线段大小比较、和与差练习题
- 格式:doc
- 大小:30.00 KB
- 文档页数:1

人教版七年级数学上册《6.2.2线段的比较与运算》 同步练习题及答案一、单选题1.借助圆规,可得图中最长的线段是( )A .BAB .CAC .DAD .EA2.“把弯曲的公路改直”能缩短路程,解释这个现象的数学依据是( ) A .经过两点,有且仅有一条直线 B .经过一点有无数条直线 C .两点之间,线段最短D .垂线段最短3.若点C 在线段AB 上,线段5cm AB =,3cm BC =则线段AC 的长是( ) A .4cmB .8cmC .2cmD .1cm4.如图所示,点C 是线段AB 的中点,点D 在线段CB 上,且6AD BD -=,若18AB =,则CD 的长( )A .3B .4C .5D .65.如图,一只蚂蚁从“A ”处爬到“B ”处(只能向上、向右爬行),爬行路线共有( )A .3条B .4条C .5条D .6条6.台湾的省会为台北市,在地图上如果把城市看作一点,下列城市与台北市之间的距离最大的是( ) A .吉林市B .西安市C .海口市D .福州市7.如图,线段18cm AB =,点C 在线段AB 上,P ,Q 是线段AC 的三等分点,M ,N 是线段BC 的三等分点,则线段PN 的长为( )A .6B .9C .12D .158.B 是线段AD 上一动点,沿A 至D 的方向以2cm/s 的速度运动.C 是线段BD 的中点10cm AD =.在运动过程中,若线段AB 的中点为E .则EC 的长是( ) A .2cmB .5cmC .2cm 或5cmD .不能确定二、填空题9.已知点C 在线段AB 上6,2AB BC ==,则AC = .10.线段10cm AB =,点C 在线段AB 上,点M 、N 分别是线段AC BC 、的中点,则MN = . 11.P 为线段AB 上一点,且25AP AB =,M 是AB 的中点,若3cm PM =,则AB = . 12.已知点C 在线段AB 上20AC =,30BC =点M 是AC 的中点且点N 是BC 的三等分点,则线段MN 的长度为 .13.已知点M 是线段AB 上一点,若14AM AB =,点N 是直线AB 上的一动点,且AN BN MN -=,则MNAB= .三、解答题14.如图,已知线a 、b ,求作一条线段c ,使2c a b =-. 要求:不写画法,保留必要的作图痕迹.15.如图,A 、B 、C 、D 四点在一条直线上,根据图形填空:(1)图中共有线段_______条;(2)若C 是BD 的中点16cm AD =,2AB BC =求线段AC 的长.16.如图所示,A 、B 、C 是一条公路上的三个村庄,A ,B 间的路程为100km ,A ,C 间的路程为40km ,现欲在C ,B 之间建一个车站P ,设P ,C 之间的路程为km x .(1)若P 为线段BC 的中点,求AP 的长;(2)用含x 的代数式表示车站P 到三个村庄的路程之和;(3)若车站P 到三个村庄的路程之和为102km ,则车站应建在何处?(4)若要使车站P 到三个村庄的路程总和最小,问车站应建在何处?最短路程是多少?参考答案题号 1 2 3 4 5 6 7 8 答案 CCCAA ACB1.C【分析】用圆规量出四条线段,再进行比较即可.此题考查了比较线段的长短,会用圆规度量各线段是本题的关键. 【详解】通过用圆规比较图中的四条线段,其中最长的DA故选:C . 2.C【分析】本题主要考查了线段的性质,熟记两点之间,线段最短是解题的关键.根据“两点之间,线段最短”进行判断即可.【详解】解:“把弯曲的公路改直”能缩短路程,解释这个现象的数学依据是“两点之间,线段最短”. 故选:C . 3.C【分析】本题考查线段的加减,根据AC BC AB +=求解即可. 【详解】∵点C 在线段AB 上 ∵AC BC AB += ∵5cm AB = 3cm BC = ∵532cm AC AB BC =-=-= 故选:C . 4.A【分析】本题考查了与线段中点有关的计算,根据图示正确找到线段之间的和差关系是解题关键.根据192AC BC AB === 9,9AD AC CD CD BD BC CD CD =+=+=-=-即可求解. 【详解】解:∵点C 是线段AB 的中点18AB = ∵192AC BC AB === ∵9,9AD AC CD CD BD BC CD CD =+=+=-=- ∵6AD BD -=∵()9926CD CD CD +--== ∵3CD =故选:A 5.A【分析】只能向上或向右走,就是最短的路线,可以用列举的方法进行求解. 【详解】解:如图,根据规则可得:,,,A C D B A E D B A E F B →→→→→→→→→ 一共有3种不同的走法. 故选:A .【点睛】本题考查了线段问题,利用求最短路线的方法:清晰的分类是解题的关键. 6.A【分析】本题考查了点与点之间的距离,根据点与点之间的距离并结合生活常识即可得出答案. 【详解】解:在地图上如果把城市看作一点,与台北市之间的距离最大的是吉林市 故选:A . 7.C【分析】本题考查了两点间的距离,n 等分点的定义,数形结合是解题的关键.由三等分点的定义得23PC AC =23CN BC =然后由两点间的距离求解即可.【详解】解:∵P ,Q 是线段AC 的三等分点,M ,N 是线段BC 的三等分点 ∵23PC AC =23CN BC =∵22221812cm 3333PN PC CN AC BC AB =+=+==⨯=. 故选C . 8.B【分析】根据线段中点的性质,做出线段AD ,按要求标出各点大致位置,列出EB ,BC 的表达式,即可求出线段EC .【详解】设运动时间为t则AB=2t ,BD=10-2t∵C 是线段BD 的中点,E 为线段AB 的中点 ∵EB=2AB =t ,BC=2BD=5-t ∵EC=EB+BC=t+5-t=5cm 故选:B .【点睛】此题考查对线段中点的的理解和运用,涉及到关于动点的线段的表示方法,难度一般,理解题意是关键. 9.4【分析】本题主要考查了线段的和差计算,根据线段的和差关系列式求解即可. 【详解】解;∵点C 在线段AB 上 6,2AB BC == ∵624AC AB BC =-=-= 故答案为:4. 10.5cm /5厘米【分析】本题考查与线段中点有关的运算,根据线段中点得到12MC AC =,12NC BC = 结合MN MC NC=+求解即可. 【详解】解:如图∵点C 在线段AB 上,点M 、N 分别是线段AC BC 、的中点 ∵12MC AC =12NC BC =∵线段10cm AB = ∵()115cm 22MN MC NC AC BC AB =+=+== 故答案为:5cm . 11.30cm /30厘米【分析】本题考查线段的和差,线段的中点,根据线段中点的定义得到12AM AB =,从而根据线段的和差得到110PM AM AP AB =-=,即10AB PM =,即可解答. 【详解】解:如图∵点M 是AB 的中点2∵25AP AB =∵1212510PM AM AP AB AB AB =-=-=∵()1010330cm AB PM ==⨯=. 故答案为:30cm 12.30或20/20或30【分析】本题主要考查了线段中点的相关计算,线段的和差计算,解题的关键是数形结合,先求出1102AM MC AC ===,分两种情况:当点N 是靠近B 点的三等份点时,当点N 是靠近C 点的三等份点时,分别画出图形,求出结果即可.【详解】解:∵20AC =,点M 是AC 的中点 ∵1102AM MC AC === 当点N 是靠近B 点的三等份点时,如图所示:∵21030303MN CM CN =+=+⨯=; 当点N 是靠近C 点的三等份点时,如图所示:∵11030203MN CM CN =+=+⨯=综上分析可知,线段MN 的长是30或20. 故答案为:30或20.13.1或12【分析】分两种情况:当点N 在线段AB 上,当点N 在线段AB 的延长线上,然后分别进行计算即可解答. 【详解】解:分两种情况:当点N 在线段AB 上,如图:AN BN MN -= AN AM MN -=BN AM ∴=414BN AB 12MN AB AM BNAB 12MN AB; 当点N 在线段AB 的延长线上,如图:AN BN MN -= AN BN AB -=AB MN ∴=1MNAB∴= 综上所述:MNAB的值为1或12故答案为:1或12.【点睛】本题考查了两点间的距离,分两种情况进行计算是解题的关键. 14.作图见详解【分析】画射线AM ,用尺规在射线AM 上取AB a ,取BC a =,再以C 点为起点,向反方向取CD b =,则AD 即为所求线段c .【详解】解:如图如下AB a ,BC a = 以C 点为起点,向反方向,即CB 方向取CD b = ∵2AD c a b ==-.【点睛】本题主要考查线段的加减,掌握尺规作图的方法是解题的关键. 15.(1)6; (2)12cm .【分析】本题考查线段的和差和中点有关的计算,熟练掌握线段和差倍分的计算是解题的关键. (1)根据线段定义数出线段即可;(2)根据图形,由线段和差和线段中点求解即可.【详解】(1)解:图中线段有AB AC AD BC BD CD 、、、、、,共6条线段故答案为:6;(2)解:∵C 是BD 中点 ∵12BC CD BD == ∵2AB BC =又∵AD AB BC CD =++ 16cm AD = ∵162BC BC BC =++ ∵4cm BC =∵4cm CD = 28cm AB BC == ∵12cm AC AB BC =+=. 16.(1)70km (2)()100km x +(3)车站应建在村庄C 的右侧2km 处(4)车站建在村庄C 处,路程和最小,最短路程是100km【分析】本题考查了线段长的计算、代数式的应用、一元一次方程的应用等知识,根据题意画出图形分类讨论是解题关键.(1)根据AC BC AB +=计算出BC ,再根据P 为线段BC 的中点,即可解答; (2)由题意列出车站P 到三个村庄的路程,再求和即可; (3)由题意得100102x +=解方程即可得到答案;(4)由题意得车站到三个村庄的总路程为()100100x +=,根据代数式的特点求出最小值,找到车站位置即可.【详解】(1)解:100km,40km,AB AC AC BC AB ==+=∵()1004060km BC AB AC =-=-=. 又∵P 为线段BC 的中点 ∵()30km PB BC ==∵()1003070km AP AB PB =-=-=; (2)解:车站P 到三个村庄的路程之和为()()()4010040100km PA PB PC x x x x ⎡⎤++=++-++=+⎣⎦;(3)解:若车站P 到三个村庄的路程之和为102km ,则100102x += 故2x =即车站应建在村庄C 的右侧2km 处;(4)解:要使车站P 到三个村庄的路程总和最小,即100x +最小,故取0x = 这时车站建在村庄C 处,路程和最小,最短路程是100km .。

2.4线段的和与差【基础练习】知识点1线段和与差的表示1.根据图1填空:(1)CD=BD-;(2)BC=-AB;(3)AC=AB+=AD-.图12.如图2,下列关系式中与图不符的是 ()图2A.AD-CD=ACB.AB+BC=ACC.BD-BC=AB+BCD.AD-BD=AC-BC3.在直线l上顺次取三个点A,B,C,使得线段AB=9 cm,BC=1 cm,那么A,C两点间的距离是.4.已知线段AB=3 cm,延长线段BA到点C,使BC=2AB,求AC的长.知识点2线段和与差的作图5.[教材例1变式]已知线段a,b,小雪作出了如图3所示的图形,其中AD是所求线段,则线段AD=(用含a,b的式子表示).图36.如图4,已知线段a,b(a>b),画线段AB,使AB=2a-2b.(不写画法,保留作图痕迹)图4知识点3线段的中点7.如图5,因为C是线段AB的中点,所以=, =2=2. 图5=128.点M在线段AB上,下面给出的四个式子中,不能判定M是线段AB的中点的是()A.AB=2AMB.BM=1AB2C.AM=BMD.AM+BM=AB9.如图6,C,D是线段AB上的两点,D是线段AC的中点.若AB=10 cm,BC=4 cm,则AD的长为()图6A.2 cmB.3 cmC.4 cmD.6 cm10.如图7,已知线段AB=6 cm,线段AB的延长线上有一点C,且BC=4 cm,若M为线段AB的中点,则MC的长为cm.图711.如图8,B是线段AC上一点,且AC=6,BC=2.(1)求线段AB的长;(2)如果O是线段AC的中点,求线段OB的长.图8【能力提升】12.如图9,已知线段AB=12,C为AB的中点,点D在线段AC上,且AD∶BC=1∶3,则BD的长度为()图9A.4B.8C.10D.613.已知线段AB=8 cm,在直线AB上画线段BC,使它等于3 cm,则线段AC等于()A.11 cmB.5 cmC.11 cm或5 cmD.8 cm或11 cm14.如图10,已知线段AB的长度为a,线段CD的长度为b,则图中所有线段的长度和为()图10A.3a+bB.3a-bC.a+3bD.2a+2bAB,若AC=15,D为线段AC的中点,则BD的长为() 15.延长线段AB到点C,使BC=14A.4.5B.3.5C.2.5D.1.516.如图11,已知线段AB的长为16 cm,点M在AB上,AM BM=1 3,P,Q分别为AM,AB的中点,则PQ的长为.图1117.如图12,已知线段AB=80 cm,M为AB的中点,点P在MB上,N是PB的中点,且NB=14 cm,求MP的长.图1218.画线段MN=3 cm,在线段MN上取一点Q,使MQ=NQ,延长线段MN至点A,使AN=1MN;延2长线段NM至点B,使BN=3BM,根据所画图形解答下列各题:(1)求线段BM的长度;(2)求线段AN的长度;(3)Q是哪些线段的中点?图中共有多少条线段?19.如图13,点C在线段AB上,M,N分别是AC,BC的中点.(1)若AC=9,BC=6,求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=a ,其他条件不变,猜想MN的长度,并说明理由.用一句简洁的话描述你发现的结论;(3)若点C在线段AB的延长线上,且满足AC-BC=b,M,N分别为AC,BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.图13答案1.(1)BC (2)AC (3)BC CD2.C3.10 cm [解析] 如图,AC=AB+BC=9+1=10(cm).4.解:如图所示.因为BC=2AB ,AB=3 cm, 所以BC=6 cm,所以AC=BC-AB=6-3=3(cm).5.2a-b6.略7.AC BC AB AB AC BC 8.D9.B [解析] 因为D 是线段AC 的中点,所以AC=2AD.因为AC=AB-BC=10-4=6(cm),所以AD=3 cm .10.7 [解析] 因为M 是线段AB 的中点,AB=6 cm,所以MB=12AB=3 cm .因为BC=4 cm,所以MC=MB+BC=3+4=7(cm).11.解:(1)由线段的和差,得AB=AC-BC=6-2=4. (2)由O 是线段AC 的中点,得OC=12AC=12×6=3. 由线段的和差,得OB=OC-BC=3-2=1.12.C [解析] 因为AB=12,C 为AB 的中点,所以AC=BC=6.因为AD ∶BC=1∶3,所以AD=2,所以BD=AB-AD=12-2=10.13.C [解析] 由于点C 的位置不确定,故要分两种情况讨论: (1)当点C 在点B 右侧时,如图①所示,AC=AB+BC=8+3=11(cm).图① 图②(2)当点C 在点B 左侧时,如图②所示,AC=AB-BC=8-3=5(cm). 综上,线段AC 等于5 cm 或11 cm.14.A [解析] 因为线段AB 的长度为a ,所以AB=AC+CD+DB=a.因为线段CD 的长度为b ,所以AD+CB=a+b ,所以图中所有线段的长度和为AB+AC+CD+DB+AD+CB=a+a+a+b=3a+b.15.A [解析] 如图.因为BC=14AB ,所以AC=BC+AB=14AB+AB=54AB.因为AC=15,所以AB=12.因为D 是线段AC 的中点,所以AD=12AC=12×15=7.5,所以BD=AB-AD=12-7.5=4.5.16.6 cm [解析] 因为AB=16 cm,AM BM=1 3,所以AM=4 cm .因为P ,Q 分别为AM ,AB 的中点,所以AP=12AM=2 cm,AQ=12AB=8 cm,所以PQ=AQ-AP=6 cm . 17.解:因为N 是PB 的中点,NB=14 cm, 所以PB=2NB=2×14=28(cm). 因为M 是AB 的中点,所以AM=MB=12AB=12×80=40(cm), 所以MP=MB-PB=40-28=12(cm). 18.[解析] 正确作出图形是解题的关键.解:根据题意画出图形,如图所示.(1)因为MN=3 cm,点Q在线段MN上,MQ=NQ,所以MQ=NQ=1.5 cm.BN,又因为BM=13所以BM=MQ=NQ=1.5 cm.MN,MN=3 cm,(2)因为AN=12所以AN=1.5 cm.(3)由题意,知BM=MQ=QN=NA,所以Q既是线段MN的中点,也是线段AB的中点.图中共有10条线段,它们分别是线段BM,BQ,BN,BA,MQ,MN,MA,QN,QA,NA.19.解:(1)因为AC=9,M是AC的中点,AC=4.5.所以CM=12因为BC=6,N是BC的中点,BC=3,所以CN=12所以MN=CM+CN=4.5+3=7.5,所以线段MN的长为7.5.a.理由:(2)MN=12因为M,N分别是AC,BC的中点,所以MC=12AC ,CN=12BC ,所以MN=MC+CN=12AC+12BC=12(AC+BC )=12AB=12a.结论:当C 为线段AB 上一点,且M ,N 分别是AC ,BC 的中点时,MN=12a. (3)能.如图.结论:MN=12b.理由:因为M 是AC 的中点,所以CM=12AC. 因为N 是BC 的中点,所以CN=12BC ,所以MN=CM-CN=12(AC-BC )=12b.。

和差问题练习题(关键是学会画线段图)
姓名
1.爸爸买回算术本语文本共30本,已知算术本比语文本多4本,问爸爸买回的算术本和语文本各有多少本?(基本题)
2.一个长方形的周长是112厘米,宽比长短12厘米。
求这个长方形的长、宽分别是多少厘米?(提示根据周长这个条件求出一条长与一条宽的和)
3.用长170厘米的铁丝围成一个长方形,使长比宽多10厘米。
长方形的长和宽各是多少厘米?
4.小诺沿长与宽相差30米的游泳池跑了5圈,做下小前的准备活动。
已知小诺共跑了700米,那么游泳池的长,宽分别是多少米?
5.减法算式中,被减数、减数、差三数之和是2002,减数比差大123,减数是多少?(提示:减数加差等于被减数,先求出减数加差的和)
6.小明期末考试时语文和数学的平均分数是94分,数学比语文多8分,问语文和数学各得了几分?(提示根据平均分这个条件求出语文和数学分数的和)
7.某工厂去年与今年的平均产值为96万元,今年比去年多10万元,今年与去年的产值各是多少万元?
8.甲、乙两人同时以相同的速度打字,2分钟共打了240个字,已知甲每分钟比乙多打10个字.问甲、乙两人每分钟各打多少个?。

和差问题练习题(关键是学会画线段图)
姓名
1、一年级两个班共有学生100人,一班比二班多4人。
一班和二班各有学生多少人?
2.一个长方形的周长是72厘米,宽比长短12厘米。
求这个长方形的长、宽分别是多少厘米?(提示根据周长这个条件求出一条长与一条宽的和)
3.把长84厘米的铁丝围成一个使长比宽多6厘米的长方形。
长和宽各是多少厘米?
4.小诺沿长与宽相差40米的操场跑了5圈,已知小诺共跑了800米,那么操场的长,宽分别是多少米?
5.减法算式中,被减数、减数、差三数之和是520,减数比差大40,减数是多少?(提示:减数加差等于被减数,先求出减数加差的和)
6.陈红和李玲平均身高为130厘米,陈红比李玲高8厘米,陈红和李玲身高各是多少厘米?
7.小敏和他爸爸的平均年龄是29岁,爸爸比他大26岁。
小敏和他爸爸的年龄各是多少岁?
8.师徒两人做零件,2小时共做了90个,已知徒弟每小时比师傅少做13个,问师徒两人每小时各做多少个?。


《2.4 线段的和与差》数学七年级上册冀教版课后练习1.已知线段AB=3厘米,延长BA到C使BC=5厘米,则AC的长是()A.2厘米B.8厘米C.3厘米D.11厘米2.如图,点C是线段AB上的点,点D是线段BC的中点,AB=10,AC=6,则线段CD的长是()A.4 B.3 C.2 D.13.如图,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点.则BD等于()A.2 B.3 C.4 D.54.如图,已知线段AB=10cm,点N在AB上,NB=2cm,M是AB中点,那么线段MN的长为()A.5cm B.4cm C.3cm D.2cm5.如图所示,C是线段AB的中点,D是线段BC的中点,下列等式不正确的是()A.CD=AD﹣BC B.CD=C.CD=AB﹣BD D.CD=AC﹣BD 6.如图,已知CB=4,DB=7,D是AC的中点,那么AC=.7.如图,已知线段a、b、c(a>c),用圆规和直尺作一条线段,使它等于a+2b﹣c.8.如图,已知点C是线段AB的中点,点D是线段AC的中点,点E是线段BC 的中点.(1)若线段DE=11cm,求线段AB的长.(2)若线段CE=4cm,求线段DB的长.1.A2.C3.B4.C5.B6.67.略8.解:如图:(1)因为点D是线段AC的中点,点E是线段BC的中点,所以AC=2CD,BC=2CE,所以AB=AC+BC=2(DC+CE)=2DE=22cm;(2)因为点E是线段BC的中点,所以BC=2CE=8cm.因为点C是线段AB的中点,点D是线段AC的中点,所以DC=AC=BC=4cm,所以DB=DC+CB=4+8=12cm.。


D 第30题2题图 2.4线段的和与差课后训练案【基础篇】1.点C 是线段AB 的中点,若AC =5cm ,则AB =_______;若D 是线段CB 的中点,则DB =_____cm ,DB =_____AC ,DB =______AD ,DB =______AB .2.如果A ,B ,C 在同一直线上,线段AB =5cm,BC =3cm,那么A ,C 两点间的距离一定是_______.3.点C 分AB 为2∶3,点D 分AB 为1∶4,若AB 为5 cm ,则AC =_____cm ,BD =_______cm ,CD =_______cm. 4.已知线段AB ,延长线段AB 至C ,使BC =12AB ,再反向延长线段AB 至D ,使AD =32AB ,那么线段CD 的中点是_______.5. 画线段AB =6.8cm ,用刻度尺找出它的中点M ,在找出线段MB 的中点N ,求出线段AN 的长度.6.如图:AB =20cm ,C 是AB 上一点,且AC =12cm ,D 是AC 的中点,E 是BC 的中点,求线段DE 的长.7.如图,AD =12BD ,E 是BC 的中点,BE =2cm ,AC =10cm ,求线段DE 的长.【提高篇】1. 如图,C 为AB 的中点,D 是BC 的中点,则下列说法错误的是( )A .CD =AC -BDB .CD =12AB -BD C .CD =23BC D .AD =BC +CD 2.同一平面上的两点M ,N 距离是17cm,若在该平面上有一点P 和M ,N •两点的距离的和等于25cm,那么下列结论正确的是( )A .P 点在线段MN 上B .P 点在直线MN 外C .P 点在直线MN 上D .P 点可能在直线MN 上,也可能在直线MN 外7题图ADCB EC6题图_ D_ C _ A _ B_ N _ M 3题图3.如图,B,C 是线段A,D 上任意两点,M 是AB 的中点,N 是CD 的中点, 若MN=a ,BC=b ,•则AD 的长是( )A .2a-bB .a-bC .a+bD .2(a-b )4. 如图,B 、C 是线段AD 上两点,且AB :BC :CD =2:4:3,M 是AD 的中点,CD =6cm ,求线段MC 的长.【拓展篇】1.已知线段AB =8,平面上有一点P .(1)若AP =5,PB 等于多少时,P 在线段AB 上?(2)当P 在线段AB 上,并且P A =PB 时,确定P 点的位置,并比较P A +PB 与AB 的大小.2.如图所示,点C 在线段AB 上,线段AC =8cm ,BC =6cm ,点M ,N 分别是AC ,BC 的中点,求 ⑴线段MN 的长度.⑵根据⑴中的计算过程和结果,设AC +BC =m ,其它条件不变,你能猜测MN 的长度吗?说明理由. ⑶若题中的条件改变为“点C 在直线AB 上”,其它条件不变,结果会有变化吗?若有变化,请求出结果.3.如图点C 在线段AB 上,AC = 8cm ,CB = 6cm ,点M 、N 分别是AC 、BC 的中点. (1)求线段MN 的长;(2)若C 为线段AB 上任一点,满足AC + CB = a cm ,其它条件不变,你能猜想MN 的长度吗?并说明理由.(3)若C 在线段AB 的延长线上,且满足AC BC = b cm ,M 、N 分别为AC 、BC 的中点,你能猜想MN 的长度吗?请画出图形.2题图 A M C N B 3题图A BC M NABCMD。

4.2比较线段的长短同步习题一.选择题1.如图,点C,D在线段AB上.则下列表述或结论错误的是()A.若AC=BD,则AD=BC B.AC=AD+DB﹣BCC.AD=AB+CD﹣BC D.图中共有线段12条2.下列说法中,正确的是()A.过两点有且只有一条直线B.连接两点的线段叫做两点间的距离C.两点之间,直线最短D.到线段两个端点距离相等的点叫做线段的中点3.下列生活现象:①用两个钉子就可以把木条固定在墙上;②从A地到B地架设电线,总是尽可能沿着线段AB架设;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④把弯曲的公路改直,就能缩短路程.其中能用“两点之间,线段最短”来解释的现象个数有()A.1B.2C.3D.44.下列说法正确的个数是()①射线MN与射线NM是同一条射线;②两点确定一条直线;③两点之间直线最短;④若2AB=AC,则点B是AC的中点A.1个B.2个C.3个D.4个5.如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若AB=10,CD =4,则EF的长为()A.6B.7C.5D.86.若线段AB=13cm,MA+MB=17cm,则下列说法正确的是()A.点M在线段AB上B.点M在直线AB上,也有可能在直线AB外C.点M在直线AB外D.点M在直线AB上7.已知点A,B,C在同一直线上,若AB=20cm,AC=30cm,点M、N分别是线段AB、AC中点,求线段MN的长是()A.5cm B.5cm或15cm C.25cm D.5cm或25cm 8.已知点A,B,C为平面内三点,给出下列条件:①AC=BC;②AB=2BC;③AC=BC =AB.选择其中一个条件就能得到“点C是线段AB中点”的是()A.①B.③C.①或③D.①或②或③9.如图,从A地到B地的最短路线是()A.A→F→E→B B.A→C→E→B C.A→D→G→E→B D.A→G→E→B 10.如图,B、C两点把线段AD分成2:4:3的三部分,M是AD的中点,CD=6,则线段BM等于()A.3B.4C.5D.6二.填空题11.点A到原点的距离为4,且位于原点的左侧,若一个点从A处向右移动2个单位长度,再向左移动7个单位长度,此时终点所表示的数为.12.已知如图,C是线段AB上的一点,N是线段BC的中点,若AB=10,AC=6,则AN =.13.如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=.14.已知点A、B、C都在直线l上,且AB=8cm,BC=5cm,则AC=cm.15.如图,C、D两点是线段AB的三等分点,点M、N分别是线段AC、BD的中点,则MN=AB.三.解答题16.如图,点C在线段AB上,AB=9,AC=2CB,D是AC的中点,求AD长.17.如图,已知点B在线段AC上,AB=8cm,BC=10cm,点P,Q分别为AB,AC的中点.(1)线段AC的长为cm,线段PC的长为cm;(2)求线段PQ的长.18.如图中,已经线段AB的长为28cm,在AB的延长线上取一点C,使,E为AC的中点,D为AB的中点,求线段DE的长.参考答案1.解:A、若AC=BD,则AD=BC,正确,不符合题意;B、AC=AD+DB﹣BC,正确,不符合题意;C、AD=AB+CD﹣BC,正确,不符合题意;D、图中共有线段6条,符合题意,故选:D.2.解:A、过两点有且只有一条直线,故符合题意;B、连接两点的线段的长度叫做两点的距离,故不符合题意;C、两点之间,线段最短,故不符合题意;D、在线段上且到线段两个端点距离相等的点叫做线段的中点,故不符合题意;故选:A.3.解:①用两个钉子就可以把木条固定在墙上,利用的是两点确定一条直线,故此选项不合题意;②从A地到B地架设电线,总是尽可能沿着线段AB架设,能用“两点之间,线段最短”来解释,故此选项符合题意;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,利用的是两点确定一条直线,故此选项不合题意;④把弯曲的公路改直,就能缩短路程,能用“两点之间,线段最短”来解释,故此选项符合题意.故选:B.4.解:①射线MN的端点是M,射线NM的端点是N,故不是同一条射线,故选项错误;②两点确定一条直线;正确;③两点之间线段最短,而不是两点之间直线最短,故选项错误;④若2AB=AC,则点B是AC的中点,错误,因为点A,B,C不一定在同一条直线上,故选项错误;.故选:A.5.解:由线段的和差,得AC+DB=AB﹣CD=10﹣4=6.∵点E是AC的中点,∴AE=AC,∵点F是BD的中点,∴BF=BD,∴AE+BF=(AC+DB)=3.由线段的和差,得EF=AB﹣(AE+BF)=10﹣3=7.故选:B.6.解:当点M在线段AB上时,MA+MB=AB,∵AB=13cm,MA+MB=17cm,∴M点不在线段AB上;当点M在线段AB的延长线上时,AB=AM﹣BM=13cm,∵MA+MB=17cm,∴AM=15cm,BM=2cm;当点M在线段BA的延长线上时,AB=BM﹣AM=13cm,∵MA+MB=17cm,∴BM=15cm,AM=2cm;当点M不在直线AB上时,则构成△ABM,∵AM+BM>AB,∴17cm>13cm成立,∴点M不在直线AB上;综上所述,点M可能在直线AB上,也可能在直线AB外,故选:B.7.解:(1)当点C位于点B的右边时,MN=(AC﹣AB)=5cm,(2)当点C位于点A的左边时,MN=(AC+AB)=25cm故线段MN的长为5cm或25cm.故选:D.8.解:①点C在线段AB上,且AC=BC,则C是线段AB中点故①不符合题意;②AB=2BC,C不一定是线段AB中点故②不符合题意;③AC=BC=AB,则C是线段AB中点,故③符合题意.故选:B.9.解:因为两点之间线段最短,从A地到B地,最短路线是最少走曲线,沿直线,行走即为A→F→E→B.故选:A.10.解:由AB:BC:CD=2:4:3,CD=6,得AB=4,BC=8.由线段的和差,得AD=AB+BC+CD=4+8+6=18.由线段中点的性质,得AM=MD=AD=9.由线段的和差,得BM=AM﹣AB=9﹣4=5,故选:C.11.解:∵点A到原点的距离为4,且位于原点的左侧,∴点A表示的数为﹣4,∵一个点从A处向右移动2个单位长度,再向左移动7个单位长度,∴﹣4+2﹣7=﹣9,故答案为:﹣9.12.解:∵AB=10,AC=6,∴CB=10﹣6=4,∵N是线段BC的中点,∴CN=2,∴AN=AC+CN=6+2=8.13.解:对C点的位置分情况讨论如下:①C点在A点的左边,∵AC:CB=1:2,BD:AB=2:3,假设AC=3k,则AB=3k,BD=2k,∴CD=3k+3k+2k=8k,∵CD=12,∴k=1.5,∴AB=4.5;②C点在线段AB上,∵AC:CB=1:2,BD:AB=2:3,假设AC=k,则CB=2k,BD=2k,∴CD=CB+BD=4k,∵CD=12,∴k=3,∴AB=AC+CB=3k=9;③C点在B点后,不符合题意,舍去;∴综上所述,AB=4.5或9.14.解:如图1所示:∵AB=8cm,BC=5cm,∴AC=AB+BC=8+5=13cm;如图2所示:AC=AB﹣BC=8﹣5=3cm.故答案为:3或13.15.解:∵点C、D是线段AB的三等分点,∴AC=CD=BD=AB,M和N分别是AC和BD的中点,∴MC=AC=AB,DN=BD=AB,∴MN=MC+DN+CD=AB+AB+AB=AB,故答案为:.16.解:∵点C在线段AB上,AC=2CB,AB=9,∴AC=6,∵D是AC的中点,∴AD=AC,∴AD=3.17.解:(1)由图可知,AC=AB+BC,∵AB=8cm,BC=10cm,∴AC=18cm,∵P是AB的中点,∴AP=4cm,∴PC=AC﹣AP=18﹣4=14(cm);故答案为18,14;(2)∵点P分别为AB的中点,∴P A=PB=AB=4(cm),∵点Q分别为AC的中点,∴AQ=QC=AC=9(cm),∴PQ=AQ﹣P A=9﹣4=5(cm),∴线段PQ的长为5 cm.18.解:∵AB的长为28cm,,∴BC=×28=16,∴AC=AB+BC=44,∵E为AC的中点,D为AB的中点,∴AD=AB==14,AE=AC=44=22,∴DE=AE=AD=22﹣14=8.。

4.3 线段的长短比较1.线段的长短比较比较线段长短的方法有两种:(1)叠合法:先把两条线段的一端重合,另一端点落在同一侧,从而确定两条线段的长短,这是从“形”的方面进行比较.当两条线段能够放在一起而又不要求知道相差的具体数值时,可用此法.将线段AB 放到线段CD 上,使点A 和点C 重合,点B 和点D 在重合点的同侧.①如果点B 和点D 重合,如图,就说线段AB 与线段CD 相等,记作AB=CD.②如果点B 在线段CD 上,如图,就说线段AB 小于线段CD ,记作AB <CD.③如果点B 在线段CD 外,如图,就说线段AB 大于线段CD ,记作AB >CD.(2)度量法:先分别量出每条线段的长度,再根据度量的结果确定两条线段的大小,这是从“数”的方面进行比较.当两条线段的长短差别不太明显,而又不便放在一起比较,或需要求出相差的具体数值时,可用此法.对于线段AB 和CD ,我们可以用刻度尺分别量出线段AB 和CD 的长度,数值大的线段较长,数值小的线段较短,数值相等时两线段一样长.【例1】 如图,已知AB >CD ,则AC 与BD 的大小关系为( ).A .AC >BDB .AC =BDC .AC <BD D .AC 和BD 的大小不能确定解析:运用叠合法或度量法直接比较,可以发现AC 与BD 的大小关系为AC >BD . 答案:A2.线段的中点如图,点C 在线段AB 上且使线段AC ,CB 相等,这样的点C 叫做线段AB 的中点.中点定义的推理步骤:(1)∵AC =CB (已知),∴点C 是线段AB 的中点(中点的定义).(2)∵点C 是线段AB 的中点(已知),∴AC =BC 或AC =12AB 或BC =12AB 或AB =2AC 或AB =2BC (中点的定义). 谈重点 对线段中点的理解线段的中点在线段上,有且只有1个,它把线段分成两条相等的线段.注意,若AC =BC ,则点C 不一定是线段AB 的中点,因为点C 不一定在线段AB 上.【例2】 如图,已知点C 为线段AB 的中点,点D 为线段BC 的中点,BD =3 cm ,求线段AB 的长度.解:∵点D 为线段BC 的中点,BD =3 cm ,∴BC =2BD =2×3=6 cm.∵C 点为线段AB 的中点,∴AB =2BC =2×6=12 cm. ∴AB 的长度为12 cm.说方法 线段的中点的应用由线段的中点这一条件得到的结论,解题过程中不一定全部写出,要根据所求问题灵活选择,一般用哪个写哪个即可.3.线段的性质(1)两点之间的所有连线中,线段最短.连接两点是指画出这两点为端点的线段.(2)两点之间线段的长度,叫做这两点之间的距离.它是一个数量.而线段本身是图形,因此不能把A ,B 两点间的距离说成是线段AB .释疑点 线段与线段的长度的区别“线段”是一个几何图形,而“线段的长度”是一个数量,二者是有区别的,但是为了书写的方便,我们常常用线段的名称表示线段的长度,如AB =2 cm.【例3】 进入新世纪,信息技术在社会的各个领域都起着至关重要的作用.2012年某中学开始安装校园网,实现办公楼、教学楼、图书馆、食堂、实验楼的联网,布线工程十分重要.已知这五座建筑物的位置及它们之间的距离,如图(1)所示(图书馆、办公楼、实验楼在同一条直线上,教学楼、办公楼、食堂在同一条直线上).假如你是布线工程的设计者,你应如何设计线路,才能使线路最短?最短线路的长是多少米?分析:联想两点之间线段最短去设计.解:布线设计图如图(2).最短线路的长为120+120+180+240=660(m).4.线段的和、差、倍、分的计算比较线段的大小,形成了线段的和、差关系,学习线段的中点及延长线形成了线段的倍、分关系.在解答有关线段的和、差、倍、分问题时,要从线段中点的定义出发,结合图形,利用线段的和差计算,寻求线段之间的大小关系,灵活运用线段中点的性质.说方法 计算线段的和、差、倍、分时应注意的问题一般要注意以下几个方面:①按照题中已知条件画出符合题意的图形是正确解题的先决条件;②观察图形,找出线段间的关系;③线段的和、差、倍、分与线段长度的和、差、倍、分是一致的.其运算方法和顺序结合与有理数运算类似.【例4】 已知线段AC 和BC 在一条直线上,如果AC =5 cm ,BC =3 cm ,求线段AC 和线段BC 的中点间的距离.解:设AC ,BC 的中点分别为M ,N ,由线段中点定义得AM =MC =12AC ,BN =CN =12BC . 如图,MN =MC +CN =12AC +12BC =12(AC +BC )=12×8=4(cm).如图,MN =MC -CN =12AC -12BC =12(AC -BC )=12×2=1(cm).5.方程思想在线段计算中的应用有些已知条件中的关系比较复杂,无法或很难由已知条件直接推导出待求的线段的长度,这时我们可以挖掘隐含条件,引进未知数,然后以线段的和、差、倍、分作为相等关系,构造出方程来解决问题.说方法 方程思想在线段计算中的应用当题目提供某一线段长时,我们一般考虑使用含未知数的代数式再表示这条线段的长,即可得到一个方程,从而求出未知数的值.【例5】 如图,B ,C 两点把线段AD 分成2∶3∶4三部分,M 是AD 中点,CD =8,求MC 的长.分析:由AB ∶BC ∶CD =2∶3∶4,可设AB =2x ,BC =3x ,CD =4x ,CD =4x =8而求得x 值,进而求出MC 长.解:设AB =2x ,由AB ∶BC ∶CD =2∶3∶4,得BC =3x ,CD =4x ,∴AD =(2+3+4)x =9x .∵CD =8,∴4x =8,x =2.∴AD =9x =18.∵M 是AD 中点,∴MC =MD -CD =12AD -CD =12×18-8=1.6.线段的和、差、倍、分的计算的应用生活中涉及线段的和、差、倍、分的运算问题比较常见,主要涉及路线、路径问题.解决这类问题的关键是画出线段示意图,将实际问题转化为线段的计算问题.然后运用线段的和、差、倍、分及中点的性质寻找由已知线段推导出未知线段的思维过程,对于这一推理过程较为困难,有时要借助于方程思想方法来解决问题.解技巧 结合图形解线段应用题有关线段的计算都是由已知,经过和、差或中点进行转化,求未知线段的过程,因此要结合图形,分析各线段关系,找出它们的联系,通过和、差、倍、分的运算解决.注意学会利用画线段图的方式解决.【例6】 李红、王明、张江三人的家恰好与学校在一条笔直的街道上.已知李红家到学校的距离是500米,张江家正好在李红与学校的中间,王明家在李红和张江家的中间,那么王明家到学校的距离是多少米?分析:此题考查学生对线段性质、线段的中点、两点间的距离知识的综合运用.首先要能用画线段图的方式来解决此类问题(如下图).解:由题可知:AD =500米.因为C 是AD 的中点,所以AC =CD =12AD =500×12=250. 因为B 是AC 的中点,所以BC =12AC =250×12=125. 王明到学校的距离BD =BC +CD =125+250=375.即王明到学校的距离是375米.7.线段的性质的应用两点之间的所有连线中,线段最短,这是线段的重要的性质,其在实际生活和生产中的应用十分广泛.涉及这类问题主要为河道由曲改直等最短路径问题,解决这类问题的关键是根据实际问题中要解决的问题画出恰当几何图形,将实际问题转化为数学问题,然后运用线段的性质来解决.【例7】某市汽车站A到火车站F有四条不同的路线,如图所示,其中路线最短的是().A.从A经过BME到FB.从A经过线段BE到FC.从A经过折线BCE到FD.从A经过折线BCDE到F解析:本题只需考虑点B到点E之间的距离最短即可.答案:B。
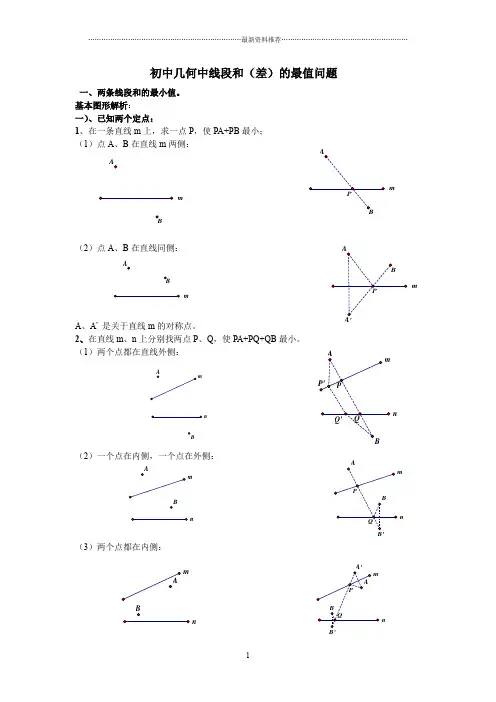
初中几何中线段和(差)的最值问题一、两条线段和的最小值。
基本图形解析: 一)、已知两个定点:1、在一条直线m 上,求一点P ,使PA+PB 最小; (1)点A 、B 在直线m 两侧:(2)点A 、B 在直线同侧:A 、A ’ 是关于直线m 的对称点。
2、在直线m 、n 上分别找两点P 、Q ,使PA+PQ+QB 最小。
(1)两个点都在直线外侧:(2)一个点在内侧,一个点在外侧:(3)两个点都在内侧:mmB mA Bmn mnn mnnnm(4)、台球两次碰壁模型变式一:已知点A 、B 位于直线m,n 的内侧,在直线n 、m 分别上求点D 、E 点,使得围成的四边形ADEB 周长最短.填空:最短周长=________________变式二:已知点A 位于直线m,n 的内侧, 在直线m 、n 分别上求点P 、Q 点PA+PQ+QA 周长最短.二)、一个动点,一个定点: (一)动点在直线上运动:点B 在直线n 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B )1、两点在直线两侧:2、两点在直线同侧:mnm nm nm(二)动点在圆上运动点B 在⊙O 上运动,在直线m 上找一点P ,使PA+PB 最小(在图中画出点P 和点B ) 1、点与圆在直线两侧:2、点与圆在直线同侧:三)、已知A 、B 是两个定点,P 、Q 是直线m 上的两个动点,P 在Q 的左侧,且PQ 间长度恒定,在直线m 上要求P 、Q 两点,使得PA+PQ+QB 的值最小。
(原理用平移知识解) (1)点A 、B 在直线m 两侧:过A 点作AC ∥m,且AC 长等于PQ 长,连接BC,交直线m 于Q,Q 向左平移PQ 长,即为P 点,此时P 、Q 即为所求的点。
(2)点A 、B 在直线m 同侧:mmmmQ Q练习题1.如图,∠AOB =45°,P 是∠AOB 内一点,PO =10,Q 、R 分别是OA 、OB 上的动点,求△PQR 周长的最小值为 .2、 如图1,在锐角三角形ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D ,M,N 分别是AD 和AB 上的动点,则BM+MN 的最小值为 . 3、如图,在锐角三角形ABC 中 ,AB=BAC=45,BAC 的平分线交BC 于D ,M 、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是多少?4、如图4所示,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是AC 边上一点.若AE=2,EM+CM 的最小值为 .5、如图3,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.6、 如图4,等腰梯形ABCD 中,AB=AD=CD=1,∠ABC=60°,P 是上底,下底中点EF 直线上的一点,则PA+PB 的最小值为 .Q7、如图5菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为.8、如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是9、如图,圆柱形玻璃杯,高为12cm,底面周长为18cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为________cm.10、如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为11、如图,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.则PB+PE的最小值是12、如图6所示,已知正方形ABCD的边长为8,点M在DC上,且DM=2,N是AC上的一个动点,则DN+MN的最小值为.13、如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为.14、如图7,在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为cm.(结果不取近似值).15、如图,⊙O的半径为2,点A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一动点,则P A+PC的最小值是.16、如图8,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,P是直径MN上一动点,则PA+PB的最小值为( )(A)2 (B) (C)1 (D)2解答题1、如图9,正比例函数y=x的图象与反比例函数y=(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为M,已知三角形OAM的面积为1.(1)求反比例函数的解析式;(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.2、如图,一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c 与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).(1)求此二次函数的解析式;(2)设此抛物线的顶点为P,对称轴与AC相交于点Q,求点P和点Q的坐标;(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.3、如图10,在平面直角坐标系中,点A的坐标为(1,),△AOB的面积是.(1)求点B的坐标;(2)求过点A、O、B的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△AOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;4.如图,抛物线y =35x 2-185x +3和y 轴的交点为A ,M 为OA 的中点,若有一动点P ,自M 点处出发,沿直线运动到x 轴上的某点(设为点E ),再沿直线运动到该抛物线对称轴上的某点(设为点F ),最后又沿直线运动到点A ,求使点P 运动的总路程最短的点E ,点F 的坐标,并求出这个最短路程的长.5.如图,已知在平面直角坐标系xOy 中,直角梯形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =AB =2,OC =3,过点B 作BD ⊥BC ,交OA 于点D .将∠DBC 绕点B 按顺时针方向旋转,角的两边分别交y 轴的正半轴、x 轴的正半轴于点E 和F . (1)求经过A 、B 、C 三点的抛物线的解析式;(2)当BE 经过(1)中抛物线的顶点时,求CF 的长; (3)在抛物线的对称轴上取两点P 、Q (点Q 在点P 的上方),且PQ =1,要使四边形BCPQ 的周长最小,求出P 、Q 两点的坐标.6.如图,已知平面直角坐标系,A,B两点的坐标分别为A(2,-3),B(4,-1)若C(a,0),D(a+3,0)是x轴上的两个动点,则当a为何值时,四边形ABDC的周长最短.7、如图11,在平面直角坐标系中,矩形的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.(1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标;(2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标.二、求两线段差的最大值问题 (运用三角形两边之差小于第三边) 基本图形解析:1、在一条直线m 上,求一点P ,使PA 与PB 的差最大; (1)点A 、B 在直线m 同侧:解析:延长AB 交直线m 于点P ,根据三角形两边之差小于第三边,P ’A —P ’B <AB ,而PA —PB=AB 此时最大,因此点P 为所求的点。
三等分点
三、简答题
1、如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,求AD的长度。
2、线段AD=6cm ,线段AC=BD=4cm ,E 、F 分别是线段AB 、CD 中点,求EF 。
3、如图:4AB =cm ,3BC =cm ,如果O 是线段AC 的中点.
求线段OB 的长度.(括号内注理由)
解:∵ AC= + =7 (cm ),
又∵ O 为AC 的中点,
( ) ∴OC= AC= (㎝),( )
∴0.5OB OC BC =-=(cm ).
4、如图4,线段,线段,点
是的中点,在上取一点,使,求的长
5、如图,点C 在线段AB 上,AC = 8 cm ,CB = 6 cm ,点M 、N 分别是AC 、BC 的中点。
(1)求线段MN 的长;
(2)若C 为线段AB 上任一点,满足AB CB acm +=,其它条件不变,你能猜想MN 的
长度吗?并说明理由。
(3)若C 在线段AB 的延长线上,且满足AC CB bcm -=,M 、N 分别为AC 、BC 的中
点,你能猜想MN 的长度吗?请画出图形,写出你的结论,并说明理由。
A B。
小学生数学用线段解题练习题# 小学生数学用线段解题练习题## 一、基础线段问题1. 题目一:画一条线段AB,如果线段AB的长度是8厘米,那么线段AB的中点C到A点的距离是多少厘米?2. 题目二:已知线段CD的长度是10厘米,如果点E是线段CD的中点,求线段CE的长度。
3. 题目三:线段EF被点G平分,EF的长度是12厘米,求GF的长度。
4. 题目四:线段HI的长度是15厘米,如果点J是线段HI的三等分点,求HJ和IJ的长度。
5. 题目五:线段KL的长度是20厘米,如果点M和N分别是线段KL的四等分点,求MN的长度。
## 二、线段的和与差6. 题目六:线段MN的长度是6厘米,线段OP的长度是4厘米,求线段MN和OP的和。
7. 题目七:如果线段PQ的长度是9厘米,线段RS的长度是3厘米,求线段PQ比RS长多少厘米。
8. 题目八:线段TU的长度是14厘米,如果从TU上减去线段VW的长度,VW的长度是5厘米,求剩余的长度。
9. 题目九:线段XY的长度是18厘米,线段YZ的长度是12厘米,求线段XY比YZ长多少厘米。
10. 题目十:线段AB的长度是11厘米,线段CD的长度是7厘米,求线段AB比CD长多少厘米。
## 三、线段的倍数关系11. 题目十一:线段EF的长度是2厘米,如果线段GH是EF的3倍,求GH的长度。
12. 题目十二:线段IJ的长度是5厘米,如果线段KL是IJ的一半,求KL的长度。
13. 题目十三:线段MN的长度是8厘米,如果线段OP是MN的1.5倍,求OP的长度。
14. 题目十四:线段PQ的长度是10厘米,如果线段RS是PQ的四分之一,求RS的长度。
15. 题目十五:线段TU的长度是6厘米,如果线段VW是TU的两倍,求VW的长度。
## 四、线段的组合问题16. 题目十六:线段XY的长度是7厘米,线段YZ的长度是3厘米,如果线段XZ是XY和YZ的和,求XZ的长度。
17. 题目十七:线段AB的长度是9厘米,线段BC的长度是6厘米,如果线段AC是AB和BC的差,求AC的长度。
初中数学冀教版七年级上册第二章2.4线段的和与差练习题一、选择题1.有下列生活,生产现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”来解释的现象有()A. ①②B. ①③C. ②④D. ③④2.如图,点C是线段AB上的点,点M、N分别是AC、BC的中点,若AC=6cm,MN=5cm,则线段MB的长度是()A. 6cmB. 7cmC. 8cmD. 10cm3.如图,已知线段AB=6cm,在线段AB的延长线上有一点C,且BC=4cm,若点M为AB中点,那么MC的长度为()A. 5cmB. 6cmC. 7cmD. 无法确定4.某公共汽车运营线路AD段上有A,B,C,D四个汽车站,如图所示,现在要在AD段上修建一个加油站M(加油站不在汽车站内),为了使加油站选址合理,要求A,B,C,D四个车站到加油站M的路程总和最小,则加油站M应建在()A. A,B之间B. B,C之间C. C,D之间D. A,D之间任意位置5.如果A、B、C三点在同一直线上,且线段AB=8cm,BC=6cm,若M、N分别为AB、BC的中点,那么M、N两点之间的距离为()A. 7cmB. 1cmC. 7cm或1cmD. 无法确定6.如图,已知线段AB=12cm,M是AB中点,点N在AB上,NB=2cm,那么线段MN的长为()A. 2cmB. 3cmC. 4cmD. 5cm7.如图,线段AB=BC=CD=DE=1cm,图中所有线段的长度之和为()A. 25cmB. 20cmC. 15cmD. 10cm8.下列两个生产生活中的现象:①植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;②把弯曲的公路改直,就能缩短路程.其中可用公理“两点之间,线段最短”来解释的现象有()A. 只有①B. 只有②C. ①②D. 无9.如图,M是线段AB的中点,NB为MB的四分之一,MN=a,则AB表示为()A. 83a B. 43a C. 2a D. 1.5a10.下列说法①过两点有且只有一条直线;②两点之间线段最短;③到线段两个端点距离相等的点叫线段的中点;④线段的中点到线段的两个端点的距离相等,其中正确的有__个。
《4.3 线段的长短比较》基础练习1. 为比较两条线段AB与CD的大小,小明将点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,则().A. AB>CDB. AB<CDC. AB=CDD. 以上都有可能2. 如图①,把弯曲的河道改直,能够缩短航程,这样做的根据是().图①A.两点之间,直线最短B.两点确定一条线段C.两点确定一条直线D.两点之间,线段最短3. 若线段AB=5 cm,CD=50 mm,则下列判断正确的是().A.AB=CD B.AB>CD C.AB<CD D.不能确定4. 如图②,已知线段AD>BC,则线段AC与BD的关系是().A.AC>BD B.AC=BD C.AC<BD D.不能确定图②5. 两点间的距离是指( ).A.一条直线的长度B.一条射线的长度C.连接两点的线段D.连接两点线段的长度6. 如图③,下列关系式中与图形不符的式子是().图③A.AD-CD=AB+BC B.AC-BC=AD-BDC.AC-AB=AD-BD D.AD-AC=BD-BC7.下列说法中正确的是( ).A.延长射线OA B.作直线AB的延长线C.延长线段AB到C,使AC= AB. D.延长线段AB到C,使AC=2AB.8.如图④,由A到B有①②③④四条路线,那么最短的路线是( ).图④A. ①B. ②C. ③D. ④9.如图⑤,C是AB的中点,D是BC的中点.下面等式不正确的是( ).图⑤A. CD=AC-DBB. CD=AD-BCC. CD=AB-BDD. CD=AB10. 把一段弯曲的公路改为直路,可以缩短路程,其理由是( ).A. 两点之间线段最短B. 两点确定一条直线C. 线段有两个端点D. 线段可以比较大小11. 如图⑥,线段AC=BD,那么AB=________.图⑥12. 线段的中点只有________个,线段的五等分点有________个.13. 如图⑦,从城市A到城市B有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.图⑦14. 如图⑧,请根据图形完成下列填空:图⑧(1)AD=AC+_________;(2)AC=AB-_______=AD-_______;(3)AC+CB=AD+________.15. 两根木条,一根长80 cm,一根长120 cm,将它们的一端重合,顺次放在同一条直线上,此时两根木条的中点间的距离是多少?答案和解析【答案】1. A2. D3. A4. A5. D6. B7. D8. B9. D 10. A11. CD12. 1 513. 两点之间,线段最短14. (1)CD(2) BC CD(3)BD15. 100cm.【解析】1. 解:由点A与点C重合使两条线段在一条直线上,点B在CD的延长线上,得AB>CD.故选A. 比较线段长短时,叠合法是一种较为常用的方法.2. 解:把弯曲的河道改直缩短航程的根据是:两点之间,线段最短.故选D.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.3. 解:CD=50 mm=5 cm,AB=5 cm,故AB=CD.故选A.本题考查了比较线段的长短的知识,解题关键是将线段的单位统一后再进行比较.4. 解:因为AD>BC,所以AC+CD>BD+CD,所以AC>BD,故选A.本题考查了比较线段的长短的知识,解题关键是由已知得到AC+CD>BD+CD.5. 解:两点间的距离是指连接两点线段的长度.故选D.此题考查的是两点间的距离的定义,连结两点的线段的长度叫做两点之间的距离.6. 解:AD-CD=AC=AB+BC,故A正确;AC-BC=AB=AD-BD,故B正确;AC-AB=BC,AD-BD=AB,故C错误;AD-AC=CD=BD-BC,故D正确.故选C.本题考查了线段的和差,解题关键是找出线段之间的等量关系.7. 解:射线、直线是不可度量的,无法“延长”,故A、B错误;延长线段AB到C,则AC>AB,故C错误,D正确.故选D.本题考查了对线段、射线、直线的语言描述,属于基础题.8. 解:根据两点之间,线段最短,则最短路线为路线②,故选B.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.9. 解:因为C是AB的中点,所以AC=BC=AB,又因为D是BC的中点,所以CD=BD=BC,所以CD=BC-DB=AC-DB,故A正确;CD=AD-AC=AD-BC,故B正确;CD=BC-DB=AB-BD,故C正确;CD=BC=AB,故D错误.故选D.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.10. 解:由把弯曲的公路改为直路,路程变短了可知,应用了“两点之间线段最短”.故选A.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.11. 解:由图可知,AB=AC-BC,CD=BD-BC,因为AC=BD,所以AB=CD.故答案为CD.本题考查了线段的和差,解题关键是找到线段之间的等量关系.12. 解:线段的中点只有1个,线段的五等分点有4个.故答案为1,5.此题考查的是对线段的中点和等分点的认识,若将线段n等分,则线段的等分点有(n-1)个. 13. 解:从城市A到城市B有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为两点之间,线段最短.故答案为两点之间,线段最短.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.14. 解:(1)AD=AC+CD;(2)AC=AB-BC=AD-CD;(3)AC+CB=AD+BD.故答案为(1)CD;(2) BC,CD;(3)BD.本题考查了线段的和差,解题关键是找到线段之间的等量关系.15. 解:由题意,得80 cm的一半是40 cm,120 cm的一半是60 cm,故两根木条的中点间的距离是40+60=100(cm).本题考查了线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.《4.3 线段的长短比较》提高练习1. 如图①,若点C为线段AB上一点,且AB=16,AC=10,则AB的中点D与BC的中点E的距离为().图①A.8B.5C.3D.22. 下列说法正确的是().A. 两点之间的所有连线中,直线最短B. 若P是线段AB的中点,则AP=BPC. 若AP=BP,则P是线段AB的中点D. 两点之间的线段叫作这两点之间的距离3. 如图②,AB=12 cm,点C是AB的中点,点D是BC的中点,则AD的长为().图②A.3 cm B.6 cm C.9 cm D.7.5 cm4.如果点B在线段AC上,那么下列各表达式中:①AB=AC;②AB=BC;③AC=2AB;④AB +BC=AC.能表示点B是线段AC的中点的有( ).A.1个B.2个C.3个D.4个5. 如图③,笔直公路的同一旁有三棵树A,B,C,量得A,B两棵树之间的距离为5米,B,C两棵树之间的距离为3米,一个公路路标恰好在A,C两棵树的正中间点O处,则点O与点B之间的距离是( ).图③A.1米B.2米C.3米D.4米6. 点A,B,C在同一条直线上,线段AB=5 cm,线段BC=2 cm,则A,C两点间的距离是( ). A.3.5cm B.3cm C.7cm D.7cm或3cm7.已知:线段AB=4cm,延长AB至点C,使AC=11cm.点D是AB中点,点E是AC中点,则DE的长为( ).A.3.5cm B.3cm C.4cm D.4.5cm8. 如图④,一只蚂蚁从A处沿着圆柱的表面爬到B处,请画出示意图且标出最短路线,并说明理由.图④9. 如图⑤,李明想从A村到B村,你能帮他找到一条最近的路线吗?请说明理由.图⑤10. 如图⑥,AB=16cm,C是AB上的一点,且AC=10cm,D是AC的中点,E是BC的中点,求线段DE的长.图⑥答案和解析【答案】1. B2. B3. C4. C5. A6. D7. A8. 线段AB即为最短路线.9.能,最近的路线为A→C→F→B.10. 8cm.【解析】1. 解:因为AB=16,AC=10,所以CB=AB-AC=16-10=6.又因为D是AB中点,E是BC中点,所以BD=AB=×16=8,BE=CB=×6=3,所以DE=BD-BE=8-3=5.故选B.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.2. 解:两点之间的所有连线中,线段最短,故A选项错误;当P是线段AB的中点时,AP=BP,但是只知道AP=BP,不能判断P是线段AB的中点,故B选项正确,C选项错误;两点之间线段的长度叫作这两点之间的距离,故D选项错误.故选B.本题主要考查了线段的基本性质,线段的中点的定义以及两点之间的距离的定义,数量掌握这些概念和性质是解题关键.3. 解:因为AB=12 cm,点C是AB的中点,所以AC=BC=AB=6cm,又因为点D是BC的中点,所以CD=BD=BC=3cm,所以AD=AB-BD=12-3=9( cm),故选C.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.4. 解:如果点B在线段AC上,能表示点B是线段AC的中点的有:①AB=AC;②AB=BC;③AC=2AB. 共3个.故选C.此题考查的是线段的中点的定义,解题关键是熟练掌握线段的中点的判定.5. 解:根据题意可知,AB=5m,BC=3m,点O是线段AC的中点,则OC=AC=(AB+BC)=×(5+3)=4(m),所以OB=OC-BC=4-3=1(m),故点O与点B之间的距离是1m.故选A.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.6. 解:已知AB=5 cm,BC=2 cm,(1)当点B在点A、C之间时,AC=AB+BC=5+2=7(cm);(2)当点C在点A、B之间时,AC=AB-BC=5-2=3(cm),故A,C两点间的距离是7cm或3cm.故选D.此题考查的是线段的和差,需要分两种情况进行讨论:(1)点B在点A、C之间;(2)点C在点A、B之间.7. 解:因为AB=4cm,点D是AB中点,所以AD=2cm.因为AC=11cm,点E是AC中点,所以AE=5.5cm.所以DE=AE-AD=5.5-2=3.5cm故选A.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.8.解:将圆柱沿过点A的高剪开,侧面展开成平面图形,如图4. 因为两点之间线段最短,所以线段AB即为最短路线.将圆柱沿着过点A的高剪开,侧面展开成平面图形,再根据线段的性质即可得到最短路线.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.9. 解:能,最近的路线为A→C→F→B. 理由如下:因为从A村到C村的距离是一定的,所以从A村到B村的远近取决于C村到B村的距离.把C,B看成两个点.因为两点之间线段最短,且F在线段CB上,所以从C到F再到B最近.所以最近的路线为A→C→F→B.本题考查了线段的性质,熟记两点之间线段最短是解题的关键.分析出“从A村到B村的远近取决于C村到B村的距离”.10. 解:解法一:因为D是AC中点,AC=10 cm,所以DC=AC=5 cm.又因为AB=16 cm,AC=10 cm,所以BC=AB-AC=16-10=6(cm).又因为E是BC的中点,所以CE=BC=3(cm).所以DE=DC+CE=5+3=8(cm).解法二:因为D是AC的中点,E是BC的中点,所以DC=AC,CE=BC,所以DE=DC+CE=AC+BC=(AC+BC)=AB=×16=8(cm).由上可得DE的长为8 cm.可以运用中点的定义先求出线段DC和CE的长,再求其和;也可以运用中点的定义直接得DE=DC+CE=AC+BC=(AC+BC)=AB,再代入数即可.对于求线段的长度问题,解法不唯一,应根据具体的题目,灵活选择简单的计算方法.《4.3 线段的长短比较》培优练习1. 点M,N都在线段AB上,且M分AB为2 : 3两部分,N分AB为3 : 4两部分,若MN=2 cm,则AB的长为( )A.60 cm B.70 cm C.75 cm D.80 cm2. C、D是线段AB上顺次两点,M、N分别是AC、BD中点,若CD=a,MN=b,则AB的长为( ).A.2b-a B.b-a C.b+a D.2a+2b3. 延长线段AB到点C,使BC=AB,延长BA到点D,使DA=AB,已知DC=6 cm,线段DC 的中点E和点A之间的距离为().A.3 cm B.2 cm C.2.5 cm D.3.5 cm4. 已知线段AB=2cm,延长AB到C,使BC=2AB,若D为AB的中点,则线段DC的长为______.5. 如图,B,C两点把线段AD分成2 : 3 : 4的三部分,点E是线段AD的中点,EC=2 cm,求:(1)AD的长;(2)AB : BE.答案和解析【答案】1. B2. A3. B4. 5cm5. (1) 36cm;(2)4 : 5.【解析】1. 解:因为M分AB为2 : 3两部分,N分AB为3 : 4两部分,所以AM=AB,AN=AB,所以MN=AN-AM=AB-AB=AB,又因为MN=2 cm,所以AB=70cm.故选B.根据线段的比可得,AM=AB,AN=AB,则可以求出MN与AB之间的关系,利用已知条件MN=2 cm,即可得到AB的长度.此题考查的是线段的比和线段的和差,熟练掌握比的意义是解题的关键.2. 解:因为C、D是线段AB上顺次两点,M、N分别是AC、BD中点,所以AM=CM=AC,BN=DN=BD,所以MN=CM+CD+DN,因为CD=a,MN=b,所以CM+DN=b-a,即AC+BD=b-a,所以AC+BD=2(b-a),所以AB=AC+CD+BD=2(b-a)+a=2b-a.故选A.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.3. 解:因为BC=AB,DA=AB,所以DC=DA+AB+BC=AB+AB+AB=2AB,因为DC=6 cm,所以AB=3cm,所以DA=1cm,又因为点E是线段DC的中点,所以DE=DC=3cm,所以AE=DE-DA=3-1=2(cm),故线段DC的中点E和点A之间的距离为2 cm,故选B.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.4. 解:因为AB=2cm,BC=2AB,所以BC=4cm,又因为D为AB的中点,所以AD=BD=AB=1cm,所以DC=BD+BC=1+4=5(cm).故答案为5cm.本题考查了线段的和差,注意理解线段的中点的概念,利用中点的性质转化线段之间的倍分关系是解题的关键.5. 解:(1)设AB=2x,则BC=3x,CD=4x.由线段的和差,得AD=AB+BC+CD=9x.由E为AD的中点,得ED=AD=x.由线段的和差,得CE=DE-CD=x-4x=x=2(cm).解得x=4.所以AD=9x=36(cm).(2)AB=2x=8(cm),BC=3x=12(cm).由线段的和差,得BE=BC-CE=12-2=10(cm).所以AB : BE=8 : 10=4 : 5.(1)根据线段的比,可设出未知数x,根据线段的和差,可得方程,根据解方程,可得x的值,根据x的值,可得AD的长度;(2)根据线段的和差,可得线段BE的长,根据比的意义,可得答案.在遇到线段之间比的问题时,往往设出未知数,列方程解答.。
线段长度比较、和与差练习题
1. 如图,C ,D 是线段AB 上两点,若CB=4cm ,DB=7cm ,且D 是AC 的中点,则AC 的长等于( )
A .3cm
B .6cm
C .11cm
D .14cm
2. 已知线段AB ,在BA 的延长线上取一点C ,使CA=3AB ,则线段CA 与线段CB 之比为( )
A .3:4
B .2:3
C .3:5
D .1:2 3. 如图,点C 是线段AB 的中点,点D 是线段BC 的中点,下面等式不正确的是( )
A .CD=AD-BC
B .CD=AC-DB
C .CD=21AB-B
D D .CD=3
1AB 4. 已知线段AB=16cm ,O 是线段AB 上一点,M 是AO 的中点,N 是BO 的中点,则MN=( )
A .10cm
B .6cm
C .8cm
D .9cm
5. 已知线段AB=5cm ,在直线AB 上画线段BC=2cm ,则AC 的长是( )
A .3cm
B .7cm
C .3cm 或7cm
D .无法确定
6. 如图,O 是线段AB 的中点,C 在线段OB 上,AC=4,CB=3,则OC 的长等于( )
A .0.5
B .1
C .1.5
D .2
7. 如图所示,数轴上有点A 和点B ,则线段AB 的长为( )
A .4.5
B .-4.5
C .4.5或-4.5
D .0.5
8. 已知:点C 在直线AB 上,线段AB=6,点D 是AC 中点,BC=4那么A 、D 之间的距离是( )
A .5
B .2.5
C .5或1
D .5或2.5 9. 如图,线段AB=8cm ,C 为AB 上一点,且AC=3.2cm ,又知M 是AB 的中点,N 是AC 的中点,求M 、N 两点间的距离.1070.如图,线段AB=8cm ,C 为AB 上一点,且AC=3.2cm ,又知M 是AB 的
2.4
10. 用刻度尺画一条线段AB=4cm ,延长AB 到C ,使BC=3AB ,D 为BC 的中点,E 为AB 的中点,画图并计算DE 的长.8。