证明线段和差练习题(三角形全等)

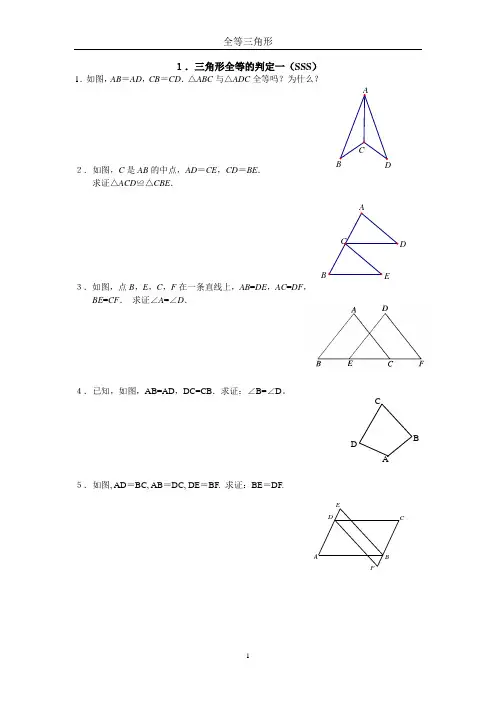
FE DCBA1．如图，AB ＝AD ，CB ＝CD ．△ABC 与△ADC 全等吗？为什么？２．如图，C 是AB 的中点，AD ＝CE ，CD ＝BE ．求证△ACD ≌△CBE ．３．如图，点B ，E ，C ，F 在一条直线上，AB =DE ，AC =DF ，BE =CF ． 求证∠A =∠D ．４．已知，如图，AB=AD ，DC=CB ．求证：∠B=∠D 。

５．如图, AD ＝BC, AB ＝DC, DE ＝BF. 求证：BE ＝DF.AD C B1．如图，AC 和BD 相交于点O ，OA =OC ，OB =OD ．求证DC ∥AB ．2．如图，△ABC ≌△A B C '''，AD ，A D ''分别是△ABC ，△A B C '''的对应边上的中线，AD 与A D ''有什么关系？证明你的结论．3．如图，已知AC ⊥AB ，DB ⊥AB ，AC ＝BE ，AE ＝BD ，试猜想线段CE 与DE 的大小与位置关系，并证明你的结论．4．已知：如图，AD ∥BC ，AD=CB ，求证：△ADC ≌△CBA ．5．已知：如图AD ∥BC ，AD=CB ，AE=CF 。

求证：△AFD ≌△CEB ．6．已知，如图，AB=AC ，AD=AE ，∠1=∠2。

求证：△ABD ≌△ACE ．C EDBAE B CFD A BC D 2 AC B ED1H F ED CB A 7．已知:如图,点B,E,C,F 在同一直线上,AB ∥DE,且AB=DE,BE=CF. 求证:AC ∥DF ．8．已知:如图,AD 是BC 上的中线 ,且DF=DE ．求证:BE ∥CF ．9．如图, 在△ABC 中, 分别延长中线BE 、CD 至F 、H, 使EF ＝BE, DH ＝CD, 连结AF 、AH ． 求证：(1) AF ＝AH ；(2)点A 、F 、H 三点在同一直线上； (3)HF ∥BC.10．如图, 在△ABC 中, AC ⊥BC, AC ＝BC, 直线EF 交AC 于F, 交AB 于E, 交BC 的延长线于D, 连结AD 、BF, CF ＝CD. 求证：BF ＝AD, BF ⊥AD.11．证明：如果两个三角形有两条边和其中一边上的中线对应相等，那么这两个三角形全等．（提示：首先分清已知和求证，然后画出图形，再结合图形用数学符号表示已知和求证）AB E F12．证明：如果两个三角形有两条边和第三边上的中线对应相等，那么这两个三角形全等．13.已知：如图，正方形ABCD ，BE =CF ，求证：(1)AE =BF ； （2）AE ⊥BF . 14．已知：E 是正方形ABCD 的边长AD 上一点，BF 平分∠EBC ，交CD 于F ，求证BE=AE+CF.（提示：旋转构造等腰）15.如图,△ABD 和△ACE 是△ABC 外两个等腰直角三角形,∠BAD=∠CAE=900.（1）判断CD 与BE 有怎样的数量关系;（2）探索DC 与BE 的夹角的大小.（3）取BC 的中点M ，连MA ，探讨MA 与DE 的位置关系。

初中几何中线段和差的最大值与最小值练习题(最全)初中几何中线段和（差）的最值问题一、两条线段和的最小值基本图形解析：一）已知两个定点：1、在一条直线m上，求一点P，使PA+PB最小。

1）点A、B在直线m两侧：在直线m上找到点P使得PA=PB，则PA+PB最小。

2）点A、B在直线同侧：在直线m上找到点A'，使得A'是关于直线m的对称点，再找到点P使得PA'+PB最小，则PA+PB最小。

2、在直线m、n上分别找两点P、Q，使PA+PQ+QB最小。

1）两个点都在直线外侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。

2）一个点在内侧，一个点在外侧：在直线m上找到点P，使其与A点连线垂直直线m，再在直线n上找到点Q，使其与B点连线垂直直线n，使PA+PQ+QB最小。

3）两个点都在内侧：在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，再找到点P和Q，使得PA'+PQ+QB'最小，则PA+PQ+QB最小。

4）、台球两次碰壁模型变式一：已知点A、B位于直线m,n的内侧，在直线n、m分别上求点D、E点，使得围成的四边形ADEB周长最短。

在直线m上找到点A'，使得A'是关于直线m的对称点，在直线n上找到点B'，使得B'是关于直线n的对称点，连接A'和B'，交直线m和n于D和E，使ADEB为矩形，则ADEB周长最短。

变式二：已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短。

在直线m上找到点A'，使得A'是关于直线m的对称点，连接AA'，在直线n上找到点Q，使得A'Q垂直直线n，连接AQ，使得PA+PQ+QA最小。

备考2021年九年级数学中考复习专题：全等三角形性质与判定（五）1．“截长补短法”证明线段的和差问题：先阅读背景材料，猜想结论并填空，然后做问题探究．背景材料：（1）如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°．探究图中线段BE，EF，FD之间的数量关系．探究的方法是，延长FD到点G．使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出的结论是．探索问题：（2）如图2，若四边形ABCD中，AB＝AD，∠B+∠D＝180°，E，F分别是BC，CD 上的点，且∠EAF＝∠BAD，上述结论是否仍然成立？成立的话，请写出推理过程．2．已知：如图，∠BAC的角平分线与BC的垂直平分线DG交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F．（1）求证：BE＝CF；（2）若AF＝6，△ABC的周长为20，求BC的长．3．如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AF＝CE．（1）求证：△ABE≌△CDF；（2）若∠BCE＝30°，∠CBE＝70°，求∠CFD的度数．4．如图，在△ABC中，∠ACB＝90°，CD是AB边上的中线，点E为CD的中点，过C 作CF∥AB交AE的延长线于点F，连接BF．（1）求证：△ADE≌△FCE；（2）四边形BDCF是怎样的特殊四边形？请加以证明．5．如图，△ABC是等边三角形，点D是边BC边上的任意一点（除B、C外），以AD为边作等边△ADE，过点C作CF∥DE交AB于点F．求证：EF＝CD．6．如图所示，在四边形ABCD中，AC与BD交于O，AB＝AD，CB＝CD．BE⊥CD于E，BE与AC交于F．CF＝2BO．（1）求证：△BEC是等腰直角三角形；（2）求tan∠ACD的值．7．如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将△ABE沿AE所在直线折叠，点B的对应点是点B′，连接AB′并延长交直线DC于点F．（1）当点F与点C重合时如图（1），易证：DF+BE＝AF（不需证明）；（2）当点F在DC的延长线上时如图（2），当点F在CD的延长线上时如图（3），线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．8．如图，四边形ABCD为正方形，E为对角线AC上的点，连接BE并作BE⊥EF，交边CD于点F，过点F作FG⊥AC交对角线AC于点G．（1）请在图中找出与BE长度相等的边并加以证明：（2）求的值．9．如图，在△ABC中，AB＝AC，∠BAC＝90°，AE是过点A的一条直线，且B、C在AE 的两侧，BD⊥AE于D，CE⊥AE于E．（1）求证：△ABD≌△CAE；（2）若DE＝3，CE＝2，求BD．10．如图，在△ABC中，AB＝BC，CD⊥AB于点D，CD＝BD，BE平分∠ABC，交AC于E．交CD于F．点H是BC边的中点，连接DH，交BE于点G，连接CG．（1）求证：CE＝BF；（2）判断△ECG的形状，并证明你的结论．°．参考答案1．证明：（1）在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF；故答案为：EF＝BE+DF．（2）解：结论EF＝BE+DF仍然成立；理由：延长FD到点G．使DG＝BE．连结AG，在△ABE和△ADG中，，∴△ABE≌△ADG（SAS），∴AE＝AG，∠BAE＝∠DAG，∵∠EAF＝∠BAD，∴∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF＝∠BAD﹣∠EAF＝∠EAF，∴∠EAF＝∠GAF，在△AEF和△GAF中，，∴△AEF≌△AGF（SAS），∴EF＝FG，∵FG＝DG+DF＝BE+DF，∴EF＝BE+DF．2．（1）证明：连接DB、DC．∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE＝DF，∵DG垂直平分BC，∴DB＝DC，在Rt△BED和Rt△CFD中，，∴Rt△BED≌Rt△CFD（HL），∴BE＝CF；（2）解：∵∠DAE＝∠DAF，∠AED＝∠AFD＝90°，AD＝AD，∴△AED≌△AFD（AAS），∴AF＝AE＝6，由（1）得：BE＝CF，∵△ABC的周长＝AB+AC+BC，＝AE+EB+AF﹣CF+BC，＝AE+AF+BC＝20，∴BC＝20﹣12＝8．3．（1）证明：∵AB∥CD，∴∠BAE＝∠FCD，∵AF＝CE，∴AE＝CF，又∵AB＝CD，∴△ABE≌△CDF（SAS）．（2）解：∵∠BCE＝30°，∠CBE＝70°，∴∠AEB＝∠BCE+∠CBE＝30°+70°＝100°，∵△ABE≌△CDF，∴∠CFD＝∠AEB＝100°．4．证明：（1）∵CF∥AB，∴∠CF A＝∠BAF，∠ADC＝∠FCD，∵点E为CD的中点，∴DE＝CE，∴△ADE≌△FCE（AAS）；（2）解：四边形BDCF是菱形．证明如下：∵△ADE≌△FCE，∴AD＝CF，∵CD是Rt△ABC的中线，∴CD＝AD＝BD，∴CF＝BD，且CF∥AB，∴四边形BDCF是平行四边形，且CD＝BD，∴四边形BDCF是菱形．5．证明：∵△AED是等边三角形，△ABC是等边三角形，∴AD＝AE＝ED，AB＝CA＝BC，∠ADE＝60°，∠B＝∠F AC＝60°，∵ED∥FC，∴∠EDB＝∠FCB，∵∠BDA＝∠ADE+∠EDB＝60°+∠EDB，∠AFC＝∠B+∠FCB＝60°+∠FCB，∴∠BDA＝∠AFC，在△ABD和△CAF中，，∴△ABD≌△CAF（AAS），∴AD＝FC，∵AD＝ED，∴ED＝CF，又∵ED∥CF，∴四边形EDCF是平行四边形，∴EF＝CD．6．证明：（1）∵AB＝AD，CB＝CD，∴AC垂直平分BD，∴BD＝2BO，∵CF＝2BO，∴CF＝BD，∵∠DBE+∠BDE＝90°，∠BDE+∠DCO＝90°，∴∠DBE＝∠FCE，又∵∠BED＝∠CEF，∴△BDE≌△CFE（AAS），∴BE＝CE，又∵BE⊥CD，∴△BEC是等腰直角三角形；（2）如图，连接DF，∵△BDE≌△CFE，∴DE＝EF，∴DF＝EF，∵AC垂直平分BD，∴BF＝DF＝EF，∴BE＝BF+EF＝（+1）EF，∴CE＝（+1）EF，∴tan∠ACD＝＝﹣1．7．解：（1）由折叠可得AB＝AB′，BE＝B′E，∵四边形ABCD是正方形，∴AB＝DC＝DF，∠B′CE＝45°，∴B′E＝B′F，∴AF＝AB′+B′F，即DF+BE＝AF；（2）图（2）的结论：DF+BE＝AF；图（3）的结论：BE﹣DF＝AF；图（2）的证明：延长CD到点G，使DG＝BE，连接AG，需证△ABE≌△ADG，∵CB∥AD，∴∠AEB＝∠EAD，∵∠BAE＝∠B′AE，∴∠B′AE＝∠DAG，∴∠GAF＝∠DAE，∴∠AGD＝∠GAF，∴GF＝AF，∴BE+DF＝AF；图（3）的证明：在BC上取点M，使BM＝DF，连接AM，需证△ABM≌△ADF，∵∠BAM＝∠F AD，AF＝AM∵△ABE≌AB′E∴∠BAE＝∠EAB′，∴∠MAE＝∠DAE，∵AD∥BE，∴∠AEM＝∠DAB，∴∠MAE＝∠AEM，∴ME＝MA＝AF，∴BE﹣DF＝AF．8．解：（1）BE＝EF，证明如下：如图1，过P作MN∥AD，交AB于M，交CD于N，∵BE⊥EF，∴∠BEF＝90°，∴∠MEB+∠NEF＝90°，∵四边形ABCD是正方形，∴∠BAD＝∠D＝90°，∵AD∥MN，∴∠BME＝∠BAD＝∠ENF＝∠D＝90°，∴∠MEB+∠MBE＝90°，∴∠NEF＝∠MBE，Rt△ENC中，∠ECN＝45°，∴△ENC是等腰直角三角形，∴EN＝CN，∵∠BME＝∠ENC＝∠ABC＝90°，∴四边形MBCN是矩形，∴BM＝CN，∴BM＝EN，∴△BME≌△ENF（ASA），∴BE＝EF；（2）如图2，设正方形ABCD的中心为点O，连接OB，∵点O是正方形ABCD对角线AC的中点，∴OB⊥AC，∴∠AOB＝90°，∴∠AOB＝∠EGF＝90°，∴∠OBE+∠BEO＝90°，∵∠BEF＝90°，∴∠BEO+∠GEF＝90°，∴∠OBE＝∠GEF，由（1）得：BE＝EF，∴△OBE≌△GEF（AAS），∴OB＝EG，∵∠BAO＝45°，∴，∴．9．（1）证明：∵BD⊥AE于D，CE⊥AE于E，∠BAC＝90°，∴∠BDA＝∠AEC＝90°，∠DBA+∠BAD＝90°，∠BAD+∠EAC＝90°，∴∠DBA＝∠EAC，在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）；（2）解：由（1）知，△ABD≌△CAE，则BD＝AE，AD＝CE．∵DE＝3，CE＝2∴AE＝AD+DE＝CE+DE＝5．∴BD＝AE＝5．10．证明：（1）∵AB＝BC，BE平分∠ABC，∴BE⊥AC，CE＝AE，∴∠A+∠ACD＝90°，∵CD⊥AB，∴∠A+∠DBF＝90°∴∠ACD＝∠DBF，在△ADC和△FDB中，∠ACD＝∠DFB，CD＝BD，∠ADC＝∠BDF，∴△ADC≌△FDB（ASA）；∴AC＝BF，又∵CE＝AE，∴CE＝BF；（2）△ECG为等腰直角三角形．∵点H是BC边的中点，∴GH垂直平分BC，∴GC＝GB，∵∠DBF＝∠GBC＝∠GCB＝∠ECF，得∠ECG＝45°，又∵BE⊥AC，∴△ECG为等腰直角三角形；。

利用三角形全等证明线段和差倍分问题1. 已知：D 是AB 中点，∠ ACB=90°，求证：12CD AB2. 已知：AD 平分∠BAC ，∠B=2∠C ，求证： AC=AB+BD3. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BECDB4·如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD 上。

求证：BC=AB+DC。

5·已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE6．如图，已知AD ∥BC ，∠P AB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．7．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ． 求证：BD =2CE ．8·在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.PEDCB A F E DCBA9·如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD 相等吗？请说明理由10·如图，已知在△ABC中，∠BAC为直角，AB=AC，D为AC上一点，CE⊥BD于E．（1）若BD平分∠ABC，求证CE=12 BD；（2）若D为AC上一动点，∠AED如何变化，若变化，求它的变化范围；若不变，求出它的度数，并说明理由。

EDCB。

个性化教学辅导教案1.截长补短与线段和差：例1如图2-9所示．已知正方形ABCD中，M为CD的中点，E为MC上一点，且∠BAE=2∠DAM．求证：AE=BC+CE．分析证明一条线段等于两条线段和的基本方法有两种：(1)通过添辅助线“构造”一条线段使其为求证中的两条线段之和(BC+CE)，再证所构造的线段与求证中那一条线段相等．(2)通过添辅助线先在求证中长线段(AE)上截取与线段中的某一段(如BC)相等的线段，再证明截剩的部分与线段中的另一段(CE)相等．我们用(1)法来证明．证延长AB到F，使BF=CE，则由正方形性质知AF=AB+BF=BC+CE．下面我们利用全等三角形来证明AE=AF．为此，连接EF交边BC于G．由于对顶角∠BGF=∠CGE，所以Rt△BGF≌Rt△CGE(AAS)，从而于是Rt△ABG≌Rt△ADM(SAS)，所以过G引GH⊥AE于H．因为AG是∠EAF的平分线，所以GB=GH，从而Rt△GBF≌Rt△GHE(HL)，所以∠F=∠HEG，则AF=AE(底角相等的三角形是等腰三角形)，即AE=BC+CE．说明我们也可以按分析(2)的方法来证明结论，为此可先作∠BAE的平分线AG交边BC于G，再作GH⊥AE于H，通过证明△ABG≌△AHG知AB=AH=BC．下面设法证明HE=CE即可，请同学们自证．练习：1.如图所示，已知AC//BD,EA,EB 分别平分∠CAB 和∠DBA ，点E 在CD 上，求证：AB=AC+BD2.在四边形ABCD 中，AC 平分∠BAD ，C E ⊥AB 于点 E ，且∠B+∠D=180° ，求证：AE=AD+BEE3．在三角形ABC 中，∠C=2∠B ，∠1=∠2求证：AB=AC+CDBC4.已知：如图，ABCD 是正方形，∠FAD =∠FAE . 求证：BE+DF=AE. FEDCBA5. 如图所示，ABC ∆是边长为1的正三角形，BDC ∆是顶角为120︒的等腰三角形，以D 为顶点作一个60︒的MDN ∠，点M 、N 分别在AB 、AC 上，求AMN ∆的周长．6.已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和.ACB ∠，BD 、CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．7.如图，已知在ABC ∆中，3ABC C ∠=∠，12∠=∠，BE AE ⊥．求证：2AC AB BE -=．21ECBANM DC B AD OECB A截长补短与角：例1如图，在ABC ∆中，60BAC ∠=︒，AD 是BAC ∠的平分线，且AC AB BD =+，求ABC ∠的度数.由已知条件可以想到将折线ABD “拉直”成AE ，利用角平分线AD 可以构造全等三角形.同样地，将AC 拆分成两段，之后再利用三角形全等亦可，此思路也是十分自然的. 需要说明的是，无论采取哪种方法，都体现出关于角平分线“对称”的思想.上述方法我们分别称之为“补短法”和“截长法”，它们是证明等量关系时优先考虑的方法.练习：1.在正ABC ∆内取一点D ，使DA DB =，在ABC ∆外取一点E ，使DBE DBC ∠=∠，且BE BA =，求BED ∠.DECBA2.五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°，求证：AD 平分∠CDECEDB AABDEFCD C BA3.在四边形ABCD 中，AC 平分∠BAD ，C E ⊥AB 于E ，并且AE=1/2（AB+AD ）， 求证：∠B+∠D=180°。

全等三角形中线段的和、差问题证明线段的和、差问题，通常采用的方法就是截长补短法，这也是初中数学几何题中一种常用辅助线的添加方法，截长就是在一条线上截取成两段，补短就是在一条边上延长，使其等于一条所求边。

例题1：已知：在△ABC中，∠BAC＝90°，AB＝AC，AE是过点A的一条直线，且BD⊥AE，垂足为点D，CE⊥AE，垂足为点E．（1）当直线AE处于如图①的位置时，有BD＝DE+CE，请说明理由；（2）当直线AE处于如图②的位置时，则BD、DE、CE的关系如何？请说明理由．证明：（1）∵∠BAC＝90°，∴∠2+∠3＝90°，∵BD⊥AE，∴∠1+∠3＝90°，∴∠1＝∠2，在△ABD和△CAE中，，∴△ABD≌△CAE，∴BD＝AE，AD＝CE，∵AE＝AD+DE，∴BD＝DE+CE；（2）BD＝DE﹣CE，理由如下：∵∠BAC＝90°，∴∠2+∠3＝90°，∵BD⊥AE，∴∠1+∠3＝90°，∴∠1＝∠2，在△ABD和△CAE中，，∴△ABD≌△CAE，∴BD＝AE，AD＝CE，∵AE＝DE﹣AD，∴BD＝DE﹣CE．例题2：阅读下面材料：小明遇到这样一个问题：如图1，在四边形ABCD中，E是BC的中点，AE是∠BAD的平分线，AB∥DC，求证：AD＝AB+DC．小明发现以下两种方法：方法1：如图2，延长AE、DC交于点F；方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．（1）根据阅读材料，任选一种方法，证明：AD＝AB+DC；用学过的知识或参考小明的方法，解决下面的问题：（2）如图4，在四边形ABCD中，AE是∠BAD的平分线，E是BC的中点，∠BAD＝60°，∠ABC＝180°﹣∠BCD，求证：CD＝CE．解：（1）方法1：如图2，延长AE、DC交于点F；∵AB∥DF，∴∠B＝∠ECF，∵BE＝EC，∠BEA＝∠CEF，∴△ABE≌△FCE（ASA），∴AB＝CF，∵EA平分∠BAD，∴∠BAE＝∠DAF＝∠F，∴AD＝DF，∴AD＝CD+AB．方法2：如图3，在AD上取一点G使AG＝AB，连接EG、CG．∵AB＝AG，∠BAE＝∠GAE，AE＝AE，∴△BAE≌△GAE（SAS），∴BE＝EG＝EC，∠AEB＝∠AEG，∴∠EGC＝∠ECG，∵∠BEG＝∠EGC+∠ECG，∴∠BEA＝∠ECG，∴AE∥CG，∴∠EAG＝∠CGD，∵AB∥CD，AE∥CG，∴∠BAE＝∠DCG，∴∠DCG＝∠DGC，∴CD＝DG，∴AD＝AB+CD．（2）证明：如图4中，作CM∥AB交AE的延长线于M，CM交AD于N，连接EN．由（1）可知：AN＝NM，AE＝EM，∴EN平分∠ANM，∵∠BAD＝60°，MN∥AB，∴∠MND＝∠BAD＝60°，∴∠ENM＝∠ENA＝60°，∴∠CND＝∠CNE，∵∠B+∠ECN＝180°，∠ABC＝180°﹣∠BCD，∴∠NCE＝∠NCD，∵CN＝CN，∴△CNE≌△CND（ASA），∴CE＝CD．习题1．如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC 的延长线于点F．（1）求证：△DAE≌△CFE；（2）若AB＝BC+AD，求证：BE⊥AF；（3）在（2）的条件下，若∠D＝90°，AD＝，AF＝10，则点E到AB的距离是．（直接写出结果即可，不用写出演推过程）2．如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一直线上，连接BE．（1）如图1，若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°①求证：AD＝BE；②求∠AEB的度数．（2）如图2，若∠ACB＝∠DCE＝120°，CM为△DCE中DE边上的高，BN为△ABE 中AE边上的高，试证明：AE＝2CM+BN．3．（1）已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．（2）如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE 是否成立？若成立，请你给出证明：若不成立，请说明理由．4．如图：在△ABC中，∠ACB＝90°，AC＝BC，过点C在△ABC外作直线MN，AM⊥MN 于M，BN⊥MN于N．（1）求证：MN＝AM+BN．（2）若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由．5．如图，△ABC的两条高AD，BE交于点F，∠ABC＝45°，∠BAC＝60°．（1）求证：DF＝DC；（2）连接CF，求证：AB＝AC+CF．6．如图，在△ABC中，∠ABC＝45°，CD⊥AB，垂足为D，DH⊥BC，垂足为H．点E在边AC上，BE分别与CD、DH相交于点F、G．（1）求证：BG＝CG；（2）若AB＝BC，且BE⊥AC．①求证：BF＝CA；②求证：BG＝CE+EF7．在△BCF中，点D是边CF上的一点，过点D作AD∥BC，过点B作BA∥CD交AD于点A，点G是BC的中点，点E是线段AD上一点，且∠CDG＝∠ABE＝∠EBF．（1）若∠F＝60°，∠C＝45°，BC＝2，请求出AB的长；（2）求证：CD＝BF+DF．8．如图，E是BC的中点，DE平分∠ADC．（1）如图1，若∠B＝∠C＝90°，求证：AE平分∠DAB；（2）如图2，若DE⊥AE，求证：AD＝AB+CD．9．四边形ABCD中，∠ABC+∠D＝180°，AC平分∠BAD，CE⊥AB于E，CF⊥AD于F．求证：（1）△CBE≌△CDF；（2）AB+DF＝AF．10．（1）如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，求证：AD＝DC+AB，（2）如图②，在四边形ABCD中，AB∥DC，F是DC延长线上一点，连接AF，E是BC的中点，若AE是∠BAF的平分线，求证：AB＝AF+CF．11．如图所示，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC的延长线于点F．（1）判断FC与AD的数量关系，并说明理由；（2）若AB＝BC+AD，则BE⊥AF吗？为什么？12．探究：如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥m于点D，CE⊥m于点E，求证：△ABD≌△CAE．应用：如图②，在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC，求证：DE＝BD+CE．13．如图，已知∠MAN＝120°，AC平分∠MAN，∠ABC+∠ADC＝180°，求证：①DC＝BC；②AD+AB＝AC．14．（1）如图①，已知：△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥m 于D，CE⊥m于E，求证：DE＝BD+CE；（2）拓展：如图②，将（1）中的条件改为：△ABC中，AB＝AC，D、A、E三点都在直线m上，并且∠BDA＝∠AEC＝∠BAC＝α，α为任意锐角或钝角，请问结论DE＝BD+CE 是否成立？如成立，请证明；若不成立，请说明理由；（3）应用：如图③，在△ABC中，∠BAC是钝角，AB＝AC，∠BAD＞∠CAE，∠BDA ＝∠AEC＝∠BAC，直线m与BC的延长线交于点F，若BC＝2CF，△ABC的面积是12，求△ABD与△CEF的面积之和．全等三角形中线段的和、差问题参考答案与试题解析一．解答题（共16小题）1．【解答】（1）证明：∵AD∥BC，∴∠ADC＝∠ECF，∵E是CD的中点，∴DE＝EC，∵在△ADE与△FCE中，，∴△ADE≌△FCE（ASA）；（2）证明：由（1）知△ADE≌△FCE，∴AE＝EF，AD＝CF，∵AB＝BC+AD，∴AB＝BC+CF，即AB＝BF，在△ABE与△FBE中，，∴△ABE≌△FBE（SSS），∴∠AEB＝∠FEB＝90°，∴BE⊥AE；（3）解：在（2）的条件下有△ABE≌△FBE，∴∠ABE＝∠FBE，∴E到BF的距离等于E到AB的距离，由（1）知△ADE≌△FCE，∴AE＝EF＝AF＝5，∵∠D＝90°，∴DE＝＝＝，∴CE＝DE＝，∵CE⊥BF，∴点E到AB的距离为．2．【解答】（1）①证明：∵∠CAB＝∠CBA＝∠CDE＝∠CED＝50°，∴∠ACB＝∠DCE＝180°﹣2×50°＝80°，∵∠ACB＝∠ACD+∠DCB，∠DCE＝∠DCB+∠BCE，∴∠ACD＝∠BCE，∵△ACB，△DCE都是等腰三角形，∴AC＝BC，DC＝EC，在△ACD和△BCE中，∴△ACD≌△BCE（SAS），∴AD＝BE．②解：∵△ACD≌△BCE，∴∠ADC＝∠BEC，∵点A、D、E在同一直线上，且∠CDE＝50°，∴∠ADC＝180°﹣∠CDE＝130°，∴∠BEC＝130°，∵∠BEC＝∠CED+∠AEB，∠CED＝50°，∴∠AEB＝∠BEC﹣∠CED＝80°．（2）证明：∵△ACD≌△BCE，∴∠DAC＝∠EBC，∵△ACB，△DCE都是等腰三角形，∠ACB＝∠DCE＝120°∴∠CAB＝∠CBA＝∠CDE＝∠CED＝30°，∵CM⊥DE，∴∠CMD＝90°，DM＝EM，∴ME＝CM，∴DE＝2CM，∵∠BEN＝∠BAE+∠ABE＝∠BAE+∠EBC+∠CBA＝∠BAE+∠DAC+∠CBA＝30°+30°＝60°，∴∠NBE＝30°，∴BE＝2EN，EN＝BN，∴BE＝BN，∵AD＝BE，∴AE＝AD+DE，∴AE＝2CM+BN．3．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．4．【解答】证明：（1）∵AM⊥MN，BN⊥MN，∴∠AMC＝∠CNB＝90°，∵∠ACB＝90°，∴∠MAC+∠ACM＝90°，∠NCB+∠ACM＝90°，∴∠MAC＝∠NCB，在△AMC和△CNB中，∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，△AMC≌△CNB（AAS），AM＝CN，MC＝NB，∵MN＝NC+CM，∴MN＝AM+BN；（2）结论：MN＝BN﹣AM．∵AM⊥MN，BN⊥MN，∴∠AMC＝∠CNB＝90°，∵∠ACB＝90°，∴∠MAC+∠ACM＝90°，∠NCB+∠ACM＝90°，∴∠MAC＝∠NCB，在△AMC和△CNB中，∠AMC＝∠CNB，∠MAC＝∠NCB，AC＝CB，△AMC≌△CNB（AAS），AM＝CN，MC＝NB，∵MN＝CM﹣CN，∴MN＝BN﹣AM．5．【解答】（1）证明：∵AD⊥BC，∴∠ADB＝∠ADC＝90°，∵∠ABC＝45°，∴∠DBA＝∠DAB＝45°，∴BD＝DA，∵BE⊥AC，∴∠BEC＝90°，∴∠DAC+∠C＝90°，∠CBE+∠C＝90°，∴∠DAC＝∠DBF，在△BDF和△ADC中，，∴△BDF≌△ADC（ASA），∴DF＝DC．（2）证明：延长FE到K，使得EK＝EF，连接CF．∵∠BAC＝60°，∠ABC＝45°，∴∠ACB＝180°﹣60°﹣45°＝75°，∵DF＝DC，∠FDC＝90°，∴∠FCD＝∠DFC＝45°，∴∠ECF＝30°，∵∠CEF＝90°，∴CF＝2EF，∵FK＝2EF，∴CF＝FK，∵AE⊥FK，EF＝EK，∴AF＝AK，∴∠K＝∠AFE，∠EAF＝∠EAF，∵∠ADC＝90°，∠ACD＝75°，∴∠DAC＝15°，∴∠EAF＝∠EAK＝15°，∴∠K＝90°﹣15°＝75°，∴∠BAK＝∠BAD+∠DAK＝75°，∴∠BAK＝∠K，∴BA＝BK，∴AB＝BF+FK＝BF+CF．6．【解答】证明：（1）∵CD⊥AB，∴∠CDB＝90°，∵∠ABC＝45°，∴∠DBC＝∠DCB＝45°，∴DB＝DC，∵DH⊥BC，∴BH＝CH，∴GB＝GC．（2）①∵BA＝BC，BE⊥AC，∠ABC＝45°，∴∠ABE＝∠CBE＝22.5°，∴∠A＝∠ACB＝67.5°，∵∠ADC＝90°，∴∠ACD＝∠DBF＝22.5°，∵∠BDF＝∠ADC＝90°，BD＝DC，∴△BDF≌△CDA（SAS），∴BF＝AC．②作DN∥BC交AC于点N，连接FN．∵△BDF≌△CDA，∴DF＝AD，∵DN∥BC，∴∠NDC＝∠DCB＝45°，∵DN＝DB，∴△NDA≌△NDF（SAS），∴∠A＝∠DFN＝67.5°∵∠DFN＝∠FCN+∠CNF，∠FCN＝22.5°，∴∠CNF＝45°，∴NE＝EF，∵∠NDC＝∠GDB＝45°，BD＝DC，∠DBG＝∠DCN，∴△BDG≌△CDN（ASA），∴BG＝CN，∵CN＝EN+EC＝EF+CE，∴BG＝EC+EF．7．【解答】解：（1）过点E作EH⊥AB交AB于点H．∵AD∥BC，AB∥CD，∴四边形ABCD为平行四边形．∴AB＝DC，∠DAB＝∠DBC，在△CGD和△AEB中，，∴△CGD≌△AEB，∴∠DGC＝∠BEA，∴∠DGB＝∠BED，∵AD∥BC，∴∠EDG+∠DGB＝180°，∴∠EDG+∠BED＝180°∴EB∥DG，∴四边形BGDE为平行四边形，∴BG＝ED，∵G是BD的中点，∴BG＝BC，∴BC＝AD，ED＝BG＝AD，∵BC＝2，∴AE＝AD＝，在Rt△AEH中，∵∠EAB＝45°，sin∠EAB＝sin 45°＝＝，∴EH＝，∵∠EHA＝90°，∴△AHE为等腰直角三角形，∴AH＝EH＝，∵∠F＝60°，∴∠FBA＝60°，∵∠EBA＝∠EBF，∴∠EBA＝30°，在Rt△EHB中，tan∠EBH＝tan 30°＝＝，∴HB＝3，∴AB＝3+（2）连接EF，延长FE交AB与点M．∵∠A＝∠EDF，AE＝DE，∠AEM＝∠DEF，∴△AEM≌△DEF（ASA），∴DF＝AM，ME＝EF，又∵∠EBA＝∠EBF，∴△MBF是等腰三角形∴BF＝BM，又∵AB＝AM+BM，∴CD＝BF+DF．8．【解答】解：（1）如图1，延长DE交AB的延长线于F，∵∠ABC＝∠C＝90°，∴AB∥CD，∴∠CDE＝∠F，又∵E是BC的中点，∴CE＝BE，∴△CDE≌△BFE（AAS），∴DE＝FE，即E为DF的中点，∵DE平分∠ADC，∴∠CDE＝∠ADE，∴∠ADE＝∠F，∴AD＝AF，∴AE平分∠DAB；（2）如图2，在DA上截取DF＝DC，连接EF，∵DE平分∠ADC，∴∠CDE＝∠FDE，又∵DE＝DE，∴△CDE≌△FDE（SAS），∴CE＝FE，∠CED＝∠FED，又∵E是BC的中点，∴CE＝BE，∴FE＝BE，∵∠AED＝90°，∴∠AEF+∠DEF＝90°，∠AEB+∠DEC＝90°，∴∠AEF＝∠AEB，又∵AE＝AE，∴△AEF≌△AEB（SAS），∴AF＝AB，∴AD＝AF+DF＝AB+CD．9．【解答】证明：（1）∵AC平分∠BAD，CE⊥AB，CF⊥AD∴CE＝CF∵∠ABC+∠D＝180°，∠ABC+∠EBC＝180°∴∠EBC＝∠D．在△CBE与△CDF中，，∴△CBE≌△CDF（AAS）；（2）在Rt△ACE与Rt△ACF中，，∴Rt△ACE≌Rt△ACF（HL），∴AE＝AF，∴AB+DF＝AB+BE＝AE＝AF．10．【解答】（1）证明：如图①中，延长AE交DC的延长线于点F，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠F，在△AEB和△FEC中，，∴△AEB≌△FEC（AAS），∴AB＝FC，∵AE是∠BAD的平分线，∴∠BAE＝∠EAD，∵AB∥CD，∴∠BAE＝∠F，∴∠EAD＝∠F，∴AD＝DF，∴AD＝DF＝DC+CF＝DC+AB．（2）如图②，延长AE交DF的延长线于点G，∵E是BC的中点，∴CE＝BE，∵AB∥DC，∴∠BAE＝∠G，在△AEB和△GEC中，，∴△AEB≌△GEC（AAS），∴AB＝GC，∵AE是∠BAF的平分线，∴∠BAG＝∠F AG，∵AB∥CD，∴∠BAG＝∠G，∴∠F AG＝∠G，∴F A＝FG，∴AB＝CG＝AF+CF．11．【解答】（1）解：结论：CF＝AD．理由：∵AD∥BC，∴∠ADC＝∠ECF，∵E是CD的中点，∴DE＝EC，∵在△ADE与△FCE中，，∴△ADE≌△FCE（ASA），∴FC＝AD；（2）结论：BE⊥AF．理由：由（1）知△ADE≌△FCE，∴AE＝EF，AD＝CF，∵AB＝BC+AD，∴AB＝BC+CF，即AB＝BF，∵△ADE≌△FCE，∴AE＝EF，∴BE⊥AE；12．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS）；（2）设∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．13．【解答】证明：①在AN上截取AE＝AC，连接CE，如图所示：∵AC平分∠MAN，∠MAN＝120°，∴∠CAB＝∠CAD＝60°，∴△ACE是等边三角形，∴∠AEC＝60°，AC＝EC＝AE，又∵∠ABC+∠ADC＝180°，∠ABC+∠EBC＝180°，∴∠ADC＝∠EBC，在△ADC和△EBC中，，∴△ADC≌△EBC（AAS），∴DC＝BC，AD＝BE；②由①得：AD＝BE，∴AB+AD＝AB+BE＝AE，∴AB+AD＝AC．14．【解答】（1）证明：∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）解：结论DE＝BD+CE成立；理由如下：∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（3）解：∵∠BAD＞∠CAE，∠BDA＝∠AEC＝∠BAC，∴∠CAE＝∠ABD，在△ABD和△CEA中，，∴△ABD≌△CEA（AAS），∴S△ABD＝S△CEA，设△ABC的底边BC上的高为h，则△ACF的底边CF上的高为h，∴S△ABC＝BC•h＝12，S△ACF＝CF•h，∵BC＝2CF，∴S△ACF＝6，∵S△ACF＝S△CEF+S△CEA＝S△CEF+S△ABD＝6，∴△ABD与△CEF的面积之和为6．。

四、利用全等三角形证线段之间的和差倍分问题证一条线段等于其它两条线段的和或差，常将其转化成证明线段的相等问题，常用的方法如下：(1)利用图形中已有的线段和差关系进行证明。

(2)延长一条线段，作出两条线段的和，然后证明这条线段等于第三条线段。

(3)在第三条线段上截取一段等于第一条线段，然后证余下的线段等于第二条线段。

后两种方法，就是通常所说的截长补短。

例1.已知：如图在△ABC中，∠ABC的平分线与∠ACB相邻外角∠ACG的平分线相交于D，DE∥BC交AB于E，交AC于F，求证：EF=BE-CF分析：要证EF=BE-CF，而图中EF=ED-FD，若证出BE=ED，CF=FD，则此题可证出。

（证明略）例2.已知：如图，四边形ABCD中，AC平分∠BAD，CE⊥AB 于E，且∠B+∠D=180°，求证：AE=AD+BE分析：要证AE=AD+BE，则可转化为证AE-BE=AD，则需找到一条线段使它等于AE-BE，再证其与AD相等，在EA上截取EF=BE，连结CF，问题转化为证AF=AD，即要证出△AFC≌△ADC证明：在EA上截取EF=BE，连结CF∵CE⊥AB于E（已知）∴CF=CB（在线段垂直平分线上的点，到线段两个端点的距离相等）∴∠1=∠B（等边对等角）∵∠1+∠2=180°（平角定义）∠B+∠D=180°（已知）∴∠2=∠D（等角的补角相等）（再往下证明略）3.如图，△ABC是等边三角形，∠BDC=120°，且BD=CD,∠MDN=60°，AB=12cm. (1)证明MN=BM＋NC.（2）求△AMN的周长。

（3）若点M、N分别是AB、CA延长线上的点，，请说明BM、MN、NC之间的关系。

分析：（1）证明MN=BM＋NC.是典型的三条线段之间的关系的题型，这种题型一般是采用“截长补短法”来证明。

“截长法”是在最长的线段MN上找一点F，将MN截为两部分(如图4)，比如截为MN=MF＋NF,且使MF=BM（或NF=NC）.再求证剩余的线段NF=NC，从而得到MN=BM＋NC。

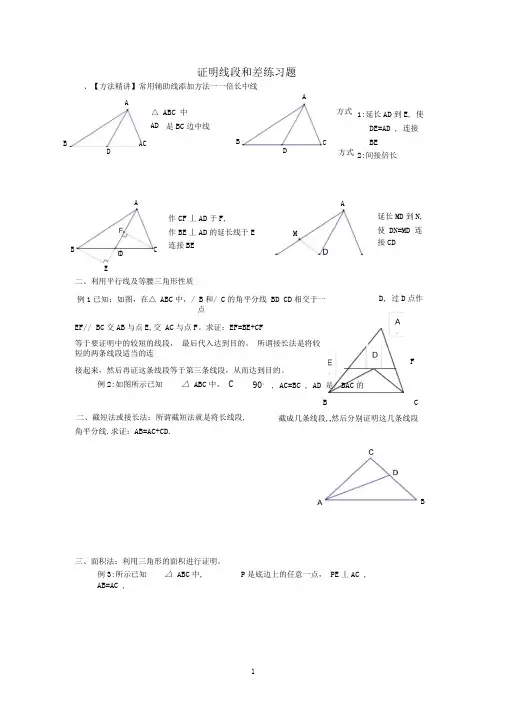
证明线段和差练习题、【方法精讲】常用辅助线添加方法一一倍长中线二、利用平行线及等腰三角形性质例1已知：如图，在△ ABC 中，/ B 和/ C 的角平分线 BD CD 相交于一点EF// BC 交AB 与点E,交 AC 与点F 。

求证：EF=BE+CF等于要证明中的较短的线段， 最后代入达到目的。

所谓接长法是将较短的两条线段适当的连接起来，然后再证这条线段等于第三条线段，从而达到目的。

角平分线.求证：AB=AC+CD.三、面积法：利用三角形的面积进行证明。

例3:所示已知 △ ABC 中, AB=AC ,P 是底边上的任意一点， PE 丄AC ,是BC 边中线方式 1:延长AD 到E , 使DE=AD , 连接BE2:间接倍长过D 点作二、截短法或接长法：所谓截短法就是将长线段,BC截成几条线段,A然后分别证明这几条线段例2:如图所示已知△ ABC 中， C90° , AC=BC , AD 是/ BAC 的A△ ABC 中AD BA CDA方式 BCDAC BD EAM延长MD 到N, 使 DN=MD 连接CD作CF 丄AD 于F , 作BE 丄AD 的延长线于E连接BED, FBPD! AB, BF 是腰AC 上的高，E D F 为垂足。

求证：①PE+PD=BF例4、如图①，在正方形 ABCD 中，则有结论 EF=BE+FD 成立；（1 ）如图②， E 、F 分别是BC 、CD 上的点，且/ EAF 成立？若成立，请证明？若不成立，请说明理由。

（2）若将（1）中的条件改为：在四边形 到点E ,延长CD 到点F ,使得/ EAF 仍然是/ BAD的一半，则结论 成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明。

2 — 1 — 8所示已知^ ABC 中,ACB 90 , AC=BC , E 是 AB 上的一点，BD 丄CE , AF 丄CE 垂足分别为 D 、F ,/ B=2/ C,求证:D练习题1. 如图2 — 1 — 3所示已知 三角形ABC 中, AD 平分/ BACB=2 /C,求证: AB+BD=AC.②当P 点在BC 的延长线上时, PE PD PF 之间满足什么关系式?E 、F 分别是 BC 、CD 上的点，且/ EAF=45 ° , 在四边形 ABCD 中，AB=AD , / B= / D=90 ° , 是/ BAD的一半，那么结论 EF=BE+FD 是否仍然ABCD 中，AB=AD , / B+ / D=180 °，延长 BCEF=BE+FD 是否仍然DF+AF=CF.2. 如图PC3、•已知：P 是等腰三角形 ABC 的底边BC 上的任意一点，过P 作AB 、AC 的平行线交 AC 、AB 于Q 、R.证明：PQ+PR 的值不随P 点的变 化而变化•且PQ+PR 为定值•4、已知:如图所示，在 ABC 中,D\E 是BC 上的点，BD=CE,过D,E 作AB 的平行线 DF,EG,分别交AC 于F,G 。

线段和差处理技巧---截长补短法
【方法技巧】在处理线段和差问题时，常考虑截长补短．截长法是在较长线段上
截取一段等于某一短线段，再证剩下的那一段等于另一短线段即可．补短法一般有两种方式：一种是将某短线段延长，使延长的一部分等于另一短线段．另一种是将某短线段直接延长至等于较长的线段．无论是截长法还是补短法都是要将几条线段的和差问题转
化为证两条线段相等的问题，一般都要通过构造出两对全等三角形来解决问题．例：如图，△ABC中，∠CAB＝∠CBA＝45°，CA＝CB，点E为BC的中点，CN⊥AE交AB于N.
[来源:Z,xx,]
(1)求证：∠1＝∠2；
(2)求证：AE＝CN＋EN.(请用多种方法证明)
方法一：直接截长法
【解题过程】
证明：在AE上截取一段AF等于短边CN，再证EF＝EN即可，[来源:学#科#网Z#X#X#K]
故可先证△AFC≌△CNB，再证△CFE≌△BNE.[来源:Z_xx_]
方法二：间接截长法[来源:]
【解题过程】
证明：作∠ACF＝45°交AE于F，先证△ACF≌△CBN，再证△CFE≌△BNE，此法实质是间接地在AE上截取AF＝CN.
[来源:学科网ZXXK]
方法三：直接补短法
【解题过程】。

人教版_部编版八年级数学上册第十二章第二节三角形全等的判定考试复习题六（含答案)阅读下列材料，然后解决问题：截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用．具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题．(1)如图①，在△ABC中，若AB＝12，AC＝8，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，把AB、AC、2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是；(2)问题解决：如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB 于点E，DF交AC于点F，连接EF，求证：BE＋CF＞EF；(3)问题拓展：如图③，在四边形ABCD中，∠B＋⊥D＝180°，CB＝CD，⊥BCD＝140°，以C为顶点作一个70°角，角的两边分别交AB，AD于E，F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．【答案】(1)210<<(2)证明见解析(3)BE＋DF＝EFAD【解析】试题分析：（1）延长AD至E，使DE=AD，连接BE．由SAS证明△BDE△△CDA，得出BE=AC=6，在△ABE中，由三角形的三边关系求出AE的取值范围，即可得出AD的取值范围；（2）延长FD至点G，使DG＝DF，连接BG，EG．同（1）得△BDG△△CDF，得出BG＝CF，由线段垂直平分线的性质得出EF＝EG，在△BEG中，由三角形的三边关系得出BE＋BG>EG即可得出结论；（3）延长AB至点G，使BG=DF，连接CG．证出△CBG＝△D，由SAS 证明△CBG△△CDF，得出CG＝CF，△BCG＝△DCF，证出△ECG=70°=△ECF，再由SAS证明△ECG△△ECF，得出EG=EF，即可得出结论．解：（1）延长AD至E，使DE=AD，连接BE，如图△所示：△AD是BC边上的中线，△BD=CD，在△BDE和△CDA中，△BD=CD，△BDE=△CDA，DE=AD，△△BDE△△CDA（SAS），△BE=AC=6，在△ABE中，由三角形的三边关系得：AB﹣BE＜AE＜AB+BE，△12﹣8＜AE＜12+8，即4＜AE＜20，△2＜AD＜10；(2)证明：延长FD至点G，使DG＝DF，连接BG，EG．△点D是BC的中点，△DB＝DC．在△BDG和△CDF中，△DG=DF，△BDG=△CDF，DB=DC，△△BDG△△CDF(SAS)，△BG＝CF．△ED△FD，即ED△FG．又△FD＝GD，△EF＝EG．在△BEG中，△BE＋BG>EG，△BE＋CF>EF．(3)解：BE＋DF＝EF．证明如下：如图，延长AB至点G，使BG＝DF，连接CG．△△ABC＋△D＝180°，△ABC＋△CBG＝180°，△△CBG＝△D．在△CBG和△CDF中，△BG=DF，△CBG=△CDF，CB=CD，△△CBG△△CDF(SAS)，△CG＝CF，△BCG＝△DCF，．△△BCD＝140°，△ECF＝70°，△△DCF＋△BCE＝70°，△△BCE＋△BCG＝70°，△△ECG＝△ECF＝70°．在△ECG和△ECF中，△CE=CE，△ECG=△ECF，CG=C，△△ECG△△ECF(SAS)，△EG＝EF．△BE＋BG＝EG，△BE＋DF＝EF．点睛：本题考查了三角形的三边关系、全等三角形的判定与性质等知识；本题综合性强，有一定难度，通过作辅助线证明三角形全等是解决问题的关键．62．如图，△ABC是等边三角形，点D，E，F分别是AB，BC，CA上的点．(1)若AD＝BE＝CF，问△DEF是等边三角形吗？试证明你的结论；(2)若△DEF是等边三角形，问AD＝BE＝CF成立吗？试证明你的结论．【答案】（1）△DEF是等边三角形，证明见解析；（2）AD＝BE＝CF成立，证明见解析.【解析】试题分析：(1)由SAS易证△ADF△△BED△△CFE，所以DF=DE=EF，即△DEF 是等边三角形；(2)先证明△1+△2=120°，△2+△3=120°．可得△1=△3．同理△3=△4．则△ADF△△BED△△CFE，故能证明AD=BE=CF.解：(1)△DEF是等边三角形．证明如下：∵△ABC是等边三角形，∴∠A＝∠B＝∠C，AB＝BC＝CA.又∵AD＝BE＝CF，∴DB＝EC＝FA.∴△ADF≌△BED≌△CFE，∴DF＝ED＝FE.∴△DEF是等边三角形．(2)AD＝BE＝CF成立．证明如下：如图，∵△DEF是等边三角形，∴DE＝EF＝FD，∠FDE＝∠DEF＝∠EFD＝60°.∴∠1＋∠2＝120°.∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∴∠2＋∠3＝120°，∴∠1＝∠3.同理∠3＝∠4，易证△ADF≌△BED≌△CFE(AAS)，∴AD＝BE＝CF.点睛：本道题主要考查了等边三角形的性质与判定、全等三角形的性质与判定，熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解答本题的关键.63．已知点P是Rt△ABC斜边AB上一动点(不与点A，B重合)，分别过点A，B向直线CP作垂线，垂足分别为点E，F，点Q为斜边AB的中点．(1)如图①，当点P与点Q重合时，AE与BF的位置关系是________，QE 与QF的数量关系是________；(2)如图②，当点P在线段AB上且不与点Q重合时，试判断QE与QF的数量关系，并说明理由．(温馨提示：直角三角形斜边上的中线等于斜边的一半)【答案】(1)AE∥BF,QE＝QF;(2) QE=QF，理由见解析.【解析】【分析】(1)根据AAS推出△AEQ和△BFQ全等即可得出答案；(2)延长EQ交BF于D，求出△AEQ和△BDQ全等，根据全等三角形的性质得出EQ=QD，根据直角三角形斜边上中点性质得出即可．【详解】(1)如图1,当点P与点Q重合时，AE与BF的位置关系是AE△BF，QE与QF的数量关系是QE=QF,理由：∵Q为AB的中点，△AQ=BQ，△AE△CQ，BF△CQ，△AE△BF，△AEQ=△BFQ=90°，△△AEQ△△BFQ，△QE=QF；(2)QE=QF证明：如图2，延长EQ交BF于D,∵由(1)知：AE△BF，△△AEQ=△BDQ，△△AEQ△△BDQ，△EQ=DQ，△△BFE=90°，△QE=QF．【点睛】本题主要考查的就是三角形全等的证明与应用，难度中等．在解决这个问题的时候，我们要学会利用添加辅助线构造三角形全等，对直角三角形性质(直角三角形斜边上的中线等于斜边的一半)的应用也要非常的熟练．64．如图，已知线段m，n，如果以线段m，n分别为等腰三角形的底或腰作三角形，能作出几个等腰三角形？请作出．不写作法，保留作图痕迹．【答案】能作出两个等腰三角形【解析】试题分析：以m为底时，以底的两个端点为圆心，n长为半径画弧交于一点，则这个点就是顶点；以n为底时，以底的两个端点为圆心，m长为半径画弧交于一点，则这个点就是顶点，则这样的三角形就有两个．试题解析：如图所示：能画出两个等腰三角形．一个以m 为底，以n 为腰；另一个以n 为底，以m 为腰．65．如图,点A 、D 、E 在直线l 上,∠BAC=90°,AB=AC,BD ⊥l 于D,CE ⊥l 于E,求证:DE=BD+CE.【答案】证明见解析.【解析】【分析】根据已知条件及互余关系可证△ABD ≌△CAE ，则BD=AE ，AD=CE ，由DE=AD+AE ，得出线段DE=BD+CE ．【详解】∵∠BAC=90°，BD ⊥DE ，CE ⊥DE ，∴∠DAB+∠DBA=∠DAB+∠EAC ，∴∠DBA=∠EAC ；在△ABD 与△CAE 中，DBA EAC BDA AEC AB AC ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝ ， ∴△ABD ≌△CAE （AAS ），∴BD=AE ，AD=CE ，∴DE=BD+CE ．66．如图，己知△ABC 是等边三角形，点P 在△ABC 内，点Q 在△ABC 外，分别连接AP 、BP 、AQ 、CQ ，∠ABP=∠ACQ, BP=CQ.(1)求证：△ABP ≌△ACQ ；(2)连接PQ,求证△APQ 是等边三角形；(3)连接P 设△CPQ 是以∠PQC 为顶角的等腰三角形，且∠BPC=100︒，求∠APB 的度数.【答案】(1)答案见解析；（2）答案见解析；（3）160°【解析】试题分析:易证AB =AC ，△BAC =60°，即可证明△ABP △△ACQ ，可得△BAP =△CAQ ，AP =AQ ，即可求得△PAQ =60°，即可解题．（1）证明： △ △ABC 是等边三角形，∴ AB=AC .在△ABP 和△ACQ 中ABP ACQ AB AC BP CQ =⎧⎪∠=∠⎨⎪=⎩， ∴ △ABP ≌ △ACQ ( SAS ).（2）证明： △ △ABP ≌ △ACQ ，∴ AP AQ =,BAP CAQ ∠=∠ ，∴ BAP PAC CAQ PAC ∠+∠=∠+∠，∴ BAC PAQ ∠=∠ .△ △ABC 是等边三角形，∴ 060BAC ∠=，∴ 060PAQ ∠= ，∴ △APQ 是等边三角形.（3）解： 如图示△ △CPQ 是等腰三角形，∠PQC 为顶角， ∴ QPC QCP ∠=∠ .设0QPC x ∠=， 0180PQC QPC QCP ∠=-∠-∠=001802x - . △ △APQ 是等边三角形，∴ 060APQ AQP ∠=∠=，∴ 00000601802240-2AQC AQP PQC x x ∠=∠+∠=+-=. △ △ABP ≌ △ACQ ，∴ APB AQC ∠=∠，∴ 002402APB x ∠=- .△ 0360APB APQ QPC BPC ∠+∠+∠+∠=，又∵ 000100,60,,BPC APQ QPC x ∠=∠=∠=∴ 240-260100360x x +++=，解得 40x =，∴ 000240240160APB ∠=-⨯= .点睛: 本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，考查了正三角形的判定，本题中求证△ABP ≌△ACQ 是解题的关键．67．已知：如图所示，△ABC 中，∠ABC=45°，高AE 与高BD 交于点M ，BE=4，EM=3.（1）求证：BM=AC ；（2）求△ABC 的面积.【答案】(1)证明见解析;(2)14【解析】试题分析：（1）由同角的余角相等，得到△BME =△C ，再由△ABE 是等腰直角三角形，得到AE =BE ，即可证明△BEM △△AEC ，从而得到结论；（2）由△BEM △△AEC ，得到BE 、EM 的长，进而得到BC 的长，根据三角形面积公式即可求出结论．试题解析：解：（1）△AE 、BD 为△ABC 的高， △△BEM =△AEC =△BDC =90°，△△EBM +△C =△EBM +△BME =90°， △△BME =△C ．又△△ABC =45°，△△ABC =△BAE =45°，△AE =BE ．在△BEM 和△AEC 中，△△BEM =△AEC ，△BME=△C，BE=AE，△△BEM△△AEC(AAS) ，△BM=AC；（2）△△BEM△△AEC，△BE=AE=4，EM=EC=3，△BC=BE+EC=7，△△ABC的面积=12×BC×AE=12×7×4=14．68．已知：如图所示，在△ABC中，AB=AC，D是BC的中点，DE⊥AB 于E，DF⊥AC于F．求证：BE＝CF【答案】证明见解析【解析】试题分析：由AB=AC，得到∠B=∠C，再由AAS得到△BED≌△CFD，即可得出BE=CF．试题解析：证明：∵AB=AC，∴∠B=∠C．∵DE⊥AB，DF⊥AC，∴∠BED=∠CFD=90°．又∵D是BC的中点，∴BD=CD．在△BED和△CFD 中，△△B=△C，△BED=△CFD=90°，BD=CD，∴△BED≌△CFD(AAS) ，∴BE ＝CF．69．如图，在△ABC中，AB＝AC，AD⊥BC于点D，CE⊥AB于点E，AE＝CE，试说明：(1)△AEF≌△CEB；(2)∠ABF＝2∠FBD；【答案】（1）详见解析；（2）详见解析.【解析】试题分析：()1根据等角的余角相等易得EAF ECB ∠=∠，此时根据ASA 结合已知条件即可得出结论；()2根据△AEF ≌△CEB 得EF EB =，得到.EBF EFB ∠=∠AD 垂直平分,BC 得到FB FC =，根据等边对等角得到.FBD FCD ∠=∠根据三角形外角的性质得到2EFB FBD FCD FBD ∠=∠+∠=∠，即可证明.试题解析：(1)因为AD BC CE AB ⊥⊥，， 所以90AEF CEB ∠=∠=︒， 9090.AFE EAF CFD ECB ∠∠=︒∠∠=︒＋，＋又因为AFE CFD ∠=∠， 所以.EAF ECB ∠=∠在△AEF 和△CEB 中，AEF CEB AE CEEAF ECB ∠=∠⎧⎪=⎨⎪∠=∠⎩， 所以△AEF ≌△CEB (ASA)．(2)由△AEF ≌△CEB 得EF EB =，所以.EBF EFB ∠=∠在△ABC 中，AB AC AD BC ⊥＝，，所以BD CD =.所以FB FC = .所以.FBD FCD ∠=∠因为2EFB FBD FCD FBD ∠=∠+∠=∠，所以2EBF FBD ∠=∠，即2.ABF FBD ∠=∠70．如图，B 、D 、C 三点在一条直线上，∠ADB=∠ADC=90°，BD=DE ，∠DAC=45°；（1）线段AB 、CE 的关系为 ；（2）若BD=a ，AD=b ，AB=c ，请利用此图的面积式证明勾股定理．【答案】(1) AB=CE ，AB ⊥CE,理由见解析；（2）证明见解析.【解析】试题分析：（1）先由边角边证得△ADB ≌△CDE ，可得AB=CE ，∠BAD=∠ECD ；延长CE 和AB 交于点F ，由同角的余角相等即可证得∠BFC=90°，即AB ⊥CE ；（2）把△ABC 面积分成ΔABE ΔBDE ΔACD S S S ++，由三角形的面积公式即可证明. 试题解析：（1）线段AB 、CE 的关系为：AB=CE ，AB ⊥CE ，∵∠ADB=∠ADC=90°，∠DAC=45°，∴△ACD 是等腰直角三角形，∴AD=CD ，∵BD=ED ，∴△ADB ≌△CDE （SAS ），∴∠BAD=∠ECD ，延长CE 交AB 于点F ，如图：∵∠BAD+∠ABD=90°，∴∠ECD +∠ABD=90°，即AB ⊥CE ；（2）如图，设EF=x ，∵ ΔABC ΔABE ΔBDE ΔACD S S S S =++， ∴1111AB CF AB EF BD DE DC AD 2222⋅=⋅+⋅+⋅， ∵BD=a ，AB=c ，AD=b ，∴易得 AB=CE=c ，BD=DE=a ，AD=CD=b ， ∴221111c c x cx a b 2222+=++（）， 即： 22211111c cx cx a b 22222+=++， ∴222111c a b 222=+， ∴222a b c +=.点睛：此题考查了三角形全等的判定、同角的余角相等以及勾股定理的证明，此题主要利用了三角形的面积公式为底×高÷2.。

1专题13 利用全等三角形的性质解决线段的证明与计算问题知识对接考点一、全等三角形的性质 （1）全等三角形对应边相等； （2）全等三角形对应角相等.考点二、怎样解运用全等三角形性质的问题证明两条线段相等或两个角相等时，常证明两条线段或两个角所在的三角形全等,运用全等三角形的性质，即全等三角形的对应边相等、对应角相等得到.专项训练一、单选题1．（2021·福建九年级）如图，点E ，F 在线段BC 上，ABF 与DEC 全等，点 A 和点D ，点B 和点C 是对应点，AF 和DE 交于点 M ，则与EM 相等的线段是（ ）A ．BEB ．EFC ．FCD ．MF【答案】D 【分析】根据ABF 与DEC 全等，点A 和点D ，点B 和点C 是对应点，可得AFB DEC ∠=∠，则有EM FM =． 【详解】解：∵ABF 与DEC 全等，点A 和点D ，点B 和点C 是对应点， ∵AFB DEC ∠=∠， ∵EM FM =， 故选：D ． 【点睛】本题考查了全等三角形的性质，等腰三角形的判定与性质，熟悉相关性质是解题的关键．2．（2021·山东九年级）如图，在菱形ABCD 中，6AB =，60BCD ∠=︒，E 是AD 中点，BE 交AC 于点F ，连接DF ，则DF 的长为（ ）A ．4BC ．D ．【答案】C 【分析】连接DB ， 四边形ABCD 为菱形，∵BCD =60°，可得∵ABD 为等边三角形，求出AF 的长度，再证明∵AEF ∵∵DEF ，即可求出DF 的长度． 【详解】 如图：连接DB∵四边形ABCD 为菱形，∵BCD =60°， ∵∵BCD =∵BAD =60°，∵AB =AD ，∵DAC =∵BAC =12∵DAB =30°，即∵ABD 为等边三角形， 又E 为AD 的中点， ∵BE ∵AD ，∵AE =12AD =12AB =3，cos ∵EAF =AE AF = cos AF 又在∵AEF 和∵DEF 中，∵AEF =∵DEF =90°，AE =DE ，EF =EF ，3∵∵AEF ∵∵DEF ， ∴DF =AF故选：C ． 【点睛】本题考查了菱形的性质，等边三角形的判定和性质，全等三角形的判定和性质，以及特殊锐角三角函数值，熟悉并灵活运用以上性质式解题的关键．3．（2021·天津和平·）如图，在AOB 中，15,6,OAB AOB OB OC ∠=∠=︒=平分AOB ∠，点P 在射线OC 上，点Q 为边OA 上一动点，则PA PQ +的最小值是（ ）A ．1B ．2C ．3D ．4【答案】C 【分析】在射线OB 上截取一点Q '，使得OQ OQ '=，则OPQ OPQ ∆≅∆'，可得PQ PQ ='．作AH OB ⊥于H ．可得PA PQ PA PQ +=+'，推出当A 、P 、Q '共线，且垂直OB 时，PA PQ +'的值最小，最小值为AH ，【详解】解：在射线OB 上截取一点Q '，使得OQ OQ '=，则OPQ OPQ ∆≅∆'，可得PQ PQ ='．作AH OB ⊥于H ． ∵'PA PQ PA PQ +=+，∵当A 、P 、Q '共线，且垂直OB 时，PA PQ +'的值最小，即最小值为AH ∵15OAB AOB ∠=∠=∵6OB AB ==，30OA B AO H B A B ∠+∠=∠=， 在Rt ABH 中， ∵·sin303AH AB ==，+的最小值为3，∵PA PQ故选C．【点睛】本题考查轴对称-最短问题、全等三角形，等腰三角形的性质、三角函数等知识，解题的关键在于能够熟练的掌握相关知识点．4．（2021·江苏南通田家炳中学九年级）如图，在直角坐标系中，已知点A(6，0)，点B为y轴正半轴上一动点，连接AB，以AB为一边向下作等边∵ABC，连接OC，则OC的最小值（）A B．3C．D．【答案】B【分析】以OA为对称轴作等边∵AMN，由“SAS”可证∵ANC∵∵AMB，可得∵AMB=∵ANC=60°，由直角三角形的性质可求∵AEN=30°，EO= ，则点C在EN上移动，当OC'∵EN时，OC'有最小值，即可求解．【详解】解：如图，以OA为对称轴作等边∵AMN，延长CN交x轴于E，∵∵ABC是等边三角形，∵AMN是等边三角形，∵AM=AN，AB=AC，∵MAN=∵BAC，∵AMN=60°=∵ANM，∵∵BAM=∵CAN，∵∵ANC∵∵AMB（SAS），∵∵AMB=∵ANC=60°，∵∵ENO=60°，∵AO=6，∵AMB=60°，AO∵BO，∵MO=NO=∵∵ENO=60°，∵EON=90°，5∵∵AEN=30°，， ∵点C 在EN 上移动，∵当OC'∵EN 时，OC'有最小值， 此时，O'C=12EO=3， 故选：B ．【点睛】本题考查了全等三角形的判定和性质，等边三角形的性质，垂线段最短，锐角三角函数，确定点C 的运动轨迹是解题的关键．5．如图，已知：在∵ABCD 中，E 、F 分别是AD 、BC 边的中点，G 、H 是对角线BD 上的两点，且BG ＝DH ，则下列结论中不正确的是（ ）A ．GF ∵FHB ．GF ＝EHC ．EF 与AC 互相平分D ．EG ＝FH【答案】A 【分析】连接EF 交BD 于O ，易证四边形EGFH 是平行四边形，然后证明是否得出选项． 【详解】连接EF 交BD 于点O ，在平行四边形ABCD 中的AD=BC ，∵EDH=∵FBG ， ∵E 、F 分别是AD 、BC 边的中点， ∵DE∵BF,DE=BF=12BC ，∵四边形AEFB 是平行四边形,有EF∵AB ， ∵点E 是AD 的中点，∵点O 是BD 的中点，根据平行四边形中对角线互相平分，故点O 也是AC 的中点，也是EF 的中点，故C 正确，又∵BG=DH,∵∵DEH∵∵BFG ， ∵GF=EH ，故B 正确，∵DHE=∵BGF ，∵∵GHE=∵HGF ， ∵∵EHG∵∵FGH ， ∵EG=HF ，故D 正确，∵GF∵EH ，即四边形EHFG 是平行四边形，而不是矩形，故∵GFH 不是90度， ∵A 不正确． 故选A. 【点睛】本题考查平行四边形的判定与性质和全等三角形的判定与性质，解题的关键是熟练掌握平行四边形的判定与性质和全等三角形的判定与性质.6．如图，ABC DEC ≌△△，A 和D ，B 和E 是对应点，B 、C 、D 在同一直线上，且5CE =，7AC =，则BD 的长为（ ）A ．12B ．7C ．2D ．14【答案】A 【分析】7根据全等三角形的性质即可得到结论． 【详解】解：如图，ABC DEC ∆≅∆，A 和D ，B 和E 是对应点，B 、C 、D 在同一直线上，且5CE =，7AC =，5BC EC ∴==，7CD AC ==，12BD BC CD ∴=+=．故选：A ． 【点睛】本题主要考查的是全等三角形的性质，熟练掌握全等三角形的性质是解题的关键． 7．如图：若ABE ACF ≌，且5,2==AB AE ，则EC 的长为（ ）A ．2B ．2.5C ．3D ．5【答案】C 【分析】根据全等三角形的性质得AC=AB=5，由EC=AC ﹣AE 求解即可． 【详解】解：∵ABE ACF ≌，AB=5， ∵AC=AB=5， ∵AE=2，∵EC=AC ﹣AE=5﹣2=3， 故选：C ． 【点睛】本题考查了全等三角形的性质、线段的和与差，熟练运用全等三角形的性质是解答的关键． 8．如图，ABC ADE △≌△，点D 在边BC 上，则下列结论中一定成立的是（ ）A．AC DE==B．AB BDC．ABD ADB∠=∠∠=∠D．EDC AED【答案】C【分析】根据全等三角形的性质可直接进行排除选项．【详解】△≌△，解：∵ABC ADE∵AB=AD，BC=DE，AC=AE，∵B=∵ADE，∵C=∵E，∵∵ABD=∵ADB，故A、B、D都是错误的，C选项正确；故选C．【点睛】本题主要考查全等三角形的性质，熟练掌握全等三角形的性质是解题的关键．9．如图，∵ACE∵∵DBF，AE//DF，AB＝3，BC＝2，则AD的长度等于（）A．2B．8C．9D．10【答案】B【分析】根据全等三角形的对应边相等解答．【详解】解：由图形可知，AC＝AB＋BC＝3＋2＝5，∵∵ACE∵∵DBF，∵BD＝AC＝5，9∵CD ＝BD−BC ＝3， ∵AD ＝AC ＋CD ＝5＋3＝8， 故选：B ． 【点睛】本题考查的是全等三角形的性质，掌握全等三角形的对应边相等是解题的关键．10．（2021·河北）如图，已知平行四边形ABCD ，3CD cm =，依下列步骤作图，并保留作图痕迹： 步骤1：以B 为圆心，BE 长为半径画弧∵，分别交AB ，BC 于点E ，F ； 步骤2：以A 为圆心，以BE 长为半径画弧∵，交AD 于点G ；步骤3：以G 为圆心，以EF 长为半径画弧∵，弧∵和弧∵交于点H ，过H 作射线，交BC 于点M ．则下列叙述不正确．．．的是：（ ）A ．AMC C ∠=∠B ．AM CD =C ．AM 平分BAD ∠ D ．BEF AGH ∆∆≌【答案】C 【分析】由作图痕迹，可以得到∵EBF∵∵GAH ，从而有∵EBF=∵GAH ，因此可以判断A 、B 、D 正确，因为C 不一定成立，故可以得到解答． 【详解】解：如图，连结E 、F 和G 、H ，由已知，在∵EBF 和∵GAH 中，AG=EB ，AH=BF ，HG=EF ，∵∵EBF∵∵GAH ，故D 正确； ∵∵EBF∵∵GAH ，∵∵EBF=∵GAH ，由平行四边形的性质可得：∵AMB=∵GAH ，∵∵EBF=∵AMB ，∵AB=AM ，又由平行四边形的性质可得：AB=CD ，∵AM=CD ，故B 正确；∵∵AMB+∵AMC=180°，∵∵EBF+∵AMC=180°，又由平行四边形的性质可得：∵EBF+∵C=180°，∵∵AMC=∵C ，故A 正确； ∵∵BAM=∵MAD 不一定成立，∵C 不正确， 故选C ． 【点睛】本题考查三角形全等的判定和应用，熟练掌握作一个角等于已知角的作法和依据是解题关键． 二、填空题11．如图，矩形ABCD 中，AD ＝2，E 为CD 上一点，连接AE ，将∵ADE 沿AE 折叠，点D 恰好落在BC 上，记为D ′，再将∵D ′CE 沿D ′E 折叠，若点C 的对应点C ′落在AE 上，则AB 的长为___．【分析】由折叠的性质得到ADE AD ED CE D C E ∆∆⎧⎨∆∆'''⎩'≌≌，能得到345∠=∠=∠，再用平角的性质得到34560∠=∠=∠=︒，再由1490∠+∠=︒，得到1230∠=∠=︒，可以求出6∠，最后可以求出cos AB AD BAD ''=⨯∠． 【详解】 如图：由折叠的性质得：ADE AD E D CE D C E ∆∆⎧⎨∆∆'''⎩'≌≌11∵123435AD AD ∠=∠∠=∠=⎧⎨∠=∠'⎩；； ∵345∠=∠=∠ ∵345180∠+∠+∠=︒ ∵34560∠=∠=∠=︒ ∵1490∠+∠=︒ ∵1230∠=∠=︒∵6901230∠=︒-∠-∠=︒ ∵'Rt ABD 中，'30BAD ∠=︒∵cos cos AB AD BAD AD BAD '''=⨯∠=⨯∠2==【点睛】本题考查了矩形与折叠，全等三角形的性质，三角函数，掌握它们的性质是解题的关键．12．（2021·江苏扬州市·九年级二模）如图，Rt ∵ABC ∵Rt ∵FDE ，∵ABC ＝∵FDE ＝90°，∵BAC ＝30°，AC ＝4，将Rt∵FDE 沿直线l 向右平移，连接BD 、BE ，则BD +BE 的最小值为___．【答案】【分析】根据平面直角坐标系，可以假设(E m ，则(1D m +，，则BD BE +求BD BE +的最小值，相当于在x 轴上找一点(,0)R m ，使得R 到(1M -，，N 的距离和的最小值，如图1中，作点N 关于x 轴的对称点N '，连接MN '交x 轴题意R ，连接RN ，此时RM RN +的值最小，最小值MN ='的长． 【详解】解：建立如图坐标系，在Rt ABC ∆中，90ABC ∠=︒，4AC =，30BAC ∠=︒， 122BC AC ∴==，AB ==∴斜边AC 上的高ABC FDE ∆≅∆，4EF AC ∴==，斜边EF∴可以假设(E m ，则(1D m +，，BD BE ∴+欲求BD BE +的最小值，相当于在x 轴上找一点(,0)R m ，使得R 到(1M -，，N 的距离和的最小值，如图1中，作点N 关于x 轴的对称点N '，连接MN '交x 轴题意R ，连接RN ，此时RM RN +的值最小，最小值MN ='BD BE ∴+的最小值为故答案为：13【点睛】本题考查轴对称最短问题，平面直角坐标系，勾股定理等知识，解题的关键是学会用转化的思想思考问题，属于中考填空题中的压轴题．13．（2021·浙江金华·九年级）如图，在ABC 中，1841B C ∠=︒∠=︒，，点D 是BC 的中点，点E 在AB 上，将BDE 沿DE 折叠，若点B 的落点B '在射线CA 上，则BA 与B D '所夹锐角的度数是________．【答案】80︒． 【分析】根据折叠可得三角形全等，根据全等三角形的性质以及中点的性质可得BD B D '=， DC DB '=，由等腰三角形性质以及三角形外角定理求得BDB '∠度数，在BOD 中根据内角和即可求得BA 与B D '所夹锐角的度数． 【详解】如下图，连接DE ，BA 与B D '相交于点O ，将 ∵BDE 沿 DE 折叠， BDE B DE '∴△≌△，BD B D '∴=,又∵D 为BC 的中点，BD DC =，BD B D '∴=，41DB C C '∴==︒∠∠, BDB DB C C =''∴=+︒∠∠∠82,18080BOD B BDB '∴=︒--=︒∠∠∠, 即BA 与B D '所夹锐角的度数是80︒．故答案为：80︒． 【点睛】本题考察了轴对称的性质、全等三角形的性质、中点的性质、三角形的外角以及内角和定理，综合运用以上性质定理是解题的关键．14．（2021·广东）如图，点M 是Rt ∵ABC 斜边AB 的中点，过点M 作DM ∵CM ，交AC 于点D ，若AD ＝2，BC ＝5，则CD ＝_______【分析】延长CM ，使CD ＝MN ，连接AN ，证明()AMN BMC SAS ∆∆≌，由全等三角形的性质得出5BC AN ==，NAM B ∠=∠，由勾股定理求出DN =【详解】解：延长CM ，使CD ＝MN ，连接AN ， 如图所示：∵点M 是Rt ABC ∆斜边AB 的中点， ∵AM BM =， 在AMN ∆和BMC ∆中， AM BM AMN BMC MN CM =⎧⎪∠=∠⎨⎪=⎩， ∵()AMN BMC SAS ∆∆≌，15∵5BC AN ==，NAM B ∠=∠， ∵//AN BC ， ∵90BCA ∠=︒， ∵90NAD ∠=︒，∵DN == ∵DM CM ⊥，CM MN =，∵CD DN ==【点睛】本题考查了全等三角形的判定与性质，勾股定理，中垂线的性质，直角三角形的性质，熟练掌握全等三角形的判定与性质是解题的关键．15．（2021·浙江）如图，已知： Rt Rt 90ABC CEF ABC CEF ∠=∠=︒≌，，306A AC ∠=︒=，．现将CEF △绕点C 逆时针旋转α度，线段CF 与直线AB 交于点O ，连接OE ．则当OE OB =时，线段OA 的长为________．【答案】【分析】过E 作EH ∵CF 于H ，得出ABC CEF ≅，设OF=x ，则OC=6-x ，根据勾股定理得出结果． 【详解】解：过E 作EH ∵CF 于H ， ∵ABC CEF ≅，∵6CF AC == ，30A ∠=︒， ∵9060EFC A ∠=︒-∠=︒， 设OF =x ，则OC =6-x ， 在Rt ∆OCB 中，2222(6)9OB OC BC x =-=--，在Rt ∆FEH 中，EH =EF FH =EF ·cos60º=32， ∵OH =x -32，在Rt ∆OEH 中，222223()2OE EH OH x =+=-+，又∵OE =OB ，∵2223()(6)92x x -+=--解得x =2，∵BO∵AO =AB -BO =故答案为【点睛】本题考查了全等三角形的性质，勾股定理及特殊角的三角函数，正确作出辅助线是解题的关键． 三、解答题16．（2021·云南）如图，AC ∵BD ，垂足点E 是BD 的中点，且AB =CD ，求证：AB //CD .【答案】详见解析 【分析】17先证明,BE DE = 再利用斜边直角边公理证明()Rt ABE Rt CDE HL ≌，可得A C ∠=∠，从而可得答案． 【详解】证明：∵点E 是BD 的中点 ∵BE ED =. ∵AC BD ⊥∵90AEB DEC ∠=∠=︒. 在Rt ABE △和Rt CDE △中AB CDBE ED =⎧⎨=⎩∵()Rt ABE Rt CDE HL ≌， ∵A C ∠=∠， ∵//AB CD ． 【点睛】本题考查的是利用斜边直角边证明两个三角形全等，以及全等三角形的性质，平行线的判定，掌握以上知识是解题的关键．17．如图，在正方形ABCD 中，点E 在BC 边的延长线上，点F 在CD 边的延长线上，且CE DF =,连接AE 和BF 相交于点M ． 求证：AE BF = ．【答案】证明见解析． 【分析】利用正方形的性质证明：AB=BC=CD ，∵ABE=∵BCF=90°，再证明BE=CF ，可得三角形的全等，利用全等三角形的性质可得答案． 【详解】证明：∵四边形ABCD 为正方形，∵AB=BC=CD ，∵ABE=∵BCF=90°， 又∵CE=DF ，∵CE+BC=DF+CD 即BE=CF ， 在∵BCF 和∵ABE 中，BE CF ABE BCF AB BC =⎧⎪∠=∠⎨⎪=⎩∵ABE BCF △△≌（SAS ）， ∵AE=BF ． 【点睛】本题考查的是正方形的性质，三角形全等的判定与性质，掌握以上知识是解题的关键． 18．（2021·吉林）综合与实践在数学活动课上，老师出示了这样一个问题：如图1，在ABC 中，90ACB ∠=︒，6AC =，8BC =，点D 为BC 边上的任意一点．将C ∠沿过点D 的直线折叠，使点C 落在斜边AB 上的点E 处．问是否存在BDE 是直角三角形？若不存在，请说明理由；若存在，求出此时CD 的长度．探究展示：勤奋小组很快找到了点D 、E 的位置．如图2，作CAB ∠的角平分线交BC 于点D ，此时C ∠沿AD 所在的直线折叠，点E 恰好在AB 上，且90BED ∠=︒，所以BDE 是直角三角形．问题解决:（1）按勤奋小组的这种折叠方式，CD 的长度为 ．（2）创新小组看完勤奋小组的折叠方法后，发现还有另一种折叠方法，请在图3中画出来． （3）在（2）的条件下，求出CD 的长． 【答案】（1）3；（2）见解析；（3）247CD = 【分析】（1）由勾股定理可求AB 的长，由折叠的性质可得AC=AE=6，CD=DE ，∵C=∵BED=90°，由勾股定理可求解；（2）如图所示，当DE∵AC，∵EDB=∵ACB=90°，即可得到答案；（3）由折叠的性质可得CF=EF，CD=DE，∵C=∵FED=90°，∵CDF=∵EDF=45°，可得DE=CD=CF=EF，通过证明∵DEB∵∵CAB，可得DE BD＝，即可求解．AC BC【详解】（1）∵∵ACB=90°，AC=6，BC=8，∵10AB=，由折叠的性质可得：∵ACD∵∵AED，∵AC=AE=6，CD=DE，∵C=∵BED=90°，∵BE=10-6=4，∵BD2=DE2+BE2，∵（8-CD）2=CD2+16，∵CD=3，故答案为：3；（2）如图3，当DE∵AC，∵BDE是直角三角形，（3）∵DE∵AC，∵∵ACB=∵BDE=90°，由折叠的性质可得：∵CDF∵∵EDF，∵CF=EF，CD=DE，∵C=∵FED=90°，∵CDF=∵EDF=45°，∵EF=DE，∵DE=CD=CF=EF，∵DE∵AC，∵∵DEB∵∵CAB，19∵DE BD AC BC ＝， ∵886DE DE -＝， ∵DE=247， ∵247CD =【点睛】此题考查几何变换综合题，全等三角形的性质，折叠的性质，相似三角形的判定和性质，勾股定理等知识，灵活运用这些性质进行推理是解题的关键．19．（2021·陕西西北工业大学附属中学九年级）如图，在平行四边形ABCD 中，E 为BC 边上一点，且B AEB ∠=∠．求证：AC DE =．【答案】证明见解析. 【详解】试题分析：由平行四边形的性质得：AB=DC ，180ABC BCD ∠+∠=︒，证得AEC BCD ∠=∠，从而可证AEC ∵DCE ，故可得结论.试题解析：∵四边形ABCD 是平行四边形， ∵AB DC =，180ABC BCD ∠+∠=︒． ∵AB DC =，∵ABE AEB ∠=∠，AE DC =． ∵180AEC AEB ∠+∠=︒， ∵AEC BCD ∠=∠． 又EC EC =， ∵AEC ∵DCE ， ∵AC ED =．20．（2021·广东九年级）如图，已知点E 、C 在线段BF 上，且BE =CF ，CM ∵DF ，（1）作图：在BC 上方作射线BN ，使∵CBN =∵1，交CM 的延长线于点A （用尺规作图法，保留作图痕迹，21不写作法）；（2）在（1）的条件下，求证：AC =DF ．【答案】（1）作图见解析；（2）证明见解析【详解】试题分析：（1）∵以E 为圆心，以EM 为半径画弧，交EF 于H ，∵以B 为圆心，以EM 为半径画弧，交EF 于P ，∵以P 为圆心，以HM 为半径画弧，交前弧于G ，∵作射线BG ，则∵CBN 就是所求作的角．（2）证明∵ABC ∵∵DEF 可得结论．试题解析：（1）如图，（2）∵CM ∵DF ，∵∵MCE =∵F ，∵BE =CF ，∵BE +CE =CF +CE ，即BC=EF ，在∵ABC 和∵DEF 中，∵1{CBN BC EF MCE F∠∠∠∠＝＝＝ ∵∵ABC ∵∵DEF ，∵AC =DF ．【点睛】本题考查了基本作图-作一个角等于已知角，同时还考查了全等三角形的性质和判定；熟练掌握五种基本作图：（1）作一条线段等于已知线段．（2）作一个角等于已知角．（3）作已知线段的垂直平分线．（4）作已知角的角平分线．（5）过一点作已知直线的垂线．21．定义：一条对角线垂直平分另一条对角线的四边形叫做筝形，如图，筝形ABCD 的对角线AC 、BD 相交于点O ．且AC 垂直平分BD ．（1）请结合图形，写出筝形两种不同类型的性质：性质1： ；性质2： ．（2）若AB ∵CD ，求证：四边形ABCD 为菱形．【答案】（1）对角线互相垂直，是轴对称图形；（2）见解析【分析】（1）由筝形的定义即可得出结论；（2）由垂直平分线的性质得出AB=AD ，BO=DO ，同理：BC=DC ，由AS 证明∵AOB∵∵CDO ，得出AB=CD ，因此AB=CD=BC=AD ，即可得出四边形ABCD 为菱形．【详解】解：（1）由筝形的定义得：对角线互相垂直，即AC∵BD ；是轴对称图形，对称轴为AC ；故答案为对角线互相垂直，是轴对称图形；（2）∵AC 垂直平分BD ，∵AB ＝AD ，BO ＝DO ，同理：BC ＝DC ，∵AB∵CD ，∵∵ABO ＝∵ODC ，在∵ABO 和∵CDO 中，ABO ODC BO DOAOB DOC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∵∵AOB∵∵CDO （ASA ），∵AB ＝CD ，∵AB ＝CD ＝BC ＝AD ，∵四边形ABCD 为菱形．【点睛】本题考查了菱形的判定、筝形的性质、线段垂直平分线的性质、全等三角形的判定与性质；熟练掌握筝形的性质，证明三角形全等是解题的关键．22．（2021·湖北黄石·）如图，D 是ABC 的边AB 上一点，//CF AB ， DF 交AC 于E 点，DE EF =．23（1）求证：ADE ∵CFE ；（2）若5AB =，4CF =，求BD 的长．【答案】（1）证明见详解；（2）1．【分析】（1）根据ASA 证明即可；（2）根据（1）可得ADE CFE ∆≅∆，即由AD CF =，根据BD AB AD AB CF 求解即可．【详解】（1）证明：//AB FC ，∴∠=∠ADE F ，在ADE ∆和CFE ∆中，ADE FDE EF AED CEFADE CFE ASA ；（2）由（1）得ADE CFE ∆≅∆AD CF ∴=∵541BD AB AD AB CF ．【点睛】本题考查全等三角形的判定和性质、平行线的性质等知识，熟练掌握基本知识是解题的关键． 23．（2021·江苏南京·南师附中新城初中）如图,在正方形ABCD 中,E ､F ､G ､H 分别是各边上的点,且AE BF CG DH ===．求证:（1）AHE BEF ≌△△; （2）四边形EFGH 是正方形．【答案】（1）见解析;（2）见解析【分析】（1）在正方形ABCD 中,由AE BF CG DH ===可得:AH BE CF DG ===,即可求证;（2）由（1）可用同样的方法证得EBF FCG △≌△,FCG GDH ≌△△,可得到FCG GDH ≌△△,然后证明90HEF ∠=︒,即可求证．【详解】（1）证明:∵四边形ABCD 为正方形,∵AB BC CD DA ===,90A B ∠=∠=︒．又∵AE BF DH CG ===,∵AH BE CF DG ===．∵()SAS AHE BEF ≌△△ （2）由（1）得,AHE BEF ≌△△, 同理,EBF FCG △≌△,FCG GDH ≌△△, ∵EF FG GH HE ===,AEH BFE ∠=∠,∵90B ∠=︒,∵90EFB FEB ∠+∠=︒,∵90AEH FEB ∠+∠=︒,∵90HEF ∠=︒,∵四边形EFGH 为正方形．【点睛】本题主要考查了正方形的性质和判定,三角全等的判断和性质,熟练掌握并会灵活应用相应知识点是解题的关键．25。

人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定微专题全等三角形应用的常见类型老师告诉你全等三角形的对应边相等、对应角相等，为我们提供了解决线段相等，角相等的新思路、新方法，因此，判定两个三角形全等是解决线段相等，角相等的问题的基础，全等三角形的判定和性质的应用是各类考试的必考内容之一，主要题型有证明线段、角相等关系、和差关系、位置关系等.类型一、全等三角形在证明线段相等角相等中的应用【典例剖析】例1-1．如图，在△ABC中，∠C=90°，BD是∠ABC的平分线，DE⊥AB于点E，点F在BC上，连接DF，且AD=DF．（Ⅰ）求证：CF=AE；（Ⅱ）若AE=3，BF=4，求AB的长．例1-2．如图，点B在线段AC上，BD∥CE，AB=EC，DB=BC．求证：AD=EB．【针对训练】1．已知：如图，AB∥DE，AB=DE，AF=DC．求证：∠B=∠E．2．如图，在中，，、分别为、上一点，．若，求证：．3．如图，CA=CD，CB=CE，AB=DE，AB与DE交于点M．（1）求证：∠ACD=∠BCE；（2）连MC，若∠BMC=78°，求∠BMD的度数．类型二、全等三角形在证明线段和差关系的应用【典例剖析】例2-1．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；例2-2．综合与实践：数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．（1）发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：_____，∠BDC=_____°；（2）类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；（3）拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：_____；【针对训练】1．已知：四边形中，，，，对角线相交于点O，且平分，过点A作，垂足为H．判断线段之间的数量关系：___________；并证明你的结论．2．如图1，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE．连结BE，CD，作AF⊥CD，垂足为F，交BE于点G．（1）若∠GAE=70°，求∠ADC的度数；（2）如图2，作EH⊥GF，垂足为H，HF=7，求EH+DF的长；（3）求证：BG=EG．3．如图，AD是△ABC的中线，BE⊥AD，垂足为E，CF⊥AD，交AD的延长线于点F，G是DA延长线上一点，连接BG．（1）求证：BE=CF；（2）若BG=CA，求证：GA=2DE．类型三、全等三角形在证明线段位置关系的应用【典例剖析】例3-1．如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．例3-2．已知AB=CD，AD=BC．求证：①AD∥BC；②∠B=∠D．【针对训练】1．两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC⊥BE．2．如图，，，，在同一条直线上，于点，于点，，，求证：．3．如图，点A ，B ，C ，D 在一条直线上，AB=CD ，CE ∥BF ，CE=BF ，求证：AE ∥DF ．类型四、全等三角形在线段或角的计算中的应用 【典例剖析】例4-1．如图，AB DC =，ABC DCB ∠=∠.（1）求证：BD CA =；（2）若62A ∠=︒，75ABC ∠=︒.求ACD ∠的度数.例4-2．如图，在 ABC △中，AD 是BC 边上的中线，E 是AB 边上一点，过点C 作//CF AB 交ED 的延长线于点F ，（1）求证：BDE CDF ≌△△；（2）当AD BC ⊥，1AE =，2CF =时，求AC 的长.【针对训练】1．如图.点A ，B ，C ，D 在同一条直线上，点E ，F 分别在直线AB 的两侧，且AE BF =，A B ∠=∠，ACE BDF ∠=∠.（1）求证：ACE BDF △△≌； （2）若8AB =，2AC =，求CD 的长.2．如图，四边ABCD 中，对角线AC 、BD 交于点O ，AB AC =，点E 是BD 上一点，且ABD ACD ∠=∠，EAD BAC ∠=∠.（1）求证：AE AD =；（2）若8BD =，5DC =，求ED 的长.3．如图,以ABC △的两边AC ,BC 为边分别向外作ADC △和BEC △,使得BCD ACE ∠=∠,CD CE =,D E ∠=∠.（1）求证:ADC BEC ≌△△;（2）若60CAD ∠=︒,110ABE ∠=︒,求ACB ∠的度数.4．如图,C 是线段AB 的中点,CD 平分ACE ∠,CE 平分BCD ∠,CD CE =.（1）求证:ACD BCE ≅△△; （2）若50D ∠=︒,求B ∠的度数.类型五、全等三角形在生活实际中的应用 【典例剖析】例5-1．小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点O 处用一根细绳悬挂一个小球A ，小球A 可以自由摆动，如图，OA 表示小球静止时的位置．当小明用发声物体靠近小球时，小球从OA 摆到OB 位置，此时过点B 作BD ⊥OA于点D ，当小球摆到OC 位置时，OB 与OC 恰好垂直（图中的A 、B 、O 、C 在同一平面上），过点C 作CE ⊥OA 于点E ，测得CE=15cm,OE=8cm. （1）试说明：OE=BD ； （2）求DE 的长．例5-2．如图，小明在游乐场玩两层型滑梯，每层楼梯的高度相同（EH=HD ），都为2.5米，他想知道左右两个滑梯BC 和EF 的长度是否相等，于是制定了如下方案：课题 探究两个滑梯的长度是否相等 测量工具长度为6米的米尺 测量步骤①测量出线段FD 的长度②测量出线段AB 的长度测量数据DF=2.5米，AB=5米（1）根据小明的测量方案和数据，判断两个滑梯BC 和EF 的长度是否相等？并说明理由． （2）试猜想左右两个滑梯BC 和EF 所在直线的位置关系，并加以证明．【针对训练】1．如图，小明站在堤岸凉亭A点处，正对他的S点停有一艘游艇，他想知道凉亭与这艘游艇之间的距离，于是制定了如下方案．课题测凉亭与游艇之间的距离测量工具皮尺等测量方案示意图测量步骤①小明沿堤岸走到电线杆B旁；②再往前走相同的距离，到达C点；③然后他向左直行，当看到电线杆与游艇在一条直线上时停下来．测量数据AB=10米，BC=10米，CD=5米（1）凉亭与游艇之间的距离是_____米．（2）请你说明小明做法的正确性．2．如图，这是王玲家的养鱼塘，王玲想要测量鱼塘的宽AB，请你帮助她设计一个不必下水而且简单可行的方案，并说明理由，要求在原图上画出该方案的示意图．3．雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．人教版八年级数学上名师点拨精练第12章全等三角形12.2 三角形全等的判定微专题全等三角形应用的常见类型（解析版）老师告诉你全等三角形的对应边相等、对应角相等，为我们提供了解决线段相等，角相等的新思路、新方法，因此，判定两个三角形全等是解决线段相等，角相等的问题的基础，全等三角形的判定和性质的应用是各类考试的必考内容之一，主要题型有证明线段、角相等关系、和差关系、位置关系等.类型一、全等三角形在证明线段相等角相等中的应用【典例剖析】例1-1．如图，在△ABC中，∠C=90°，BD是∠ABC的平分线，DE⊥AB于点E，点F在BC上，连接DF，且AD=DF．（Ⅰ）求证：CF=AE；（Ⅱ）若AE=3，BF=4，求AB的长．【解析】（Ⅰ）通过HL证明Rt△CDF≌Rt△EDA，即可得出结论；（Ⅱ）通过HL证明△BED≌△BCD，得BE=BC，再进行等量代换即可．证明：（Ⅰ）∵∠C=90°，AD是∠BAC的平分线，DE⊥AB，∴DE=DC，∠AED=90°，在Rt△CDF与Rt△EDA中，，∴Rt△CDF≌Rt△EDA（HL），∴CF=AE；（Ⅱ）∵CF=AE，AE=3，∴CF=3，∵BF=4，∴BC=BF+CF=4+3=7，∵DE⊥AB，∴∠DEB=90°，∵∠C=90°，∴∠DEB=∠C，∵BD是∠ABC的平分线，∴∠ABD=∠CBD，在△BED和△BCD中，，∴△BED≌△BCD（AAS），∴BE=BC=7，∴AB=BE+AE=7+3=10．例1-2．如图，点B在线段AC上，BD∥CE，AB=EC，DB=BC．求证：AD=EB．【解析】由平行线的性质可得∠A=∠EBC，由“AAS”可证△ABD≌△BEC，可得BD=EC．证明：∵BD∥CE，∴∠ABD=∠C，在△ABD和△ECB中，∴△ABD≌△ECB（SAS），∴AD=EB．【针对训练】1．已知：如图，AB∥DE，AB=DE，AF=DC．求证：∠B=∠E．【解析】由AF=DC，得AC=DF，由AB∥DE，得∠A=∠D，即可证△ABC≌△DEF（SAS），故∠B=∠E．证明：∵AF=DC，∴AF+CF=DC+CF，即AC=DF，∵AB∥DE，∴∠A=∠D，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS），∴∠B=∠E．2．如图，在中，，、分别为、上一点，．若，求证：．【答案】见解析【解析】先根据条件得出，，再根据判定，即可得到．解：证明：，，，，，，，在与中，，，．【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的性质等知识；熟练掌握等腰三角形的性质，证明三角形全等是解题的关键．3．如图，CA=CD，CB=CE，AB=DE，AB与DE交于点M．（1）求证：∠ACD=∠BCE；（2）连MC，若∠BMC=78°，求∠BMD的度数．【解析】（1）根据SSS证明△ABC≌△DEC，进而利用全等三角形的性质解答即可；（2）根据AAS证明△AGC≌△DHC，进而利用全等三角形的性质解答即可．证明：（1）在△ABC和△DEC中，，∴△ABC≌△DEC（SSS），∴∠ACB=∠DCE，∴∠ACD=∠BCE；（2）过C作CG⊥AB于G，CH⊥DE于H，∵△ABC≌△DEC，∴∠A=∠D，AC=DC，∵∠AGC=∠DHC=90°，在△AGC和△DHC中，，∴△AGC≌△DHC（AAS），∴CG=CH，∴MC平分∠BMD，∴∠BMD=2∠BMC=2×78°=156°．类型二、全等三角形在证明线段和差关系的应用【典例剖析】例2-1．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD-BE；【解析】（1）①由已知推出∠ADC=∠BEC=90°，因为∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，推出∠DAC=∠BCE，根据AAS即可得到答案；②由（1）得到AD=CE，CD=BE，即可求出答案；（2）与（1）证法类似可证出∠ACD=∠EBC，能推出△ADC≌△CEB，得到AD=CE，CD=BE，代入已知即可得到答案．（1）①证明：∵AD⊥DE，BE⊥DE，∴∠ADC=∠BEC=90°，∵∠ACB=90°，∴∠ACD+∠BCE=90°，∠DAC+∠ACD=90°，∴∠DAC=∠BCE，在△ADC和△CEB中，∴△ADC≌△CEB（AAS）．②证明：由（1）知：△ADC≌△CEB，∴AD=CE，CD=BE，∵DC+CE=DE，∴AD+BE=DE．（2）证明：∵BE⊥EC，AD⊥CE，∴∠ADC=∠BEC=90°，∴∠EBC+∠ECB=90°，∵∠ACB=90°，∴∠ECB+∠ACE=90°，∴∠ACD=∠EBC，在△ADC和△CEB中，∴△ADC≌△CEB（AAS），∴AD=CE，CD=BE，∴DE=EC-CD=AD-BE．例2-2．综合与实践：数学模型可以用来解决一类问题，是数学应用的基本途径．通过探究图形的变化规律，再结合其他数学知识的内在联系，最终可以获得宝贵的数学经验，并将其运用到更广阔的数学天地．（1）发现问题：如图1，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=30°，连接BE，CF，延长BE交CF于点D．则BE与CF的数量关系：_____，∠BDC=_____°；（2）类比探究：如图2，在△ABC和△AEF中，AB=AC，AE=AF，∠BAC=∠EAF=120°，连接BE，CF，延长BE，FC交于点D．请猜想BE与CF的数量关系及∠BDC的度数，并说明理由；（3）拓展延伸：如图3，△ABC和△AEF均为等腰直角三角形，∠BAC=∠EAF=90°，连接BE，CF，且点B，E，F在一条直线上，过点A作AM⊥BF，垂足为点M．则BF，CF，AM之间的数量关系：_____；【答案】(1)BE=CF;(2)30;(3)BF=CF+2AM;【解析】（1）根据等腰三角形的性质，利用SAS证明△ABE≌△ACF即可得出结论；（2）根据等腰三角形的性质，利用SAS证明△BAE≌△CAF即可得出结论；（3）根据等腰直角三角形的性质，利用SAS证明△BAE≌△CAE即可得出结论；（4）根据直径所对的圆周角是直角，先找到点P，利用勾股定理计算出BP，再利用第3小题的结论得到三角形的高，△ABP的面积即可求出．解：（1）BE=CF，∠BDC=30°，理由如下：如图1所示：∵△ABC和△ADE都是等腰三角形，∴AB=AC，AE=AF，又∵∠BAC=∠EAF=30°，∴△ABE≌△ACF（SAS），∴BE=CF，∴∠ABE=∠ACD，∵∠AOE∠ABE+∠BAC，∠AOE=∠ACD+∠BDC，∴∠BDC=∠BAC=30°；（2）BE=CF，∠BDC=60°，理由如下：如图2所示：证明：∵∠BAC=∠EAF=120°，∴∠BAC-∠EAC=∠EAF-∠EAC，即∠BAE=∠CAF，又∵△ABC和△AEF都是等腰三角形，∴AB=AC，AE=AF，∴△BAE≌△CAF（SAS）∴BE=CF，∴∠AEB=∠AFC，∵∠EAF=120°，AE=AF，∴∠AEF=∠AFE=30°，∴∠BDC=∠BEF-∠EFD=∠AEB+30°-（∠AFC-30°）=60°；（3）BF=CF+2AM，理由如下：如图3所示：∵△ABC和△AEF都是等腰三角形，∴∠CAB=∠EAF=90°，AB=AC，AE=AF，∴∠CAB-∠CAE=∠FAE-∠CAE，即：∠BAE=∠CAF，∴△BAE≌△CAE（SAS），∴BE=CF，∵AM⊥BF，AE=AF，EAF=90°，∴EF=2AM，∵BF=BE+EF，∴BF=CF+2AM；【针对训练】1．已知：四边形中，，，，对角线相交于点O，且平分，过点A作，垂足为H．判断线段之间的数量关系：___________；并证明你的结论．【答案】，证明见解析【解析】先证明是等边三角形，再证明，最后根据三角形内角和定理证明，在上截取，先证明，得出，再证明，得出，即可解决问题．，证明：∵，，∴是等边三角形，∴，∵，平分，∴，∴，∵，，，∴，在上截取，∵，∴，又，∴，∴，∴∵，∴，∴，∵，∴．【点睛】此题主要考查了全等三角形的判定和性质、等边三角形的判定和性质，三角形内角和定理，角平分线的定义等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．2．如图1，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE．连结BE，CD，作AF⊥CD，垂足为F，交BE于点G．（1）若∠GAE=70°，求∠ADC的度数；（2）如图2，作EH⊥GF，垂足为H，HF=7，求EH+DF的长；（3）求证：BG=EG．【解析】（1）由∠ADC+∠DAF=90°，∠GAE+∠DAF=90°，得∠ADC=∠GAE=70°；（2）可证明△EAH≌△ADF，EH=AF，AH=DF，则EH+DF=AF+AH=HF=7；（3）作EH⊥FG于点H，BI⊥FG交FG的延长线于点I，可证明△BAI≌△ACF，得BI=AF，而EH=AF，所以BI=EH，可证明△BGI≌△EGH，则BG=EG．（1）解：如图1，∵AF⊥CD，∴∠AFD=90°，∴∠ADC+∠DAF=90°，∵∠DAE=90°，∴∠GAE+∠DAF=90°，∴∠ADC=∠GAE=70°，∴∠ADC的度数是70°．（2）解：如图2，∵EH⊥GF，∴∠EHA=∠AFD=90°，由（1）得∠EAH=∠ADF，在△EAH和△ADF中，，∴△EAH≌△ADF（AAS），∴EH=AF，AH=DF，∴EH+DF=AF+AH=HF=7，∴EH+DF的长是7．（3）证明：如图3，作EH⊥FG于点H，BI⊥FG交FG的延长线于点I，∴∠I=∠EHG=∠AFC=90°，∵∠BAC=90°，∴∠BAI=∠ACF=90°-∠CAF，在△BAI和△ACF中，，∴△BAI≌△ACF（AAS），∴BI=AF，由（2）得EH=AF，∴BI=EH，在△BGI和△EGH中，，∴△BGI≌△EGH（AAS），∴BG=EG．3．如图，AD是△ABC的中线，BE⊥AD，垂足为E，CF⊥AD，交AD的延长线于点F，G是DA延长线上一点，连接BG．（1）求证：BE=CF；（2）若BG=CA，求证：GA=2DE．【解析】（1）利用AAS证明△BED≌△CFD，得BE=CF；（2）利用HL证明Rt△BGE≌Rt△CAF，得GE=AF，从而解决问题．证明：（1）∵AD是△ABC的中线，∴BD=CD，∵BE⊥AD，CF⊥AD，∴∠BED=∠F，在△BED和△CFD中，，∴△BED≌△CFD（AAS），∴BE=CF；（2）在Rt△BGE和Rt△CAF中，，∴Rt△BGE≌Rt△CAF（HL），∴GE=AF，∴AG=EF．∵△BED≌△CFD，∴DE=DF，∴GA=2DE．类型三、全等三角形在证明线段位置关系的应用【典例剖析】例3-1．如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC．CF平分∠DCE．求证：（1）△ACD≌△BEC；（2）CF⊥DE．【解析】（1）根据平行线性质求出∠A=∠B，根据SAS推出即可．（2）根据全等三角形性质推出CD=CE，根据等腰三角形性质求出即可．证明：（1）∵AD∥BE，∴∠A=∠B，在△ACD和△BEC中∴△ACD≌△BEC（SAS），（2）∵△ACD≌△BEC，∴CD=CE，又∵CF平分∠DCE，∴CF⊥DE．例3-2．已知AB=CD，AD=BC．求证：①AD∥BC；②∠B=∠D．【解析】①连接AC，由AB=CD，BC=DA，AC=CA，根据全等三角形的判定定理“SSS”证明△ABC≌△CDA，得∠ACB=∠CAD，则AD∥BC；②由△ABC≌△CDA，得∠B=∠D．证明：①连接AC，在△ABC和△CDA中，，∴△ABC≌△CDA（SSS），∴∠ACB=∠CAD，∴AD∥BC．②△ABC≌△CDA，∴∠B=∠D．【针对训练】1．两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC．（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC⊥BE．【解析】（1）根据等腰直角三角形的性质，可以得出△ABE≌△ACD；（2）由△ABE≌△ACD可以得出∠B=∠ACD-45°，进而得出∠DCB=90°，就可以得出结论．（1）△ABE≌△ACD．证明：∵△ABC与△AED均为等腰直角三角形，∴AB=AC，AE=AD，∠BAC=∠EAD=90°．∴∠BAC+∠CAE=∠EAD+∠CAE．即∠BAE=∠CAD，在△ABE与△ACD中，，∴△ABE≌△ACD；（2）证明∵△ABE≌△ACD，∴∠ACD=∠ABE=45°，又∵∠ACB=45°，∴∠BCD=∠ACB+∠ACD=90°，∴DC⊥BE．2．如图，，，，在同一条直线上，于点，于点，，，求证：．【答案】见解析【解析】先证明，利用全等三角形的性质解题即可．证明：∵，∴，又∵∴在和中，，∴∴∴【点睛】本题考查全等三角形的判定和性质，平行线的判定，掌握全等三角形的判定方法是解题的关键．3．如图，点A，B，C，D在一条直线上，AB=CD，CE∥BF，CE=BF，求证：AE∥DF．【解析】根据平行线的性质得出∠ACE=∠DBF，求出AC=BD，根据全等三角形的判定得出△AEC≌△DFB，根据全等三角形的性质得出∠A=∠D，根据平行线的判定得出即可．证明：∵CE∥BF，∴∠ACE=∠DBF，∵AB=CD，∴AB+BC=CD+BC，即AC=BD ，在△AEC 和△DFB 中，，∴△AEC ≌△DFB （SAS ）， ∴∠A=∠D ， ∴AE ∥DF ．类型四、全等三角形在线段或角的计算中的应用 【典例剖析】例4-1．如图，AB DC =，ABC DCB ∠=∠.（1）求证：BD CA =；（2）若62A ∠=︒，75ABC ∠=︒.求ACD ∠的度数. 答案：（1）见详解 （2）32︒解析：（1）证明：在ABC △与DBC △中，AB DC ABC DCB BC CB ∠∠⎧⎪⎨⎪⎩＝＝＝， ()SAS ABC DCB ∴≌△△，BD CA ∴=；（2）ABC DCB ≌△△，75ABC ∠=︒75ABC DCB ∴∠=∠=︒， 62A ∠=︒，75ABC ∠=︒. 180756243ACB ∴∠=︒-︒-︒=︒，754332ACD DCB ACB ∴∠=∠-∠=︒-︒=︒.例4-2．如图，在 ABC △中，AD 是BC 边上的中线，E 是AB 边上一点，过点C 作//CF AB 交ED 的延长线于点F ，（1）求证：BDE CDF ≌△△；（2）当AD BC ⊥，1AE =，2CF =时，求AC 的长. （1）答案：见解析 解析：//CF AB ，B FCD ∴∠=∠，BED F ∠=∠，AD 是BC 边上的中线，BD CD ∴=， BDE CDF∴≌△△；（2）答案：3解析：BDE CDF≌△△， 2BE CF ∴==，123AB AE BE ∴=+=+=， AD BC ⊥，BD CD =， 3AC AB ∴==.【针对训练】1．如图.点A ，B ，C ，D 在同一条直线上，点E ，F 分别在直线AB 的两侧，且AE BF =，A B ∠=∠，ACE BDF ∠=∠.（1）求证：ACE BDF △△≌；（2）若8AB =，2AC =，求CD 的长. 答案：（1）见解析 （2）4解析：（1）在ACE △和BDF △中，ACE BDF A BAE BF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()AAS ACE BDF ∴△△≌；（2）ACE BDF ≌△△，2AC =，2BD AC ∴==，又8AB =，4CD AB AC BD ∴=--=.2．如图，四边ABCD 中，对角线AC 、BD 交于点O ，AB AC =，点E 是BD 上一点，且ABD ACD ∠=∠，EAD BAC ∠=∠.（1）求证：AE AD =；（2）若8BD =，5DC =，求ED 的长. 答案：（1）见解析 （2）3 解析：（1）BAC EAD ∠=∠，BAC EAC EAD EAC ∴∠-∠=∠-∠，即：BAE CAD ∠=∠， 在ABE △和ACD △中，ABD ACD AB ACBAE CAD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ASA ABE ACD ∴≌△△，AE AD ∴=；（2）()ASA ABE ACD ≌△△，BE CD ∴=， 8BD =，5DC =，853ED BD BE BD CD ∴=-=-=-=.3．如图,以ABC △的两边AC ,BC 为边分别向外作ADC △和BEC △,使得BCD ACE ∠=∠,CD CE =,D E ∠=∠.（1）求证:ADC BEC ≌△△;（2）若60CAD ∠=︒,110ABE ∠=︒,求ACB ∠的度数. 答案：（1）见解析 （2）80︒ 解析:（1）证明:BCD ACE ∠=∠,BCD ACB ACE ACB ∴∠-∠=∠-∠,即ACD BCE ∠=∠. 又CD CE =,D E ∠=∠,()ADC BEC ASA ∴△≌△;（2）由（1）得ADC BEC △≌△,60CBE CAD ∴∠=∠=︒,AC BC =, CAB CBA ∴∠=∠. 110ABE ∠=︒,1106050CAB CBA ABE CBE ∴∠=∠=∠-∠=︒-︒=︒, 180180505080ACB CAB CBA ∴∠=︒-∠-∠=︒-︒-︒=︒.4．如图,C 是线段AB 的中点,CD 平分ACE ∠,CE 平分BCD ∠,CD CE =.（1）求证:ACD BCE ≅△△; （2）若50D ∠=︒,求B ∠的度数. 答案：（1）证明见解析; （2）70︒. 解析:（1）点C 是线段AB 的中点,AC BC ∴=,又CD 平分ACE ∠,CE 平分BCD ∠,12∴∠=∠,23∠=∠,13∴∠=∠在ACD △和BCE △中,13CD CE AC BC =⎧⎪∠=∠⎨⎪=⎩ACD BCE ∴≅△△（2）123180∴∠+∠+∠=︒12360∴∠=∠=∠=︒ ACD BCE ≅△△ 50E D ∴∠=∠=︒180370B E ∴∠=-∠-∠=︒︒.类型五、全等三角形在生活实际中的应用 【典例剖析】例5-1．小明在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：在一个支架的横杆点O 处用一根细绳悬挂一个小球A ，小球A 可以自由摆动，如图，OA 表示小球静止时的位置．当小明用发声物体靠近小球时，小球从OA 摆到OB 位置，此时过点B 作BD ⊥OA于点D ，当小球摆到OC 位置时，OB 与OC 恰好垂直（图中的A 、B 、O 、C 在同一平面上），过点C 作CE ⊥OA 于点E ，测得CE=15cm,OE=8cm. （1）试说明：OE=BD ； （2）求DE 的长．【解析】（1）利用AAS 证明△COE ≌△OBD ，可得结论；（2）利用全等三角形性质可得答案．解：（1）∵OB⊥OC，∴∠BOD+∠COE=90°，∵CE⊥OA，BD⊥OA，∴∠CEO=∠ODB=90°，∴∠BOD+∠B=90°，∴∠COE=∠B，∵OC=BO，∴△COE≌△OBD（AAS），∴OE=BD；（2）∵△COE≌△OBD，∴CE=OD=15cm,∴DE=OD-OE=7cm.例5-2．如图，小明在游乐场玩两层型滑梯，每层楼梯的高度相同（EH=HD），都为2.5米，他想知道左右两个滑梯BC和EF的长度是否相等，于是制定了如下方案：课题探究两个滑梯的长度是否相等测量工具长度为6米的米尺①测量出线段FD的长度测量步骤②测量出线段AB的长度测量数据DF=2.5米，AB=5米（1）根据小明的测量方案和数据，判断两个滑梯BC和EF的长度是否相等？并说明理由．（2）试猜想左右两个滑梯BC和EF所在直线的位置关系，并加以证明．【解析】（1）证明△BAC≌△EDF（SAS），由全等三角形的性质得出BC=EF；（2）延长BC交EF于点M，由全等三角形的性质得出∠BMF=90°，则可得出结论．解：（1）BC=EF．理由：∵EH=DH=2.5米，∴ED=5米，∴AB=DE，由题意可知四边形CADH为矩形，∴CA=DH=2.5米，∵DF=2.5米，∴CA=DF，∵∠BAC=∠EDF=90°，∴△BAC≌△EDF（SAS），∴BC=EF；（2）BC⊥EF．理由：延长BC交EF于点M，∵∠EDF=90°，∴∠F+∠EDF=90°，∵△BAC≌△EDF，∴∠B=∠DEF，∴∠B+∠F=90°，∴∠BMF=90°，∴EF⊥BM．【针对训练】1．如图，小明站在堤岸凉亭A点处，正对他的S点停有一艘游艇，他想知道凉亭与这艘游艇之间的距离，于是制定了如下方案．课题测凉亭与游艇之间的距离测量工具皮尺等测量方案示意图测量步骤①小明沿堤岸走到电线杆B旁；②再往前走相同的距离，到达C点；③然后他向左直行，当看到电线杆与游艇在一条直线上时停下来．测量数据AB=10米，BC=10米，CD=5米（1）凉亭与游艇之间的距离是_____米．（2）请你说明小明做法的正确性．【答案】5【解析】根据全等三角形的判定和性质即可得到结论．解：（1）凉亭与游艇之间的距离是5米；故答案为：5．（2）理由：在△ABS与△CBD中，，∴△ABS≌△CBD（ASA），∴AS=CD=5米．2．如图，这是王玲家的养鱼塘，王玲想要测量鱼塘的宽AB，请你帮助她设计一个不必下水而且简单可行的方案，并说明理由，要求在原图上画出该方案的示意图．【解析】方案设计为：从A点出发沿与AB垂直的方向到C点，再沿AC方向走到D点，使CD=AC，接着从B点出发，沿与AD垂直的方向走到E点，使E、C、B共线，则测出DE的长解能得到AB 的宽；然后根据全等三角形的判断方法证明△ACB≌△DCE，从而得到AB=DE．解：方案设计为：从A点出发沿与AB垂直的方向到C点，再沿AC方向走到D点，使CD=AC，接着从B点出发，沿与AD垂直的方向走到E点，使E、C、B共线，则测出DE的长解能得到AB的宽．理由如下：∵AD⊥AB，BE⊥AD，∴∠BAC=∠EDC，∵∠BCA=∠ECD，AC=DC，∴△ACB≌△DCE（ASA），∴AB=DE．3．雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．【解析】∠BAD与∠CAD相等，证角相等，常常通过把角放到两个全等三角形中来证，本题OA=OA公共边，可考虑SSS证明三角形全等，从而推出角相等．解：雨伞开闭过程中二者关系始终是：∠BAD=∠CAD，理由如下：∵AB=AC，AE=AB，AF=AC，∴AE=AF，在△AOE与△AOF中，，∴△AOE≌△AOF（SSS），∴∠BAD=∠CAD．。

附典型题解答：例1：在△DEF中，DE=DF，点B在EF边上，且△EBD=60°，C是射线BD上的一个动点（不与点B重合，且BC≠BE），在射线BE上截取BA=BC，连接AC．（1）当点C在线段BD上时，△若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系；△如图2，若点C不与点D重合，请证明AE=BF+CD；（2）当点C在线段BD的延长线上时，用等式表示线段AE，BF，CD之间的数量关系（直接写出结果，不需要证明）．分析：（1）△如图1，根据已知条件得到△ABC是等边三角形，由等边三角形的性质得到AD=AB=BC，△DAB=△ABC=60°，由邻补角的性质得到△EAD=△FBD=120°，推出△ADE△△BDF，根据全等三角形的性质即可得到结论；△证明：在BE上截取BG=BD，连接DG，得到△GBD是等边三角形．同理，△ABC也是等边三角形．求得AG=CD，通过△DGE△△DBF，得到GE=BF，根据线段的和差即可得到结论；（2）如图3，连接DG，由（1）知，GE=BF，AG=CD，根据线段的和差和等量代换即可得到结论；如图4，连接DG，由（1）知，GE=BF，AG=CD，根据线段的和差和等量代换即可得到结论．解：（1）△如图1，△BA=BC，△EBD=60°，△△ABC是等边三角形，△AD=AB=BC，△DAB=△ABC=60°，△△EAD=△FBD=120°，△DE=DF，△△E=△F，在△AEC 与△BCF 中，⎪⎩⎪⎨⎧=∠=∠∠=∠BD AD FBDEAD FE △△ADE△△BDF ，△AE=BF ； 故答案为：AE=BF ；△证明：如图2，在BE 上截取BG=BD ，连接DG ， △△EBD=60°，BG=BD ， △△GBD 是等边三角形．同理，△ABC 也是等边三角形．△AG=CD ， △DE=DF ，△△E=△F ． 又△△DGB=△DBG=60°， △△DGE=△DBF=120°，在△DGE 与△DBF 中，⎪⎩⎪⎨⎧=∠=∠∠=∠BD DG FBD EGD F E △△DGE△△DBF ，△GE=BF ， △AE=BF+CD ； （2）如图3，连接DG ，由（1）知，GE=BF ，AG=CD ， △AE=EG -AG ；△AE=BF -CD ， 如图4，连接DG ，由（1）知，GE=BF ，AG=CD ，△AE=AG -EG ； △AE=CD -BF ．点评 ：本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的性质，正确的作出辅助线是解题的关键．例2：在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）如图1，当点D在线段BC上时，如果∠BAC=90°，则∠BCE= 度；（2）设∠BAC=α，∠BCE=β，∠BAC≠90°时①如图2，当点D在线段BC上移动，则α、β之间有怎样的数量关系？请说明理由；②当点D在线段BC的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时α与β之间的数量关系（不需证明）．证明．（3）当点D在线段BC的反向延长线上移动时，请在图（3）中画出完整图形并猜想角α与β之间的数量关系是___，线段BC、DC、CE之间的数量关系是___，并写出证明过程．解：（1）如图1，△BCE=90°，故答案为90（2）①当点D在线段BC上移动，α+β=180°；理由如下：∵∠DAE=∠BAC，∴∠DAE-∠DAC=∠BAC-∠DAC，∴∠CAE=∠BAD，在△ABD和△ACE中，⎪⎩⎪⎨⎧=∠=∠=AEADCAEBADACAB∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，∵∠BAC+∠ABD+∠ACB=180°，∴∠BAC+∠ACE+∠ACB=180°，∴∠BAC+∠BCE=180°，即α+β=180°；②当点D在线段BC的延长线上α=β；理由如下：∵∠DAE=∠BAC，∴∠DAE+∠CAD=∠BAC+∠CAD，∴∠BAD=∠CAE，在△BAD和△CAE中，⎪⎩⎪⎨⎧=∠=∠=AEADCAEBADACAB∴△ABD ≌△ACE （SAS ）， ∴∠ABD=∠ACE ，BD=CE ，∵∠ACD=∠ABD+∠BAC=∠ACE+∠DCE ， ∴∠BAC=∠DCE ，即α=β；（3）当点D 在线段BC 的反向延长线上移动时，α>β，BC+CD>CE ；如图所示：连接BE ， ∵∠DAE=∠BAC ，∴∠DAE+∠DAB=∠BAC+∠DAB ， ∴∠BAE=∠CAD ，在△BAE 和△CAD 中，⎪⎩⎪⎨⎧=∠=∠=AD AE CAD BAE ACAB∴△BAE ≌△CAD （SAS ）， ∴∠ABE=∠ACD ，BE=CD ， ∵AB=AC ， ∴∠ABC=∠ACB ，∵∠ABC+∠ABE+∠DBE=180°，∠BAC+∠ABC+∠ACB=180°， ∴∠DBE=∠BAC=α， ∵∠DBE>∠BCE=β， ∴α>β， ∵BC+BE>CE ， ∴BC+CD>CE ．点评：该题主要考查了等腰直角三角形的性质、全等三角形的判定及其性质等几何知识点及其应用问题；应牢固掌握等腰直角三角形的性质、全等三角形的判定及其性质等几何知识点例3：在△ABC中，AB=AC，射线BM、BN在△ABC内部，分别交线段AC于点G、H。

(文末带解析)八年级数学全等三角形典型例题及答题技巧单选题1、如图，已知AB∥DC ， AD∥BC ， BE=DF，则图中全等三角形的总对数是A．3B．4C．5D．62、工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在∠AOB的两边OA、OB上分别在取OC=OD，移动角尺，使角尺两边相同的刻度分别与点C、D重合，这时过角尺顶点M的射线OM就是∠AOB的平分线．这里构造全等三角形的依据是（）A．SAS B．ASA C．AAS D．SSS3、小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1、2、3、4的四块），你认为将其中的哪一些块带去，就能配一块与原来一样大小的三角形？应该带（）A．第1块B．第2块 C．第3块D．第4块4、如图，B，C，E，F四点在一条直线上，下列条件能判定△ABC与△DEF全等的是（）A．AB∥DE，∠A=∠D，BE=CF B．AB∥DE，AB=DE，AC=DFC．AB∥DE，AC=DF，BE=CF D．AB∥DE，AC∥DF，∠A=∠D5、如图，△ABC和△EDF中，∠B＝∠D＝90°，∠A＝∠E，点B，F，C，D在同一条直线上，再增加一个条件，不能判定△ABC≌△EDF的是( )A．AB＝EDB．AC＝EFC．AC∥EFD．BF＝DC6、有一个小口瓶（如图所示），想知道它的内径是多少，但是尺子不能伸到里边直接测，于是拿两根长度相同的细木条，把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（）A．边角边B．角边角C．边边边D．角角边7、如图是作ΔABC的作图痕迹，则此作图的已知条件是（）A．已知两边及夹角B．已知三边C．已知两角及夹边D．已知两边及一边对角8、有一个小口瓶（如图所示），想知道它的内径是多少，但是尺子不能伸到里边直接测，于是拿两根长度相同的细木条，把两根细木条的中点固定在一起，木条可以绕中点转动，这样只要量出AB的长，就可以知道玻璃瓶的内径是多少，那么△OAB≌△OCD理由是（）A．边角边B．角边角C．边边边D．角角边填空题9、如图，若△ABC≌△A1B1C1，且∠A＝110°，∠B＝40°，则∠C1＝______°．10、已知△ABC≌△DEF，BC=EF=5cm，△ABC的面积是20cm2，那么△DEF中EF边上的高是______cm．11、如图，在△ABC中，已知AD是△ABC的角平分线，作DE⊥AB，已知AB＝4，AC＝2，△ABD的面积是2，则△ADC的面积为___．12、如图，△ABC≌△DEF，BE＝5，BF＝1，则CF＝_____．13、如图，AB⊥BC于B，DC⊥BC于C，AB=6，BC=8，CD=2，点P为BC边上一动点，当BP＝________时，形成的R t△ABP与R t△PCD全等．解答题14、已知：如图，点A、B、C、D在一条直线上，EA//FB,EA=FB,AB=CD．（1）求证：△ACE≌△BDF；（2）若∠A=40,∠D=80°，求∠E的度数．15、如图，三角形纸片中，AB=8cm，BC=6cm，AC=5cm．沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，求△ADE的周长(文末带解析)八年级数学全等三角形_00A参考答案1、答案：D解析：根据全等三角形的判定方法进行判断．全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件．解：∵AB∥DC，AD∥BC，∴∠DAC=∠BCA，∠CDB=∠ABD，∠DCA=∠BAC，∠ADB=∠CBD，又∵BE=DF，∴由∠ADB=∠CBD，DB=BD，∠ABD=∠CDB，可得△ABD≌△CDB；由∠DAC=∠BCA，AC=CA，∠DCA=∠BAC，可得△ACD≌△CAB；∴AO=CO，DO=BO，由∠DAO=∠BCO，AO=CO，∠AOD=∠COB，可得△AOD≌△COB；由∠CDB=∠ABD，∠COD=∠AOB，CO=AO，可得△COD≌△AOB；由∠DCA=∠BAC，∠COF=∠AOE，CO=AO，可得△AOE≌△COF；由∠CDB=∠ABD，∠DOF=∠BOE，DO=BO，可得△DOF≌△BOE；故选D．小提示：本题主要考查了全等三角形的判定与性质的运用，解题时注意：若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，或者是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．2、答案：D解析：根据全等三角形的判定条件判断即可．解：由题意可知OC=OD,MC=MD在△OCM和△ODM中{OC=OD OM=OM MC=MD∴△OCM≅△ODM(SSS)∴∠COM=∠DOM∴OM就是∠AOB的平分线故选：D小提示：本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键．3、答案：B解析：本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．解：1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素，所以不能带它们去，只有第2块有完整的两角及夹边，符合ASA，满足题目要求的条件，是符合题意的．故选：B．小提示：本题主要考查三角形全等的判定，看这4块玻璃中哪个包含的条件符合某个判定．判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．4、答案：A解析：根据全等三角形的判定条件逐一判断即可．解：A、∵AB∥DE，∴∠ABC=∠DEF，∵BE=CF，∴BE+CE=CF+CE，即BC=EF在△ABC和△DEF中∵{∠A=∠D∠ABC=∠DEFBC=EF∴△ABC≌△DEF(AAS)，故A符合题意；B、∵AB∥DE，∴∠ABC=∠DEF，再由AB=DE，AC=DF，不可以利用SSA证明两个三角形全等，故B不符合题意；C、∵AB∥DE，∴∠ABC=∠DEF，再由AC=DF，BE=CF，不可以利用SSA证明两个三角形全等，故C不符合题意；D、∵AB∥DE,AC∥DF，∴∠ACB=∠DFE，∠ABC=∠DEF，再由∠A=∠D，不可以利用AAA证明两个三角形全等，故D不符合题意；故选A．小提示：本题主要考查了全等三角形的判定，熟知全等三角形的判定条件是解题的关键．5、答案：C解析：根据全等三角形的判定方法即可判断.A. AB＝ED，可用ASA判定△ABC≌△EDF；B. AC＝EF，可用AAS判定△ABC≌△EDF；C. AC∥EF，不能用AAA判定△ABC≌△EDF，故错误；D. BF＝DC，可用AAS判定△ABC≌△EDF；故选C.小提示：此题主要考查全等三角形的判定，解题的关键是熟知全等三角形的判定方法. 6、答案：A解析：OC=OA,∠AOB=∠COD,OB=OD,根据SAS得：△OAB≌△OCD.则AB=CD.故选A.7、答案：C解析：观察ΔABC的作图痕迹，可得此作图的条件.解：观察ΔABC的作图痕迹，可得此作图的已知条件为：∠α，∠β，及线段AB, 故已知条件为：两角及夹边，故选C.小提示：本题主要考查三角形作图及三角形全等的相关知识.8、答案：A解析：OC=OA,∠AOB=∠COD,OB=OD,根据SAS得：△OAB≌△OCD.则AB=CD.故选A.9、答案：30解析：本题实际上是全等三角形的性质以及根据三角形内角和等于180°来求角的度数．∵△ABC≌△A1B1C1，∴∠C1=∠C，又∵∠C=180°-∠A-∠B=180°-110°-40°=30°，∴∠C1=∠C=30°．故答案为30．小提示：本题考查了全等三角形的性质；解答时，除必备的知识外，还应将条件和所求联系起来，即将所求的角与已知角通过全等及三角形内角之间的关系联系起来．10、答案：8解析：利用全等三角形对应边相等，以及对应边上的高也相等，利用面积法求出EF边上的高即可．解：∵△ABC≌△DEF，BC=EF=5cm，△ABC的面积是20cm2，∴1BC•h=20，即h=8，2则△DEF中EF边上的高是8cm，所以答案是：8．小提示：此题考查了全等三角形的性质，熟练掌握全等三角形的性质是解本题的关键．11、答案：1解析：先根据三角形面积公式计算出DE= 1，再根据角平分线的性质得到点D到AB和AC的距离相等，然后利用三角形的面积公式计算△ADC的面积．∵DE⊥AB，∴S△ABD=1× DE × AB= 2，2∴DE=2×2=1，4∵AD是△ABC的角平分线，∴点D到AB和AC的距离相等，∴点D到AC的距离为1，∴S△ADC=1×2×1= 1．2所以答案是：1．小提示：本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等，属于基础题，熟练掌握角平分线的性质是解题的关键．12、答案：3解析：先利用线段和差求EF＝BE﹣BF＝4，根据全等三角形的性质BC=EF，再结合线段和差求出FC 可得答案．解：∵BE＝5，BF＝1，∴EF＝BE﹣BF＝4，∵△ABC≌△DEF，∴BC＝EF＝4，∴CF＝BC﹣BF＝4-1=3，所以答案是：3．小提示：本题考查全等三角形的性质，线段和差,解题的关键是根据全等三角形的性质得出BC=EF．13、答案：2解析：当BP=2时，R t△ABP≌R t△PCD，由BC=8可得CP=6，进而可得AB=CP，BP=CD，再结合AB⊥BC、DC⊥BC可得∠B=∠C=90°，可利用SAS判定△ABP≌△PCD．当BP=2时，R t△ABP≌R t△PCD．理由如下：∵BC=8，BP=2，∴PC=6，∴AB=PC．∵AB⊥BC，DC⊥BC，∴∠B=∠C=90°．在△ABP和△PCD中，∵{AB=PC=6∠B=∠C=90°BP=CD=2，∴△ABP≌△PCD(SAS)．所以答案是：2．小提示：本题考查了全等三角形的判定，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）是解题的关键．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角相等时，角必须是两边的夹角．14、答案：（1）见解析；（2）60°解析：（1）首先利用平行线的性质得出，∠A=∠FBD，根据AB=CD即可得出AC=BD，进而得出△EAC≌△FBD即可；（2）根据全等三角形的性质和三角形内角和解答即可．证明：（1）∵EA∥FB，∴∠A=∠FBD，∵AB=CD，∴AB+BC=CD+BC，即AC=BD，在△EAC与△FBD中，{EA=FB ∠A=∠FBD AC=BD,∴△EAC≌△FBD（SAS）（2）∵△EAC≌△FBD，∴∠ECA=∠D=80°，∵∠A=40°，∴∠E=180°-40°-80°=60°，答：∠E的度数为60°．小提示：此题主要考查了全等三角形的判定与性质等知识，解题时注意：两边及其夹角分别对应相等的两个三角形全等．根据已知得出△EAC≌△FBD是解题关键．15、答案：7cm解析：根据翻折变换的性质可得DE=CD，BE=BC，然后求出AE，再根据三角形的周长列式求解即可．解：∵BC沿BD折叠点C落在AB边上的点E处，∴DE=CD，BE=BC，∵AB=8cm，BC=6cm，∴AE=AB-BE=AB-BC=8-6=2cm，∴△ADE的周长=AD+DE+AE，=AD+CD+AE，=AC+AE，=5+2，=7cm．小提示：本题考查了翻折变换的性质，熟记翻折前后两个图形能够完全重合得到相等的线段是解题的关键．。

人教版_部编版八年级数学上册第十二章第二节三角形全等的判定考试复习题一（含答案)已知，如图，点A 、D 、B 、E 在同一直线上，AC EF =，AD BE =，A E ∠=∠，CHD ∠=110°，求HBD ∠的度数．【答案】55°【解析】【分析】先根据SAS 即可证明ABC EDF ∆≅∆；可知HDB HBD ∠=∠，再利用三角形的外角关系即可求出HBD ∠的度数．【详解】解：AD BE =，AB ED ∴=，在ABC ∆和EDF ∆中，AC EF A E AB ED =⎧⎪∠=∠⎨⎪=⎩， ()ABC EDF SAS ∴∆≅∆；ABC EDF ∆≅∆，HDB HBD ∴∠=∠，110CHD HDB HBD ∠=∠+∠=︒，55HBD ∴∠=︒．【点睛】本题考查了全等三角形的判定和性质以及三角形的外角关系，属于基础性题目．解题关键是由SAS 证明ABC EDF ∆≅∆．72．如图所示，D 是BC 上一点，AB AD =，BC DE =，AC AE =，AC 与DE 交于点F ．求证：C E ∠=∠．【答案】证明见解析．【解析】【分析】利用“边边边”证明ABC ∆和ADE ∆全等，根据全等三角形对应角相等证明即可；【详解】证明：在ABC ∆和ADE ∆中，AB AD BC DE AC AE =⎧⎪=⎨⎪=⎩， ()ABC ADE SSS ∴∆≅∆，C E ∴∠=∠（全等三角形对应角相等）；【点睛】本题考查了全等三角形的判定与性质，熟练掌握三角形全等的判定方法是解题的关键．73．如图所示，在ABC 中，90BAC ∠=︒，AB AC =，MN 是经过点A 的直线，,BD MN CE MN ⊥⊥，垂足分别为D ，E ．（1）求证：①BAD ACE =∠∠；②BD AE =；（2）请写出BD ，CE ，DE 三者间的数量关系式，并证明．【答案】（1）①见解析；②见解析；（2）BD=CE+DE ，证明见解析．【解析】【分析】（1）①根据∠BAD+∠CAE=90°，∠ACE+∠CAE=90°，即可得出∠BAD=∠ACE ；②根据全等三角形的判定方法（AAS ）得出△ABD ≌△CAE ，从而得出BD=AE ；（2）根据△ABD ≌△CAE ，得出BD=AE ，AD=CE ，再根据AE=AD+DE ，即可得出BD ，DE ，CE 三者间的数量关系．【详解】解：（1）△△△BAC=90°，△△BAD+△CAE=90°，△CE △MN ，△△ACE+△CAE=90°，△△BAD=△ACE ；△△BD △MN ，CE △MN ，△△BDA=△AEC=90°，在△ABD 和△CAE 中，∵∠BDA ＝∠AEC ，∠BAD ＝∠ACE ，AB ＝AC ，△△ABD △△CAE ，△BD=AE ；（2）△△ABD △△CAE ，△BD=AE ，AD=CE ，△AE=AD+DE ，△BD=CE+DE ．【点睛】本题主要考查了直角三角形的性质，余角的性质，以及全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．74．如图，点E 在ABC 外部，点D 在BC 边上，DE 交AC 于点F ，若123∠=∠=∠，AC AE =，试说明：ABC ADE △≌△的理由．【答案】证明见详解．【解析】【分析】根据已知，利用三角形的内角和得到∠E=∠C ，再由已知可得∠BAC=∠DAE ，又因为AC=AE ，所以根据AAS 可判定△ABC ≌△ADE ．【详解】∵∠2=∠3，∠AFE=∠CFD ，∴∠C=∠E ；∵∠1=∠2，∴∠1+∠DAF=∠2+∠DAF即：∠BAC=∠DAE ．又∵AC=AE ，∠C=∠E ，∴△ABC ≌△ADE ．【点睛】此题考查三角形内角和及全等三角形的判定的理解及运用，准确识图，熟练掌握和运用相关知识是解题的关键．75．如图ABC 中，60,,ABC AD CE ︒∠=分别平分,BAC ACB AD CE∠∠、、相交于点P ．（1）求CPD ∠的度数；（2）求证：AE CD AC +=【答案】（1）∠CPD=60°；（2）详见解析【解析】【分析】（1）根据三角形的内角和定理及角平分线的定义，三角形的外角性质即可求出；（2）在AC 上截取AF=AE ，先证明△APE ≌△APF （SAS ），再证明△CFP ≌△CDP （ASA ），根据全等三角形的性质证明AE CD AC +=即可．【详解】解：（1）∵∠ABC=60°，∴∠BAC+∠ACB=180°-60°=120°，又∵AD 、CE 分别平分∠∠、BAC ACB ， ∴12CAD BAC ∠=∠，12ACE ACB ∠=∠ ∴111()60222CAD ACE BAC ACB BAC ACB ∠+∠=∠+∠=∠+∠=︒， 又∵∠CPD 是△ACP 的外角，∴∠CPD=∠CAD+△ACE=60°，∴∠CPD=60°．（2）如图，在AC 上截取AF=AE ，连接PF ，∵∠CPD=60°，∴∠APC=120°，∠APE=60°∵AD 平分∠BAC ，CE 平分∠ACB ，∴∠BAD=∠CAD ，∠ACE=∠BCE在△APE 与△APF 中AE AF BAD CAD AP AP =⎧⎪∠=∠⎨⎪=⎩， ∴△APE ≌△APF （SAS ）∴∠APF=∠APE=60°，∴∠CPF=△AOC-△APF=60°，在△CFP 与△CDP 中，ACE BCE CP CPCPD CPF ∠=⎧⎪=⎨⎪∠=∠⎩∴△CFP ≌△CDP （ASA ）∴CD=CF∴AC=AF+CF=AE+CD ，即AE CD AC +=．【点睛】本题考查了全等三角形的判定及性质、三角形内角和定理与角平分线的角度计算问题，解题的关键是通过在AC 上截取AF=AE 构造全等三角形．76．如图，点E 在四边形ABCD 的边AD 上，90BAE BCE ACD ∠=∠=∠=︒，且BC CE =，求证：AD AE AB =+．【答案】详见解析【解析】【分析】根据等量代换证明出∠ACB=△DCE 及∠ABC=△DEC ，再证明△ABC ≌△DEC （ASA ），由全等三角形的性质即可证明结论．【详解】解：∵90BCE ACD ∠=∠=︒∴∠ACB+∠ACE=△DCE+△ACE∴∠ACB=△DCE又∵90BAE BCE ∠=∠=︒，四边形ABCE 的内角和为360°，∴∠ABC+∠AEC=180°，又∵∠AEC+△DEC=180°，∴∠ABC=△DEC在△ABC 与△DEC 中ABC DEC BC CEACB DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEC （ASA ）△AB=DE∴AD=AE+DE=AE+AB即AD AE AB =+．【点睛】本题考查了全等三角形的判定，结题的关键是通过等量代换证明∠ACB=△DCE 及∠ABC=△DEC ．77．如图，A ，B ，D ，F 在同直线上，AD BF =，AE BC =，A B ∠=∠，求证：（1）AEF BCD ≌；（2）//AE BC ．【答案】（1）见解析；（2）见解析【解析】【分析】（1）由AD=BF 得出AF=BD ，根据SAS 即可证得△AEF ≌△BCD ；（2）由∠A=∠B，根据平行线的判定方法：内错角相等，两直线平行即可证明.【详解】解：（1）∵AD=BF ，∴AD+DF=BF+FD ，即AF=BD ，在△AEF 和△BCD 中，AE BC A B AF BD =⎧⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△BCD （SAS ）；（2）∵∠A=∠B ，∴AE ∥BC.【点睛】本题考查了全等三角形的判定与性质和平行线的判定，比较简单，熟记全等三角形的判定方法SAS 是解决问题的关键．78．在数学活动课上，数学老师出示了如下题目：如图①，在四边形ABCD 中，E 是边CD 的中点，AE 是BAD ∠的平分线，AD BC ∥．求证：AB AD BC =+．小聪同学发现以下两种方法：方法1：如图②，延长AE 、BC 交于点F ．方法2：如图③，在AB 上取一点G ，使AG AD =，连接EG 、CG ．（1）请你任选一种方法写出这道题的完整的证明过程；（2）如图④，在四边形ABCD 中，AE 是BAD ∠的平分线，E 是边CD 的中点，60BAD ∠=︒，11802D BCD ∠+∠=︒，求证：CB CE =．【答案】（1）方法1：证明见解析；方法2：证明见解析；（2）证明见解析．【解析】【分析】（1）方法1：先根据角平分线的定义、平行线的性质得出BAF DAE F ∠=∠=∠，再根据等腰三角形的性质可得AB BF =，根据三角形全等的判定定理与性质得出AD FC =，然后根据线段的和差即可得证；方法2：先根据角平分线的定义得出DAE GAE ∠=∠，再根据三角形全等的判定定理与性质可得,DE GE D AGE =∠=∠，然后根据线段中点的定义、等腰三角形的性质可得ECG EGC ∠=∠，最后根据平行线的性质、平角的定义可得BCG BGC ∠=∠，由等腰三角形的定义可得BG BC =，由此根据线段的和差即可得证；（2）如图（见解析），参照方法1构造辅助线，先根据等腰三角形的性质得出EF 平分AFG ∠，从而有12EFC AFG ∠=∠，再根据平行线的性质、角的和差得出60EFC BFC ∠=∠=︒，ECF BCF ∠=∠，然后根据三角形全等的判定定理与性质即可得证．【详解】（1）方法1：如图②，延长AE 、BC 交于点FAE ∵是BAD ∠的平分线BAF DAE ∴∠=∠//AD BCDAE F ∴∠=∠BAF F ∴∠=∠AB BF FC BC ∴==+E 是边CD 的中点DE CE ∴=在ADE 和FCE △中，DAE FAED FECDE CE∠=∠⎧⎪∠=∠⎨⎪=⎩ ()ADE FCE AAS ∴≅AD FC ∴=AB FC BC AD BC ∴=+=+；方法2：如图③，在AB 上取一点G ，使AG AD =，连接EG 、CGAE ∵是BAD ∠的平分线DAE GAE ∴∠=∠在ADE 和AGE 中，AD AGDAE GAEAE AE =⎧⎪∠=∠⎨⎪=⎩()ADE AGE SAS ∴≅,DE GE D AGE ∴=∠=∠E 是边CD 的中点DE CE ∴=CE GE ∴=ECG EGC ∴∠=∠//AD BC180D BCD ︒∴∠+∠=，即180D ECG BCG ∠+∠+∠=︒180AGE EGC BCG ∴∠+∠+∠=︒，即180AGC BCG ∠+∠=︒又180AGC BGC ∠+∠=︒BCG BGC ∴∠=∠BG BC ∴=AB AG BG AD BC ∴=+=+；（2）如图，过点C 作//CG AD ，交AE 延长线于点G ，延长GC 交AB 于点F ，连接EF由方法1可知：,AF GF AE GE ==AFG ∴是等腰三角形EF ∴平分AFG ∠12EFC AFG ∴∠=∠ //CG AD ，60BAD ∠=︒60,180120BFC BAD AFG BAD ∴∠=∠=︒∠=︒-∠=︒60EFC ∴∠=︒//CG AD180D ECF ∴∠+∠=︒ 11802D BCD ︒∠+∠=，即1()1802D ECF BCF ∠+∠+∠=︒ 1()2ECF ECF BCF ∴∠=∠+∠ ECF BCF ∴∠=∠在ECF △和BCF 中，60EFC BFC CF CF ECF BCF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩()ECF BCF ASA ∴≅CB CE ∴=．【点睛】本题考查了角平分线的定义、平行线的性质、三角形全等的判定定理与性质等知识点，较难的是题（2），参照方法1，通过作辅助线，构造全等三角形是解题关键．79．如图，在ABC 和DBE 中，点D 在边AC 上，BC 与DE 交于点P ，AB DB =，A BDE ∠=∠，ABD CBE ∠=∠．（1）求证：ABC DBE ≅；（2）若 2.5AD DC ==，4BC =，求CDP 与BEP △的周长和．【答案】（1）证明见解析；（2）CDP 与BEP △的周长和为15.5．【解析】【分析】（1）先根据角的和差得出ABC DBE ∠=∠，再根据三角形全等的判定定理即可得证；（2）先根据三角形全等的性质得出5,4AC DE BC BE ====，再根据三角形的周长公式、线段的和差即可得．【详解】（1）ABD CBE ∠=∠ABD CBD CBE CBD ∴∠+∠=∠+∠，即ABC DBE ∠=∠在ABC 和DBE 中，A BDE AB DB ABC DBE ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABC DBE ASA ∴≅；（2） 2.5AD DC ==5AC AD DC ∴=+=由（1）知，ABC DBE ≅5,4AC DE BC BE ∴====CDP ∴与BEP △的周长和为CD CP DP PE BP BE +++++()()CD CP BP DP PE BE =+++++CD BC DE BE =+++2.5454=+++15.5=即CDP 与BEP △的周长和为15.5．【点睛】本题考查了三角形全等的判定定理与性质、角的和差等知识点，熟记三角形全等的判定定理与性质是解题关键．80．如图，在ABC 和DEF 中，点B 、F 、C 、E 在同一直线上，AB DE =，BF CE =，AB DE ∥，求证：ABC DEF △≌△．【答案】证明见解析．【解析】【分析】先根据线段的和差可得BC EF =，再根据平行线的性质可得B E ∠=∠，然后根据三角形全等的判定定理即可得证．【详解】BF CE =BF CF CE CF ∴+=+，即BC EF =//AB DEB E ∴∠=∠在ABC和DEF中，BC EFB E AB DE=⎧⎪∠=∠⎨⎪=⎩()ABC DEF SAS∴≅△△．【点睛】本题考查了线段的和差、平行线的性质、三角形全等的判定定理，熟记三角形全等的判定定理是解题关键．。

全等三角形简单模型【模型讲解】模型1、平移全等模型，如下图：【巩固训练】1．如图，AB DE =，A D ∠=∠，要说明ABC DEF △≌△，需添加的条件不能是（）A ．//AB DE B ．//AC DF C ．AC DE ⊥D ．AC DF =【答案】C 【分析】直接根据三角形证明全等的条件进行判断即可；【详解】A 、∵AB ∥DE ，∴∠ABC=∠DEC ，∴根据ASA 即可判定三角形全等，故此选项不符合题意；B 、∵AC ∥DF ，∴∠DFE=∠ACB ，∴根据AAS 即可判定三角形全等，故此选项不符合题意；C 、AC ⊥DE ，不符合三角形全等的证明条件，故此选项符合题意；D 、∵AC=DF ，∴根据SAS 即可判定三角形全等，故此选项不符合题意；故选：C ．【点睛】本题考查了三角形证明全等所需添加的条件，正确掌握知识点是解题的关键；2．如图：已知AD BE =，BC EF =且//BC EF ，求证：ABC DEF ≌△△．【答案】见解析【分析】由AD=BE 可求得AB=DE ，再结合条件可证明△ABC ≌△DEF ．【详解】证明：∵AD BE =∴AD BD BE BD +=+∴AB DE=又∵//BC EF ∴ABC DEF∠=∠在ABC 和DEF 中AB DE ABC DEF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ABC DEF △≌△（SAS ）【点睛】本题主要考查全等三角形的判定方法，掌握全等三角形的判定方法是解题的关键，即SSS 、SAS 、ASA 、AAS 和HL ．3．如图，在△ABC 和△DEF 中，B ，E ，C ，F 在同一条直线上，AB //DE ，AB =DE ，∠A =∠D ．（1）求证：ABC DEF ≌；（2）若BF =11，EC =5，求BE的长．【答案】（1）见解析；（2）BE =3．【分析】（1）根据平行线的性质由AB ∥DE 得到∠ABC ＝∠DEF ，然后根据“ASA”可判断△ABC ≌△DEF ；（2）根据三角形全等的性质可得BC ＝EF ，由此可求出BE ＝CF ，则利用线段的和差关系求出BE ．【详解】（1）证明：∵AB ∥DE ，∴∠ABC ＝∠DEF ，在△ABC 和△DEF 中A D AB DE ABC DEF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF （ASA ）；（2）解：∵△ABC ≌△DEF ，∴BC ＝EF ，∴BC －EC ＝EF －EC ，即BE ＝CF ，∵BF ＝11，EC ＝5，∴BF －EC ＝6．∴BE ＋CF ＝6．∴BE ＝3．【点睛】本题考查了全等三角形的判定与性质，掌握全等三角形的判定与性质是解答此题的关键．4．如图，已知点C 是AB 的中点，CD ∥BE ，且CD BE =．（1）求证：△ACD ≌△CBE ．（2）若87,32A D ∠=︒∠=︒，求∠B的度数．【答案】（1）见解析；（2）61【分析】（1）根据SAS 证明△ACD ≌△CBE ；（2）根据三角形内角和定理求得∠ACD ，再根据三角形全等的性质得到∠B=∠ACD ．【详解】（1）∵C 是AB 的中点，∴AC ＝CB ，∵CD//BE ，∴ACD CBE ∠=∠，在△ACD 和△CBE 中，AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩，∴ACD CBE ∆≅∆；（2）∵8732A D ︒︒∠=∠=，，∴180180873261ACD A D ︒︒︒︒︒∠=-∠-∠=--=，又∵ACD CBE ∆≅∆，∴61B ACD ︒∠=∠=．【点睛】考查了全等三角形的判定和性质，解题关键是根据SAS 证明△ACD ≌△CBE ．5．如图，AB//CD ，AB=CD 点E 、F 在BC 上，且BF=CE ．（1）求证：△ABE ≌△DCF （2）求证:AE//DF ．【答案】（1）见详解；（2）见详解【分析】（1）由题意易得B C ∠=∠，BE CF =，然后问题可得证；（2）由（1）可得DFC AEB ∠=∠，则有EFD AEF ∠=∠，然后问题可得证．【详解】证明：（1）∵AB ∥CD ，∴B C ∠=∠，∵BF =CE ，∴CF EF BE EF +=+，∴BE CF =，∵AB =CD ，∴ABE DCF △≌△（SAS ）；（2）由（1）可得：ABE DCF △≌△，∴DFC AEB ∠=∠，∵180,180DFC EFD AEF AEB ∠+∠=︒∠+∠=︒，∴EFD AEF ∠=∠，∴//AE DF ．【点睛】本题主要考查三角形全等的判定及性质，熟练掌握全等三角形的判定定理是解题的关键．6.如图1，A ，B ，C ，D 在同一直线上，AB ＝CD ，DE ∥AF ，且DE ＝AF ，求证：△AFC ≌△DEB ．如果将BD 沿着AD 边的方向平行移动，如图2，3时，其余条件不变，结论是否成立？如果成立，请予以证明；如果不成立，请说明理由．【思路】可以根据已知利用SAS 判定△AFC ≌△DEB ．如果将BD 沿着AD 边的方向平行移动，如图（2）、（3）时，其余条件不变，结论仍然成立．可以利用全等三角形的常用的判定方法进行验证．【解答过程】解：∵AB ＝CD ，∴AB +BC ＝CD +BC ，即AC ＝BD ．∵DE ∥AF ，∴∠A ＝∠D ．在△AFC 和△DEB 中，AF DE∠A ∠D AC DB，∴△AFC ≌△DEB （SAS ）．在（2），（3）中结论依然成立．如在（3）中，∵AB ＝CD ，∴AB ﹣BC ＝CD ﹣BC ，即AC ＝BD ，∵AF ∥DE ，∴∠A ＝∠D ．在△ACF 和△DEB 中，AF DE∠A ∠D AC DB，∴△ACF ≌△DEB （SAS ）．模型2.对称（翻折）全等模型，如下图：【巩固训练】1．如图，四边形ABCD 的对角线AC ，BD 相交于点O ，ABO ADO △≌△，下列结论：①AC BD ⊥；②CB CD =；③ABC ADC △≌△；④DA DC =，其中正确结论的序号是__________．【答案】①②③【分析】根据全等三角形的性质得出AB=AD ，∠BAO =∠DAO ，∠AOB =∠AOD =90°，OB=OD ，再根据全等三角形的判定定理得出△ABC ≌△ADC ，进而得出其它结论.【详解】由△ABO ≌△ADO 得：AB=AD ，∠AOB =∠AOD =90°，∴AC ⊥BD ∠BAC =∠DAC ，又AC =AC ，所以，有△ABC ≌△ADC ，∴CB=CD ，所以，①②③正确．由已知条件得不到DA=DC ，故④不正确．故答案为：①②【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定方法:SSS ，SAS ，ASA ，AAS ，以及HL ，是解题的关键.2．如图，已知ACB DBC ∠=∠，若要使得ABC DCB ∆≅∆，则添加的一个条件不能是（）A ．A D∠=∠B ．ABC DCB ∠∠=C ．AB =DC D ．AC =DB【答案】C 【分析】根据全等三角形的判定方法对各选项进行判断，即可得出结论．【详解】解：∵ACB DBC ∠=∠，BC ＝CB ，A 、当添加∠A ＝∠D 时，可利用“AAS”判断△ABC ≌△DCB ，故此选项不符合题意；B 、当添加ABC DCB ∠=∠时，可利用“ASA”判断△ABC ≌△DCB ，故此选项不符合题意；C 、当添加AB=DC 时，利用“SSA”不能判断△ABC ≌△DCB ，故此选项符合题意；D 、当添加AC=DB 时，可利用“SAS”判断△ABC ≌△DCB ，故此选项不符合题意．故选：C ．【点睛】本题考查了全等三角形的判定：全等三角形的判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．3．如图，12∠=∠，BC EC =，请补充一个条件：______，能使用“ASA ”方法判定ABC DEC ≌△△．【答案】∠B ＝∠E【分析】已知∠1＝∠2，就是已知∠ACB ＝∠DCE ，则根据三角形的判定定理“ASA ”即可证【详解】可以添加∠B ＝∠E ．理由是：∵∠1＝∠2，∴∠1+∠BCE ＝∠2+∠BCE ，∴∠ACB ＝∠DCE ，∴在△ABC 和△DEC 中，ACB DCE BC EC B E ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△ABC ≌△DEC （ASA ）．故答案是：∠B＝∠E【点睛】本题考查了三角形全等的判定，熟练掌握“两角及夹边对应相等的两个三角形全等”是解题关键．4．在数学课上，林老师在黑板上画出如图所示的图形（其中点B 、F 、C 、E 在同一直线上），并写出四个条件：①AB ＝DE ，②BF ＝EC ，③∠B ＝∠E ，④∠1＝∠2．请你从这四个条件中选出三个作为题设，另一个作为结论，组成一个真命题，并给予证明．题设：；结论：．（均填写序号）证明：【答案】①②③；④；证明过程见解析；【分析】根据三个不同的情况进行讨论分析即可；【详解】情况一：题设①②③，结论④；∵BF=EC ，∴BF CF EC CF +=+，即BC EF =，在△ABC 和△DEF 中，AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩，∴ABC DEF ≅ ，∴12∠=∠；情况二：题设①③④，结论③；在△ABC 和△DEF 中，12B E AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ABC DEF ≅ ，∴BC EF =，∴BC FC EF FC -=-，即BF EC =；情况三：题设②③④，结论①；∵BFEC =，∴BF CF EC CF +=+，即BC EF =，在△ABC 和△DEF 中，12BC EF B E ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ABC DEF ≅ ，∴AB DE =；故答案为：①②③；④．【点睛】本题主要考查了全等三角形的判定与性质，准确分析证明是解题的关键．5．如图，在ABC 中，点D ，E 分别是AB 、AC 边上的点，BD CE =，ABE ACD ∠=∠，BE 与CD 相交于点F ，求证：AB AC =．【答案】见详解；【分析】依题意，BD =CE ，∠ABE =∠ACD ，∠BFD =∠CFE ，可得△BDF ≌△CEF ，可得DF =EF ，BF =CF ；可得CD =BE ，可得△ABE ≌△ACD ，即可；【详解】由题知：BD =CE ，∠ABE =∠ACD ，又∠BFD 和∠CFE 为对顶角，∴∠BFD =∠CFE ；在△BDF 和△CEF 中ABE ACD BFD CFE BD CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BDF ≌△CEF （AAS ）；∴DF =EF ，BF =CF ；又CD =DF +CF ，BE =BF +EF ；∴CD =BE ；在△ABE 和△ACD 中A A ABE ACD BE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABE ≌△ACD （AAS ）；∴AB =AC ；【点睛】本题主要考查对顶角相等、用AAS 证明全等及其性质，熟练构造出全等的三角形是关键；6．如图，已知∠C ＝∠F ＝90°，AC ＝DF ，AE ＝DB ，BC 与EF 交于点O ，（1）求证：Rt△ABC≌Rt△DEF；（2）若∠A＝51°，求∠BOF的度数．【答案】（1）见解析；（2）78°【分析】（1）由AE＝DB得出AE＋EB＝DB＋EB，即AB＝DE，利用HL即可证明Rt△ABC ≌Rt△DEF；（2）根据直角三角形的两锐角互余得∠ABC＝39°，根据全等三角形的性质得∠ABC＝∠DEF＝39°，由三角形外角的性质即可求解．【详解】（1）证明：∵AE＝DB，∴AE＋EB＝DB＋EB，即AB＝DE．又∵∠C＝∠F＝90°，AC＝DF，∴Rt△ABC≌Rt△DEF．（2）∵∠C＝90°，∠A＝51°，∴∠ABC＝∠C－∠A＝90°－51°＝39°．由（1）知Rt△ABC≌Rt△DEF，∴∠ABC＝∠DEF．∴∠DEF＝39°．∴∠BOF＝∠ABC＋∠BEF＝39°＋39°＝78°．【点睛】本题主要考查直角三角形的两锐角互余，三角形外角的性质，全等三角形的判定与性质，证明三角形全等是解题的关键．模型3.旋转全等模型，如下图：【巩固训练】1．如图，△ABC和△AED共顶点A，AD＝AC，∠1＝∠2，∠B＝∠E．BC交AD于M，DE交AC于N，甲说：“一定有△ABC≌△AED．”乙说：“△ABM≌△AEN．”那么（）A ．甲、乙都对B ．甲、乙都不对C ．甲对、乙不对D ．甲不对、乙对【答案】A 【分析】利用AAS 判定△ABC ≌△AED ，则可得到AB=AE ，再利用ASA 判定△ABM ≌△AEN ．【详解】∵∠1＝∠2，∴∠1+∠MAC ＝∠2+∠MAC ，∴∠BAC ＝∠EAD，在△BAC 和△EAD 中，B E BAC EAD AC AD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BAC ≌△EAD ，∴甲说的正确；∵△BAC ≌△EAD （AAS ），∴AB=AE ，在△BAM 和△EAN 中，12B E AB AE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BAM ≌△EAN （ASA ），∴乙说的正确；故选A ．【点睛】本题考查了三角形全等的判定方法，根据题目的特点，补充适当条件，活用判定定理是解题的关键．2．如图，已知AB AD =，BC DE =，且10CAD ∠=︒，25B D ∠=∠=︒，120EAB ∠=︒，则EGF ∠的度数为（）A ．120︒B ．135︒C ．115︒D ．125︒【答案】C【分析】由已知得△ABC ≌△ADE ，故有∠BAC =∠DAE ，由∠EAB =120°及∠CAD =10°可求得∠AFB 的度数，进而得∠GFD 的度数，在△FGD 中，由三角形的外角等于不相邻的两个内角的和即可求得∠EGF 的度数．【详解】在△ABC 和△ADE 中AB AD B D BC DE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE （SAS ）∴∠BAC =∠DAE∵∠EAB =∠BAC +∠DAE +∠CAD =120°∴∠BAC =∠DAE ()112010552=⨯︒-︒=︒∴∠BAF =∠BAC +∠CAD =65°∴在△AFB 中，∠AFB =180°-∠B -∠BAF =90°∴∠GFD =90°在△FGD 中，∠EGF =∠D +∠GFD =115°故选：C【点睛】本题考查了三角形全等的判定和性质、三角形内角和定理，关键求得∠BAC 的度数．3．已知：如图，C 为线段BE 上一点，AB//DC ，AB=EC ，BC=CD ．求证：∠A=∠E．【答案】见详解【分析】直接利用全等三角形的判定方法得出△ABC ≌△ECD ，即可得出答案．【详解】证明：∵AB ∥DC ，∴∠B ＝∠ECD ，在△ABC 和△ECD 中，AB EC B ECD BC CD ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABC ≌△ECD （SAS ），∴∠A ＝∠E （全等三角形的对应角相等）．【点睛】此题主要考查了全等三角形的判定与性质，正确掌握全等三角形的判定方法是解题关键．4．如图，,,,AC BC DC EC AC BC DC EC ⊥⊥==，求证：（1）ACE BCD ∆≅∆；（2）AE BD ⊥．【答案】（1）见解析；（2）见解析【分析】（1）根据垂直得到90ACB DCE ∠=∠=︒，求出DCB ECA ∠=∠，即可得到结果；（2）设AC 交BD 于N ，AE 交BD 于O ，根据全等三角形的性质得到A B ∠=∠，再根据已知条件转换即可；【详解】证明：()1AC BC ⊥Q ，DC EC ⊥，90ACB DCE ∴∠=∠=︒，ACB ACD DCE ACD ∴∠+∠=∠+∠，∴∠=∠DCB ECA ，在DCB ∆和ECA ∆中，AC BC DCB ECA CD CE =⎧⎪∠=∠⎨⎪=⎩，()DCB ECA SAS ∴∆≅∆；()2如图，设AC 交BD 于N ，AE 交BD 于O ，∆≅∆ DCB ECA ，A B ∴∠=∠，∠=∠ AND BNC ，90∠+∠=︒B BNC ，90∴∠+∠=︒A AND ，90∴∠=︒AON ，AE BD ∴⊥．【点睛】本题主要考查了全等三角形的判定与性质，准确证明是解题的关键．。

辅助线模型考点分析：全等三角形是初中数学中的重要内容之一，是今后学习其他知识的基础。

判断三角形全等的公理有 SAS、ASA、AAS、SSS 和 HL，如果所给条件充足，则可直接根据相应的公理证明，但是如果给出的条件不全，就需要根据已知的条件结合相应的公理进行分析，先推导出所缺的条件然后再证明。

一些较难的证明题要构造合适的全等三角形，把条件相对集中起来，再进行等量代换，就可以化难为易了。

典型例题人说几何很困难，难点就在辅助线。

辅助线，如何添？把握定理和概念。

还要刻苦加钻研，找出规律凭经验。

全等三角形辅助线找全等三角形的方法：（1）可以从结论出发，寻找要证明的相等的两条线段（或两个角）分别在哪两个可能全等的三角形中；（2）可以从已知条件出发，看已知条件可以确定哪两个三角形全等；（3）可从条件和结论综合考虑，看它们能确定哪两个三角形全等；（4）若上述方法均不可行，可考虑添加辅助线，构造全等三角形。

三角形中常见辅助线的作法：①延长中线构造全等三角形；②利用翻折，构造全等三角形；③引平行线构造全等三角形；④作连线构造等腰三角形。

常见辅助线的作法有以下几种：（1）遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”。

例1：如图，Δ ABC 是等腰直角三角形，∠BAC=90°，BD 平分∠ABC交AC 于点D，CE 垂直于 BD，交BD 的延长线于点E。

求证：BD=2CE。

思路分析：1）题意分析：本题考查等腰三角形的三线合一定理的应用2）解题思路：要求证 BD=2CE，可用加倍法，延长短边，又因为有 BD 平分∠ABC 的条件，可以和等腰三角形的三线合一定理结合起来。

解答过程：证明：延长BA，CE 交于点F，在ΔBEF 和ΔBEC 中，∵∠1=∠2，BE=BE，∠BEF=∠BEC=90°，∴ΔBEF≌ΔBEC，∴EF=EC，从而CF=2CE。

又∠1+∠F=∠3+∠F=90°，故∠1=∠3。

2020—2021八年级上学期专项冲刺卷（人教版）专项12.5 三角形全等的判定（HL ）姓名：___________考号：___________分数：___________（考试时间：100分钟 满分：120分）一、 选择题（本大题共12小题，每小题3分，共36分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．如图，在ABC 中，BE AC ⊥于点E ，AF 分别交BE ，BC 于点F ，D ，AE BE =，若依据“HL ”说明AEF BEC ≌，则下列所添条件合理的是（ ）A ．EF CE =B ．AFEC ∠=∠ C ．BD AD ⊥ D ．AF BC =【答案】D【分析】 根据“HL ”进行判断即可．【详解】解：由题意得，AEF 和BEC △中，有一组直角边对应相等，即AE BE =缺少斜边对应相等，即AF BC =，故选：D ．【点睛】此题主要考查了“HL ”的应用，熟练掌握直角三角形的判定方法是解答此题的关键．2．如图，在ABC 中，90C ∠=︒，DE AB ⊥于点D ，BC BD =．如果3cm AC =，那么AE DE +=（ ）A ．2cmB ．4cmC ．3cmD ．5cm【答案】C【分析】通过HL 判定定理可证Rt∆BDE ≅Rt∆BCE ，得到ED=EC ，即可求解．【详解】在Rt BCE 和Rt BDE △中，BC BD =，BE BE =，∴()Rt Rt HL BCE BDE ≌△△， ∴ED EC =，∴3cm AE DE AE EC AC +=+==．故选：C ．【点睛】本题考查了全等三角形的性质和判定，注意:直角三角形全等的判定定理有SAS ，ASA ，AAS ，SSS ，HL ，全等三角形的对应边相等.3．如图，已知在ABC 和DEF 中，AB DE =，BC EF =，下列条件中不能判定ABC DEF △≌△的是（ ）A ．AC DF =B ．B E ∠=∠C ．AB AC ⊥且ED DF ⊥ D ．C F ∠=∠【答案】D【分析】根据三角形全等的判定条件可直接排除选项．【详解】解：A 、若AC DF =，则根据“SSS”可判定ABC DEF △≌△，故不符合题意；B 、若B E ∠=∠，则根据“SAS”可判定ABC DEF △≌△，故不符合题意；C 、若AB AC ⊥且ED DF ⊥，则根据“HL”可判定ABC DEF △≌△，故不符合题意； D 、若C F ∠=∠，则不能判定ABC DEF △≌△，故符合题意；故选D ．【点睛】本题主要考查三角形全等的判定，熟练掌握三角形全等的条件是解题的关键．4．如图，AB BC ⊥，CD BC ⊥，AC BD =，则能证明ABC DCB ≅的判定法是( )A ．SASB ．AASC ．SSSD ．HL【答案】D【分析】 直接证明全等三角形，即可确定判断方法.【详解】解：∵AB BC ⊥，CD BC ⊥，∴ABC 与△DCB 均为直角三角形，又AC DB =，BC CB =，∴()ABC DCB HL ≅,故选：D.【点睛】本题考查全等三角形的判定定理，属于基础题.5．用三角尺画角平分线：如图，先在AOB ∠的两边分别取OM ON =，再分别过点M ，N 作OA ，OB 的垂线，交点为P ．得到OP 平分AOB ∠的依据是（ ）A ．HLB ．SSSC ．SASD ．ASA【答案】A【分析】 利用垂直得到90PMO PNO ∠=∠=，再由OM ON =，OP OP =即可根据HL 证明()HL ≌PMO PNO △△，由此得到答案.【详解】∵PM OA ⊥，PN OB ⊥，∴90PMO PNO ∠=∠=．∵OM ON =，OP OP =，∴()HL ≌PMO PNO △△， ∴POA POB ∠=∠，故选：A ．【点睛】此题考查三角形全等的判定定理：SSS 、SAS 、ASA 、AAS 、HL ，根据题中的已知条件确定对应相等的边或角，由此利用以上五种方法中的任意一种证明两个三角形全等.6．如图，在Rt ABC 和Rt ADE △中，90,,ACB AED AB AD AC AE ∠=∠===，则下列说法不正确的是（ ）A ．BC DE =B ．BAE DAC ∠=∠ C ．OC OE =D ．EAC ABC ∠=∠【答案】D【分析】 根据HL 定理分别证明Rt △ABC ≌Rt △ADE 和Rt △AEO ≌Rt △ACO ，根据全等三角形的性质可判断各选项．【详解】解：解：∵90,,ACB AED AB AD AC AE ∠=∠===，∴Rt △ABC ≌Rt △ADE （HL ）∴BC DE =，∠BAC=∠DAE ，故A 选项正确；∴∠BAC-∠EAC=∠DAE-∠EAC ，即BAE DAC ∠=∠，故B选项正确；连接AO，∵AE=AC，AO=AO，∴Rt△AEO≌Rt△ACO（HL），∴OC OE=，故C选项正确；无法得出EAC ABC∠=∠，故D选项错误；故选：D．【点睛】本题全等三角形的性质与判断．掌握证明直角三角形全等的HL定理是解题关键．7．如图，在Rt△ABC中，∠ACB=90°，BC=5cm，在AC上取一点E使EC=BC，过点E作EF⊥AC，连接CF，使CF=AB，若EF=12cm，则AE的长为（）A．5cm B．6cm C．7cm D．8cm【答案】C【分析】根据已知条件证明Rt△ABC≌Rt△FCE，即可求出答案．【详解】∵EF⊥AC，∴∠CEF=90°，在Rt△ABC和Rt△FCE中BC CE BA CF=⎧⎨=⎩，∴Rt△ABC≌Rt△FCE（HL），∴AC=FE=12cm，∵EC=BC=5cm ，∴AE=AC-EC=12-5=7cm ，故选：C ．【点睛】本题考查了全等三角形的判定和性质，掌握知识点是解题关键．8．已知，如图AB BD ⊥，ED BD ⊥，AB CD =，AC CE =，则ACE ∠等于（ ）A ．90︒B ．120︒C ．80︒D ．100︒【答案】A【分析】 由题中条件可得Rt △ABC ≌Rt △CDE ，再通过角之间的转化，进而可得出结论．【详解】解：∵AB ⊥BD ，ED ⊥BD ，∴∠D=∠B=90°，在Rt △ABC 和Rt △CDE 中，AB CD AC CE=⎧⎨=⎩， ∴Rt △ABC ≌Rt △CDE （HL ），∴∠DCE=∠A ，∵∠B=90°，∴∠BAC+∠ACB=90°，∴∠ECD+∠ACB=90°，∴∠ACE=180°-90°=90°．故选：A ．【点睛】本题主要考查了直角三角形全等的判定及性质，解决本题的关键是证明Rt △ABC ≌Rt △CDE ． 9．已知，如图，B 、C 、E 三点在同一条直线上，AC ＝CD ，∠B ＝∠E ＝90°，AB ＝CE ，则不正确的结论是（ ）A ．∠A 与∠D 互为余角B ．∠A ＝∠2C ．△ABC ≌△CEDD ．∠1＝∠2【答案】D【分析】 根据HL 证Rt ABC Rt CED ≌，根据全等三角形的性质即可求出答案.【详解】∵∠B ＝∠E ＝90°，∴在Rt ABC 和Rt CED 中AC CD AB CE =⎧⎨=⎩， ∴Rt ABC Rt CED ≌（HL ），故C 正确，∴∠A ＝∠2，∠1＝∠D ，∵∠1+∠A ＝90°，∴∠A+∠D ＝90°，∠1+∠2＝90°，∴∠A 与∠D 互为余角，故A 、B 正确；D 错误，故选：D ．【点睛】本题考查了全等三角形的性质和判定，关键是推出Rt ABC Rt CED ≌．10．如图，AC DF =，AC BC ⊥，DF DE ⊥，且AE BF =，70A ∠=︒，那么DEF ∠的度数是（ ）A ．10︒B ．20︒C ．30D ．40︒【答案】B【解析】【分析】 首先求出AB=FE ，利用HL 证明Rt △ACB ≌Rt △FDE ，得到70F A ∠=∠=︒，然后根据直角三角形两锐角互余得出答案.【详解】解：∵AE BF =，∴AB=FE ，∵AC BC ⊥，DF DE ⊥，∴在Rt △ACB 和Rt △FDE 中，AB FE AC DF=⎧⎨=⎩， ∴Rt △ACB ≌Rt △FDE （HL ），∴70F A ∠=∠=︒，∴907020DEF ∠=︒-︒=︒，故选：B.【点睛】本题考查全等三角形的判定和性质以及直角三角形两锐角互余的性质，正确寻找证明三角形全等的条件是解题关键.11．如图，在ABC ∆中，90,︒∠=C D 是AC 上一点，DE AB ⊥于点E ，BE BC =连接BD ，若AC=8cm ，则AD DE +等于（ ）A ．6cmB ．7cmC ．8cmD ．9cm【答案】C【分析】 根据已知条件证明BCD BED ≅，证明DC=DE 即可；【详解】∵DE AB ⊥，∴90DEB ∠=︒，在Rt BCD 和Rt BED 中，()()已知公共边BE BC BD BD ⎧=⎪⎨=⎪⎩， ∴BCD BED ≅，∴DC=DE ，又∵AC=8cm ，∴8+=AD DE cm ．故答案选C ．【点睛】本题主要考查了三角形的全等，准确利用HL 定理是解题的关键．12．如图，有两个长度相同的滑梯，左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等，两个滑梯的倾斜角ABC ∠和DFE ∠之间的关系是（ ）A ．ABC DFE ∠=∠B ．ABC DFE ∠>∠ C ．100ABC DFE ∠+∠=︒D ．90∠+∠=︒ABC DFE【答案】D【分析】根据HL 定理判定()≌Rt ABC Rt DEF HL ，即可得到结果；【详解】由题意可知BC FE =，AC DF =，AC AB ⊥，DE DF ⊥，ABC ∴与DEF 为直角三角形．∴在Rt ABC 与Rt DEF △中，BC EF AC DF=⎧⎨=⎩，()Rt ABC Rt DEF HL ∴≌，ACB DFE ∴∠=∠．90ABC ACB ∠∠=︒＋，90ABC DFE ∴∠+∠=︒．故选D ．【点睛】本题主要考查了全等三角形的判定，准确理解是解题的关键．二、 填空题（本大题共6小题，每小题3分，共18分）13．如图，在Rt ABC ∆中，90C ∠=︒，D 为BC 上一点，连接AD ，过D 点作DE AB ⊥，且DE DC =．若5AB =，3AC =，则EB =__．【答案】2【分析】先根据HL 证明ADE ADC ∆≅∆，得出AE =AC =3，再根据BE =AB -AE 即可得出答案．【详解】解：∵90C ∠=︒，DE AB ⊥，在Rt ADE ∆和Rt ADC ∆中，AD AD DE DC=⎧⎨=⎩， Rt ADE Rt ADC(HL)∴∆≅∆，3AC AE ∴==，2BE AB AE ∴=-=，故答案为2．【点睛】本题考查了全等三角形的性质与判定，熟练掌握三角形的判定方法是解题的关键．14．如图，在Rt △ABC 中，∠C =90°，D 为BC 上一点，连接AD ，过D 点作DE ⊥AB ，且DE =DC ．若AB =5，AC =3，则EB =____．【答案】2【分析】先证明△AED ≌△ACD 得到AE=AC=3，最后根据线段的和差即可解答．【详解】解：∵∠C =90°，DE ⊥AB ，∴△AED 和△ACD 都是直角三角形，在Rt △AED 和Rt △ACD 中，DE=DC,AD=AD ，∴△AED ≌△ACD （HL ），∴AE=AC=3，∴BE=AB-AC=5-3=2．故填：2．【点睛】本题主要考查了全等三角形的判定与性质，掌握运用HL 证明三角形全等是解答本题的关键． 15．如图，点D 在BC 上，DE ⊥AB 于点E ，DF ⊥BC 交AC 于点F ，BD ＝CF ，BE ＝CD ．若∠AFD ＝145°，则∠EDF ＝_____．【答案】55°【分析】由∠AFD ＝145°可求得∠CFD=35°，证明Rt △BDE ≌△Rt △CFD ，根据对应角相等推知∠BDE=∠CFD=35°，进而可求出∠EDF 的值．【详解】解：∵∠DFC+∠AFD=180°，∠AFD=145°，∴∠CFD=35°．又∵DE ⊥AB ，DF ⊥BC ，∴∠BED=∠CDF=90°，在Rt △BDE 与△Rt △CFD 中，BE CD BD CF=⎧⎨=⎩， ∴Rt △BDE ≌△Rt △CFD （HL ），∴∠BDE=∠CFD=35°，∴∠EDF =180°-90°-35°=55°．故答案是：55°．【点睛】本题考查了全等三角形的判定与性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．16．如图，在Rt ABC △中，90C ∠=︒，10AC =，5BC =，线段PQ AB =，P ，Q 两点分别在线段AC 和过点A 且垂直于AC 的射线AD 上运动，当AQ =______时，ABC 和PQA △全等．【答案】5或10【分析】分两种情况：当AQ=5时，当AQ=10时，利用全等三角形的判定及性质定理得到结论．【详解】分两种情况：当AQ=5时，∵5BC =，∴AQ=BC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴ABC ≌△PQA （HL ）；当AQ=10时，∵10AC =，∴AQ=AC ，∵AD ⊥AC ，∴∠QAP=∠ACB=90︒，∵AB=PQ ，∴△ABC ≌△QPA ，故答案为：5或10．【点睛】此题考查全等三角形的判定及性质定理，运用分类思想，动点问题，熟记三角形的判定定理及性质定理是解题的关键．17．如图，//MN PQ ，AB PQ ⊥，点A ，D ，B ，C 分别在直线MN 与PQ 上，点E 在AB 上，7AD BC +=，AD EB =，DE EC =，则AB =________．【答案】7【分析】先根据平行线的性质证出∠DAE=∠EBC=90°，再利用HL 证出Rt ADE ≌Rt BEC △，从而得出AE=BC ，AD=BE ，然后利用等量代换即可求出结论．【详解】解：∵AB PQ ⊥，∴∠EBC=90°∵//MN PQ∴∠DAE=180°－∠EBC=90°∴∠DAE=∠EBC在Rt ADE 和Rt BEC △中AD EB DE EC =⎧⎨=⎩∴Rt ADE ≌Rt BEC △∴AE=BC ，AD=BE∴AB=AE ＋BE=BC ＋AD=7故答案为：7．【点睛】此题考查的是全等三角形的判定及性质和平行线的性质，掌握全等三角形的判定及性质和平行线的性质是解题关键．18．如图，在△ABC 中，∠C ＝90°，DE ⊥AB 于D ，BC ＝BD ，若AC ＝4cm ，则AE +DE ＝_____．【答案】4cm【分析】根据题意由条件可证明Rt △CBE ≌Rt △DBE ，则可求得DE ＝EC ，可求得答案．【详解】解：∵DE ⊥AB ，∠C ＝90°，∴∠C ＝∠BDE ＝90°，在Rt △CBE 和Rt △DBE 中BE BE BC BD =⎧⎨=⎩∴Rt △CBE ≌Rt △DBE （HL ），∴CE ＝DE ，∴AE+DE ＝AE+CE ＝AC ＝4cm ，故答案为：4cm ．【点评】本题主要考查全等三角形的判定和性质，证得Rt △CBE ≌Rt △DBE 得到CE ＝DE 是解题的关键．三、解答题（本大题共6小题，共66分，解答应写出文字说明、演算步骤或推理过程） 19．如图，点C 、D 、E 、F 在同一条直线上，90A B ︒∠=∠=，AC BF =，CD EF =，AE 与BD 相交于点O ．（1）求证：EA DB =；（2）若55C ︒∠=，求∠BOE 的度数．【答案】（1）见解析；（2）70︒．【分析】（1）先证出CE FD =，再用HL 证明Rt ACE △≌Rt BFD ，即可得出结论；（2）先由直角三角形的性质得35AEC ︒∠=，再由全等三角形的性质得35AEC BDF ︒∠=∠=，然后由三角形的外角性质即可得出答案．【详解】（1）证明：CD EF =，∴CD DE EF DE +=+，即CE FD =，90A B ︒∠=∠=，∴ACE 和BFD △是直角三角形，在Rt ACE △和Rt BFD 中，CE FD AC BF =⎧⎨=⎩， ∴Rt ACE △≌()Rt BFD HL ，∴EA DB =；（2）解：90A ︒∠=，55C ︒∠=，∴905535AEC ︒︒︒∠=-=，由（1）得：Rt ACE △≌Rt BFD ，∴35AEC BDF ︒∠=∠=，∴70BOE AEC BDF ︒∠=∠+∠=．【点睛】本题主要考查了三角形全等的判定和性质，三角形外角性质，熟练掌握用HL 定理证明两个直角三角形全等是解题的关键．20．已知：如图，AB =CD ，DE ⊥AC ，BF ⊥AC ，E ，F 是垂足，DE =BF ．求证：（1）AE =CF ；（2）AB ∥CD ．【答案】（1）证明见解析；（2）证明见解析．【分析】（1）利用HL 定理即可证明△ABF ≌△CDE ，证明AF =CE ，据此即可得到AE =CF ；（2）根据△ABF ≌△CDE 即可证得∠A =∠C ，然后利用平行线的判定定理证明．【详解】证明：（1）∵DE ⊥AC ，BF ⊥AC ，∴∠DEC =∠BF A =90°，∴在Rt △ABF 和Rt △CDE 中，AB CD DE BF =⎧⎨=⎩， ∴△ABF ≌△CDE （HL ）；∴AF =CE ，即AF -EF =CE -EF∴AE =CF ；（2）∵△ABF ≌△CDE ，∴∠A =∠C ，∴CD ∥AB ．【点睛】本题考查了全等三角形的判定与性质以及平行线的判定，正确证明△ABF ≌△CDE 是关键． 21．如图，已知AE BD =，AC BC ⊥，DF EF ，垂足分别为点C ，F ，且BC EF =．（1）求证：ABC ≌DEH △；（2）求证：//AC DF ．【答案】（1）见详解；（2）见详解．【分析】（1）根据HL 证明两个三角形全等即可．（2）利用全等三角形的性质证明∠A=∠D 即可解决问题．【详解】（1）证明：∵AC BC ⊥，DF EF ，∴90C F ∠=∠=︒，∵AE BD =，∴AB DE =，∵BC EF =，∴Rt ABC △≌Rt DEF △（HL ）．（2）∵ABC ≌DEF ，∴A D ∠=∠，∴//AC DF ．【点睛】本题考查全等三角形的判定和性质，平行线的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．22．已知：如图，BE CD ⊥于点E ，BE DE =，BC DA =．（1）求证：BCE DAE △△≌（2）判断DF 与BC 的位置关系，并说明理由．【答案】（1）证明见解析；（2）DF BC ⊥，理由见解析【分析】（1）根据HL 即可证得；（2）根据（1）中全等可得B D ∠=∠，易证90D C ∠+∠=，即可证得．【详解】证明（1）∵BE DE =，BC DA =∴()BCE DAE HL △△≌（2）位置关系：DF BC ⊥BCE DAE △△≌B D ∴∠=∠BE CD ⊥90B C ∴∠+∠=90D C ∴∠+∠=90CFD ∴∠=DF BC ∴⊥【点睛】本题考查全等三角形证明方法，掌握HL 是解题的关键．23．如图，在ABC 中，,90,AB CB ABC F ︒=∠=为AB 延长线上一点，点E 在BC 上，且AE CF =．（1）求证：Rt ABE Rt CBF ≌；（2）若22CAE ︒∠=，求ACF ∠的度数．【答案】（1）见解析；（2）=68ACF ∠︒【分析】（1）根据旋转全等模型容易找到Rt ABE ∆和Rt CBF ∆全等的条件，从而可以证明Rt ABE Rt CBF ∆≅∆；（2）由Rt ABC ∆是等腰直角三角形易求45BCA BAC ∠=∠=︒，23EAB ∠=︒，根据Rt ABE Rt CBF ∆≅∆得23EAB FCB ∠=∠=︒，再由ACF FCB BCA ∠=∠+∠即可求.【详解】（1）证明：90ABC ∠=︒，90ABE CBF ∴∠=∠=︒，在Rt ABE ∆和Rt CBF ∆中，AB CB AE CF =⎧⎨=⎩， Rt ABE Rt CBF(HL)∴∆≅∆；（2）AB CB =，90ABC ∠=︒，45BCA BAC ∴∠=∠=︒，又∵22CAE ∠=︒，CAB CAE EAB ∠=∠+∠，23EAB ∴∠=︒，Rt ABE Rt CBF ∆≅∆，EAB FCB ∴∠=∠，23FCB ∴∠=︒，234568ACF FCB BCA ∴∠=∠+∠=︒+︒=︒，即68ACF ∠=︒．【点睛】本题考查全等三角形的判定与性质，解题的关键是明确题意，找出所要证明结论需要的条件． 24．如图，在ABC 中，C 90∠=︒，DE AB ⊥于点D ，DB BC =．（1）证明：BCE BDE ．（2）求证：AC AE DE =+．【答案】（1）见解析；（2）见解析【分析】（1）利用HL 可证明Rt △BCE ≌Rt △BDE ；（2）根据Rt △BCE ≌Rt △BDE 可得DE=CE ，从而可得AC=AE+CE=AE+DE ．【详解】解：（1）∵DE ⊥AB ，∴∠EDB=∠C=90°，在Rt △BCE 和Rt △BDE 中，BC BD BE BE=⎧⎨=⎩， ∴Rt △BCE ≌Rt △BDE （HL ）；（2）∵Rt △BCE ≌Rt △BDE ，∴CE=DE ，∴AC=AE+CE=AE+DE ．【点睛】本题主要考查三角形全等的判定和性质，证得Rt △BCE ≌Rt △BDE 是本题解题的关键．。