例题-线段的和与差

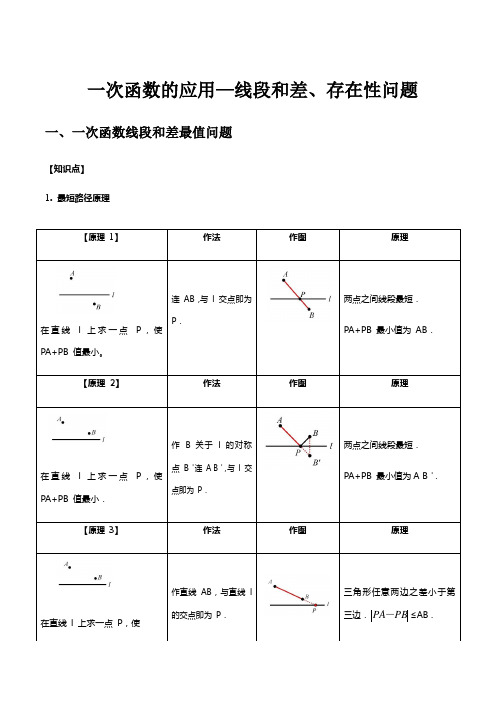
一次函数的应用—线段和差、存在性问题一、一次函数线段和差最值问题【知识点】1. 最短路径原理【原理1】作法作图原理在直线l 上求一点P，使PA+PB 值最小。

连AB，与l 交点即为P．两点之间线段最短．PA+PB 最小值为AB．【原理2】作法作图原理在直线l 上求一点P，使PA+PB 值最小．作 B 关于l 的对称点B＇连A B＇，与l 交点即为P．两点之间线段最短．PA+PB 最小值为A B＇．【原理3】作法作图原理在直线l 上求一点P，使作直线AB，与直线l的交点即为P．三角形任意两边之差小于第三边．≤AB .PBPA－（1）求线段和最小时动点坐标或直线解析式； （2）求三角形周长最小值；（3）求线段差最大时点的坐标或直线解析式。

3. 口诀：“和小异，差大同”（一）一次函数线段和最小值问题【例题讲解】★★☆例题1．在平面直角坐标系xOy 中，y 轴上有一点P ，它到点(4,3)A ，(3,1)B 的距离之和最小，则点P 的坐标是( ) A ．(0,0)B ．4(0,)7C ．5(0,)7D ．4(0,)5【答案】C的值最大 .【原理 4】作法作图原理在直线 l 上求一点 P ，使的值最大 .作 B 关于 l 的对称点 B ＇作直线 A B ＇，与 l 交点即为 P ．三角形任意两边之差小于第三边．≤A B ＇ .PB PA －PB PA －PB PA －【解析】解：作A 关于y 轴的对称点C ，连接BC 交y 轴于P ，则此时AP PB +最小，即此时点P 到点A 和点B 的距离之和最小，(4,3)A ，(4,3)C ∴-，设直线CB 的解析式是y kx b =+，把C 、B 的坐标代入得：3413k bk b =-+⎧⎨-=+⎩，解得：47k =-，57b =，4577y x ∴=-+，把0x =代入得：57y =， 即P 的坐标是5(0,)7，故选：C ．【备注】本题考查了轴对称-最短路线问题，一次函数的解析式，坐标与图形性质等知识点，关键是能画出P 的位置，题目比较典型，是一道比较好的题目．★★☆练习1．如图，在平面直角坐标系中，已知点(2,3)A ，点(2,1)B -，在x 轴上存在点P 到A ，B 两点的距离之和最小，则P 点的坐标是 ．【答案】(1,0)-【解析】解：作A 关于x 轴的对称点C ，连接BC 交x 轴于P ，则此时AP BP +最小，A 点的坐标为(2,3)，B 点的坐标为(2,1)-，(2,3)C ∴-，设直线BC 的解析式是：y kx b =+，把B 、C 的坐标代入得：2123k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩．即直线BC 的解析式是1y x =--，当0y =时，10x --=，解得：1x =-，P ∴点的坐标是(1,0)-．故答案为：(1,0)-．【备注】本题考查了一次函数图象上点的坐标特征，用待定系数法求一次函数的解析式，轴对称-最短路线问题的应用，关键是能找出P 点，题目具有一定的代表性，难度适中．★★☆练习2．如图，直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，以线段AB 为边在第一象限内作正方形ABCD ．若点P 为x 轴上的一个动点，求当PC PD +的长最小时点P 的坐标．【答案】详见解析【解析】解：直线34120x y +-=与x 轴、y 轴分别交于点B 、A 两点，则点A 、B 的坐标分别为：(0,3)，(4,0)，如图所示，过点C 作CH x ⊥轴交于点H ，90ABO BAO ∠+∠=︒，90ABO CBH ∠+∠=︒，CBH BAO ∴∠=∠，又90AOB CHB ∠=∠=︒，AB BC =，()AOB BHC AAS ∴∆≅∆，4CH OB ∴==，3HB OA ==，故点(7,4)C ，同理可得点(3,7)D ，确定点C 关于x 轴的对称点(7,4)C '-，连接C D '交x 轴于点P ，则此时PC PD +的长最小，将点C '、D 的坐标代入一次函数表达式并解得： 直线CD 的表达式为：116144y x =-+， 当0y =时，6111x =，故点61P，0)．(11【备注】本题考查的是一次函数上坐标点的特征，涉及到点的对称性、正方形性质等，本题的难点在于：通过证明三角形全等，确定点C、D的坐标．★★☆例题2．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，3OB=，D为边OB的中点，若E为x轴上的一个动点，当CDE∆的周长最小时，求点E OA=，4的坐标()A．(3,0)-B．(1,0)C．(0,0)D．(3,0)【答案】B【解析】解：如图，作点D关于x轴的对称点D'，连接CD'与x轴交于点E，连接DE．若在边OA上任取点E'与点E不重合，连接CE'、DE'、D E''由DE CE D E CE CD D E CE DE CE'+'=''+'>'='+=+，可知CDE∆的周长最小．OB=，D为边OB的中点，42∴=，OD∴，(0,2)D在矩形OACB 中，3OA =，4OB =，D 为OB 的中点，3BC ∴=，2D O DO '==，6D B '=，//OE BC ，Rt ∴△D OE Rt '∽△D BC '，∴OE D OBC D B '=' 即236OE = 1OE =，∴点E 的坐标为(1,0)故选：B ．【备注】此题主要考查轴对称--最短路线问题，解决此类问题，一般都是运用轴对称的性质，将求折线问题转化为求线段问题，其说明最短的依据是三角形两边之和大于第三边．★★☆练习1．如图，在平面直角坐标系中，点A 、B 的坐标分别为(1,4)和(3,0)，点C 是y 轴上的一个动点，连接AC 、BC ，当ABC ∆的周长最小值时，ABC ∆的面积为 ．【答案】3【解析】解：如图，作点A 关于y 轴的对称点A '，连接A B '交y 轴于点C '，此时ABC ∆'的周长最小，设直线A B ' 的解析式为y kx b =+，(1,4)A '-，(3,0)B ，∴430k b k b -+=⎧⎨+=⎩，1k ∴=-，3b =，∴直线A B ' 的解析式为3y x =-+，当0x =时，3y =，(0,3)C ∴'，ABC AA BAA C S SS∆'''∴=-11242122=⨯⨯-⨯⨯ 413=-=．所以ABC ∆'的面积为3．故答案为：3．【备注】本题考查了轴对称、最短路线问题、坐标与图形性质、三角形的面积，解决本题的关键是掌握轴对称的性质．★★☆练习2．如图，在平面直角坐标系中，直线122y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边 在第二象限内作正方形ABCD ．（1）求点A 、B 的坐标，并求边AB 的长；（2）求点C 和点D 的坐标；（3）在x 轴上找一点M ，使MDB ∆的周长最小，请求出M 点的坐标，并直接写出MDB ∆的周长最小值．【答案】详见解析【解析】解： （1）对于直线122y x =+， 令0x =，得到2y =；令0y =，得到4x =-，(4,0)A ∴-，(0,2)B ，即4OA =，2OB =， 则224225AB =+=；（2）过D 作DE x ⊥轴，过C 作CF y ⊥轴，四边形ABCD 为正方形，AB BC AD ∴==，90ABC BAD BFC DEA AOB ∠=∠=∠=∠=∠=︒，90FBC ABO ∠+∠=︒，90ABO BAO ∠+∠=︒，90DAE BAO ∠+∠=︒，FBC OAB EDA ∴∠=∠=∠，()DEA AOB BFC AAS ∴∆≅∆≅∆，2AE OB CF ∴===，4DE OA FB ===，即426OE OA AE =+=+=，246OF OB BF =+=+=，则(6,4)D -，(2,6)C -；（3）如图所示，连接BD ，找出B 关于y 轴的对称点B '，连接DB '，交x 轴于点M ，此时BM MD DM MB DB +=+'='最小，即BDM ∆周长最小，(0,2)B ，(0,2)B ∴'-，设直线DB '解析式为y kx b =+，把(6,4)D -，(0,2)B '-代入得：642k b b -+=⎧⎨=-⎩，解得：1k =-，2b =-，∴直线DB '解析式为2y x =--，令0y =，得到2x =-，则M 坐标为(2,0)-， 此时MDB ∆的周长为21062+．【备注】本题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，坐标与图形性质，勾 股定理，全等三角形的判定与性质，正方形的性质，对称性质，以及一次函数与坐标轴的交点，熟练掌握 性质及定理是解本题的关键（二）一次函数线段差最大值问题【例题讲解】★★☆例题1．已知，如图点(1,1)A ，(2,3)B -，点P 为x 轴上一点，当||PA PB -最大时，点P的坐标为( )A ．1(,0)2B ．5(,0)4C ．1(,0)2-D ．(1,0)【答案】A【解析】解：作A 关于x 轴对称点C ，连接BC 并延长交x 轴于点P ， (1,1)A ，C ∴的坐标为(1,1)-，连接BC ，设直线BC 的解析式为：y kx b =+，∴123k b k b +=-⎧⎨+=-⎩， 解得：21k b =-⎧⎨=⎩， ∴直线BC 的解析式为：21y x =-+， 当0y =时，12x =， ∴点P 的坐标为：1(2，0)，当B ，C ，P 不共线时，根据三角形三边的关系可得：||||PA PB PC PB BC -=-<，∴此时||||PA PB PC PB BC -=-=取得最大值．故选：A ．【备注】此题考查了轴对称、待定系数法求一次函数的解析式以及点与一次函数的关系．此题难度较大，解题的关键是找到P 点，注意数形结合思想与方程思想的应用．★★☆练习1．平面直角坐标系中，已知(4,3)A 、(2,1)B ，x 轴上有一点P ，要使PA PB -最大，则P 点坐 标为【答案】(1,0)【解析】解：(4,3)A 、(2,1)B ，x 轴上有一点P ，||PA PB AB ∴-，∴当A ，B ，P 三点共线时，PA PB -最大值等于AB 长，此时，设直线AB 的解析式为y kx b =+，把(4,3)A 、(2,1)B 代入，可得3412k b k b =+⎧⎨=+⎩， 解得11k b =⎧⎨=-⎩， ∴直线AB 的解析式为1y x =-，令0y =，则1x =，P ∴点坐标为(1,0)，故答案为：(1,0)． 【备注】本题主要考查了坐标与图形性质，利用待定系数法求得直线AB 的解析式是解决问题的关键． ★★☆练习2．如图，在平面直角坐标系中，点A 的坐标为(0,4)，点B 的坐标为(6,0)，点P 在一次函数1322y x =+的图象上运动，则PB PA -的最大值为( )A ．2B ．233C ．4D ．143【答案】C【解析】解：如图，作点A 关于直线1322y x =+的对称点K ，连接AK 交直线于H ，连接PK ．AK PH ⊥，(0,4)A ，∴直线AK 的解析式为24y x =-+，由132224y x y x ⎧=+⎪⎨⎪=-+⎩，解得12x y =⎧⎨=⎩， (1H ∴，20，AH KH =，(2,0)K ∴．PB PA PB PK KB ∴-=-，∴当点P 在BK 的延长线上时，P B P K BK '-'=的值最大，最大值为624-=，故选：C ．【备注】本题考查一次函数图象上的点的特征、轴对称等知识，解题的关键是学会利用对称解决最值问题 属于中考常考题型．【题型知识点总结】一次函数最短路径问题注意事项：1. 根据“和小异，差大同”判断是否需要作对称；2. 作对称时注意要选取动点运动的直线为对称轴作某一定点的对称点。

中考复习专题之线段(和差)最值问题之对称对称问题，指的是通过对称的方式求得线段(和差)最值的问题类型，包含一次对称即将军饮马问题、二次对称、过河修桥问题等. 1.将军饮马问题“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。

而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。

如图，将军在图中点A 处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？如图，在直线上找一点P 使得PA+PB 最小？这个问题的难点在于PA+PB 是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．作点A 关于直线的对称点A'，连接PA'，则PA'=PA ，所以PA+PB=PA'+PB当A'、P 、B 三点共线的时候，PA'+PB =A'B ，此时为最小值（两点之间线段最短） 作端点（点A 或点B ）关于折点（上图P 点）所在直线的对称，化折线段为直线段．2.二次对称问题在OA 、OB 上分别取点M 、N ，使得△PMN 周长最小．AB 将军军营河此处M 、N 均为折点，分别作点P 关于OA （折点M 所在直线）、OB （折点N 所在直线）的对称点，化折线段PM +MN +NP 为P'M +MN +NP ’’，当P'、M 、N 、P''共线时，△PMN 周长最小． 3.过河修桥问题已知人在图中点A 村庄，现要过河去往B 村，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？考虑MN 长度恒定，只要求AM +NB 最小值即可．问题在于AM 、NB 彼此分离，所以首先通过平移，使AM 与NB 连在一起，将AM 向下平移使得M 、N 重合，此时A 点落在A ’位置．问题化为求A'N +NB 最小值，显然，当A'、N 、B 共线时，AM+MN+BN 的值最小，并得出桥应建的位置． 【问题扩展1】已知将军在图中点A 处，现要过两条河去往B 点的军营，桥必须垂直于河岸建造，问：桥建在何处能使路程最短？BB考虑PQ 、MN 均为定值，所以路程最短等价于AP +QM +NB 最小，对于这彼此分离的三段，可以通过平移使其连接到一起．AP 平移至A'Q ，NB 平移至MB ’，化AP +QM +NB 为A'Q +QM +MB'．当A'、Q 、M 、B ’共线时，A'Q +QM +MB'取到最小值，再依次确定P 、N 位置． 【问题扩展1】如图，将军在A 点处，现在将军要带马去河边喝水，并沿着河岸走一段路，再返回军营，问怎么走路程最短？已知A 、B 两点，MN 长度为定值，求确定M 、N 位置使得AM +MN +NB 值最小？【分析】考虑MN 为定值，故只要AM +BN 值最小即可．将AM 平移使M 、N 重合，AM =A'N ，将AM +BN 转化为A'N +NB ．构造点A 关于MN 的对称点A''，连接A''B ，可依次确定N 、M 位置，可得路线．军营BBB军营河练习题1.如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为___________．2.如图，正方形ABCD 的边长是4，M 在DC 上，且DM =1， N 是AC 边上的一动点，则△DMN 周长的最小值是___________．3.如图，在Rt △ABO 中，∠OBA =90°，A （4,4），点C 在边AB 上，且AC :CB =1:3，点D 为OB 的中点，点P 为边OA 上的动点，当点P 在OA 上移动时，使四边形PDBC 周长最小的点P 的坐标为( ) A ．(2,2)B ．5(2，5)2C ．8(3，8)3D ．(3,3)4.如图，在△ABC 中，AC =BC ，∠ACB =90°，点D 在BC 上，BD =3，DC =1，点P 是AB 上的动点，则PC +PD 的最小值为( ) A ．4B ．5C ．6D ．75.如图，在等边△ABC 中，AB =6， N 为AB 上一点且BN =2AN ， BC 的高线AD 交BC 于点D ，M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________．6.如图，在Rt △ABD 中，AB =6，∠BAD =30°，∠D =90°，N 为AB 上一点且BN =2AN ， M 是AD 上的动点，连结BM ，MN ，则BM +MN 的最小值是___________．7.如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为( ) A ．3B ．4C．D．8.如图，在锐角三角形ABC 中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是( ) AB ．2C．D ．49.如图，在菱形ABCD 中，AC=BD =6，E 是BC 的中点，P 、M 分别是AC 、AB 上的动点，连接PE 、PM ，则PE +PM 的最小值是( )A ．6B．C．D ．4.5P OBAMNNMD CBAPDCBAA BCDMNN M D BAE AFCDBNM DCBA10.如图，矩形ABOC 的顶点A 的坐标为（-4,5），D 是OB 的中点，E 是OC 上的一点，当△ADE 的周长最小时，点E 的坐标是( ) A ．4(0,)3B ．5(0,)3C ．(0,2)D ．10(0,)311.如图，在矩形ABCD 中，AB =6，AD =3，动点P 满足13PAB ABCD S S ∆=矩形，则点P 到A 、B 两点距离之和P A +PB 的最小值为( )A．B．C．D12.如图，矩形ABCD 中，AB =10，BC =5，点E 、F 、G 、H 分别在矩形ABCD 各边上，且AE =CG ，BF =DH ，则四边形EFGH 周长的最小值为( ) A．B．C．D．13.如图，∠AOB =60°，点P 是∠AOB 内的定点且OPM 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是( )ABC ．6D ．314. 如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N （3,0）是OB 上的一定点，点M 是ON 的中点，∠AOB =30°，要使PM +PN 最小，则点P 的坐标为 ． 15.如图，已知正比例函数y =kx （k >0）的图像与x 轴相交所成的锐角为70°，定点A 的坐标为（0，4），P 为y 轴上的一个动点，M 、N 为函数y =kx （k >0）的图像上的两个动点，则AM +MP +PN 的最小值为____________．16.如图，在平面直角坐标系中，矩形ABCD 的顶点B 在原点，点A 、C 在坐标轴上，点D 的坐标为（6，4），E 为CD 的中点，点P 、Q 为BC 边上两个动点，且PQ =2，要使四边形APQE 的周长最小，则点P 的坐示应为______________．17.如图，矩形ABCD 中，AD =2，AB =4，AC 为对角线，E 、F 分别为边AB 、CD 上的动点，且EF ⊥AC 于点M ，连接AF 、CE ，求AF +CE 的最小值．EPDCBAMDCBAPHFGEDCB AA BMOPN18.如图，在平面直角坐标系中，Rt△OAB 的直角顶点A 在x 轴的正半轴上，顶点B的坐标为(3)，点C 的坐标为(12，0)，点P 为斜边OB 上一动点，则PA+PC 的最小值为___________． 19.如图，△ AOB=30 °，点 M 、 N 分别在边 OA 、OB 上，且 OM=1 ，ON=3，点 P 、Q 分别在边 OB 、OA 上，则 MP+PQ+QN 的最小值 _________20.如图，在矩形ABCD 中，AB=4，BC=8，E 为CD 边的中点．若P ，Q 为BC 边上的两动点，且PQ=2，则当BP=___时，四边形APQE 的周长最小．21.如图在河的两侧有两个村庄，A 离河为60米，B 离河是30米，AB 的水平距离为120米，河的宽度为30米，问桥修在何处会使得从A 经过桥到B 的路程最小，最小值为多少？参考答案1.82.63.C4.B5.6. 7.C 8.C 9.C 10.B 11.A 12.B 13.D14.3(215. 16.8(,0)3 17.520.2+ 21.180A B CDEFMyxPCBAO Q P ED CB A。

专题6.4 线段的和差模块一：知识清单1.线段的和与差：如下图，有AB +BC ＝AC ，或AC ＝a +b ；AD ＝AB -BD .2.线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点． 如下图，有：12AM MB AB ==.①线段中点的等价表述：如上图，点M 在线段上，且有12AM AB =，则点M 为线段AB 的中点. ②除线段的中点（即二等分点）外，类似的还有线段的三等分点、四等分点等. 如下图，点M ,N ,P 均为线段AB 的四等分点，则有AB PB NP MN AM 41====. PNMBA模块二：同步培优题库全卷共24题 测试时间：80分钟 试卷满分：100分一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2022·江苏·盐城市大丰区实验初级中学七年级阶段练习）已知点M 在线段AB 上，在①AB ＝2AM ；②BM ＝12AB ；③AM ＝BM ；④AM +BM ＝AB 四个式子中，能说明M 是线段AB 的中点的式子有（ ） A ．1个 B ．2个 C ．3个 D ．4个【答案】C【分析】根据线段中点的定义，借助图形逐一判断即可． 【详解】解：如图：∵AB =2AM ，∴点M 是线段AB 的中点， ∵BM =12AB ，∴点M 是线段AB 的中点， ∵AM =BM ，∴点M 是线段AB 的中点， 故①②③都能说明点M 是线段AB 的中点，根据：④AM +BM =AB ，不能判断点M 是线段AB 的中点，故选：C ．【点睛】本题考查了线段中点的定义，借助图形分析是解题的关键．2．（2022·安徽合肥·七年级期末）如图，已知线段AB＝4 cm，延长AB至点C，使AC＝11 cm．点D 是AB的中点，点E是AC的中点，则DE的长为（）A．3 cm B．3.5 cm C．4 cm D．4.5 cm【答案】B【分析】根据线段中点得出AD＝2cm，AE＝5.5cm，结合图形即可得出结果．【详解】解：∵AB＝4 cm，点D是AB的中点，∴AD＝12AB＝2cm．∵AC＝11cm，点E是AC的中点，∴AE＝12AC＝5.5 cm．∴DE＝AE－AD＝5.5－2＝3.5cm故选：B．【点睛】题目主要考查线段中点的计算，找准线段间的数量关系是解题关键．3．（2022·浙江·七年级期末）如图，已知A B C D E、、、、五点在同一直线上，点D是线段AB的中点，点E是线段BC的中点，若线段12AC=，则线段DE等于（）A．6 B．7 C．8 D．9【答案】A【分析】首先根据D点是线段AB的中点，点E是线段BC的中点，可得AD=BD，BE=CE；然后根据线段AC=12，可得BD+CD=12，据此求出CE+CD=6，即可判断出线段DE等于6．【详解】解：∵D点是线段AB的中点，∴AD=BD，∵点E是线段BC的中点，∴BE=CE，∵AC=12，∴AD+CD=12，∴BD+CD=12，又∵BD=2CE+CD，∴2CE+CD+CD=12，即2（CE+CD）=12，∴CE+CD=6，即线段DE等于6．故选：A．【点睛】此题主要考查了两点间的距离的求法，要熟练掌握，解答此题的关键是要明确线段的中点的性质，并能推得AD=BD，BE=CE．4．（2022·安徽·桐城市第二中学七年级期末）已知线段AB=10cm，线段AC=16cm，且AB、AC在同一条直线上，点B在A、C之间，此时AB、AC的中点M、N之间的距离为（）A．13cm B．6cm C．3cm D．1.5cm【答案】C【分析】首先根据题意，结合中点的性质，分别算出AN、AM的长，然后再根据线段之间的数量关系进行计算，即可得出结果．【详解】解：如图，∵16AC=cm，又∵AC 的中点为N ，∴8cm AN =， ∵10AB =cm ，∵AB 的中点为M ，∴5cm AM =，∴853cm MN AN AM =-=-=．故选：C【点睛】本题考查中点的性质、线段的和、差关系，解本题的关键在充分利用数形结合思想解决问题． 5．（2022·浙江·七年级期中）如图，点M 为线段AB 的中点，C 为线段MB 上的任意一点（不与点M ，B 重合）．在同一直线上有一点N ，若1223CN AC <<，则（ ）A ．点N 不能在射线AP 上B ．点N 不能在线段AM 上C ．点N 不能在线段MB 上D ．点N 不能在射线BQ 上【答案】A【分析】当N 在C 点的左侧时，根据题意，可知CN AC <，结合图排除B ， 当N 在C 点的右侧时，当C 点接近M 点时，111222AC AM MB <=,可排除C ；当C 点接近B 点时，1122AC AB MB <=，则可排除D ． 【详解】213CN AC <<，CN AC ∴<， ①当N 在C 点的左侧时，结合图则，点N 不能在射线AP 上，故A 符合题意； N ∴在线段AM 上，故B 错误；②当N 在C 点的右侧时，当C 点接近M 点时，111222AC AM MB <=,此时点N 在线段MB 上；故C 错误；当C 点接近B 点时，1122AC AB MB <=，此时点N 在射线BQ 上，故D 错误故选A ． 【点睛】本题考查了线段的和差关系，比例关系，根据C 是动点，分情况讨论是解题的关键． 6．（2022·河北唐山·七年级期末）如图所示，长为12cm 的线段AB 的中点为M ，C 将线段MB 分为MC 和CB ，且:1:3MC MB =，则线段AC 的长为（ ）A ．10B ．9C ．8D ．7【答案】C【分析】根据中点的定义，可求出AM 和BM 的长度，根据MC 和MB 的比例关系，可求出MC 的长度，最后用AM 加上CM 即可求出AC 的长．【详解】∵点M 为AB 中点，∴AM =BM =12AB =6cm ， ∵:1:3MC MB =，∴13MC MB ==2cm ，∴AC =AM +MC =8cm ；故选：C【点睛】本题主要考查了中点的定义和成比例线段，熟练地根据中点的定义和线段间的比例关系求出需要线段的长度是解题的关键．7．（2022·重庆·西南大学附中七年级期末）如图，点D 为线段AB 的中点，点C 为DB 的中点，若16AB =，13DE AE =，则线段EC 的长（ ）A ．7B ．203C ．6D ．5【答案】C【分析】应用一条线上的线段和差关系进行计算即可得出答案． 【详解】解：∵点D 为线段AB 的中点， ∴AD ＝BD ＝12AB ＝12×16＝8，∵AD ＝AE ＋DE ，DE ＝13AE ，∴AE ＋13AE ＝8，∴AE ＝6，DE ＝2，∵点C 为DB 的中点，∴CD ＝12BD ＝12×8＝4， ∴CE ＝DE ＋CD ＝2＋4＝6，故选：C ．【点睛】本题主要考查了一条线上各个线段关系，看清图中线段关系，熟练掌握两点间的距离计算方法进行求解是解决本题的关键．8．（2022·浙江·）定义：当点C 在线段AB 上，AC nAB =时，我们称n 为点C 在线段AB 上的点值，记作A C B d n =※．甲同学猜想：点C 在线段AB 上，若2AC BC =，则23C AB d =※．乙同学猜想：点C 是线段AB 的三等分点，则13C AB d =※ 关于甲乙两位同学的猜想，下列说法正确的是（ ） A ．甲正确，乙不正确 B ．甲不正确，乙正确 C ．两人都正确D ．两人都不正确【答案】A【分析】本题根据题目所给A C B d n =※的定义对两人的猜想分别进行验证即可得到答案，对于乙的猜想注意进行分类讨论．【详解】解：甲同学：点C 在线段AB 上，且2AC BC =， ∴23AC AB =，∴23C AB d =※，∴甲同学正确．乙同学：点C 在线段AB 上，且点C 是线段AB 的三等分点，∴有两种情况， ①当13AC AB =时，13C AB d =※，②当23AC AB =时，23C AB d =※，∴乙同学错误．故选：A ．【点睛】本题主要考查对于新定义和线段的等分点的理解，对于线段的三等分点注意分类讨论即可． 9．（2022·绍兴市柯桥区七年级开学考试）如图，线段 CD 在线段 AB 上，且 CD =1，若线段AB 的长度是一个正整数，则图中以A ，B ，C ，D 这四点中任意两点为端点的所有线段长度之和可能是（ ）A ．4B ．3C ．2D ．1【答案】A【分析】根据数轴和题意可知，所有线段的长度之和是AC +CD +DB +AD +CB +AB ，然后根据CD =1，线段AB 的长度是一个正整数，可以解答本题．【详解】解：由题意可得，图中以A ，B ，C ，D 这四点中任意两点为端点的所有线段长度之和是： AC +CD +DB +AD +CB +AB =(AC +CD +DB )+(AD +CB )+AB =AB +AB +CD +AB =3AB +CD ，∵CD =1，线段AB 的长度是一个正整数，AB ＞CD ，∴长度之和减1是3的倍数，而只有4-1=3是3的倍数，故选A ．【点睛】本题考查两点间的距离，线段的和差，解题的关键是数形结合，找出所求问题需要的条件． 10．（2022•松江区期末）如图，已知点C 为线段AB 的中点，D 为CB 上一点，下列关系表示错误的是（ ）A ．CD ＝AC ﹣DB B ．BD +AC ＝2BC ﹣CD C ．2CD ＝2AD ﹣ABD ．AB ﹣CD ＝AC ﹣BD【思路点拨】根据图形可以明确线段之间的关系，对线段CD 、BD 、AD 进行和、差转化，即可发现错误选项．【答案】解：∵C 是线段AB 的中点， ∴AC ＝BC ，AB ＝2BC ＝2AC ，∴CD ＝BC ﹣BD ＝AB ﹣BD ＝AC ﹣BD ； ∵BD +AC ＝AB ﹣CD ＝2BC ﹣CD ； ∵CD ＝AD ﹣AC ，∴2CD ＝2AD ﹣2AC ＝2AD ﹣AB ；∴选项A 、B 、C 均正确． 而答案D 中，AB ﹣CD ＝AC +BD ； ∴答案D 错误符合题意．故选：D ．【点睛】本题考查的是线段的长度计算，熟练进行线段的和、差、倍、分计算是解决本题的关键． 二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）11．（2022·湖北·老河口市第四中学七年级阶段练习）C 是线段AB 上一点，D 是BC 的中点，若12cm AB =，2cm =AC ，则BD 的长为______．【答案】5cm【分析】根据题意画出图形，先求出BC ，再根据线段中点的定义详解． 【详解】解：如图，12cm AB =，2cm =AC ，12210(cm)BC AB AC ∴=-=-=．D 是BC 的中点，11105(cm)22BD BC ∴==⨯=．故答案是：5cm ．【点睛】本题考查了两点间的距离，主要利用了线段中点的定义，熟记概念是解题的关键，作出图形更形象直观．12．（2022·浙江丽水·七年级期末）如图，P 是线段MN 上一点，Q 是线段PN 的中点．若MN =10，MP =6，则MQ 的长是____．【答案】8【分析】首先求得NP =4，根据点Q 为NP 中点得出PQ =2，据此即可得出MQ 的长． 【详解】解：∵MN =10，MP =6，∴NP = MN- MP =4， ∵点Q 为NP 中点，∴PQ =QN =12NP =2，∴MQ =MP +PQ =6+2=8，故答案为：8．【点睛】此题主要考查了两点之间的距离，根据中点的定义得出PQ =2是解题关键．13．（2022·宁夏·景博中学七年级期末）如图，点C 为线段AB 的中点，点D 在线段CB 上，AB ＝10，DB ＝4，则CD ＝________．【答案】1【分析】先根据线段中点的定义可得5BC =，再根据CD BC DB =-即可得．【详解】解：点C 为线段AB 的中点，且10AB =，152BC AB ∴==， 4DB =，541CD BC DB =∴=--=，故答案为：1．【点睛】本题考查了与线段中点有关的计算，熟练掌握线段之间的运算是解题关键．14．（2022·陕西渭南·七年级期末）如图，AD =12BD ，E 是BC 的中点，BE =15AC =2cm ，则线段DB的长为_______cm ．【答案】4【分析】根据BE =15AC =2cm 可以求得AC 长，进而得出AB 、BC 的长，即可求得DB 的长．【详解】解：∵BE =15AC =2(cm)，∴AC =5BE =10(cm)，∵E 是BC 的中点，∴BC =2BE =2×2=4(cm)，∴AB =AC -BC =10-4=6(cm)， ∵AD =12DB ，∴AD +DB =AD +2AD =6(cm)，∴AD =2cm ，∴DB =4cm ，故答案为：4．【点睛】本题主要考查的是线段的和差倍分计算和线段中点的概念，找出线段间的数量关系是解决此类问题的关键．15．（2022·山东威海·期末）如图，点C ，点D 在线段AB 上，点E ，点F 分别为AC ，BD 的中点．若AB m =，CD n =，则EF 的长为________．【答案】12m +12n【分析】先根据中点的定义可得EC =12AC 、DF =12BD ，再根据线段的和差可得AC +BD =AB -CD =m -n ，最后根据EF =EC +CD +DF 求解即可．【详解】解：∵点E 、点F 分别为AC 、BD 的中点∴EC =12AC ,DF =12BD ∵AB m =，CD n =∴AC +BD =AB -CD =m -n∴EF =EC +CD +DF =12AC +CD +12BD =12(AC +BD )+CD =12( m -n )+n =12m +12n ．故答案为12m +12n ． 【点睛】本题主要考查了中点的定义、线段的和差等知识点，通过识图、明确线段间的关系成为解答本题的关键．16．（2022·浙江·）已知 A B C 、、三点在同一条直线上，且线段4cm,6cm AB BC ==，点D E 、分别是线段AB BC 、的中点点F 是线段DE 的中点，则BF =_______cm ．【答案】12或52【分析】根据中点定义求出BD 、BE 的长度，然后分①点C 在AB 的延长线上时，求出DE 的长度，再根据中点定义求出EF 的长，然后根据BF =BE -EF 代入数据进行计算即可得解；②点C 在AB 的反向延长线上时，求出DE 的长度，再根据中点定义求出EF 的长，然后根据BF =BE -EF 代入数据进行计算即可得解． 【详解】解：D 、E 分别是线段AB 、BC 的中点，4AB cm =，6BC cm =，114222BD AB cm ∴==⨯=，116322BE BC cm ==⨯=， ①如图1，点C 在AB 的延长线上时，235DE BD BE cm =+=+=，点F 是线段DE 的中点，1155222EF DE cm ∴==⨯=，此时，51322BF BE EF cm =-=-=； ②如图2，点C 在AB 的反向延长线上时，321DE BE BD cm =-=-=，点F 是线段DE 的中点，1111222EF DE cm ∴==⨯=，此时，15322BF BE EF =-=-=， 综上所述，12BF =或52cm ．故答案为：12或52．【点睛】本题考查了两点间的距离，线段中点的定义，难点在于要分情况讨论，作出图形更形象直观． 17．（2022•和平区期末）已知线段AB ＝12，M 是AB 的中点，点C 是直线AB 上一点，且AC ＝5BC ，则C 、M 两点间的距离为 ．【思路点拨】根据线段中点的性质推出AM ＝BM ＝AB ＝×12＝6，并分点C 在点B 左侧和点C 在点B 左侧两种情况进行讨论，由题意作出相关的图形，结合图形当点C 在点B 左侧时，MC ＝BM ﹣BC ；当点C 在点B 右侧时，MC ＝BM +BC ，利用线段之间的和差关系进行求解即可． 【答案】解：∵AB ＝12，M 是AB 的中点， ∴AM ＝BM ＝AB ＝×12＝6， 当点C 在点B 左侧时，如图1，∵AC ＝5BC ，∴AB ＝AC +BC ＝6BC ，∴MC＝BM﹣BC＝AB﹣AB＝AB＝×12＝4；当点C在点B右侧时，如图2，∵AC＝5BC，∴AB＝AC﹣BC＝4BC＝12，∴BC＝3，∴MC＝BM+BC＝6+3＝9，综上所述，C、M两点间的距离为4或9．故答案为：4或9．【点睛】本题考查两点间的距离及线段的和差，解题的关键是根据题意进行分类讨论（点C在点B 左侧时和点C在点B左侧时），注意结合图形联系线段中点的性质和线段之间的和差关系进行求解．18．（2022·北京海淀区·七年级期末）已知线段6cmAB=，若M是AB的三等分点，N是AM的中点，则线段MN的长度为________．【答案】1cm或2cm【分析】分两种情况考虑点M是AB的三等分点，求出AM的长，由中点定义求出MN即可．【详解】当M是AB的左三等分点，∵AB=6cm，∴AM=11AB=6=233⨯cm，∵N是AM的中点，∴AN=NM=11AM=2=1 22⨯，当M是AB的右三等分点，∵AB=6cm，∴AM=22AB=6=433⨯cm，∵N是AM的中点，∴AN=NM=11AM=4=2 22⨯，线段MN的长度为1cm或2cm．故答案为：1cm或2cm．【点睛】本题考查线段的三等分点，线段的中点计算，掌握线段三等分的性质，线段的中点的性质，会利用分类思想求线段AM是解题关键．三、解答题（本大题共6小题，共46分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）19．（2022·山东郓城县·七年级期末）某摄制组从A市到B市有一天的路程，由于堵车中午才赶到一个小镇（D ），只行驶了原计划的三分之一（原计划行驶到C 地），过了小镇，汽车赶了400千米，傍晚才停下来休息（休息处E ），司机说：再走从C 地到这里路程的二分之一就到达目的地了，问：A ，B 两市相距多少千米．【答案】A ，B 两市相距600千米．【分析】根据题意可知DE 的距离且可以得到12AD DC =，12EB CE =，11()22AD EB DC CE DE +=+=，由1=2AB AD EB DE DE DE =+++计算即可得出结果．【详解】如图，由题意可知，400DE =千米，12AD DC =，12EB CE =， ∴ 111()400200222AD EB DC CE DE +=+==⨯=（千米）∴ 200400600AB AD EB DE =++=+=（千米） 答：A ，B 两市相距600千米．【点睛】本题考查了求解线段长度在实际生活中的应用，能够找出线段之间的等量关系是解题关键． 20．（2022·辽宁大连市·）已知点D 为线段AB 的中点，点C 在线段AB 上．（1）如图1，若8cm,6cm AC BC ==，求线段CD 的长；（2）如图2，若2BC CD =，点E 为BD 中点，18cm AE =，求线段AB 的长． 【答案】（1）1cm ；（2）24cm【分析】（1）先求出AB 的长，再根据中点定义求出BD 的长，进而可求CD 的长； （2）设cm CD x =，用含x 的代数式表示出AE ，然后列方程求出x ，进而可求AB 的长． 【详解】解：（1）∵8cm,6cm AC BC ==，∴8614cm AB AC BC =+=+=， ∵点D 为线段AB 的中点，∴11147cm 22BD AB ==⨯=． ∵CD BD BC =-，∴761cm CD =-=．∴线段CD 的长为1cm ． （2）设cm CD x =．∵2BC CD =，∴2cm BC x =∵BD CD BC =+，∴23cm BD x x x =+=．∵E 为BD 中点，∴13cm 22DE BD x ==． 又∵D 为AB 中点，∴3cm AD BD x ==．∵AE AD DE =+，∴393cm 22AE x x x =+=． ∵18cm AE =，∴918,42x x ==，∴2624cm AB BD x ===，∴线段AB 的长为24cm ．【点睛】本题考查了线段中点的有关计算，如果点C 把线段AB 分成相等的两条线段AC 与BC ，那么点C 叫做线段AB 的中点，这时AC =BC =12AB ，或AB =2AC =2BC ． 21．（2022·浙江·七年级期末）如图，线段8cm AB C =,是线段AB 上一点，M 是AB 的中点，N 是AC 的中点．（1）3cm AC =，求线段CM NM 、的长；（2）若线段AC m =，线段BC n =，求MN 的长度（m n <用含,m n 的代数式表示）．【答案】（1）CM =1cm ，NM =2.5cm ；（2）12n【分析】（1）求出AM 长，代入CM =AM -AC 求出即可；分别求出AN 、AM 长，代入MN =AM -AN 求出即可；（2）分别求出AM 和AN ，利用AM -AN 可得MN ． 【详解】解：（1）8AB cm =，M 是AB 的中点，142AM AB cm ∴==， 3AC cm =，431CM AM AC cm ∴=-=-=；8AB cm =，3AC cm =，M 是AB 的中点，N 是AC 的中点， 142AM AB cm ∴==，11.52AN AC cm ==，4 1.52.5MN AM AN cm ∴=-=-=；（2）AC m =，BC n =，AB AC BC m n ∴=+=+，M 是AB 的中点，N 是AC 的中点，11()22AM AB m n ∴==+，1122AN AC m ==，111()222MN AM AN m n m n ∴=-=+-=．【点睛】本题考查了两点之间的距离，线段中点的定义的应用，解此题的关键是求出AM 、AN 的长． 22.（2022·平山县七年级期末）已知点A ，B ，C 在同一条直线上，点M ，N 分别是AC ，BC 的中点．（1）如图1，若点C 在线段AB 上，AC =6cm ，CB =4cm ，则线段MN 的长为 cm ； （2）若点C 在线段AB 上，且AC +CB =acm ，则线段MN 的长度为 cm ；（3）如图2，若点C 在线段AB 的延长线上，且AC -BC =bcm ，猜测MN 的长度，写出你的结论，并说明理由．【答案】（1）5，（2）12a ，（3）MN =12b ．理由见解析．【分析】（1）根据中点的定义求解；（2）与（1）同理，根据中点的定义求解；（3）根据MN=CM-CN 求解．【详解】解：（1）由题意可得：113222MC AC CN CB====，，∴MN=MC+CN=3+2=5，故答案为5；（2）与（1）同理有：1122MC AC CN CB==，，∴()11112222MC CN AC CB AC CB a+=+=+=，故答案为12a，（3）结论为：MN=12b，理由如下：当点C在线段AB的延长线时，如图：则AC＞BC，因为M是AC的中点，所以CM=12AC，因为点N是BC的中点，所以CN=12BC，所以MN=CM-CN=12（AC-BC）=12b．【点睛】本题考查中点的应用，熟练掌握中点的意义、线段的四则运算及准确画图是解题关键．23．（2022·杭州市七年级月考）已知点C在线段AB上，AC＝2BC，点D、E在直线AB上，点D在点E的左侧，（1）若AB＝18，DE＝8，线段DE在线段AB上移动，①如图1，当E为BC中点时，求AD的长；②当点C是线段DE的三等分点时，求AD的长；（2）若AB＝2DE，线段DE在直线上移动，且满足关系式32AD ECBE+=，则CDAB＝．【答案】（1）①AD＝7；②AD＝203或243；（2）1742或116【分析】（1）根据已知条件得到BC＝6，AC＝12，①由线段中点的定义得到CE＝3，求得CD＝5，由线段的和差得到AD＝AC﹣CD＝12﹣5＝7；②当点C线段DE的三等分点时，可求得CE＝13 DE＝83或CE＝23DE＝163，则CD＝163或83，由线段的和差即可得到结论；（2）当点E在线段BC之间时，，设BC＝x，则AC＝2BC＝2x，求得AB＝3x，设CE＝y，得到AE＝2x+y，BE＝x﹣y，求得y＝27x，当点E在点A的左侧，设BC＝x，则DE＝1.5x，设CE＝y，求得DC＝EC+DE＝y+1.5x，得到y＝4x，于是得到结论．【详解】解：（1）∵AC＝2BC，AB＝18，∴BC＝6，AC＝12，①∵E为BC中点，∴CE＝3，∵DE＝8，∴CD＝5，∴AD＝AC﹣CD＝12﹣5＝7；②∵点C是线段DE的三等分点，DE＝8，∴CE＝13DE＝83或CE＝23DE＝163，∴CD＝163或CD＝83，∴AD＝AC﹣CD＝12﹣163＝203或12-83=243；（2）当点E在线段BC之间时，如图，设BC＝x，则AC＝2BC＝2x，∴AB＝3x，∵AB＝2DE，∴DE＝1.5x，设CE＝y，∴AE＝2x+y，BE＝x﹣y，∴AD＝AE﹣DE＝2x+y﹣1.5x＝0.5x+y，∵32AD ECBE+=，∴0.532x y yx y++=-，∴y＝27x，∴CD＝1.5x﹣27x＝1714x，∴171714342==xCDAB x；当点E在点A的左侧，如图，设BC＝x，则DE＝1.5x，设CE＝y，∴DC＝EC+DE＝y+1.5x，∴AD＝DC﹣AC＝y+1.5x﹣2x＝y﹣0.5x，∵32AD ECBE+=，BE＝EC+BC＝x+y，∴0.532y x yx y-+=+，∴y＝4x，∴CD＝y+1.5x＝4x+1.5x＝5.5x，BD＝DC+BC＝y+1.5x+x＝6.5x，∴AB＝BD﹣AD＝6.5x﹣y+0.5x＝6.5x﹣4x+0.5x＝3x，∴5.51136==CD xAB x，当点E在线段AC上及点E在点B右侧时，无解，综上所述CDAB的值为1742或116．故答案为：1742或116．【点睛】本题考查了两点间的距离，利用了线段中点的性质、线段的和差、准确识图分类讨论DE的位置是解题的关键．24．（2022·浙江·七年级课时练习）小明在学习了比较线段的长短时对下面一道问题产生了探究的兴趣：如图1，点C在线段AB上，M，N分别是AC，BC的中点．若AB＝12，AC＝8，求MN的长．(1)根据题意，小明求得MN＝___________；(2)小明在求解（1）的过程中，发现MN的长度具有一个特殊性质，于是他先将题中的条件一般化，并开始深入探究．设AB＝a，C是线段AB上任意一点（不与点A，B重合），小明提出了如下三个问题，请你帮助小明解答．①如图1，M，N分别是AC，BC的中点，则MN＝______________；②如图2，M，N分别是AC，BC的三等分点，即13AM AC=，13BN BC=，求MN的长；③若M，N分别是AC，BC的n等分点，即1AM ACn=，1BN BCn=，则MN＝___________；∴MN=12 a；故答案为：12 a；②∵AM=13AC，BN=13BC，∴CM=23AC，CN=23BC，∴MN=CM+CN=23AC+23BC=23AB，∵AB=a，∴MN=23 a；③∵AM=1nAC，BN=1nBC，∴CM=1nn-AC，CN=1nn-BC，∴MN=CM+CN=1nn-AC+1nn-BC=1nn-AB，∵AB=a，∴MN=1nn-a，故答案为：1nn-a．【点睛】本题考查了线段的中点、线段的和差，解题的关键是掌握线段中点的定义及线段和差运算．25．（2022·深圳市高级中学初一期末）如图，P是线段AB上一点，AB=12cm，C、D两点分别从P、B 出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上），运动的时间为t.（1）当t=1时，PD=2AC，请求出AP的长；（2）当t=2时，PD=2AC，请求出AP的长；（3）若C、D运动到任一时刻时，总有PD=2AC，请求出AP的长；（4）在（3）的条件下，Q是直线AB上一点，且AQ﹣BQ=PQ，求PQ的长.【答案】（1）4cm；（2）4cm；（3）4cm；（4）4cm或12cm分析：(1) 观察图形可以看出，图中的线段PC和线段BD的长分别代表动点C和D的运动路程. 利用“路程等于速度与时间之积”的关系可以得到线段PC和线段BD的长，进而发现BD=2PC. 结合条件PD=2AC，可以得到PB=2AP. 根据上述关系以及线段AB的长，可以求得线段AP的长.(2) 利用“路程等于速度与时间之积”的关系结合题目中给出的运动时间，可以求得线段PC和线段BD的长，进而发现BD=2PC. 根据BD=2PC和PD=2AC的关系，依照第(1)小题的思路，可以求得线段AP 的长.(3) 利用“路程等于速度与时间之积”的关系可知，只要运动时间一致，点C 与点D 运动路程的关系与它们运动速度的关系一致. 根据题目中给出的运动速度的关系，可以得到BD =2PC . 这样，本小题的思路就与前两个小题的思路一致了. 于是，依照第(1)小题的思路，可以求得线段AP 的长. (4) 由于题目中没有指明点Q 与线段AB 的位置关系，所以应该按照点Q 在线段AB 上以及点Q 在线段AB 的延长线上两种情况分别进行求解. 首先，根据题意和相关的条件画出相应的示意图. 根据图中各线段之间的关系并结合条件AQ -BQ =PQ ，得到AP 和BQ 之间的关系，借助前面几个小题的结论，即可求得线段PQ 的长.【解析】(1) 因为点C 从P 出发以1(cm/s)的速度运动，运动的时间为t =1(s)，所以111PC =⨯=(cm). 因为点D 从B 出发以2(cm/s)的速度运动，运动的时间为t =1(s)，所以212BD =⨯=(cm).故BD =2PC. 因为PD =2AC ，BD =2PC ，所以BD +PD =2(PC +AC )，即PB =2AP .故AB =AP +PB =3AP . 因为AB =12cm ，所以1112433AP AB ==⨯=(cm). (2) 因为点C 从P 出发以1(cm/s)的速度运动，运动的时间为t =2(s)，所以122PC =⨯=(cm). 因为点D 从B 出发以2(cm/s)的速度运动，运动的时间为t =2(s)，所以224BD =⨯=(cm).故BD =2PC. 因为PD =2AC ，BD =2PC ，所以BD +PD =2(PC +AC )，即PB =2AP .故AB =AP +PB =3AP . 因为AB =12cm ，所以1112433AP AB ==⨯=(cm). (3) 因为点C 从P 出发以1(cm/s)的速度运动，运动的时间为t (s)，所以PC t =(cm).因为点D 从B 出发以2(cm/s)的速度运动，运动的时间为t (s)，所以2BD t =(cm).故BD =2PC. 因为PD =2AC ，BD =2PC ，所以BD +PD =2(PC +AC )，即PB =2AP .故AB =AP +PB =3AP . 因为AB =12cm ，所以1112433AP AB ==⨯=(cm). (4) 本题需要对以下两种情况分别进行讨论.(i) 点Q 在线段AB 上(如图①).因为AQ -BQ =PQ ，所以AQ =PQ +BQ .因为AQ =AP +PQ ，所以AP =BQ .因为13AP AB =，所以13BQ AP AB ==. 故13PQ AB AP BQ AB =--=.因为AB =12cm ，所以1112433PQ AB ==⨯=(cm).(ii) 点Q 不在线段AB 上，则点Q 在线段AB 的延长线上(如图②). 因为AQ -BQ =PQ ，所以AQ =PQ +BQ .因为AQ =AP +PQ ，所以AP =BQ . 因为13AP AB =，所以13BQ AP AB ==.故1433AQ AB BQ AB AB AB =+=+=.因为AB=12cm，所以411233PQ AQ AP AB AB AB=-=-==(cm).综上所述，PQ的长为4cm或12cm.点睛：本题是一道几何动点问题. 分析图形和题意，找到代表动点运动路程的线段是解决动点问题的重要环节. 利用速度、时间和路程的关系，常常可以将几何问题与代数运算结合起来，通过运算获得更多的线段之间的关系，从而为解决问题提供有利条件. 另外，分情况讨论的思想也是非常重要的，在思考问题时要注意体会和运用.。

线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是：1、两点这间线段最短。

2、三角形的任意两边之和大于第三边（找和的最小值）。

3、三角形的任意两边之差小于第三边（找差的最大值）。

作图找点的关键：充分利用轴对称，找出对称点，然后，使三点在一条直线上。

即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。

证明此类问题，可任意另找一点，利用以上原理来证明。

一两条线段差的最大值：（1）两点同侧：如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB，︱PA－PB︱＜ABp'（2两点异侧：如图，如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：1、作B关于直线L的对称点B。

B2、连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB、PB。

︱PA－PB︱=︱PA－PB︱＜AB（三角形任意两边之差小于第三边）二、两条线段和的最小值问题：（1））两点同侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（三角形的任意两边之和大于第三边（找和的最小值），P A＋PB=AB（2）两点异侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（两点之间线段最短）三、中考考点：08年林金钟老师的最后一题：如图，在矩形ABCO中，B（3，2），E（3，1），F（1，2）在X轴与Y轴上是否分别存在点M、N，使得四边形EFNM的周长最小？若存在，请求出周长的最小值，若不存在，请说明理由。

提示：EF长不变。

即求F N＋NM＋MF的最小值。

利用E关于X轴的对称点E，F的对称点F，把这三条线段搬到同一条直线上。

一、以正方形为载体，求线段和的最小值例1. 如图1，四边形ABCD 是正方形，边长是4，E 是BC 上一点，且CE ＝1，P 是对角线BD 上任一点，则PE ＋PC 的最小值是_____________。

ABCP中考数学复习线段和差最值系列之费马点皮耶·德·费马，17世纪法国数学家，有“业余数学家之王”的美誉，之所以叫业余并非段位不够，而是因为其主职是律师，兼职搞搞数学．费马在解析几何、微积分等领域都有卓越的贡献，除此之外，费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等．言归正传，今天的问题不是费马提出来的，是他解决的，故而叫费马点． 问题：在△ABC 内找一点P ，使得P A +PB +PC 最小．【分析】在之前的最值问题中，我们解决的依据有：两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等．以上依据似乎都用不上，怎么办？若点P 满足∠PAB=∠BPC=∠CPA=120°，则PA+PB+PC 值最小，P 点称为该三角形的费马点．一、如何作费马点问题要从初一学到的全等说起：（1）如图，分别以△ABC 中的AB 、AC 为边，作等边△ABD 、等边△ACE ． （2）连接CD 、BE ，即有一组手拉手全等：△ADC ≌△ABE ．（3）记CD 、BE 交点为P ，点P 即为费马点．（到这一步其实就可以了）（4）以BC 为边作等边△BCF ，连接AF ，必过点P ，有∠P AB =∠BPC =∠CP A =120°．在图三的模型里有结论：（1）∠BPD =60°；（2）连接AP ，AP 平分∠DPE ．有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°．但是在这里有个小小的要求，细心的同学会发现，这个图成立的一个必要条件是∠BAC <120°，若120BAC ∠≥︒ ,这个图就不是这个图了，会长成这个样子：EB ACAB CDE此时CD 与BE 交点P 点还是我们的费马点吗？显然这时候就不是了，显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和．所以，是的，你想得没错，此时三角形的费马点就是A 点！当然这种情况不会考的，就不多说了．二、为什么是这个点为什么P 点满足∠P AB =∠BPC =∠CP A =120°，P A +PB +PC 值就会最小呢？归根结底，还是要重组这里3条线段：P A 、PB 、PC 的位置，而重组的方法是构造旋转！在上图3中，如下有△ADC ≌△ABE ，可得：CD =BE ．类似的手拉手，在图4中有3组，可得：AF =BE =CD ．巧的，它们仨的长度居然一样长！更巧的是，其长度便是我们要求的P A +PB +PC 的最小值，这一点是可以猜想得到的，毕竟最小值这个结果，应该也是个特别的值！ 接下来才是真正的证明：考虑到∠APB =120°，∴∠APE =60°，则可以AP 为边，在PE 边取点Q 使得PQ =AP ，则△APQ 是等边三角形．△APQ 、△ACE 均为等边三角形，且共顶点A ，故△APC ≌△AQE ，PC =QE ． 以上两步分别转化P A =PQ ，PC =QE ，故P A +PB +PC =PB +PQ +QE =BE ．没有对比就没有差别，我们换个P 点位置，如下右图，同样可以构造等边△APQ ，同样有△APC ≌△AQE ，转化P A =PQ ，PC =QE ，显然，P A +PB +PC =PB +PQ +QE >BE ．还剩下第3个问题！如果说费马点以前还算是课外的拓展内容，那现在，已经有人把它搬上了中考舞台！【中考再现】问题背景：如图1，将△ABC 绕点A 逆时针旋转60°得到△ADE ，DE 与BC 交于点P ，可推出结论：P A +PC =PE ．问题解决：如图2，在△MNG 中，MN =6，∠M =75°，MG=O 是△MNG 内一点，则点O 到△MNG 三个顶点的距离和的最小值是______．【分析】本题的问题背景实际上是提示了解题思路，构造60°的旋转，当然如果已经了解了费马点问题，直接来解决就好了！如图，以MG 为边作等边△MGH ，连接NH ，则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值．（此处不再证明）过点H 作HQ ⊥NM 交NM 延长线于Q 点，根据∠NMG =75°，∠GMH =60°，可得∠HMQ =45°，∴△MHQ 是等腰直角三角形， ∴MQ =HQ =4，∴NH== 练习题1.如图，在△ABC 中，△ACB=90°，AB=AC=1，P 是△ABC 内一点，求P A +PB +PC 的最小值．2. 如图，已知矩形ABCD ，AB =4，BC =6，点M 为矩形内一点，点E 为BC 边上任意一点，则MA +MD +ME 的最小值为______．NG图2图1ABCD EPHGN M464Q HGN MABCDME3.如图，矩形ABCD中，AB=10，BC=15，现在要找两点E、F，则EA+EB+EF+FC+FD的最小值为__________4.如图，等腰Rt∆ABC中，AB=4，P为∆ABC内部一点，则PA+PB+PC的最小值为_______5.如图，∆ABC中，AB=4，,∠ABC=75°，P为∆ABC内的一个动点，连接PA、PB、PC，则PA+PB+PC的最小值为________6.如图，P为正方形ABCD对角线BD上一动点，若AB=2，则PA+PB+PC的最小值为______7.在Rt∆ABC中，∠ACB=90°，AC=1，，点O为Rt∆ABC内一点，连接AO、BO、CO，且∠AOC=∠COB=∠BOA=120°，则OA+OB+OC=_______8.如图，在四边形ABCD中，∠B=60°，AB=BC=3，AD=4，∠BAD=90°，点P是四边形内部一点，则PA+PB+PD的最小值是______9.如图，点P是矩形ABCD对角线BD上的一个动点，已知AB=2，，则PA+PB+PC 的最小值为_______10.如图，菱形ABCD的对角线AC上有一动点P，BC=6，∠ABC=150°，则PA+PB+PD的最小值为__________11.已知，在∆ABC中，∠ACB=30°点P是ABC内一动点，则PA+PB+PC的最小值为__________12.如图，设点P到等边三角形ABC两顶点A、B的距离分别为2则PC的最大值为______13.如图，设点P到正方形ABCD两顶点A、D的距离为2PC的最大值为________14.如图，设点P到正方形ABCD两顶点A、D的距离为2则PO的最大值为_________.15.如图，在Rt∆ABC中，∠BAC=90⁰，AB=AC，点D是BC边上一动点，连接AD，把AD 绕点A逆时针旋转90⁰，得到AE，连接CE、DE，点F是DE的中点，连接CF问题：在点D运动的过程中，在线段AD上存在一点P，使PA+PB+PC的值最小，当PA+PB+PC 取最小值时，AP的长为m，用含有m的式子表示CE的长.参考答案1.7.8.7 9.3 10. 12.2+13.2+1 15.32m +。

线段和差问题的截长补短方案（一题多解）系列文章之一线段和差问题与截长补短法（含答案）四川崇州 平生曜曜数学好玩，因为定题型、树模型，招式路数皆可寻。

几何中的线段和差问题，截长补短法在实施过程中都有四种截长方案，八种补短方案，可谓十二重关。

本文即将推出一道线段和差问题，希望同学们努力破之。

作者曾闲着没事碰巧把这十二种方案都尝试成功了，所以对于同学而言这十二关障的破解就不再是渺茫的探求，而是一个已经有了答案的考题。

同学们尽管去尝试，要深信这十二种方案皆能破题，但也仅限于本文所推题目而已，至于其它的线段和差问题十二关障能否一一告破就不好说了。

比如本人正在攻克一道线段和差问题，被弄得昏天地转，仍未冲破牛角，现在只得将之当作休闲佐料耳。

作者打心底告诉各位同学，把一道“典型题”做透了，会领悟n 多，积淀一抹多。

但说得再多也是空谈，当你正真去把它做实，你才能感受到其中的丰富与藕联，而后你再通过提炼啊，总结啊，什么，什么的，定能铸就非凡的解题技艺。

数学可玩，因为按需补、应需造，综合分析可当道。

好了，大家来凑凑热闹，去感受那应需而生的几何构造是如何美妙？ 如图，等边⊿ABC 中M 、N 分别为线段AB 、BC 上的两点，且BM=CN ，AN 、CM 相交于点E ，将⊿ABC 绕点C 旋转，使CB 与CA 重合得到⊿ACD ，连结DE.（1）、求证：⊿BCM ≌⊿CAN ； （2）、求∠AED 的度数； （3）、求证：AE + CE = DE ；第一篇章：探讨第（1）、（2）问的解答第（1）问的解答（1）、∵⊿ABC 是等边三角形 ， ∴ BC = AC ，∠B =∠ACN又∵BM = CN ，∴⊿BCM ≌⊿CAN .第（2）问的解答〈分析一〉：通过量角器测量，可大胆猜想ο∠AED，怎样求证？60= Array由（1）题，容易证获CAN=∠，BCM∠再由外角性质易证ο∠AEM，从而∠=60得ο∠AEC，那么关键环节来了！120=在四边形AECD中，欲证边AD所对“帆尖角”ο60∠ACD，所以=60=∠AED，考虑到边AD所对另一“帆尖角”ο只需去求证“A、E、C、D”四点共圆即可。

中考复习专题：线段和或差的最值问题引例：如图，有一圆形透明玻璃容器，高15cm，底面周长为24cm，在容器内壁柜上边缘4cm的A处，停着一只小飞虫，一只蜘蛛从容器底部外向上爬了3cm的B处时（B 处与A处恰好相对），发现了小飞虫，问蜘蛛怎样爬去吃小飞虫最近？它至少要爬多少路？（厚度忽略不计）．Ⅰ．专题精讲：最值问题是一类综合性较强的问题，而线段和（差）问题，要归归于几何模型：（1）归于“两点之间的连线中，线段最短”凡属于求“变动的两线段之和的最小值”时，大都应用这一模型．（2）归于“三角形两边之差小于第三边”凡属于求“变动的两线段之差的最大值”时，大都应用这一模型．Ⅱ．典型例题剖析:一．归入“两点之间的连线中，线段最短”Ⅰ．“饮马”几何模型：条件：如下左图，A、B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA＋PB的值最小．模型应用：1．如图，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．则PB+PE的最小值是 2．如图，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P 是OB上一动点，则PA+PC的最小值是．3．如图，在锐角△ABC中，AB＝42，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是．第1题第2题第3题第4题中考专题：线段和（差）最值问题4．如图，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AD＝4，AB＝5，BC＝6，点P是AB上一个动点，模型应用：当PC＋PD的和最小时，PB的长为__________．5．如图，等腰梯形ABCD中，AB＝AD＝CD＝1，∠ABC＝60°，P是上底，下底中点EF直线上的一点，则PA+PB的最小值为．6．如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为．第5题第6题第7题7．已知A(－2，3)，B(3，1)，P点在x轴上，若PA＋PB长度最小，则最小值为． 8．已知：如图所示，抛物线y＝－x2＋bx＋c与x轴的两个交点分别为A(1，0)，B(3，0)．（1）求抛物线的解析式；（2）设点P在该抛物线上滑动，且满足条件S△PAB＝1的点P有几个？并求出所有点P的坐标；（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小？若存在，求出点M的坐标；若不存在，请说明理由．Ⅱ．台球两次碰壁模型已知点A位于直线m，n 的内侧，在直线m、n分别上求点P、Q点，使PA+PQ+QA周长最短.变式：已知点A、B位于直线m，n 的内侧，在直线m、n分别上求点D、E点，使得围成的四边形ADEB周长最短.中考复习专题：线段和或差的最值问题第 2 页共 6 页1．如图，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR周长的最小值．2．如图，已知平面直角坐标系，A，B两点的坐标分别为A(2，－3），B(4，－1）设M，N分别为x轴和y轴上的动点，请问：是否存在这样的点M(m，0），N(0，n),使四边形ABMN的周长最短？若存在，请求出m＝______，n ＝ ______（不必写解答过程）；若不存在，请说明理由．中考赏析：1．著名的恩施大峡谷（A）和世界级自然保护区星斗山（B）位于笔直的沪渝高速公路X同侧，AB=50km、B到直线X的距离分别为10km和40km，要在沪渝高速公路旁修建一服务区P，向A、B两景区运送游客．小民设计了两种方案，图（1）是方案一的示意图（AP与直线X垂直，垂足为P），P到A、B的距离之和S1＝PA＋PB，图（2）是方案二的示意图（点A关于直线X的对称点是A'，连接BA'交直线X于点P），P到A、B 的距离之和S2＝PA＋PB．（1）求S1、S2，并比较它们的大小；（2）请你说明S2＝PA＋PB的值为最小；（3）拟建的恩施到张家界高速公路Y与沪渝高速公路垂直，建立如图（3）所示的直角坐标系，B到直线Y的距离为30km，请你在X旁和Y旁各修建一服务区P、Q，使P、A、B、Q组成的四边形的周长最小．并求出这个最小值．2．如图，抛物线y＝35x2－185＋3和y轴的交点为A，M为OA的中点，若有一动点P，自M点处出发，沿直线运动到x轴上的某点（设为点E），再沿直线运动到该抛物线对称轴上的某点（设为点F），最后又沿直线运动到点A，求使点P运动的总路程最短的点E，点F的坐标，并求出这个最短路程的长．Ⅲ．已知A、B是两个定点，P、Q是直线m上的两个动点，P在Q的左侧，且PQ间长度恒定,在直线m上要求P、Q两点，使得PA+PQ+QB的值最小．(原理用平移知识解) （1）点A、B在直线m两侧：（2）点A、B在直线m同侧：中考复习专题：线段和或差的最值问题第 3 页共 6 页实战演练：1．如图，已知平面直角坐标系，A，B两点的坐标分别为A(2，－3），B(4，－1）若C(a，0)，D(a+3，0)是x轴上的两个动点，则当a ＝______时，四边形ABDC的周长最短．2．如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；（2）若E、F为边OA上的两个动点，且EF＝2，当四边形CDEF的周长最小时，求点E、F的坐标.3．如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半二．求两线段差的最大值问题(运用三角形两边之差小于第三边) 轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．几何模型：在一条直线m上，求一点P，使PA－PB的差最大；（1）点A、B在直线m同侧：（2）点A、B在直线m异侧：（1）求经过A、B、C三点的抛物线的解析式；（2）当BE经过（1）中抛物线的顶点时，求CF的长；（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ＝1，要使四边形BCPQ的周长最小，求出P、Q两点的坐标．模型应用：1. 如图，抛物线y＝－12x－x＋2的顶点为A，与y 轴交于点B．(1)求点A、点B的坐标；(2)若点P是x轴上任意一点，求证：PA－PB≤AB；4．如图，已知点A（－4，8）和点B（2，n）在抛物线y＝ax2上．(3)当PA－PB最大时，求点P的坐标.（1）求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ＋QB最短，求出点Q的坐标；（2）平移抛物线y＝ax2，记平移后点A的对应点为A′，点B的对应点为B′，点C（－2，0）和点D（－4，0）是x轴上的两个定点．①当抛物线向左平移到某个位置时，A′C＋CB′最短，求此时抛物线的函数解析式；②当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？好题赏析：（2010?宁德）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD （不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM＋CM的值最小；②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；（3）当AM＋BM＋CM的最小值为3＋1时，求正方形的边长．变式：如图四边形ABCD是菱形，且∠ABC＝60，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的是（）①若菱形ABCD的边长为1，则AM＋CM的最小值1；②△AMB≌△ENB；③S四边形AMBE=S四边形ADCM；④连接AN，则AN⊥BE；⑤当AM＋BM＋CM的最小值为2时，菱形ABCD的边长为2．A．①②③ B．②④⑤ C．①②⑤ D．②③⑤。

《6.4 线段的和差》课时同步练习2020-2021年数学浙教新版七（上）一．选择题（共16小题）1．已知AB＝1.5，AC＝4.5，且A，B，C三点不共线，若BC的长为整数，则BC的长为（）A．3B．6C．3或6D．4或52．两根木条，一根长20cm，另一根长24cm，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为（）A．2cm B．4cm C．2cm或22cm D．4cm或44cm 3．点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC＝2，则AC 等于（）A．3B．2C．3或5D．2或64．某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（）A．两点之间线段最短B．两点确定一条直线C．垂线段最短D．经过直线外一点，有且只有一条直线与这条直线平行5．如图，C、D是线段AB上的两点，且D是线段AC的中点，若AB＝10cm，BC＝4cm，则AD的长为（）A．2cm B．3cm C．4cm D．6cm6．A，B，C三点在同一直线上，线段AB＝5cm，BC＝4cm，那么A，C两点的距离是（）A．1cm B．9cmC．1cm或9cm D．以上答案都不对7．如图，点C是线段AB上一点，点M是AC的中点，点N是BC的中点，如果MC比NC 长2cm，AC比BC长（）A．2cm B．4cm C．1cm D．6cm8．如果延长线段AB到C，使得，那么AC：AB等于（）A．2：1B．2：3C．3：1D．3：29．如图，将一根绳子对折以后用线段AB表示，现从P处将绳子剪断，剪断后的各段绳子中最长的一段为60cm，若AP＝PB，则这条绳子的原长为（）A．100cm B．150cmC．100cm或150cm D．120cm或150cm10．如图，C、D是线段AB上的两个点，CD＝3cm，M是AC的中点，N是DB的中点，AB＝9.8cm，那么线段MN的长等于（）A．5.4cm B．6.4cm C．6.8cm D．7cm11．数轴上A、B、C三点所表示的数分别为a、b、c，且C在AB上．若|a|＝|b|，AC：CB ＝1：3，则下列b、c的关系式，何者正确？（）A．|c|＝|b|B．|c|＝|b|C．|c|＝|b|D．|c|＝|b|12．如图所示，某同学的家在A处，书店在B处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（）A．A→C→D→B B．A→C→F→B C．A→C→E→F→B D．A→C→M→B 13．把一条弯曲的公路改成直道，可以缩短路程．用几何知识解释其道理正确的是（）A．两点确定一条直线B．垂线段最短C．两点之间线段最短D．三角形两边之和大于第三边14．如图，线段AB＝18cm，BC＝6cm，D为BC的中点，则线段AD的长为（）A．12 cm B．15cm C．13cm D．11 cm15．下列说法不正确的是（）A．两点之间的连线中，线段最短B．若点B为线段AC的中点，则AB＝BCC．若AP＝BP，则点P为线段为AB的中点D．直线与射线不能比较大小16．如图：A、B、C、D四点在一条直线上，若AB＝CD，下列各式表示线段AC错误的是（）A．AC＝AD﹣CD B．AC＝AB+BC C．AC＝BD﹣AB D．AC＝AD﹣AB 二．解答题（共8小题）17．如图，点C是线段AB上一点，点M、N、P分别是线段AC，BC，AB的中点．（1）若AB＝10cm，则MN＝cm；（2）若AC＝3cm，CP＝1cm，求线段PN的长．18．已知：如图，在直线l上顺次有A、B、C三点，AB＝4cm，AB＞BC，点O是线段AC 的中点，且OB＝cm，求：B、C两点之间的距离．19．如图，点B、C把线段MN分成三部分，其比是MB：BC：CN＝2：3：4，P是MN的中点，且MN＝18cm，求PC的长．20．如图，已知线段AB和CD的公共部分BD＝AB＝CD，线段AB、CD的中点E、F 之间距离是10cm，求AB，CD的长．21．如图，已知点C为AB上一点，AC＝12cm，CB＝AC，D、E分别为AC、AB的中点，求DE的长．22．如图，C为线段AD上一点，点B为CD的中点，且AD＝8cm，BD＝2cm．（1）图中共有多少条线段？（2）求AC的长．（3）若点E在直线AD上，且EA＝3cm，求BE的长．23．如图，P是线段AB上任一点，AB＝12cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2cm/s，D点的运动速度为3cm/s，运动的时间为ts．（1）若AP＝8cm，①运动1s后，求CD的长；②当D在线段PB上运动时，试说明AC＝2CD；（2）如果t＝2s时，CD＝1cm，试探索AP的值．24．如图，点C在线段AB上，AC＝16cm，CB＝12cm，点M、N分别是AC、BC的中点．（1）求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB＝a cm，其它条件不变，你能猜想MN的长度吗？并说明理由．（3）若C在线段AB的延长线上，且满足AC﹣BC＝b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，不要说明理由．参考答案一．选择题（共16小题）1．解：∵BC边长为整数，A、B、C不共线，∴3＜BC＜6，∴BC＝4或5．故选：D．2．解：如图，设较长的木条为AB＝24cm，较短的木条为BC＝20cm，∵M、N分别为AB、BC的中点，∴BM＝12cm，BN＝10cm，∴①如图1，BC不在AB上时，MN＝BM+BN＝12+10＝22cm，②如图2，BC在AB上时，MN＝BM﹣BN＝12﹣10＝2cm，综上所述，两根木条的中点间的距离是2cm或22cm；故选：C．3．解：此题画图时会出现两种情况，即点C在线段AB内，点C在线段AB外，所以要分两种情况计算．点A、B表示的数分别为﹣3、1，AB＝4．第一种情况：在线段AB外，AC＝4+2＝6；第二种情况：在线段AB内，AC＝4﹣2＝2．故选：D．4．解：某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是两点之间线段最短．故选：A．5．解：∵AB＝10cm，BC＝4cm，∴AC＝AB﹣BC＝6cm，又点D是AC的中点，∴AD＝AC＝3cm，答：AD的长为3cm．故选：B．6．解：第一种情况：C点在AB之间上，故AC＝AB﹣BC＝1cm；第二种情况：当C点在AB的延长线上时，AC＝AB+BC＝9cm．故选：C．7．解：∵点M是AC的中点，点N是BC的中点，∴AC＝2MC，BC＝2NC，∴AC﹣BC＝（MC﹣NC）×2＝2×2＝4（cm），即AC比BC长4cm．故选：B．8．解：如图，∵BC＝AB，∴AC＝AB+BC＝AB+AB＝AB，∴AC：AB＝3：2．故选：D．9．解：当PB的2倍最长时，得PB＝30cm，AP＝PB＝20cm，AB＝AP+PB＝50cm，这条绳子的原长为2AB＝100cm；当AP的2倍最长时，得AP＝30cm，AP＝PB，PB＝AP＝45cm，AB＝AP+PB＝75cm，这条绳子的原长为2AB＝150cm．故选：C．10．解：∵M是AC的中点，N是DB的中点，CD＝3cm，AB＝9.8cm，∴MC+DN＝（AB﹣CD）＝3.4cm，∴MN＝MC+DN+CD＝3.4+3＝6.4cm．故选：B．11．解：∵C在AB上，AC：CB＝1：3，∴|c|＝，又∵|a|＝|b|，∴|c|＝|b|．故选：A．12．解：根据两点之间的线段最短，可得C、B两点之间的最短距离是线段CB的长度，所以想尽快赶到书店，一条最近的路线是：A→C→F→B．故选：B．13．解：要想缩短两地之间的里程，就尽量是两地在一条直线上，因为两点间线段最短．故选：C．14．解：∵AB＝18cm，BC＝6cm，∴AC＝AB﹣BC＝12cm又∵D为BC的中点，∴CD＝BC＝3于是AD＝AC+CD＝12+3＝15故选：B．15．解：A．线段公理，此项正确；B．中点的性质，中点将线段分成长度相等的两条线段，此项正确；C．A、B、P三点不一定在同一条直线上，因此点P不一定是线段AB的中点，此项错误；D．直线具有两边无限延伸性，射线具有一边无限延伸性，故直线与射线不能比较大小，此项正确；故选：C．16．解：∵A、B、C、D四点在一条直线上，AB＝CD，∴AC＝AD﹣CD＝AD﹣AB＝AB+BC，故选：C．二．解答题（共8小题）17．解：（1）∵M、N分别是AC、BC的中点，∴MC＝AC，CN＝BCMN＝MC+CN＝．故填：5．（2）∵AC＝3，CP＝1，∴AP＝AC+CP＝4，∵P是线段AB的中点，∴AB＝2AP＝8∴CB＝AB﹣AC＝5，∵N是线段CB的中点，CN＝CB＝，∴PN＝CN﹣CP＝．18．解：∵AB＝4cm，OB＝cm∴OA＝AB﹣OB＝3.5而O是线段AC的中点，∴AC＝2OA＝7∴BC＝AC﹣AB＝7﹣4＝3故B、C两点之间的距离为3cm．19．解：设MB＝2x，则BC＝3x，CN＝4x，因为P是MN中点，所以MP＝MN＝×（2x+3x+4x）＝x＝9．解得x＝2，∴PC＝MC﹣MP＝2x+3x﹣x＝0.5x＝1．20．解：设BD＝xcm，则AB＝3xcm，CD＝4xcm，AC＝6xcm．∵点E、点F分别为AB、CD的中点，∴AE＝AB＝1.5xcm，CF＝CD＝2xcm．∴EF＝AC﹣AE﹣CF＝6x﹣1.5x﹣2x＝2.5xcm．∵EF＝10cm，∴2.5x＝10，解得：x＝4．∴AB＝12cm，CD＝16cm．21．解：∵AC＝12cm，CB＝AC，∴CB＝6cm，∴AB＝AC+BC＝12+6＝18cm，∵E为AB的中点，∴AE＝BE＝9cm，∵D为AC的中点，∴DC＝AD＝6cm，所以DE＝AE﹣AD＝3cm．22．解：（1）图中共有6条线段；（2）∵点B为CD的中点．∴CD＝2BD．∵BD＝2cm，∴CD＝4cm．∵AC＝AD﹣CD且AD＝8cm，CD＝4cm，∴AC＝4cm；（3）当E在点A的左边时，则BE＝BA+EA且BA＝6cm，EA＝3cm，∴BE＝9cm当E在点A的右边时，则BE＝AB﹣EA且AB＝6cm，EA＝3cm，∴BE＝3cm．23．解：（1）①由题意可知：CP＝2×1＝2cm，DB＝3×1＝3cm ∵AP＝8cm，AB＝12cm∴PB＝AB﹣AP＝4cm∴CD＝CP+PB﹣DB＝2+4﹣3＝3cm②∵AP＝8，AB＝12，∴BP＝4，AC＝8﹣2t，∴DP＝4﹣3t，∴CD＝DP+CP＝2t+4﹣3t＝4﹣t，∴AC＝2CD；（2）当t＝2时，CP＝2×2＝4cm，DB＝3×2＝6cm，当点D在C的右边时，如图所示：由于CD＝1cm，∴CB＝CD+DB＝7cm，∴AC＝AB﹣CB＝5cm，∴AP＝AC+CP＝9cm，当点D在C的左边时，如图所示：∴AD＝AB﹣DB＝6cm，∴AP＝AD+CD+CP＝11cm综上所述，AP＝9cm或11cm24．解：（1）∵点M、N分别是AC、BC的中点，AC＝16cm，CB＝12cm，∴CM＝AC＝8cm，CN＝BC＝6cm，∴MN＝CM+CN＝8cm+6cm＝14cm，即线段MN的长是14cm；（2）解：∵点M、N分别是AC、BC的中点，AC+CB＝acm，∴CM＝AC，CN＝BC，∴MN＝CM+CN＝AC+BC＝（AC+BC）＝acm，即线段MN的长是acm；（3）解：如图：MN＝b，理由是：∵点M、N分别是AC、BC的中点，AC﹣CB＝bcm，∴CM＝AC，CN＝BC，∴MN＝CM﹣CN＝AC﹣BC＝（AC﹣BC）＝bcm，即线段MN的长是bcm；。

第8讲线段和差问题的处理方法知识导航1．等量代换法；2．截长补短法．【板块一】等量代换方法技巧通过用图中相等的线段来代换另一条线段，将线段的和差问题转化为证两线段相等的问题，通过全等得到线段等，直接代换，将分散的线段转化到同一直线上解决问题．【例1】如图，点D为BC上一点，AB＝AC，AD＝AE，∠BAC＝∠DAE．求证：BC＝CD＋CE．【例2】如图，在△ABC中，∠BAC＝90°，AB＝AC，直线DE过点A，BD⊥DE于D，CE⊥DE于E．（1）如图1，求证：DE＝CE＋BD；（2）如图2，求证：DE＝CE－BD．针对练习11．如图，在△ABC中，AB＝BC，点D为AB中点，∠ABC＝∠BAE＝90°，BE⊥CD交AC于F．求证：CD＝BF＋DF．【板块二】截长补短方法技巧和宜并之差宜贴，短则补之长则截．截长：在长线段中截取一段等于另两条中的一条，然后证明剩下部分等于另一条；补短：将一条短线段延长，延长部分等于另一条短线段，然后证明新线段等于长线段；或者将短线段直接延长至等于长线段。

无论截长还是补短都需要将几条线段的和差问题转化为证两条线段相等的问题，一般情况要通过两对全等实现。

模型一角平分线与线段和差类【例3】如图，在△ABC中，AB＝AC，BD是△ABC的角平分线．（1）若∠BAC＝90°，求证：BC＝AB＋AD；（2）若∠BAC＝108°，求证：BC＝AB＋CD；（3）若∠BAC＝100°，求证：BC＝BD＋AD．【例4】如图，在△ABC中，∠A＝60°，∠ABC与∠ACB的平分线BD，CE交于点I．求证：BC＝BE＋CD．模型二倍半角与线段和差类【例5】如图，在△ABC中，∠CAB＝2∠B．CD平分∠ACB．求证；BC＝AC＋AD．(请尝试用两种方法证明）模型三垂直与线段和差类【例6】如图，在△ABC中，∠BAC＝120°，AD⊥BC于D，且AB＋BD＝DC，求∠C的度数．模型四等边三角形与线段和差类【例7】如图，△ABC为等边三角形，∠ADC＝60°．求证：AD＝BD＋CD．（请用两种方法证明）针对练习21．如图，在四边形ABCD中，AD//BC，点E为AB上一点，CE平分∠BCD，DE平分∠ADC．求证：CD＝AD＋BC．2．如图，在△ABC中，AB＝AC，∠BAC＝90°，点D为AC中点，AE⊥BD于E，交BC 于F，连接DF．求证：BD－AF＝DF．。

4、应用题1 延长线段AB 到C, 使BC=AB,D 为AC 中点,且CD=5cm,求AB 的长.2 A 、B 、C 、D 四个点在同一直线上,且AB=8cm,BC=3cm,AD=2cm,求CD 的长.3、如图,点C 在线段AB 上,AC = 8厘米,CB = 6厘米,点M 、N 分别是AC 、BC 的中点; 1 求线段MN 的长；2 若C 为线段AB 上任一点,满足AC + CB = a 厘米,其它条件不变,你能猜想MN 的长度吗并说明理由;3) 若C 在线段AB 的延长线上,且满足AC BC = b 厘米,M 、N 分别为AC 、BC 的中点,你 能猜想MN 的长度吗请画出图形,写出你的结论,并说明理由;4 AD ＝12BD,E 是BC 的中点,BE ＝2cm,AC ＝10cm,求线段DE 的长． 5 如图,量出以下图形中各条线段的长度,比较它们的大小．并比较一个三角形中任意两边的和与第三边的关系．可以得出什么结论6思考小老鼠该怎么爬才能最快吃到汉堡包呢7 A 、B 、C 、D 四个小区在同一条路上,为了给小区的居民出行带来方便准备在这条路上增设一个车站,车站应建在哪里使车站与各个小区的距离和最短,请同学们设计出方案． 四．课后作业：1、如图,A 、B 、C 、D 、四点在一条直线上,图中有 条线段.2、根据所示图形填空,理解截取、顺次截取的意义,熟练掌握基本画图语句.已知线段a 、b,画出一条线段,使它等于a+b.解：1画射线OP ；2在射线OP 上顺次截取 =a, =b.线段 就是所要画的线段.3、根据所示图形填空,理解截取、顺次截取的意义,熟练掌握基本画图语句.已知线段a 、b,画出一条线段,使它等于a-b.解法一：1画射线OP ；2在射线OP 上截取 =a,在线段 上截取 =b.线段 就是所要画的线段.解法二：1画射线OP ；A A D CB E。