圆弧面蜗杆数控车削加工的宏程序

数控宏程序FANUC数控车本文档不做商业用途，尽供大家相互学习。

二次上传时间2022/11/15 shen245194831第一章编程代码----------------------------------------------------------1 1．准备功能G------------------------------------------------------------1 2．辅助功能M-----------------------------------------------------------6 第二章用户宏程序-------------------------------------------------------71. 运算符号---------------------------------------------------------------72．转移和循环-----------------------------------------------------------7 3．运算指令--------------------------------------------------------------8第三章宏程序编程------------------------------------------------------11 1．车V型圆锥- --------------------------------------------------------11 2．车U圆弧-------------------------------------------------------------12 3．方程曲线车削加工-------------------------------------------------13 5．车梯形螺纹36×6--------------------------------------------------14 6．蜗杆-------------------------------------------------------------------15 7．加工多件--------------------------------------------------------------17 第四章自动编程---------------------------------------------------------------21 1．UG建模--------------------------------------------------------------------21 2．创建几何体----------------------------------------------------------------24 附录--------------------------------------------------------------------------29第一章编程代码1．准备功能G00快速定位 G01直线插补 G02顺弧插补G03逆弧插补 G04暂停G9,G60,G64准确/连续停G20英制输入 G21米制输入 G40取消刀具补偿G41建立左刀具补偿 G42建立右刀具补偿G50坐标设定/主轴最高速设定G70精车循环格式： G70 P(ns) Q(nf)ns: 精加工形状程序的第一个段号。

蜗杆传动装置主要应用在减速机构中，在很多机械设备上要应用，如车、铣、刨、磨等设备上都要应用。

蜗杆因螺距大、螺旋槽深，在普通车床上加工比较耗时，且劳动强度较大，并对工人技术要求较高，而在数控车床上采用宏程序加工蜗杆，只需通过变量参数设置就能完成蜗杆加工时的分层、分头、借刀等动作，减轻了劳动强度，提高了生产效率。

1 蜗杆相关尺寸分析根据蜗杆齿廓形状的不同，常用蜗杆的齿形分轴向直廓蜗杆和法向直廓蜗杆两种。

轴向直廓蜗杆的轴向齿廓为直线，在垂直于轴线的截面内，齿形是阿基米德螺旋线，又称阿基米德蜗杆。

法向直廓蜗杆是法向齿廓为直线，在垂直于轴线的截面内，齿形是延长渐开线，又称延长渐开线蜗杆。

在加工法向直廓蜗杆、轴向直廓蜗杆时，法向直廓蜗杆的制造比较困难，一般轴向直廓蜗杆在机械设备中应用的最多，下面根据轴向直廓蜗杆计算相关尺寸。

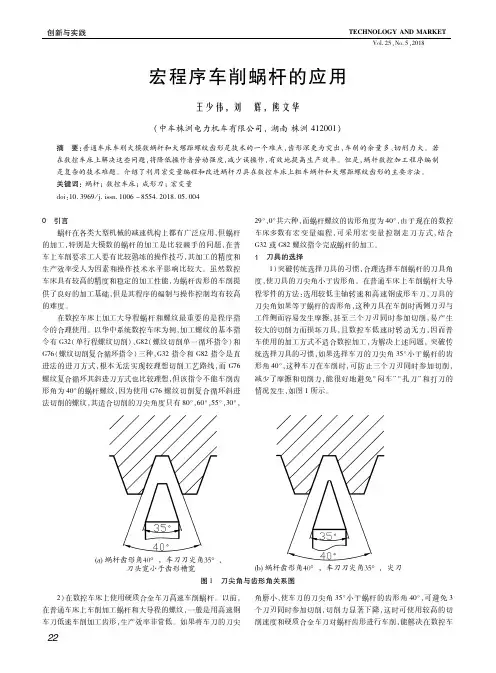
(1)根据图1计算轴向直廓蜗杆部分理论几何尺寸螺距：P=πx m =3.14*4=12.56 m m全齿高：h=2.2m x =2.2*4=8.8 m m 轴向齿顶宽：a s =0.843mx=0.843*4=3.372 m m轴向齿根槽宽：f e =0.697mx=0.697*4=2.788 m m分度圆直径：d 1=d -2mx=60-8=52 m m齿根圆直径：f d =d -4.4mx=60-17.6=42.4 m m轴向齿厚：x s =p/2=12.56/2=6.28 mm(2)根据图1尺寸公差要求计算蜗杆几何尺寸根据轴向齿厚尺寸公差取中间公差值得到的尺寸6.205 m m ，在分度圆直径、全齿高不变的情况下齿根槽宽和齿顶宽的尺寸发生了变化。

齿根槽宽增加了0.075 m m ，尺寸为2.863 m m ，蜗杆车刀刀头刃宽为2.5 m m ，齿顶宽减少了0.075 m m，尺寸为3.297 m m。

2 蜗杆编程工艺分析(1)加工方法选择 在车床上加工蜗杆一般采用直进法、斜进法、左右借刀法三种加工方法，在数控车床上加工大模数蜗杆我采用左右借刀法加工。

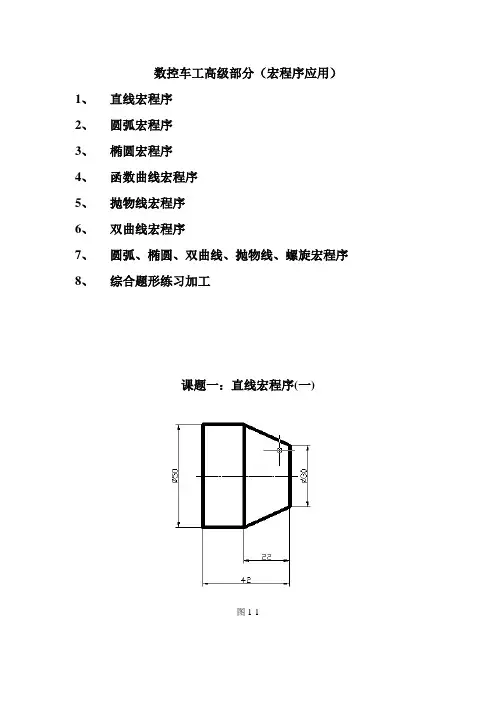
数控车工高级部分（宏程序应用）1、直线宏程序2、圆弧宏程序3、椭圆宏程序4、函数曲线宏程序5、抛物线宏程序6、双曲线宏程序7、圆弧、椭圆、双曲线、抛物线、螺旋宏程序8、综合题形练习加工课题一：直线宏程序(一)图1-1直线方程式：X=KZ+B解题思路：1、直线两点（X 30 , Z 0）(X 50 , Z -22).2、根据线形方程式得：30=K*0+B50=K*(-22)+B得：B=30K=-0.90903、方程式为：X=-0.9090Z+304、长度宏变量范围：Z0 ~Z-225、设自变量#1=0 #2=-226、应用循环语言WHILE [ ] DO1END1精加工程序内容：O0001；M03 S1000；T0101；G00 X55 Z2；#1=0；#2=-22；WHILE [ #1GE#2 ] DO1；#3= -0.9090*#1+30；G01 X[#3] Z[#1] F0.1#1=#1-0.05END1;G00 X100 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X55 Z2；#1=0；#2=-22；WHILE [ #2LE#1 ] DO1；#3= -0.9090*#2+30；G01 X[#3+1] F0.25;G01 Z[#2+0.5] F0.1;G00 U1 W0.5;Z2;#2=#2+2;END1;G00 X100 Z100;M30;课题一：直线宏程序(二)图1-2直线方程式：X=KZ+B解题思路：1、直线两点（X 50 , Z -20）(X 30 , Z -42).2、根据线形方程式得：50=K*-20+B30=K*(-42)+B得：B=68.18K=0.90903、方程式为：X=0.9090Z+68.184、长度宏变量范围：Z-20 ~Z-425、设自变量#1=-20 #2=-426、应用循环语言WHILE [ ] DO1END1精加工程序内容：O0001；M03 S1000；T0101；G00 X55 Z-20；#1=-20；#2=-42；WHILE [ #1GE#2 ] DO1；#3= 0.9090*#1+68.18；G01 X[#3] Z[#1] F0.1#1=#1-0.05END1;G00 X100 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X55 Z-20；#1=-20；#2=-42；WHILE [ #1GE#2 ] DO1；#3= 0.9090*#1+68.18；G01 X[#3+1] Z[#1-0.5] F0.25;G01 Z[#2]G00 U1 W0.5;Z [#1-0.5];#1=#1-2;END1;G00 X100 Z100;M30;课题一：直线宏程序(三)直线方程式：X=KZ+B解题思路：1、直线两点（X 44, Z 0）(X 30 , Z –40).2、根据线形方程式得：44=K*0+B30=K*(-40)+B得：B=44K=0.353、方程式为：X=0.35Z+444、长度宏变量范围：Z0 ~Z-405、设自变量#1=0 #2=-406、应用循环语言WHILE [ ] DO1END1精加工程序内容：O0001；M03 S1000；T0101；G00 X28 Z2；#1=0；#2=-40；WHILE [ #1GE#2 ] DO1；#3= 0.35*#1+44；G01 X[#3] Z[#1] F0.1#1=#1-0.05END1;G00 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X28 Z2；#1=0；#2=-40；WHILE [ #2LE#1 ] DO1；#3= 0.35*#2+44；G01 X[#3-1] F0.25;Z[#2+0.5];G00 U-1 W0.5;Z 2;#2=#2+2;END1;G00 Z100;M30;课题一：直线宏程序(四)直线方程式：图示右斜线直线方程式：X=KZ+B图示左斜线直线方程式：X=KZ+B解题思路：1、直线两点（X 50, Z -20）(X 30 , Z –42).2、直线两点（X30, Z –58）(X 50 , Z –80).3、根据右斜线形方程式得：50=K*-20+B30=K*(-42)+B得：B=68.18K=0.90904、根据左斜线形方程式得：30=K*-58+B50=K*(-80)+B得：B=-22.722K=-0.90905、方程式为：图示右斜线直线方程式：X=0.9090Z+68.18图示左斜线直线方程式：X=-0.9090Z-22.7226、长度宏变量范围：Z-20 ~Z-42 Z-58 Z-807、设自变量#1=-20 #2=-42 #3=58 #4=-808、应用循环语言WHILE [ ] DO1END1精加工程序内容(一)：O0001；M03 S1000；T0101；G00 X55 Z-20；#1=-20；#2=-42；#3=-58;#4=-80;WHILE [ #1GE#2 ] DO1；#5= 0.090*#1+68.18；G01 X[#5] Z[#1] F0.1;W-16;#6=-0.090*#3-22.722G01 X[#6] Z[#3]F0.15;#1=#1-0.05#3=#3-0.05END1;G00 X100 Z100;M30;精加工也可这样编写（二）：O0001；M03 S1000；T0101；G00 X55 Z-20；#1=-20；#2=-42；#3=-58;#4=-80;WHILE [ #1GE#2 ] DO1；#5= 0.090*#1+68.18；G01 X[#5] Z[#1] F0.1;#1=#1-0.05END1G01 W-16 F0.15;WHILE [ #3GE#4 ] DO2；#6=-0.090*#3-22.722G01 X[#6] Z[#3]F0.15;#3=#3-0.05END2;G00 X100 Z100;M30;精加工也可这样编写（三）：O0001；M03 S1000；T0101；G00 X55 Z-20；#1=-20；#2=-42；#3=-58;#4=-80;WHILE [ #1GE#2 ] DO1；WHILE [ #3GE#4 ] DO2；#5= 0.090*#1+68.18；#6=- 0.090*#1-22.722;G01 X[#5] Z[#1] F0.1;G01 W-16;G01 X[#6] Z[#3] F0.1;#1=#1-0.05;#3=#3-0.05;END2;END1;G00 X100 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X55 Z-20；#1=-20；#2=-42；#3=-58;#4=-80;WHILE [ #1GE#2 ] DO1；WHILE [ #3GE#4 ] DO2；#5= 0.090*#1+68.18；#6=- 0.090*#1-22.722;G01 X[#5+1] Z[#1-0.5] F0.1;G01 X[#6+1] Z[#3+0.5] F0.1;G00 U1 W0.5;Z [#1-0.5];#1=#1-1;#3=#3-1;END2;END1;G00 X100 Z100;M30;课题二：椭圆宏程序(一)1、椭圆第一种应用方程式：X=A*2*SIN(a) Z=B*CON(a)A:为X轴方的长度(平行与X轴的椭圆轴) B:为Z轴方向的长度(平行与z轴的椭圆轴)2、椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1A:为X轴方的长度B:为Z轴方向的长度第一种方程式应用解题；3、角度宏变量范围：a=0 ∽ a=904、设自变量#1=0 #2=90 #3=10 #4=255、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55 Z2；#1=0；#2=90；#3=10；#4=25；WHILE [ #1LE#2 ] DO1；#5=2*#4*SIN（#1）；#6=#3*CON（#1）；G01 X [#5] Z[#6-10] F0.15#1=#1+0.1;END1;G00 X100 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X55 Z2；#1=0；#2=90；#3=10；#4=25；WHILE [ #2GE#1 ] DO1；#5=2*#4*SIN（#2）；#6=#3*CON（#2）；G01 X [#5+1] F0.25;Z[#6-10+0.5] F0.25;G00 U1 W0.5;Z2;#2=#2+3;END1;G00 X100 Z100;M30;椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1编程:1、长度宏变量范围：z=0 ∽ z=-102、公式分析化简得:X=SQRT[[1-Z*Z/B*B]*A*A]4、设自变量#1=0 #2=-10 #3=10 #4=255、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55 Z2；#2=0#3=10；#4=25；WHILE [ #1GE#2 ] DO1；#5=2*SQRT[[1-#1*#1/#3*#3]*#4*#4] G01 X [#5] Z[#1-10] F0.15#1=#1+0.1;END1;G00 X100 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X55 Z2；#1=10；#2=0；#3=10；WHILE [ #2GE#1 ] DO1；#5=2*SQRT[[1-#2*#2/#3*#3]*#4*#4]G01 X [#5+1] F0.25;Z[#2-10+0.5] F0.25;G00 U1 W0.5;Z2;#2=#2+3;END1;G00 X100 Z100;M30;课题二：椭圆宏程序(二)1、椭圆第一种应用方程式：X=A*2*SIN(a) Z=B*CON(a)A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)2\椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)第一种方程式应用解题；3、角度宏变量范围：a=0 ∽ a=1504、设自变量#1=90 #2=150 #3=25 #4=405、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X30Z2；#1=90；#2=150；#4=40；WHILE [ #1LE#2 ] DO1；#5=2*#3*SIN（#1）；#6=#4*CON（#1）；G01 X [#5] Z[#6] F0.15#1=#1+0.1;END1;G00 U-2;G00 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=90；#2=150；#3=25；WHILE [ #2GE#1 ] DO1；#5=2*#3*SIN（#2）；#6=#4*CON（#2）；G01 X [#5-1] F0.25;Z[#6+0.5] F0.25;G00 U-1 W0.5;Z2;#2=#2+3;END1;G00 Z100;M30;椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1编程:3、长度宏变量范围：z=0 ∽ z=-304、公式分析化简得:X=SQRT[[1-Z*Z/B*B]*A*A]4、设自变量#1=0 #2=-30 #3=25 #4=405、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X30 Z2；#1=0；#2=-30#3=25；#4=40；WHILE [ #1GE#2 ] DO1；#5=2*SQRT[[1-#1*#1/#4*#4]*#3*#3] G01 X [#5] Z[#1] F0.15#1=#1-0.1;END1;G00 U-2;G00 Z100;M30;粗加工程序内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=0；#2=-30；#3=25；#4=40；WHILE [ #2GE#1 ] DO1；#5=2*SQRT[[1-#2*#2/#4*#4]*#3*#3] G01 X [#5-1] F0.25;Z[#2+0.5] F0.25;G00 U-1 W0.5;Z2;#2=#2-3;END1;G00 Z100;M30;课题二：椭圆宏程序(三)1、椭圆第一种应用方程式：X=A*2*SIN(a) Z=B*CON(a)A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)2、椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)第一种方程式应用解题；2、角度宏变量范围：a=0 ∽ a=1504、设自变量#1=0 #2=150 #3=25 #4=405、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55Z2；#1=0；#2=150；#3=25；#4=40；WHILE [ #1LE#2 ] DO1；#5=2*#3*SIN（#1）；#6=#4*CON（#1）-40；G01 X [#5] Z[#6] F0.15#1=#1+0.1;END1;G00 X150;G00 Z100;M30;粗加工程序右边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=0；#2=90；#3=25；#4=40；WHILE [ #2GE#1 ] DO1；#5=2*#3*SIN（#2）；#6=#4*CON（#2）-40；G01 X [#5+1] F0.25;Z[#6+0.5] F0.25;Z2;#2=#2+3;END1;G00 Z100;M30;粗加工程序左边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=90；#2=150；#3=25；#4=40；WHILE [ #1LE#2 ] DO1；#5=2*#3*SIN（#1）；#6=#4*CON（#1）-40；G01 X [#5+1] Z[#6-0.5] F0.25;Z-80;Z[#6-0.5];#1=#1+3;END1;G00 Z100;M30;椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1编程:5、长度宏变量范围：z=0 ∽ z=-306、公式分析化简得:X=SQRT[[1-Z*Z/B*B]*A*A]4、设自变量#1=40 #2=-30 #3=25 #4=405、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55 Z2；#1=40；#2=-30#3=25；#4=40；WHILE [ #1GE#2 ] DO1；#5=2*SQRT[[1-#1*#1/#4*#4]*#3*#3] G01 X [#5] Z[#1-40] F0.15#1=#1-0.1;END1;G00X150;G00 Z100;M30;粗加工程序右边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=40；#2=0；#3=25；#4=40；WHILE [ #2LE#1 ] DO1；#5=2*SQRT[[1-#2*#2/#4*#4]*#3*#3] G01 X [#5+1] F0.25;Z[#2+0.5-40] F0.25;G00 U1 W0.5;Z2;#2=#2+3;END1;G00 Z100;M30;粗加工程序左边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=0；#2=-30；#3=25；#4=40；WHILE [ #1GE#2 ] DO1；#5=2*SQRT[[1-#1*#1/#4*#4]*#3*#3]G01 X [#5+1] Z[#1-0.5-40] F0.25;Z-80G00 U1 W0.5;Z[#1-0.5-40];#1=#1-3;END1;G00 X150 Z100;M30;课题二：椭圆宏程序(四)3、椭圆第一种应用方程式：X=A*2*SIN(a) Z=B*CON(a)A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)2、椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1A:为X轴方的长度(平行与X轴的椭圆轴)B:为Z轴方向的长度(平行与z轴的椭圆轴)第一种方程式应用解题；4、角度宏变量范围：a=24.397 ∽ a=155.6034、设自变量#1=24.397 #2=155.603 #3=20 #4=505、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55 Z-16.93；#1=24.397 ;#2=155.603;#3=20;#4=50;WHILE [ #1LE#2 ] DO1；#5=80-2*#3*SIN（#1）-13.477；#6=#4*CON（#1）-50；G01 X [#5] Z[#6] F0.15#1=#1+0.1;END1;G00 X150;G00 Z100;M30;粗加工程序右边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=0；#2=90；#3=25；#4=40；WHILE [ #2GE#1 ] DO1；#5=2*#3*SIN（#2）；#6=#4*CON（#2）-40；G01 X [#5+1] F0.25;Z[#6+0.5] F0.25;G00 U1 W0.5;Z2;#2=#2+3;END1;G00 Z100;M30;粗加工程序左边内容:O0001；M03 S650；T0101；G00 X30 Z2；#1=90；#2=150；#3=25；#4=40；WHILE [ #1LE#2 ] DO1；#5=2*#3*SIN（#1）；#6=#4*CON（#1）-40；G01 X [#5+1] Z[#6-0.5] F0.25;Z-80;G00 U1 W0.5;Z[#6-0.5];#1=#1+3;END1;G00 Z100;M30;椭圆第二种应用方程式：X*X/A*A+Z*Z/B*B=1编程:7、长度宏变量范围：z=0 ∽ z=-308、公式分析化简得:X=SQRT[[1-Z*Z/B*B]*A*A]4、设自变量#1=40 #2=-30 #3=25 #4=405、应用循环语言WHILE [ ] DO1END1精加工编程内容：O0001；M03 S1000；T0101；G00 X55 Z2；#1=33.07；#2=-33.07#3=20；#4=50；WHILE [ #1GE#2 ] DO1；#5=80-2*SQRT[[1-#1*#1/#4*#4]*#3*#3] G01 X [#5] Z[#1-50] F0.15#1=#1-0.1;END1;G00X150;G00 Z100;M30;粗加工平行方式编程内容：O0001；M03 S1000；T0101；G00 X55 Z-16.93；#1=33.07；#2=-33.07#3=20；#4=50；#7=10；#8=0；WHILE [ #7GE#8 ] DO2；WHILE [ #1GE#2 ] DO1；#5=80-2*SQRT[[1-#1*#1/#4*#4]*#3*#3]; G01 X [#5+#7] Z[#1-50] F0.15;#1=#1-0.1;END1;G00 X60;Z-16.93;#7=#7-1;END2;G00X150;G00 Z100;M30;左右两边粗加工内容：O0001；M03 S1000；T0101；G00 X55 Z-16.93；#1=33.07；#2=0；#10=-33.07#3=20；#4=50；WHILE [ #1GE#2 ] DO1；WHILE [ #10LE#2 ] DO2；#5=80-2*SQRT[[1-#1*#1/#4*#4]*#3*#3] #6=80-2*SQRT[[1-#10*#10/#4*#4]*#3*#3] G01 X [#5+1] Z[#1-50-0.5] F0.15;Z[#10-50+0.5];G00U2;X [#6+1] Z [#1-50];#1=#1-1;#10=#10+1;END2;END1;G00X150;G00 Z100;M30;课题四:函数曲线宏程序正弦函数曲线方程式：X=A+SIN(Ａ);解题思路：1、A:为正弦函数曲线零线在回转体工件两边上下的中心直径距离¤40MM.2、根据线形方程式得：SIN(A)角度A为正弦函数曲线的变量方式:共角度度数为720°(90 ----810)3、将共长60与共角度720°等分成1000等分。

数控车床上加工蜗杆的通用宏程序广数 980TD数控车床上加工蜗杆的通用宏程序摘要很多中小型企业会遇到要在数控车床上加工大螺距梯形螺纹和蜗杆 (由于这些企业条件限制(往往不能编制好加工程序 (本文以实例探讨了数控车床中加工蜗杆和梯形螺纹通用宏程序的设计和编程(让中小企业也能轻松地应用宏程序加工蜗杆和梯形螺纹。

关键词宏程序梯形螺纹蜗杆一、前言今年本人应某中小型企业邀请(去帮他们处理数控车床加工中遇到的一些问题。

经交流得知(他们要加工一批蜗杆 ( 并从宜昌纺织机械厂请了位师傅编了个很长的程序 (但加工时还是很快损坏了刀具。

我查阅了相关说明书(并无这方面内容 (上网搜索 (也没有找到免费的可以直接使用的相关文章 (因此本人参考部分资料 (给他们编制了一个通用的加工蜗杆和梯形螺纹的程序(告诉他们使用方法后 (遇到蜗杆和梯形螺纹就可以直接套用该程序 (这样即使对宏程序不太熟悉的工人也可以加工蜗杆和梯形螺纹了。

二、加工螺纹的一般方法在数控车床加工螺纹一般有四种方法；直进法、斜进法、左右切削法和切槽刀粗切槽法四种。

1、直进法；如图 1 所示 (螺纹刀间歇性进给到牙深处 (采用此种方法加工梯形螺纹时(螺纹车刀的三面都参与切削 (导致加工排屑困难( 切削力和切削热增加(刀尖磨损严重(进刀量过大时 ( 还可能产生扎刀现象。

很显然(加工大螺距梯形螺纹和蜗杆是不可取的。

2、斜进法；如图 2 所示(螺纹车刀沿牙型角方向斜向间歇进给到牙深处(采用此种方法加工梯形螺纹时(螺纹车刀始终只有一侧刀刃参加切削(从而排屑比较顺利(刀尖的受力和受热情况有所改善(在车削中不易引起扎刀现象。

1/4页3、左右切削法；如图3所示 (螺纹车刀沿牙型角方向交错间隙进给至牙深(该方法同于斜进法(在数控车床上采用宏程序编程来实现。

3、切槽刀粗切槽法；如图 4 所示 (该方法先用切槽刀粗切槽(再用梯形螺纹车刀加工螺纹两侧面(这种方法在数控车中较难实现。

三、蜗杆和大螺距梯形螺纹特点和加工方法车削加工蜗杆和大导程螺纹(无论用斜进法还是左右切削法(切削抗力非常大( 以前只能用高速钢车刀低速车削加工(生产效率非常低。

基于宏程序在数控车床上加工圆弧面蜗杆徐军平,聂荣臻(常州刘国钧高等职业技术学校,江苏常州213004)摘要:以Fanuc 0i 系统数控车床为例,阐述了运用宏程序解决圆弧面蜗杆的加工问题,并提供了相应的程序。

关键词:数控车床;蜗杆;宏程序中图分类号:TS 642文献标识码:Ａ文章编号:2095-2953(2014)05-0054-02Application of Macro Programs to Circular Worm Process on CNC LathesXU Jun-ping,NIE Rong-zhen(Changzhou Liu Guojun Higher Vocational School,Changzhou Jiangsu 213004,China)Abstract :With Fanuc 0i s ys te m CNC la the s a s an e xa m ple ,the applica tio n o f m acro pro g ra m s to s o lve the proble m s w ith the pro ce s s ingo f circula r wo rm s iss ta te d,with corre s po ndingprog ra m spro vide d.Key words :CNC la the ;wo rm ;m a cro蜗杆是机械传动中常用的零件,具有牙槽窄而深、螺旋升角大、精度要求高、工件的长度和直径比值较大等特征。

本文以Fanuc 数控系统为例,介绍在圆弧曲面上加工圆弧牙型蜗杆的宏程序编程和加工方法[1-2]。

1宏程序格式宏程序的编制在数控编程中属于难点部分。

在一般的程序编制中,程序中地址字符后为一个常量,一个程序只能描述所加工平面的几何图形,缺乏灵活性和适用性。

宏程序中地址字符也是一个变量,可以通过赋值语句改变所加工零件的形状,使整个程序都具有通用性。

在数控车床上快速车削蜗杆的方法在数控车床上车削较大导程的蜗杆、梯形螺纹和锯齿螺纹,由于工件的齿形深,需要切除的毛坯余量多,一般是选择较低的切削速度和高速钢成形刀,使用G32和G76等指令车削,加工精度特别是表面粗糙度很难达到图纸要求,加工难度较大.针对出现的加工精度低、生产效率低等特点,说明如何有效地发挥数控车床的高精度,高速度、定位精度高、生产效率高的优势.我们以沈阳CAK3675v华中数控系统的车床来论述快速车削蜗杆的方法.如图1蜗杆数控车床成形刀硬质合金宏程序蜗杆和大导程螺纹车削的进刀方法有多种,如直进法、左右切削法、斜进法和切槽法等.以前车削蜗杆等大导程零件的方法是：选用较低主轴转速数控车床最低速为100转/分时转动无力和高速钢成形车刀,车削蜗杆时的生产效率低.为解决上述问题,我认为应从刀具材料、几何形状及角度和车削方法来谈谈快速车削蜗杆和大导程螺纹的方法.一、突破传统选择刀具的习惯,合理选择车削蜗杆的刀具角度,使刀具的刀尖角小于齿形角车削蜗杆刀具的刀尖角如果等于蜗杆的齿形角.这种刀具在车削时两侧刀刃与工件侧面容易发生摩擦,甚至三个刀刃同时参加切削,易产生较大的切削力而损坏刀具.如果选择车刀的刀尖角35小于蜗杆的齿形角40,如图2这种车刀在车削时,可防止三个刀刃同时参加切削,减少了摩擦、切削力,能很好地避免“闷车”、“扎刀”和打刀的情况发生.二、在数控车床上使用硬质合金车刀高转速车削蜗杆成为现实以前,车削加工蜗杆和大导程螺纹,只能用高速钢车刀低速车削加工,生产效率非常低.如果将车刀的刀尖角磨小,使车刀的刀尖角35小于蜗杆的齿形角40,可避免三个刀刃同时参加切削,切削刀显剧下降,这时可使用较高的切削速度和硬质合金车刀对蜗杆进行车削.当工件直径、导程越大时,可获得的线速度越高,加工出的工件表面质量越好,而且生产效率明显提高.彻底解决在数控车床不能用硬质合金刀具车削蜗杆和大导程螺纹零件.只要数控车床能承受,尽可能选择较高的线速度,在车削模数Ms＝4时,选用350转/分钟.如图3图2 刀尖角35小于齿形角40 图3 硬质合金车刀三、利用数控车床的精度高、定位准,用车削斜面的方法代替成形刀车削蜗杆,能保证蜗杆的齿形角如果蜗杆车刀的刀尖角直接决定被加工螺纹牙形角的大小,这显然是用成形刀来车削蜗杆.当使用成形刀车削较大导程蜗杆工件时,有可能整过刀刃甚至是三个刀刃同时参加切削,切削力陡增.由于数控车床在低转速转动时无力,用成形刀在数控车床上车削蜗杆或大导程螺纹会出现“闷车”和“扎刀”.为解决以上问题,可用左右分层车削斜面的方法取代成形刀法来车削蜗杆和大导程螺纹,可彻底避免在车削中经常出现三个刀刃同时参加切削而导致切削力增大、排屑不畅、“闷车”和“扎刀”等现象.车削斜面的方法是：车螺纹时,车刀在第一次往复车削后,刀尖在通过轴线剖面的牙侧上车削出了A点,经过多次往复循环车削,刀尖在通过轴线剖面的牙侧上分别车削出了B、C、D、E、F……N个点,将ACEN和BDF等多个点分别连接起来成为两条倾斜的直线,形成了蜗杆两侧的齿面和齿形角.如图4图4 蜗杆齿侧的形成四、使用宏程序能满足加工加工要求粗车如图1模数Ms＝4的蜗杆,大约只需10分钟左右.粗车蜗杆的加工宏程序如下：%0001T0303M03S350F1001＝蜗杆全齿高2＝齿根槽宽W＝3= 刀头宽t＝WHLIE 1GE04＝12+ 计算X轴尺寸.齿根圆为5＝1TAN20PI/1802+2 计算Z轴尺寸WHLIE 5GE3G00 X50 Z8 M08 循环起点G00 Z8+5-3/2 Z轴向右边移动G82 X4 Z-87 车蜗杆G00 Z8-5-3/2 Z轴向右边移动G82 X4 Z-87 车蜗杆5＝5-3 每次循环的切削宽度ENDW1= 每次循环的切削深度ENDWG0X150Z8M09M30精车时必须修改粗车的宏程序如下：1、测量粗车后的法向齿厚Sn/Cos20=Sx轴向齿厚.2、将宏程序的程序段2＝修改为2＝+ Sx/2轴向齿厚/23、将宏程序的程序段1=修改为1=4、将宏程序的WHLIE 5GE3、5＝5-3、ENDW删除.5、将修改后的宏程序重新调用加工一次,精车蜗杆大约只需10分钟左右.修改后,精车蜗杆宏程序如下：%0001T0303M03S350F1001＝蜗杆全齿高2＝+ Sx/2 齿根槽宽+轴向齿厚Sx/23= 刀头宽t＝WHLIE 1GE04＝12+ 计算X轴尺寸.齿根圆为5＝1TAN20PI/1802+2 计算Z轴尺寸G00 X50 Z8 M08 循环起点G00 Z8+5-3/2 Z轴向右边移动G82 X4 Z-87 车蜗杆G00 Z8-5-3/2 Z轴向右边移动G82 X4 Z-87 车蜗杆1= 每次循环的切削深度ENDWG0X150Z8M09M30五、结束语在数控车床上快速车削蜗杆和大导程螺纹的方法有三个特点：一是摆脱了在普通车床上车削蜗杆要求工人有较高的操作技能和技巧.二是解决了数控车床不能车削大导程的蜗杆和螺纹.三是充分利用了数控车床的精度高、定位准的特点,突破了传统的选择蜗杆车刀的习惯,将刀具的刀尖角选得小于齿形角,车削时防止了三个刀刃同时参加切削,排屑顺利,减小了切削力,使用硬质合金车刀,高速切削蜗杆和大导程螺纹成为现实在数控车床上加工较大直径和较大导程的蜗杆优势更大.粗车和精车如图1的蜗杆大约需要20分钟左右的时间,生产效率有了较大的提高,是普通车床的10倍左右.在数控车床上车削蜗杆和大导程螺纹注意三点：一是要求有编辑和修改宏程序、准备车刀和安装工件的能力.二是用硬质合金车刀车削梯形螺纹,不能选用过高的主轴转速,应考虑车床的承受能力.如车削模数Ms＝4的蜗杆,主轴转速可选350转/分左右,否则,会由于大滑板换向太快而影响车床丝杆和螺母的精度.三是如果被切削的工件直径较小,车削时的线速度较低,车削出齿侧的表面粗糙度只能达到左右.当车削较小直径的工件时,可在数控车床上粗车,留下较小的精车余量,然后选用高速钢车刀低速精车来解决工件的表面粗糙度.资料来源。

数控车床上加工蜗杆的通用宏程序摘要很多中小型企业会遇到要在数控车床上加工大螺距梯形螺纹和蜗杆，由于这些企业条件限制，往往不能编制好加工程序，本文以实例探讨了数控车床中加工蜗杆和梯形螺纹通用宏程序的设计和编程，让中小企业也能轻松地应用宏程序加工蜗杆和梯形螺纹。

关键词宏程序梯形螺纹蜗杆一、前言今年本人应某中小型企业邀请，去帮他们处理数控车床加工中遇到的一些问题。

经交流得知，他们要加工一批蜗杆，并从宜昌纺织机械厂请了位师傅编了个很长的程序，但加工时还是很快损坏了刀具。

我查阅了相关说明书，并无这方面内容，上网搜索，也没有找到免费的可以直接使用的相关文章，因此本人参考部分资料，给他们编制了一个通用的加工蜗杆和梯形螺纹的程序，告诉他们使用方法后，遇到蜗杆和梯形螺纹就可以直接套用该程序，这样即使对宏程序不太熟悉的工人也可以加工蜗杆和梯形螺纹了。

二、加工螺纹的一般方法在数控车床加工螺纹一般有四种方法：直进法、斜进法、左右切削法和切槽刀粗切槽法四种。

1、直进法：如图1所示，螺纹刀间歇性进给到牙深处，采用此种方法加工梯形螺纹时，螺纹车刀的三面都参与切削，导致加工排屑困难，切削力和切削热增加，刀尖磨损严重，进刀量过大时，还可能产生扎刀现象。

很显然，加工大螺距梯形螺纹和蜗杆是不可取的。

2、斜进法：如图2所示，螺纹车刀沿牙型角方向斜向间歇进给到牙深处，采用此种方法加工梯形螺纹时，螺纹车刀始终只有一侧刀刃参加切削，从而排屑比较顺利，刀尖的受力和受热情况有所改善，在车削中不易引起扎刀现象。

3、左右切削法：如图3所示，螺纹车刀沿牙型角方向交错间隙进给至牙深，该方法同于斜进法，在数控车床上采用宏程序编程来实现。

3、切槽刀粗切槽法：如图4所示，该方法先用切槽刀粗切槽，再用梯形螺纹车刀加工螺纹两侧面，这种方法在数控车中较难实现。

三、蜗杆和大螺距梯形螺纹特点和加工方法车削加工蜗杆和大导程螺纹，无论用斜进法还是左右切削法，切削抗力非常大，以前只能用高速钢车刀低速车削加工，生产效率非常低。

浅析在数控车床用宏程序加工蜗杆方法作者：黄广和来源：《学校教育研究》2020年第05期摘要：蜗杆在通常加工中常用低速加工，工人加工劳动量大，加工难度高，工作效率低。

本文以实例探讨数控车床中高速加工蜗杆通用宏程序的设计和编程，以减少工人劳动强度，提高加工效率。

关键词：数控车加工、蜗杆加工、宏程序编程本文以下图为例，讲解在数控车床上如何利用宏程序编程加工蜗杆的实例。

一、加工工艺的安排1.锅杆在数控车床上进行加工编程的内容十分复杂，工艺的安排在蜗杆的加工过程中起到了重要的作用。

首先关于起刀点，要设置在蜗杆的右侧起刀，编程也应当将起点设置在右端面。

另外为了应对背吃刀量的问題，加工过程中对蜗杆的全齿和削法也有着明确的规定。

还有一夹一顶的装夹方式是被优先选用的装夹方式，对蜗杆生产来说误差也是一个很重要的方面，在数控车床加工中，减小误差是十分重要的。

2.相关数据的计算。

在蜗杆加工编程的过程中，很重要的事就是对蜗杆相关参数进行计算。

其中起刀点是一项主要需要测算的项目之一，它计算的依据主要是距离、转程、导程，在计算起刀点的过程中升速段和减速段是主要被参考的对象，另外在蜗杆加工之前还有许多的数据需要经过严密的计算才能够确定并且投入加工生产中。

3.蜗杆的加工方法。

由于蜗杆导程大，牙高深，所以无论用斜进法还是左右切削法，切削抗力非常大。

如果要在数控车床上用高速加工蜗杆，因此我采用了“分层切削"的方法来加工。

把螺纹或蜗杆的牙槽分成若干层，转化成若干个较浅的螺纹槽来进行切削，这样可以有效地控制切除余量，保证表面质量和刀具的使用寿命。

（如图2）二、蜗杆加工宏程序编程宏程序，简单的说，它就是一种利用变量来进行表示的一种程序，它的变量分三种，即有：局部变量、公共变量、系统变量，蜗杆加工时利用宏程序来控制蜗杆的灵活性，在编程过程中，参数的不同就会加工出不同型号的锅杆，而参数的改变常被用于加工相似的蜗杆，用这样的方式，可以提高蜗杆加工的效率。