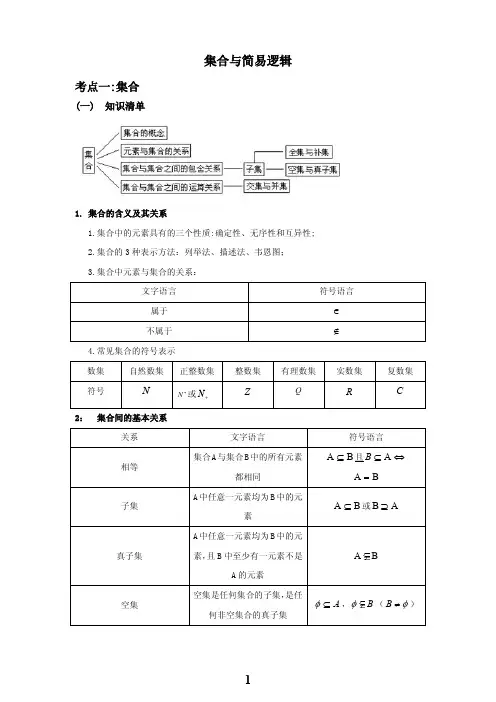
2012年高考数学 高考试题+模拟新题分类汇编专题A 集合与常用逻辑用语 文

北京市2012年高考数学最新联考试题分类大汇编
一、选择题：
2. (2012年3月北京市朝阳区高三一模文科)若集合{}2
1,A m =，{}3,4B =，则
“2m =”是“{}4=B A I ”的
A ．充分不必要条件
B ．必要不充分条件
C ．充分必要条件
D ．既不充分也不必要条件
【答案】A
7．(北京市西城区2012年4月高三第一次模拟文)设等比数列{}n a 的前n 项和为n S ．则“10a >”是“32S S >”的（ C ）
（A ）充分而不必要条件
（B ）必要而不充分条件 （C ）充要条件 （D ）既不充分又不必要条件
【答案】A
（2）(北京市东城区2012年4月高考一模文科)若集合},0{2
m A =，}2,1{=B
，则
6．(2012年3月北京市丰台区高三一模文科)若函数1(),0,()2,0,x x f x x a x ⎧≤⎪=⎨⎪-+>⎩ 则“a =1”是“函数y =f (x )在R 上单调递减”的
(A) 充分不必要条件
(B) 必要不充分条件 (C) 充要条件
(D) 既不充分也不必要条件
【答案】A。

《人民解放战争的胜利 》 班级 姓名 小组 编号 一、学习目标：1.重庆谈判双方的主要代表及签订的文件；2.刘邓大军挺进大别山，人民解放战争转入反攻；3.三大战役、渡江战役的基本情况及示意图；4.人民解放战争胜利的主要原因。

二、课堂目标重难点： 1.重点:重庆谈判；三大战役和渡江战役。

2.难点：人民军解放战争胜利的主要原因。

三、自主学习教材第94---99 页，完成下列练习： 1. 重庆谈判：时间：1945年8月-10月；代表：共产党---毛泽东、（ ）、王若飞。

国民党----张治中、邵力子。

结果：签订《 》。

2全面内战爆发：时间：1946年6月；标志：国民党军队围攻（ ）解放区。

3. 粉碎敌人重点进攻：时间：1947年3月；指挥者及战术：（ ）“蘑菇战术”； 结果：粉碎了敌人对陕北的重点进攻。

4. 刘、邓大军挺进（ ）：1947年夏，影响：揭开了战略反攻的序幕。

5. 三大战役：（ ）战役：解放东北全境；（ ）战役：基本上解放了长江以北的华东和中原地区；（ ）战役：解放华北全境。

6. 渡江战役：时间：1949年2月，战线：东起（ ），西至（ ）；结果：统治中国22年的南京国民党政权垮台。

四 课堂练习： 材料 毛泽东于1949年4月的一首七律：钟山风雨起苍黄，百万雄师过大江。

虎踞龙盘今胜昔，天翻地覆慨而慷。

宜将剩勇追穷寇，不可沽名学霸王。

天若有情天亦老，人间正道是沧桑。

请回答：1.“百万雄师过大江”指的是什么历史事件？此事件得以发动的军事基础是什么？ 2.诗中“宜将剩勇追穷寇，不可沽名学霸王”中的“霸王”是指谁？诗句的寓意是什么？ 3.“百万雄师过大江”的结果是什么？ 初中学习网，资料共分享！我们负责传递知识！。

A 单元 集合与常用逻辑用语A1 集合及其运算2．A1、B7[2012·某某卷] 设集合A ＝{x |－3≤2x －1≤3}，集合B 为函数y ＝lg(x －1)的定义域，则A ∩B ＝( )A ．(1,2)B ．[1,2]C ．[1,2)D ．(1,2]2．D [解析] 根据已知条件，可求得A ＝[]－1，2，B ＝()1，＋∞，所以A ∩B ＝[]－1，2∩()1，＋∞＝(]1，2.1．A1[2012·全国卷] 已知集合A ＝{x |x 是平行四边形}，B ＝{x |x 是矩形}，C ＝{x |x 是正方形}，D ＝{x |x 是菱形}，则( )A ．A ⊆B B ．C ⊆B C ．D ⊆C D ．A ⊆D1．B [解析] 本小题主要考查特殊四边形的定义．解题的突破口为正确理解四种特殊四边形的定义及区别．因为正方形是邻边相等的矩形，故选B. 2．A1[2012·某某卷] 已知集合M ＝{1,2,3,4}，N ＝{－2,2}，下列结论成立的是( ) A ．N ⊂M B ．M ∪N ＝MC ．M ∩N ＝ND ．M ∩N ＝{2}2．D [解析] 因为集合M ＝{1,2,3,4}，N ＝{－2,2}，所以M ∩N ＝{2}．所以D 正确．2．A1[2012·某某卷] 设集合U ＝{1,2,3,4,5,6}，M ＝{1,3,5}，则∁U M ＝( ) A ．{2,4,6} B ．{1,3,5} C ．{1,2,4} D ．U2．A [解析] 因为U ＝{1,2,3,4,5,6}，M ＝{1,3,5}，所以∁UM ＝{2,4,6}，所以选择A.1．A1[2012·某某卷] 已知集合A ＝{x |x 2－3x ＋2＝0，x ∈R }，B ＝{x |0＜x <5，x ∈N }，则满足条件A ⊆C ⊆B 的集合C 的个数为( )A ．1B ．2C ．3D ．4 1．D[解析] 易知A ＝{1,2}，B ＝{x |0<x <5，x ∈N }＝{1,2,3,4}．又因为A ⊆C ⊆B ，所以集合C 必须含有元素1,2，且可能含有元素3,4，原题即求集合{3,4}的子集个数，即有22＝4个．故选D.1．A1[2012·某某卷] 设集合M ＝{－1,0,1}，N ＝{x |x 2＝x }，则M ∩N ＝( ) A ．{－1,0,1} B ．{0,1} C ．{1} D ．{0}1．B [解析] 本题考查集合的运算，意在考查集合交集的简单运算．由题意得集合N ＝{0,1}，利用韦恩图，或者直接运算得M ∩N ＝{0,1}．[易错点] 本题的易错为求集合M ，N 的并集运算，错选A.1．A1[2012·某某卷] 已知集合A ＝{1,2,4}，B ＝{2,4,6}，则A ∪B ＝________.1．{1,2,4,6} [解析] 考查集合之间的运算．解题的突破口为直接运用并集定义即可．由条件得A ∪B ＝{1,2,4,6}．2．A1[2012·某某卷] 若全集U ＝|x ∈R |x 2≤4|，则集合A ＝{x ∈R ||x ＋1|≤1}的补集∁UA 为( )A ．{x ∈R |0<x <2}B ．{x ∈R |0≤x <2}C ．{x ∈R |0<x ≤2} D．{x ∈R |0≤x ≤2}2．C [解析] ∵集合U ＝{x |－2≤x ≤2}，A ＝{x |－2≤x ≤0}，∴∁UA ＝{x |0<x ≤2}，故选C.1．A1[2012·课标全国卷] 已知集合A ＝{x |x 2－x －2<0}，B ＝{x |－1<x <1}，则( ) A ．A B B ．B A C ．A ＝B D ．A ∩B ＝∅1．B [解析] 易知集合A ＝{x |－1<x <2}，又已知B ＝{x |－1<x <1}，所以B A .故选B. 2．A1[2012·某某卷] 已知全集U ＝{0,1,2,3,4,5,6,7,8,9}，集合A ＝{0,1,3,5,8}，集合B ＝{2,4,5,6,8}，则(∁U A )∩(∁U B }＝( )A ．{5,8}B ．{7,9}C ．{0,1,3}D ．{2,4,6}2．B [解析] 本小题主要考查集合的概念及基本运算．解题的突破口为弄清交集与补集的概念以及运算性质．法一：∵∁U A ＝{2,4,6,7,9}，∁U B ＝{0,1,3,7,9}，∴(∁U A )∩(∁U B )＝{7,9}． 法二：∵A ∪B ＝{0,1,2,3,4,5,6,8}， ∴(∁U A )∩(∁U B )＝∁U (A ∪B )＝{7,9}． 2．A1[2012·某某卷] 已知全集U ＝{0,1,2,3,4}，集合A ＝{1,2,3}，B ＝{2,4}，则(∁U A )∪B 为( )A ．{1,2,4}B ．{2,3,4}C ．{0,2,4}D ．{0,2,3,4}2．C [解析] 本题考查集合间的关系及交、并、补的运算，考查运算能力，容易题． ∵U ＝{0,1,2,3,4}，A ＝{1,2,3}，B ＝{2,4}，∴∁U A ＝{0,4}，(∁U A )∪B ＝{0,2,4}．1．A1[2012·某某卷] 集合M ＝{x |lg x >0}，N ＝{x |x 2≤4}，则M ∩N ＝( ) A ．(1,2) B ．[1,2) C ．(1,2] D ．[1,2]1．C [解析] 本小题主要考查集合的概念及基本运算以及对数函数的性质、一元二次不等式的解法．解题的突破口为解对数不等式以及一元二次不等式．对于lg x >0可解得x >1；对于x 2≤4可解得－2≤x ≤2，根据集合的运算可得1<x ≤2，故选C.2．A1[2012·某某卷] 若集合A ＝{x |2x －1＞0}，B ＝{x ||x |＜1}，则A ∩B ＝________. 2.⎝ ⎛⎭⎪⎫12，1 [解析] 考查集合的交集运算和解绝对值不等式，此题的关键是解绝对值不等式，再利用数轴求解．解得集合A ＝⎝ ⎛⎭⎪⎫12，＋∞，集合B ＝(－1,1)，求得A ∩B ＝⎝ ⎛⎭⎪⎫12，1. 1．A1[2012·某某卷] 设集合A ＝{a ，b }，B ＝{b ，c ，d }，则A ∪B ＝( ) A ．{b } B ．{b ，c ，d }C ．{a ，c ，d }D ．{a ，b ，c ，d }1．D [解析] 由已知A ∪B ＝{a ，b }∪{b ，c ，d }＝{a ，b ，c ，d }．2．J3[2012·某某卷] (1＋x )7的展开式中x 2的系数是( ) A ．21 B ．28 C ．35 D ．422．A [解析] 根据二项展开式的通项公式T r ＋1＝C r 7x r ，取r ＝2得x 2的系数为C 27＝7×62＝21.1．A1[2012·某某卷] 设全集U ＝{1,2,3,4,5,6}，集合P ＝{1,2,3,4}，Q ＝{3,4,5}，则P ∩(∁U Q )＝( )A ．{1,2,3,4,6}B ．{1,2,3,4,5}C ．{1,2,5}D ．{1,2}1．D [解析] 本题考查集合的表示、集合交集、补集的运算，考查学生对集合基础知识的掌握情况，属于基础题．因为∁U Q ＝{1,2,6}，则P ∩(∁U Q )＝{1,2}，答案为D.10．A1、E3、B6[2012·某某卷] 设函数f (x )＝x 2－4x ＋3，g (x )＝3x－2，集合M ＝{x ∈R |f (g (x ))>0|，则N ＝{x ∈R |g (x )<2}，则M ∩N 为( )A ．(1，＋∞) B．(0,1) C ．(－1,1) D ．(－∞，1)10．D [解析] 因为f (g (x ))＝[g (x )]2－4g (x )＋3，所以解关于g (x )不等式[g (x )]2－4g (x )＋3＞0，得g (x )＜1或g (x )＞3，即3x －2＜1或3x－2＞3，解得x ＜1或x ＞log 35，所以M ＝(－∞，1)∪(log 35，＋∞)，又由g (x )＜2，即3x －2＜2,3x＜4，解得x ＜log 34，所以N ＝(－∞，log 34)，故M ∩N ＝(－∞，1)，选D.A2 命题及其关系、充分条件、必要条件5．A2[2012·某某卷] 设x ∈R ，则“x ＞12”是“2x 2＋x －1＞0”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．A [解析] 当x >12时，2x 2＋x －1>0成立；但当2x 2＋x －1>0时，x >12或x <－1.∴“x >12”是“2x 2＋x －1>0”充分不必要条件．5．A2[2012·某某卷] 已知命题p ：∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≥0，则綈p 是( )A ．∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≤0B ．∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≤0C ．∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<0D ．∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<05．C [解析] 本小题主要考查存在性命题与全称命题的关系．解题的突破口为全称命题的否定是存在性命题，存在性命题的否定是全称命题．故∀x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)≥0的否定是∃x 1，x 2∈R ，(f (x 2)－f (x 1))(x 2－x 1)<0，故而答案选C.1．A2[2012·某某卷] 命题“若p 则q ”的逆命题是( ) A ．若q 则p B ．若綈p 则綈q C ．若綈q 则綈p D ．若p 则綈q1．A [解析] 根据原命题与逆命题的关系，交换条件p 与结论q 的位置即可，即命题“若p 则q ”的逆命题是“若q 则p ”，选A.3．A2[2012·某某卷] 命题“若α＝π4，则tan α＝1”的逆否命题是( )A ．若α≠π4，则tan α≠1B ．若α＝π4，则tan α≠1C ．若tan α≠1，则α≠π4D ．若tan α≠1，则α＝π43．C [解析] 本题考查命题的逆否命题，意在考查考生对命题的逆否命题的掌握．解题思路：根据定义，原命题：若p 则q ，逆否命题：若綈q 则綈p ，从而求解．命题“若α＝π4，则tan α＝1”的逆否命题是“若tan α≠1，则α≠π4”，故选C. [易错点] 本题易错一：对四种命题的概念不清，导致乱选；易错二：把命题的逆否命题与命题的否定混淆．4．A2、H2[2012·某某卷] 设a ∈R ，则“a ＝1”是“直线l 1：ax ＋2y －1＝0与直线l 2：x ＋2y ＋4＝0平行”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．C [解析] 本题考查了简易逻辑、两直线平行等基础知识，考查了学生简单的逻辑推理能力．若a ＝1，则直线l 1：ax ＋2y －1＝0与l 2：x ＋2y ＋4＝0平行；若直线l 1：ax ＋2y －1＝0与l 2：x ＋2y ＋4＝0平行，则2a －2＝0即a ＝1.∴“a ＝1”是“l 1：ax ＋2y －1＝0与l 2：x ＋2y ＋4＝0平行”的充要条件．16．A2、H5[2012·某某卷] 对于常数m 、n ，“mn ＞0”是“方程mx 2＋ny 2＝1的曲线是椭圆”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件16．B [解析] 考查充分条件和必要条件，以及椭圆方程．判断充分条件和必要条件，首先要确定条件与结论．条件是“mn >0”，结论是“方程mx 2＋ny 2＝1的曲线是椭圆”， 方程mx 2＋ny 2＝1的曲线是椭圆，可以得出mn >0，且m >0，n >0，m ≠n ，而由条件“mn >0”推不出“方程mx 2＋ny 2＝1的曲线是椭圆”．所以为必要不充分条件，选B.4．A2、L4[2012·某某卷] 设a ，b ∈R ，i 是虚数单位，则“ab ＝0”是“复数a ＋bi为纯虚数”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．B [解析] 本小题主要考查充要条件的概念以及复数的相关知识，解题的突破口为弄清什么是纯虚数，然后根据充要条件的定义去判断．a ＋b i ＝a －b i ，若a ＋bi 为纯虚数，a＝0且b ≠0，所以ab ＝0不一定有a ＋b i 为纯虚数，但a ＋bi 为纯虚数，一定有ab ＝0，故“ab＝0”是“复数a ＋bi为纯虚数”的必要不充分条件，故选B.A3 基本逻辑联结词及量词5．A3、C4[2012·某某卷] 设命题p ：函数y ＝sin2x 的最小正周期为π2；命题q ：函数y ＝cos x 的图象关于直线x ＝π2对称．则下列判断正确的是( )A ．p 为真B ．綈q 为假C ．p ∧q 为假D ．p ∨q 为真5．C [解析] 本题考查含量词命题间的真假关系及三角函数的图象与性质，考查推理能力，容易题．∵函数y ＝sin2x 的最小正周期为π，∴命题p 为假命题；函数y ＝cos x 的图象的对称轴所在直线方程为x ＝kπ，k ∈Z ，∴命题q 为假命题，由命题间的真假关系得p ∧q 为假命题．14． A3、B3、E3[2012·卷] 已知f (x )＝m (x －2m )(x ＋m ＋3)，g (x )＝2x－2，若∀x ∈R ，f (x )<0或g (x )<0，则m 的取值X 围是________．14．(－4,0) [解析] 本题考查函数图像与性质、不等式求解、逻辑、二次函数与指数函数等基础知识和基本技能，考查分类讨论的数学思想、分析问题和解决问题以及综合运用知识的能力．由已知g (x )＝2x－2<0，可得x <1，要使∀x ∈R ，f (x )<0或g (x )<0，必须使x ≥1时，f (x )＝m (x －2m )(x ＋m ＋3)<0恒成立，当m ＝0时，f (x )＝m (x －2m )(x ＋m ＋3)＝0不满足条件，所以二次函数f (x )必须开口向下，也就是m <0，要满足条件，必须使方程f (x )＝0的两根2m ，－m －3都小于1，即⎩⎪⎨⎪⎧2m <1，－m －3<1， 可得m ∈(－4,0)． 4． A3[2012·某某卷] 命题“存在实数x ，使x >1”的否定．．是( ) A ．对任意实数x ，都有x >1 B ．不存在实数x ，使x ≤1 C ．对任意实数x ，都有x ≤1 D ．存在实数x ，使x ≤14．C [解析] 对结论进行否定同时对量词做对应改变，原命题的否定应为：“对任意实数x ，都有x ≤1”．A4 单元综合 2012模拟题1．[2012·某某一中月考] 已知集合A＝{x|－5≤2x－1≤3，x∈R}，B＝{x|x(x－8)≤0，x∈Z}，则A∩B＝( )A．(0,2) B．[0,2]C．{0,2} D．{0,1,2}1.D [解析] A∩B是A，B中的所有公共元素组成的集合，由题易求得A＝{x|－2≤x≤2}，B＝{0,1,2,3,4,5,6,7,8}，故A∩B＝{0,1,2}．2．[2012·某某师大附中月考] 已知集合U＝{1,2,3,4,5}，集合A＝{x|x2－3x＋2＝0}，B＝{x|x＝2a，a∈A}，则集合∁U(A∪B)中元素的个数为( )A．1 B．2C．3 D．42．B [解析] A＝{1,2}，B＝{2,4}，∴A∪B＝{1,2,4}，∴∁U(A∪B)＝{3,5}．3．[2012·某某一模] 己知命题p：∀x∈R，ln(e x＋1)>0，则綈p为( )A．∃x∈R，ln(e x＋1)<0B．∀x∈R，ln(e x＋1)<0C．∃x∈R，ln(e x＋1)≤0D．∀x∈R，ln(e x＋1)≤03．C [解析] p：∀x∈R，ln(e x＋1)>0的否定是∃x∈R，ln(e x＋1)≤0.4．[2012·某某两校联考] 设p：16－x2<0，q：x2＋x－6>0，则綈q是綈p的( ) A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件4．A [解析] ∵p：16－x2<0⇒x>4或x<－4，q：x2＋x－6>0⇒x>2或x<－3，∴綈p：－4≤x≤4，綈q：－3≤x≤2，∴{x|－3≤x≤2}{x|－4≤x≤4}，∴綈q⇒綈p，綈p不能推出綈q，綈q是綈p的充分不必要条件．5．[2012·武昌元月调研] 已知集合A＝{(x，y)||x－a|＋|y－1|≤1}，B＝{(x，y)|(x －1)2＋(y－1)2≤1}，若A∩B≠∅，则实数a的取值X围为________．5．[－1,3] [解析] 作出|x|＋|y|<1的图象，利用平移，知集合A是中心为M(a,1)，边长为eq \r(2)的正方形内部(包括边界)，又集合B是圆心为N(1,1)，半径为1的圆的内部(包括边界)，易知MN的长度不大于1＋1时，即eq \r((a－1)2)≤2，∴－1≤a≤3，故实数a的取值X围为[－1,3]．。

题型四：图解法解集合问题 例 7、 已知集合 M= x | A． C． [ 3,3]
2 2

x2 y2 x y 1 ，N= y | 1 ，则 M N （ ） 9 4 3 2
B． {(3,0), ( 2,0)} D． 3,2
变式 1. 已知集合 A {( x, y ) | x, y 为实数，且 x y 1} ， B {( x, y ) | x, y 为实数，且
(2)“p 且 q” p∧q 形式的复合命题真假： 当 p、q 为真时，p 且 q 为真；当 p、q 中至少有一个为假时，p 且 q 为假. （一假必假） p q p且q 真 真 假 假 真 假 真 假 真 假 假 假
(3)“p 或 q” p∨q 形式的复合命题真假： 当 p、q 中至少有一个为真时，p 或 q 为真；当 p、q 都为假时，p 或 q 为假. （一真必真） p q P或q 真 真 假 假 真 假 真 假 真 真 真 假
4.全称量词与存在量词 数学命题中出现“全部”、 “所有”、 “一切”、 “任何”、 “任意”、 “每一个”等与“存 在着”、“有”、“有些”、“某个”、“至少有一个”等的词语，在逻辑中分别称为全称 量词与存在性量词（用符号分别记为“ ”与“ ”来表示） ；由这样的量词构成的命题 分别称为全称命题与存在性命题。 一般地，全称命题 P： xM,有 P（x）成立；其否定命题┓P 为：x∈M,使 P（x）不 成立。存在性命题 P：xM，使 P（x）成立；其否定命题┓P 为： xM,有 P（x）不成立。 用符号语言表示： P:M, p(x）否定为 P: M, P（x） P:M, p(x）否定为 P: M, P（x）
例 15. “a=1”是“直线 x+y=0 和直线 x-ay=0 互相垂直”的（ A.充分而不必要条件 C.充要条件 B.必要而不充分条件 D.既不充分也不必要条件

精品解析：北京市2012年高考数学最新联考试题分类大汇编（2）常
用逻辑用语试题解析
一、选择题：
2. (2012年3月北京市朝阳区高三一模文科)若集合{}2
1,A m
=，{}3,4B =，则
“2m =”是“{}4=B A ”的
A ．充分不必要条件
B ．必要不充分条件
C ．充分必要条件
D ．既不充分也不必要条件 【答案】A
7．(北京市西城区2012年4月高三第一次模拟文)设等比数列{}n a 的前n 项和为n S ．则“10a >”是“32S S >”的（ C ） （A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件
（D ）既不充分又不必要条件
【答案】A
（2）(北京市东城区2012年4月高考一模文科)若集合},0{2
m A =，}2,1{=B
，则
6．(2012年3月北京市丰台区高三一模文科)若函数
1(),0,()2
,0,x
x f x x a x ⎧≤⎪=⎨⎪-+>⎩ 则“a =1”是“函数y =f (x )在R 上单调递减”的 (A) 充分不必要条件
(B) 必要不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
【答案】A。

【学习目标】 理解议论文中论据和论点的关系，能把握文章的中心论点 理解议论文的基本思路 理解和分析常见的论证方法 领会议论性语言严密、概括的特点 了解立论、驳论两种基本论证方式，理清文章的论证结构 善于表达通过自己的思考作出的判断。

【教学步骤】 引入：1、议论文的特点：以议论为主要的表达方式，可兼用其他表达方式；以鲜明的态度表明观点或主张；以充分的材料证明其观点或主张。

2、议论文的三要素： 论点——对所论述的问题所持的观点、态度。

论点有中心论点、分论点两种，有的议论文只有中心论点，有的议论文中心论点、分论点均有。

论据——对论点进行论证的材料、依据。

论据有事实论据（代表性的确凿的事例与史实、统计的数字等）；道理论据（自然科学的定义、定理，名言警句，俗语谚语等） 论证——用论据证明论点的过程和方法。

3、议论文的分类： 立论——从正面论述其观点、说明其观点的正确。

驳论——批驳错误观点，然后确立其正确观点。

议论文按论证方式分类可分为：立论文和驳论文。

把握中心论点 从题目入手 ①题目即为观点。

例：《多一些宽容》、《人的高贵在于灵魂》；②有的题目是论题，从文中找出直接回答这个论题的语句，就能把握论点。

例：《论美》《学问与智慧》《成功》 从文中运用的论据推断出论点。

论据是支撑论点的材料。

即抓住文中所运用的事实或道理论据用来证明什么，尤其要抓住的是作者对论据所阐述的话，也能把握论点。

捕捉文章的“中心句”。

根据论点常见位置[一般在篇首或篇末，也有在篇中的]来寻找。

审视是不是中心论点，也要慎重，必须通读全文，才可确认。

放在结尾的，往往先提出分论点，层层论述，在结尾处归纳出中心论点。

要很好地研究文章和题目的各种关系，才能归纳出来。

放在文中的这种文章，往往观点的提出有一个过程，经过一番论辩后，再提出中心论点，一般驳论性的文章、读后感一类文章，好采取此种方法。

不管放在何处，只要留心题目、论点的位置、分析议论展开后的段落、层次结构，中心论点是可以找到的。

山东省各市2012届高三数学（理）下学期模拟考试题分类解析集合与常用逻辑用语1、（2012滨州二模）设全集U ＝R ，A ＝{x|0.5x >0.25},B={x|y=ln(1-x)}，则()U A C B ⋂＝ （A ）{x|x ≥1} （B ）{x|1≤x<2} （C ）{x|0<x ≤1} （D ）{x|x ≤1} 答案：B解析：A ＝{x|x ＜2}，B={x|x ＜1}，U C B ＝{x| x ≥1}，所以()U A C B ⋂＝{x|1≤x<2} 2、（2012德州二模）1．已知全集U ＝R ，集合{|A x y ==，{|log (2)}a B x y x ==+，则集合()U A B =A ．（-2，-1）B ．(2,1]--C ．(,2)-∞-D ．(1,)-+∞答案：B解析：集合A ＝{x|x ＞－1} ，()U A ＝{x|x ≤－1}，B ＝{x|x ＞－2} ，所以，()U A B ＝{x|－2＜x ≤－1}，故选B 。

3、（2012德州一模）设全集U 是实数集R ，若2{4},N={|1<3}UM x|x x x =>≤，则M N =( )A ．{|-21}x x ≤<B ．{|2}x x <C ．{|-22}x x ≤≤D ．{|1<2}x x ≤ 答案：D 解析：2{4}={|22}UM x|x x x x =>><-或，所以{|-22}M x x =≤≤，M N ＝{|1<2}x x ≤，因些，选D 。

4、（2012济南3月模拟）设p :|4x -3|≤1，q : 2x -(2a +1)x +a (a +1)≤0，若非p 是非q 的必要而不充分条件，则实数a 的取值范围是 A. 10,2⎡⎤⎢⎥⎣⎦ B. 10,2⎛⎫⎪⎝⎭C. （－∞，0］∪1,2⎡⎫+∞⎪⎢⎣⎭D.（－∞，0）∪1,2⎛⎫+∞ ⎪⎝⎭【答案】A【解析】由|4x -3|≤1解得121≤≤x ，由2x -(2a +1)x +a (a +1)≤0得0 )1)((≤---a x a x ，即1+≤≤a x a ，若非p 是非q 的必要而不充分条件，则q 是p 的必要而不充分条件，所以有⎪⎩⎪⎨⎧≥+≤1121a a ，即⎪⎩⎪⎨⎧≥≤021a a ，所以210≤≤x ，选A. 5、（2012济南三模）1、若全集U =R ，集合{235}A x x =+<，B =｛3|log (2)x y x =+｝，则()UC AB =A ．{}14≥-≤x x x 或B ．{}14>-<x x x 或 C ．{}12>-<x x x 或 D ．{}12≥-≤x x x 或答案：D解析：因为}14{}532{<<-=<+=x x x x A ，}2}{02{})2(log {3->>+=+==x x x x x y x B ，所以}12{<<-=⋂x x B A ，所以}21{)(-≤≥=⋂x x x B A C U 或，选D.6、（2012莱芜3月模拟）已知全集U =R ，集合{|13}A x x =<≤，{|2}B x x =>，则U A B 等于(A){|12}x x <≤(B){|12}x x ≤< (C ){|12}x x ≤≤(D){|13}x x ≤≤【答案】A【解析】}2{≤=x x B C U ，所以}21{}2{}31{≤<=≤⋂≤<=⋂x x x x x x B C A U ，选A.7、（2012临沂3月模拟）集合{}022≤--=x x x A ，{}1<=x x B ，则=⋂)(B C A R（A ）{}1>x x （B ）{}21≤≤x x （C ）{}21≤<x x （D ）{}1≥x 【答案】B【解析】{}2}1{022≤≤-=≤--=x x x x x A ，所以}1{≥=x x B C R ，所以}21{≤≤=⋂x x B A ，选B.8、（2012临沂二模）设{}213A x x =-≤，{}0B x x a =->，若A B ⊆，则实数a 的取值范围是（A ）()-∞，-1 （B ）(1]-∞-， （C ）(2)-∞-， （D ）(2]-∞-，【答案】A【解析】集合}21{}3123{≤≤-=≤-≤-=x x x x A ，而}{a x x B >=，因为A B ⊆，所以1-<a ，选A.9、（2012青岛二模）已知集合{},3M m =-,{}22730,N x x x x =++<∈Z ,如果M N ≠∅,则m 等于A ．1-B ．2-C ．2-或1-D ．32-【答案】C【解析】1}2{}213{},0372{2--=∈-<<-=∈<++=，，Z x x x Z x x x x N ,因为φ≠⋂N M ，所以1-=m 或2-=m ，选C.10、（2012青岛3月模拟）已知实数集R ，集合{|22},M x x =-≤集合{|N x y =，则R ()MN =A.{|01}x x ≤<B.{|01}x x ≤≤C. {|14}x x <≤D. {|14}x x ≤≤ B 【解析】R ()MN ={}{|04}1x x x x ≤≤≤{|01}x x =≤≤.11、（2012日照5月模拟）已知集合{}{}222|,,1|x y x N R x x y y M -==∈-==，则N M ⋂=（A ）),1[+∞- （B ）)2,1[- （C ）),2[+∞ （D ）ø答案：B 解析：{}{}.].2,1[],2,2[2|),,1[,1|22B N M x y x N R x x y y M 选-=⋂∴-=-==+∞-=∈-==12、（2012泰安一模）设{}{}R x y y Q R x x y y P x∈==∈+-==,2,,12，则 A.Q P ⊆B.P Q ⊆C.Q P C R ⊆D.P C Q R ⊆【答案】C【解析】{}{}1,12≤=∈+-==y y R x x y y P ，{}{}0,2>=∈==y y R x y y Q x，所以}1{>=y y P C R ，所以Q P C R ⊆，选C.13、（2012威海二模）已知集合1{1,10,}10A =,{|lg ,}B y y x x A ==∈,则A B = A.1{}10B. {10}C. {1}D. ∅ 【答案】C【解析】}1,1,0{}101lg,10lg ,1lg {},lg {-=====∈==y y y y A x x y y B ，所以}1{=B A ,选C.14、（2012烟台二模）设全集{}{}U 2,1,0,1,2,3,M 0,1,2=--=，{}N 0,1,2,3=，则()U C M ∩N ＝A.{}0,1,2B.{}2,1,3--C.{}0,3D.{}3答案：D解析：U C M ＝{－2，－1，3}，所以，()U C M ∩N ＝{}3，选D 。

2012年高考数学按章节分类汇编（人教A文：选修1-1理：选修2-1）第一章常用逻辑用语一、选择题．（2012年高考（安徽理））设平面与平面相交于直线,直线在平面内,直线在平面内,且,则“”是“”的（ ）A．充分不必要条件 B．必要不充分条件 C．充要条件 D．即不充分不必要条件．（2012年高考（浙江文））设a∈R ,则“a=1”是“直线l1:ax+2y=0与直线l2 :x+(a+1)y+4=0平行的（ ）A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件．（2012年高考（浙江理））设aR,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的（ ）A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件．（2012年高考（重庆文））命题“若p则q”的逆命题是（ ）A．若q则p B．若p则 q C．若则 D．若p则．（2012年高考（天津文））设,则“”是“”的（ ）A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件．（2012年高考（上海文））对于常数、,“”是“方程的曲线是椭圆”的（ ）A．充分不必要条件. B．必要不充分条件C．充分必要条件. D．既不充分也不必要条件.．（2012年高考（山东文））设命题p:函数的最小正周期为;命题q:函数的图象关于直线对称.则下列判断正确的是（ ）A．p为真 B．为假 C．为假 D．为真．（2012年高考（辽宁文））已知命题p:x1,x2R,(f(x2)f(x1)(x2x1)≥0,则p是（ ）A．x1,x2R,(f(x2)f(x1)(x2x1)≤0 B．x1,x2R,(f(x2)f(x1)(x2x1)≤0C．x1,x2R,(f(x2)f(x1)(x2x1)<0D．x1,x2R,(f(x2)f(x1)(x2x1)<0．（2012年高考（湖南文））命题“若α=,则tanα=1”的逆否命题是（ ）A．若α≠,则tanα≠1 B．若α=,则tanα≠1C．若tanα≠1,则α≠ D．若tanα≠1,则α=．（2012年高考（湖北文））设,则“”是“”的（ ）A．充分条件但不是必要条件, B．必要条件但不是充分条件C．充分必要条件 D．既不充分也不必要的条件．（2012年高考（湖北文））命题“存在一个无理数,它的平方是有理数”的否定是（ ）A．任意一个有理数,它的平方是有理数 B．任意一个无理数,它的平方不是有理数C．存在一个有理数,它的平方是有理数 D．存在一个无理数,它的平方不是有理数．（2012年高考（安徽文））命题“存在实数,,使”的否定是（ ）A．对任意实数, 都有 B．不存在实数,使C．对任意实数, 都有 D．存在实数,使．（2012年高考（上海春））设为所在平面上一点.若实数满足,则“”是“点在的边所在直线上”的[答]（ ）A．充分不必要条件. B．必要不充分条件.C．充分必要条件. D．既不充分又不必要条件.．（2012年高考（辽宁理））已知命题p:x1,x2R,(f(x2)f(x1))(x2x1)≥0,则p是（ ）A．x1,x2R,(f(x2)f(x1))(x2x1)≤0 B．x1,x2R,(f(x2)f(x1))(x2x1)≤0C．x1,x2R,(f(x2)f(x1))(x2x1)<0D．x1,x2R,(f(x2)f(x1))(x2x1)<0．（2012年高考（江西理））下列命题中,假命题为（ ）A．存在四边相等的四边形不是正方形B．z1,z2∈c,z1+z2为实数的充分必要条件是z1,z2互为工复数C．若x,y∈CR,且x+y>2,则x,y至少有一个大于1D．对于任意n∈N,C°+C1.+C°.都是偶数．（2012年高考（湖南理））命题“若α=,则tanα=1”的逆否命题是（ ）A．若α≠,则tanα≠1 B．若α=,则tanα≠1C．若tanα≠1,则α≠ D．若tanα≠1,则α=．（2012年高考（湖北理））命题“,”的否定是（ ）A．,B．,C．,D．,．（2012年高考（福建理））下列命题中,真命题是（ ）A． B．C．的充要条件是 D．是的充分条件．（2012年高考（重庆理））已知是定义在R上的偶函数,且以2为周期,则“为[0,1]上的增函数”是“为[3,4]上的减函数”的（ ）A．既不充分也不必要的条件 B．充分而不必要的条件 C．必要而不充分的条件 D．充要条件．（2012年高考（四川理））设、都是非零向量,下列四个条件中,使成立的充分条件是（ ）A． B． C． D．且19 ．（2012年高考（天津理））设,则“”是“为偶函数”的（ ）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件二、解答题．（2012年高考（湖南理））已知数列{a n}的各项均为正数,记A(n)=a1+a2++a n,B(n)=a2+a3++a n+1,C(n)=a3+a4++a n+2,n=1,2。

2012年高考数学理科试题分类汇编：集合与简易逻辑2012年高考真题理科数学解析分类汇编1集合与简易逻辑1.【2012高考浙江理1】设集合A={x|1＜x＜4}，集合B={x|-2x-3≤0},则A∩（CRB）=A.(1,4)B.(3,4)C.(1,3)D.(1,2)∪（3,4）【答案】B【解析】B={x|-2x-3≤0}=，A∩（CRB）={x|1＜x＜4}=。

故选B.2.【2012高考新课标理1】已知集合；则中所含元素的个数为（）【答案】D【解析】要使,当时，可是1，2，3，4.当时，可是1，2，3.当时，可是1，2.当时，可是1，综上共有10个，选D.3.【2012高考陕西理1】集合，，则（）A.B.C.D.【答案】C.【解析】，，故选C.4.【2012高考山东理2】已知全集，集合，则为（A）（B）（C）（D）【答案】C【解析】,所以,选C.5.【2012高考辽宁理1】已知全集U=｛0,1,2,3,4,5,6,7,8,9｝，集合A=｛0,1,3,5,8｝，集合B=｛2,4,5,6,8｝，则为(A){5,8}(B){7,9}(C){0,1,3}(D){2,4,6}【答案】B【命题意图】本题主要考查集合的补集、交集运算，是容易题.【解析】1.因为全集U=｛0,1,2,3,4,5,6,7,8,9｝，集合A=｛0,1,3,5,8｝，集合B=｛2,4,5,6,8｝，所以，所以为{7,9}。

故选B2.集合为即为在全集U中去掉集合A和集合B中的元素，所剩的元素形成的集合，由此可快速得到答案，选B【点评】采用解析二能够更快地得到答案。

6.【2012高考辽宁理4】已知命题p：x1，x2R，(f(x2)f(x1))(x2x1)≥0，则p是(A)x1，x2R，(f(x2)f(x1))(x2x1)≤0(B)x1，x2R，(f(x2)f(x1))(x2x1)≤0(C)x1，x2R，(f(x2)f(x1))(x2x1)(D)x1，x2R，(f(x2)f(x1))(x2x1)【答案】C 【解析】命题p为全称命题，所以其否定p应是特称命题，又(f(x2)f(x1))(x2x1)≥0否定为(f(x2)f(x1))(x2x1)【点评】本题主要考查含有量词的命题的否定，属于容易题。

第一部分 集合与常用逻辑用语1.（2012湖南卷文）设集合M={-1,0,1}，N={x |x 2=x }，则M∩N=( ) A.{-1，0，1} B.{0,1} C.{1} D.{0} 【答案】B【解析】{}0,1N = M={-1,0,1} ∴M∩N={0,1} 2. （2012湖南卷文）命题“若α=4π，则tan α=1”的逆否命题是( )A.若α≠4π，则tan α≠1 B. 若α=4π，则tan α≠1C. 若tan α≠1，则α≠4πD. 若tan α≠1，则α=4π【答案】C【解析】因为“若p ，则q ”的逆否命题为“若p ⌝，则q ⌝”，所以 “若α=4π，则tan α=1”的逆否命题是 “若tan α≠1，则α≠4π”.3.（2012年天津卷文）设x ∈R ，则“x >12”是“2x 2+x -1>0”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件 【解析】不等式0122>-+x x 的解集为21>x 或1-<x ，所以“21>x ”是“0122>-+x x ”成立的充分不必要条件，选A.4. （2012年北京卷理）已知集合A={x ∈R|3x +2＞0} B={x ∈R|（x +1）(x -3)＞0} 则A∩B=( )A （-∞，-1）B （-1，-23） C （-23,3）D (3,+∞)【解析】32}023|{->⇒>+∈=x x R x A ，利用二次不等式可得1|{-<=x x B 或}3>x 画出数轴易得：}3|{>=x x B A ．故选D ． 5.（2012年福建卷理）下列命题中，真命题是( ) A ．0,00≤∈∃x eR x B ．22,x R x x >∈∀C ．0=+b a 的充要条件是1-=ba D ．1,1>>b a 是1>ab 的充分条件【答案】D6.（2012年广东卷理）设集合U {1,23,4,5,6}=，，M {1,2,4}=则M U =ð( ) A ．U B ．{1,3,5} C ．{3,5,6} D ．{2,4,6}【答案】C（2012年上海卷文）2、若集合{}210A x x =->，{}1B x x =<，则A B ⋂＝ (2012年安徽文)（2）设集合A={3123|≤-≤-x x }，集合B 为函数)1lg(-=x y 的定义域，则A ⋂B=（A ） （1，2） （B ）[1，2] （C ） [ 1，2） （D ）（1，2 ] 【解析】选D{3213}[1,2]A x x =-≤-≤=-，(1,)(1,2]B A B =+∞⇒=(2012年安徽文)（4）命题“存在实数x ，使x > 1”的否定是（A ） 对任意实数x , 都有x > 1 （B ）不存在实数x ，使x ≤ 1（C ） 对任意实数x , 都有x ≤ 1 （D ）存在实数x ，使x ≤ 1 【解析】选C存在---任意，1x >---1x ≤（2012年山东卷理）2 已知全集 ={0,1,2,3,4}，集合A={1,2,3,}，B={2,4} ，则（CuA ） B 为A {1,2,4}B {2,3,4}C {0,2,4}D {0,2,3,4}解析：}4,2,0{)(},4,0{==B A C A C U U 。

集合与常用逻辑用语(高考真题+模拟新题)课标文数2.A1[2011·安徽卷] 集合U ＝{1,2,3,4,5,6}，S ＝{1,4,5}，T ＝{2,3,4}，则S ∩(∁U T )等于( )A ．{1,4,5,6}B ．{1,5}C ．{4}D ．{1,2,3,4,5} 课标文数2.A1[2011·安徽卷] B 【解析】 S ∩(∁U T )＝{1,4,5} ∩{1,5,6}＝{1,5}．课标理数8.A1[2011·安徽卷] 设集合A ＝{1,2,3,4,5,6}，B ＝{4,5,6,7,8}，则满足S ⊆A 且S ∩B ≠∅的集合S 的个数是( )A ．57B ．56C ．49D ．8 课标理数8.A1[2011·安徽卷] B 【解析】 集合S 的个数为26－23＝64－8＝56.课标理数1.A1，E3[2011·北京卷] 已知集合P ＝{x |x 2≤1}，M ＝{a }．若P ∪M ＝P ，则a 的取值范围是( )A ．(－∞，－1]B ．[1，＋∞)C ．[－1,1]D ．(－∞，－1]∪[1，＋∞) 课标理数1.A1，E3[2011·北京卷] C 【解析】 由P ∪M ＝P ，可知M ⊆P ，而集合P ＝{x |－1≤x ≤1}，所以－1≤a ≤1，故选C.课标文数1.A1，E3[2011·北京卷] 已知全集U ＝R ，集合P ＝{x |x 2≤1}，那么∁U P ＝( ) A ．(－∞，－1) B ．(1，＋∞)C ．(－1,1)D ．(－∞，－1)∪(1，＋∞) 课标文数1.A1，E3[2011·北京卷] D 【解析】 因为集合P ＝{x |－1≤x ≤1}，所以∁U P ＝{x |x <－1或x >1}，故选D.大纲文数1.A1[2011·全国卷] 设集合U ＝{1,2,3,4}，M ＝{1,2,3}，N ＝{2,3,4}，则∁U (M ∩N )＝( )A ．{1,2}B ．{2,3}C ．{2,4}D ．{1,4} 大纲文数 1.A1[2011·全国卷] D 【解析】 ∵M ∩N ＝{2,3}，∴∁U (M ∩N )＝{1,4}，故选D.课标理数1.A1，L4[2011·福建卷] i 是虚数单位，若集合S ＝{－1,0,1}，则( )A ．i ∈SB ．i 2∈SC ．i 3∈S D.2i∈S课标理数1.A1、L4[2011·福建卷] B 【解析】 由i 2＝－1，而－1∈S ，故选B.课标文数1.A1[2011·福建卷] 若集合M ＝{－1,0,1}，N ＝{0,1，2}，则M ∩N 等于( ) A ．{0,1} B ．{－1,0,1} C ．{0,1,2} D ．{－1,0,1,2} 课标文数1.A1[2011·福建卷] A 【解析】 由已知M ＝{－1,0,1}，N ＝{0,1,2}，得M ∩N ＝{0,1}，故选A.课标文数12.A1，M1[2011·福建卷] 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[k ]，即[k ]＝{5n ＋k |n ∈Z }，k ＝0,1,2,3,4.给出如下四个结论：①2011∈[1]； ②－3∈[3]；③Z ＝[0]∪[1]∪[2]∪[3]∪[4]；④“整数a ，b 属于同一‘类’”的充要条件是“a －b ∈[0]”．其中，正确结论的个数是( ) A ．1 B ．2 C ．3 D ．4 课标文数12.A1，M1[2011·福建卷] C 【解析】 因为2011＝5×402＋1，则2011∈[1]，结论①正确；因为－3＝5×(－1)＋2，则－3∈[2]，结论②不正确；因为所有的整数被5除的余数为0,1,2,3,4五类，则Z ＝[0]∪[1]∪[2]∪[3]∪[4]，结论③正确；若整数a ，b 属于同一“类”[k ]，可设a ＝5n 1＋k ，b ＝5n 2＋k (n 1，n 2∈Z )，则 a －b ＝5(n 1－n 2)∈[0]；反之，若a －b ∈[0]，可设a ＝5n 1＋k 1，b ＝5n 2＋k 2(n 1，n 2∈Z )，则 a －b ＝5(n 1－n 2)＋(k 1－k 2)∈[0]；∴k 1＝k 2，则整数a ，b 属于同一“类”，结论④正确，故选C.课标理数2.A1[2011·湖北卷] 已知U ＝{y |y ＝log 2x ，x >1}，P ＝⎩⎨⎧⎭⎬⎫y |y ＝1x ，x >2，则∁U P ＝( )A.⎣⎡⎭⎫12，＋∞B.⎝⎛⎭⎫0，12 C.()0，＋∞ D.(]－∞，0∪⎣⎡⎭⎫12，＋∞课标理数 2.A1[2011·湖北卷] A 【解析】 因为U ＝{y |y ＝log 2x ，x >1}＝{y |y >0}，P ＝⎩⎨⎧⎭⎬⎫y |y ＝1x ，x >2＝⎩⎨⎧⎭⎬⎫y ⎪⎪ 0<y <12，所以∁U P ＝⎩⎨⎧⎭⎬⎫y ⎪⎪y ≥12＝⎣⎡⎭⎫12，＋∞.课标文数1.A1[2011·湖北卷] 已知U ＝{1,2,3,4,5,6,7,8}，A ＝{1,3,5,7}，B ＝{2,4,5}，则 ∁U (A ∪B )＝( )A ．{6,8}B ．{5,7}C ．{4,6,7}D ．{1,3,5,6,8} 课标文数 1.A1[2011·湖北卷] A 【解析】 因为A ∪B ＝{}1，2，3，4，5，7，所以∁U ()A ∪B ＝{}6，8.课标文数1.A1[2011·湖南卷] 设全集U ＝M ∪N ＝{1,2，3,4,5}，M ∩∁U N ＝{2,4}，则N ＝( )A ．{1,2,3}B ．{1,3,5}C ．{1,4,5}D ．{2,3,4} 课标文数1.A1[2011·湖南卷] B 【解析】 (排除法)由M ∩∁U N ＝{2,4}，说明N 中一定不含有元素2,4，故可以排除A 、C 、D ，故选B.课标文数2.A1[2011·江西卷] 若全集U ＝{1,2,3,4,5,6}，M ＝{2,3}，N ＝{1,4}，则集合{5,6}等于( )A ．M ∪NB ．M ∩NC ．(∁U M )∪∁U N )D ．(∁U M )∩(∁U N ) 课标文数2.A1[2011·江西卷] D 【解析】 方法一： ∵M ∪N ＝{1,2,3,4}，∴(∁U M )∩(∁U N )＝∁U (M ∪N )＝{5,6}．故选D. 方法二：∵∁U M ＝{1,4,5,6}，∁U N ＝{2,3,5,6}， ∴(∁U M )∩(∁U N )＝{5,6}．故选D.课标理数2.A1[2011·辽宁卷] 已知M ，N 为集合I 的非空真子集，且M ，N 不相等，若N ∩∁I M ＝∅，则M ∪N ＝( )A ．MB ．NC ．ID ．∅ 课标理数2.A1[2011·辽宁卷] A 【解析】 N ∩∁I M ＝∅⇒N ⊆M ，所以M ∪N ＝M ，故选A.课标文数1.A1[2011·辽宁卷] 已知集合A ＝{x |x ＞1}，B ＝{x |－1＜x ＜2}，则A ∩B ＝( ) A ．{x |－1＜x ＜2} B ．{x |x ＞－1} C ．{x |－1＜x ＜1} D ．{x |1＜x ＜2} 课标文数1.A1[2011·辽宁卷] D 【解析】 由图1－1知A ∩B ＝{x |1<x <2}，故选D.课标文数1.A1[2011·课标全国卷] 已知集合M ＝{0,1,2,3,4}，N ＝{1,3,5}，P ＝M ∩N ，则P 的子集共有( )A ．2个B ．4个C ．6个D ．8个 课标文数1.A1[2011·课标全国卷] B 【解析】 因为M ＝{}0，1，2，3，4，N ＝{}1，3，5，所以P ＝M ∩N ＝{}1，3，所以集合P 的子集共有∅，{}1，{}3，{}1，34个．课标理数1.A1[2011·山东卷] 设集合M ＝{x |x 2＋x －6<0}，N ＝{x |1≤x ≤3}，则M ∩N ＝( )A ．[1,2)B ．[1,2]C ．(2,3]D ．[2,3] 课标理数1.A1[2011·山东卷] A 【解析】 由解不等式知识知M ＝{x |－3<x <2}，又N ＝{x |1≤x ≤3}，所以M ∩N ＝{x |1≤x ＜2}．课标理数7.A1[2011·陕西卷] 设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝x ⎪⎪⎪⎪⎪⎪x －1i ＜2，i 为虚数单位，x ∈R ，则M ∩N 为( )A ．(0,1)B ．(0,1]C ．[0,1)D ．[0,1] 课标理数7.A1[2011·陕西卷] C 【解析】 对于M ，由基本不等式得y ＝|cos 2x －sin 2x |＝|cos2x |，故0≤y ≤1.对于N ，因为x －1i＝x ＋i ，由⎪⎪⎪⎪x －1i <2，得x 2＋1<2，所以－1<x <1，故M ∩N ＝[0,1)，故答案为C.课标文数8.A1，L4[2011·陕西卷] 设集合M ＝{y |y ＝|cos 2x －sin 2x |，x ∈R }，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪⎪⎪⎪⎪x i ＜1，i 为虚数单位，x ∈R ，则M ∩N 为( ) A ．(0,1) B ．(0,1] C ．[0,1) D ．[0,1] 课标文数8.A1，L4[2011·陕西卷] C 【解析】 对M ，由基本不等式得y ＝|cos 2x －sin 2x |＝|cos2x |，故0≤y ≤1.对N ，⎪⎪⎪⎪x i <1，即|－x i|<1，所以－1<x <1，故M ∩N ＝[0,1)，故答案为C.课标数学1.A1[2011·江苏卷] 已知集合A ＝{－1,1,2,4}，B ＝{－1,0,2}, 则A ∩B ＝________. 课标数学1.A1[2011·江苏卷] {－1,2} 【解析】 因为集合A ，B 的公共元素为－1,2，故A ∩B ＝{－1,2}．课标数学1.A1[2011·江苏卷] 已知集合A ＝{－1,1,2,4}，B ＝{－1,0,2}, 则A ∩B ＝________. 课标数学1.A1[2011·江苏卷] {－1,2} 【解析】 因为集合A ，B 的公共元素为－1,2，故A ∩B ＝{－1,2}．大纲文数1.A1[2011·四川卷] 若全集M ＝{1,2,3,4,5}，N ＝{2,4}，则∁M N ＝( ) A ．∅ B ．{1,3,5}C ．{2,4}D ．{1,2,3,4,5}大纲文数1.A1[2011·四川卷] B 【解析】 ∁M N ＝{1,3,5}，所以选B.课标理数13.A1[2011·天津卷] 已知集合A ＝{x ∈R ||x ＋3|＋|x －4|≤9}，B ＝x ∈R ⎪⎪x ＝4t ＋1t －6，t ∈(0，＋∞)，则集合A ∩B ＝________.课标理数13.A1[2011·天津卷] {x |－2≤x ≤5} 【解析】 ∵A ＝{}x ∈R ||x ＋3|＋|x －4|≤9 ＝{}x ∈R |－4≤x ≤5，B ＝⎩⎨⎧⎭⎬⎫x ∈R ⎪⎪x ＝4t ＋1t －6，t ∈()0，＋∞ ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ∈R ⎪⎪x ≥24t ×1t －6，t ∈()0，＋∞ ＝{x ∈R |x ≥－2}∴A ∩B ＝{x ∈R |－4≤x ≤5}∩{x |x ≥－2}＝{x |－2≤x ≤5}．课标文数9.A1[2011·天津卷] 已知集合A ＝{x ∈R ||x －1|<2}，Z 为整数集，则集合A ∩Z 中所有元素的和等于________．课标文数9.A1[2011·天津卷] 3 【解析】 A ＝{x ∈R ||x －1|<2}＝{x |－1<x <3}．∴A ∩Z ＝{0,1,2}，即0＋1＋2＝3.课标文数1.A1[2011·浙江卷] 若P ＝{x |x <1}，Q ＝{x |x >－1}，则( ) A ．P ⊆Q B ．Q ⊆P C ．∁R P ⊆Q D ．Q ⊆∁R P 课标文数1.A1[2011·浙江卷] C 【解析】 P ＝{x |x <1}，∴∁R P ＝{x |x ≥1}．又∵Q ＝{x |x >－1}，∴Q ⊇∁R P ，故选C.大纲文数2.A1[2011·重庆卷] 设U ＝R ，M ＝{x |x 2－2x >0}，则∁U M ＝( ) A ．[0,2] B ．(0,2)C ．(－∞，0)∪(2，＋∞)D ．(－∞，0]∪[2，＋∞) 大纲文数2.A1[2011·重庆卷] A 【解析】 解不等式x 2－2x ＞0，得x ＞2或x ＜0. 即集合M ＝{x |x ＞2或x ＜0}， ∴∁U M ＝{x |0≤x ≤2}．故选A.课标理数7.A2[2011·安徽卷] 命题“所有能被2整除的整数都是偶数”的否定．．是( ) A ．所有不能被2整除的整数都是偶数B ．所有能被2整除的整数都不是偶数C ．存在一个不能被2整除的整数是偶数D ．存在一个能被2整除的整数不是偶数 课标理数7.A2[2011·安徽卷] D 【解析】 本题是一个全称命题，其否定是特称命题，同时将命题的结论进行否定，答案为D.课标文数20.D2，A2[2011·北京卷] 若数列A n ：a 1，a 2，…，a n (n ≥2)满足|a k ＋1－a k |＝1(k ＝1,2，…，n －1)，则称A n 为E 数列．记S (A n )＝a 1＋a 2＋…＋a n .(1)写出一个E 数列A 5满足a 1＝a 3＝0；(2)若a 1＝12，n ＝2000，证明：E 数列A n 是递增数列的充要条件是a n ＝2011； (3)在a 1＝4的E 数列A n 中，求使得S (A n )＝0成立的n 的最小值． 课标文数20.D2，A2[2011·北京卷] 【解答】 (1)0,1,0,1,0是一个满足条件的E 数列A 5. (答案不唯一，0，－1,0,1,0；0，±1,0,1,2；0，±1,0，－1，－2；0，±1,0，－1,0都是满足条件的E 数列A 5)(2)必要性：因为E 数列A n 是递增数列，所以a k ＋1－a k ＝1(k ＝1,2，…，1999)．所以A n 是首项为12，公差为1的等差数列． 所以a 2000＝12＋(2000－1)×1＝2011， 充分性：由于a 2000－a 1999≤1. a 1999－a 1998≤1. ……a 2－a 1≤1.所以a 2000－a 1≤1999，即a 2000≤a 1＋1999. 又因为a 1＝12，a 2000＝2011. 所以a 2000＝a 1＋1999.故a k ＋1－a k ＝1>0(k ＝1,2，…，1999)，即E 数列A n 是递增数列． 综上，结论得证．(3)对首项为4的E 数列A n ，由于 a 2≥a 1－1＝3， a 3≥a 2－1≥2， ……a 8≥a 7－1≥－3， ……所以a 1＋a 2＋…＋a k >0(k ＝2,3，…，8)．所以对任意的首项为4的E 数列A n ，若S (A n )＝0，则必有n ≥9.又a 1＝4的E 数列A 9：4,3,2,1,0，－1，－2，－3，－4满足S (A 9)＝0， 所以n 的最小值是9.课标理数2.A2[2011·福建卷] 若a ∈R ，则“a ＝2”是“(a －1)(a －2)＝0”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分又不必要条件 课标理数2.A2[2011·福建卷] A 【解析】 若a ＝2，则(a －1)(a －2)＝0成立；若(a －1)(a －2)＝0，则a ＝2或a ＝1，则a ＝2是(a －1)(a －2)＝0的充分而不必要条件，故选A.课标文数3.A2[2011·福建卷] 若a ∈R ，则“a ＝1”是“|a |＝1”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分又不必要条件 课标文数3.A2[2011·福建卷] A 【解析】 若a ＝1，则|a |＝1成立；若|a |＝1，则a ＝－1或a ＝1，则a ＝1是|a |＝1的充分而不必要条件，故选A.课标理数9.A2[2011·湖北卷] 若实数a ，b 满足a ≥0，b ≥0，且ab ＝0，则称a 与b 互补．记φ(a ，b )＝a 2＋b 2－a －b ，那么φ(a ，b )＝0是a 与b 互补的( )A ．必要而不充分的条件B ．充分而不必要的条件C ．充要条件D ．既不充分也不必要的条件 课标理数9.A2[2011·湖北卷] C 【解析】 若φ(a ，b )＝0，则a 2＋b 2＝a ＋b ，两边平方整理得ab ＝0，且a ≥0，b ≥0，所以a ，b 互补；若a ，b 互补，则a ≥0，b ≥0，且ab ＝0，所以a ＋b ≥0，此时有φ()a ，b ＝()a ＋b 2－2ab －()a ＋b ＝()a ＋b 2－()a ＋b ＝()a ＋b －()a ＋b ＝0，所以“φ()a ，b ＝0”是a 与b 互补的充要条件．课标文数10.A2[2011·湖北卷] 若实数a ，b 满足a ≥0，b ≥0，且ab ＝0，则称a 与b 互补．记φ(a ，b )＝a 2＋b 2－a －b ，那么φ(a ，b )＝0是a 与b 互补的( )A ．必要而不充分的条件B ．充分而不必要的条件C ．充要条件D ．既不充分也不必要的条件 课标文数10.A2[2011·湖北卷] C 【解析】 若φ(a ，b )＝0，则a 2＋b 2＝a ＋b ，两边平方整理得ab ＝0，且a ≥0，b ≥0，所以a ，b 互补；若a ，b 互补，则a ≥0，b ≥0，且ab ＝0，所以a ＋b ≥0，此时有φ()a ，b ＝()a ＋b 2－2ab －()a ＋b ＝()a ＋b 2－()a ＋b ＝()a ＋b －()a ＋b ＝0，所以“φ()a ，b ＝0”是a 与b 互补的充要条件．课标理数2.A2[2011·湖南卷] 设集合M ＝{1,2}，N ＝{a 2}，则“a ＝1”是“N ⊆M ”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件D ．既不充分又不必要条件 课标理数2.A2[2011·湖南卷] A 【解析】 当a ＝1时，N ＝{1}，此时有N ⊆M ，则条件具有充分性；当N ⊆M 时，有a 2＝1或a 2＝2得到a 1＝1，a 2＝－1，a 3＝2，a 4＝－2，故不具有必要性，所以“a ＝1”是“N ⊆M ”的充分不必要条件， 故选A.课标文数3.A2[2011·湖南卷] “x >1”是“|x |>1”的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分又不必要条件 课标文数3.A2[2011·湖南卷] A 【解析】 由不等式||x >1得x <－1或x >1.当x >1时，一定有||x >1成立，则条件具有充分性；当||x >1不一定有x >1，则不具有必要性，故选A.课标理数8.A2[2011·江西卷] 已知α1，α2，α3是三个相互平行的平面，平面α1，α2之间的距离为d 1，平面α2，α3之间的距离为d 2，直线l 与α1，α2，α3分别相交于P 1，P 2，P 3，那么“P 1P 2＝P 2P 3”是“d 1＝d 2”的( )A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件课标理数5.A2[2011·山东卷] 对于函数y ＝f (x )，x ∈R ，“y ＝|f (x )|的图象关于y 轴对称”是“y ＝f (x )是奇函数”的( )A ．充分而不必要条件B ．必要而不充分条件C．充要条件D．既不充分也不必要条件课标理数5.A2[2011·山东卷] B【解析】由判定充要条件方法之一——定义法知，由“y ＝f(x)是奇函数”可以推出“y＝|f(x)|的图象关于y轴对称”，反过来，逆推不成立，所以选B.课标文数5.A2[2011·山东卷] 已知a，b，c∈R，命题“若a＋b＋c＝3，则a2＋b2＋c2≥3”的否命题是()A．若a＋b＋c≠3，则a2＋b2＋c2<3B．若a＋b＋c＝3，则a2＋b2＋c2<3C．若a＋b＋c≠3，则a2＋b2＋c2≥3D．若a2＋b2＋c2≥3，则a＋b＋c＝3课标文数5.A2[2011·山东卷] A【解析】命题的否命题是原命题的条件与结论分别否定后组成的命题，所以选择A.课标理数1.A2[2011·陕西卷] 设a，b是向量，命题“若a＝－b，则|a|＝|b|”的逆命题是()A．若a≠－b，则|a|≠|b| B．若a＝－b，则|a|≠|b|C．若|a|≠|b|，则a≠－b D．若|a|＝|b|，则a＝－b课标理数1.A2[2011·陕西卷] D【解析】利用原命题和逆命题之间的关系“如果第一个命题的条件和结论分别是第二个命题的结论和条件，那么这两个命题叫做互逆命题．如果把其中一个命题叫做原命题，那么另一个命题叫做原命题的逆命题．即原命题：若p，则q；逆命题：若q，则p”，故答案为D.课标文数1.A2[2011·陕西卷] 设a，b是向量，命题“若a＝－b，则|a|＝|b|”的逆命题是()A．若a≠－b，则|a|≠|b|B．若a＝－b，则|a|≠|b|C．若|a|≠|b|，则a≠－b D．若|a|＝|b|，则a＝－b课标文数1.A2[2011·陕西卷] D【解析】利用原命题和逆命题之间的关系“如果第一个命题的条件和结论分别是第二个命题的结论和条件，那么这两个命题叫做互逆命题．如果把其中一个命题叫做原命题，那么另一个命题叫做原命题的逆命题．即原命题：若p，则q；逆命题：若q，则p”，故答案为D.大纲文数5.A2[2011·四川卷] “x＝3”是“x2＝9”的()A．充分而不必要的条件B．必要而不充分的条件C．充要条件D．既不充分也不必要的条件大纲文数5.A2[2011·四川卷] A【解析】x＝3⇒x2＝9，但x2＝9⇒x＝±3，所以“x＝3”是“x2＝9”的充分不必要条件．大纲理数5.A2[2011·四川卷] 函数f(x)在点x＝x0处有定义是f(x)在点x＝x0处连续的() A．充分而不必要的条件B．必要而不充分的条件C．充要条件D．既不充分也不必要的条件大纲理数5.A2[2011·四川卷] B【解析】在x＝x0处连续不仅需要有定义，还需要在该点处的极限值与函数值相等，所以函数在x＝x0处有定义是在该点处连续的必要不充分条件．所以选B.课标理数2.A2[2011·天津卷] 设x，y∈R，则“x≥2且y≥2”是“x2＋y2≥4”的() A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件课标理数2.A2[2011·天津卷] A 【解析】 当x ≥2且y ≥2时，一定有x 2＋y 2≥4；反过来当x 2＋y 2≥4，不一定有x ≥2且y ≥2，例如x ＝－4，y ＝0也可以，故选A.课标文数 4.A2[2011·天津卷] 设集合A ＝{x ∈R |x －2>0}，B ＝{x ∈R |x <0}，C ＝{x ∈R |x (x －2)>0}，则“x ∈A ∪B ”是“x ∈C ”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 课标文数4.A2[2011·天津卷] C 【解析】 ∵A ＝{x ∈R | x －2>0}，B ＝{x ∈R |x <0}， ∴A ∪B ＝{x ∈R |x <0或x >2}．又∵C ＝{x ∈R |x (x －2)>0}＝{x ∈R |x <0或x >2}， ∴A ∪B ＝C ，即“x ∈A ∪B ”是“x ∈C ”的充分必要条件．课标理数7.A2[2011·浙江卷] 若a ，b 为实数，则“0<ab <1”是“a <1b 或b >1a”的( )A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 课标理数7.A2[2011·浙江卷] A 【解析】 当a >0，b >0时，由0<ab <1两边同除b 可得a <1b 成立；当a <0，b <0时，两边同除以a 可得b >1a 成立，∴“0<ab <1”是“a <1b 或b >1a”的充分条件．反过来，若ab <0，由a <1b 或b >1a得不到0<ab <1.大纲理数2.A2[2011·重庆卷] “x ＜－1”是“x 2－1＞0”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件D ．既不充分也不必要条件 大纲理数2.A2[2011·重庆卷] A 【解析】 解不等式x 2－1＞0，得x ＜－1或x ＞1， 因此当x ＜－1成立时，x 2－1＞0成立；而当x ＜－1或x ＞1成立时，x ＜－1不一定成立．故选A.课标理数20.D5，A3[2011·北京卷] 若数列A n ：a 1，a 2，…，a n (n ≥2)满足|a k ＋1－a k |＝1(k ＝1,2，…，n －1)，则称A n 为E 数列．记S (A n )＝a 1＋a 2＋…＋a n .(1)写出一个满足a 1＝a 5＝0，且S (A 5)＞0的E 数列A 5；(2)若a 1＝12，n ＝2000.证明：E 数列A n 是递增数列的充要条件是a n ＝2011； (3)对任意给定的整数n (n ≥2)，是否存在首项为0的E 数列A n ，使得S (A n )＝0？如果存在，写出一个满足条件的E 数列A n ；如果不存在，说明理由．课标理数20.D5，A3[2011·北京卷] 【解答】 (1)0,1,2,1,0是一个满足条件的E 数列A 5. (答案不唯一，0,1,0,1,0也是一个满足条件的E 数列A 5) (2)必要性：因为E 数列A n 是递增数列， 所以a k ＋1－a k ＝1(k ＝1,2，…，1999)．所以A n 是首项为12，公差为1的等差数列． 所以a 2000＝12＋(2000－1)×1＝2011. 充分性：由于a 2000－a 1999≤1， a 1999－a 1998≤1， ……a 2－a 1≤1，所以a 2000－a 1≤1999，即a 2000≤a 1＋1999. 又因为a 1＝12，a 2000＝2011， 所以a 2000＝a 1＋1999，故a k ＋1－a k ＝1＞0(k ＝1,2，…，1999)，即E 数列A n 是递增数列． 综上，结论得证．(3)令c k ＝a k ＋1－a k (k ＝1,2，…，n －1)，则c k ＝±1， 因为a 2＝a 1＋c 1， a 3＝a 1＋c 1＋c 2， ……a n ＝a 1＋c 1＋c 2＋…＋c n －1，所以S (A n )＝na 1＋(n －1)c 1＋(n －2)c 2＋(n －3)c 3＋…＋c n －1 ＝(n －1)＋(n －2)＋…＋1－[(1－c 1)(n －1)＋(1－c 2)·(n －2)＋…＋(1－c n －1)] ＝n (n －1)2－[(1－c 1)(n －1)＋(1－c 2)(n －2)＋…＋(1－c n －1)]．因为c k ＝±1，所以1－c k 为偶数(k ＝1,2，…，n －1)， 所以(1－c 1)(n －1)＋(1－c 2)(n －2)＋…＋(1－c n －1)为偶数，所以要使S (A n )＝0，必须使n (n －1)2为偶数，即4整除n (n －1)，亦即n ＝4m 或n ＝4m ＋1(m ∈N *)．当n ＝4m (m ∈N *)时，E 数列A n 的项满足a 4k －1＝a 4k －3＝0，a 4k －2＝－1，a 4k ＝1(k ＝1,2，…，m )时，有a 1＝0，S (A n )＝0；当n ＝4m ＋1(m ∈N *)时，E 数列A n 的项满足a 4k －1＝a 4k －3＝0，a 4k －2＝－1，a 4k ＝1(k ＝1,2，…，m )，a 4m ＋1＝0时，有a 1＝0，S (A n )＝0；当n ＝4m ＋2或n ＝4m ＋3(m ∈N *)时，n (n －1)不能被4整除，此时不存在E 数列A n ，使得a 1＝0，S (A n )＝0.课标文数4.A3[2011·北京卷] 若p 是真命题，q 是假命题，则( ) A ．p ∧q 是真命题 B ．p ∨q 是假命题 C ．綈p 是真命题 D ．綈q 是真命题 课标文数4.A3[2011·北京卷] D 【解析】 p 是真命题，则綈p 是假命题；q 是假命题，则綈q 是真命题，故应选D.课标文数4.A3[2011·辽宁卷] 已知命题p ：∃n ∈N,2n ＞1000，则綈p 为( ) A ．∀n ∈N,2n ≤1000 B ．∀n ∈N,2n ＞1000 C ．∃n ∈N,2n ≤1000 D ．∃n ∈N,2n ＜1000 课标文数4.A3[2011·辽宁卷] A 【解析】 命题p 用语言叙述为“存在正整数n ，使得2n>1000成立”，所以它的否定是“任意的正整数n ，使得2n ≤1000成立”，用符号表示为“∀n ∈N,2n≤1000”课标理数2.A4[2011·广东卷] 已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且y ＝x }，则A ∩B 的元素个数为( )A ．0B ．1C ．2D ．3 课标理数2.A4[2011·广东卷] C 【解析】 集合A 表示以原点为圆心的单位圆，集合B 表示过原点的直线，显然有两个交点，故选C.课标理数8.A4[2011·广东卷] 设S 是整数集Z 的非空子集，如果∀a ，b ∈S ，有ab ∈S ，则称S 关于数的乘法是封闭的，若T ，V 是Z 的两个不相交的非空子集，T ∪V ＝Z ，且∀a ，b ，c ∈T ，有abc ∈T ；∀x ，y ，z ∈V ，有xyz ∈V ，则下列结论恒成立的是( )A ．T ，V 中至少有一个关于乘法是封闭的B ．T ，V 中至多有一个关于乘法是封闭的C ．T ，V 中有且只有一个关于乘法是封闭的D ．T ，V 中每一个关于乘法都是封闭的课标理数8.A4[2011·广东卷] A 【解析】 T 全部是偶数，V 全部是奇数，那么T ，V 对乘法是封闭的，但如果T 是全部偶数和1,3，那么此时T ，V 都符合题目要求，但是在V 里面，任意取的数是－1和－3，那么相乘等于3，而V 里面没有3，所以V 对乘法不封闭．排除B 、C 、D 选项，所以“至少一个”是对的．课标文数2.A4[2011·广东卷] 已知集合A ＝{(x ，y )|x ，y 为实数，且x 2＋y 2＝1}，B ＝{(x ，y )|x ，y 为实数，且x ＋y ＝1}，则A ∩B 的元素个数为( )A ．4B ．3C ．2D ．1 课标文数2.A4[2011·广东卷] C 【解析】 集合A 表示以原点为圆心的单位圆，集合B 表示过点(1,0)，(0,1)的直线，显然有两个交点，故选C.课标理数2.A4[2011·江西卷] 若集合A ＝{x |－1≤2x ＋1≤3}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x －2x ≤0，则A ∩B＝( )A ．{x |－1≤x <0}B ．{x |0<x ≤1}C ．{x |0≤x ≤2}D ．{x |0≤x ≤1}课标理数2.A4[2011·江西卷] B 【解析】 ∵A ＝{x |－1≤x ≤1}，B ＝{x |0<x ≤2}，∴A ∩B ＝{x |0<x ≤1}．故选B.[2011·广东广雅中学期末] 下列说法正确的是( )A ．命题“若x 2＝1，则x ＝1”的否命题为：“若x 2＝1，则x ≠1”B ．“x ＝－1”是“x 2－5x －6＝0”的必要不充分条件C ．命题“存在x ∈R ，使得x 2＋x ＋1＜0”的否定是：“对任意x ∈R, 均有x 2＋x ＋1＜0”D ．命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题[2011·湖南六校联考] 已知命题p：“∀x∈R，∃m∈R,4x－2x＋1＋m＝0”，且命题綈p是假命题，则实数m的取值范围为________．[2011·丰台期末] 若X是一个集合，τ是一个以X的某些子集为元素的集合，且满足：①X 属于τ，∅属于τ；②τ中任意多个元素的并集属于τ；③τ中任意多个元素的交集属于τ.则称τ是集合X上的一个拓扑．已知集合X＝{a，b，c}，对于下面给出的四个集合τ：①τ＝{∅，{a}, {c}, {a, b, c}}；②τ＝{∅，{b}, {c}, {b, c}, {a, b, c}}；③τ＝{∅，{a}, {a, b}, {a, c}}；④τ＝{∅，{a, c}, {b, c}, {c}, {a, b, c}}．其中是集合X上的拓扑的集合τ的序号是________．- 11 -。

2012高考数学新题分类汇编 推理与证明（高考真题+模拟新题）课标理数10.M1，D2，B11[2011·福建卷] 已知函数f (x )＝e x＋x .对于曲线y ＝f (x )上横坐标成等差数列的三个点A 、B 、C ，给出以下判断：①△ABC 一定是钝角三角形； ②△ABC 可能是直角三角形； ③△ABC 可能是等腰三角形； ④△ABC 不可能是等腰三角形． 其中，正确的判断是( )A ．①③B ．①④C ．②③D ．②④课标理数10.M1，D2，B11[2011·福建卷] B 【解析】 解法一：(1)设A 、B 、C 三点的横坐标分别为x 1，x 2，x 3(x 1<x 2<x 3),∵ f ′(x )＝e x＋1>0，∴ f (x )在(－∞，＋∞)上是增函数，∴ f (x 1)<f (x 2)<f (x 3)，且f x 1＋x 32<f x 1＋f x 32，∵ BA →＝(x 1－x 2，f (x 1)－f (x 2))，BC →＝(x 3－x 2，f (x 3)－f (x 2))， ∴ BA →·BC →＝(x 1－x 2)(x 3－x 2)＋(f (x 1)－f (x 2))(f (x 3)－f (x 2))<0， ∴ ∠ABC 为钝角，判断①正确，②错；(2)若△ABC 为等腰三角形，则只需AB ＝BC ，即(x 1－x 2)2＋(f (x 1)－f (x 2))2＝(x 3－x 2)2＋(f (x 3)－f (x 2))2， ∵ x 1，x 2，x 3成等差数列，即2x 2＝x 1＋x 3， 且f (x 1)<f (x 2)<f (x 3)，只需 f (x 2)－f (x 1)＝f (x 3)－f (x 2)，即2f (x 2)＝f (x 1)＋f (x 3)，即 f ⎝ ⎛⎭⎪⎫x 1＋x 32＝f x 1＋f x 32，这与f ⎝ ⎛⎭⎪⎫x 1＋x 32<f x 1＋f x 32相矛盾， ∴△ABC 不可能是等腰三角形，判断③错误，④正确，故选B. 解法二：(1)设A 、B 、C 三点的横坐标为x 1，x 2，x 3(x 1<x 2<x 3),图1－3∵ f ′(x )＝e x＋1>0，∴ f (x )在(－∞，＋∞)上是增函数，画出f (x )的图象(大致)∴ f (x 1)<f (x 2)<f (x 3)，且f x 1＋x 32<f x 1＋f x 32，如图1－2，设直线AB 、BC 的倾斜角分别为α和β，由0<k AB <k BC ，得α<β<π2，故∠ABC ＝π－(β－α)为钝角，判断①正确，②错误；由x 1，x 2，x 3成等差数列，得x 2－x 1＝x 3－x 2， 若△ABC 为等腰三角形，只需AB ＝BC ，则 f (x 2)－f (x 1)＝f (x 3)－f (x 2)，由0<k AB <k BC ，知上式不成立，判断③错误，④正确，故选B.课标理数15.B1，M1[2011·福建卷] 设V 是全体平面向量构成的集合，若映射f ：V →R 满足：对任意向量a＝(x1，y1)∈V，b＝(x2，y2)∈V，以及任意λ∈R，均有f(λa＋(1－λ)b)＝λf(a)＋(1－λ)f(b)．则称映射f具有性质P.现给出如下映射：①f1：V→R，f1(m)＝x－y，m＝(x，y)∈V；②f2：V→R，f2(m)＝x2＋y，m＝(x，y)∈V；③f3：V→R，f3(m)＝x＋y＋1，m＝(x，y)∈V.其中，具有性质P的映射的序号为________．(写出所有具有性质P的映射的序号) 课标理数15.B1，M1[2011·福建卷] 【答案】①③【解析】设a＝(x1，y1)∈V，b＝(x2，y2)∈V，则λa＋(1－λ)b＝λ(x1，y1)＋(1－λ)(x2，y2)＝(λx1＋(1－λ)x2，λy1＋(1－λ)y2)，①f1(λa＋(1－λ)b)＝λx1＋(1－λ)x2－[λy1＋(1－λ)y2]＝λ(x1－y1)＋(1－λ)(x2－y2)＝λf1(a)＋(1－λ)f1(b)，∴映射f1具有性质P；②f2(λa＋(1－λ)b)＝[λx1＋(1－λ)x2]2＋[λy1＋(1－λ)y2]，λf2(a)＋(1－λ)f2(b)＝λ(x21 ＋y1 ) ＋ (1－λ)(x22 ＋y2 )，∴f2(λa＋(1－λ)b)≠λf2(a)＋(1－λ)f2(b)，∴映射f2不具有性质P；③f3(λa＋(1－λ)b)＝λx1＋(1－λ)x2＋(λy1＋(1－λ)y2)＋1＝λ(x1＋y1＋1)＋(1－λ)(x2＋y2＋1)＝λf3(a)＋(1－λ)f3(b)，∴映射f3具有性质P.故具有性质P的映射的序号为①③.课标文数12.A1，M1[2011·福建卷] 在整数集Z中，被5除所得余数为k的所有整数组成一个“类”，记为[k]，即[k]＝{5n＋k|n∈Z}，k＝0,1,2,3,4.给出如下四个结论：①2011∈[1]；②－3∈[3]；③Z＝[0]∪[1]∪[2]∪[3]∪[4]；④“整数a，b属于同一‘类’”的充要条件是“a－b∈[0]”．其中，正确结论的个数是( )A．1 B．2 C．3 D．4课标文数12.A1，M1[2011·福建卷] C 【解析】因为2011＝5×402＋1，则2011∈[1]，结论①正确；因为－3＝5×(－1)＋2，则－3∈[2]，结论②不正确；因为所有的整数被5除的余数为0,1,2,3,4五类，则Z＝[0]∪[1]∪[2]∪[3]∪[4]，结论③正确；若整数a，b属于同一“类”[k]，可设a＝5n1＋k，b＝5n2＋k(n1，n2∈Z)，则a－b＝5(n1－n2)∈[0]；反之，若a－b∈[0]，可设a＝5n1＋k1，b＝5n2＋k2(n1，n2∈Z)，则a－b＝5(n1－n2)＋(k1－k2)∈[0]；∴k1＝k2，则整数a，b属于同一“类”，结论④正确，故选C.课标理数7.M1[2011·江西卷] 观察下列各式：55＝3125,56＝15625,57＝78125，…，则52011的末四位数字为( )A．3125 B．5625C．0625 D．8125课标理数7.M1[2011·江西卷] D 【解析】∵55＝3125,56＝15625,57＝78125,58＝390625,59＝1953125,510＝9765625，…，∴5n(n∈Z且n≥5)的末四位数字呈周期性变化，且最小正周期为4，记5n(n∈Z且n≥5)的末四位数为f(n)，则f(2011)＝f(501×4＋7)＝f(7)，∴52011与57的末四位数相同，均为8125.故选D.课标文数6.M1[2011·江西卷] 观察下列各式：72＝49,73＝343,74＝2401，…，则72011的末两位数字为( )A．01 B．43 C．07 D．49课标文数 6.M1[2011·江西卷] B【解析】∵75＝16807,76＝117649,77＝823543,78＝5764801，…，∴7n(n∈Z且n≥2)的末两位数字呈周期性变化，且最小正周期为4，记7n(n∈Z且n≥2)的末两位数为f(n)，则f(2011)＝f(502×4＋3)＝f(3)，∴72011与73的末两位数相同，均为43.课标理数15.M1[2011·山东卷] 设函数f(x)＝xx＋2(x>0)，观察：f1(x)＝f(x)＝xx＋2，f2(x)＝f(f1(x))＝x3x＋4，f3(x)＝f(f2(x))＝x7x＋8，f4(x)＝f(f3(x))＝x15x＋16，……根据以上事实，由归纳推理可得：当n∈N*且n≥2时，f n(x)＝f(f n－1(x))＝________.课标理数15.M1[2011·山东卷]xn－x＋2n【解析】观察1,3,7,15，…，与对应项的关系，显然满足2n－1，观察2,4,8,16，…与对应项的关系，显然满足2n，故f n(x)＝x－x＋2.课标理数13.M1[2011·陕西卷] 观察下列等式1＝12＋3＋4＝93＋4＋5＋6＋7＝254＋5＋6＋7＋8＋9＋10＝49……照此规律，第n个等式为________________________________________________________________________．课标理数13.M1[2011·陕西卷] n＋(n＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2【解析】由每一行分析发现规律是以后每一个数都比前一个数大1，再对每一行的第一个数分析找规律为以后每一个数都比前一个数大1，对每一行的最后一个数分析找规律为1,4,7,10，…，(3n－2)，对结果找规律为12,32,52，…，(2n－1)2，所以第n个等式为n＋(n ＋1)＋(n＋2)＋…＋(3n－2)＝(2n－1)2.课标文数13.M1[2011·陕西卷] 观察下列等式1＝12＋3＋4＝93＋4＋5＋6＋7＝254＋5＋6＋7＋8＋9＋10＝49照此规律，第五个等式应为________________________________．课标文数13.M1[2011·陕西卷] 5＋6＋7＋8＋9＋10＋11＋12＋13＝81 【解析】因为1＝1第一个式子左边1个数，右边1；2＋3＋4＝9第二个式子左边2个数，从2开始加，加3个数，右边3的平方；3＋4＋5＋6＋7＝25第三个式子左边5个数，从3开始加，加5个数，右边5的平方；4＋5＋6＋7＋8＋9＋10＝49第四个左边7个数，从4开始加，加7个数，右边7的平方，故第五项为5＋6＋7＋8＋9＋10＋11＋12＋13＝81.课标理数22.B9，M3[2011·湖南卷] 已知函数f (x )＝x 3，g (x )＝x ＋x . (1)求函数h (x )＝f (x )－g (x )的零点个数，并说明理由；(2)设数列{a n }(n ∈N *)满足a 1＝a (a >0)，f (a n ＋1)＝g (a n )，证明：存在常数M ，使得对于任意的n ∈N *，都有a n ≤M .课标理数22.B9，M3[2011·湖南卷] 【解答】 (1)由h (x )＝x 3－x －x 知，x ∈[0，＋∞)，而h (0)＝0，且h (1)＝－1<0，h (2)＝6－2>0，则x ＝0为h (x )的一个零点，且h (x )在(1,2)内有零点．因此，h (x )至少有两个零点．解法一：h ′(x )＝3x 2－1－12x －12，记φ(x )＝3x 2－1－12x －12，则φ′(x )＝6x ＋14x －32.当x ∈(0，＋∞)时，φ′(x )>0，因此φ(x )在(0，＋∞)上单调递增，则φ(x )在(0，＋∞)内至多只有一个零点．又因为φ(1)>0，φ⎝ ⎛⎭⎪⎫33<0，则φ(x )在⎝ ⎛⎭⎪⎫33，1内有零点，所以φ(x )在(0，＋∞)内有且只有一个零点．记此零点为x 1，则当x ∈(0，x 1)时，φ(x )<φ(x 1)＝0；当x ∈(x 1，＋∞)时，φ(x )>φ(x 1)＝0.所以，当x ∈(0，x 1)时，h (x )单调递减．而h (0)＝0，则h (x )在(0，x 1]内无零点； 当x ∈(x 1，＋∞)时，h (x )单调递增，则h (x )在(x 1，＋∞)内至多只有一个零点，从而h (x )在(0，＋∞)内至多只有一个零点．综上所述，h (x )有且只有两个零点．解法二：由h (x )＝x ⎝⎛⎭⎪⎫x 2－1－x －12，记φ(x )＝x 2－1－x －12，则φ′(x )＝2x ＋12x －32.当x ∈(0，＋∞)时，φ′(x )>0，从而φ(x )在(0，＋∞)上单调递增，则φ(x )在(0，＋∞)内至多只有一个零点．因此h (x )在(0，＋∞)内也至多只有一个零点．综上所述，h (x )有且只有两个零点．(2)记h (x )的正零点为x 0，即x 30＝x 0＋x 0. (i)当a <x 0时，由a 1＝a ，即a 1<x 0.而a 32＝a 1＋a 1<x 0＋x 0＝x 30，因此a 2<x 0.由此猜测：a n <x 0.下面用数学归纳法证明． ①当n ＝1时，a 1<x 0显然成立．②假设当n ＝k (k ≥1)时，a k <x 0成立， 则当n ＝k ＋1时，由a 3k ＋1＝a k ＋a k <x 0＋x 0＝x 30知，a k ＋1<x 0. 因此，当n ＝k ＋1时，a k ＋1<x 0成立．故对任意的n ∈N *，a n <x 0成立．(ii)当a ≥x 0时，由(1)知，h (x )在(x 0，＋∞)上单调递增，则h (a )≥h (x 0)＝0，即a 3≥a ＋a .从而a 32＝a 1＋a 1＝a ＋a ≤a 3，即a 2≤a .由此猜测：a n ≤a .下面用数学归纳法证明．①当n ＝1时，a 1≤a 显然成立．②假设当n ＝k (k ≥1)时，a k ≤a 成立，则当n ＝k ＋1时，由a 3k ＋1＝a k ＋a k ≤a ＋a ≤a 3知，a k ＋1≤a .因此，当n ＝k ＋1时，a k ＋1≤a 成立．故对任意的n ∈N *，a n ≤a 成立．综上所述，存在常数M ＝max{x 0，a }，使得对于任意的n ∈N *，都有a n ≤M .课标数学23.M4[2011·江苏卷] 设整数n ≥4，P (a ，b )是平面直角坐标系xOy 中的点，其中a ，b ∈{1,2,3，…，n }，a >b .(1)记A n 为满足a －b ＝3的点P 的个数，求A n ；(2)记B n 为满足13(a －b )是整数的点P 的个数，求B n .课标数学23.M4[2011·江苏卷] 【解答】 (1)点P 的坐标满足条件：1≤b ＝a －3≤n －3，所以A n ＝n －3.(2)设k 为正整数，记f n (k )为满足题设条件以及a －b ＝3k 的点P 的个数．只要讨论f n (k )≥1的情形．由1≤b ＝a －3k ≤n －3k 知f n (k )＝n －3k ，且k ≤n －13.设n －1＝3m ＋r ，其中m ∈N *，r ∈{0,1,2}，则k ≤m .所以B n ＝∑m k ＝1f n (k )＝∑mk ＝1 (n －3k )＝mn －3m m ＋2＝m n －3m －2. 将m ＝n －1－r 3代入上式，化简得B n ＝n －n －6－r r －6.所以B n＝⎩⎪⎨⎪⎧n n －6，n3是整数，n －n －6，n3不是整数.[2011·福州一模] 否定“自然数a ，b ，c 中恰有一个偶数”时，正确的反设为( ) A ．a ，b ，c 都是奇数 B ．a ，b ，c 都是偶数C ．a ，b ，c 中至少有两个偶数D ．a ，b ，c 中至少有两个偶数或都是奇数[2011·汕头期末] 设直角三角形的两条直角边的长分别为a ，b ，斜边长为c ，斜边上的高为h ，则有①a 2＋b 2>c 2＋h 2，②a 3＋b 3<c 3＋h 3， ③a 4＋b 4>c 4＋h 4，④a 5＋b 5<c 5＋h 5. 其中正确结论的序号是_______；进一步类比得到的一般结论是____________________．。

2012年高考理科数学试题选编1-集合与常用逻辑用语虢镇中学 数学教研组2 2012年高考理科数学试题选编1-集合与简易逻辑一、选择题 集合 1.全国新课标（1）已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈；则B 中所含元素的个数为（ ） ()A 3 ()B 6 ()C 8 ()D 102.北京1．已知集合A={x ∈R|3x+2＞0} B={x ∈R|（x+1）(x-3)＞0} 则A ∩B=A （-∞，-1）B （-1，-23） C （-23,3）D (3,+∞) 3.广东 2．设集合U {1,23,4,5,6}=，，M {1,2,4}=则M U = A ．UB ．{1,3,5}C ．{3,5,6}D ．{2,4,6}4.湖南1.设集合M={-1,0,1}，N={x|x 2≤x}，则M ∩N= A.{0} B.{0,1} C.{-1,1} D.{-1,0,0} 5.辽宁1. 已知全集{}=0,1,2,3,4,5,6,7,8,9U ，集合{}=0,1,3,5,8A ，集合{}=2,4,5,6,8B ，则()()=U U C A C BA ．{}5,8B ．{}7,9C ．{}0,1,3D ．{}2,4,66.陕西1. 集合{|lg 0}Mx x =>，2{|4}N x x =≤，则MN =（ ）A ． (1,2) B. [1,2) C. (1,2] D. [1,2] 7.全国大纲 2．已知集合{}{1,3,,1,,A m B m A B A ==⋃=，则m =A ．0或3B ．0或3C ．1或3D ．1或38.浙江 1．设集合A ＝{x |1＜x ＜4}，B ＝{x |x 2－2x －3≤0}，则A ∩(C R B )＝A ．(1，4)B ．(3，4)C ．(1，3)D ．(1，2) 9.山东2 已知全集={0,1,2,3,4}，集合A={1,2,3,}，B={2,4} ，则（CuA ）B 为A {1,2,4}B {2,3,4}C {0,2,4}D {0,2,3,4}10.江西 1．若集合A=｛-1，1｝，B=｛0，2｝，则集合｛z ︱z =x +y ,x ∈A,y ∈B｝中的元素的个数为（ ）A ．5 B.4 C.3 D.2简易逻辑11.福建 3.下列命题中，真命题是（ ）A ．0,00≤∈∃x e R x B ．22,x R x x >∈∀C ．0=+b a 的充要条件是1-=baD ．1,1>>b a 是1>ab 的充分条件 12.天津 （２）设R ϕ∈，则“=0ϕ”是“()=cos(+)f x x ϕ()x R ∈为偶函数”的（A ）充分而不必要条件 （Ｂ）必要而不充分条件 （Ｃ）充分必要条件 （Ｄ）既不充分也不必要条件虢镇中学 数学教研组3 13.湖北 2．命题“∈∃0x Q ，Q x ∈3”的否定是 A ．∉∃0x Q ，Q x ∈3B ．∈∃0x Q ，Q x ∉30 C ．∉∀0x Q ，Q x ∈3D ．∉∀0x Q ，Q x ∉314.湖南 2.命题“若α=4π，则tan α=1”的逆否命题是 A.若α≠4π，则tan α≠1 B. 若α=4π，则tan α≠1C. 若tan α≠1，则α≠4πD. 若tan α≠1，则α=4π15. 辽宁 4. 已知命题()()()()122121:,,--0p x x R f x f x x x ∀∈≥，则p ⌝是A ．()()()()122121,,--0x x R f x f x x x ∃∈≤B ．()()()()122121,,--0x x R f x f x x x ∀∈≤C ．()()()()122121,,--<0x x R f x f x x x ∃∈ D ．()()()()122121,,--<0x x R f x f x x x ∀∈16．江西 5.下列命题中，假命题为（ ） A ．存在四边相等的四边形不．是正方形 B ．1212,,z z C z z ∈+为实数的充分必要条件是12,z z 为共轭复数 C ．若,x y ∈R ，且2,x y +>则,x y 至少有一个大于1D ．对于任意01,nn n n n N C C C ∈+++都是偶数二、填空题 集合 1.天津（11）已知集合={||+2|<3}A x R x ∈，集合={|()(2)<0}B x R x m x ∈--,且=(1,)A B n -，则=m ,=n .2. 江苏 1．已知集合{124}A =，，，{246}B =，，，则A B = ．3.四川13、设全集{,,,}Ua b c d =，集合{,}A a b =，{,,}B b c d =，则=）（）（B C A C U U _______。

《借书不还，天打雷劈》 ⊙收获平台一、积累与运用。

1．逐段朗读课文，边读边摘抄文中的下列各类词语。

成语：?四字语：?尊称：?文言词语：?2．任选以上的四个词语连词组段，要求中心明确，语句连贯，有幽默趣味。

? 二、课文第五、六段写了借书不还的两类人，为什么分别称为“恶客”、“雅贼”？这两种人有什么不同？＊三、课文第九段叙写了“吾友李大人”借书不还，“我”最终以智取回，并施以“薄惩”的事。

这一段的叙述语言有什么特点？请举例说明。

⊙发展空间阅读下面的文字，完成文后各题（2003年四川省中考）。

① 有些人只会空想，不会做事。

他们凭空想了许多念头，滔滔不绝地说了许多空话，可是从来没认真做过一件事。

②也有些人只顾做事，不动脑筋。

他们一天忙到晚，做他们一向做惯的或者别人要他们做的事。

他们做事的方法只是根据自己的习惯，或者别人的命令，或一般人的通例。

自己一向这样做，别人要他们这样做，一般人都这样做，他们就“依葫芦画瓢”，照样做去。

到底为什么要做这件事，为什么要这样做，有没有更好的办法，他们从来不想一想。

③我们瞧不起前一种人，说他们是“空想家”。

可是往往赞美后一种人，说他们能够“埋头苦干”。

能够苦干固然是好的，但是只顾埋着头，不肯动动脑筋来想想自己做的事，其实并不值得赞美。

④这种埋头做事不动脑筋的人简直是——说得不客气一点——跟牛马一样。

拉磨的牛成年累月地在鞭子下绕着石磨转，永远不会想一想为什么要做这件事，为什么要这样做，有没有更好的办法。

能够这样想的只有人。

人在劳动中不断地动脑筋，想办法，才清清楚楚地知道自己做这件事为什么目的，有什么意义，有什么缺点，才渐渐想出节省劳力，提高效率的方法。

人类能够这样劳动，能够一面做，一面 想，所以文化能够不断地进步。

要不，今天的人类就只能像几万年以前的人类一样，过着最原始最简单的生活了。

⑤一事不做，凭空设想，那是“空想”。

不动脑筋，埋头苦干，那是“死做”。

无论什么事情，工作也好，学习也好，“空想”和“死做”都不会得到进步。

2012高考试题分类汇编（常用逻辑用语）考点1 简单的命题1.（2012·四川卷·文理）下列命题正确的是A.若两条直线和同一个平面所成的角相等，则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C.若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面，则这两个平面平行1.（2012·福建卷·理科）下列命题中，真命题是A.0x R ∃∈，00x e ≤B.x R ∀∈，2 2x x >C.0a b +=的充要条件是1a b=- D.1,1a b >>是1ab >的充分条件 2.（2012·江西卷·理科）下列命题中，假命题为A.存在四边相等的四边形不是正方形B.C z z ∈21,, 12z z +为实数的充分必要条件是12,z z 互为共轭复数C.若,x y R ∈，且2x y +>，则,x y 至少有一个大于1D.对于任意n N *∈,n nn n C C C +++ 10都是偶数 3.（2012·湖南卷·文理科）命题“若4πα=，则tan 1α=”的逆否命题是 A.若4πα≠，则tan 1α≠ B.若4πα=，则tan 1α≠C.若tan 1α≠，则4πα≠ D.若tan 1α≠，则4πα=考点2 充分、必要条件1.（2012·山东卷·理科）设0a >且1a ≠，则“函数()x f x a =在R 上是减函数” 是“函数3()(2)g x a x =-在R 上是增函数”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件2.（2012·安徽卷·理科）设平面α与平面β相交于直线m ，直线a 在平面α内，直线b 在平面β内，且b ⊥m ，则“α⊥β”是“a ⊥b ”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件3.（2012·浙江卷·文理）设a R ∈，则“1a =”是“直线1l ：210ax y +-=与直线2l ：(1)40x a y +++=平行的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件4.（2012·福建卷·文科）已知向量(1,2)a x =- ，(2,1)b = ，则a b ⊥ 的充要条件是 A.12x =- B.1x =- C.5x = D.0x = 5.（2012·四川卷·文理）设a ，b 都是非零向量，下列四个条件中，使a b a b = 成立的充分条件是A.a =- bB.a ∥bC.2a = bD.a ∥b 且a = b6.（2012·天津卷·理科）设R ∈ϕ,则“0=ϕ”是“))((cos )(R x x x f ∈+=ϕ为偶函数”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分与不必要条件7.（2012·天津卷·文科）设R x ∈，则“x >21”是“2210x x +->”的 A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件8.（2012·北京卷·文理）设,a b R ∈，i 是虚数单位，“0a =”是“复数a bi +是纯虚数”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.（2012·陕西卷·文理）设,a b R ∈，i 是虚数单位，则“0ab =”是“复数b a i+为纯虚数”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件10.（2012·湖北卷·文科）设,,a b c R ∈,则“1abc =”是a b c≤++”的A.充分条件但不是必要条件，B.必要条件但不是充分条件C.充分必要条件D.既不充分也不必要的条件11.（2012·重庆卷·理科）已知()f x 是定义在R 上的偶函数，且以2为周期，则“()f x 为[]0,1上的增函数”是“()f x 为[]3,4上的减函数”的A.既不充分也不必要的条件B.充分而不必要的条件C.必要而不充分的条件D.充要条件12.（2012·上海卷·文科）对于常数m 、n ，“0mn >”是“方程221mx ny +=的曲线是椭圆”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件考点3 全称命题、特称命题1.（2012·安徽卷·文科）命题“存在实数x ，使1x >”的否定是A. 对任意实数x , 都有1x >B.不存在实数x ，使1x ≤C. 对任意实数x , 都有1x ≤D.存在实数x ，使1x ≤2.（2012·辽宁卷·文理）已知命题p ：12,x x R ∀∈，2121(()())()0f x f x x x --≥，则p ⌝是A.12,x x R ∃∈,2121(()())()0f x f x x x --≤B.12,x x R ∀∈，2121(()())()0f x f x x x --≤C.12,x x R ∃∈，2121(()())()0f x f x x x --<D.12,x x R ∀∈，2121(()())()0f x f x x x --<3.（2012·湖北卷·理科）命题“0R x C Q ∃∈,30x Q ∈”的否定是A.0R x C Q ∃∉,30x Q ∈B.0R x C Q ∃∈,30x Q ∉C.0R x C Q ∀∈,30x Q ∈D.0R x C Q ∀∈,30x Q ∉4.（2012·湖北卷·文科）命题“存在一个无理数，它的平方是有理数”的否定是A.任意一个有理数，它的平方是有理数B.任意一个无理数，它的平方不是有理数C.存在一个有理数，它的平方是有理数D.存在一个无理数，它的平方不是有理数考点4 复合命题1.（2012·山东卷·文科）设命题p ：函数sin 2y x =的最小正周期为2π； 命题q ：函数cos y x =的图象关于直线2x π=对称.则下列判断正确的是A.p 为真B.q ⌝为假C.p q ∧为假D.p q ∨为真。