小学数学单元双向细目表
- 格式:doc
- 大小:112.00 KB
- 文档页数:12
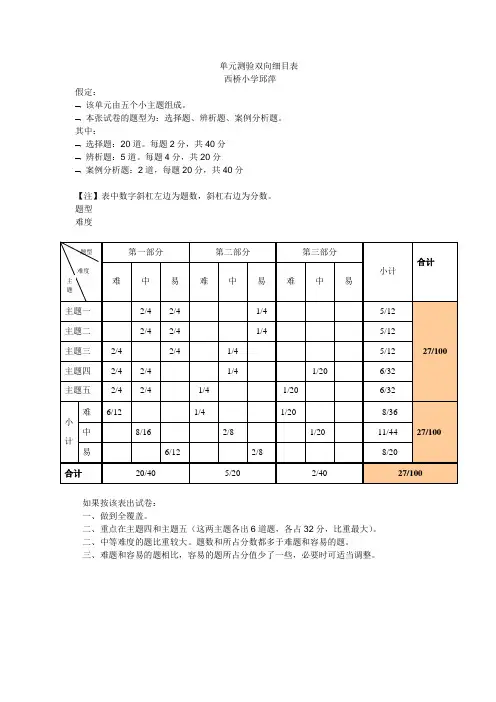
单元测验双向细目表
西桥小学邱萍
假定:
⌝该单元由五个小主题组成。
⌝本张试卷的题型为:选择题、辨析题、案例分析题。
其中:
⌝选择题:20道。
每题2分,共40分
⌝辨析题:5道。
每题4分,共20分
⌝案例分析题:2道,每题20分,共40分
【注】表中数字斜杠左边为题数,斜杠右边为分数。
题型
难度
如果按该表出试卷:
一、做到全覆盖。
二、重点在主题四和主题五(这两主题各出6道题,各占32分,比重最大)。
二、中等难度的题比重较大。
题数和所占分数都多于难题和容易的题。
三、难题和容易的题相比,容易的题所占分值少了一些,必要时可适当调整。

小学数学单元测验双向细目表一、简介本文档旨在提供一份小学数学单元测验的双向细目表,帮助老师们对学生的研究情况有更清晰的了解。
通过此表,可以系统地记录学生的掌握程度,以便针对性地进行教学和辅导。
此外,双向细目表也可以作为学生和家长们了解研究进展的参考。
二、双向细目表格式说明1. 基本信息栏- 学生姓名:填写学生姓名- 学号:填写学生学号- 学年学期:填写学年和学期- 班级:填写学生所在班级2. 单元测验内容栏- 标题:填写测验的单元名称- 日期:填写测验日期3. 学生表现栏(逐个单元记录)- 项目:记录测验中的具体项目,如填空题、选择题等- 正确答案:填写该项目的正确答案- 学生答案:填写学生在测验中的答案,并标注是否正确4. 综合评价栏- 学生的优点:简要记录学生在本次测验中的亮点和优秀表现- 学生的不足:简要记录学生在本次测验中的不足之处和需要提升的地方- 改进建议:针对学生在本次测验中的不足,提出具体的改进和辅导建议三、使用方法1. 打开双向细目表模板,填写基本信息栏中的学生姓名、学号、学年学期和班级。
2. 在单元测验内容栏中填写测验的单元名称和日期。
3. 在学生表现栏中按照测验内容逐个记录学生的答案。
4. 在综合评价栏中给出学生的优点、不足和改进建议。
5. 根据需要,可以复制多份学生表现栏,记录多位学生的情况。
四、注意事项1. 确保填写的学生基本信息准确无误,以免造成混淆。
2. 在记录学生答案时,标注正确与否,便于后期统计与分析。
3. 综合评价栏中的优点、不足和改进建议要具体明确,便于学生和家长们理解并采取行动。
4. 定期更新和归档测验记录,方便跟踪研究进展和进行后续的教学辅导。
5. 鼓励学生根据综合评价栏中的改进建议,针对不足进行反思和努力提高。
五、总结通过使用此双向细目表,我们可以更好地了解学生在数学研究中的掌握情况,分析研究缺失点,为学生提供有针对性的辅导。
同时,学生和家长们也可以通过综合评价栏了解研究进展和改进方向。

数学试题双向细目表I. 整数与有理数A. 基本概念1. 整数的定义及性质2. 有理数的定义及性质B. 整数与有理数的运算1. 加法与减法2. 乘法与除法3. 混合运算C. 整数与有理数的应用1. 温度计算2. 货币兑换问题II. 代数表达式与方程式A. 代数表达式1. 变量与常数2. 四则运算3. 代数表达式化简B. 方程式1. 一元一次方程式2. 一元二次方程式3. 解方程应用题III. 几何A. 基本概念1. 点、线、面的定义2. 角的定义与性质B. 图形的性质与分类1. 三角形2. 四边形3. 圆与圆的构造C. 坐标系与向量1. 平面直角坐标系2. 向量的定义与运算IV. 概率与统计A. 概率1. 随机事件与样本空间2. 概率的计算3. 事件的复合与互斥B. 统计1. 数据的收集与整理2. 平均数与中位数3. 概率统计应用题V. 函数与图像A. 函数概念与性质1. 函数的定义2. 函数的图像与性质B. 常见函数类型1. 线性函数与非线性函数2. 幂函数与指数函数3. 对数函数与三角函数C. 函数的运算与应用1. 函数的加减与乘除2. 函数的复合与反函数VI. 三角函数A. 基本概念与性质1. 弧度与角度的换算2. 三角函数的定义B. 三角函数的图像与周期性1. 正弦函数与余弦函数2. 正切函数与余切函数C. 三角函数的应用1. 三角函数方程的解法2. 三角函数在几何中的应用VII. 数列与数学归纳法A. 数列的概念与性质1. 等差数列与等比数列2. 通项公式与求和公式B. 数学归纳法1. 数学归纳法的原理2. 数学归纳法的应用VIII. 解析几何A. 平面解析几何1. 平面直角坐标系2. 点、线、圆的方程B. 空间解析几何1. 空间直角坐标系2. 直线与平面的方程3. 空间图形的分类IX. 近似计算A. 有效数字与误差1. 有效数字的定义2. 误差的计算与表示B. 近似计算方法1. 数的四舍五入2. 数的科学记数法3. 近似计算的应用X. 排列组合与概率A. 排列与组合1. 排列的定义与计算2. 组合的定义与计算B. 概率统计1. 事件的概率计算2. 投掷与抽取问题的概率XI. 三角函数与复数A. 三角函数的复数表示1. 克莱布斯-戴维(C-D)公式2. 欧拉公式与复数表示B. 复数的运算与性质1. 复数的加减与乘除2. 复数的共轭与模XII. 微积分基础A. 导数的定义与性质1. 导数的定义2. 导数的性质与计算B. 函数的极值与应用1. 函数的极大值与极小值2. 函数的应用问题XIII. 平面向量A. 向量的概念与性质1. 向量的定义与表示2. 向量的性质与运算B. 向量的应用1. 向量的坐标表示2. 向量运算在几何中的应用XIV. 几何证明A. 平面几何证明1. 各种基本几何定理的证明2. 几何图形性质的证明B. 空间几何证明1. 空间几何定理的证明2. 空间图形性质的证明XV. 指数与对数函数A. 指数函数与对数函数的性质1. 指数函数的定义与性质2. 对数函数的定义与性质B. 指数与对数函数的应用1. 指数增长问题2. 对数衰减问题。
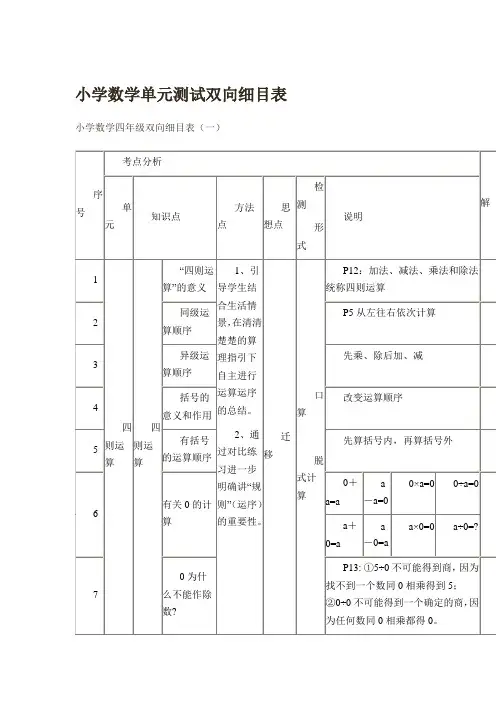
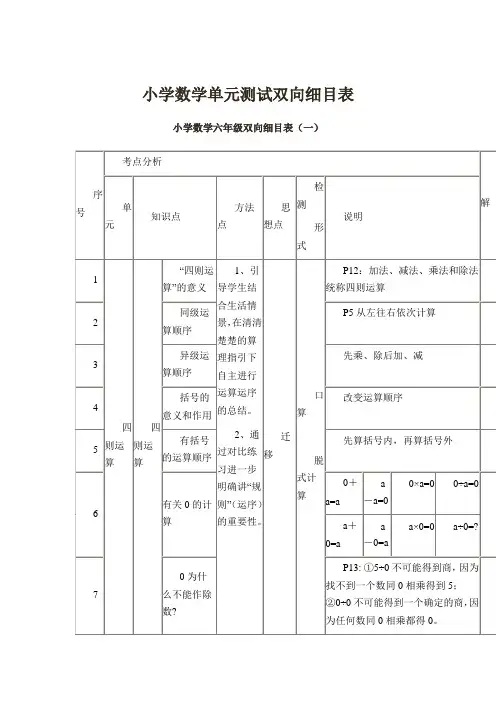
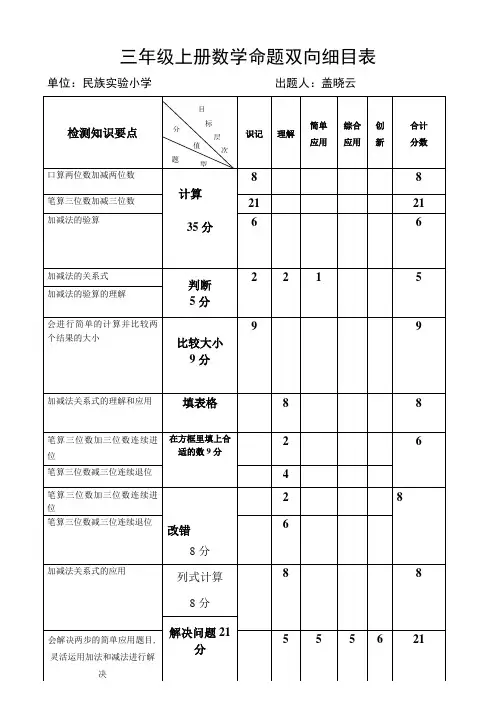
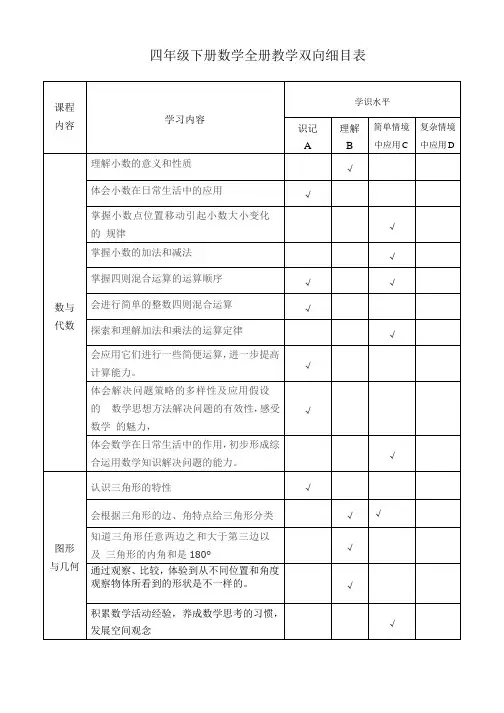

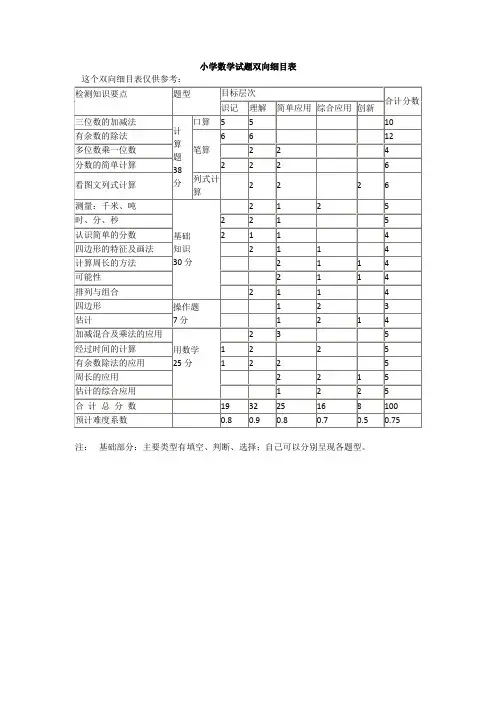
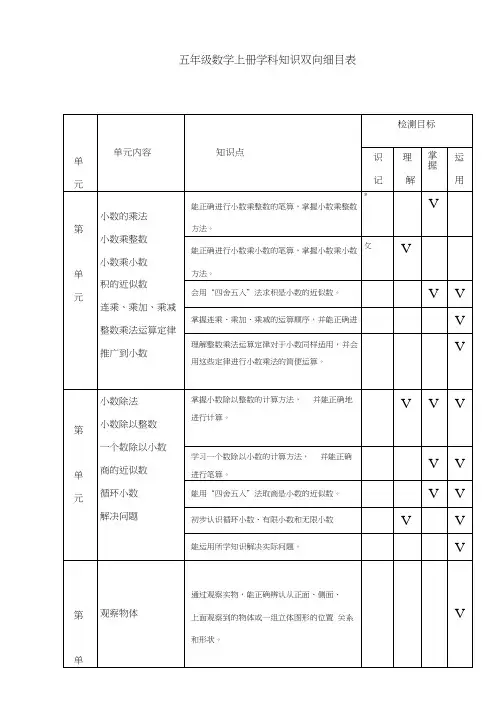
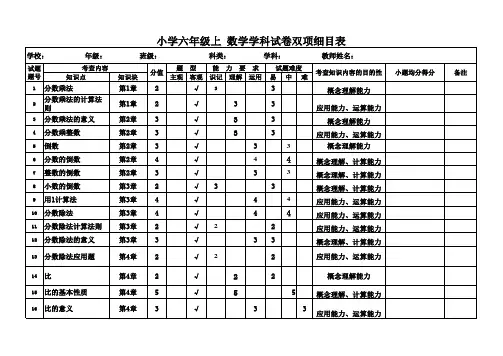
小学数学1-12册双向细目表知识点册数单元(知识块) 知识点教学目标(目的性)第一册一、数一数数数量在10以内的物体的个数体会学习数学的乐趣,提高学习数学的兴趣,建立学好数学的信心。
二、比一比比多少、比长短、比高矮1.了解多少,长短、高矮的概念 2.会比较多少,长短、高矮三、1~5的认识和加减法比大小,认识“<、>”;序数;数的分解和组成;加减法;简单图画应用题;0的认识1.认识符号“=”“<”“>”,会使用这些符号表示数的大小,掌握5以内各数的组成2.初步知道加减法的含义和加减法算式中各部分名称,初步知道加法和减法的关系,比较熟练的计算5以内的加减法。
四、认识物体和图形长方体、正方体、圆柱、球;长方形、正方形、三角形、圆直观认识长方体、正方体、圆柱,长方形、正方形、三角形和圆。
五、分类根据不同标准进行简单的分类初步了解分类的方法,会进行简单的分类六、6~10的认识和加减法6和7;8和9;10;连加连减;加减混合1.掌握6到10的数字顺序以及各数的组成2. 比较熟练的计算一位数的加法和10以内的减法。
七、11~20各数的认识认识11~20熟练地数出数量在20以内的物体个数,会读、写11-20各数八、认识钟表整时和几时半初步认识钟表,会认识整时和半时九、20以内的进位加法简单图画应用题中出现单位名称熟练计算20以内的进位加法人教版小学数学1-12册双向细目表知识点第二册后”、“左、右”的基本含义,初步了解它们的相对性。
2.使学生会用上、下、左右、前、后描述物体的相对位置。
3.使学生能够在具体情境中,根据行、列确定物体的位置。
二、20以内的退位减法20以内的退位减法、用数学(出现与图画结合,但语言叙述较完整的应用题;出现依据条件提问题的不完整应用题)1.使学生经历与他人交流各自算法的过程,能够比较熟练地口算20以内的退位减法。
2.使学生初步学会用加法和减法解决简单的问题。
三、图形的拼组平面图形的特征和图形之间的关系;立体图形的特征和图形之间的关系。
人教版一年级年级数学上册单元教学目标双向细目表
第五单元
2.使学生初步学会用加法和减法解决简单的问题。
3.通过数学学习,使学生初步体验数学与日常生活的密切联系,感受数学在日常生活中的作用。
说明:
1、学习内容的排列顺序与教材的编排相一致。
2、学习水平分A\B\C\D四级水平(A:识记;B:理解;C:再现性的情景应用;
D:生成性的情景应用)。
3、对于每一知识要点技能要点所需达到的学习水平,可在空格中直接打“√”。
4、识记—了解、认识、感知、初步体会、初步学会。
理解—说明、表达、解释、懂得、领会;
再现性的情景运用—掌握、会用、归纳等;
生成性的情景应用—会推导、说明、研究讨论、解决问题、总结评价等。