分数除法的意义。
- 格式：docx
- 大小：3.30 KB
- 文档页数：2
下载文档原格式
合集下载
分数除法的意义教学反思
分数除法的意义教学反思分数除法是小学数学中一个重要的知识点，也是学生很容易混淆和理解困难的内容之一。
作为数学教师，我深感对于分数除法的意义进行教学反思是非常必要和重要的。
首先，分数除法是数学中的一种运算，它的意义在于将分数进行分割和平均。
在实际生活中，我们经常会遇到将一些物品或者资源进行平均分配的情况，而分数除法正是解决这种问题的有效工具。
例如，我们可以用分数除法来计算一个蛋糕要平均分给几个人，或者一块土地要平均分给几户人家，这些都是生活中常见的实际问题。
其次，分数除法的意义在于培养学生的逻辑思维和数学应用能力。
分数除法是一个相对抽象和复杂的概念，需要学生能够正确理解和运用分数的概念，进行运算和解决问题。
这既需要学生具备较强的逻辑思维能力，能够理解和分析问题，找出合适的解决方法，又需要学生能够将数学知识应用于实际问题，通过数学计算得出准确的答案。
通过分数除法的学习，可以培养学生的思维能力和数学应用能力，为以后的数学学习打下坚实的基础。
然而，在实际的教学中，我发现学生对于分数除法的理解和掌握存在一些困难和误区。
一方面，学生容易将分数除法与整数除法混淆，不正确地运用分数除法的规则和方法。
他们往往会忽略分数除法的独特性，将其视为整数除法的简单拓展，导致运算结果错误。
例如，当计算3/4 ÷ 1/2时，部分学生会错误地将除法运算符和乘法运算符混淆，得出1/12的错误答案。
另一方面，学生在解决实际问题时，对于如何将问题抽象为数学运算仍存在一定困难。
由于实际问题具有一定的复杂性和变化性，学生需要能够将问题准确地转化成数学运算，进行求解。
然而，我在教学中发现许多学生缺乏此项能力，导致在解决实际问题时困惑和错误频发。
针对以上问题，我认为对于分数除法的意义进行教学反思，有以下几点值得关注和改进。
首先，我应该注重分数除法的定义和基本规则的教学，提高学生对分数除法的整体理解。
在课堂教学中，我将引入生活中常见的例子，通过实物展示和情境模拟等方式，帮助学生理解分数除法的意义，强调分数除法是一种分割和平均的运算方法，并与实际问题相结合进行深入讲解。
分数除法的意义和分数除以整数
整数除法
整数除法运算中，被除数除以除 数，商为整数或小数，余数可有 可无。
计算方法的比较
分数除法
分数除法的计算通常包括两个步骤， 首先将除数的倒数求出，然后将被除 数与这个倒数相乘。
整数除法
整数除法的计算通常是通过连续减法 或乘法逆元（如果存在）来实现的。
应用场景的比较
分数除法
分数除法在解决涉及分数的问题时非常有用，如分配、比较大小、求解方程等。 它可以帮助我们更精确地表示和处理与分数相关的数量关系。
在未来的学习中，我们将继续深入学习分数的四则运算，包括加法、减法、乘法和除法。通过熟练掌握这些运算规则 ，我们将能够更灵活地运用分数来解决各种问题。
拓展到复杂数学问题
随着学习的深入，我们将接触到更复杂的数学问题，如分式方程、不等式等。这些问题将要求我们综合运用分数的知 识和技巧，提高我们的数学素养和解决问题的能力。
在分数除法中，被除数称为“分 子”，除数称为“分母”，运算结 果称为“商”。
分数除法与乘法的关系
分数除法可以转化为乘法运算，即被 除数除以除数等于被除数乘以除数的 倒数。
通过将除法转化为乘法，可以简化运 算过程，提高计算效率。
分数除法的运算规则
分数除以整数时，可以将整数看 作分母为1的分数，然后进行除
当分数除以整数时，可以将除法转化为乘法，即除以一个数等于乘以这个数的倒数。这样 ，我们就可以利用乘法运算来简化分数除法的计算过程。
分数除法的应用
分数除法在实际生活中有着广泛的应用，如计算平均分、求解比例问题等。掌握分数除法 的方法，有助于我们更好地理解和解决这些问题。
对未来学习的展望
深入学习分数运算
分数除法在求图形周长中的应用
对于一些由多个不同长度线段组成的图形，如多 边形、不规则图形等，可以通过分数除法来计算 某一线段与周长的比例。
整数除法运算中，被除数除以除 数，商为整数或小数，余数可有 可无。
计算方法的比较
分数除法
分数除法的计算通常包括两个步骤， 首先将除数的倒数求出，然后将被除 数与这个倒数相乘。
整数除法
整数除法的计算通常是通过连续减法 或乘法逆元（如果存在）来实现的。
应用场景的比较
分数除法
分数除法在解决涉及分数的问题时非常有用，如分配、比较大小、求解方程等。 它可以帮助我们更精确地表示和处理与分数相关的数量关系。
在未来的学习中，我们将继续深入学习分数的四则运算，包括加法、减法、乘法和除法。通过熟练掌握这些运算规则 ，我们将能够更灵活地运用分数来解决各种问题。
拓展到复杂数学问题
随着学习的深入，我们将接触到更复杂的数学问题，如分式方程、不等式等。这些问题将要求我们综合运用分数的知 识和技巧，提高我们的数学素养和解决问题的能力。
在分数除法中，被除数称为“分 子”，除数称为“分母”，运算结 果称为“商”。
分数除法与乘法的关系
分数除法可以转化为乘法运算，即被 除数除以除数等于被除数乘以除数的 倒数。
通过将除法转化为乘法，可以简化运 算过程，提高计算效率。
分数除法的运算规则
分数除以整数时，可以将整数看 作分母为1的分数，然后进行除
当分数除以整数时，可以将除法转化为乘法，即除以一个数等于乘以这个数的倒数。这样 ，我们就可以利用乘法运算来简化分数除法的计算过程。
分数除法的应用
分数除法在实际生活中有着广泛的应用，如计算平均分、求解比例问题等。掌握分数除法 的方法，有助于我们更好地理解和解决这些问题。
对未来学习的展望
深入学习分数运算
分数除法在求图形周长中的应用
对于一些由多个不同长度线段组成的图形，如多 边形、不规则图形等，可以通过分数除法来计算 某一线段与周长的比例。
分数除法的意义
二、新知探究
(一)、教学例1
1、课件出示自学提纲:
（1）出示插图及乘法应用题，学生列式计算。
（2）学生把这道乘法应用题改编成两道除法应用题，并解答。
（3）将100克化成千克，300克化成千克，得出三道分数乘、除法算式。
2、学生自学后小组间交流
3、全班汇报：
100×3＝300（克）
A、3盒水果糖重300克，每盒有多重？300÷3＝100（克）
在教学中注重了以下几点：
1、强调知识的迁移和类推。在教学中，先复习整数除法意义再进行分数除法意义的教学，可以使学生利用知识的迁移和类推很容易得出分数除法的意义。
2、以自主探索为主。提供给学生自主学习的机会，给学生充分思考的空间和时间。
课题
分数除法的意义与分数除以整数
页码
28,29页
课型
计算
设计者
张小花
教学
目标
1、通过实例，使学生知道分数除法的意义与整数除法的意义是相同的，并使学生掌握分数除以整数的计算法则。
2、动手操作，通过直观认识使学生理解整数除以分数，引导学生正确地总结出计算法则，能运用法则正确地进行计算。
3、培养学生观察、比较、分析的能力和语言表达能力，提高计算能力。
B、300克水果糖，每盒100克，可以装几盒？300÷100＝3（盒）
4、引导学生通过整数题组和分数题组的对照，小组讨论后得出：
分数除法的意义与整数除法相同，都是已知两个因数的积与其
中一个因数，求另个一个因数。都是乘法的逆运算。
（二）、巩固分数除法意义的练习：P28“做一做”
（三）、教学例2
（1）学生拿出课前准备好的纸，小组讨论操作，如何把这张纸的平均分成2份，并通过操作得出每份是这张纸的几分之几。
(一)、教学例1
1、课件出示自学提纲:
（1）出示插图及乘法应用题，学生列式计算。
（2）学生把这道乘法应用题改编成两道除法应用题，并解答。
（3）将100克化成千克，300克化成千克，得出三道分数乘、除法算式。
2、学生自学后小组间交流
3、全班汇报：
100×3＝300（克）
A、3盒水果糖重300克，每盒有多重？300÷3＝100（克）
在教学中注重了以下几点：
1、强调知识的迁移和类推。在教学中，先复习整数除法意义再进行分数除法意义的教学，可以使学生利用知识的迁移和类推很容易得出分数除法的意义。
2、以自主探索为主。提供给学生自主学习的机会，给学生充分思考的空间和时间。
课题
分数除法的意义与分数除以整数
页码
28,29页
课型
计算
设计者
张小花
教学
目标
1、通过实例，使学生知道分数除法的意义与整数除法的意义是相同的，并使学生掌握分数除以整数的计算法则。
2、动手操作，通过直观认识使学生理解整数除以分数，引导学生正确地总结出计算法则，能运用法则正确地进行计算。
3、培养学生观察、比较、分析的能力和语言表达能力，提高计算能力。
B、300克水果糖，每盒100克，可以装几盒？300÷100＝3（盒）
4、引导学生通过整数题组和分数题组的对照，小组讨论后得出：
分数除法的意义与整数除法相同，都是已知两个因数的积与其
中一个因数，求另个一个因数。都是乘法的逆运算。
（二）、巩固分数除法意义的练习：P28“做一做”
（三）、教学例2
（1）学生拿出课前准备好的纸，小组讨论操作，如何把这张纸的平均分成2份，并通过操作得出每份是这张纸的几分之几。
分数除法的意义分数除以整数
分数除法的重要性
在数学、科学和工程等领域，分数除 法是解决各种问题的基础。它有助于 理解分数的性质，比较大小，以及解 决与分数有关的实际问题，如分数的 加减、乘除等运算。
分数除以整数的计算方法和技巧
分数除以整数的计算方法
将分数除以整数，可以通过乘以整数的倒数来简化计算。例如，将分数a/b除以整数c，可以表示为(a/b) × (1/c)。
分数除以整数在数学题目中的应用
解决几何问题
在几何问题中，经常需要将分数除以整数来计算图形的面积 或周长。例如，计算一个矩形的面积，需要将长和宽相乘， 如果长和宽是用分数表示的，就需要用到分数除法。
解决代数问题
在代数问题中，经常需要将分数除以整数来计算表达式的值 。例如，解方程时需要将方程中的项相除或相乘，如果项是 用分数表示的，就需要用到分数除法。
03
分数除以整数的实例
分数除以整数的实际应用
分数在商业计算中的应用
在商业计算中，经常需要将分数除以整数来计算商品的比例或分配。例如，将 一块蛋糕分成若干等份，每份蛋糕所占的比例可以用分数表示，如果要将这个 比例分配给几个人，就需要将分数除以整数的数量。
分数在科学实验中的应用
在科学实验中，经常需要将分数除以整数来计算实验结果。例如，化学实验中 经常需要将溶液稀释成不同的比例，这时候就需要用到分数除法。
分数除以整数在日常生活中的应用
家庭理财
在家庭理财中，经常需要将分数除以整数来计算投资回报率或贷款利率。例如，如果一个家庭的月收入是1000元， 而每月的支出是800元，那么这个家庭每月的结余就是1000元 - 800元 = 200元，这个结余占月收入的 200/1000 = 1/5。
健康管理
在健康管理中，经常需要将分数除以整数来计算身体指标的正常范围。例如，如果一个成年人的血压是120/80毫 米汞柱，而正常血压范围是90/60毫米汞柱 - 140/90毫米汞柱，那么这个成年人的血压就是正常范围之内。
在数学、科学和工程等领域，分数除 法是解决各种问题的基础。它有助于 理解分数的性质，比较大小，以及解 决与分数有关的实际问题，如分数的 加减、乘除等运算。
分数除以整数的计算方法和技巧
分数除以整数的计算方法
将分数除以整数，可以通过乘以整数的倒数来简化计算。例如，将分数a/b除以整数c，可以表示为(a/b) × (1/c)。
分数除以整数在数学题目中的应用
解决几何问题
在几何问题中，经常需要将分数除以整数来计算图形的面积 或周长。例如，计算一个矩形的面积，需要将长和宽相乘， 如果长和宽是用分数表示的，就需要用到分数除法。
解决代数问题
在代数问题中，经常需要将分数除以整数来计算表达式的值 。例如，解方程时需要将方程中的项相除或相乘，如果项是 用分数表示的，就需要用到分数除法。
03
分数除以整数的实例
分数除以整数的实际应用
分数在商业计算中的应用
在商业计算中，经常需要将分数除以整数来计算商品的比例或分配。例如，将 一块蛋糕分成若干等份，每份蛋糕所占的比例可以用分数表示，如果要将这个 比例分配给几个人，就需要将分数除以整数的数量。
分数在科学实验中的应用
在科学实验中，经常需要将分数除以整数来计算实验结果。例如，化学实验中 经常需要将溶液稀释成不同的比例，这时候就需要用到分数除法。
分数除以整数在日常生活中的应用
家庭理财
在家庭理财中，经常需要将分数除以整数来计算投资回报率或贷款利率。例如，如果一个家庭的月收入是1000元， 而每月的支出是800元，那么这个家庭每月的结余就是1000元 - 800元 = 200元，这个结余占月收入的 200/1000 = 1/5。
健康管理
在健康管理中，经常需要将分数除以整数来计算身体指标的正常范围。例如，如果一个成年人的血压是120/80毫 米汞柱，而正常血压范围是90/60毫米汞柱 - 140/90毫米汞柱，那么这个成年人的血压就是正常范围之内。
分数除法的意义和分数除以整数
分数除法的运算符号：÷
分数除法的运算性质：除以一 个数等于乘以这个数的倒数
分数除法与乘法的关系
分数除法可以转化为乘法运算 分数除以一个整数等于分数乘以这个整数的倒数 分数除法用于解决实际问题如分东西、计算百分比等 分数除法在数学中具有重要意义是进一步学习的基础
分数除它 可以用来解决各种 实际问题如计算面 积、体积、比例等。
题目：把一张纸 平均分成4份每 份是它的(1/4)如 果取3份就是 (3/4)。
题目：把一张纸 平均分成5份每 份是它的(1/5) 如果取4份就是 (4/5)。
题目：把一张纸 平均分成6份每 份是它的(1/6) 如果取5份就是 (5/6)。
题目：把一张纸 平均分成7份每 份是它的(1/7) 如果取6份就是 (6/7)。
分数除以整数在化学计算中的应用例如溶液的配制和反应速率的计算。 在物理学中分数除以整数可以用于计算各种物理量例如力、速度、加速度等。 在生物学中分数除以整数可以用于表示生物种群的数量变化和生长率。 在经济学中分数除以整数可以用于分析经济数据和预测市场趋势。
分数除以整数的练习题及解 析
第五章
练习题
● 答案：3/8 ● 解析：将一张纸的(3/4)平均分成2份每份是这张纸的(3/4)÷2=(3/4)×(1/2)=3/8。
● 题目：把一张纸的(7/8)平均分成5份每份是这张纸的几分之几？ 答案：7/40 解析：将一张纸的(7/8)平均分成5份每份是 这张纸的(7/8)÷5=(7/8)×(1/5)=7/40。
数的实际应用。
分数除以整数在数学中的实例
分数除以整数可以用于解决实际问题例如计算时间和距离。 分数除以整数在数学中可以用于解决几何问题例如计算面积和周长。 分数除以整数在数学中可以用于解决分数运算问题例如计算分数的加减乘除。 分数除以整数在数学中可以用于解决比例问题例如计算比例和百分比。
分数乘法和分数除法的计算方法和意义
分数乘法和分数除法的计算方法和意义分数乘法和分数除法是分数运算中非常重要的两个运算，它们的计算方法和意义如下:分数乘法:分数乘法是将两个分数相乘，得到一个新的分数。
分数乘法的计算方法可以分为以下几步:1. 将两个分数的分母取公倍数，最小公倍数为两者的分子之和。
2. 将两个分数的分子相乘，得到一个分数的分子。
3. 将两个分数的分母乘以各自分子的倍数，使得新的分母等于公倍数。
4. 将新的分子乘以各自分母的倍数，得到新的分母。
5. 将第一步中得到的分数分子与第二步中得到的分数分子相加，得到新的分数的分子。
6. 将第三步中得到的分数分母与第四步中得到的分数分母相加，得到新的分数的分母。
7. 将新的分数的分子和分母分别相乘，得到乘积。
分数除法:分数除法是将一个分数除以另一个分数，得到一个新的分数。
分数除法的计算方法可以分为以下几步:1. 将两个分数的分子取公倍数，最小公倍数为两者的分母之和。
2. 将一个分数的分子乘以另一个分数的分母的倍数，得到一个新的分数的分子。
3. 将一个分数的分母乘以另一个分数的分子的倍数，得到一个新的分数的分母。
4. 将新的分子乘以新的分母的倍数，得到新的分母。
5. 将两个分数的分母相乘，得到新的分数的分母。
6. 将一个分数的分子除以另一个分数的分母，得到一个新的分数的分子。
7. 将一个分数的分母除以另一个分数的分子，得到一个新的分数的分母。
8. 将第一步中得到的分数分子与第二步中得到的分数分子相加，得到新的分数的分子。
9. 将第三步中得到的分数分母与第四步中得到的分数分母相加，得到新的分数的分母。
10. 将新的分数的分子和分母分别相乘，得到乘积。
分数乘法和分数除法的意义在于，它们可以用来解决实际问题中的分数问题，并且可以方便地将分数转化为小数或者百分数进行计算。
例如，在日常生活中，我们经常需要计算两个数量的比值，可以用分数乘法来表示:设甲数为 a，乙数为 b，则甲数与乙数的比值可以用分数表示为:a/b = (a×b)/b其中，(a×b)/b 表示甲数与乙数相乘后得到的比例。
分数除法的意义和计算法则
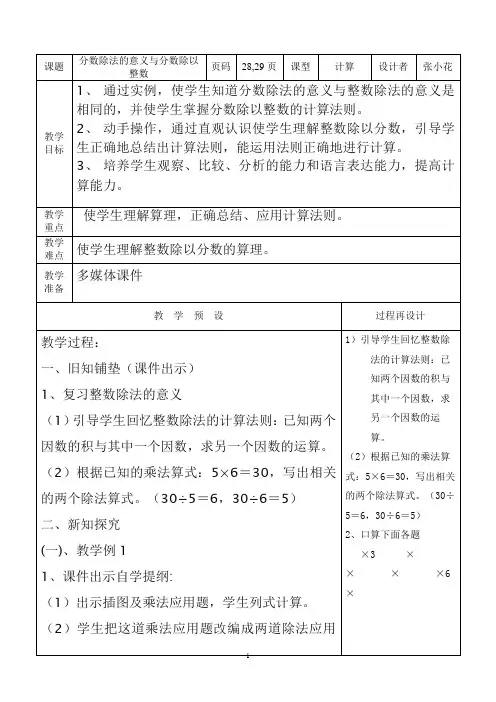
分数除法的意义和计算法则导读：本文是关于分数除法的意义和计算法则，希望能帮助到您！教学目标1．使学生理解分数除法的意义与整数除法的意义相同，就是已知两个因数的积与其中一个因数，求另一个因数的运算．2．掌握分数除以整数的计算法则，并能正确的进行计算．3．培养学生分析能力、知识的迁移能力和语言表达能力．教学重点正确归纳出分数除以整数的计算法则，并能正确的进行计算．教学难点正确归纳出分数除以整数的计算法则，并能正确的进行计算．教学过程一、复习引新（一）说出下面各数的倒数．0.3 6（二）已知126×45＝5670，直接说出5670÷45和5670÷126的得数，再说说你是怎样想的，根据是什么．（学生回答后教师总结：根据整数除法的意义，不用计算就能知道这两题的结果，谁还记得整数除法的意义是什么？已知两个因数的积与其中一个因数，求另一个因数的运算．）（三）引新：同学们想不想知道分数除法的意义吗？分数除法如何计算呢？这节课我们就一起来学习分数除法．（板书课题：分数除法的意义和计算法则）二、新授教学（一）．教学分数除法的意义（演示课件：分数除法的意义）1．每人吃半块月饼，4个人一共吃多少块月饼？教师提问：半块月饼用分数怎么表示？求4个人一共吃多少块月饼就是求几个？求4个是多少怎样列算式？（）2．两块月饼，平均分给4人，每人分得多少块？怎样列式？列式：2÷43．两块月饼，分给每人半块，可以分给几个人？列式：教师提问：说一说结果是多少？你是如何得出结果的？4．组织学生讨论：分数除法的意义．总结：分数除法的意义与整数除法的意义相同，都是已知两个因数的积与其中一个因数，求另一个因数的运算．5．练习反馈．根据：，写出，（二）教学分数除以整数的计算法则1．出示例1．把米铁丝平均分成2段，每段长多少米（演示课件：分数除以整数）（1）求每段长多少米怎样列算式？（2）以小组为单位讨论一下得多少呢？米平均分成2段就是要把6个米平均分成2份，每份是3个米是米．（3）教师板书整理．（米）2．教师质疑：如果把米铁丝平均分成3段、6段怎样计算？也可以这样想：把米铁丝平均分成3段，就是求米的是多少，列式是：把米铁丝平均分成6段，就是求米的是多少，列式是：3．教师继续质疑：如果把米铁丝平均分成4段每段长多少米？怎样计算？（米）为什么采用转化成分数乘法这种方法比较好呢？组织学生观察在转变中，什么变了，什么没变？讨论分数除以整数的计算法则．4．学生边概括教师边板书：分数除以整数（0除外）等于分数乘以这个整数的倒数．三、巩固练习（一）计算下面各题．学生独立完成，教师巡视，进行个别辅导．（二）求未知数1． 2．（三）判断．1．分数除法的意义与整数除法的意义相同．（）2．已知两个分数的积与其中一个分数，求另一个分数，用除法解答．（）3．（）4．（）5．（）（四）解答下面各题．1．把平均分成4份，每份是多少？2．什么数乘以6等于？3．一个正方形的周长是米，它的边长是多少米？四、课堂总结这节课我们学习了哪些知识？分数除法的意义是什么？分数除以整数的计算法则是什么？还有什么问题？五、课后作业（一）计算下面各题．（二）解下列方程．六、板书设计分数除法。
分数除法的六种意义
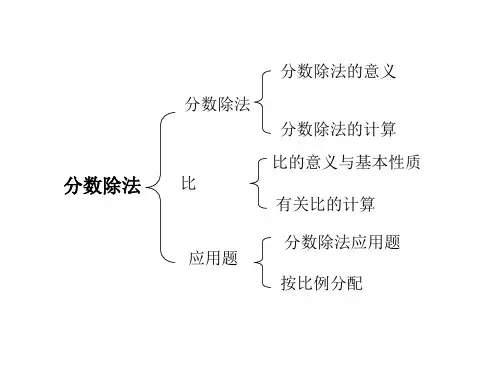
分数除法的六种意义
为了解决人类对数学的晦涩难懂，在数学里定义了分数除法，以帮助更好地理解数学问题。
分数除法可以分为六种主要意义：
1．比例：当两个数的比例一致时，可以表示为分数除法，从而更加准确地表述比例的概念。
2．分组：当需要划分同等大小的不同组时，可以使用分数除法进行分组，这样可以更好地表达总数量和分组数量的关系。
3．分配：当需要在一个或多个等份物品中均匀分配是，可以使用分数除法，这样可以准确地计算每一份物品的数量。
4．移除：当需要在一组物品中移除一定数量是，可以使用分数除法，这样可以精确的计算移除的数量。
5．做题：当解决一些常见的数学问题时，可以使用分数除法，这样可以得出更精确的答案。
6．其他：分数除法还可用于涉及到百分比计算，数量级转换等等。
分数除法的意义(例)
在化学中，分数的除法也经常用到。例如，在计算化学反 应速率时，常常需要用到分数的除法。例如，某个化学反 应的速率是$frac{1}{2}$摩尔/升·秒，反应物的浓度是 $frac{3}{4}$摩尔/升，那么反应速率是多少？这就需要用 到分数的除法来计算。
分数除法的运算规则
02
PART ONE
分数除以整数
例如，$frac{8}{9} div frac{4}{7} = frac{8}{9} times frac{7}{4} = frac{14}{9}$，表示将 $frac{8}{9}$平均分成$frac{4}{7}$份，每份 为$frac{14}{9}$。
分数除法运算的注 意事项
PART ONE
避免混淆除法与乘法
分数除法是指将一个分数除以另一个分数的运算。具体来说，分数a除以分数b，等于分数a乘以分数的倒 数。例如，$frac{2}{3} div frac{4}{5} = frac{2}{3} times frac{5}{4}$。
分数除法在日常生活中的应用
分数的除法在日常生活中的应用非常广泛，例如在计算时 间和速度时，常常需要用到分数的除法。例如，某人走路 的速度是$frac{3}{4}$公里/小时，他走了$frac{5}{6}$小 时，那么他走了多少公里？这就需要用到分数的除法来计 算。
除法与乘法的运算符号不同，除 法使用“÷”或“/”，而乘法使 用“×”。在进行分数除法时， 应明确区分除法与乘法的运算符 号，避免混淆。
除法与乘法的意义不同，除法表 示将一个数分成若干等份，而乘 法表示将一个数加到自己若干次。 理解这两种运算的意义有助于更 好地掌握分数除法的运算。
注意运算顺序
在处理复杂的分数除法运算时，应注意运算的顺序，避免因运算顺 序错误而导致结果错误。 在进行分数除法时，应遵循运算的优先级顺序，即先进行乘除运算， 再进行加减运算。在进行分数除法时，应先处理分子和分母的乘除 关系，然后再进行加减运算。
分数除法的运算规则
02
PART ONE
分数除以整数
例如，$frac{8}{9} div frac{4}{7} = frac{8}{9} times frac{7}{4} = frac{14}{9}$，表示将 $frac{8}{9}$平均分成$frac{4}{7}$份，每份 为$frac{14}{9}$。
分数除法运算的注 意事项
PART ONE
避免混淆除法与乘法
分数除法是指将一个分数除以另一个分数的运算。具体来说，分数a除以分数b，等于分数a乘以分数的倒 数。例如，$frac{2}{3} div frac{4}{5} = frac{2}{3} times frac{5}{4}$。
分数除法在日常生活中的应用
分数的除法在日常生活中的应用非常广泛，例如在计算时 间和速度时，常常需要用到分数的除法。例如，某人走路 的速度是$frac{3}{4}$公里/小时，他走了$frac{5}{6}$小 时，那么他走了多少公里？这就需要用到分数的除法来计 算。
除法与乘法的运算符号不同，除 法使用“÷”或“/”，而乘法使 用“×”。在进行分数除法时， 应明确区分除法与乘法的运算符 号，避免混淆。
除法与乘法的意义不同，除法表 示将一个数分成若干等份，而乘 法表示将一个数加到自己若干次。 理解这两种运算的意义有助于更 好地掌握分数除法的运算。
注意运算顺序
在处理复杂的分数除法运算时，应注意运算的顺序，避免因运算顺 序错误而导致结果错误。 在进行分数除法时，应遵循运算的优先级顺序，即先进行乘除运算， 再进行加减运算。在进行分数除法时，应先处理分子和分母的乘除 关系，然后再进行加减运算。
分数除法中的余数有什么意义？
分数除法中的余数有什么意义？
当我们进行分数除法时，结果往往包含一个整数部分和一个真
分数部分，如7/4=1 3/4。
这时，我们常常会忽略余数部分3/4，而
只重视商数部分1。
但余数部分实际上也有其独特的数学意义。
在数学上，余数实际上是被除数减去除数乘上商数所得到的数值。
在分数除法中，除数与商数都是分数，所以余数也自然而然地
成为了分数。
这个分数除了表达剩余的部分外，还具有其他的意义。
一、分数除法的几何意义
我们可以将7/4=1 3/4表示为一个面积为7/4个单位的小矩形被
每个边长为1个单位的小正方形所填满，整数部分1表示矩形的宽，而余数部分3/4则表示矩形面积中剩余的部分。
二、分数除法的分解意义
我们可以将7/4=1 3/4分解为1个单位和3/4个单位两部分。
1
个单位是商数，表示被除数中包含有几个除数，而3/4个单位则是
余数部分，表示余下的部分。
这样的分解可以让我们更加清晰地了解被除数的构成。
三、分数除法的循环意义
在一些特定的分数除法中，商数与余数部分会循环出现。
比如22/7的结果为3 1/7，其中7是循环出现的除数，3是商数，1/7是余数部分。
这里的循环出现可以用分数的形式表示为1/7，说明余数部分1/7会不断重复出现。
因此，分数除法中的余数并没有被忽视，它具有几何、分解、循环等多种意义。
在理解分数除法的同时，我们也需要充分认识到余数部分的重要性。
(本文内容参考自网络)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
分数除法的意义。
分数除法是数学中的一种运算方法，它的意义在于将一个分数除以另一个分数，得到一个新的分数或一个小数。
分数除法的结果可以用于比较两个分数的大小、求解实际问题中的比率和比例关系等。
我们来看一下分数除法的基本概念。
在分数除法中，被除数表示被分成若干等份的部分，而除数表示每份的大小。
例如，如果有一个被分成8份的糖果，而每份糖果的大小是1/4，那么我们可以用分数除法来计算每份糖果的数量，即8 ÷ 1/4。
按照分数除法的计算规则，我们可以将除法转化为乘法，即8 × 4/1，最终结果为32个糖果。
分数除法的意义之一是比较两个分数的大小。
通过将两个分数进行除法运算，我们可以得到它们的商。
如果一个分数的商比另一个分数的商大，那么我们可以说这个分数比另一个分数大；反之，如果一个分数的商比另一个分数的商小，那么我们可以说这个分数比另一个分数小。
例如，对于分数2/3和3/4，我们可以进行除法运算，得到2/3 ÷ 3/4 = 8/9和3/4 ÷ 2/3 = 9/8。
由于8/9比9/8小，所以我们可以说2/3比3/4小。
分数除法的另一个意义是求解实际问题中的比率和比例关系。
在很多实际问题中，我们需要计算不同物体的比率或者比例关系。
例如，假设一个水果篮中有3个苹果和4个橙子，我们可以用分数除法来
计算苹果和橙子的比率。
即3 ÷ 4，结果为3/4。
这意味着苹果和橙子的比率是3比4，或者可以说每个苹果对应4/3个橙子。
分数除法还可以用于计算小数。
当我们将一个分数除以另一个分数时，如果无法整除，我们就可以得到一个小数。
例如，将1/2除以1/3，我们可以得到1/2 ÷ 1/3 = 3/2。
由于3不能整除2，所以我们可以将这个分数转化为小数，即1.5。
这表明将一个分数除以另一个分数，可以得到一个小数表示。
分数除法在数学中有着重要的意义。
它不仅可以用于比较两个分数的大小，还可以用于求解实际问题中的比率和比例关系，以及计算小数。
通过掌握分数除法的运算规则和意义，我们可以更好地理解和应用分数除法，提高数学运算的能力。