高考一轮课时训练理算法的概念与流程

【高中数学】盘点高考数学一轮备考算法初步知识点1：算法的概念(1)算法概念：在数学上，现代意义上的算法通常是指可以用计算机来解决的某一类问题是程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成.(2)算法的特点:①有限性：一个算法的步骤序列是有限的，必须在有限操作之后停止，不能是无限的.②确定性：算法中的每一步必须就是确认的并且能够有效地继续执行且获得确认的结果，而不应就是模棱两可.③顺序性与正确性：算法从初始步骤开始，分为若干明确的步骤，每一个步骤只能有一个确定的后继步骤，前一步是后一步的前提，只有执行完前一步才能进行下一步，并且每一步都准确无误，才能完成问题.④不唯一性：解某一个问题的数学分析不一定就是唯一的，对于一个问题可以存有相同的算法.⑤普遍性：很多具体的问题，都可以设计合理的算法去解决，如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.2：程序框图(1)程序框图基本概念：①程序画法的概念：程序框图又称流程图，就是一种用规定的图形、指向线及文字说明去精确、直观地则表示算法的图形。

一个程序框图包括以下几部分：表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明。

②形成程序侧边的图形符号及其促进作用学习这部分知识的时候，要掌握各个图形的形状、作用及使用规则，画程序框图的规则如下：1、采用标准的图形符号。

2、框图通常按从上到下、从左到右的方向画。

3、除推论框外，大多数流程图符号只有一个步入点和一个选择退出点。

推论侧边具备少于一个选择退出点的唯一符号。

4、推论框分两大类，一类推论框是是否两分支的推论，而且存有且仅有两个结果;另一类就是多分支推论，存有几种相同的结果。

5、在图形符号内叙述的语言必须非常简洁确切。

3：算法的三种基本逻辑结构：顺序结构、条件结构、循环结构。

(1)顺序结构：顺序结构就是最简单的算法结构，语句与语句之间，侧边与框之间就是按从上到下的顺序展开的，它就是由若干个依次继续执行的处置步骤共同组成的，它就是任何一个算法都有赖于的一种基本算法结构。

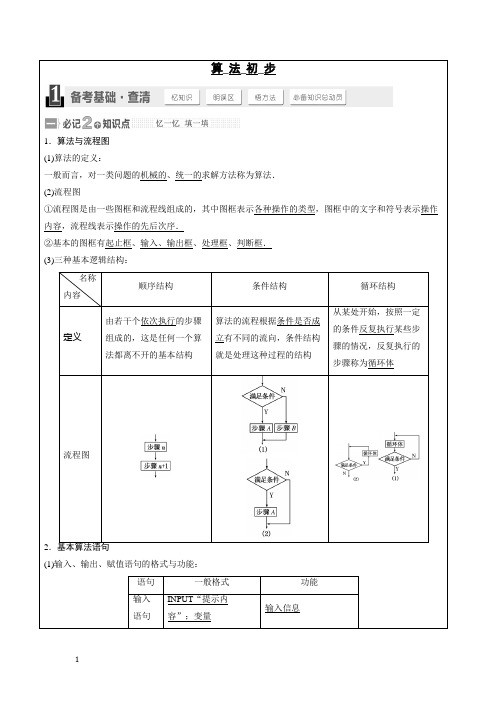
算_法_初_步1．算法与流程图(1)算法的定义：一般而言，对一类问题的机械的、统一的求解方法称为算法．(2)流程图①流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作内容，流程线表示操作的先后次序．②基本的图框有起止框、输入、输出框、处理框、判断框．(3)三种基本逻辑结构：名称内容顺序结构条件结构循环结构定义由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤称为循环体流程图2．基本算法语句(1)输入、输出、赋值语句的格式与功能：语句一般格式功能输入语句INPUT“提示内容”；变量输入信息输出语句PRINT“提示内容”；表达式输出常量、变量的值和系统信息赋值语句变量＝表达式将表达式所代表的值赋给变量(2)条件语句的格式及框图：①IF－THEN格式：②IF－THEN－ELSE格式：(3)循环语句的格式及框图：①UNTIL语句：②WHILE语句：1．易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．2．易忽视循环结构中必有条件结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．3．易混淆当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．[试一试]1．执行如图所示的算法流程图，若输入x＝2，则输出y的值为________．2．如图是一个算法流程图，则输出的k的值是________．识别算法流程图运行和完善流程图的步骤识别运行算法流程图和完善流程图是高考的热点．解答这一类问题，第一，要明确流程图的顺序结构、条件结构和循环结构；第二，要识别运行流程图，理解框图所解决的实际问题；第三，按照题目的要求完成解答．对流程图的考查常与数列和函数等知识相结合，进一步强化框图问题的实际背景．[练一练]1．(2014·深圳调研)若执行图中的框图，输入N＝13，则输出的数等于________．2．运行如图所示的流程图，若输出的结果是62，则判断框中整数M的值是________．考点一算法的基本结构1．(2012·江苏高考)下图是一个算法流程图，则输出的k的值是________．2．(2013·安徽高考改编)如图所示，程序框图(算法流程图)的输出结果为________．3．(2014·南昌模拟)若如下框图所给的程序运行结果为S＝20，那么判断框中应填入的关于k的条件是________．[类题通法]1．解决流程框图问题要注意几个常用变量：(1)计数变量：用来记录某个事件发生的次数，如i＝i＋1.(2)累加变量：用来计算数据之和，如S＝S＋i.(3)累乘变量：用来计算数据之积，如p＝p×i.2．处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．考点二算法的交汇性问题算法是高考热点内容之一，算法的交汇性问题是新课标高考的一大亮点，归纳起来常见的命题角度有：(1)与统计的交汇问题；(2)与函数的交汇问题；(3)与概率的交汇问题.角度一与统计的交汇问题1．(2014·荆州模拟)图(1)是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…，A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是________．角度二与函数的交汇问题2．(2014·北京海淀模拟)执行如图所示的算法流程图，输出的k值是________．角度三与概率的交汇问题3．如图是用模拟方法估计圆周率π值的流程图，P表示估计结果，则图中空白框内应填入________．[类题通法]解决算法的交汇性问题的方法(1)读懂流程图、明确交汇知识；(2)根据给出问题与流程图处理问题；(3)注意框图中结构的判断．考点三基本算法语句[典例](2013·南京、盐城一模)如图是一算法的伪代码，执行此算法，最后输出的n的值为________．n←6s←0While s<15s←s＋nn←n－1End WhilePrint n[类题通法]1．输入语句、输出语句和赋值语句基本对应于算法的顺序结构．2．在循环语句中也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套格式，这些语句需要保证算法的完整性，否则就会造成程序无法执行．[针对训练]运行下面的程序时，WHILE循环语句的执行次数是________．N←0WHILE N<20N←N＋1N←N*NWENDPRINT NEND[课堂练通考点]1．(2013·济南模拟)阅读算法流程图，运行相应的程序，输出的结果为________．2．(2014·福州模拟)执行如图所示的流程图，若输入的x值为2，则输出的x值为________．3．(2013·广东高考改编)执行如图所示的程序框图，若输入n的值为4，则输出s的值为________．4．(2013·惠州模拟)如图所示是一个算法的流程图，则输出S的值是________．[课下提升考能]1．(2014·大连模拟)在如图所示的流程图中，输入A＝192，B＝22，则输出的结果是________．2．当a＝1，b＝3时，执行完如图的一段程序后x的值是________．IF a<b THENx←a＋bELSEx←a－bEND IF3．图中的算法伪代码运行后，输出的S为________．I←1While I<8S←2×I＋3I←I＋2End WhilePrint S4．按如图所示的流程图运行后，输出的结果是63，则判断框中的整数M的值是________．5．(2013·东城模拟)某算法流程图如图所示，执行该程序，若输入的x值为5，则输出的y值为________．6．(2014·南通调研)已知实数x∈[1,9]，执行如图所示的流程图，则输出的x不小于55的概率为________．7．(2014·徐州摸底)已知某算法的流程图如图所示，则程序运行结束输出的结果为________．8．(2013·长春第三次调研)执行如图所示的流程图，若输出的k＝5，则输入的整数p的最大值为________．9．(2014·台州模拟)按如图所示的流程图运算，若输入x＝20，则输出的k＝________. 10．(2013·湖南高考)执行如图所示的程序框图，如果输入a＝1，b＝2，则输出的a的值为________．11．(2014·湖北八校联考)执行如图所示的流程图，输出的S的值为________．12．(2014·湘潭模拟)执行如图所示的流程图，输出的结果是________．。

盘点高考数学一轮备考算法初步知识点数学可以提升一团体的思想，可以开发你的大脑，小编预备了算法初步知识点，希望你喜欢。

1：算法的概念(1)算法概念：在数学上，现代意义上的算法通常是指可以用计算机来处置的某一类效果是顺序或步骤，这些顺序或步骤必需是明白和有效的，而且可以在有限步之内完成.(2)算法的特点:①有限性：一个算法的步骤序列是有限的，必需在有限操作之后中止，不能是有限的.②确定性：算法中的每一步应该是确定的并且能有效地执行且失掉确定的结果，而不应当是模棱两可.③顺序性与正确性：算法从初始步骤末尾，分为假定干明白的步骤，每一个步骤只能有一个确定的后继步骤，前一步是后一步的前提，只要执行完前一步才干停止下一步，并且每一步都准确无误，才干完成效果.④不独一性：求解某一个效果的解法不一定是独一的，关于一个效果可以有不同的算法.⑤普遍性：很多详细的效果，都可以设计合理的算法去处置，如心算、计算器计算都要经过有限、事前设计好的步骤加以处置.2：顺序框图(1)顺序框图基本概念：①顺序构图的概念：顺序框图又称流程图，是一种用规则的图形、指向线及文字说明来准确、直观地表示算法的图形。

一个顺序框图包括以下几局部：表示相应操作的顺序框;带箭头的流程线;顺序框外必要文字说明。

②构成顺序框的图形符号及其作用学习这局部知识的时分，要掌握各个图形的外形、作用及运用规那么，画顺序框图的规那么如下：1、运用规范的图形符号。

2、框图普通按从上到下、从左到右的方向画。

3、除判别框外，大少数流程图符号只要一个进入点和一个参与点。

判别框具有超越一个参与点的独一符号。

4、判别框分两大类，一类判别框是与否两分支的判别，而且有且仅有两个结果;另一类是多分支判别，有几种不同的结果。

5、在图形符号内描画的言语要十分精练清楚。

3：算法的三种基本逻辑结构：顺序结构、条件结构、循环结构。

(1)顺序结构：顺序结构是最复杂的算法结构，语句与语句之间，框与框之间是按从上到下的顺序停止的，它是由假定干个依次执行的处置步骤组成的，它是任何一个算法都离不开的一种基本算法结构。

高考数学一轮复习算法的概念要点数学在人类历史进展和社会生活中发挥着不可替代的作用，小编预备了算法的概念要点，具体请看以下内容。

算法的概念(1)算法概念：在数学上，现代意义上的算法通常是指能够用运算机来解决的某一类问题是程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成.(2)算法的特点:①有限性：一个算法的步骤序列是有限的，必须在有限操作之后停止，不能是无限的.②确定性：算法中的每一步应该是确定的同时能有效地执行且得到确定的结果，而不应当是模棱两可.③顺序性与正确性：算法从初始步骤开始，分为若干明确的步骤，每一个步骤只能有一个确定的后继步骤，前一步是后一步的前提，只有执行完前一步才能进行下一步，同时每一步都准确无误，才能完成问题.④不唯独性：求解某一个问题的解法不一定是唯独的，关于一个问题能够有不同的算法.死记硬背是一种传统的教学方式,在我国有悠久的历史。

但随着素养教育的开展,死记硬背被作为一种僵化的、阻碍学生能力进展的教学方式,慢慢为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。

事实上,只要应用得当,“死记硬背”与提高学生素养并不矛盾。

相反,它恰是提高学生语文水平的重要前提和基础。

“教书先生”可能是市井百姓最为熟悉的一种称呼，从最初的门馆、私塾到晚清的学堂，“教书先生”那一行当如何说也确实是让国人景仰甚或敬畏的一种社会职业。

只是更早的“先生”概念并非源于教书，最初显现的“先生”一词也并非有传授知识那般的含义。

《孟子》中的“先生何为出此言也？”；《论语》中的“有酒食，先生馔”；《国策》中的“先生坐，何至于此？”等等，均指“先生”为父兄或有学问、有德行的长辈。

事实上《国策》中本身就有“先生长者，有德之称”的说法。

可见“先生”之原意非真正的“教师”之意，倒是与当今“先生”的称呼更接近。

看来，“先生”之本源含义在于礼貌和尊称，并非具学问者的专称。

称“老师”为“先生”的记载，首见于《礼记?曲礼》，有“从于先生，不越礼而与人言”，其中之“先生”意为“年长、资深之传授知识者”，与教师、老师之意差不多一致。

第一节 算法初步程序框图与算法语句 1．算法的含义、程序框图(1)了解算法的含义，了解算法的思想．(2)理解程序框图的三种基本逻辑结构：顺序结构、条件结构、循环结构． 2．基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义．知识点一 算法与程序框图 1．算法(1)算法通常是指按照一定规则解决某一类问题的明确和有限的步骤． (2)应用：算法通常可以编成计算机程序，让计算机执行并解决问题． 2．程序框图定义：程序框图又称流程图，是一种用程序框、流程线及文字说明来表示算法的图形． 易误提醒 易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．[自测练习]1.如果执行右边的程序框图，输入x ＝－12，那么其输出的结果是( )A ．9B ．3 C. 3 D.19解析：依题意得，执行完第1次循环后，x ＝－12＋3＝－9≤0；执行完第2次循环后，x ＝－9＋3＝－6≤0；执行完第3次循环后，x ＝－6＋3＝－3≤0；执行完第4次循环后，x ＝－3＋3＝0≤0；执行完第5次循环后，x ＝0＋3＝3>0，程序结束．结合题中的程序框图可知，最后输出的结果是 3.答案：C2．如图，按如下程序框图，若输出结果为170，则判断框内应补充的条件为()A．i>7？B．i>9?C．i>10? D．i>11?解析：∵21＋23＋25＋27＝170，∴判断框内应补充的条件为i>7或i≥9，故选A.答案：A知识点二三种基本逻辑结构及相应语句名称示意图相应语句顺序结构①输入语句：INPUT“提示内容”；变量②输出语句：PRINT “提示内容”；表达式③赋值语句：变量＝表达式条件结构IF__条件__THEN语句体END__IFIF__条件__THEN 语句体1 ELSE语句体2 END__IF循环结构直到型循环结构DO循环体LOOP__UNTIL条件当型循环结构WHILE条件循环体WEND易误提醒易忽视循环结构中必有选择结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．易混淆当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．[自测练习]3．如图是一个程序框图，则输出的n的值是________．解析：该程序框图共运行5次，各次2n的值分别是2,4,8,16,32，所以输出的n的值是5.答案：54．当a＝1，b＝3时，执行完下面一段过程后x的值是________．IF a<b THENx＝a＋bELSEx＝a－bEND IF解析：∵a<b，∴x＝a＋b＝4.答案：4考点一算法的基本结构|1．(2015·高考天津卷)阅读如图所示的程序框图，运行相应的程序，则输出的S的值为()A．－10B．6C．14D ．18解析：执行程序框图可知，i ＝2，S ＝18；i ＝4，S ＝14；i ＝8，S ＝6.故输出S 的值为6. 答案：B2．(2016·威海一模)根据给出的程序框图，计算f (－1)＋f (2)＝( )A ．0B ．1C ．2D ．4解析：输入－1，满足x ≤0，所以f (－1)＝4×(－1)＝－4； 输入2，不满足x ≤0，所以f (2)＝22＝4， 即f (－1)＋f (2)＝0.故选A. 答案：A3．(2015·高考重庆卷)执行如图所示的程序框图，若输出k 的值为8，则判断框内可填入的条件是( )A ．s ≤34B ．s ≤56C ．s ≤1112D ．s ≤2524解析：第一次循环，得k ＝2，s ＝12；第二次循环，得k ＝4，s ＝12＋14＝34；第三次循环，得k ＝6，s ＝34＋16＝1112；第四次循环，得k ＝8，s ＝1112＋18＝2524，此时退出循环，输出k ＝8，所以判断框内可填入的条件是s ≤1112，故选C.答案：C1．解决程序框图问题要注意几个常用变量：(1)计数变量：用来记录某个事件发生的次数，如i ＝i ＋1.(2)累加变量：用来计算数据之和，如S＝S＋i.(3)累乘变量：用来计算数据之积，如p＝p×i.2．处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．考点二算法的交汇性问题|算法是高考热点内容之一，算法的交汇性问题是新课标高考的一大亮点，归纳起来常见的探究角度有：1．与统计的交汇问题．2．与函数的交汇问题．3．与不等式的交汇问题．4．与数列求和的交汇问题．探究一与统计的交汇问题1．如图是某县参加2016年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1，A2，…，A10(如A2表示身高(单位：cm)在[150,155)内的学生人数)．图(2)是统计图(1)中身高在一定范围内学生人数的一个程序框图．现要统计身高在160～180 cm(含160 cm，不含180 cm)的学生人数，则在流程图中的判断框内应填写()A．i<6？B．i<7?C．i<8? D．i<9?解析：统计身高在160～180 cm的学生人数，即求A4＋A5＋A6＋A7的值．当4≤i≤7时，符合要求．答案：C探究二与函数的交汇问题2．(2015·高考山东卷)执行如图所示的程序框图，输出的T的值为________．解析：开始n ＝1，T ＝1，因为1<3，所以T ＝1＋⎠⎛01x 1d x ＝1＋12x 2| 10＝1＋12×12＝32，n ＝1＋1＝2；因为2<3，所以T ＝32＋⎠⎛01x 2d x ＝32＋13x 3| 10＝32＋13×13＝116，n ＝2＋1＝3.因为3<3不成立，所以输出T ，即输出的T 的值为116.答案：116探究三 与不等式的交汇问题3．关于函数f(x)＝⎩⎪⎨⎪⎧－x ，1<x ≤4，cos x ，－1≤x ≤1的程序框图如图所示，现输入区间[a ，b]，则输出的区间是________．解析：由程序框图的第一个判断条件为f(x)>0，当f(x)＝cos x ，x ∈[－1,1]时满足．然后进入第二个判断框，需要解不等式f ′(x)＝－sin x ≤0，即0≤x ≤1.故输出区间为[0,1]．答案：[0,1]第3题图 第4题图 探究四 与数列求和的交汇问题4．(2015·高考湖南卷)执行如图所示的程序框图，如果输入n ＝3，则输出的S ＝( ) A.67 B.37 C.89D.49解析：第一次循环，S ＝11×3，此时i ＝2，不满足条件，继续第二次循环，S ＝11×3＋13×5，此时i ＝3，不满足条件，继续第三次循环，S ＝11×3＋13×5＋15×7＝12⎣⎡⎦⎤⎝⎛⎭⎫1－13＋⎝⎛⎭⎫13－15＋⎝⎛⎭⎫15－17＝37， 此时i ＝4>3，退出循环，输出S 的值为37，选B.答案：B解决算法交汇问题的三个关键点(1)读懂程序框图，明确交汇知识； (2)根据给出问题与程序框图处理问题； (3)注意框图中结构的判断．考点三 算法基本语句|按照如图程序运行，则输出K 的值是________． X ＝3 K ＝0 DO X ＝2] [解析] 第一次循环，X ＝7，K ＝1； 第二次循环，X ＝15，K ＝2； 第三次循环，X ＝31，K ＝3； 终止循环，输出K 的值是3. [答案] 3算法语句应用的关注点(1)输入语句、输出语句和赋值语句基本对应于算法的顺序结构．(2)在循环语句中也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套格式，这些语句需要保证算法的完整性，否则就会造成程序无法执行．(2015·高考江苏卷)根据如图所示的伪代码，可知输出的结果S为________．S←1I←1While I<8S←S＋2I←I＋3End WhilePrint S解析：该伪代码运行3次，故输出的S为7.答案：725.变量的含义理解不准致误【典例】(2015·高考全国卷Ⅰ)执行如图所示的程序框图，如果输入的t＝0.01，则输出的n＝()A．5B．6C．7D．8[易错点析](1)读不懂程序框图，把执行循环体的次数n误认为是变量S的值，没有注意到n的初始值为0.(2)对循环结构：①判断条件把握不准；②循环次数搞不清楚；③初始条件容易代错．[解析]由程序框图可知，S ＝1－12＝12，m ＝14，n ＝1，12>0.01；S ＝12－14＝14，m ＝18，n ＝2，14>0.01； S ＝14－18＝18，m ＝116，n ＝3，18>0.01； S ＝18－116＝116，m ＝132，n ＝4，116>0.01； S ＝116－132＝132，m ＝164，n ＝5，132>0.01； S ＝132－164＝164，m ＝1128，n ＝6，164>0.01； S ＝164－1128＝1128，m ＝1256，n ＝7，1128<0.01，输出n ＝7，故选C. [答案] C[方法点评] (1)要分清是当型循环结构还是直到型循环结构；要理解循环结构中各变量的具体含义以及变化规律．(2)在处理含有循环结构的算法问题时，关键是确定循环的次数，循环中有哪些变量，且每一次循环之后的变量S 、n 值都要被新的S 、n 值所替换．[跟踪练习] 执行如图所示的程序框图，则输出S 的值为( )A ．3B ．－6C ．10D ．－15解析：第一次执行程序，得到S ＝0－12＝－1，i ＝2； 第二次执行程序，得到S ＝－1＋22＝3，i ＝3； 第三次执行程序，得到S ＝3－32＝－6，i ＝4； 第四次执行程序，得到S ＝－6＋42＝10，i ＝5；第五次执行程序，得到S ＝10－52＝－15，i ＝6，到此结束循环，输出的S ＝－15. 答案：DA 组 考点能力演练1．定义运算a ⊗b 为执行如图所示的程序框图输出的S 值，则⎝⎛⎭⎫2cos 5π3⊗⎝⎛⎭⎫2tan 5π4的值为( )A ．4B ．3C ．2D ．－1解析：由程序框图可知，S ＝⎩⎪⎨⎪⎧a (a －b )，a ≥b ，b (a ＋1)，a <b ，2cos5π3＝1,2tan 5π4＝2,1<2， 所以⎝⎛⎭⎫2cos 5π3⊗⎝⎛⎭⎫2tan 5π4＝2(1＋1)＝4. 答案：A2．(2016·贵州模拟)阅读如图所示的程序框图，运行相应的程序，输出s 的值等于( )A ．－3B ．－10C ．0D ．－2解析：第一次循环k ＝0＋1＝1，s ＝2×1－1＝1，满足k <4；第二次循环k ＝1＋1＝2，s ＝2×1－2＝0，满足k <4；第三次循环k ＝2＋1＝3，s ＝2×0－3＝－3，满足k <4；第四次循环k ＝3＋1＝4，不满足k <4，输出的s ＝－3，故选A.答案：A3．(2016·长春模拟)阅读如图所示的程序框图，运行相应的程序．若输出的S 为1112，则判断框中填写的内容可以是( )A ．n ＝6?B ．n <6?C ．n ≤6?D ．n ≤8?解析：∵12＋14＋16＝1112，∴n ＝6时满足条件，而n ＝8时不满足条件，∴n ≤6，故选C.答案：C4.某程序框图如图所示，若输出的S ＝120，则判断框内为( )A ．k >4?B ．k >5?C ．k >6?D ．k >7?解析：依题意，进行第一次循环时，k ＝1＋1＝2，S ＝2×1＋2＝4；进行第二次循环时，k ＝2＋1＝3，S ＝2×4＋3＝11；进行第三次循环时，k ＝3＋1＝4，S ＝2×11＋4＝26；进行第四次循环时，k ＝4＋1＝5，S ＝2×26＋5＝57；进行第五次循环时，k ＝5＋1＝6，S ＝2×57＋6＝120，此时结束循环，因此判断框内应为“k >5？”，选B.答案：B5.某流程图如图所示，现输入如下四个函数，则可以输出的函数是( )A ．f (x )＝x 2B ．f (x )＝|x |xC ．f (x )＝e x －e －xe x ＋e －xD ．f (x )＝1＋sin x ＋cos x1＋sin x －cos x解析：由框图可知输出函数为奇函数且存在零点，依次判断各选项，A 为偶函数，B 不存在零点，不符合，对于C ，由于f (－x )＝e －x －e xe －x ＋e x ＝－f (x )，即函数为奇函数，且存在零点为x ＝0，对于D ，由于其定义域不关于原点对称，故其为非奇非偶函数，故选C.答案：C6．(2016·南京模拟)根据如图所示的伪代码，最后输出的S 的值为________． S ＝0For I From 1 To 10S ＝S ＋I End For Print S解析：这是一个1＋2＋3＋…＋10的求和，所以输出的S 的值为55. 答案：557．执行如图所示的程序框图，输出的S 的值为______．解析：S ＝sin 1×π3＋sin 2×π3＋sin 3×π3＋sin 4×π3＋sin5×π3＋sin 6×π3＋…＋sin 2 013×π3 ＝⎝⎛sin1×π3＋sin 2×π3＋sin 3×π3＋sin 4×π3＋⎭⎫sin5×π3＋sin6×π3×335＋sin 1×π3＋sin2×π3＋sin 3×π3＝ 3. 答案： 38．(2016·黄冈模拟)随机抽取某中学甲、乙两个班各10名同学，测量它们的身高获得身高数据的茎叶图如左下图，在样本的20人中，记身高在[150,160)，[160,170)，[170,180)，[180,190)的人数依次为A 1，A 2，A 3，A 4.右下图是统计样本中身高在一定范围内的人数的算法框图．若图中输出的S ＝18，则判断框应填________．解析：本题考查程序框图与统计交汇问题．由于i 从2开始，也就是统计大于或等于160的所有人数，于是就要计算A 2＋A 3＋A 4，因此，判断框应填i <5或i ≤4.答案：i <5或i ≤49．给出以下10个数：5,9,80,43,95,73,28,17,60,36.要求把大于40的数找出来并输出．试画出该问题的算法程序框图．解：程序框图如下：10．某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示：队员i 1 2 3 4 5 6 三分球个数a 1a 2a 3a 4a 5a 6统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如上图所示． (1)试在判断框内填上条件； (2)求输出的s 的值．解：(1)依题意，程序框图是统计6名队员投进的三分球的总数． ∴判断框内应填条件“i ≤6？”．(2)6名队员投进的三分球数分别为a 1，a 2，a 3，a 4，a 5，a 6.故输出的s ＝a 1＋a 2＋…＋a 6.B 组 高考题型专练1．(2014·高考江西卷)阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为( )A ．7B ．9C ．10D ．11解析：执行程序框图，第一次循环：i ＝1，S ＝lg 13>－1，否；执行第二次循环：i ＝3，S＝lg 13＋lg 35＝lg 15>－1，否；执行第三次循环：i ＝5，S ＝lg 15＋lg 57＝lg 17>－1，否；执行第四次循环：i ＝7，S ＝lg 17＋lg 79＝lg 19>－1，否；执行第五次循环：i ＝9，S ＝lg 19＋lg 911＝lg 111<－1，是，结束循环，输出i 为9，故选B.答案：B2．(2014·高考新课标全国卷Ⅰ)执行下面的程序框图，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )A.203B.72C.165D.158解析：第一次循环，M ＝32，a ＝2，b ＝32，n ＝2；第二次循环，M ＝83，a ＝32，b ＝83，n＝3；第三次循环，M ＝158，a ＝83，b ＝158，n ＝4，退出循环，输出M 为158，故选D.答案：D3．(2015·高考全国卷Ⅱ)程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的a ＝( )A ．0B ．2C ．4D ．14解析：第一次执行，输入a ＝14，b ＝18，因为a <b ，所以b ＝18－14＝4；第二次执行，因为a ＝14，b ＝4，a >b ，所以a ＝14－4＝10；第三次执行，因为a ＝10，b ＝4，a >b ，所以a ＝10－4＝6；第四次执行，因为a ＝6，b ＝4，a >b ，所以a ＝6－4＝2；第五次执行，因为a ＝2，b ＝4，a <b ，所以b ＝4－2＝2，此时a ＝b ＝2，故选B.答案：B4.根据框图，当输入x 为2 016时，输出的y ＝( )A．2 B．4C．10 D．28解析：由题意可得，x依次为2 016，2 014，2 012，…，0，－2，执行y＝3－(－2)＋1＝10，故输出的y＝10，选C.答案：C。

算法的概念与流程图一、教学目标1．了解算法的含义，能用自然语言描述算法．2．了解流程图的三种基本逻辑结构，能识别简单的流程图所描述的算法． 二、基础知识回顾与梳理【回顾要求】1. 阅读必修三第5—15页，完成以下任务：（1）理解算法的概念，学习算法的自然语言表示，认识算法的特征、作用和优势。

（2）流程图是怎么构成的？如何用流程图描述基本的算法结构？ （3）构成程序框的图形符号有哪些？其作用是什么？ （4）算法的三种基本逻辑结构各有什么特点？2. 第13页例4你会写出算法吗？阅读教材上的求解过程。

3. 在教材上的空白处做以下题目：第15页练习第1题。

【要点解析】1．算法的概念：可以用计算机来解决的某一类问题的程序或步骤，这些程序和步骤必须是明确和有效的，且能在有限步之内完成．算法的特点：确定性、有限性、顺序性，正确性．2．流程图：是由一些图框和带箭头的流线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作的内容，带箭头的流线表示操作的先后次序． 【教学建议】结合某一流程图说明 3．构成程序框的图形符号及其作用4．算法的三种基本逻辑结构：顺序结构、选择（条件）结构、循环结构．5．以下框图中表示顺序结构的是 ，表示选择结构的是 ，表示循环结构的是 ．图1图3答案：图1，图2与图3、图4与图5【教学建议】本题主要是帮助学生了解三种流程图常见结构．要结合上述流程图的构成，说明程序框的图形符号及其作用三、诊断练习1、教学处理：课前由学生自主完成4道小题，并要求将解题过程扼要地写在学习笔记栏。

课前抽查批阅部分同学的解答，了解学生的思路及主要错误。

将知识问题化，通过问题驱动，使教学言而有物，帮助学生内化知识，初步形成能力。

点评时要简洁，要点击要害。

2、诊断练习点评题1：计算机执行下面的程序段后，输出的结果是________.【分析与点评】本题用到了顺序结构．题2：下面流程图的功能是 ． 【分析与点评】（1）本题中流程图的作用是求输入值的绝对值． （2）选择结构的作用是在算法中通过对条件的判断，根据条件是否成立而选择不同流向的算法结构．分段函数求值的算法设计中常用到选择结构．（3）循环结构和选择结构共同点都要用到判断框，但它们是有区别的，好好体会．题3：一个算法如下： 第一步：S 取值0，i 取值1；第二步：若i 不大于10,则执行下一步；否则执行第六步； 第三步：计算S+i 且将结果代替S ； 第四步：用i+2结果代替i ； 第五步：转去执行第二步；第六步：输出S.则运行以上步骤输出的结果为________.【分析与点评】（1）这是用自然语言表示的算法，虽说是最初始的形式，但理解起来不及图形语言来得直观，易懂，亦可将它转化为流程图形式，更便于理解；（2）它实质上是一个含有循环结构的求满足一定条件的正奇数和的算法。

第10章算法初步、推理与证明10.1 算法的含义与流程图考纲要求1．了解算法的含义和算法的基本思想．2．了解流程图中的三种基本的算法结构：顺序结构、选择结构和循环结构，并能解决相关的简单问题．1．算法(1)定义：一般而言，对一类问题的________、________求解方法称为算法．(2)找到了某种算法是指使用一系列运算规则能在______求解某类问题，其中的每条规则必须是__________、________.(3)算法从初始步骤开始，每一个步骤只能有________的后继步骤，从而组成一个步骤序列，序列的终止表示问题得到________或指出问题____________．2．流程图定义：流程图是由一些________和流程线组成的，其中图框表示各种__________，图框中的文字和符号表示__________，流程线表示__________．3．三种基本逻辑结构(1)顺序结构是由__________________组成的，这是任何一个算法都离不开的基本结构．其结构形式为(2)选择结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式，也称为分支结构．其结构形式为(3)循环结构是指在算法中，需要________________的结构．反复执行的处理步骤称为________．循环结构又分为__________和__________．其结构形式为1．已知一个学生的语文成绩为89，数学成绩为96，外语成绩为99，求他的总分和平均成绩的一个算法为：S1令A←89，B←96，C←99；S2____________________；S3____________________；S4输出计算的结果．2．如图所表示的算法功能是________，输出结果为i＝________，i＋2＝________.(第2题图) (第3题图)3．某算法的流程图如图所示，则输出量y与输入量x满足的关系式是__________．4．如图是求函数值的流程图，当输出y的值为1时，则输入的x的值为__________．(第4题图) (第5题图)5．在如图所示的流程图中，输出的结果是__________．1．如何正确画出流程图？提示：在画流程图时首先要进行结构的选择．若所要解决的问题不需要分情况讨论，只用顺序结构就能解决；若所要解决的问题要分若干种情况讨论时，就必须引入选择结构；若所要解决的问题要进行许多重复的步骤，且这些步骤之间又有相同的规律时，就必须引入变量，应用循环结构．2．选择结构的主要作用是什么？提示：分类是算法中经常发生的事情，选择结构的主要作用就是表示分类．在分类不止两类的情况下通常用在选择结构中“嵌套”选择结构的方法去实现．一、算法的设计【例1】已知点P(x0，y0)和直线l：Ax＋By＋C＝0，求点P(x0，y0)到直线l的距离d，写出其算法并画出流程图．方法提炼设计算法应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)将解决问题的过程划分为若干个步骤；(4)用简练的语言将各个步骤表示出来．请做针对训练3二、算法的选择结构【例2】如图是一个算法的流程图，当输入的值为3时，输出的结果为__________．方法提炼利用选择结构解决算法问题时，要引入判断框，要根据题目的要求引入一个或多个判断框．而判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要逐个分析判断框内的条件．请做针对训练2三、算法的循环结构【例3】(2012江苏南京高三模拟)在如图所示的流程图中，若输入n的值为11，则输出A的值为__________．方法提炼利用循环结构表示算法，第一要确定是利用当型循环结构，还是直到型循环结构；第二要选择准确的表示累加的变量；第三要注意在哪一步开始循环．请做针对训练1对流程图的考查有两种常见题型：一是补齐流程图的条件；二是理解流程图的功能，得到输出结果．因此，读懂流程图是解答本节内容的关键．分析江苏近三年的试卷，每年都有一道算法的填空题．要求理解流程图的功能，得到输出结果，难度不大．1．流程图如图所示，如果输入x＝5，则输出的结果为________．2．已知函数y ＝⎩⎪⎨⎪⎧－1，x >0，0，x ＝0，1，x <0.写出求该函数的函数值的算法及流程图．3．计算下面梯形的面积：上底为3，下底为7，高为6，试设计该问题的算法，并画出流程图．参考答案基础梳理自测 知识梳理1．(1)机械的 统一的(2)有限步骤内 明确定义的 可行的 (3)一个确定 解答 没有解答2．图框 操作的类型 操作的内容 操作的先后次序 3．(1)若干个依次执行的处理步骤(3)重复执行同一操作 循环体 当型循环 直到型循环 基础自测1．计算总分D ←A ＋B ＋C 计算平均成绩E ←D32．求积是624的相邻两个偶数 24 263．y ＝⎩⎪⎨⎪⎧x －2，x >1，2x，x ≤14．1 解析：若x ＜0，得x ＝2，不成立．若x ≥0，得x ＝1，所以x ＝1. 5．20考点探究突破【例1】 解：算法如下：第一步 输入x 0，y 0及直线方程的系数A ，B ，C ； 第二步 计算Z 1＝Ax 0＋By 0＋C ；第三步 计算Z 2＝A 2＋B 2；第四步 计算d ＝|Z 1|Z 2；第五步 输出d . 流程图如图所示．【例2】10 解析：∵3＜5，∴执行流程图中的“Y ”，即y ＝32＋1＝10.【例3】13 解析：经计算A 值是以－3，－12，13，2为一个周期循环的，当i ＝10时，A＝－12，10＜11；i ＝11，A ＝13，退出循环，输出A ＝13.演练巩固提升 针对训练1．325 解析：第1次运行后，x ＝5×3－2＝13＜200；第2次运行后，x ＝13×3－2＝37＜200；第3次运行后，x ＝37×3－2＝109＜200；第4次运行后，x ＝109×3－2＝325＞200，故输出的结果为325.2．解：算法如下：S1 输入x ；S2 如果x ＞0，则y ←－1，如果x ＝0，则y ←0，如果x ＜0，则y ←1；S3 输出函数值y .流程图如下图所示．3．解：算法如下：S1 输入a ，b ，h ；S2 S ＝12(a ＋b )·h ； S3 输出S .流程图为：。

第101课时 算法的含义及流程图
[复习巩固]
1、运行如图所示的程序，其输出结果为__________
2、右边的流程图最后输出的n 的值是________
3、五个用流程图表示的算法如图所示，则其运行后输出的结果为___________
4、已知伪代码如图，则输出的结果S=_________
5、一个算法的流程图如下图所示，则输出S 为_________
6、如图给出的是计算
20
1614121++++ 的值的一个程序框图，其中判断框内应填入的条件是________
[典型例题]
例1：根据如图所示的算法流程图，可知输出的结果i 为________
_________
例3：定义函数CONRND（a，b）是产生区间（a，b）内的任何一个实数的随机数函数，如图所示的程序框图可用来估计π的值。

现在N输入的值为100，结果m的输出值为21，则由此可估计π的近似值为______
[巩固练习]
1、如果执行右面的程序框图，那么输出的S=______
2、阅读下列程序：
输出的结果是______
3、如果执行下面的程序框图，那么输出的S=________
4、某算法的伪代码如图所示，如果输出的y值是4，那么输入的x的所有可能值是_______
5、计算机执行如图所示程序后，输出的结果是________
6、如图，将一个体积为27cm2的正方体木块表面涂上蓝色，然后锯成体积为1 cm3的小正方体，从中任取一块，则这一块恰有两面涂有蓝色的概率是________。