下载文档原格式
弧垂计算简易公式弧垂是指从圆弧上某一点到弦线的垂线长度，是在工程测量中常用的一种计算方法。
弧垂计算简易公式是指通过一定的公式计算出弧垂的长度，本文将详细介绍弧垂计算的公式及其应用。
一、弧垂计算公式弧垂计算公式是通过圆弧的半径、圆心角和弦长来计算弧垂的长度。
具体公式如下：h = R - Rcosθ其中，h表示弧垂的长度，R表示圆弧的半径，θ表示圆心角的大小（单位为弧度）。
这个公式的推导过程比较简单，可以通过以下步骤得到：1. 画出圆弧和弦线，并标出圆心角θ。
2. 连接圆心和圆弧上的某一点，得到垂线。
3. 根据正弦定理可得：sin(θ/2) = h/2R4. 化简得：h = 2Rsin(θ/2)5. 再根据半角公式可得：sin(θ/2) = cos(π/2 - θ/2)6. 代入上式得：h = 2Rcos(π/2 - θ/2)7. 化简得：h = R - Rcosθ这就是弧垂计算的简易公式。
二、弧垂计算的应用弧垂计算的应用非常广泛，特别是在道路、铁路、桥梁等工程建设中。
下面以道路工程为例，介绍弧垂计算的应用。
在道路工程中，弧垂常用于计算曲线的设计和施工。
曲线是指道路中的弯道，它的设计和施工需要考虑到车辆的行驶安全和舒适性。
曲线的设计需要满足一定的几何条件，其中之一就是弧垂的限制。
具体来说，曲线的设计需要满足以下条件：1. 曲线的半径不能太小，否则车辆容易失控。
2. 曲线的弧垂不能太大，否则车辆行驶不稳定。
3. 曲线的长度不能太长，否则车辆行驶时间过长。
因此，在曲线的设计中，需要根据车辆的行驶速度、车辆类型和道路的地形条件等因素，计算出合适的曲线半径和弧垂。
具体计算方法如下：1. 根据车辆的行驶速度和车辆类型，确定曲线的设计速度。
2. 根据曲线的设计速度和地形条件，确定曲线的最小半径。
3. 根据曲线的最小半径和设计速度，计算出曲线的最大弧垂。
4. 根据曲线的最大弧垂和设计速度，计算出曲线的最大长度。
5. 根据曲线的最小半径、最大弧垂和最大长度，确定曲线的具体形状。
f D-----代表档距弧垂（m）L D-----代表档距（m）L观-----观测档档距【实际（m）】『θ为仪器看对面一基挂线点的角度』挂点高差：Φ=tg-1（h/L观）注：h为基与基的高差。
f =f D/(cosΦ)＊（L观/L D）2注：一般在弧垂资料上有个计算公式。
a =呼高—塔尺读数—瓷瓶长度注：当在耐张塔看弧垂时就不减瓷瓶长。
b =（2f—a）2c =（2f—a）注：当c为负值时弧垂看不到。
检查公式f =1/4×｛a＋)tgL｝2注：tgθ为挂线点，tgΦ为观tgθ—(*Φ弧垂切点计算代表弧垂（f D-----代表档距弧垂（m））1、在综合表找查数据。
2、要把地线，导线分开.不要搞混。
计算！（如：观测档距为220m）在表中找到220m左右的数据来进行计算。
例：在表中找到220m档距左右的数据分别为.200（0.5），250(0.7)设：220（X ） 如下：（200）（0.5）、(220)(X)、（250）（0.7） 5.0200220--X =X --7.0220250 求出X 值，X 就是F d（1）在孤立档ΔL=L316f ×Δf f —观测档设计弧垂。
Δf —弧垂变量（弧垂大为正，小为负）（需要调整的数）（2）在连续档ΔL=16L db 2×f c /(3L c 4)×Δf c ×ΣL （备用） L c —观测档的档距。
f c —观测档要求的弧垂。
Δf c --观测档的弧垂变量（大为正，小为负）（同上Δf ） ΣL —紧线段长度L db —代表档距ΔL=8 L db 2/3L C 4×(2f c ×Δf c ＋Δf c 2)×ΣL （专用）。
档外角度法档外角度法观测弧垂是将仪器架设在观测档外某处较高位置、中相导线正下方观测弧垂，如图4-4（a ）、（b ）所示。
调整架空线张力，使架空线稳定时的弧垂与经纬仪的弧垂观测垂直角θ的视线相切，弧垂即为测定。
档外角度法观测角θ，悬链线式按下式计算：11a b htg l l θ--±=+（4-8）抛物线式按下式计算：()()(){}21222211484881616/tghl lf l f hl lf l f hf af f h l l θ-⎡⎤=±--+±--+±+--⎢⎥⎣⎦（4-9）式中θ——档外经纬仪垂直观测角度值（正值表示仰角，负值表示俯值）a ——悬挂点A 下垂线至档外经纬仪横轴中心的垂直截距，m ；b ——档外经纬仪视线A 1B 1对于悬挂点B 下垂线的垂直截距，m ；h ——观测档的两悬挂点高差（经纬仪侧的悬挂点A 较低时，其前的“±”号只取+号；经纬仪侧的悬挂点A 较高时，其前的“±”号只取-号），m ；l ——观测档的档距，m ；iiBL L 1a 1Aθfab(a)hLL 1θaABbha 1(b)f图4-4 档外角度法观测弧垂1l ——架空线中线下方档外弧垂观测点至A 点的水平距离，m ；f ——观测档的弧垂值，m 。
测算方法和观测步骤如下：（1）、（2）测定方法与档内角度法相同；（3）、a 、h 值可以从平断面图和铁塔结构图中查出，但现场应复核，测法见图4-5。
高差按下式计算：12a l tg ϕ=（4-10）()11h l l tg a ϕ=+- （4-11）式中2ϕ、1ϕ——分别为观测A 、B 悬挂点的垂直角；（4）、根据已知的1l 、l 、f 、h 及a 的数据，按式（4-8）或（4-9），即可算出弧垂观测角θ值；（5）、弧垂观测方法与档端角度法相同，但须注意，因仪器正在架空线的下方，在紧线时，应防止架空线起落碰撞观测人员和仪器。
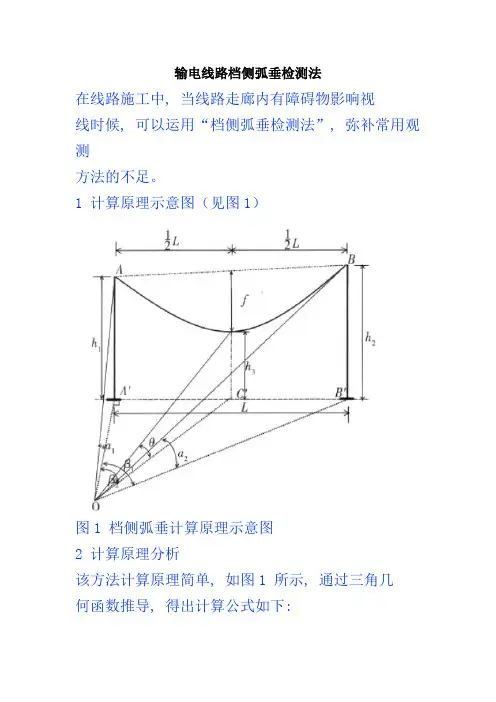
输电线路档侧弧垂检测法
在线路施工中, 当线路走廊内有障碍物影响视
线时候, 可以运用“档侧弧垂检测法”, 弥补常用观测
方法的不足。
1 计算原理示意图（见图1）
图1 档侧弧垂计算原理示意图
2 计算原理分析
该方法计算原理简单, 如图1 所示, 通过三角几
何函数推导, 得出计算公式如下:
式中L———观测档档距;
2 实际操作方法简介
2.1 把经纬仪置于垂直于铁塔侧面2 倍塔高以外
的地方, 最远距离不限, 以镜头能看清导地线为宜。
2.2 调整仪器位置, 使仪器竖丝对穿铁塔左右侧中心螺栓或左右侧挂点螺栓为准, 证明仪器垂直于铁塔中心桩侧面。
2.3 分别测出a1、a2 和β1
, 然后根据公式便可计算
出弧垂值f 或观测角θ, 用以观测或检查弧垂。
3 实际应用分析
3.1 误差分析: 本方法和其他方法一样, 也会受到仪器位置和观测角度偏差等的影响, 但是由于本方法弧垂观测点在档距中央, 即导地线弧垂点上, 所以
观测更为精确。
通过多次测量对比证明, 本方法受误差因素影响相对较小, 完全能够满足施工需要。
3.2 在本方法公式基础上稍加变动, 也可用于检测相邻下一档的弧垂, 此方法适用于观测档外地形不便时, 把仪器置于前一档或下一档铁塔侧面即可。
3.3 根据本方法的计算原理, 可以测量档内导线任意距离点的位置, 非常适合导线间隔棒检查、安装, 从而避免了间隔棒安装在高空测量的不便和危险。
用这种方法检查安装间隔棒已经在施工中应用, 并取得了良好效果。
3.4 本方法缺点: 不能进行导线子线间超平观测, 只能逐个检测每一根导线, 或按扇形面估测, 在这方面增加了工作量。
一、前言架空线路设计和施工都需要进行导线力学计算．笔者编制了导线应力、弧垂计算的BASIC 程序，用户只需按屏幕显示的表格键入导线参数、气象条件，计算机即能完成计算全过程，并将计算结果打印制表。
各种计算项目采用菜单选择，用户使用非常方便。
本文就该程序的设计方法及特点作一简单介绍，以供参考．二、架空导线应力、孤垂的计算机算法1．导线比载计算导线的综合比载是垂直比载（自重、冰重）、水平比载（风压）的矢量和．对各种气象情况的综合比载可用下式表示：式中：q——导线的单位重量（千克／千米）S——导线的计算截面（毫米2）d——导线的计算外径（毫米）b——导线覆冰厚度（毫米）v——设计风速（米／秒）C——风荷载体形系数，当线径d＜17毫米时，C=1.2，当线径≥17毫米时，C=1.1；覆冰时不论线径大小C=1.2α——风速不均匀系数，根据不同风速取值。
（程序框图略）2．临界档距计算及有效临界档距判别根据工程需要，导统应力孤垂的计算项目有时多达十种，即最大风速、覆冰情况、安装情况、事故断线、最低气温、最高气温、外过电压（有风、无风）、内过电压、平均气温。
这十种情况对应十种气象条件．但导线选用应力的控制条件只可能是其中的4种情况，即最低气温、最大风速、覆冰情况和平均气温．这4种控制条件的两两组合有6个临界档距。
一般地n种控制条件有=n(n－1)／2个临界档距，其中有效临界档距有0～（n—1）个。
两个控制条件的临界档距为式中：E——导线弹性模数（千克／毫米２）a——导线温度线膨胀系数（l／℃）δi、δj——两种控制条件的限定应力（最大使用应力或年平均运行应力上限）（千克／毫米２）ti、tj——两种控制条件的气温（℃）gi、gj——两种控制条件的比载（千克／米•毫米２）。
由式（2－1）可知，若将n个控制条件的g／δ值由小到大排列，再比较各δ＋aEt，并满足下式：不满足式（2－2）的控制条件不起作用舍去。
当两种控制条件的g／δ相同时，舍去δ＋aEt 较大者；若两者的δ＋aEt相同，舍去g／δ较小者，则所有满足式（2－2）的控制条件均有实数解的临界档距，把满足（2－2）式的控制条件由小到大编为序号1、2、3、…c（c≤n），并相应建立C－l个临界档距数栏。
100弧垂=（观测档距÷100）2 ×代表档距所查数据弧垂=（观测档距÷代表档距）2 ×代表档距所查数据线线6：导线、避雷线弧垂：最大误差÷标准弧垂代表档距L= (a13+a23+a33)÷(a1+ a2+a3) a表示档距弧垂量：导线长度比：100米约1米；《要求观测档弧垂=(要求观测档档距/已知观测档档距)2×已知观测档弧垂》转角塔倾斜率：（10°内）3‰；（10°—30°）4‰；（30°—60°）7‰；（60°—90°）9‰；倾斜率×视点=整数÷视点=倾斜值倾斜值= 一个数值2+另一个数值2根开×倾斜率=要求垫的高度观测档：耐张段超过5档，要求用2个观测档耐张段超过12档，要求用3个观测档交叉点净距：测量得出D（米）、∠1（度）、∠2（度）[Tan(∠1-270°)—Tan(∠2-270°)]×D换算至最高温度时的净距/温度=交叉点净距—{[（要求档档距/观测档档距）2×（观测档10°弧垂—观测档0°弧垂）]/10}×39《角度换算：例10°23，44，，计算机上用10.2344然后（→DEG）键换算。
》线线6：实测弧垂最大值，相间偏差为0；其于的减弧垂最大值。
220kV跳线对塔身最近安全距离：不小于2米紧线表格：弧垂误差最大值/标准弧垂=检查栏第三项相间弧垂误差=弧垂误差值下线最大—弧垂误差值下线最小子线间弧垂误差、子线间弧垂=下线不能小于上线接地离变电所2公里内5欧姆，2公里外10欧姆压接：（压后）铝管长度：导线模子测量数据×0.866×0.993＋0.2 (mm) （压后）钢管长度：钢管模子测量数据×0.866×0.993＋0.2 (mm) LGJ—300/25导线直径：23.76mmLGJ—300/25耐张线夹：铝管：长度：400（压前）直径：40 （压后）直径：34.6钢管：长度：90（压前）直径：14 （压后）直径：12.24导线直线压接管：（搭接）铝管：长度：400直径：（压前）40 （压后）34.6钢管：长度：90直径：（压前）20 （压后）17.4地线直线接续管：（LXXGJ—50）钢管：长度：240直径：（压前）18 （压后）15.68LGJ—240/30导线直径：21.6mmLGJ—240/30 导线耐张NY—240/30（压接管）铝管：长度：390直径：（压前）36 压后（31.16）钢管：长度：100直径：（压前）16 压后（13.96）直线接续管：JYD—240/30铝管：长度：460直径：36钢管：长度：100直径：20LGJ—185/25铝：32钢：14240导线有压接，240导线以下用洋枪夹头LGJQ——400/50 比重： 1.511米/公斤LGJ——240 比重：0.922米/公斤LGJ——185 比重：0.7326米/公斤基础：L（线净长）+（8f平方（弧垂）/3L）=所得长度扣除两端金具串工程施工项目问题一、开工第一步1、施工组织措施2、算出材料用量3、打出材料表并分配给施工队伍4、线路复测分坑5、基础施工作业指导书6、现浇台阶基础分坑制模尺寸表7、转角塔基础预高值表8、基础配置图9、现浇台阶式基础分坑图10、（基础施工作业指导）书审批表11、监理报审表12、安全协议13、承包合同14、配合比报告15、技术交底记录表16、文件发放登记表立塔计算1、组塔方法：外抱杆、内抱杆、落地抱杆、悬浮抱杆立塔2、计算目的：吊重、抱杆倾角、拉线对地夹角、控制绳对地夹角、垂偏角3、计算对象：控制绳、抱杆、起吊滑车、转向滑车、拉线4、吊重计算：G=1.1×1.2×图重1.1为平衡系数1.2为冲击系数G5以抱杆头为中心，拉线与滑车的连绳的压力TTG N FPxαβ以O点为原点Ex=0 Tsinβ-Pcosα=0 (1)Ey=0 Tcosβ-Psinα-G=0 (2)T=Gcosα/cos(α+β)P=G×sinβ/cos(α+β)α=arctg H1/L1H1为已组立塔高L1为地锚到转向滑车距离6、抱杆力系：精确法O，TZ1=T/n×ηn为工作绳数η为效率2吨千斤套Z2Z0=T/（1+1.05+1.052）1吨物 1.05吨动力（滑轮磨擦系数）滚动磨擦系数为1.015走一走二滑车：n为3 η为0.907。
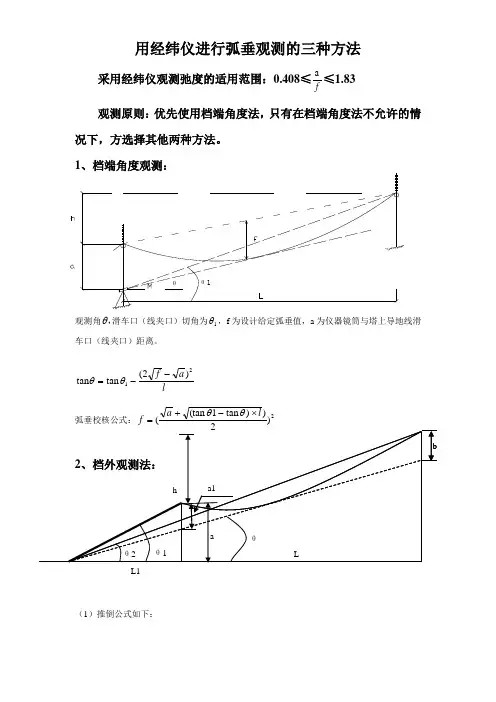
用经纬仪进行弧垂观测的三种方法采用经纬仪观测弛度的适用范围：0.408≤fa ≤1.83观测原则：优先使用档端角度法，只有在档端角度法不允许的情况下，方选择其他两种方法。
1、档端角度观测：观测角，θ滑车口（线夹口）切角为1θ，f 为设计给定弧垂值，a 为仪器镜筒与塔上导地线滑车口（线夹口）距离。
la f 21)2(tan tan --=θθ弧垂校核公式：2)))tan 1(tan (l a f ⨯-+=θθ（1）推倒公式如下：L1 θθ1)3()2(2)(111121111————）—（—θθθθtg L a a F b a a tg L L h tg L a L L ba h tg -==+-+==+-+=将（2）、（3）式代入（1）式得到()[]()[]C B B tg atg L L h tg L a fa h F L C LFL h F L B fa h F tg FL Lh LF tg L -+-=-+==--=+-==--++-+22111221212222)(1641)84(20164)1628(）（令θθθθθ弧垂校核公式：211)2)tan 2tan )()tan 1(tan (θθθθ-⨯++-⨯=（L L L f3、档内观测法：θθ2θ1()[]()[]C B B tg atg L L h tg L a fa h F L C LFL h F L B fa h F tg FL Lh LF tg L -+-=--==--=--==--+--+22111221212222)(1641)84(20164)1628(）（令θθθθθ弧垂校核公式：211)2)tan 2tan )()1tan (tan (θθθθ-⨯-++⨯=（L L L f4、★正弦定理：R ccb b a a 2sin sin sin === ★余弦定理：a c c ab a b b ac b c c b a cab b a c b ac c a b a bc c b a cos cos cos cos cos cos cos 2cos 2cos 2222222222+=+=+=-+=-+=-+=、、。
弧垂计算公式
弧垂计算公式是在测量工程中常用的一种计算方法，用于确定水平线与曲线之间的垂直距离，以便确定工程设计的准确性和可行性。
本文将介绍弧垂计算公式的原理和应用，并结合实例进行说明。
我们来了解一下弧垂计算公式的原理。
在测量工程中，弧垂是指曲线上某一点到其切线的垂直距离。
为了计算弧垂，我们需要利用曲线的半径和曲线的弧长这两个参数。
弧垂计算公式的基本原理是利用曲线的半径和弧长之间的关系来确定弧垂的大小。
具体而言，弧垂计算公式可以表示为：h = (L^2) / (24R)，其中h表示弧垂，L表示弧长，R表示曲线的半径。
根据这个公式，我们可以通过已知的曲线半径和弧长来计算出弧垂的值。
下面我们通过一个实例来说明弧垂计算公式的应用。
假设我们需要在一条半径为100米的曲线上测量弧垂，已知曲线的弧长为50米。
根据弧垂计算公式，我们可以得到：h = (50^2) / (24*100) = 10.42米。
因此，在这个例子中，曲线上某一点到其切线的垂直距离为10.42米。
弧垂计算公式在实际工程中有广泛的应用。
例如，在道路建设中，设计人员需要根据道路的曲线半径和弧长来确定道路的坡度和高差，以确保车辆行驶的安全和舒适性。
此外，在铁路建设中，弧垂计算公式也可以用于确定铁轨的高差和坡度，以确保列车行驶的稳定性
和安全性。
总结一下，弧垂计算公式是一种常用的测量计算方法，通过已知的曲线半径和弧长来确定弧垂的大小。
它在工程设计和建设中起着重要的作用，能够确保工程的准确性和可行性。
希望通过本文的介绍，读者对弧垂计算公式有了更深入的了解。
