波浪作用力公式介绍

波浪力计算公式波浪力是描述海浪对海岸或其他结构物的冲击力的物理量。

它是指海浪作用于单位长度海岸线或结构物上的力量。

波浪力的计算公式可以使用斯托克斯公式来表示。

斯托克斯公式是描述波浪力计算的经典公式，它基于假设波浪是理想的正弦波。

根据斯托克斯公式，波浪力可以表示为：F = 0.5 * ρ * g * H^2 * L其中，F是波浪力，ρ是水的密度，g是重力加速度，H是波高，L 是波长。

波浪力的计算公式可以帮助我们了解海浪对海岸线或其他结构物的冲击程度。

通过计算波浪力，我们可以评估海岸线的稳定性，预测海岸侵蚀的风险，设计合适的防护工程等。

在海岸工程中，波浪力的计算是一个重要的任务。

通过对波浪力的计算，可以确定合适的海岸保护结构的尺寸和类型。

根据波浪力的大小，我们可以选择适当的海岸防护工程，如堤防、防波堤、海堤等，以减轻海浪对海岸的冲击。

除了海岸工程，波浪力的计算在海洋工程和海洋能利用领域也具有重要意义。

在海洋工程中，波浪力的计算可以用于设计海上平台、船舶和海洋结构物的稳定性。

在海洋能利用领域，波浪力的计算可以用于评估波浪能量的潜力和设计波浪能发电设备。

波浪力的计算公式是基于理想的正弦波假设。

然而，在实际情况中，海浪往往是复杂的，包含多种频率和方向的波浪成分。

因此，在实际应用中，需要考虑更复杂的波浪模型和数值方法来计算波浪力。

波浪力的计算公式是描述海浪对海岸线或其他结构物冲击力的重要工具。

它可以帮助我们评估海岸侵蚀的风险，设计合适的海岸防护工程，以及评估海洋工程和海洋能利用的可行性。

通过深入研究波浪力的计算公式，我们可以更好地理解海洋与人类活动的相互作用，保护海岸环境，促进可持续发展。

波浪力计算公式引言：在海洋工程中，波浪力是一个重要的参数，用于估计波浪对结构物的作用力。

波浪力的计算可以通过波浪力计算公式来实现。

本文将介绍波浪力计算公式的原理和应用，并探讨波浪力计算的相关问题。

一、波浪力计算公式的原理波浪力计算公式是根据波浪理论和结构动力学原理推导出来的。

其基本原理是根据波浪的特性和结构物的几何形状，通过计算波浪作用下的压力和力矩，进而得到波浪力的大小和方向。

二、常用的波浪力计算公式1. Morison公式：Morison公式是最常用的波浪力计算公式之一，适用于波浪作用下的柱状结构物。

该公式基于马克思-赫茨伯格(Morison)定律，考虑了波浪作用下的惯性力和阻力。

其表达式为：F = 0.5 * ρ * Cd * A * (dV/dt) + ρ * Cp * A * V * |V|其中，F为波浪力，ρ为水的密度，Cd和Cp分别为阻力系数和惯性系数，A为结构物的横截面积，V为波浪速度，dV/dt为波浪加速度。

2. Goda公式：Goda公式是一种改进的波浪力计算公式，适用于不规则波浪作用下的结构物。

该公式考虑了波浪的频率谱和结构物的响应特性，能更准确地估计波浪力。

其表达式为：F = ∫∫ (0.5 * ρ * Hs * g * S(f) * A * R(f)^2 * |H(f)|^2 * cos(θ))^0.5 df dθ其中，F为波浪力，ρ为水的密度，Hs为波浪高度，g为重力加速度，S(f)为波浪频率谱密度函数，A为结构物的横截面积，R(f)为结构物的响应函数，H(f)为波浪高度频谱密度函数，θ为波浪方向。

三、波浪力计算的应用波浪力计算公式广泛应用于海洋工程中的结构设计和安全评估。

通过计算波浪力，可以评估结构物的稳定性和安全性，为结构物的设计和施工提供依据。

例如，在海上风电场中，需要计算波浪力来评估风机基础的稳定性；在海岸工程中，需要计算波浪力来评估海堤的稳定性。

四、波浪力计算的相关问题1. 如何确定阻力系数和惯性系数？阻力系数和惯性系数是波浪力计算公式中的重要参数，可以通过试验或数值模拟来确定。

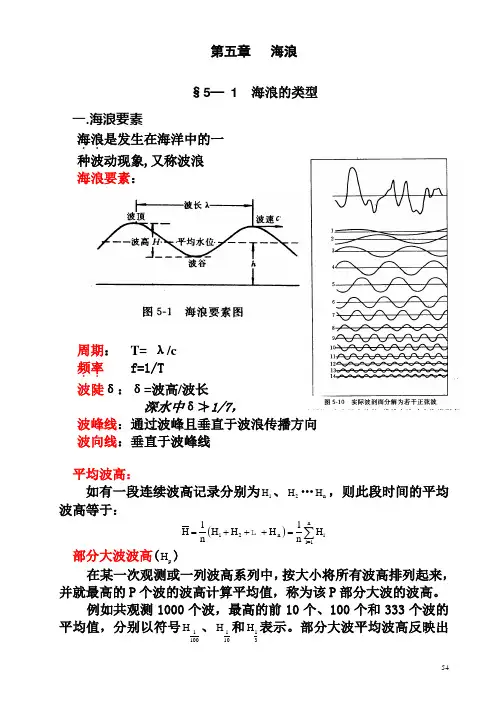
第五章海浪§5— 1 海浪的类型一.海浪要素 海浪．．是发生在海洋中的一 种波动现象,又称波浪 海浪要素：周期： T= λ/c 频率．．f=1/T 波陡δ：δ=波高/波长深水中δ≯1/7，波峰线：通过波峰且垂直于波浪传播方向 波向线：垂直于波峰线平均波高：如有一段连续波高记录分别为1H 、2H …n H ，则此段时间的平均波高等于：()n12n i i=111H H H H H n n =+++=∑L 部分大波波高(p H )在某一次观测或一列波高系列中，按大小将所有波高排列起来，并就最高的P 个波的波高计算平均值，称为该P 部分大波的波高。

例如共观测1000个波，最高的前10个、100个和333个波的平均值，分别以符号1100H 、110H 和13H 表示。

部分大波平均波高反映出海浪的显著部分或特别显著部分的状态。

习惯上将13H称为有效波高（或称有义波高）。

最大波高maxH：指某次观测中，实际出现的最大的一个波高。

各种波高间的换算111100103H H H2.663, 2.032,1.598H H H===111100100101111033H H H1.311,1.666,1.272H H H===二.海浪运动机理深水：水质点以近似于圆形的轨道作圆周运动运动半径：随着水深的增加而减小h=λ/2时;r↓→4% r0（r0=a）浅水：（h＜λ/20）运动波及海底。

三.海浪的分类1.按海水深度分深度深: 表面波（深水波）：h↑→r↓深度浅: 长波（浅水波h＜λ/20）运动波及海底。

2.按周期分3.按生成原因分：．．．．．．．风浪、潮波、海啸4.按受力情况分：自由波：涌浪受迫波：潮波5.按波形前进与否分：进行波；驻波。

6.按边界条件分①微小振幅波H/λ很小，H可忽略所有运动方程式都是线性的。

②有限振幅波：H不可忽略a.斯托克斯波有“质量运移”b.孤立波H/λ＜1/10; 运动集中在波峰附近c.摆线波7.内波§5—2 海浪的形成一.海浪形成假说(1)形成毛细波(2)风以法向压力形式给波浪传递能量(3)空气小涡流加强了水质点的运动(4) 波长较短的波由风取得能量转给波长较长的波二、海浪的消衰1.分子粘滞性消耗的能量2.涡动消耗能量3.空气的阻力4.海底摩擦5.波浪破碎三.海浪的状态1.海浪三要素风速：大于0风时：状态相同的风作用的时间风区：状态相同的风作用的海区风大不一定浪大．．．．．．．2.定常状态风区一定，海浪达最大；风区增加，海浪高度增加；风区是限制因素。

波浪力计算公式引言：波浪力是指波浪对于物体施加的力量，它是海洋工程中一个重要的参数。

通过对波浪力进行准确的计算，可以帮助我们设计和构建海洋结构物，预测其受力情况，从而确保结构的安全性和稳定性。

本文将介绍波浪力的计算公式及其应用。

一、波浪力的定义波浪力是波浪作用在物体上的力量，它的大小与波浪的高度、周期、波浪传播方向以及物体的形状和尺寸等因素有关。

波浪力的计算是海洋工程中的一个重要问题，也是一项挑战性的任务。

二、波浪力的计算公式波浪力的计算公式可以用以下公式表示：F = 0.5 * ρ * g * H^2 * L其中，F为波浪力，ρ为水的密度，g为重力加速度，H为波浪高度，L为波长。

三、波浪力的应用波浪力的计算在海洋工程中有着广泛的应用。

例如，在设计海洋平台、堤坝、海底管道等结构物时，需要考虑波浪对这些结构物施加的力量。

通过使用波浪力计算公式，可以预测结构物在不同波浪条件下的受力情况，从而指导工程设计和施工过程。

在海洋工程中，波浪力的计算还可以用于预测海洋结构物的疲劳寿命。

由于波浪力是结构物受力的主要因素之一，通过对波浪力进行准确的计算，可以评估结构物的疲劳损伤程度，为结构物的维护和修复提供依据。

波浪力的计算还可以应用于海洋能利用领域。

波浪能和潮汐能是海洋能资源中的两个重要组成部分。

通过准确计算波浪力，可以评估波浪能装置的性能和效益，为海洋能的开发和利用提供科学依据。

四、波浪力计算的挑战和改进尽管波浪力的计算公式已经相对成熟，但在实际应用中仍然存在一些挑战。

例如，波浪力的计算需要准确测量波浪的高度、周期和波长等参数，这对于海洋工程来说是一项技术难题。

另外，波浪力的计算还需要考虑波浪与结构物之间的相互作用，这也增加了计算的复杂性。

为了解决这些问题，研究人员正在不断改进波浪力的计算方法。

一方面，他们致力于改进波浪参数的测量技术，例如利用遥感技术和数值模拟方法来获取更准确的波浪参数。

另一方面，他们还在研究波浪与结构物之间的相互作用机理，以提高波浪力计算的准确性。

波浪激励力的表达式
【原创版】
目录
1.波浪激励力的概念
2.波浪激励力的表达式推导
3.波浪激励力的应用
正文
一、波浪激励力的概念
波浪激励力，是指在海洋工程、船舶工程等领域中，用于描述波浪对物体作用力的一种力。

在实际应用中，波浪激励力会导致结构物的振动和疲劳损伤，因此研究波浪激励力具有重要意义。

二、波浪激励力的表达式推导
波浪激励力的表达式通常由波浪的统计特性和物体的运动特性共同
决定。

根据线性波浪理论，波浪激励力可以表示为：
F = ∫ρg(t) * ∫(u/t) * cos(k * x - ω * t) dk dt
其中，F 表示波浪激励力，ρ表示水的密度，g(t) 表示波浪的加速度，u 表示物体的位移，k 表示波浪的波数，ω表示波浪的角频率，t 表示时间。

三、波浪激励力的应用
波浪激励力的表达式在海洋工程、船舶工程等领域具有广泛的应用。

例如，在设计海上平台时，需要根据波浪激励力计算结果，选择合适的抗风浪措施，以保证平台的稳定性和安全性。

此外，波浪激励力计算结果还可以用于评估船舶在波浪中的航行性能和结构强度。

第1页共1页。

波浪计算公式(二)波浪计算公式1. 波长计算公式•公式：波长（λ） = 速度（v） / 频率（f）•示例：如果一个波的速度是10m/s，频率为5Hz，那么波长可以计算为：λ = 10m/s / 5Hz = 2m2. 频率计算公式•公式：频率（f） = 速度（v） / 波长（λ）•示例：假设波的速度是15m/s，波长为3m，那么频率可以通过以下计算得到：f = 15m/s / 3m = 5Hz3. 速度计算公式•公式：速度（v） = 波长（λ） * 频率（f）•示例：当波长为4m，频率为2Hz时，速度可以计算如下：v = 4m * 2Hz = 8m/s4. 能量计算公式•公式：能量（E）= 振幅（A）^2 * 密度（ρ） * 波速（v） * 波速（v）•示例：如果振幅为3，密度为2kg/m^3，波速为10m/s，那么能量可以通过以下方式计算：E = (3)^2 * 2kg/m^3 * 10m/s *10m/s = 900 J5. 群速度计算公式•公式：群速度（v_g）= 速度（v） / 折射率（n）•示例：假设波的速度为20m/s，折射率为，那么群速度可以计算如下：v_g = 20m/s / = /s6. 相速度计算公式•公式：相速度（v_p）= 波长（λ） * 频率（f）•示例：如果一个波的波长为6m，频率为3Hz，那么相速度可以通过以下公式计算：v_p = 6m * 3Hz = 18m/s7. 相位差计算公式•公式：相位差（Δφ）= 2π * (距离（d）/ 波长（λ）)•示例：当两个波的距离为4m，波长为2m时，相位差可以通过以下公式计算：Δφ = 2π * (4m / 2m) = 4π8. 反射率计算公式•公式：反射率（R）= (电磁波的反射强度) / (电磁波的入射强度)•示例：如果电磁波的反射强度为10 W/m^2，入射强度为5 W/m^2，那么反射率可以计算如下：R = 10 W/m^2 / 5 W/m^2 = 2以上是一些与波浪计算相关的公式和示例解释。

2 波浪荷载的计算理论2.1 直墙上的波浪力（1）直墙上的立波浪力二阶浅水立波的波压力公式：222()1()sin 2[1(32)cos 2]41(csc 22cos 2)2ch z kd ch z kd p z AA cth kd cth kd chkd chkd A h kd cth kd ωτωτωτ++=-+-+-++令 kd →∞，得二阶深水立波的波压力公式：22211sin cos 2(1cos 2)24z z p z Ae A A e ωτωτωτ=-++-+ （2）直墙上的破波浪力1）远破波的波压力计算在静水面以上高度为H （推进波的波高）处得波压力为0，静水面处得波压力P s 为12s p K K H γ=其中 γ——海水容重1K ——与海底坡度i 有关的系数2K ——与坡坦有关的系数在静水面以上的波浪力的分布按直线变化。

在静水面以下z=H/2处得波浪附加应力P s 为0.7z s p p =在墙底处的波浪附加压力P d 为当d/H ≤1.7时，0.6d s p p =当d/H>1.7时，0.5d s p p =墙底面上的波浪浮托力P u 为2d u bp p u = （b 为墙底宽度，u 为波浪浮托力分布图的折减系数，可取0.7） 2）近破波的波压力计算静水面处得波压力P s 为：当2/3≥d 1>1/3时，111.25(1.80.16)(10.13)s H H p H d d γ=--； 当1/3≥d 1≥1/4时，1111.25[(13.936.4)(0.67) 1.03](10.13)s d H H p H d d d γ=--+-。

在墙底处的波浪附加压力P d 为0.6d s p p =在计算单位长度堤身上的近破波的总波浪力P 时运用下面的公式：当2/3≥d 1>1/3时，11.25(1.90.17)s H p H d γ=-；当1/3≥d 1≥1/4时，1111.25[(14.838.8)(0.67) 1.1]s d H p Hd d d γ=--+。

波浪对桩柱作用力的计算分析港口码头、跨海桥梁、海洋工程中经常遇到波浪力对桩柱的作用，水中的桩柱结构所受的水平力主要来自波浪的作用。

对于一般的桩柱结构，当桩柱的直径D与波浪的波长L的比值D/L<0.2时，称此结构为小尺度结构物；当D/L>0.2时，则称为大尺度结构物[1]。

港口码头、跨海桥梁、海洋工程常用的桩柱结构，一般为小尺度结构物，因此本文重点探究小尺度结构物的波浪力计算。

1 波浪力的计算方法国内外对波浪力的计算理论相差不大，都是基于Morison公式[2]內对波浪力的计算主要有《海港水文规范》规定的方法，国外对波浪力的计算有美国的API、挪威的DNV等标准提出的方法。

基于Morison理论的波浪力计算公式如下：（公式-1）（公式-2）（公式-3）上式中：PD是波浪力的速度分力（也叫拖曳力）；PI是波浪力的惯性分力；CD是速度力系数；CM是质量力系数；D是桩柱直径；dz是桩柱上每一小分段的长度；A是桩柱的断面积。

u、u/t——分别为水质点轨道运动的水平速度和水平加速度；是圆频率；t是时间，当波峰通过柱体中心线时t=0；H、T分别是波高和波周期。

美国的API规范给出拖曳力系数取0.6～1.0，惯性力系数取2.0。

国内的《海港水文规范》给出拖曳力系数取1.2，惯性力系数取2.0。

《海港水文规范》提出的拖曳力系数和惯性力系数比较适合我国的情况，因此本文以《海港水文规范》给出拖曳力系数1.2、惯性力系数2.0进行波浪力计算。

2 波浪力随高度和时间的变化趋势本文模拟了一个我国东部沿海的项目的桩基，该项目水深10m，采用垂直的钢管桩，桩体直径2.5m。

计算海浪的波长72m，波高3.9m，波周期7.8s。

采用Excel对周期T内的各时间点、沿桩柱各高度的拖曳力和惯性力的分力分别进行计算，然后用数值积分的方法将各分力沿桩柱高度进行积分，得出各时间点作用在桩柱上的波浪力的合力。

为考察波浪力随桩体高度变化趋势，按照公式1～3，将桩体在平均海平面以上分为10等份，在平均海平面以上分为2等份，进行拖曳力和惯性力计算。