波浪作用力计算

3.2.1 风、水流和波浪对浮体产生的作用力风、水流和波浪对浮体产生的作用力参照前苏联《波浪、冰凌和船舶对水工建筑物的荷载与作用》计算。

（1）风对浮体作用的横向分力和纵向分力见3.2.1.1。

（2）水流对浮体作用的横向分力和纵向分力水流对浮体作用的横向分力和纵向分力按以下公式计算：20.59x x x F A v =20.59y y yF A v = 式中：F x 、F y —趸船计算水流力的横向分力和纵向分力(kN)；A x 、A y —浮趸水下横向和纵向阻水面积(m 2)； v x 、v y —设计水流流速的横向和纵向分量(m/s)。

浮趸水面以下的阻水面积计算：A x =45×0.6=27m 2； A y =7×0.6=4.2m 2 作用在趸船上的水流力：20.5927 1.5538.27kN x F =⨯⨯=20.59 4.2 1.55 5.95kN y F =⨯⨯= （3）波浪对浮体的作用力波浪对浮体的横向分力和纵向分力按以下公式计算：1x x Q ghA χτρ= y y Q ghA χρ=式中：Qx 、Qy —趸船计算波浪力的横向分力和纵向分力(kN)； χ—系数，按图3-1取用，图中ds 为浮趸吃水，ds=0.6m ；τ1—系数，按表1-3.6取用，表中αl 为浮体水下部分纵向轮廓的最大水平尺寸（m ），取αl=45m ；h —取H5%波高，h=1.3m ；Ax 、Ay —浮趸水下横向和纵向阻水面积(m 2)。

图3-1 系数χ值的曲线图表1-3.1 系数τ1/0.6/200.03s d λ==，根据图3-1， 取χ=0.85。

/48.6/20 2.25l αλ==，根据表1-3.6，取τ1=0.48。

χ作用在趸船上的计算波浪力：10.850.48 1.0259.8 1.327146.79kN x x Q ghA χρ==⨯⨯⨯⨯⨯=τ 0.85 1.0259.8 1.3 4.222.83kN y y Q ghA χρ==⨯⨯⨯⨯=风、水流和波浪对浮趸的作用力计算结果见表1-3.7。

波浪力的计算需要两方面理论的支持：波浪运动理论及波浪荷载计算理论。

前者研究波浪的运动，后者在已知波浪运动的前提下计算波浪对水中物体的作用。

几种常用的波浪普： 1.P-M 谱Pierson 和Moskowitz适用于无限风速发在的波浪普。

国际船模水池会议（ITTC）推荐采用这一形式的波，故也称为ITTC波谱。

JONSWAP（Joint north sea wave project）.是一种频谱。

3.应力范围的长期分布模型：1.离散型模型，2.分段连续型模型，3.连续模型。

1. 离散模型:用Hs作为波高，Tz为波浪周期，定义一个余弦波。

然后用规则波理论计算作用在结构上的波浪力。

并用准静定的方法计算结构呢I的应力。

缺陷：没有将波浪作为一个随机过程来处理。

每一海况的应力范围只有一个确的数值。

因此又称为确定性模型。

2.分段连续型模型每一短期海况中，交变应力过程是一个均值为0的平稳正态过程。

综合所有海况中应力范围的短期分布，并得出各个海况出现的疲劳，就得到应力范围的长期分布，它的形式是分段连续的。

应力范围的两种短期分布模型：1.Rayleigh分布和Rice分布。

在某一海况中交变应力均值为。

应力峰值服从Rayleigh分布。

通过计算得出应力范围也服从Rayleigh分布。

3.在船舶及海洋工程结构疲劳可靠性分析中，希望应力范围的长期分布能用一个连续的分布函数来描述。

这就是应力范围长期分布的连续模型.最常用的就是Weibull分布。

4.有义波高：（significant wave height）所有波浪中波高最大的三分之一波浪的平均高度。

用Hs表示。

5.Stokes五阶波给出了波陡的量度（H/L）H/L越大，波就越陡。

当波高与波长的比值大到一定程度时，波会破碎。

6.波速=波长与频率的乘积 C=λ/T或者C=λf,其中f是频率。

或者T=2π/ω7.圆频率1.圆频率即2π秒内振动的次数，又叫角频率，和角速度的ω没有任何关系。

波浪力计算公式波浪力是描述海浪对海岸或其他结构物的冲击力的物理量。

它是指海浪作用于单位长度海岸线或结构物上的力量。

波浪力的计算公式可以使用斯托克斯公式来表示。

斯托克斯公式是描述波浪力计算的经典公式，它基于假设波浪是理想的正弦波。

根据斯托克斯公式，波浪力可以表示为：F = 0.5 * ρ * g * H^2 * L其中，F是波浪力，ρ是水的密度，g是重力加速度，H是波高，L 是波长。

波浪力的计算公式可以帮助我们了解海浪对海岸线或其他结构物的冲击程度。

通过计算波浪力，我们可以评估海岸线的稳定性，预测海岸侵蚀的风险，设计合适的防护工程等。

在海岸工程中，波浪力的计算是一个重要的任务。

通过对波浪力的计算，可以确定合适的海岸保护结构的尺寸和类型。

根据波浪力的大小，我们可以选择适当的海岸防护工程，如堤防、防波堤、海堤等，以减轻海浪对海岸的冲击。

除了海岸工程，波浪力的计算在海洋工程和海洋能利用领域也具有重要意义。

在海洋工程中，波浪力的计算可以用于设计海上平台、船舶和海洋结构物的稳定性。

在海洋能利用领域，波浪力的计算可以用于评估波浪能量的潜力和设计波浪能发电设备。

波浪力的计算公式是基于理想的正弦波假设。

然而，在实际情况中，海浪往往是复杂的，包含多种频率和方向的波浪成分。

因此，在实际应用中，需要考虑更复杂的波浪模型和数值方法来计算波浪力。

波浪力的计算公式是描述海浪对海岸线或其他结构物冲击力的重要工具。

它可以帮助我们评估海岸侵蚀的风险，设计合适的海岸防护工程，以及评估海洋工程和海洋能利用的可行性。

通过深入研究波浪力的计算公式，我们可以更好地理解海洋与人类活动的相互作用，保护海岸环境，促进可持续发展。

波浪力计算公式引言：在海洋工程中，波浪力是一个重要的参数，用于估计波浪对结构物的作用力。

波浪力的计算可以通过波浪力计算公式来实现。

本文将介绍波浪力计算公式的原理和应用，并探讨波浪力计算的相关问题。

一、波浪力计算公式的原理波浪力计算公式是根据波浪理论和结构动力学原理推导出来的。

其基本原理是根据波浪的特性和结构物的几何形状，通过计算波浪作用下的压力和力矩，进而得到波浪力的大小和方向。

二、常用的波浪力计算公式1. Morison公式：Morison公式是最常用的波浪力计算公式之一，适用于波浪作用下的柱状结构物。

该公式基于马克思-赫茨伯格(Morison)定律，考虑了波浪作用下的惯性力和阻力。

其表达式为：F = 0.5 * ρ * Cd * A * (dV/dt) + ρ * Cp * A * V * |V|其中，F为波浪力，ρ为水的密度，Cd和Cp分别为阻力系数和惯性系数，A为结构物的横截面积，V为波浪速度，dV/dt为波浪加速度。

2. Goda公式：Goda公式是一种改进的波浪力计算公式，适用于不规则波浪作用下的结构物。

该公式考虑了波浪的频率谱和结构物的响应特性，能更准确地估计波浪力。

其表达式为：F = ∫∫ (0.5 * ρ * Hs * g * S(f) * A * R(f)^2 * |H(f)|^2 * cos(θ))^0.5 df dθ其中，F为波浪力，ρ为水的密度，Hs为波浪高度，g为重力加速度，S(f)为波浪频率谱密度函数，A为结构物的横截面积，R(f)为结构物的响应函数，H(f)为波浪高度频谱密度函数，θ为波浪方向。

三、波浪力计算的应用波浪力计算公式广泛应用于海洋工程中的结构设计和安全评估。

通过计算波浪力，可以评估结构物的稳定性和安全性，为结构物的设计和施工提供依据。

例如，在海上风电场中，需要计算波浪力来评估风机基础的稳定性；在海岸工程中，需要计算波浪力来评估海堤的稳定性。

四、波浪力计算的相关问题1. 如何确定阻力系数和惯性系数？阻力系数和惯性系数是波浪力计算公式中的重要参数，可以通过试验或数值模拟来确定。

• 另外，在长期的波浪淘刷之下，刚性护面结构下面的 另外，在长期的波浪淘刷之下， 反滤层很容易被掏空，在此种情况下， 反滤层很容易被掏空，在此种情况下，波浪的冲击力 结合波浪对护面结构的反作用力， 结合波浪对护面结构的反作用力，往往会造成海堤的 最终破坏。因此， 最终破坏。因此，斜坡式采用混凝土板护面层进行强 度设计时，一定要进行波浪作用力的计算。 度设计时，一定要进行波浪作用力的计算。
• 2 计算内容： 计算内容： • 分为直立式护面结构和斜坡式护面结构
的波浪作用力计算。 的波浪作用力计算。
• 3 计算公式来源： 计算公式来源： • 主要来自于《海港水文规范》 主要来自于《海港水文规范》公式和原
苏联规范公式。 苏联规范公式。
正文有关条文的解释和说明 • 6.7.1 海堤工程的波浪作用力计算应采用不 规则波要素作为计算条件， 规则波要素作为计算条件，计算应取堤脚前 波长处的波浪要素， 约 1/2波长处的波浪要素 ， 当堤脚前滩涂坡 波长处的波浪要素 度较陡时，应取靠近海堤堤脚处的波浪要素。 度较陡时，应取靠近海堤堤脚处的波浪要素。 堤前波浪要素应按第6.1节 堤前波浪要素应按第 节 ～ 第 6.4节的规定 节的规定 确定。 确定。 • 6.7.2 波浪作用力可分为直立式护面和斜坡 式护面按附录G.1和附录 和附录G.2计算确定，单一 计算确定， 式护面按附录 和附录 计算确定 坡度陡墙式海堤的波浪作用力， 坡度陡墙式海堤的波浪作用力，可按相关直 立式海堤的公式估算。 立式海堤的公式估算。
• 还有一种情况是陡墙式护面结构下的防浪 墙的稳定也和波浪作用力紧密相关， 墙的稳定也和波浪作用力紧密相关，本节 就是针对此种情况下而制定的。 就是针对此种情况下而制定的。对于陡墙 式护面结构（防浪墙的稳定）、 ）、斜坡式采 式护面结构（防浪墙的稳定）、斜坡式采 用混凝土板护面层进行强度设计时， 用混凝土板护面层进行强度设计时，需进 行波浪作用力的计算。 行波浪作用力的计算。

波浪力计算公式引言：波浪力是指波浪对于物体施加的力量，它是海洋工程中一个重要的参数。

通过对波浪力进行准确的计算，可以帮助我们设计和构建海洋结构物，预测其受力情况，从而确保结构的安全性和稳定性。

本文将介绍波浪力的计算公式及其应用。

一、波浪力的定义波浪力是波浪作用在物体上的力量，它的大小与波浪的高度、周期、波浪传播方向以及物体的形状和尺寸等因素有关。

波浪力的计算是海洋工程中的一个重要问题，也是一项挑战性的任务。

二、波浪力的计算公式波浪力的计算公式可以用以下公式表示：F = 0.5 * ρ * g * H^2 * L其中，F为波浪力，ρ为水的密度，g为重力加速度，H为波浪高度，L为波长。

三、波浪力的应用波浪力的计算在海洋工程中有着广泛的应用。

例如，在设计海洋平台、堤坝、海底管道等结构物时，需要考虑波浪对这些结构物施加的力量。

通过使用波浪力计算公式，可以预测结构物在不同波浪条件下的受力情况，从而指导工程设计和施工过程。

在海洋工程中，波浪力的计算还可以用于预测海洋结构物的疲劳寿命。

由于波浪力是结构物受力的主要因素之一，通过对波浪力进行准确的计算，可以评估结构物的疲劳损伤程度，为结构物的维护和修复提供依据。

波浪力的计算还可以应用于海洋能利用领域。

波浪能和潮汐能是海洋能资源中的两个重要组成部分。

通过准确计算波浪力，可以评估波浪能装置的性能和效益，为海洋能的开发和利用提供科学依据。

四、波浪力计算的挑战和改进尽管波浪力的计算公式已经相对成熟，但在实际应用中仍然存在一些挑战。

例如，波浪力的计算需要准确测量波浪的高度、周期和波长等参数，这对于海洋工程来说是一项技术难题。

另外，波浪力的计算还需要考虑波浪与结构物之间的相互作用，这也增加了计算的复杂性。

为了解决这些问题，研究人员正在不断改进波浪力的计算方法。

一方面，他们致力于改进波浪参数的测量技术，例如利用遥感技术和数值模拟方法来获取更准确的波浪参数。

另一方面，他们还在研究波浪与结构物之间的相互作用机理，以提高波浪力计算的准确性。

Froude-Krylov假定：
F = CFK
C = F = FK + Fd
FK
FK
王 树
• C——绕射系数
青
第中 五章 大尺度结构物上的波浪力
5.1 线性绕射问题
国
海
洋 大
{ 5.1.2 绕射系数和质量系数
学
海
洋
工 程 系
对尺度较小（D/L<0.2)结构物，忽略绕射效应，
海 洋 工 程
C
5.1 线性绕射问题
国
海
洋 大
{ 5.1.1 线性绕射问题的基本方程和边界条件
学
海
洋
工 程 系
求解得到以复数形式表示的绕射波速度势；
将其与己知的入射波速度势线性迭加，可得到扰动后 波动场内任一点总速度势。
海
应用线性化的伯努利方程便可得到结构物表面上的波
洋
工 程
压强分布。
波
浪 力
若不计静压强pgz，则结构物表面上各点的波压强为:
浪
力
学
∑ =
ρgH 2
chkz chkd{[A0a
+
∞
2
m=0
(−1)m
([A2ma
cos2mθ
+
A(2m−1)b
cos(2m
−1)θ)]cosωt
∞
∑ +[A0b + 2 (−1)m([A2mb cos2mθ− A(2m−1)a cos(2m−1)θ)]sinωt} m=0
王 树 青
第中 五章 大尺度结构物上的波浪力
zc2adxo第五章大尺度结构物上的波浪力中国海洋52大直径直立圆柱上的波浪力521maccamy?fuchs公式大学海洋工?程系?海洋工程波浪力学王树青入射波速度势?ighchkzikx?ti2chkde柱坐标系速度势eikxeikrcoscoskrcosisinkrcosghchkzi?i2chkdmjmkrcoszme?itm0c2adxo第五章大尺度结构物上的波浪力中国海洋大学海洋工程系海洋工程波浪力学王树青52大直径直立圆柱上的波浪力521maccamy?fuchs公式?散射波速度势yrx?s1?s1?s?s02222r?rr??r?z222ghchkz?itzs?imbmhmkrcosme2chkdm0chmkrjmkriymkr2adxo第五章大尺度结构物上的波浪力中国海洋大学海洋工52大直径直立圆柱上的波浪力521maccamy?fuchs公式?总速度势程系海洋工程波浪力学王树青ghchkzchkdi?imjmkrcosme?it2m0?ighchkzs?it2chkdmbmhmkrcosmem0xyztixyztsxyzt?ighchkz2chkdmjmkrcosmm0mbmhmkrcosme?itm0第五章大尺度结构物上的波浪力中国海洋大学海洋工程系海洋工程波浪力学王树青52大直径直立圆柱上的波浪力521maccamy?fuchs公式?总速度势ghchkz?imjmkrcosm2chkdm0m0mbmhmkrcosme?it?确定系数bm柱面边界条件urra???i?s???0?rra??r?r?rakajmbm?kahmkrjmghchkz?it?imjmkr?hmkrcosmekr2chkdm0hm第五章大尺度结构物上的波浪力中国海洋大学海洋工程系海洋工程波浪力学王树青52大直径直立圆柱上的波浪力yrx521maccamy?fuchs公式?柱面压强?p??trakajmghchkz?itmjmka?hmkacosmeka2chkdm0hmghchkzma0a2?1a2macos2ma2m?1bcos2m?1cost2chkdm0a0b2?1a2mbcos2m?a2m?1acos2m?1sintmm0第五章大尺度结构物上的波浪力中国海洋52大直径直立圆柱上的波浪力521maccamy?fuchs公式大学海洋工?程系海洋工程波浪力学王树青任意高度z处顺波向的水平波力yrf2hy?0pasina

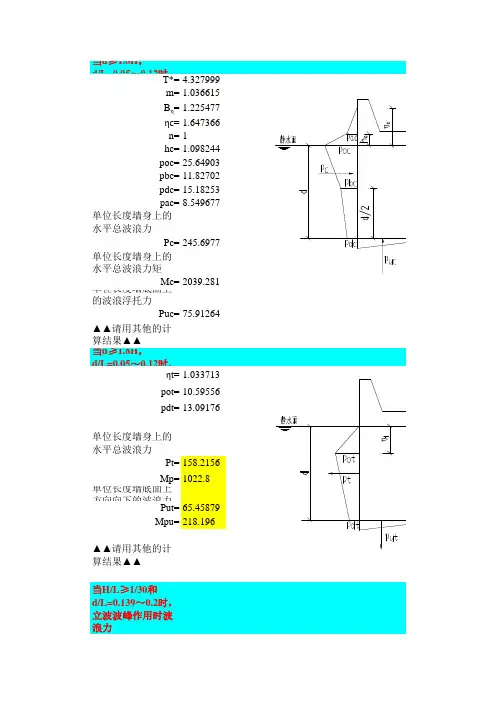
单位长度墙底面上的波浪浮托力Puc=75.91264Mp=Pu=▲▲当H/L≥1/30和0.2<d/L<0.5和d/L≥0.5时的立波波谷波浪力hs=0.169982pd'= 3.393871ps'=13.222680.169982pb'= 3.860429单位长度墙身上的总波浪力P'=111.3689单位长度墙底面上方向向下的波浪力Pu'=19.30215单位长度上波吸力产生的力矩M PB=838.5474单位长度上浮托力产生的力矩M PBU=64.34048※※请用该部分的计算结果※※远破波波浪力波峰作用力计算ps=21.13806pz=14.79664pd=10.56903单位长度墙身上的总波浪力p=188.3507Mp=1446.23墙底面上的波浪浮托力pu=36.99161Mpu=246.6107远破波波浪力波谷作用力计算p=7.4825单位长度墙身上的总波浪力P=97.01061Mp=629.0374近破波波峰作用（d1>=0.6H)Z=7.4591ps=FALSEpb=0单位长度墙身上的总波浪力P=FALSET9H 6.11d12.1APoc0.02901-0.00011 2.140829Pbc0.14574-0.024030.919769Pdc-0.18-0.00015 2.543419BPoc 1.31427-1.20064-0.67369Pbc-3.07372 2.915850.110469Pdc-0.032910.174530.650749qPoc0.037650.46443 2.916989Pbc0.0622 1.32641-2.975579Pdc0.28649-3.8676638.41959波浪力及力矩计算：一、波峰作用波浪压力强度为零处： 4.960mP H＝1331.313M PH＝18250.95P V＝354.7516M PV＝4490.801P U＝19.53622M PU＝130.2414二、波谷作用hs＝0.170m波浪压力强度最大处： 2.040mP H＝787.31M PH＝7263.211P V＝0M PV＝0P U＝19.30215M PU＝128.6811.46波长试算：40.44638840.455.1613.9313.3310I01.251.133.339.827.705480.3443760.413958,2d H<≥21/10H i<，H——立波113dd<≤113dd≤——立波8.1.4.2ηc/d=0.724693072h c/d=0.363360145Pac=12.16547429P0.01686972.5184975 -0.0355746.99529986 -0.220941.26126962 1.0409730.6430940.696269 0.887005 0.642842 0.335617d1/d=0.956927。

波浪的能量与波高的平方、波浪的运动周期以及迎波面的宽度成正比。
波浪能的大小可以用海水起伏势能的变化来进行估算，即 P＝0.5TH^2
（P为单位波前宽度上的波浪功率，单位 kw/m；
T为波浪周期，单位s；H为波高，单位m，
问题：
为何波浪的能量和波高的平方成正比，而不是和运动周期平方成正比？
公式中的0.5怎么来的？
这可能是由实验得到的经验公式。这里的P是平均能流密度，故有1/2的系数。波的能量理论上和振幅平方成正比。
那個只是估算式。重力波的相速度公式中在根號裏面有1/2，平方之後就有1/2了
ห้องสมุดไป่ตู้
。

计算竖直圆柱波浪力竖直圆柱体波浪力求解示意图本次次计算作用于竖直圆柱波浪力如图1所示竖直桩为半径是r的圆柱对df和相对海底的力分别是波浪水质点运动轨迹速度和加速度的水平分量代入线性波理论中的ucoscossincoscossinkdkdkdsinh16kdkdkdkdcoshsinhkdkdkdsinh64规则波条件下morison方程惯性力及阻力系数确定为了确定morison方程中的阻力系数cd和惯性力cm的取值国内外学者进行了大量规则波或振荡流对垂直桩柱作用力实验研究
Morison 方程计算结果
本文分别计算直径为0.5m,1m,2m,3m,4m的圆柱在30m水深，波高为4m,波浪周期为11s的单桩柱受到波 浪力的情况。 直径为0.5m的圆柱在不同相位受到波浪力如表1所示，结果曲线如图2所示。
表1 直径0.5m圆柱Morison方程结果
相位 0 0.0634665 0.126933 0.1903996 0.2538661 0.3173326 0.3807991 0.4442656 0.5077321 Fi 0 395.07977 788.5687 1178.8823 1564.449 1943.7163 2315.1568 2677.275 3028.6128 Fd 6805.2619 6777.8871 6696.2032 6561.5245 6376.0179 6142.6685 5865.2308 5548.169 5196.5847 Ft 6805.2619 7172.9669 7484.7719 7740.4068 7940.467 8086.3847 8180.3876 8225.444 8225.1975 相位 2.1578616 2.2213281 2.2847947 2.3482612 2.4117277 2.4751942 2.5386607 2.6021272 2.6655938 Fi 5186.2375 4956.9533 4707.7092 4439.5088 4153.4321 3850.631 3532.3248 3199.7951 2854.381 Fd -2088.041 -2495.919 -2918.386 -3348.645 -3779.772 -4204.832 -4616.983 -5009.595 -5376.351 Ft 3098.1964 2461.0344 1789.3231 1090.8639 373.65968 -354.2006 -1084.658 -1809.8 -2521.97 相位 4.3157232 4.3791898 4.4426563 4.5061228 4.5695893 4.6330558 4.6965224 4.7599889 4.8234554 Fi -5745.522 -5886.592 -6003.958 -6097.148 -6165.788 -6209.6 -6228.408 -6222.136 -6190.811 Fd -1015.771 -727.9824 -483.23 -285.452 -137.8305 -42.74083 -1.71308 15.407376 83.603368 Ft -6761.293 -6614.574 -6487.188 -6382.6 -6303.618 -6252.341 -6230.121 -6206.729 -6107.207

说明： 说明：单坡上的波压力计算方法是根据原 苏联国家建设委员会在1986 1986年颁布的建筑 苏联国家建设委员会在1986年颁布的建筑 标准与规范《波浪、 标准与规范《波浪、冰凌和船舶对水工建 筑物的荷载与作用》CНИП.2.06.04筑物的荷载与作用》CНИП.2.06.04-82 中计算规则波波压力的方法， 中计算规则波波压力的方法，其由试验计 算求得，并通过原型实测资料验证。 算求得，并通过原型实测资料验证。可用 于计算不规则波对单坡堤混凝土护面上的 波压力。 波压力。
ps =γK1K2H
静水面以上、以下的波浪压力强度按《规范》 静水面以上、以下的波浪压力强度按《规范》 有关规定计算。 有关规定计算。 波谷作用时波浪力计算： 波谷作用时波浪力计算：
静 静 静
d＜ 2H H /2
i
p
b
图G.1.1-2 波谷时的波压力分布图
静水面处波浪压力强度为零； 静水面处波浪压力强度为零； 静水面以下波浪压力强度计算。 静水面以下波浪压力强度计算。
G.2 斜坡式护面
G.2.1 对于斜坡式海堤，当护面层采用混凝 对于斜坡式海堤， 土板时， 土板时，护面板的稳定取决于上下两面波 浪力与浮力的作用。 浪力与浮力的作用。 G.2.2 在1.5≤m≤5.0的条件下，作用在整体 1.5≤m≤5.0的条件下 的条件下， 或装配式平板护面上的波压力分布见下图， 或装配式平板护面上的波压力分布见下图， 最大波压力p (kPa)按下式计算 按下式计算。 最大波压力p2(kPa)按下式计算。
p
Z d1 + d1
) 负 (负
Z 静 静 静 d
胸 胸 P u b
图G.2.3-1 胸墙波压力图 G.2.3-
注意：本条中的波高 均是指 均是指H 频率F的 注意：本条中的波高H均是指 F，频率 的 取值由表6.1.3确定。 确定。 取值由表 确定

G.2.3 作用于如下图的斜坡式海堤顶部胸墙 上的波浪力，当无因次参数ξ≤ξb时，可按下 列公式计算。
本条公式介绍了波峰作用时胸墙上平均压力 强度、胸墙上的波压力分布高度、单位长度 胸墙上的总波浪力、胸墙底面上的波浪浮托 力的计算公式。
静水面 d
p
d1 +Z Z
d1 (负值)
胸墙
Pu b
图G.2.3-1 胸墙波压力图
注意：本条中的波高H均是指HF，频率F的 取值由表6.1.3确定。
1. 静水面以上高度H处的波压力为零。 2. 静水面处的波浪压力强度为：
ps K1K2 H
静水面以上、以下的波浪压力强度按《规范》 有关规定计算。 波谷作用时波浪力计算：
静水面
d＜2H H/2
b
i
p
图G.1.1-2 波谷时的波压力分布图
Байду номын сангаас波浪作用力计算公式 简介
G.1 直立式护面
G.1.1 T g / d 8, d 2H,i 1/10或T g / d 8，d 1.8H,i 1/10
时，直立式海堤护面上波浪作用力可按下确 定。波峰作用下：
H
静水面
ps 0.7ps
H/2
d＜2H
pd=(0.5～0.6) ps
b
i
图G.1.1-1 波压力分布图
注意：本条中的波高H均是指HF，频率F的 取值由表6.1.3确定。
p2 k1k2 pH
3
1 2 4 5
α
图G.2.2 斜坡护面平板的波压力分布图
首先确定：最大波压力p2作用点2的垂直坐 标z2（m）：
z2
A
1 m2
1
2m2 1 A B
其次确定各压力转折点离点2的距离及各点 的波压力p：可由《规范》有关规定确定。

H1% (m)
4.44 4.37 4.33 4.19 4.07 4
H4% (m)
3.8 3.74 3.7 3.57 3.48 3.45 3.36 3.3
H13% (m)
3.11 3.06 3.03 2.92 2.84 2.79
Hmean (m)
ηmax＝ Z1 ＝ Z2 ＝ K2 ＝ K4 ＝ 柱体断面面积A＝ CM = 海水重度γ＝ PImax＝ MImax＝ 3.合力 PDmax<=0.5PImax Pmax＝ Mmax＝
0.66 查表 0m 12.16 m 0.467 0.125 0.502655 m2 2 10.25 kN/m3 12.03 kN 83.75 kNm
30.46 kN 234.19 kNm
设计波 要素表
表2-8 计算点 D (琅歧) E
100
方向
风速 重现期 (年)
300
计算 水位
计算点 水深(m)
15.82 年一遇高水位 15.48 年一遇高水位 极端高水位 15.24 15.82 年一遇高水位 15.48 年一遇高水位 极端高水位 15.24
2 1.97 1.95 1.88 1.83 1.79
Tmean (s)
7 6.9 6.9 6.8 6.7 6.6
L (m)
67.88 66.65 65.96 64.76 63.11 61.87
钢管桩的波浪力计算 一.计算资料
设计高水位 波高H 底高程 波浪周期T 圆柱直径D 13.5 4 0 6.7 0.8 m m m s m 13.5 m 70.09 m 0.1926 0.09258 145.820 m 0.005 < 按小尺度桩柱计算 H/d＝ d/L＝ 0.296 > 0.093 < 0.2 0.35

波浪对桩柱作用力的计算分析港口码头、跨海桥梁、海洋工程中经常遇到波浪力对桩柱的作用，水中的桩柱结构所受的水平力主要来自波浪的作用。

对于一般的桩柱结构，当桩柱的直径D与波浪的波长L的比值D/L<0.2时，称此结构为小尺度结构物；当D/L>0.2时，则称为大尺度结构物[1]。

港口码头、跨海桥梁、海洋工程常用的桩柱结构，一般为小尺度结构物，因此本文重点探究小尺度结构物的波浪力计算。

1 波浪力的计算方法国内外对波浪力的计算理论相差不大，都是基于Morison公式[2]內对波浪力的计算主要有《海港水文规范》规定的方法，国外对波浪力的计算有美国的API、挪威的DNV等标准提出的方法。

基于Morison理论的波浪力计算公式如下：（公式-1）（公式-2）（公式-3）上式中：PD是波浪力的速度分力（也叫拖曳力）；PI是波浪力的惯性分力；CD是速度力系数；CM是质量力系数；D是桩柱直径；dz是桩柱上每一小分段的长度；A是桩柱的断面积。

u、u/t——分别为水质点轨道运动的水平速度和水平加速度；是圆频率；t是时间，当波峰通过柱体中心线时t=0；H、T分别是波高和波周期。

美国的API规范给出拖曳力系数取0.6～1.0，惯性力系数取2.0。

国内的《海港水文规范》给出拖曳力系数取1.2，惯性力系数取2.0。

《海港水文规范》提出的拖曳力系数和惯性力系数比较适合我国的情况，因此本文以《海港水文规范》给出拖曳力系数1.2、惯性力系数2.0进行波浪力计算。

2 波浪力随高度和时间的变化趋势本文模拟了一个我国东部沿海的项目的桩基，该项目水深10m，采用垂直的钢管桩，桩体直径2.5m。

计算海浪的波长72m，波高3.9m，波周期7.8s。

采用Excel对周期T内的各时间点、沿桩柱各高度的拖曳力和惯性力的分力分别进行计算，然后用数值积分的方法将各分力沿桩柱高度进行积分，得出各时间点作用在桩柱上的波浪力的合力。

为考察波浪力随桩体高度变化趋势，按照公式1～3，将桩体在平均海平面以上分为10等份，在平均海平面以上分为2等份，进行拖曳力和惯性力计算。

Morison公式是计算波浪力的一种经典方法，可以用于估算结构物受到的波浪力的大小。

本文将Morison公式计算波浪力例题”为题，详细介绍Morison公式的原理，以及如何使用该公式进行波浪力的计算。

引言概述：在海洋工程和海洋结构物设计中，波浪力的计算对于结构的稳定性和安全性至关重要。

Morison公式是一种常用的计算波浪力的方法，被广泛应用于海洋工程领域。

该公式基于流体动力学和质量相互作用理论，能够较为准确地预测波浪对结构物的作用力。

正文内容：1. Morison公式的原理1.1 流体动力学原理流体动力学是研究流体运动及其产生的力的学科。

在Morison公式中，流体动力学原理被应用于推导出波浪力的表达式。

根据牛顿第二定律，当流体作用于物体时，会产生一个力，该力等于物体所受到的动量变化率。

利用这一原理，可以推导出Morison公式的基本形式。

1.2 质量相互作用原理质量相互作用是指在波浪作用下，流体会对物体施加一个额外的力。

在Morison公式中，质量相互作用原理被应用于计算波浪对结构物的附加作用力。

这种附加作用力是由于波浪绕过结构物时引起的涡旋效应而产生的。

2. Morison公式的计算过程2.1 确定参数在使用Morison公式计算波浪力之前，需要确定一些参数，包括波浪的特征、结构物的几何特征以及流体动力学参数。

关于波浪的特征，需要考虑波高、波长和波浪周期等；对于结构物的几何特征，需要确定结构体的截面形状和尺寸；流体动力学参数包括流体密度和流体速度等。

2.2 应用Morison公式Morison公式的基本形式是：F = Cd ρ d V (U + Vr)其中，F是波浪力，Cd是Morison公式中的阻力系数，ρ是流体密度，d是结构物的部分特征尺寸，V是波浪水速，U是流体速度，Vr是结构物表面被绕过的流体速度。

2.3 波浪力的分量根据Morison公式，波浪力可以分解为静力和动力两个分量。

静力分量是由于流体的质量相互作用引起的，与波浪的运动无关；动力分量则是由于流体的运动引起的，与波浪的运动有关。

桩基结构物波浪力的工程计算方法桩基结构物在海洋工程中具有举足轻重的地位，而波浪力是影响桩基结构物稳定性和安全性的关键因素之一。

因此，对桩基结构物波浪力的工程计算方法进行研究，对保障海洋工程的安全性和稳定性具有重要意义。

本文将围绕桩基结构物波浪力的工程计算方法展开讨论，旨在明确计算方法及其在实际工程中的应用。

桩基结构物波浪力是指海洋工程中桩基结构物受到海浪作用产生的力。

这种力的产生主要源于海浪的冲击力、海流力和重力等多种因素。

波浪力的计算公式通常根据物理力学原理进行推导，是桩基结构设计中的重要参数。

在实际工程中，波浪力的计算方法大致可分为经验法和理论法两类。

经验法主要依据实际工程数据进行拟合计算，而理论法则是基于物理力学理论进行计算。

有限元法是一种常用的数值计算方法，适用于各种复杂的工程问题。

在桩基结构物波浪力的计算中，有限元法可以将桩基和周围介质视为离散的单元体，通过对单元体进行力学分析，得到每个单元体上的力与位移关系，最终得到整个结构的应力与变形。

模拟法是通过计算机模拟海浪对桩基结构物的作用过程，从而得到结构物所受的波浪力。

这种方法需要建立海浪模型和桩基结构物模型，通过设定不同的海浪条件和结构物参数，进行大量模拟计算，最终得到不同条件下的波浪力。

为了说明上述计算方法的有效性和可行性，我们选取了一个实际案例进行详细的分析和验证。

该案例为某海上风电场桩基结构物，基础形式为单桩基础。

我们运用有限元法对该结构物进行了建模，并对其在不同海浪条件下的波浪力进行了模拟计算。

计算结果表明，在相同的海浪条件下，有限元法与模拟法得到的波浪力结果相近，证明了这两种计算方法的可靠性。

同时，通过对比分析，我们发现有限元法在处理复杂边界条件和多因素耦合问题上具有更大的优势。

本文对桩基结构物波浪力的工程计算方法进行了系统的探讨，分别介绍了经验法和理论法两种计算思路，并详细推导了其中的公式和理论。

通过实例分析和验证，说明这些方法在计算桩基结构物波浪力上的有效性和可行性。

波浪对桩柱作用力的计算波浪对桩柱作用力的计算是海洋工程中重要的研究内容。

波浪在桩柱上的作用力分为水平力和垂直力两种，其中垂直力对桩柱的稳定性影响较大。

本文将介绍波浪对桩柱作用力的计算方法及其对海洋工程的应用。

一、波浪对桩柱垂直力的计算波浪对桩柱垂直力的计算可以采用线性水波理论或非线性水波理论。

线性水波理论是一种经验公式，适用于波高小于1/7水深的情况。

非线性水波理论考虑了波浪的非线性因素，适用于波高大于1/7水深的情况。

1. 线性水波理论线性水波理论最早由Stokes提出，其公式表达如下：$$F=ρgh\cdot A$$其中，F为波浪垂直力，ρ为水密度，g为重力加速度，h为波高，A为横截面积。

Stokes公式的前提条件是波高比较小，海洋工程中较少使用。

2. 非线性水波理论非线性水波理论与线性水波理论相比，考虑了波浪的非线性因素，因此更加准确。

非线性水波理论中最常用的是Mild-Slope equation，其公式表达如下：$$F=\frac{1}{g}(\frac{∂P}{∂z})$$其中，F为波浪垂直力，g为重力加速度，P为波浪压力，z为水深。

Mild-Slope equation适用于海洋深度较大的海域，且波浪高度不太受深度影响的情况。

二、波浪对桩柱水平力的计算波浪对桩柱水平力的计算较为复杂，需要考虑波浪和桩柱之间的摩擦力和慣性力等因素。

常用的计算方法有Morison方程、Barracuda方程和Strip Theory等。

1. Morison方程Morison方程是目前海洋工程中最常用的波浪和桩柱的作用力计算方法。

该方法将桩柱的作用力分为二阶谐波力和非二阶谐波力。

其中，二阶谐波力对于波高较小的海域较为准确，而非二阶谐波力对于波高较大的海域较为准确。

Morison方程的公式表达如下：$$F_{x}=ρC_{d}D_{p}V(t)^{2}+ρC_{m}D_{p}ẋ(t)+F_{xN}$$$$F_{y}=ρC_{d}D_{p}V(t)^{2}+ρC_{m}D_{p}ẏ(t)+F_{yN}$$其中，Fx和Fy分别为水平力和横向力，ρ为水密度，Cd 为Morison方程中的阻力系数，Dp为桩柱直径，V(t)为波浪速度，Cm为Morison方程中的惯性系数，ẋ(t)和ẏ(t)分别为桩柱在水平和垂直方向上的速度，FxN和FyN分别为非二阶谐波力。