由互易定理

互易定理证明范文互易定理是数学中的一个重要定理，旨在说明在不同的域上进行变换时，求导和求积分可以互相转换。

在本文中，我将从定理的定义、证明过程以及实际应用等角度来解释互易定理。

首先，我们来定义互易定理。

在数学中，互易定理又称为傅里叶变换的互易性质。

设函数f(x)和F(k)分别表示实数轴上的两个函数，其傅里叶变换定义为：F(k) = ∫[负无穷，正无穷] f(x)·e^(-ikx) dx其中，e^(-ikx)是一个复指数函数，被称为傅里叶系数，表示一个特定频率的振幅。

互易定理指出，当函数f(x)和F(k)都在积分区间[-∞,∞]上绝对可积时，f(x)的傅里叶变换F(k)的逆变换等于f(x)自身。

也就是说，有如下关系成立：f(x) = (1/(2π))∫[负无穷，正无穷] F(k)·e^(ikx) dk接下来，我将展示互易定理的证明过程。

证明过程如下：我们首先考虑定义的傅里叶变换公式：F(k) = ∫[负无穷，正无穷] f(x)·e^(-ikx) dx现在，我们将定义傅里叶变换的逆变换：f(x) = (1/(2π))∫[负无穷，正无穷] F(k)·e^(ik x) dk为了证明互易定理，我们需要证明f(x)等于其逆傅里叶变换。

换句话说，我们需要证明：(1/(2π))∫[负无穷，正无穷] F(k)·e^(ikx) dk = f(x)我们可以通过以下步骤证明上述等式：步骤1：我们将f(x)表示为其傅里叶变换F(k)的逆变换。

f(x) = (1/(2π))∫[负无穷，正无穷] F(k)·e^(ikx) dk步骤2：然后，我们将F(k)替换为其傅里叶变换f(x)。

f(x) = (1/(2π))∫[负无穷，正无穷] [∫[负无穷，正无穷]f(x')·e^(-ikx') dx']·e^(ikx) dk步骤3：我们交换积分的顺序并进行化简。

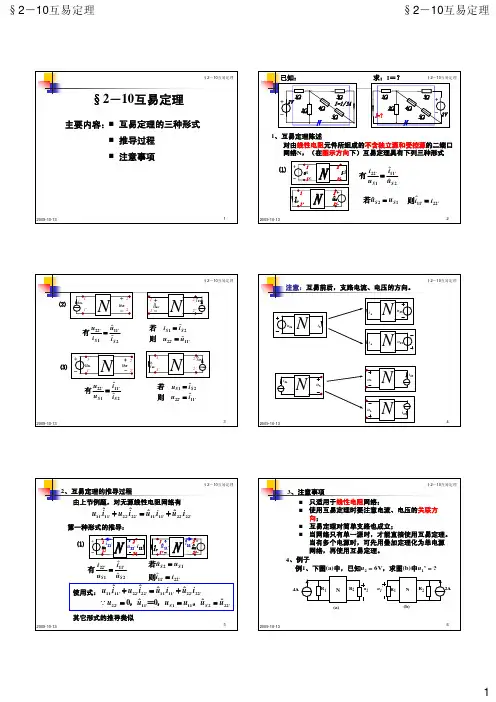
证明：设电路中有b条支路，连接αα’和证明方法同定理1证明方法同定理1☐互易定理在应用时要注意，前两种形式中，当激励是电压，响应为电流；当激励是电流，响应就是电压；第3种形式，一边激励、响应都是电流，另一边激励、响应都是电压。

从总体上说，不能全是电流或全是电压。

(注意，互易定理中各次观测的响应均为零状态响应)☐应用互易定理时，不仅有量的大小问题，而且还有方向问题。

一般电源的移动方法为：平移法和旋转法。

☐互易定理用于解平衡电桥电路和对称电路较方便。

☐互易性与无源性是互不相干的，回转器是无源器件，但不能互易。

9例4：图中N为线性无源电阻电路，图（当将3Ω支路短路求短路电流(a) (b)17从图(a)可知又因为从图(b)可知22232323()R u R i R i R i R i R R iββ=+=+=+Si i =所以223S()u R R i β=+113ˆˆˆˆR uu i R i γ=++又因为S ˆii =111S ˆˆR uR i R i ββ=-=-所以11S S 3S 13S ˆ()uR i i R i R R i βγβγ=-++=-++由于u 2应等于û1，所以可求得12()R R γβ=+(c)19网孔方程为消去控制电流i 及网孔电流i m3，得矩阵形式的网孔方程13131m1132232m 22R R R R R i u R R R R R i u γβγβββ++-+-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥+++⎣⎦⎣⎦⎣⎦若原电路电路互易，则13m13m 21m313m123m 22m32m3m1m 2()()R R i R i R i u i R i R R i R i u i i i i i γβ++-=-⎧⎪+++=⎪⎨=⎪⎪=+⎩3132R R R R γββ+-=+亦可得12()R R γβ=+。

材料力学互易定理材料力学互易定理，也称Betti第二定理或Betti-Maxwell互易定理，是材料力学分析中一个重要的定理，用于计算复杂结构的内力分布和刚度计算等问题。

本文将详细解释什么是材料力学互易定理，其背景、前提和证明过程，并简要介绍其应用和限制。

一、背景和前提材料力学互易定理是由19世纪意大利学者贝蒂 (Carlo Alberto Castigliano) 和英国学者麦克斯韦（James Clerk Maxwell）独立提出的。

这个定理的起源可以追溯到19世纪，当时的工程师们需要计算桥梁、建筑和机器的承载能力以及内力、应变等。

然而，复杂的结构往往需要进行繁琐的计算才能得出结果，这个过程既费时又费力，而且容易出错。

为了解决这个问题，贝蒂和麦克斯韦分别提出了一条定理，使得计算更为简单。

他们的定理相似，而且可以互相推导，因此被称为材料力学互易定理或Betti第二定理。

这个定理的基本思想是在复杂的力学问题中，可以通过若干次简单的计算来得出结果。

在介绍互易定理之前，先要介绍一些概念。

材料力学中的很多问题都是静力学问题，即考虑物体在稳定状态下的受力情况。

为了描述一个物体在空间中的静力学状态，需要引入一些概念：受力结构：指一个物体，包括其支撑和支承的物体。

外载荷：指作用在受力结构各部分上的外部荷载，包括重力、压力、拉力等。

位移：指受力结构的任意一个点在三维空间中的位移，包括沿x、y和z三个方向的位移。

应力：指受力结构内部任意一个点的受力情况，包括拉力、压力等。

应变：指受力结构内部任意一个点的形变情况，包括沿x、y和z三个方向上的形变。

根据上述定义，可以得到受力结构中各部分的内力和挠度，由此可以推导出材料力学互易定理。

二、定理表述材料力学互易定理的核心是内力和位移之间的关系。

它的推理方式可以描述为以下两个定理：定理一：原来的受力结构，在其任意点的位移与外载荷的乘积之和等于对其施加单位外力所引起的位移值，即W = ∫_(V)⁡(σVε)dV其中，W是原始受力结构对外力加之后的反作用位移，V是受力结构内部有位移的体积，σ是体积元素中的应力向量，ε是应力张量中的应变向量。

互易定理的应用互易定理，又称反比例定理，是一种数学定理，由欧几里得发现，也有可能是希腊数学家勒比里安提出。

它表明两个变量总是存在反比例关系，即当一个增加时，另一个就会减少，反之亦然。

本文将针对互易定理的定义及其在人们日常生活中的应用作出介绍。

首先，从数学上来说，互易定理的定义如下：若x和y是两个正数，且x y，则有 x / y = y / x 。

互易定理是一种对称定理，即把变量换位置，结果依旧不变。

它可以被用来计算一个变量的值，当另一个变量的值已知时，例如将2/4用互易定理处理，可得出4/2=2。

其次，在日常生活中，互易定理常常被用来计算金融类的问题，例如汇率的计算，人们可以根据以美元（USD）为基准计价的汇率，把其他货币的汇率折算成美元，再将美元的汇率折算回原货币，从而得出原货币的汇率。

此外，在物理上，互易定理也得到了广泛的应用。

常见的例子是摩擦力和摩擦系数之间的关系，即F=μ*N，其中F为摩擦力，N为物体表面接触的部分产生的压力，而μ则为摩擦系数。

很显然，当N增大时，F也会增大，但μ则同时减小，由此可见，F和μ之间也存在反比例关系，这正是互易定理的应用。

最后，互易定理还可以应用于流体力学和化学，例如比重的换算，在一个未知液体的情况下，可以根据比重的反比例关系，通过测定出一个熟悉的液体的比重，从而估算出未知液体的比重。

在生物学方面，同样可以利用互易定理，比如减肥的过程，当体重减少时，体质指数（BMI）会相应减少，反之亦然，因此可直观地看出二者之间存在反比例关系，同样是互易定理的应用。

综上所述，互易定理是一个十分有用的定理，其应用领域涉及到金融、物理、化学以及生物等多种领域。

本文综述了互易定理的定义及其应用，希望能够对读者有所帮助。

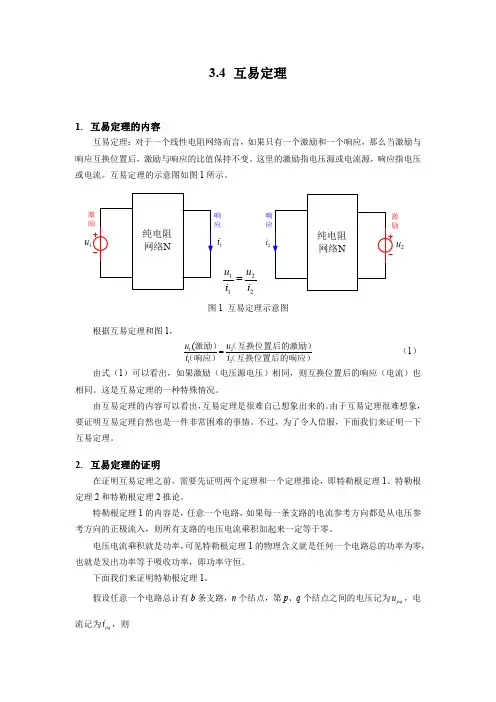
3.4 互易定理1. 互易定理的内容互易定理：对于一个线性电阻网络而言，如果只有一个激励和一个响应，那么当激励与响应互换位置后，激励与响应的比值保持不变。

这里的激励指电压源或电流源，响应指电压或电流。

互易定理的示意图如图1所示。

u 1i 2u 2i 1212u u i i =图1 互易定理示意图根据互易定理和图1，1212(u u i i =激励）（互换位置后的激励）（响应）（互换位置后的响应） （1）由式（1）可以看出，如果激励（电压源电压）相同，则互换位置后的响应（电流）也相同。

这是互易定理的一种特殊情况。

由互易定理的内容可以看出，互易定理是很难自己想象出来的。

由于互易定理很难想象，要证明互易定理自然也是一件非常困难的事情。

不过，为了令人信服，下面我们来证明一下互易定理。

2. 互易定理的证明在证明互易定理之前，需要先证明两个定理和一个定理推论，即特勒根定理1、特勒根定理2和特勒根定理2推论。

特勒根定理1的内容是，任意一个电路，如果每一条支路的电流参考方向都是从电压参考方向的正极流入，则所有支路的电压电流乘积加起来一定等于零。

电压电流乘积就是功率，可见特勒根定理1的物理含义就是任何一个电路总的功率为零，也就是发出功率等于吸收功率，即功率守恒。

下面我们来证明特勒根定理1。

假设任意一个电路总计有b 条支路，n 个结点，第p 、q 个结点之间的电压记为pq u ，电流记为pq i ，则1111111111111()02222bn n n n n n nnk kpq pq p q pq p pq q pq k p q p q p q q p u i u i u u i u i u i ===========−=−=∑∑∑∑∑∑∑∑∑ （2）由式（2）即证明了特勒根定理1。

式（2）乍一看很难理解，下面对其中的细节进行解释。

式（2）中第一个等号是将支路电压电流乘积之和转化为结点与结点之间电压与电流乘积之和。

高等数学1 互易定理-回复什么是互易定理？互易定理，也被称为傅里叶互易性质，是高等数学中一个重要的定理。

它描述了一个函数的傅里叶变换与它的自身的傅里叶变换之间的关系。

互易定理被广泛应用在信号处理、图像处理、量子力学等领域。

在本文中，我们将详细介绍互易定理的概念、定义、性质和应用。

1. 互易定理的概念互易定理是傅里叶变换理论的重要内容之一。

傅里叶变换是将一个函数在时域（时间域）上的表达转换为频域上的表达的数学工具。

互易定理表明，一个函数的傅里叶变换与其自身的傅里叶变换之间存在某种变换关系。

2. 互易定理的定义设函数f(t) 的傅里叶变换为F(w)，则互易定理可以表述为：F(t) 的傅里叶变换为f(-w)。

换句话说，一个函数在时域上的傅里叶表示对应于另一个函数在频域上的傅里叶表示。

3. 互易定理的性质互易定理具有以下性质：3.1 线性性质：如果f(t) 的傅里叶变换为F(w)，g(t) 的傅里叶变换为G(w)，那么af(t)+bg(t) 的傅里叶变换为aF(w) + bG(w)，其中a和b为常数。

3.2 平移性质：如果f(t) 的傅里叶变换为F(w)，那么e^jwtf(t) 的傅里叶变换为F(w - w0)。

即在时域上对函数进行平移，其傅里叶变换在频域上也发生了相应的平移。

3.3 对称性质：如果f(t) 为实函数且f(t) 的傅里叶变换为F(w)，那么F(t) 的傅里叶变换为2πf(-w)。

即函数在时域上的对称性对应于其傅里叶变换在频域上的反对称性。

4. 互易定理的应用互易定理在信号处理、图像处理和量子力学等领域有着广泛的应用。

4.1 信号处理中的应用：通过傅里叶变换，我们可以将一个时域上的信号转化为频域上的信号，从而实现频谱分析、滤波等操作。

互易定理可用于说明，对某个信号施加一个变换后，其频域表达将对应于原信号在另一个域中的变换。

4.2 图像处理中的应用：图像可以看作是一个二维函数，通过二维傅里叶变换，我们可以将图像在时域上的表示转化为频域上的表示。

数据库原理互易定理互易定理是数据库中的一种重要原理，指的是在进行关系运算时，操作符之间的顺序可以交换而不影响运算结果。

在关系数据库中，常用的关系运算符包括选择、投影、并、差、笛卡尔积和连接等，这些运算符是用来操作关系表的，将它们合理应用可以实现各种复杂的查询和操作。

下面我们来详细介绍一下关系运算符之间的互易定理：1. 选择操作的互易定理选择（selection）是从关系表中筛选出满足特定条件的元组，其符号为σ。

根据互易定理，选择运算符是可以交换位置的。

也就是说，若R是一个关系表，p和q是任意两个选择条件，则有：σp(σq(R)) = σq(σp(R))R ∪ S = S ∪ R4. 笛卡尔积操作和连接操作的互易定理互易定理在关系数据库中是非常重要的一个原理。

它的运用可以使关系表之间的运算更加灵活、高效，也为关系数据库的设计和查询提供了更多的可能性。

除了互易定理之外，还有一些其他的关系代数规则也非常重要。

这些规则包括结合律、分配律、交换律以及去重等规则。

1. 结合律结合律是指运算符之间的运算顺序不同，但结果不变。

对于三个表R、S、T，选择运算符符合结合律即：σp(σq(R)) = σq(σp(R))2. 分配律分配律是指关系运算符可以有两种顺序进行运算，没有影响结果，比如：R × (S ∪ T) = (R × S) ∪ (R × T)3. 交换律R ∪ S = S ∪ R4. 去重在关系数据库中，经常需要对表进行去重操作，而这个操作可以简单地表示为：以上这些关系代数规则全都非常重要，它们的存在可以让我们更快地进行表的操作，提升数据库操作效率和查询速度。

在实际应用中，我们还需要根据具体的数据情况和查询需求来选用不同的操作符和规则。

除了关系代数，我们也可以使用关系演算来进行关系运算。

关系演算包括元组关系演算和域关系演算两种形式，其中元组关系演算基于元组的集合，而域关系演算基于关系表的列。