下载文档原格式
四、互易定理对于线性单一激励的不含受控源的线性电阻电路（即仅有一个独立源作用的电阻电路）还有一个很重要的性质互易性，反映互易性的原理称作互易原理。
此原理有三种形式。
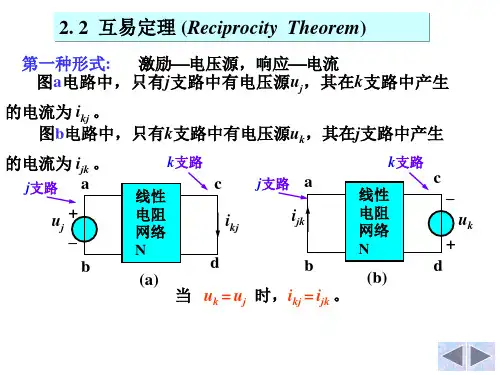
1、在图2-3-18(a)与(b)所示电路中示出了互易原理的第一种形式（N 为仅由电阻组成的线性电阻电路）图示说明对于不含受控源的单一激励的线性电阻电路，互易激励(电压源)与响应(电流)的位置，其响应与激励的比值仍然保持不变。
当激励U s1=U s2时，则I 2 =I 1。
_U ’I 2 S2 (a) (b)图2-3-18互易原理的第一种形式2、在图2-3-19(a)与(b)所示电路中示出了互易原理的第二种形式，图示说明对于不含受控源的单一激励的线性电阻电路，互易激励(电流源)与响 应(电压)的位置，其响应与激励的比值仍然保持不变。
当激励I s1=I s2时，则U 2 =U 1。
I ’U 2S2+- (a) (b)图2-3-19 互易定理第二种形式3、在图2-3-20(a)与(b)所示电路中示出了互易原理的第三种形式，图示说明对于不含受控源的单一激励的线性电阻电路，互易激励与响应的位置，且把原电压激励改换为电流激励，把原电压响应改换为电流响应，则互易位置前后响应与激励的比值仍然保持不变。
如果在数值上U s1=I s2时，则U 2 =I 1。
_U S1+ ’U 2 S2 -(a) (b)图2-3-20【例15】：电路如图2-3-21(a)所示，试求电流I 。
(a) (b)图2-3-21例15电路图【解】：原电路为一不平衡桥式电路，但为仅有一个独立源单独作用的线性电阻电路，可使用互易定理进行分析。
互易后的电路如右图所示。
此时应注意互易前后对应支路上的电压电流的参考方向必须同时关联或非关联。
在图2-3-21(b)中可以求得：A I 224241212281=+⨯++⨯+=根据分流公式：A I I 3221112=+=A II 3442413=+=由KCL 可得：A I I I 3223=-=∴原电路中所求电流AI 32=d 8V。
互易定理的条件互易定理是物理学中的一个重要定理，描述了线性系统的输入和输出之间的关系。
根据互易定理，系统的输入与输出之间的关系在时间域和频率域之间存在一种对应关系。
在下面的文章中，我会详细解释互易定理的条件，并提供相关的背景知识。
互易定理是傅里叶分析的一个关键概念，它指出了在频率域中，信号的傅里叶变换（频谱）与该信号的共轭复数的傅里叶变换之间存在一种对称关系。
具体而言，如果一个信号在时间域中的函数为f(t)，它的傅里叶变换为F(ω)，那么互易定理可以用下面的公式来表示：F(ω) = ∫[f(t) * e^(-jωt)] dt其中，F(ω)是信号f(t)在频率域中的傅里叶变换，e^(-jωt)是复指数函数，表示频率为ω的正弦波。
公式中的积分表示对信号f(t)在所有时间点上的加权求和。
为了满足互易定理，信号f(t)必须满足一些条件。
以下是互易定理的主要条件：1. 信号必须是连续的。
互易定理适用于连续信号而不是离散信号。
连续信号是在连续时间范围内定义的信号，而离散信号则是在离散时间点上定义的信号。
2. 信号必须是带限的。
带限信号是指其频谱在一定频率范围内有限。
这意味着信号在频率域中没有无限宽的频带，而是在某个频率范围内存在。
如果信号的频谱是无限宽的，那么它将无法满足互易定理。
3. 信号必须满足一定的可积条件。
具体而言，信号的幅度必须在整个时间域上是有界的，即信号的绝对值不能无限增大。
这是为了确保信号的傅里叶变换存在。
4. 信号必须具有有限的能量。
信号的能量定义为信号幅度的平方在整个时间域上的积分。
信号的能量必须是有限的，以便信号的傅里叶变换存在。
需要注意的是，互易定理通常用于描述线性时不变系统，这些系统对输入信号的响应与输入信号的傅里叶变换之间存在相似的关系。
互易定理在信号处理、通信系统、电路分析等领域中有广泛的应用。
总之，互易定理是描述线性系统中输入和输出之间关系的一个重要定理。
它要求信号是连续、带限的，并满足可积和有限能量的条件。
特勒根定理
设有电路,A B ，满足：（1）两者的拓扑图完全相同，均有n 个节点b 条支路；（2）对应的支路和节点均采用相同的编号，其中B 电路的电流、电压加“^”号；（3）各支路电流、电压参考方向均取为一致，则有： 功率守恒定理：
01
b
U I k k k =∑=
ˆˆ01b
U I k k
k =∑= 似功率守恒定理：
ˆ01
b
U I k k k =∑= 1
ˆ0b k k k U I ==∑
适用于各种电路：直流、交流；线性、非线性；
被称为基尔霍夫第三定律。
§2－2互易定理
在线性电路中，若只有一个独立电源作用，网络只含有线性电阻（不含受控源），则在一定的激励与响应的定义下，二者的位置互易后，响应与激励的比值不变。
互易定理的证明需要特勒根定理（或二端网络等效的概念）。
根据激励和响应是电压还是电流，互易定理有三种形式：
1、互易定理的第一种形式
S u
S u ˆ+-
电路在方框内仅含线性电阻，不
含任何独立电源和受控源。
电压源s u 接在端子1-1'，支路2-2'短路，其电流为2i 。
如果把激励和响应位置互
换，此时ˆs u
接于2-2'，而响应则是接于1-1'，短路电流1ˆi 。
21ˆˆs s i i u u
=，若 ˆs s u u =，则21ˆi i =。
对一个仅含线性电阻的电路，在单一电压源激励而响应为电流时，激励和响应互换位置，不改变同一激励产生的响应。
2、互易定理的第二种形式
2'
2
1'
1
21ˆˆs s u u i i
= 若ˆs s i i
=，则21ˆu u =。
3 互易定理的第三种形式
2
1ˆˆs s i u i u
= 若数值上ˆs s i u =，则数值上21ˆi u =。
例 用互易定理求下图中电流i 。
解：根据互易定理，图(a)和(b)中电流i 相同。
从图(b)中易于求得：
024
361236261236
i A ==⨯⨯++
++
00123161236
i i i A =-=++
例 互易双口的输入电流为2A 时，输入端电压为10V ，输出端电压为5V 。
把电流源移到输出端，同时在输入端跨接5Ω电阻，求5Ω电阻的电流。
例 互易双口的输入电压为10V 时，输入端电流为5A ，输出端短路电流为1A 。
把电压源移到输出端，同时在输入端跨接2Ω电阻，求2Ω电阻
的电压。
例P99，例题。
