下载文档原格式
第2章MATLAB概论1、与其他计算机语言相比较，MA TLAB语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MA TLAB系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可.4、MATLAB操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？答：在MATLAB操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock按钮，点击Undock按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的view菜单中选择Dock，菜单项就可以将独立的窗口重新防止的桌面上.5、如何启动M文件编辑/调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.6、存储在工作空间中的数组能编辑吗？如何操作？答：存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输入修改内容即可.7、命令历史窗口除了可以观察前面键入的命令外，还有什么用途？答：命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.8、如何设置当前目录和搜索路径，在当前目录上的文件和在搜索路径上的文件有什么区别？答：当前目录可以在当前目录浏览器窗口左上方的输入栏中设置，搜索路径可以通过选择操作桌面的file菜单中的Set Path菜单项来完成.在没有特别说明的情况下，只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用，如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件，如果没有特别说明，数据文件将存储在当前目录上.9、在MA TLAB中有几种获得帮助的途径？答：（1）帮助浏览器：选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器.（2）help命令：在命令窗口键入“help”命令可以列出帮助主题，键入“help 函数名”可以得到指定函数的在线帮助信息.（3）lookfor命令：在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数.（4）模糊查询：输入命令的前几个字母，然后按Tab键，就可以列出所有以这几个字母开始的命令和函数.注意：lookfor和模糊查询查到的不是详细信息，通常还需要在确定了具体函数名称后用help命令显示详细信息.第3章 MATLAB 数值运算3.1在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375，并将其赋予变量a ？ 答：在Command Window 窗口输入操作:>> a=[5 7 3;4 9 1]3.2有几种建立矩阵的方法？各有什么优点？ 答：（1）直接输入法，如a=[1 2 3 4]，优点是输入方法方便简捷；（2）通过M 文件建立矩阵，该方法适用于建立尺寸较大的矩阵，并且易于修改； （3）由函数建立，如y=sin(x)，可以由MATLAB 的内部函数建立一些特殊矩阵； （4）通过数据文件建立，该方法可以调用由其他软件产生数据.3.3在进行算术运算时，数组运算和矩阵运算各有什么要求？答：进行数组运算的两个数组必须有相同的尺寸.进行矩阵运算的两个矩阵必须满足矩阵运算规则，如矩阵a 与b 相乘（a*b ）时必须满足a 的列数等于b 的行数.渗釤呛俨匀谔鱉调硯錦。
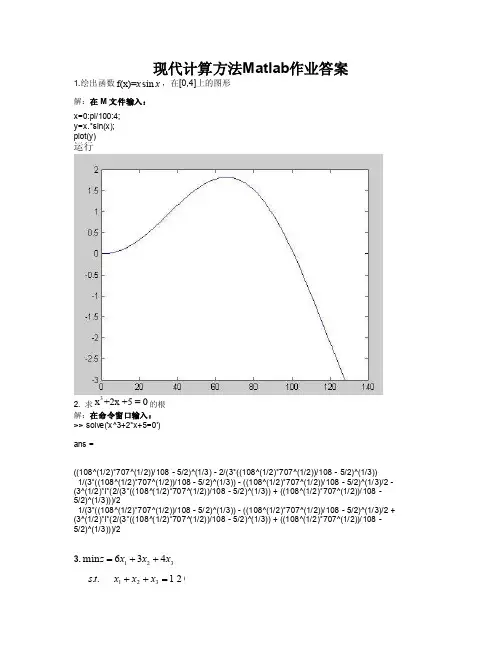
现代计算方法Matlab 作业答案1.绘出函数f(x)=sin x x ，在[0,4]上的图形解：在M 文件输入：x=0:pi/100:4;y=x.*sin(x);plot(y)运行2. 求3x +2x +5 = 0的根解：在命令窗口输入：>> solve('x^3+2*x+5=0')ans =((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3) - 2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3))1/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 -(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/21/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) - ((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)/2 +(3^(1/2)*i*(2/(3*((108^(1/2)*707^(1/2))/108 - 5/2)^(1/3)) + ((108^(1/2)*707^(1/2))/108 -5/2)^(1/3)))/23.321436min x x x z ++=120..321=++x x x t s301≥x5002≤≤x203≥x解：运用单纯形法计算此题，首先把约束条件化成标准形式：,,,,,205030120654321635241321≥=-=+=-=++x x x x x x x x x x x x x x x（1）在M 文件输入SimpleMthd 函数：function [x,minf] = SimpleMthd(A,c,b,baseVector)sz = size(A);nVia = sz(2);n = sz(1);xx = 1:nVia;nobase = zeros(1,1);m = 1;for i=1:nViaif (isempty(find(baseVector == xx(i),1)))nobase(m) = i;m = m + 1;else;endendbCon = 1;M = 0;while bConnB = A(:,nobase);ncb = c(nobase);B = A(:,baseVector);cb = c(baseVector);xb = inv(B)*b;f = cb*xb;w = cb*inv(B);for i=1:length(nobase)sigma(i) = w*nB(:,i)-ncb(i);end[maxs,ind] = max(sigma);if maxs <= 0minf = cb*xb;vr = find(c~=0 ,1,'last');for l=1:vrele = find(baseVector == l,1);if (isempty(ele))x(l) = 0;elsex(l)=xb(ele);endendbCon = 0;elsey = inv(B)*A(:,nobase(ind));if y <= 0disp('不存在最优解!');x = NaN;minf = NaN;return;elseminb = inf;chagB = 0;for j=1:length(y)if y(j)>0bz = xb(j)/y(j);if bz<minbminb = bz;chagB = j;endendendtmp = baseVector(chagB);baseVector(chagB) = nobase(ind);nobase(ind) = tmp;endendM = M + 1;if (M == 1000000)disp('找不到最优解!');x = NaN;minf = NaN;return;endend（2）在命令窗口输入：clear allA=[1 1 1 0 0 0;1 0 0 -1 0 0;0 1 0 0 1 0;0 0 1 0 0 -1];c=[6 3 4 0 0 0];b=[120;30;50;20];[xm,mf]=SimpleMthd(A,c,b,[3 4 5 6])xm =0 50 70mf =4304.计算下面函数在区间(0，1)内的最小值。
第二章非线性方程求根习题2-11. 试寻找f(x)= x 3+6.6 x2-29.05 x +22.64=0的实根上下界,及正根所在的区间，区间长度取1。
解:由笛卡儿符号规则知，f(x)=0可能有二个正根或无正根f(-x)= -x 3+6.6 x2+29.05 x +22.64=0即x 3 -6.6 x2-29.05 x -22.64=0f(-x)=0有一个正根，因此，f(x)=0有一个负根。
由定理2-3，f(x)=0的正根上界f(x)=0的负根下界x0123456 6.39f(x)++-+++++正根所在区间为(1, 2),(2, 3)。
2．你能不利用多项式的求导公式，而借鉴于余数定理的思想，构造出P n(x)=a0x n+a1x n-1+...+a n-1x+a n在x0这点上的导数值的算法吗？习题2-21.用二分法求方程x2-x-1=0的正根，要求准确到小数点后第一位a F(a)b F(b)x F(x)0-1211-11-121 1.5-0.251.5-0.2521 1.750.31251.5-0.25 1.750.3125 1.6250.3015625 1.5-0.25 1.6250.015625 1.5625-0.12109375 1.5625-0.12104375 1.6250.015625 1.59375-0.053710937 1.59375-0.053710937 1.6250.015625 1.609375-0.019287109 1.609375-0.019287109 1.6250.015625 1.6171875-0.001892089 1.6171875-0.001892089 1.6250.015625 1.621093750.006851196 1.6171875-0.001892089 1.621093750.006851196 1.6191406250.002175738 1.6171875-0.001892089 1.619140620.002475738 1.6181640630.000290904X*=1.618K=5X*=1.593752．试证明用试位法（比例求根法），求在区间[0, 1]内的一个根必然收敛。
实验6 Matlab数值计算实验目的：1、掌握数据统计与分析的方法；2、掌握数据插值和曲线拟合的方法及其应用；3、掌握多项式的常用运算。
实验内容：1.利用randn函数生成符合正态分布的10×5随机矩阵A，进行如下操作：（1）求A的最大元素和最小元素；（2）求A的每行元素的和以及全部元素的和；（3）分别对A的每列元素按升序、每行元素按降序排列。
a = randn(10,5)+10;ma = max(max(a))mi = min(min(a))s = sum(a,2)sa = sum(sum(a))p = sort(a)p1 = -sort(-a,2)2.用3次多项式方法插值计算1-100之间整数的平方根。
f = sqrt(n);interp1(n,f,(1:100),'cubic')3.某气象观测站测得某日6：00-18：00之间每隔2h的室内外温度（°C）如下表所示。
使用三次样条插值分别求出该日室内外6：30-17：30之间每隔2h 各点的近似温度，并绘制插值后的温度曲线。
n= 6:2:18;f1 = [18 20 22 25 30 28 24]; f2 = [15 19 24 28 34 32 30]; r = 6.5:2:17.5;w = interp1(n,f1,r,'spline'); w1 = interp1(n,f2,r,'spline'); subplot(211),plot(r,w) subplot(212),plot(r,w1)4. 已知lgx 在[1,101]区间10个整数采样点的函数值如下表所示，试求lgx 的5次拟合多项式p(x)，并绘制lgx 和p(x)在[1,101]区间的函数曲线。
x = linspace(1,101,10); y = log(x) /log(10); p = polyfit(x,y,5) y1 = polyval(p,x) plot(x,y,':o',x,y1,'-*') legend('sin(x)','fit')5. 有3个多项式(),(),()P x x x x P x x P x x x =+++=+=++4322123245223，试进行下列操作：（1） 求()()()()P x P x P x P x =+123。
习 题 三 解 答1、用高斯消元法解下列方程组。
（1）12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③解：⨯4②＋(-)①2，12⨯③＋(-)①消去第二、三个方程的1x ，得：1232323231425313222x x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩④⑤⑥ 再由52)4⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：1232332314272184x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩回代，得：36x =-，21x =-，19x = 所以方程组的解为(9,1,6)T x =--注意：①算法要求，不能化简。
化简则不是严格意义上的消元法，在算法设计上就多出了步骤。
实际上，由于数值计算时用小数进行的，化简既是不必要的也是不能实现的。
无论是顺序消元法还是选主元素消元法都是这样。
②消元法要求采用一般形式,或者说是分量形式，不能用矩阵，以展示消元过程。
要通过练习熟悉消元的过程而不是矩阵变换的技术。
矩阵形式错一点就是全错，也不利于检查。
一般形式或分量形式： 12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③ 矩阵形式123213142541207x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭向量形式 123213142541207x x x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭③必须是方程组到方程组的变形。
三元方程组的消元过程要有三个方程组，不能变形出单一的方程。
④消元顺序12x x →→L ，不能颠倒。
按为支援在方程组中的排列顺序消元也是存储算法的要求。
实际上，不按顺序消元是不规范的选主元素。
⑤不能化简方程，否则系数矩阵会变化，也不利于算法设计。
（2）1231231231132323110221x x x x x x x x x --=⎧⎪-++=⎨⎪++=-⎩①②③解：⨯23②＋()①11，111⨯③＋(-)①消去第二、三个方程的1x ，得： 123232311323523569111111252414111111x x x x x x x ⎧--=⎪⎪⎪-=⎨⎪⎪+=-⎪⎩④⑤⑥ 再由2511)5211⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：123233113235235691111111932235252x x x x x x ⎧⎪--=⎪⎪-=⎨⎪⎪=-⎪⎩回代，得：32122310641,,193193193x x x =-==， 所以方程组的解为 41106223(,,)193193193Tx =-2、将矩阵1020011120110011A ⎛⎫ ⎪⎪= ⎪- ⎪⎝⎭作LU 分解。
matlab教程习题答案
MATLAB教程习题答案
MATLAB是一种用于数学计算、数据分析和可视化的强大工具。
它被广泛应用于工程、科学和金融领域，因此掌握它的使用对于提高工作效率和解决问题至关重要。
在学习MATLAB的过程中，许多人会遇到各种习题，下面我们将给出一些常见习题的答案，希望能帮助大家更好地理解和掌握MATLAB的使用。
1. 编写一个MATLAB程序，计算并输出1到100之间所有奇数的和。
答案：
```matlab
sum = 0;
for i = 1:100
if mod(i, 2) == 1
sum = sum + i;
end
end
disp(sum);
```
2. 编写一个MATLAB程序，生成一个5x5的随机矩阵，并计算矩阵每一行的平均值。
答案：
```matlab
A = rand(5, 5);
row_means = mean(A, 2);
disp(row_means);
```
3. 编写一个MATLAB程序，求解以下线性方程组的解：
```
2x + 3y = 8
4x - 2y = 2
```
答案：
```matlab
A = [2, 3; 4, -2];
B = [8; 2];
X = A \ B;
disp(X);
```
通过以上习题的答案，我们可以看到MATLAB的强大功能和灵活性。
掌握这些基本的使用技巧，可以帮助我们更好地应用MATLAB解决实际问题，提高工作效率。
希望大家在学习和使用MATLAB的过程中能够不断积累经验，不断提升自己的技能水平。
腹有诗书气自华《数值计算方法与Matlab 》 样卷答案一．填空题：（每空3分,共42分）1． 8，6105.0-⨯ 。
2．)(3)1(2)1(1)(3)1(2)1(1)(3)1(3)(3)(2)1(1)(3)(2)1(1)(2)1(2)(3)(2)(1)(3)(2)(1)(1)1(1)1(22)22()1()1(222)1()222(k k k k k k k k k k k k k k k k k k k k k k k k x x x x x x x x x x x x x x x x x x x x x x x x ωωωωωωωωωωωωωω-+--=---⋅+=+--+-=---⋅+=++--=+--⋅+=+++++++++，)2,1(∈ω。
3．],[1b a C S m -∈。
4. 1e 2e ---x ，⎩⎨⎧==-=⋅--⎰,3,2,1,0;0,e 1d )(e 110k k x x g k x ，正交投影。
5. 2阶，6阶。
6．10.6658，10.9521，10.9501。
7. 4002.2)00.1(=ε，4030.2)01.1(=ε。
二．解下列各题：（每题9分，共36分）1．解：令)1(23+=t x ， （2分） 则⎰⎰-+++=+112302dt )1(25.21)1(49d 1t t x x x ⎭⎬⎫++++⎩⎨⎧++-+-≈22)6.01(25.21)6.01(9525.2198)6.01(25.21)6.01(9549 （8分）210631.10≈ （9分） 2．解：记系数矩阵为A, 对增广矩阵[]b A |作初等行运算,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--401533933112⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==5.55.115.35.405.75.401125.1,5.11,31,2l l ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=45.114005.75.4011212,3l , 所以13-=x ,2)5.75.1(5.4112=-=x x ,1)1(21321=-+-=x x x ,即方程组的解为 [1,2,-1]T . （4分）故系数矩阵A 的LU 分解为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⋅⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=4005.75.40112115.1015.1001A 。
习题一6、解：设正方形的边长为x ，则其面积为x 2，由题设知x 的近似值为x *。
记y *为y 的近似值，则E （y *）= y- y *= 2 x *（x- x *）= 20（x-x *）= 20E （x *）≤0.1 所以E （x *）= 0.005cm12、解：因为y 。
= 2，*0y = 1.41，所以*0y-y ≤12⨯210- =δ 于是有*11y y -=**00010y 110y 110y y 10--+=-≤0δ *22y y -=**2111110y 110y 110y y 10--+=-≤δ 类推有*10101010y y -≤δ=81102⨯ 即计算到10y ，其误差限为1010δ，亦即若在0y 处有误差限为δ，则 10y 的误差将扩大1010倍，可见这个计算过程是不稳定的。
习题二2、解：第一步：计算U 的第一行，L 的第二行，得116u = 122u = 131u = 141u =- 21211113l a u == 31311116l au == 41411116l a u ==-第二步：计算U 的第二行，L 的第二列，得22222112232321132424211432323112224242411222102/31/3()1/5()1/10u a l u u a l u u a l u l a l u u l a l u u =-==-==-==-==-=第三步：计算U 的第三行，L 的第三列，得33333113322334343114322443434113422333444441144224433437/109/10()/9/37U 955/370u a l u l u u a l u l u l a l u l u u u a l u l u l u =--==--=-=--=-=---=第四步：计算的第四行，得从而，6211241011411013-⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥--⎣⎦=100062111100010321161100110161109371000955370-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦由LY=b,解得Y=（6，-3，23/5，-955/370）T 由UX=Y ，解得X=（1，-1，1，-1）T 。
