2020版导与练第一轮复习理科数学 (20)

第十节变化率与导数、导数的计算知识点一 导数的概念1．函数y ＝f (x )在x ＝x 0处的导数 称函数y ＝f (x )在x ＝x 0处的瞬时变化率lim Δx →0f (x 0＋Δx )－f (x 0)Δx＝lim Δx →0Δy Δx 为函数y ＝f (x )在x ＝x 0处的导数，记作f ′(x 0)或y ′|x ＝x 0，即f ′(x 0)＝lim Δx →0ΔyΔx ＝lim Δx →0f (x 0＋Δx )－f (x 0)Δx. 2．导数的几何意义函数f (x )在点x 0处的导数f ′(x 0)的几何意义是在曲线y ＝f (x )上点P (x 0，y 0)处的切线的斜率(瞬时速度就是位移函数s (t )对时间t 的导数)．相应地，切线方程为y －y 0＝f ′(x 0)(x －x 0)．3．函数f (x )的导函数称函数f ′(x )＝lim Δx→0f (x ＋Δx )－f (x )Δx为f (x )的导函数．1．某质点的位移函数是s (t )＝2t 3－12gt 2(g ＝10 m/s 2)，则当t ＝2 s 时，它的加速度是( A )A ．14 m/s 2B ．4 m/s 2C ．10 m/s 2D ．－4 m/s 2解析：由v (t )＝s ′(t )＝6t 2－gt ，a (t )＝v ′(t )＝12t －g ，得t ＝2时，a (2)＝v ′(2)＝12×2－10＝14(m/s 2)．2．函数f (x )＝x 2在区间[1,2]上的平均变化率为3，在x ＝2处的导数为4.解析：函数f (x )＝x 2在区间[1,2]上的平均变化率为22－122－1＝3，在x ＝2处的导数为f ′(2)＝2×2＝4.3．(2018·全国卷Ⅱ)曲线y ＝2ln(x ＋1)在点(0,0)处的切线方程为y ＝2x . 解析：∵y ＝2ln(x ＋1)，∴y ′＝2x ＋1.当x ＝0时，y ′＝2，∴曲线y ＝2ln(x ＋1)在点(0,0)处的切线方程为y －0＝2(x －0)，即y ＝2x . 知识点二 导数的运算1．几种常见函数的导数2.导数的运算法则(1)[f (x )±g (x )]′＝f ′(x )±g ′(x )； (2)[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )；(3)⎣⎢⎡⎦⎥⎤f (x )g (x )′＝f ′(x )g (x )－f (x )g ′(x )[g (x )]2(g (x )≠0)．3．复合函数的导数复合函数y ＝f (g (x ))的导数和函数y ＝f (u )，u ＝g (x )的导数间的关系为y x ′＝y u ′·u x ′，即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积．4．函数y ＝x cos x －sin x 的导数为( B ) A ．x sin x B ．－x sin x C ．x cos xD ．－x cos x解析：y ′＝(x cos x )′－(sin x )′＝cos x －x sin x －cos x ＝－x sin x . 5．已知f (x )＝x ln x ，若f ′(x 0)＝2，则x 0等于( B ) A ．e 2 B ．e C.ln22D ．ln2解析：f (x )的定义域为(0，＋∞)，f ′(x )＝ln x ＋1，由f ′(x 0)＝2，即ln x 0＋1＝2，解得x 0＝e.1．求导常见易错点：①公式(x n )′＝nx n －1与(a x )′＝a x ln a 相互混淆；②公式中“＋”“－”号记混，如出现如下错误：⎣⎢⎡⎦⎥⎤f (x )g (x )′＝f ′(x )g (x )＋f (x )g ′(x )[g (x )]2，(cos x )′＝sin x .2．f ′(x 0)代表函数f (x )在x ＝x 0处的导数值；(f (x 0))′是函数值f (x 0)的导数，且(f (x 0))′＝0.3．曲线的切线与曲线的公共点的个数不一定只有一个，而直线与二次曲线相切只有一个公共点．考向一 导数的运算【例1】 求下列函数的导数． (1)y ＝x 2sin x ； (2)y ＝ln x ＋1x ； (3)y ＝cos x e x ；(4)y ＝x sin ⎝ ⎛⎭⎪⎫2x ＋π2cos ⎝ ⎛⎭⎪⎫2x ＋π2. 【解】 (1)y ′＝(x 2)′sin x ＋x 2(sin x )′ ＝2x sin x ＋x 2cos x .(2)y ′＝⎝ ⎛⎭⎪⎫ln x ＋1x ′＝(ln x )′＋⎝ ⎛⎭⎪⎫1x ′＝1x －1x 2.(3)y ′＝⎝ ⎛⎭⎪⎫cos x e x ′＝(cos x )′e x－cos x (e x)′(e x )2＝－sin x ＋cos xe x. (4)∵y ＝x sin ⎝ ⎛⎭⎪⎫2x ＋π2cos ⎝ ⎛⎭⎪⎫2x ＋π2 ＝12x sin(4x ＋π)＝－12x sin4x ，∴y ′＝－12sin4x －12x ·4cos4x ＝－12sin4x －2x cos4x .(1)对于复杂函数的求导，首先应利用代数、三角恒等变换等变形规则对函数解析式进行化简，然后求导，这样可以减少运算量，提高运算速度，减少差错.(2)利用公式求导时要特别注意除法公式中分子的符号，不要与求导的乘法公式混淆.(1)函数y ＝sin xx 的导数为y ′＝x cos x －sin x x 2. (2)已知f (x )＝(x ＋1)(x ＋2)(x ＋a )，若f ′(－1)＝2，则f ′(1)＝26. (3)函数f (x )的导函数为f ′(x )，且满足关系式f (x )＝x 2＋3xf ′(2)－ln x ，则f ′(2)的值是－74.解析：(1)∵y ＝sin xx ，∴y ′＝x (sin x )′－x ′sin x x 2＝x cos x －sin xx 2.(2)f (x )＝(x ＋1)(x ＋2)(x ＋a )＝(x 2＋3x ＋2)(x ＋a )＝x 3＋(a ＋3)x 2＋(3a ＋2)x ＋2a ，所以f ′(x )＝3x 2＋2(a ＋3)x ＋3a ＋2，所以f ′(－1)＝3×(－1)2＋2(a ＋3)×(－1)＋3a ＋2＝2，解得a ＝3，所以f ′(x )＝3x 2＋12x ＋11，所以f ′(1)＝3×12＋12×1＋11＝26.(3)∵f (x )＝x 2＋3xf ′(2)－ln x ，∴f ′(x )＝2x ＋3f ′(2)－1x ，令x ＝2，得f ′(2)＝4＋3f ′(2)－12，解得f ′(2)＝－74. 考向二 导数的几何意义方向1 已知切点求切线方程【例2】 (2018·全国卷Ⅰ)设函数f (x )＝x 3＋(a －1)x 2＋ax .若f (x )为奇函数，则曲线y ＝f (x )在点(0,0)处的切线方程为( )A ．y ＝－2xB ．y ＝－xC ．y ＝2xD ．y ＝x【解析】 解法1：因为函数f (x )＝x 3＋(a －1)x 2＋ax 为奇函数，所以f (－x )＝－f (x )，所以(－x )3＋(a －1)·(－x )2＋a (－x )＝－[x 3＋(a －1)x 2＋ax ]，所以2(a －1)x 2＝0，因为x ∈R ，所以a ＝1，所以f (x )＝x 3＋x ，所以f ′(x )＝3x 2＋1，所以f ′(0)＝1，所以曲线y ＝f (x )在点(0,0)处的切线方程为y ＝x .故选D.解法2：因为函数f (x )＝x 3＋(a －1)x 2＋ax 为奇函数，所以f (－1)＋f (1)＝0，所以－1＋a －1－a ＋(1＋a －1＋a )＝0，解得a ＝1，所以f (x )＝x 3＋x ，所以f ′(x )＝3x 2＋1，所以f ′(0)＝1，所以曲线y ＝f (x )在点(0,0)处的切线方程为y ＝x .故选D.【答案】 D 方向2 求切点坐标【例3】 设曲线y ＝e x 在点(0,1)处的切线与曲线y ＝1x (x >0)上点P 处的切线垂直，则点P 的坐标为________．【解析】 y ＝e x 的导数为y ′＝e x ，则曲线y ＝e x 在点(0,1)处的切线斜率k 1＝e 0＝1.y ＝1x (x >0)的导数为y ′＝－1x 2(x >0)，设P (m ，n )，则曲线y ＝1x (x >0)在点P 处的切线斜率k 2＝－1m 2(m >0)．因为两切线垂直，所以k 1k 2＝－1，所以m ＝1，n ＝1，则点P 的坐标为(1,1)．【答案】 (1,1)方向3 未知切点的切线问题【例4】 (1)(2019·西安八校联考)曲线y ＝x 3上一点B 处的切线l 交x 轴于点A ，△OAB (O 为原点)是以∠A 为顶角的等腰三角形，则切线l 的倾斜角为( )A ．30°B ．45°C ．60°D ．120°(2)(2019·广州市调研测试)已知直线y ＝kx －2与曲线y ＝x ln x 相切，则实数k 的值为________．【解析】 (1)解法1：因为y ＝x 3，所以y ′＝3x 2.设点B (x 0，x 30)(x 0≠0)，则k l ＝3x 20，所以切线l 的方程为y －x 30＝3x 20(x －x 0)．取y ＝0，则x ＝23x 0，所以点A (23x 0,0)．易知线段OB 的垂直平分线方程为y －x 302＝－1x 20(x －x 02)，根据线段OB 的垂直平分线过点A (23x 0,0)可得－x 302＝－1x 20(23x 0－x 02)，解得x 20＝33，所以k l ＝3x 20＝3，故切线l 的倾斜角为60°.故选C. 解法2：因为y ＝x 3，所以y ′＝3x 2.设点B (x 0，x 30)(x 0≠0)，则k l ＝3x 20，所以切线l 的方程为y －x 30＝3x 20(x －x 0)．取y ＝0，则x ＝23x 0，所以点A (23x 0,0)．由|OA |＝|AB |，得4x 209＝x 209＋x 60，又x 0≠0，所以x 20＝33，所以k l ＝3x 20＝3，故切线l 的倾斜角为60°.故选C.(2)由y ＝x ln x 得，y ′＝ln x ＋1.设直线y ＝kx －2与曲线y ＝x ln x 相切于点P (x 0，y 0)，则切线方程为y －y 0＝(ln x 0＋1)(x －x 0)，又直线y ＝kx －2恒过点(0，－2)，所以点(0，－2)在切线上，把(0，－2)以及y 0＝x 0ln x 0代入切线方程，得x 0＝2，故P (2,2ln2)．把(2,2ln2)代入直线的方程y ＝kx －2，得k ＝1＋ln2.【答案】 (1)C (2)1＋ln21.与切线有关问题的处理策略(1)已知切点A (x 0，y 0)求斜率k ，即求该点处的导数值，k ＝f ′(x 0). (2)已知斜率k ，求切点A (x 1，f (x 1))，即解方程f ′(x 1)＝k .,(3)求过某点M (x 1，y 1)的切线方程时，需设出切点A (x 0，f (x 0))，则切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)，再把点M (x 1，y 1)代入切线方程，求x 0.2.根据导数的几何意义求参数的值的思路一般是利用切点P (x 0，y 0)既在曲线上又在切线上构造方程组求解.1．(方向1)已知函数f (x )是奇函数，当x <0时，f (x )＝x ln(－x )＋x ＋2，则曲线y ＝f (x )在x ＝1处的切线方程为( B )A ．y ＝2x ＋3B ．y ＝2x －3C ．y ＝－2x ＋3D ．y ＝－2x －3解析：设x >0，则－x <0，∵f (x )为奇函数，当x <0时，f (x )＝x ln(－x )＋x ＋2，∴f (x )＝－f (－x )＝－(－x ln x －x ＋2)＝x ln x ＋x －2.∴f (1)＝－1，f ′(x )＝ln x ＋2.∴f ′(1)＝2，∴曲线y ＝f (x )在x ＝1处的切线方程是y ＝2x －3.故选B.2．(方向2)设a ∈R ，函数f (x )＝e x ＋a ·e －x 的导函数是f ′(x )，且f ′(x )是奇函数．若曲线y ＝f (x )的一条切线的斜率是32，则切点的横坐标为( A )A ．ln2B ．－ln2 C.ln22D ．－ln22解析：对f (x )＝e x ＋a ·e －x 求导得f ′(x )＝e x －a e －x ，又f ′(x )是奇函数，故f ′(0)＝1－a ＝0，解得a ＝1，故f ′(x )＝e x －e －x .设切点坐标为(x 0，y 0)，则f ′(x 0)＝e x 0－e －x 0＝32，得e x 0＝2或e x 0＝－12(舍去)，得x 0＝ln2.3．(方向3)经过原点(0,0)作函数f (x )＝x 3＋3x 2的图象的切线，则切线方程为y ＝0或9x ＋4y ＝0.解析：当(0,0)为切点时，f ′(0)＝0，故切线方程为y ＝0；当(0,0)不为切点时，设切点为P (x 0，x 30＋3x 20)(x 0≠0)，则切线方程为y －(x 30＋3x 20)＝(x －x 0)(3x 20＋6x 0)，因为切线过原点，所以x 30＋3x 20＝3x 30＋6x 20，所以x 0＝－32，此时切线方程为9x ＋4y ＝0.典例 若直线y ＝kx ＋b 是曲线y ＝ln x ＋2的切线，也是曲线y ＝ln(x ＋1)的切线，则b ＝________.【分析】 分别求出两个对应函数的导数，设出两个切点坐标，利用导数得到两个切点坐标之间的关系，进而求出切线斜率，求出b 的值．【解析】 解法1：求得(ln x ＋2)′＝1x ，[ln(x ＋1)]′＝1x ＋1.设曲线y ＝ln x ＋2上的切点为(x 1，y 1)，曲线y ＝ln(x ＋1)上的切点为(x 2，y 2)，则k ＝1x 1＝1x 2＋1，所以x 2＋1＝x 1. 又y 1＝ln x 1＋2，y 2＝ln(x 2＋1)＝ln x 1，所以k ＝y 1－y 2x 1－x 2＝2， 所以x 1＝1k ＝12，y 1＝ln 12＋2＝2－ln2，所以b ＝y 1－kx 1＝2－ln2－1＝1－ln2.解法2：设直线y ＝kx ＋b 与y ＝ln x ＋2的切点坐标为A (x 1，ln x 1＋2)，则在点A 处的切线方程为y －(ln x 1＋2)＝1x 1(x －x 1)，即为y ＝1x 1x ＋ln x 1＋1 ①，设直线y ＝kx ＋b 与y ＝ln(x ＋1)的切点坐标为B (x 2，ln(x 2＋1))，则在点B 处的切线方程为y －ln(x 2＋1)＝1x 2＋1(x －x 2)，即为y ＝1x 2＋1x ＋ln(x 2＋1)－x 2x 2＋1②，由①②表示同一直线，则⎩⎨⎧ x 1＝x 2＋1，ln x 1＋1＝ln (x 2＋1)－x 2x 2＋1，解得x 1＝12，x 2＝－12，则b ＝ln 12＋1＝1－ln2.【答案】 1－ln2已知曲线y ＝x ＋ln x 在点(1,1)处的切线与曲线y ＝ax 2＋(a ＋2)x ＋1相切，则a ＝8.解析：法1：∵y ＝x ＋ln x ，∴y ′＝1＋1x ，y ′|x ＝1＝2.∴曲线y ＝x ＋ln x 在点(1,1)处的切线方程为y －1＝2(x －1)，即y ＝2x －1.∵y ＝2x －1与曲线y ＝ax 2＋(a ＋2)x ＋1相切，∴a ≠0(当a ＝0时曲线变为y ＝2x ＋1与已知直线平行)．由⎩⎪⎨⎪⎧y ＝2x －1，y ＝ax 2＋(a ＋2)x ＋1 消去y ，得ax 2＋ax ＋2＝0.由Δ＝a 2－8a ＝0，解得a ＝8.法2：同法1得切线方程为y ＝2x －1.设y ＝2x －1与曲线y ＝ax 2＋(a ＋2)x ＋1相切于点(x 0，ax 20＋(a ＋2)x 0＋1)．∵y ′＝2ax ＋(a ＋2)，∴y ′|x ＝x 0＝2ax 0＋(a ＋2)．由⎩⎪⎨⎪⎧2ax 0＋(a ＋2)＝2，ax 20＋(a ＋2)x 0＋1＝2x 0－1，解得⎩⎨⎧ x 0＝－12，a ＝8.。

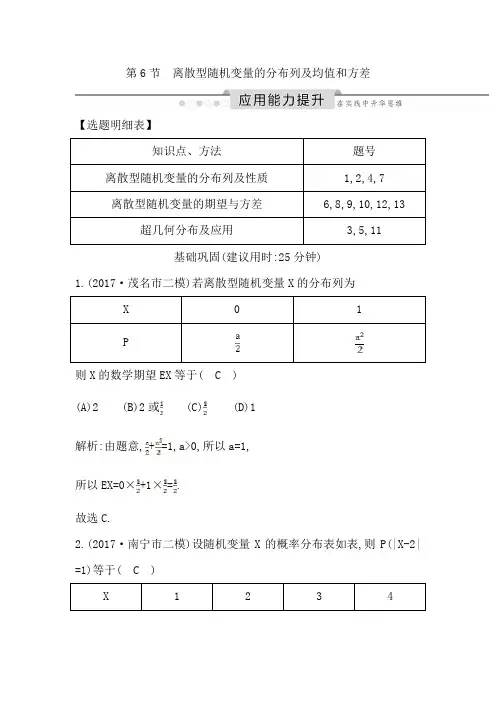
第6节离散型随机变量的分布列及均值和方差【选题明细表】基础巩固(建议用时:25分钟)1.(2017·茂名市二模)若离散型随机变量X的分布列为则X的数学期望EX等于( C )(A)2 (B)2或 (C) (D)1解析:由题意,+=1,a>0,所以a=1,所以EX=0×+1×=.故选C.2.(2017·南宁市二模)设随机变量X的概率分布表如表,则P(|X-2| =1)等于( C )(A) (B) (C) (D)解析:m=,P(|X-2|=1)=+=.故选C.3.有10张卡片,其中8张标有数字2,2张标有数字5,从中任意抽出3张卡片,设3张卡片上的数字之和为X,则X≥8的概率是( C ) (A) (B) (C) (D)解析:X的取值为6,9,12,X≥8时,P(X=9)==,P(X=12)==,所以X≥8的概率为+=.故选C.4.设随机变量ξ的分布列为P(ξ=)=ak(k=1,2,3,4,5),则P(<ξ<)等于( C )(A)(B)(C)(D)解析:由已知得分布列为由分布列的性质可得a+2a+3a+4a+5a=1,解得a=.所以P(<ξ<)=P(ξ=)+P(ξ=)+P(ξ=)=++=.故选C.5.一个袋中有4个红球,3个黑球,小明从袋中随机取球,设取到一个红球得2分,取到一个黑球得1分,从袋中任取4个球,则小明得分大于6分的概率是( A )(A)(B)(C)(D)解析:记得分为X,则X=5,6,7,8.P(X=7)==;P(X=8)==.所以P(X>6)=P(X=7)+P(X=8)=+=.6.(2017·合肥市二模)已知5件产品中有2件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为ξ,则Eξ等于( B )(A)3 (B)(C)(D)4解析:由题意知ξ的可能取值为2,3,4,P(ξ=2)=×=,P(ξ=3)=(×+×+×)×=,P(ξ=4)=1-P(ξ=2)-P(ξ=3)=,所以Eξ=2×+3×+4×=.故选B.7.设随机变量ξ等可能取1,2,3,…,n,若P(ξ<4)=0.3,则n= .解析:因为1,2,3,…,n每个值被取到的概率为,所以P(ξ<4)=P(ξ= 1)+P(ξ=2)+P(ξ=3)=++=0.3,所以n=10.答案:108.(2019·浙江宁波市二模)已知随机变量X的分布列如表:若EX=2,则a= ,DX= .解析:由随机变量X的分布列及EX=2,得解得a=0,b=,所以DX=(0-2)2×+(2-2)2×+(3-2)2×+(4-2)2×=.答案:0能力提升(建议用时:25分钟)9.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a,b,c ∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量ξ=|a-b|,则E ξ为( A )(A)(B)(C)(D)解析:因为抛物线的对称轴在y轴的左侧,所以-<0,即>0,即a,b同号.所以随机变量ξ的分布列为所以Eξ=0×+1×+2×=.故选A.10.(2019·广东汕头市二模)一个不透明的袋子中装有大小相同的12个黑球,4个白球,每次有放回地任意摸取一个球,共摸取3次,若用X 表示取到白球的次数,则X的数学期望EX与方差DX分别为, .解析:由题意,X的可能取值为0,1,2,3,摸到白球的概率为,则P(X=0)=()3=,P(X=1)=()2×=,P(X=2)=×()2=,P(X=3)=()3=.所以X的概率分布列为所以数学期望为EX=0×+1×+2×+3×=或EX=3×=;方差为DX=×(0-)2+×(1-)2+×(2-)2+×(3-)2=.答案:11.(2017·黔东南州一模)从某校高三上学期期末数学考试成绩中,随机抽取了60名学生的成绩得到如图所示的频率分布直方图.(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;(2)若用分层抽样的方法从分数在[30,50)和[130,150]的学生中抽取6人,该6人中成绩在[130,150]的有几人?(3)在(2)抽取的6人中,随机抽取3人,设分数在[130,150]内的人数为ξ,求其数学期望Eξ.解:(1)由频率分布直方图,得该校高三学生本次数学考试的平均分为0.005 0×20×40+0.007 5×20×60+0.007 5×20×80+0.015 0×20×100+0.012 5×20×120+0.002 5×20×140=92(分).(2)样本中分数在[30,50)和[130,150]的人数分别为6人和3人,所以抽取的6人中分数在[130,150]的人有6×=2(人).(3)由(2)知,抽取的6人中分数在[130,150]的有2人,依题意ξ的所有取值为0,1,2,当ξ=0时,P(ξ=0)==;当ξ=1时,P(ξ=1)==;当ξ=2时,P(ξ=2)==;所以Eξ=0×+1×+2×=1.12.(2019·天津和平区二模)甲、乙、丙均两次参加英语高考,取两次成绩中较高的为最终成绩,三人第一次成绩不低于130分的概率依次为,,.甲若第一次成绩不低于130分,则第二次成绩不低于130分的概率为,若第一次成绩在130分以下,则第二次成绩不低于130分的概率为;乙若第一次成绩不低于130分,则第二次成绩不低于130分的概率为,若第一次成绩在130分以下,则第二次成绩不低于130分的概率为;丙第二次成绩不受第一次成绩的影响,不低于130分的概率为.(1)设A为事件“甲的英语高考最终成绩不低于130分”,B为事件“乙的英语高考最终成绩不低于130分”,C为事件“丙的英语高考最终成绩不低于130分”,分别求出事件A、事件B、事件C发生的概率;(2)设甲、乙、丙中英语高考最终成绩不低于130分的人数为X,求X 的分布列与数学期望.解:(1)A为事件“甲的英语高考最终成绩不低于130分”,事件A发生的概率P(A)=+(1-)×=,B为事件“乙的英语高考最终成绩不低于130分”,事件B发生的概率P(B)=+(1-)×=,C为事件“丙的英语高考最终成绩不低于130分”,事件C发生的概率P(C)=+(1-)×=.(2)设甲、乙、丙中英语高考最终成绩不低于130分的人数为X,则X 的可能取值为0,1,2,3,P(X=0)=P()=××=,P(X=1)=P( C+B+A)=××+××+××=,P(X=2)=P(BC+A C+AB)=××+××+××=,P(X=3)=P(ABC)=××=.所以X的分布列为数学期望EX=0×+1×+2×+3×=2.13.(2019·河南洛阳市二模)某市共有户籍人口约400万,其中老人(60岁及以上)约66万,为了解老人们的身体健康状况,相关部门从这些老人中随机抽取600人进行健康评估.健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,由样本数据制得条形图如图.(1)根据条形图完成下表:并估算该市80岁及以上老人占全市户籍人口的百分比;(2)据统计,该市大约有五分之一的户籍老人无固定收入,该市政府计划给这部分老人每月发放生活补贴,标准如下:①80岁及以上老人每人每月发放生活补贴200元;②80岁以下老人每人每月发放生活补贴120元;③不能自理的老人每人每月额外发放生活补贴100元.试估算该市政府为执行此计划每年所需资金的总额(单位:亿元,保留两位小数)解:(1)80岁及以上老人大约为66×=11(万人),所以该市80岁及以上老人占全市户籍人口的百分比为×100%=2.75%.(2)设某户籍老人每月享受的生活补助为X元,X的取值为0,120,200, 220,300.则P(X=0)=,P(X=120)=×=,P(X=200)=×=,P(X=220)=×=,P(X=300)=×=.所以X的分布列为所以EX=0×+120×+200×+220×+300×=28.所以该市政府为执行此计划每年所需资金的总额为28×12×66×104=2.217 6×108≈2.22×108(元)=2.22(亿元).所以该市政府为执行此计划每年所需资金的总额约为2.22亿元.。

第20讲导数的实际应用及综合应用1．某商场销售某种商品的经验表明，该商品每日的销售量y(单位：千克)与销售价格x(单位：元/千克)满足关系式y＝ax－3＋10(x－6)2，其中3＜x＜6，a为常数．已知销售价格为5元/千克时，每日可售出该商品11千克．(1)求a的值；(2)若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大．(1)因为当x＝5时，y＝11，所以a5－3＋10(5－6)2＝11，解得a＝2.(2)由(1)知该商品每日的销售量y＝2x－3＋10(x－6)2(3＜x＜6)，所以该商场每日销售该商品所获得的利润f(x)＝[2x－3＋10(x－6)2](x－3)＝2＋10(x－3)(x－6)2(3＜x＜6)，所以f′(x)＝10[(x－6)2＋2(x－3)(x－6)]＝30(x－4)(x－6)．当x变化时，f(x)，f′(x)的变化情况如下表：x (3，4) 4 (4，6)f′(x)＋0 －f(x) 单调递增极大值42 单调递减由上表可得，x＝4是函数f(x)在区间(3,6)内的极大值点，也是最大值点，所以当x＝4时，f(x)max＝42.答：当销售价格定为4元/千克时，商场每日销售该商品所获得的利润最大．2．请你设计一个包装盒，如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A、B、C、D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上被切去的等腰直角三角形斜边的两个端点，设AE＝FB＝x(cm)．(1)若广告商要包装盒侧面积S(cm2)最大，试问x应取何值？(2)若广告商要包装盒容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．(1)根据题意，有S＝4×2x×22(60－2x)＝－8(x－15)2＋1800(0<x<30)．所以x ＝15时，包装盒侧面积S 最大． (2)根据题意，有 V ＝(2x )2×22(60－2x )＝22x 2(30－x )(0<x <30)． 所以V ′＝62x (20－x )．当0<x <20时，V ′>0，V 单调递增； 当20<x <30时，V ′<0，V 单调递减． 所以当x ＝20时，V 取极大值，也是最大值．此时，包装盒的高与底面边长的比值为22(60－2x )2x＝12，即x ＝20时，包装盒容积V (cm 3)最大，此时包装盒的高与底面边长的比值为12.3．(2017·全国卷Ⅱ)已知函数f (x )＝ax 2－ax －x ln x ，且f (x )≥0. (1)求a ；(2)证明：f (x )存在唯一的极大值点x 0，且e －2<f (x 0)<2－2.(1)f (x )的定义域为(0，＋∞)． 设g (x )＝ax －a －ln x ，则f (x )＝xg (x )，f (x )≥0等价于g (x )≥0. 因为g (1)＝0，g (x )≥0，故g ′(1)＝0，而g ′(x )＝a －1x，g ′(1)＝a －1，得a ＝1.若a ＝1，则g ′(x )＝1－1x .当0<x <1时，g ′(x )<0，g (x )单调递减； 当x >1时，g ′(x )>0，g (x )单调递增．所以x ＝1是g (x )的极小值点，故g (x )≥g (1)＝0. 综上，a ＝1.(2)由(1)知f (x )＝x 2－x －x ln x ，f ′(x )＝2x －2－ln x .设h (x )＝2x －2－ln x ，则h ′(x )＝2－1x.当x ∈(0，12)时，h ′(x )<0；当x ∈(12，＋∞)时，h ′(x )>0.所以h (x )在(0，12)上单调递减，在(12，＋∞)上单调递增．又h (e －2)>0，h (12)<0，h (1)＝0，所以h (x )在(0，12)上有唯一零点x 0，在[12，＋∞)上有唯一零点1，且当x ∈(0，x 0)时，h (x )>0；当x ∈(x 0,1)时，h (x )<0；当x ∈(1，＋∞)时，h (x )>0.因为f ′(x )＝h (x )，所以x ＝x 0是f (x )的唯一极大值点． 由f ′(x 0)＝0得ln x 0＝2(x 0－1)，故f (x 0)＝x 0(1－x 0)． 由x 0∈(0，12)得f (x 0)<14.因为x ＝x 0是f (x )在(0,1)上的最大值点， 由e －1∈(0,1)，f ′(e －1)≠0得f (x 0)>f (e －1)＝e －2. 所以e －2<f (x 0)<2－2.4．(2018·华南师大附中模拟)函数f(x)＝x 2＋m ln (1＋x)．(1)讨论f(x)的单调性；(2)若函数f(x)有两个极值点x 1，x 2，且x 1<x 2，求证：2f(x 2)>－x 1＋2x 1ln 2.f(x)的定义域是(－1，＋∞)，f′(x)＝2x 2＋2x ＋m1＋x，(1)由题设知，1＋x>0，令g(x)＝2x 2＋2x ＋m ，这是开口向上，以x ＝－12为对称轴的抛物线，g(－12)＝－12＋m ，①当g(－12)≥0，即m ≥12时，g(x)≥0，即f′(x)≥0在(－1，＋∞)上恒成立．②当g(－12)<0，即m<12时，由g(x)＝2x 2＋2x ＋m ＝0得x ＝－12±1－2m 2，令x 1＝－12－1－2m 2，x 2＝－12＋1－2m2， 则x 1<－12，x 2>－12.1)当g(－1)≤0即m ≤0时，x 1<－1，故在(－1，x 2)上，g(x)<0，即f′(x)<0，在(x 2，＋∞)上，g(x)>0，即f′(x)>0.2)当g(－1)>0时，即0<m<12时，x (－1，x 1) x 1 (x 1，x 2) x 2 (x 2，＋∞)g(x)>0 ＋ 0 － 0 ＋ f′(x)>0 ＋ 0 － 0 ＋ f(x)递增递减递增综上：m ≤0时，f(x)在(－1，－12＋1－2m 2)上单调递减，在(－12＋1－2m2，＋∞)上单调递增；0<m<12时，f(x)在(－12－1－2m 2，－12＋1－2m 2)上单调递减，在(－1，－12－1－2m2)和(－12＋1－2m2，＋∞)上单调递增； m ≥12时，f(x)在(－1，＋∞)上单调递增．(2)证明：若函数f(x)有两个极值点x 1，x 2，且x 1<x 2， 则必是0<m<12，g(0)>0，则－1<x 1<－12<x 2<0，且f(x)在(x 1，x 2)上递减，在(－1，x 1)和(x 2，＋∞)上递增，则f(x 2)<f(0)＝0， 因为x 1，x 2是g(x)＝2x 2＋2x ＋m ＝0的两个不等实根，所以⎩⎪⎨⎪⎧x 1＋x 2＝－1，x 1x 2＝m2，即x 1＝－1－x 2，m ＝2x 1x 2， 所以若证2f(x 2)>－x 1＋2x 1ln 2成立，只需证2f(x 2 ) ＝ 2x 22 ＋ 2m ln (1 ＋ x 2 ) ＝ 2x 22 ＋ 4x 1 x 2 ln (1 ＋ x 2 )＝2x 22 －4(1 ＋ x 2 )x 2 ln (1 ＋ x 2 ) >－(－1－x 2)＋2(－1－x 2)ln 2 ＝1＋x 2－2(1＋x 2)ln 2.即证2x 22 －4(1 ＋ x 2 )x 2 ln (1 ＋ x 2 )－(1＋x 2)(1－2ln 2)>0对－12<x 2<0恒成立， 设φ(x)＝2x 2－4(1＋x)x ln (1＋x)－(1＋x)(1－2ln 2)(－12<x<0)，φ′(x)＝－4(1＋2x)ln (1＋x)＋ln 4e，当－12<x<0时，1＋2x>0，ln (1＋x)<0，ln 4e>0，故φ′(x)>0，故φ(x)在(－12，0)上递增，故φ(x)>φ(－12)＝2×14－4×12×(－12)×ln 12－12×(1－2ln 2)＝0，所以2x 22 －4(1 ＋ x 2 )x 2 ln (1 ＋ x 2 )－(1＋x 2)(1－2ln 2)>0对－12<x 2<0恒成立， 所以2f(x 2)>－x 1＋2x 1ln 2.感谢您的下载!快乐分享，知识无限！由Ruize收集整理！。

集合的概念与运算1．(2018·全国卷Ⅰ)已知集合A＝{0,2}，B＝{－2，－1,0,1,2}，则A∩B＝(A)A．{0,2} B．{1,2}C．{0} D．{－2，－1,0,1,2}A∩B＝{0,2}∩{－2，－1,0,1,2}＝{0,2}．2．(2016·山东卷)设集合U＝{1,2,3,4,5,6}，A＝{1,3,5}，B＝{3,4,5}，则∁U(A∪B)＝(A)A．{2,6} B．{3,6}C．{1,3,4,5} D．{1,2,4,6}因为A＝{1,3,5}，B＝{3,4,5}，所以A∪B＝{1,3,4,5}．又U＝{1,2,3,4,5,6}，所以∁U(A∪B)＝{2,6}．3．(2018·武汉调研测试)已知集合M＝{x|x2＝1}，N＝{x|ax＝1}，若N M，则实数a 的取值集合为(D)A．{1} B．{－1,1}C．{1,0} D．{1，－1,0}M＝{x|x2＝1}＝{－1,1}，又N M，N＝{x|ax＝1}，则N＝{－1}，{1}，∅满足条件，所以a＝1，－1,0，即实数a的取值集合为{1，－1,0}．4．(2018·佛山一模)已知全集U＝R，集合A＝{0,1,2,3,4}，B＝{x|x2－2x＞0}，则图中阴影部分表示的集合为(A)A．{0,1,2} B．{1,2}C．{3,4} D．{0,3,4}因为B＝{x|x2－2x＞0}＝{x|x＞2或x＜0}，所以∁U B＝{x|0≤x≤2}，所以图中阴影部分表示的集合为A ∩(∁U B )＝{0,1,2}．5．设集合A ＝{1,2,3}，B ＝{4,5}，M ＝{x |x ＝a ＋b ，a ∈A ，b ∈B }，则集合M 中的元素个数为(B)A ．3B ．4C ．5D ．6M ＝{5,6,7,8}，所以M 中的元素个数为4.6．(2017·江苏卷)已知集合A ＝{1,2}，B ＝{a ，a 2＋3}．若A ∩B ＝{1}，则实数a 的值为 1 .因为A ∩B ＝{1}，A ＝{1,2}，所以1∈B 且2∉B .若a ＝1，则a 2＋3＝4，符合题意． 又a 2＋3≥3≠1，故a ＝1.7．已知集合A ＝{y |y ＝1x}，B ＝{y |y ＝x 2}，则A ∩B ＝ (0，＋∞) .A ＝{y |y ＝1x}＝(－∞，0)∪(0，＋∞)，B ＝{y |y ＝x 2}＝[0，＋∞)，所以A ∩B ＝(0，＋∞)．8．设集合A ＝{x |x 2－3x －4<0}，则A ∩Z ＝ {0,1,2,3} ，A ∩Z 的所有子集的个数为 16 .A ＝{x |x 2－3x －4<0}＝{x |－1<x <4}，所以A ∩Z ＝{0,1,2,3}，A ∩Z 的子集个数有24＝16个．9．(2017·山东卷)设集合M ＝{x ||x －1|<1}，N ＝{x |x <2}，则 M ∩N ＝(C) A ．(－1,1) B ．(－1,2) C ．(0,2) D ．(1,2)因为M ＝{x |0<x <2}，N ＝{x |x <2}，所以M ∩N ＝{x |0<x <2}∩{x |x <2}＝{x |0<x <2}．10．已知集合A ＝{x |y ＝lg(x －x 2)}，B ＝{x |x 2－cx <0，c >0}，若A ⊆B ，则实数c 的取值范围是(B)A ．(0,1]B ．[1，＋∞)C ．(0,1)D ．(1，＋∞)由x －x 2>0，得0<x <1，所以A ＝(0,1)，由x 2－cx <0，得0<x <c ，所以B ＝(0，c )， 因为A ⊆B ，所以c ≥1.11．已知M ＝{x |－2≤x ≤5}，N ＝{x |a ＋1≤x ≤2a －1}． (1)若a ＝3，则M ∪(∁R N )＝ R .(2)若N ⊆M ，则实数a 的取值范围为 (－∞，3] .(1)当a ＝3时，N ＝{x |4≤x ≤5}，所以∁R N ＝{x |x <4或x >5}． 所以M ∪(∁R N )＝R .(2)①当2a －1<a ＋1，即a <2时，N ＝∅， 此时满足N ⊆M .②当2a －1≥a ＋1，即a ≥2时，N ≠∅，由N ⊆M ，得⎩⎪⎨⎪⎧a ＋1≥－2，2a －1≤5，所以2≤a ≤3.综上，实数a 的取值范围为(－∞，3]．12．(2018·黄石月考)某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 人．设全集U 为某班30人，集合A 为喜爱篮球运动的15人，集合B 为喜爱乒乓球运动的10人，如图．设两者都喜欢的人数为x 人，则只喜爱篮球的有(15－x )人，只喜爱乒乓球的有(10－x )人，由此可得(15－x )＋(10－x )＋x ＋8＝30，解得x ＝3.所以15－x ＝12，即所求人数为12人．命题及其关系、充分条件与必要条件1．(2018·深圳市第二次调研)设A ，B 是两个集合，则“x ∈A ”是“x ∈A ∩B ”的(B)A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件因为x ∈A ∩B ⇒x ∈A 且x ∈B ⇒x ∈A .但x ∈A ≠> x ∈A ∩B .所以“x ∈A ”是“x ∈A ∩B ”的必要不充分条件． 2．命题“若α＝π4，则tan α＝1”的逆否命题为(C)A ．若α≠π4，则tan α≠1 B．若α＝π4，则tan α≠1C ．若tan α≠1，则α≠π4D ．若tan α≠1，则α＝π4将条件和结论分别否定后作为结论和条件即得到逆否命题．3．(2018·天津卷)设x ∈R ，则“x 3>8”是“|x |>2”的(A) A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件由x 3>8⇒x >2⇒|x |>2，反之不成立，故“x 3>8”是“|x |>2”的充分而不必要条件．4．(2018·广东肇庆一模)原命题：设a ，b ，c ∈R ，若“a >b ”，则“ac 2>bc 2”，以及它的逆命题、否命题、逆否命题中，真命题共有(C)A ．0个B ．1个C ．2个D ．4个因为当c ＝0时，由a >b ≠> ac 2>bc 2，所以原命题为假，从而逆否命题为假．又ac 2>bc 2⇒a >b ，所以逆命题为真，从而否命题为真． 故真命题共有2个．5．(2018·湖北新联考四模)若“x >2m 2－3”是“－1<x <4”的必要不充分条件，则实数m 的取值范围是(D)A ．[－3,3]B ．(－∞，－3]∪[3，＋∞)C ．(－∞，－1]∪[1，＋∞) D．[－1,1]“x >2m 2－3”是“－1<x <4”的必要不充分条件，所以(－1,4) (2m 2－3，＋∞)，所以2m 2－3≤－1，解得－1≤m ≤1.6．命题“若a >b ，则2a>2b－1”的否命题为 若a ≤b ，则2a≤2b－1 .7．(2018·北京卷)能说明“若a ＞b ，则1a ＜1b”为假命题的一组a ，b 的值依次为 1，－1(答案不唯一) .只要保证a 为正b 为负即可满足要求．当a ＞0＞b 时，1a ＞0＞1b.只要取满足上述条件的a ，b 值即可，如a ＝1，b ＝－1(答案不唯一)．8．f (x )是R 上的增函数，且f (－1)＝－4，f (2)＝2，设P ＝{x |f (x ＋t )＋1<3}，Q ＝{x |f (x )<－4}，若“x ∈P ”是“x ∈Q ”的充分不必要条件，则实数t 的取值范围为 (3，＋∞) .依题意P ＝{x |f (x ＋t )＋1<3}＝{x |f (x ＋t )<2}＝{x |f (x ＋t )<f (2)}，Q ＝{x |f (x )<－4}＝{x |f (x )<f (－1)}， f (x )是R 上的增函数，所以P ＝{x |x <2－t }，Q ＝{x |x <－1}， 要使“x ∈P ”是“x ∈Q ”的充分不必要条件， 需2－t <－1，解得t >3，所以实数t 的取值范围是(3，＋∞)．9．(2016·天津卷)设x ＞0，y ∈R ，则“x ＞y ”是“x ＞|y |”的(C) A ．充要条件 B ．充分而不必要条件C ．必要而不充分条件D ．既不充分也不必要条件(1)分别判断x >y ⇒x >|y |与x >|y |⇒x >y 是否成立，从而得到答案．当x ＝1，y ＝－2时，x >y ，但x >|y |不成立； 若x >|y |，因为|y |≥y ，所以x >y .所以“x >y ”是“x >|y |”的必要而不充分条件．10．(2017·浙江卷)已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d ＞0”是“S 4 ＋S 6＞2S 5”的(C)A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件(方法一)因为数列{a n }是公差为d 的等差数列， 所以S 4＝4a 1＋6d ，S 5＝5a 1＋10d ，S 6＝6a 1＋15d ， 所以S 4＋S 6＝10a 1＋21d,2S 5＝10a 1＋20d . 若d >0，则21d >20d,10a 1＋21d >10a 1＋20d ， 即S 4＋S 6>2S 5.若S 4＋S 6>2S 5，则10a 1＋21d >10a 1＋20d ，即21d >20d ， 所以d >0.所以“d >0”是“S 4＋S 6>2S 5”的充分必要条件． (方法二)因为S 4＋S 6>2S 5S 4＋S 4＋a 5＋a 6>2(S 4＋a 5a 6>a 5a 5＋d >a 5d >0，所以“d >0”是“S 4＋S 6>2S 5”的充分必要条件．11．(2018·武汉调研测试)在△ABC 中，角A ，B ，C 的对应边分别为a ，b ，c ，条件p ：a ≤b ＋c 2，条件q ：A ≤B ＋C 2，那么条件p 是条件q 成立的(A)A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件条件q ：A ≤B ＋C2A ≤π－A 2A ≤π3. 条件p ：a ≤b ＋c2⇒cos A ＝b 2＋c 2－a22bc≥b 2＋c 2－b ＋c222bc＝3b 2＋3c 2－2bc 8bc ≥12⇒0<A ≤π3.所以p ⇒q ，但q p .如∠A ＝60°，a ＝3，b ＝1，c ＝2，不能得到a ≤b ＋c2.所以p 是q 的充分而不必要条件．12．(2018·江西赣中南五校二模)“a >0”是“函数y ＝ax 2＋x ＋1在(0，＋∞)上单调递增”的 充分不必要 条件．当a >0时，y ＝a (x ＋12a )2＋1－14a ，在(－12a，＋∞)上单调递增，因此在(0，＋∞)上单调递增，故充分性成立．当a ＝0时，y ＝x ＋1，在R 上单调递增，因此在(0，＋∞)上单调递增．故必要性不成立．综上，“a >0”是“函数y ＝ax 2＋x ＋1在(0，＋∞)上单调递增”的充分不必要条件．简单的逻辑联结词、全称量词与存在量词1．若p 是真命题，q 是假命题，则(D) A ．p ∧q 是真命题 B ．p ∨q 是假命题 C ．﹁p 是真命题 D ．﹁q 是真命题由“且”命题一假则假，“或”命题一真则真，命题与命题的否定真假相反，得A 、B 、C 都是错误的，故选D.2．(2018·河北五校高三联考)已知命题p ：“a >b ”是“2a>2b”的充要条件；q ：∃x ∈R ，|x ＋1|≤x ，则(D)A ．﹁p ∨q 为真命题B ．p ∧q 为真命题C ．p ∧﹁q 为假命题D ．p ∨q 为真命题对于p ：因为a >b ⇒2a>2b，反之，2a>2b⇒a >b ，所以“a >b ”是“2a >2b”的充要条件，即p 是真命题．对于q ：|x ＋1|≤x ⇔⎩⎪⎨⎪⎧x ＋1≥0，x ＋1≤x 或⎩⎪⎨⎪⎧x ＋1<0，－x －1≤x .解得x ∈∅，即不等式无实数解，所以q 是假命题． 所以p ∨q 为真命题．3．命题“∃x 0∈(0，＋∞)，ln x 0＝x 0－1”的否定是(A) A ．∀x ∈(0，＋∞)，ln x ≠x －1 B ．∀x ∉(0，＋∞)，ln x ＝x －1 C ．∃x 0∈(0，＋∞)，ln x 0≠x 0－1 D ．∃x 0∉(0，＋∞)，ln x 0＝x 0－1修改原命题中的两个地方即可得其否定，∃改为∀，否定结论，即ln x ≠x －1，故选A.4．(2018·三亚校级期中)命题“对任意的x ∈R ，x 3－x 2＋1≤0”的否定是(C) A ．不存在x ∈R ，x 3－x 2＋1≤0 B ．存在x 0∈R ，x 30－x 20＋1≥0 C ．存在x 0∈R ，x 30－x 20＋1>0 D ．对任意的x ∈R ，x 3－x 2＋1>05．(2018·湖南省六校联考) 下列各组命题中，满足“p ∨q ”为真、“p ∧q ”为假、“﹁q ”为真的是(B)A ．p ：0＝∅；q ：0∈∅B ．p ：x >2是x >1成立的充分不必要条件；q ：∀x ∈{1，－1,0},2x ＋1>0C ．p ：a ＋b ≥2ab (a >0，b >0)；q ：不等式|x |>x 的解集是(－∞，0)D ．p ：y ＝1x在定义域内是增函数；q ：f (x )＝e x ＋e －x是偶函数由题意可知，满足“p ∨q ”为真、“p ∧q ”为假、“﹁q ”为真，可知p 为真、q为假．A 中，p 、q 都为假；B 中，p 为真，q 为假；C 中，p 、q 都为真；D 中，p 为假、q 为真．故选B.6．(2017·湖北武汉2月调研)命题“y ＝f (x )(x ∈M )是奇函数”的否定是(D) A ．∃x ∈M ，f (－x )＝－f (x ) B ．∀x ∈M ，f (－x )≠－f (x ) C ．∀x ∈M ，f (－x )＝－f (x ) D ．∃x ∈M ，f (－x )≠－f (x )命题“y ＝f (x )(x ∈M )是奇函数”的否定是∃x ∈M ，f (－x )≠－f (x )． 7．已知命题p ：“∃x 0∈R ，|x 0|＋x 20<0”，则﹁p 为 ∀x ∈R ，|x |＋x 2≥0 _. 8．若x ∈[0，π4]，tan x ≤m ”是真命题，则实数m 的最小值为 1 .由题意，原命题等价于tan x ≤m 在区间[0，π4]上恒成立，即y ＝tan x 在[0，π4]上的最大值小于或等于m ，又y ＝tan x 在[0，π4]上的最大值为1，所以m ≥1，即m 的最小值为1.9．(2018·湖南长郡中学联考)已知命题p ：∃x 0∈(－∞，0)，2x 0<3x 0，命题q ：∀x ∈(0，π2)，tan x >sin x ，则下列命题为真命题的个数是(B)①p ∨q ；②p ∨(﹁q )；③(﹁p )∧q ；④p ∧(﹁q )． A ．1个 B ．2个 C ．3个 D ．4个因为幂函数y ＝x α，当α<0时在(0，＋∞)上递减， 由x 0<0,2<3，得2x 0>3x 0，所以p 为假命题．因为对于x ∈(0，π2)，sin x <x <tan x ，所以q 为真命题．所以①为真，②为假，③为真，④为假． 即真命题的个数是2.10．(2018·兰州模拟)已知下列四个命题：p 1：若直线l 和平面α内的无数条直线垂直，则l ⊥α； p 2：若f (x )＝2x －2－x ，则x ∈R ，f (－x )＝－f (x )； p 3：若f (x )＝x ＋1x ＋1，则∃x 0∈(0，＋∞)，f (x 0)＝1；p 4：在△ABC 中，若A >B ，则sin A >sin B .其中真命题的个数是(B) A ．1 B ．2 C ．3 D ．4平面的斜线l 可以和平面内无数条平行直线垂直，p 1为假命题．因为f (－x )＝2－x－2x＝－f (x )，所以p 2为真命题． 因为f (x )＝x ＋1x ＋1＝x ＋1＋1x ＋1－1 ≥2x ＋1x ＋1－1＝1， 取等号的条件为x ＋1＝1x ＋1，得到x ＝－，＋∞)，所以当x ∈(0，＋∞)时，f (x )>1，不存在x 0∈(0，＋∞)，满足f (x 0)＝1，所以p 3为假命题．在△ABC 中，A >B ⇒a >b ⇒sin A >sin B ，所以p 4为真命题． 故p 2和p 4为真命题，真命题的个数为2.11．若命题“存在实数x ，使x 2＋ax ＋1<0”的否定为真命题，则实数a 的取值范围为 [－2,2] .(方法一)由题意，命题“对任意实数x ，都有x 2＋ax ＋1≥0”是真命题，故Δ＝a 2－4×1×1≤0，解得－2≤a ≤2.(方法二)若命题“存在实数x ，使x 2＋ax ＋1<0”是真命题， 则Δ＝a 2－4×1×1>0，解得a >2或a <－2.故所求的实数a 的取值范围是取其补集，即[－2,2]． 12．(2018·华南师大附中模拟)设有两个命题：p ：关于x 的不等式a x >1(a >0，且a ≠1)的解集是{x |x <0}；q ：函数y ＝lg(ax 2－x ＋a )的定义域为R .如果p ∨q 为真命题，p ∧q 为假命题，则实数a 的取值范围是 (0，12]∪(1，＋∞) .p ：“关于x 的不等式a x>1(a >0，且a ≠1)的解集是{x |x <0}”为真⇒0<a <1.q ：“函数y ＝lg(ax 2－x ＋a )的定义域为R ”为真⇒ax 2－x ＋a >0恒成立⇒⎩⎪⎨⎪⎧a >0，Δ<0⇒a >12.因为p ∨q 为真命题，p ∧q 为假命题，所以p ，q 一真一假．⎩⎪⎨⎪⎧ p 真，q 假⇒⎩⎪⎨⎪⎧ 0<a <1，a ≤12⇒0<a ≤12.⎩⎪⎨⎪⎧p 假，q 真⇒⎩⎪⎨⎪⎧a >1，a >12⇒a >1.所以实数a 的取值范围是(0，12]∪(1，＋∞)．函数及其表示1．函数y ＝x ·ln(1－x )的定义域为(B) A ．(0,1) B ．[0,1) C ．(0,1] D ．[0,1]由⎩⎪⎨⎪⎧x ≥0，1－x >0，解得0≤x <1.2．已知函数f (x )＝⎩⎪⎨⎪⎧x 2－x ， x ≤1，11－x， x >1， 则f [f (－2)]的值为(C)A.12B.15 C ．－15 D ．－12因为f (－2)＝(－2)2－(－2)＝6，所以f [f (－2)]＝f (6)＝11－6＝－15. 3．若函数f (x )的定义域为[0,2]，则函数g (x )＝f x x －1的定义域是(B)A ．[0,1]B ．[0,1)C ．[0,1)∪(1,4]D ．(0,1)因为f (x )的定义域为[0,2]，所以⎩⎪⎨⎪⎧0≤2x ≤2，x －1≠0，解得0≤x <1.4．(2018·黑龙江模拟) 设函数f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的解析式为(C) A ．3x －1 B ．3x ＋1 C ．2x －1 D ．2x ＋1g (x ＋2)＝f (x )＝2x ＋3，即g (x ＋2)＝2x ＋3，令x ＋2＝t ，所以x ＝t －2， 所以2x ＋3＝2(t －2)＋3＝2t －1， 所以g (x )＝2x －1.5．已知函数f (x )在[－1,2]上的图象如下图所示，则函数f (x )的解析式为f (x )＝ ⎩⎪⎨⎪⎧x ＋1， －1≤x ≤0，－12x ， 0＜x ≤2 .由图可知，图象是由两条直线的一段构成，故可采用待定系数法求出其表示式．当－1≤x ≤0时，设y ＝k 1x ＋b 1，将(－1,0)，(0,1)代入得k 1＝1，b 1＝1，所以y ＝x ＋1， 当0<x ≤2时，设y ＝k 2x ＋b 2，将(0,0)，(2，－1)代入得k 2＝－12，b 2＝0，所以y ＝－12x .所以f (x )＝⎩⎪⎨⎪⎧x ＋1， －1≤x ≤0，－12x ， 0＜x ≤2.6．设函数f (x )＝⎩⎪⎨⎪⎧3x －b ，x <1，2x ， x >1，若f [f (56)]＝4，则b 等于 12.因为56<1，所以f (56)＝3×56－b ＝52－b .若52－b <1，即b >32时， f (52－b )＝3(52－b )－b ＝152－4b ＝4，解得b ＝78，不满足b >32，舍去；若52－b ≥1，即b ≤32时， f (52－b )＝2(52－b )＝5－2b ＝4，解得b ＝12，满足b ≤32.故b ＝12.7．已知f (x )＝⎩⎪⎨⎪⎧x ＋2， x ≤－1，x 2， －1<x <2，－2x ＋8， x ≥2.(1)求f (3)，f [f (－2)]，f (a )(a >0)的值；(2)画出f (x )的图象，并求出满足条件f (x )>3的x 的值．(1)因为3>2，所以f (3)＝－2×3＋8＝2.因为－2<－1，所以f (－2)＝2－ 2. 又－1<2－2<2，所以f [f (－2)]＝f (2－2)＝(2－2)2＝6－4 2. 又a >0，当0<a <2时，f (a )＝a 2； 当a ≥2时，f (a )＝－2a ＋8.综上所述，f (a )＝⎩⎪⎨⎪⎧a 2， 0<a <2，－2a ＋8， a ≥2.(2)f (x )的图象如图所示．当x ≤－1时，f (x )＝x ＋2≤1，此时无解；当－1<x <2时，由x 2＝3，解得x ＝±3， 因为x ＝－3<－1，故舍去；当x ≥2时，由－2x ＋8＝3，解得x ＝52.由图知，不等式f (x )>3的解为(3，52)．8．(2018·湖北武汉调研)已知函数f (x )满足f (1x )＋1xf (－x )＝2x (x ≠0)，则f (－2)＝(C)A ．－72 B.92C.72 D ．－92令x ＝2，可得f (12)＋12f (－2)＝4，①令x ＝－12，可得f (－2)－2f (12)＝－1，②联立①②解得f (－2)＝72.9．(2017·全国卷Ⅲ)设函数f (x )＝⎩⎪⎨⎪⎧x ＋1， x ≤0，2x， x >0，则满足f (x )＋f (x －12)>1的x的取值范围是 (－14，＋∞) .由题意知，可对不等式分x ≤0,0＜x ≤12，x ＞12三段讨论．当x ≤0时，原不等式为x ＋1＋x ＋12＞1，解得x ＞－14，所以－14＜x ≤0.当0＜x ≤12时，原不等式为2x＋x ＋12＞1，显然成立．当x ＞12时，原不等式为2x＋2x －12＞1，显然成立．综上可知，x 的取值范围是(－14，＋∞)．10．函数f (x )＝－a2x 2＋－a x ＋6.(1)若f (x )的定义域为R ，求实数a 的取值范围； (2)若f (x )的定义域为[－2,1]，求实数a 的值．(1)因为对于x ∈R ，(1－a 2)x 2＋3(1－a )x ＋6≥0恒成立，所以①当a ＝1时，原不等式变为6≥0，此时x ∈R . ②当a ＝－1时，原不等式变为6x ＋6≥0，此时x R .③若a ≠±1时，则⎩⎪⎨⎪⎧1－a 2>0，Δ≤0，所以⎩⎪⎨⎪⎧1－a 2>0，－a 2－－a2，解得－511≤a <1，所以实数a 的取值范围为[－511，1]． (2)因为f (x )的定义域为[－2,1]，所以不等式(1－a 2)x 2＋3(1－a )x ＋6≥0的解集为[－2,1]， 所以x ＝－2，x ＝1是方程(1－a 2)x 2＋3(1－a )x ＋6＝0的两根，所以⎩⎪⎨⎪⎧1－a 2<0，－2＋1＝－－a 1－a 2，－2×1＝61－a2，解得a ＝2.函数的值域与最值1．已知函数f (x )的值域为[－2,3]，则函数f (x －2)的值域为(D) A ．[－4,1] B ．[0,5]C ．[－4,1]∪[0,5]D ．[－2,3]函数y ＝f (x －2)的图象是由y ＝f (x )的图象向右平移2个单位而得到的，其值域不变．2．函数y ＝16－4x的值域是(C) A ．[0，＋∞) B．[0,4] C ．[0,4) D ．(0,4)因为16－4x≥0，且4x>0，所以0≤16－4x<16，所以0≤16－4x<4.3．已知函数f (x )＝e x－1，g (x )＝－x 2＋4x －3.若有f (a )＝g (b )，则b 的取值范围为(B)A ．[2－2，2＋2]B ．(2－2，2＋2)C ．[1,3]D ．(1,3)f (a )的值域为(－1，＋∞)，由－b 2＋4b －3>－1，解得2－2<b <2＋ 2.4．(2018·重庆期中)已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋x ＋a ，x <1，1－ln x ， x ≥1的值域为R ，则实数a 的取值范围是(C)A ．(－∞，－1]B ．[－1，＋∞)C ．(－∞，54]D ．[54，＋∞)当x ≥1时，f (x )＝1－ln x ≤1.由于函数f (x )＝⎩⎪⎨⎪⎧x 2＋x ＋a ，x <1，1－ln x ， x ≥1的值域为R ，且当x <1时，f (x )＝x 2＋x ＋a ≥a －12＋14＝a －14，所以a －14≤1，解得a ≤54.5．函数y ＝x 2x 2＋1(x ∈R )的值域为 [0,1) .y ＝x 2x 2＋1＝x 2＋1－1x 2＋1＝1－1x 2＋1.因为x 2＋1≥1，所以0<1x 2＋1≤1，所以0≤y <1. 6．若关于x 的不等式x 2－4x ≥m 对任意x ∈(0,1]恒成立，则m 的取值范围为 (－∞，－3] .只需要在x ∈(0,1]时，(x 2－4x )min ≥m 即可．而当x ＝1时，(x 2－4x )min ＝－3，所以m ≤－3. 7．求下列函数的值域： (1)y ＝x ＋1x －3； (2)y ＝2x ＋4x －1； (3)y ＝|x ＋1|＋x －2.(1)y ＝x －3＋4x －3＝1＋4x －3，因为4x －3≠0，所以y ≠1， 即所求函数的值域为(－∞，1)∪(1，＋∞)． (2)因为函数的定义域为{x |x ≥1}，又函数是增函数，所以函数的值域为[2，＋∞)． (3)y ＝|x ＋1|＋|x －2|＝⎩⎪⎨⎪⎧2x －1， x ≥2，3， －1≤x ＜2，1－2x ， x ＜－1.画出函数的图象，由图象观察可知，所求函数的值域为[3，＋∞)．8．已知函数y ＝1－x ＋x ＋3的最大值为M ，最小值为m ，则m M的值为(A) A.22B. 2 C ．2 2 D ．2由⎩⎪⎨⎪⎧1－x ≥0，x ＋3≥0，得定义域为[－3,1]，y ≥0，所以y 2＝4＋2x ＋－x ＝4＋2－x ＋2＋4，当x ＝－3或x ＝1，(y 2)min ＝4，所以y min ＝2； 当x ＝－1时，(y 2)max ＝8，所以y max ＝2 2. 即m ＝2，M ＝22，所以mM ＝22. 9．已知函数f (x )满足2f (x )－f (1x )＝3x2，则f (x )的最小值为 2 2 .由2f (x )－f (1x )＝3x2， ①令①式中的x 变为1x，可得2f (1x)－f (x )＝3x 2， ②由①②可解得f (x )＝2x2＋x 2，由于x 2>0，由基本不等式可得f (x )＝2x 2＋x 2≥22x2·x 2＝2 2.当x 2＝2时取等号，因此，其最小值为2 2. 10．已知函数f (x )＝1a －1x(a ＞0，x ＞0)．(1)若f (x )在[m ，n ]上的值域是[m ，n ]，求a 的取值范围，并求相应的m ，n 的值； (2)若f (x )≤2x 在(0，＋∞)上恒成立，求a 的取值范围．(1)因为f (x )＝1a －1x(a ＞0，x ＞0)，所以f (x )在(0，＋∞)上为增函数．那么当x ∈[m ，n ]时，y ∈[m ，n ]，所以⎩⎪⎨⎪⎧fm ＝m ，fn ＝n .即m ，n 是方程1a －1x＝x 相异的两实根，由1a －1x ＝x ，得x 2－1ax ＋1＝0，由题设知：⎩⎪⎨⎪⎧m ＋n ＝1a>0，m ·n ＝1＞0，Δ＝1a 2－4＞0.所以0＜a ＜12.此时，m ＝1－1－4a 22a ，n ＝1＋1－4a22a .(2)若1a －1x≤2x 在(0，＋∞)上恒成立．那么a ≥12x ＋1x恒成立．令g (x )＝12x ＋1x(x ＞0)．所以g (x )≤122x ·1x＝24. 故a ≥24.函数的单调性1．(2018·西城区期末)下列四个函数中，定义域为R 的单调递减函数是(D) A ．y ＝－x 2B ．y ＝log 0.5xC ．y ＝1xD ．y ＝(12)xy ＝－x 2在R 上没有单调性，排除A ；y ＝log 0.5x 的定义域不是R ，排除B ；y ＝1x的定义域不是R ，排除C ；y ＝(12)x的定义域为R ，且在R 上单调递减，故选D.2．已知函数f (x )＝|x ＋a |在(－∞，－1)上是单调函数，则a 的取值范围是(A) A ．(－∞，1] B ．(－∞，－1] C ．[－1，＋∞) D．[1，＋∞)因为函数f (x )在(－∞，－a )上是单调函数，所以－a ≥－1，解得a ≤1.3．已知f (x )是R 上的减函数，则满足f (|1x|)<f (1)的实数x 的取值范围是(C)A ．(－1,1)B ．(0,1)C ．(－1,0)∪(0,1)D ．(－∞，－1)∪(1，＋∞)因为f (x )是R 上的减函数，所以f (|1x |)<f1x|>1，所以0<|x |<1，所以x∈(－1,0)∪(0,1)．4．(2018·城关区期中)已知f (x )＝⎩⎪⎨⎪⎧a －x ＋4a ， x ＜1，log a x ， x ≥1是(－∞，＋∞)上的减函数，那么a 的取值范围是(C)A ．(0,1)B ．(0，13)C ．[17，13)D ．[17，1)因为f (x )＝log a x (x ≥1)是减函数，所以0＜a <1，且f (1)＝0.因为f (x )＝(3a －1)x ＋4a (x <1)为减函数， 所以3a －1<0，所以a <13，又因为f (x )＝⎩⎪⎨⎪⎧a －x ＋4a ，x ＜1，log a x ， x ≥1是(－∞，＋∞)上的减函数，所以f (x )在(－∞，1]上的最小值大于或等于f (x )在[1，＋∞)上的最大值．所以(3a －1)×1＋4a ≥0，所以a ≥17，故a ∈[17，13)．5．函数f (x )＝log 2(4x －x 2)的单调递减区间是 [2,4) .因为4x －x 2>0，所以0<x <4，又y ＝log 2t 为增函数，所求函数f (x )的递减区间为t ＝4x －x 2(0<x <4)的递减区间是[2,4)．6．已知函数f (x )为(0，＋∞)上的增函数，若f (a 2－a )>f (a ＋3)，则实数a 的取值范围为 (－3，－1)∪(3，＋∞) .由条件得⎩⎪⎨⎪⎧a 2－a >a ＋3，a 2－a >0，a ＋3>0，即⎩⎪⎨⎪⎧a 2－2a －3>0，a >1或a <0，a >－3.解得⎩⎪⎨⎪⎧a >3或a <－1，a >1或a <0，a >－3，所以a 的取值范围为(－3，－1)∪(3，＋∞)． 7．已知函数f (x )＝2x ＋1x ＋1.(1)判断f (x )在区间[1，＋∞)上的单调性，并用定义证明你的结论； (2)求该函数在区间[1,4]上的最大值与最小值．(1)函数f (x )在[1，＋∞)上是增函数，证明如下：任取x 1，x 2∈[1，＋∞)，且x 1<x 2，则f (x 1)－f (x 2)＝2x 1＋1x 1＋1－2x 2＋1x 2＋1＝x 1－x 2x 1＋x 2＋，因为x 1－x 2<0，(x 1＋1)(x 2＋1)>0， 所以f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)． 所以函数f (x )在[1，＋∞)上为增函数． (2)由(1)知， 函数f (x )在[1,4]上是增函数， 故f (x )max ＝f (4)＝95，f (x )min ＝f (1)＝32.8．(2017·山东卷)若函数e xf (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质．下列函数中具有M 性质的是(A)A ．f (x )＝2－xB ．f (x )＝x 2C ．f (x )＝3－xD ．f (x )＝cos x(方法一)若f (x )具有性质M ，则[e x f (x )]′＝e x[f (x )＋f ′(x )]>0在f (x )的定义域上恒成立，即f (x )＋f ′(x )>0在f (x )的定义域上恒成立．对于选项A ，f (x )＋f ′(x )＝2－x－2－xln 2＝2－x(1－ln 2)>0，符合题意． 经验证，选项B ，C ，D 均不符合题意．故选A.(方法二)对于A ，e x f (x )＝(e 2)x ，因为e 2>1，所以e xf (x )为增函数．9．函数f (x )＝⎩⎪⎨⎪⎧1， x >0，0， x ＝0，－1， x <0，g (x )＝x 2·f (x －1)，则函数g (x )的递减区间是(B)A ．[0，＋∞)B ．[0,1)C ．(－∞，1)D ．(－1,1)由条件知g (x )＝⎩⎪⎨⎪⎧x 2， x >1，0， x ＝1，－x 2， x <1.如图所示，其递减区间是[0,1)．10．(2018·安徽皖江名校联考题改编)已知定义在(－2,2)上的函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]>0，x 1≠x 2，且f (a 2－a )>f (2a －2)．(1)求实数a 的取值范围；(2)求函数g (x )＝log a (x 2－x －6)的单调区间．(1)因为定义在(－2,2)上的函数f (x )满足(x 1－x 2)[f (x 1)－f (x 2)]>0，x 1≠x 2，所以f (x )在(－2,2)上单调递增， 又f (a 2－a )>f (2a －2)， 所以⎩⎪⎨⎪⎧－2<a 2－a <2，－2<2a －2<2，2a －2<a 2－a ，即⎩⎪⎨⎪⎧－1<a <2，0<a <2，a <1或a >2.所以0<a <1.即a 的取值范围为(0,1)．(2)g (x )＝log a (x 2－x －6)可以看作由y ＝log a u 与u ＝x 2－x －6的复合函数． 由u ＝x 2－x －6>0，得x <－2或x >3.因为u ＝x 2－x －6在(－∞，－2)上是减函数，在(3，＋∞)上是增函数， 因为0<a <1，所以y ＝log a x 在(0，＋∞)上是减函数，所以y ＝log a (x 2－x －6)的单调递增区间为(－∞，－2)，单调递减区间为(3，＋∞)．函数的奇偶性与周期性1．(2017·北京卷)已知函数f (x )＝3x－(13)x ，则f (x )(B)A ．是偶函数，且在R 上是增函数B ．是奇函数，且在R 上是增函数C ．是偶函数，且在R 上是减函数D ．是奇函数，且在R 上是减函数因为函数f (x )的定义域为R ，f (－x )＝3－x －(13)－x ＝(13)x －3x ＝－f (x )，所以函数f (x )是奇函数．因为函数y ＝(13)x在R 上是减函数，所以函数y ＝－(13)x在R 上是增函数．又因为y ＝3x在R 上是增函数，所以函数f (x )＝3x－(13)x 在R 上是增函数．2．设函数f (x )，g (x )的定义域都为R ，且f (x )是奇函数，g (x )是偶函数，则下列结论正确的是(C)A ．f (x )g (x )是偶函数B ．|f (x )|g (x )是奇函数C ．f (x )|g (x )|是奇函数D ．|f (x )g (x )|是奇函数因为f (x )是奇函数，g (x )是偶函数，所以f (－x )＝－f (x )，g (－x )＝g (x )， 所以f (－x )g (－x )＝－f (x )g (x )， 所以f (x )g (x )为奇函数．|f (－x )|g (－x )＝|f (x )|g (x )， 所以|f (x )|g (x )为偶函数．f (－x )|g (－x )|＝－f (x )|g (x )|，所以f (x )|g (x )|为奇函数． |f (－x )g (－x )|＝|f (x )g (x )|， 所以|f (x )g (x )|为偶函数．3．(2018·华大新高考联盟教学质量测评)设f (x )是周期为4的奇函数，当0≤x ≤1时，f (x )＝x (1＋x )，则f (－92)＝(A)A ．－34B ．－14C.14D.34f (－92)＝f (－92＋4)＝f (－12)＝－f (12)＝－12(1＋12)＝－34.4．(2018·天津一模)已知偶函数f (x )对于任意x ∈R 都有f (x ＋1)＝－f (x )，且f (x )在区间[0,2]上是递增的，则f (－6.5)，f (－1)，f (0)的大小关系为(A)A ．f (0)<f (－6.5)<f (－1)B ．f (－6.5)<f (0)<f (－1)C ．f (－1)<f (－6.5)<f (0)D ．f (－1)<f (0)<f (－6.5)由f (x ＋1)＝－f (x )，得f (x ＋2)＝－f (x ＋1)＝f (x )， 故函数f (x )是周期为2的函数． 又f (x )为偶函数，所以f (－6.5)＝f (－0.5)＝f (0.5)，f (－1)＝f (1)， 因为f (x )在区间[0,2]上是递增的， 所以f (0)<f (0.5)<f (1)， 即f (0)<f (－6.5)<f (－1)．5．(2017·山东卷)已知f (x )是定义在R 上的偶函数，且f (x ＋4)＝f (x －2)．若当x ∈[－3,0]时，f (x )＝6－x，则f (919)＝ 6 .因为f (x ＋4)＝f (x －2)，所以f [(x ＋2)＋4]＝f [(x ＋2)－2]，即f (x ＋6)＝f (x )，所以f (x )是周期为6的周期函数， 所以f (919)＝f (153×6＋1)＝f (1)． 又f (x )是定义在R 上的偶函数， 所以f (1)＝f (－1)＝6，即f (919)＝6.6．已知奇函数f (x )在定义域[－10,10]上是减函数，且f (m －1)＋f (2m －1)>0，则实数m 的取值范围为 [－92，23) .由f (m －1)＋f (2m －1)>0f (m －1)>－f (2m －1)，因为f (x )为奇函数，所以－f (x )＝f (－x )， 所以f (m －1)>f (1－2m )， 又f (x )在[－10,10]上是减函数， 所以⎩⎪⎨⎪⎧－10≤m －1≤10，－10≤2m －1≤10，m －1<1－2m ，解得－92≤m <23.7．设f (x )是定义在R 上的奇函数，且对任意实数x 恒有f (x ＋2)＝－f (x )，当x ∈[0,2]时，f (x )＝2x －x 2.(1)求证：f (x )是周期函数；(2)当x ∈[2,4]时，求f (x )的解析式； (3)计算f (0)＋f (1)＋f (2)…＋f (2019)的值．(1)证明：因为f (x ＋2)＝－f (x )，所以f (x ＋4)＝－f (x ＋2)＝f (x )． 所以f (x )是周期为4的周期函数．(2)因为x ∈[2,4]，所以－x ∈[－4，－2]，所以4－x ∈[0,2]， 所以f (4－x )＝2(4－x )－(4－x )2＝－x 2＋6x －8， 又f (x )是周期为4的奇函数， 所以f (4－x )＝f (－x )＝－f (x )， 所以f (x )＝－f (4－x )，所以f (x )＝x 2－6x ＋8，x ∈[2,4]．(3)因为f (0)＝0，f (1)＝1，f (2)＝0，f (3)＝－1， 又f (x )是周期为4的周期函数，所以f (0)＋f (1)＋f (2)＋f (3)＝f (4)＋f (5)＋f (6)＋f (7)＝…＝f (2016)＋f (2017)＋f (2018)＋f (2019)＝0，所以f (0)＋f (1)＋f (2)…＋f (2019)＝0.8．(2016·山东卷)已知函数f (x )的定义域为R .当x <0时，f (x )＝x 3－1；当－1≤x ≤1时，f (－x )＝－f (x )；当x >12时，f (x ＋12)＝f (x －12)，则f (6)＝(D)A ．－2B ．－1C ．0D ．2由题意知，当x ＞12时，f (x ＋12)＝f (x －12)，则当x ＞0时，f (x ＋1)＝f (x )． 又当－1≤x ≤1时，f (－x )＝－f (x )， 所以f (6)＝f (1)＝－f (－1)． 又当x ＜0时，f (x )＝x 3－1，所以f (－1)＝－2，所以f (6)＝2.故选D.9．(2018·全国卷Ⅲ)已知函数f (x )＝ln(1＋x 2－x )＋1，f (a )＝4，则f (－a )＝ －2 .(方法一)令g (x )＝ln(1＋x 2－x )，则f (x )＝g (x )＋1，因为1＋x 2－x >|x |－x ≥0，所以g (x )的定义域为R ， 因为g (－x )＝ln(1＋x 2＋x )＝ln 11＋x 2－x＝－g (x )， 所以g (x )为奇函数，所以f (a )＝g (a )＋1＝4，所以g (a )＝3，所以f (－a )＝g (－a )＋1＝－g (a )＋1＝－3＋1＝－2.(方法二)因为f (x )＋f (－x )＝ln(1＋x 2－x )＋1＋ln(1＋x 2＋x )＋1＝ln(1＋x 2－x 2)＋2＝2，所以f (a )＋f (－a )＝2，所以f (－a )＝－2.10．已知函数f (x )是定义在R 上的奇函数，且当x ≥0时，f (x )＝－x 2＋ax . (1)若a ＝－2，求函数f (x )的解析式； (2)若函数f (x )为R 上的单调减函数，①求a 的取值范围；②若对任意实数m ，f (m －1)＋f (m 2＋t )<0恒成立，求实数t 的取值范围．(1)当x <0时，－x >0，又因为f (x )为奇函数，且a ＝－2， 所以当x <0时，f (x )＝－f (－x )＝x 2－2x ，所以f (x )＝⎩⎪⎨⎪⎧x 2－2x ， x <0，－x 2－2x ， x ≥0.(2)①当a ≤0时，对称轴x ＝a2≤0，所以f (x )＝－x 2＋ax 在[0，＋∞)上单调递减， 由于奇函数在关于原点对称的区间上单调性相同， 所以f (x )在(－∞，0)上单调递减，又在(－∞，0)上f (x )>0，在(0，＋∞)上f (x )<0， 所以当a ≤0时，f (x )为R 上的单调减函数．当a >0时，f (x )在(0，a 2)上单调递增，在(a2，＋∞)上单调递减，不合题意．所以函数f (x )为单调减函数时，a 的取值范围为(－∞，0]． ②因为f (m －1)＋f (m 2＋t )<0， 所以f (m －1)<－f (m 2＋t )，又因为f (x )是奇函数，所以f (m －1)<f (－t －m 2)， 因为f (x )为R 上的减函数， 所以m －1>－t －m 2恒成立，所以t >－m 2－m ＋1＝－(m ＋12)2＋54对任意实数m 恒成立，所以t >54.即t 的取值范围为(54，＋∞)．二次函数1．已知a >0，函数f (x )＝ax 2＋bx ＋c ，若x 0满足关于x 的方程2ax ＋b ＝0，则下列选项的命题中为假命题的是(C)A ．∃x ∈R ，f (x )≤f (x 0)B ．∃x ∈R ，f (x )≥f (x 0)C ．∀x ∈R ，f (x )≤f (x 0)D ．∀x ∈R ，f (x )≥f (x 0)函数f (x )的最小值是f (－b2a)＝f (x 0)，等价于x ∈R ，f (x )≥f (x 0)，所以C 错误．2．若函数y ＝x 2－3x －4的定义域为[0，m ]，值域为[－254，－4]，则m 的取值范围是(D)A ．[0,4]B ．[32，4]C ．[32，＋∞) D．[32，3]二次函数的对称轴为x ＝32，且f (32)＝－254，f (3)＝f (0)＝－4，结合图象可知m ∈[32，3]．3．(2018·双桥区校级月考)设abc >0，二次函数f (x )＝ax 2＋bx ＋c 的图象可能是(D)(方法一)对于A 选项，因为a <0，－b2a<0，所以b <0，又因为abc >0，所以c >0，由图知f (0)＝c <0，矛盾，故A 错．对于B 选项，因为a <0，－b2a>0，所以b >0，又因为abc >0，所以c <0，由图知f (0)＝c >0，矛盾，故B 错．对于C 选项，因为a >0，－b2a<0，所以b >0，又因为abc >0，所以c >0，由图知f (0)＝c <0，矛盾，故C 错．故排除A ，B ，C ，选D.(方法二)当a >0时，b ，c 同号，C ，D 两图中c <0，故b <0， 所以－b2a>0，选D.4．(2018·皖北联考)已知二次函数f (x )＝－x 2＋2ax ＋1－a 在x ∈[0,1]上有最大值2，则a 的值为(D)A ．2B ．－1或－3C ．2或－3D ．－1或2因为f (x )＝－(x －a )2＋a 2－a ＋1，所以f (x )的图象是开口向下，对称轴是x ＝a 的抛物线，(1)当a <0时，对称轴x ＝a 在区间[0,1]的左边，f (x )在[0,1]上单调递减， 所以f (x )max ＝f (0)＝1－a ＝2，解得a ＝－1. (2)当0≤a ≤1时，对称轴x ＝a ∈[0,1]，f (x )在[0，a ]上单调递增，在[a,1]上单调递减，所以f (x )max ＝f (a )＝a 2－a ＋1＝2，无解．(3)当a >1时，对称轴x ＝a 在区间[0,1]的右边，f (x )在[0,1]上单调递增， 所以f (x )max ＝f (1)＝a ＝2，有a ＝2. 综上可知，a ＝－1或a ＝2.5．若x ≥0，y ≥0，且x ＋2y ＝1，那么2x ＋3y 2的最小值为 34 .由x ≥0，y ≥0，且x ＋2y ＝1，得x ＝1－2y ≥0，所以0≤y ≤12，设t ＝2x ＋3y 2，把x ＝1－2y 代入，得t ＝2－4y ＋3y 2＝3(y －23)2＋23.因为t ＝f (y )在[0，12]上单调递减，所以当y ＝12时，t 取最小值，t min ＝34.6．设f (x )＝x 2－2ax ＋1.(1)若x ∈R 时恒有f (x )≥0，则a 的取值范围是 [－1,1] ；(2)若f (x )在[－1，＋∞)上递增，则a 的取值范围是 (－∞，－1] ； (3)若f (x )的递增区间是[1，＋∞)，则a 的值是 1 .(1)由Δ≤0，得4a 2－4≤0，所以a ∈[－1,1]．(2)a ≤－1.(3)由对称轴x ＝1知a ＝1.7．已知函数f (x )＝x 2－2ax ＋5(a >1)．(1)若f (x )的定义域和值域均是[1，a ]，求实数a 的值；(2)若f (x )在区间(－∞，2]上是减函数，且对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4，求实数a 的取值范围．(1)因为f (x )＝(x －a )2＋5－a 2(a >1)， 所以f (x )在[1，a ]上是减函数， 又定义域和值域均为[1，a ]，所以⎩⎪⎨⎪⎧f＝a ，fa ＝1，即⎩⎪⎨⎪⎧1－2a ＋5＝a ，a 2－2a 2＋5＝1，解得a ＝2.(2)因为f (x )在区间(－∞，2]上是减函数，所以a ≥2. 又x ＝a ∈[1，a ＋1]，且(a ＋1)－a ≤a －1， 所以f (x )max ＝f (1)＝6－2a ，f (x )min ＝f (a )＝5－a 2， 因为对任意的x 1，x 2∈[1，a ＋1]，总有|f (x 1)－f (x 2)|≤4， 因为f (x )max －f (x )min ≤4，得－1≤a ≤3.又a ≥2，所以2≤a ≤3. 故实数a 的取值范围为[2,3]．8．(2017·浙江卷)若函数f (x )＝x 2＋ax ＋b 在区间[0,1]上的最大值是M ，最小值是m ，则M －m (B)A ．与a 有关，且与b 有关B ．与a 有关，但与b 无关C ．与a 无关，且与b 无关D ．与a 无关，但与b 有关(方法一)设x 1，x 2分别是函数f (x )在[0,1]上的最小值点与最大值点，则m ＝x 21＋ax 1＋b ，M ＝x 22＋ax 2＋b .所以M －m ＝x 22－x 21＋a (x 2－x 1)，显然此值与a 有关，与b 无关．(方法二)由题意可知，函数f (x )的二次项系数为固定值，则二次函数图象的形状一定．随着b 的变动，相当于图象上下移动，若b 增大k 个单位，则最大值与最小值分别变为M ＋k ，m ＋k ，而(M ＋k )－(m ＋k )＝M －m ，故与b 无关．随着a 的变动，相当于图象左右移动，则M －m 的值在变化，故与a 有关．9．(2018·重庆模拟)已知函数f (x )＝x 2＋mx －1，若对于任意x ∈[m ，m ＋1]，都有f (x )<0成立，则实数m 的取值范围是 (－22，0) .作出二次函数f (x )的图象，对于任意x ∈[m ，m ＋1]，都有f (x )<0，则有⎩⎪⎨⎪⎧fm ，fm ＋，即⎩⎪⎨⎪⎧m 2＋m 2－1<0，m ＋2＋m m ＋－1<0，解得－22<m <0.10．已知f (x )＝ax 2－2x (0≤x ≤1)，求f (x )的最小值．(1)当a ＝0时，f (x )＝－2x 在[0,1]上递减，所以f (x )min ＝f (1)＝－2.(2)当a >0时，f (x )＝ax 2－2x ，图象开口向上，且对称轴为x ＝1a.①当1a≤1，即a ≥1时，f (x )＝ax 2－2x 图象的对称轴在[0,1]内，所以f (x )在[0，1a ]上递减，在[1a，1]上递增，所以f (x )min ＝f (1a )＝1a －2a ＝－1a.②当1a>1，即0<a <1时，f (x )＝ax 2－2x 图象的对称轴在[0,1]的右侧，所以f (x )在[0,1]上递减， 所以f (x )min ＝f (1)＝a －2.(3)当a <0时，f (x )＝ax 2－2x 的图象的开口向下，且对称轴x ＝1a<0，在y 轴的左侧，所以f (x )＝ax 2－2x 在[0,1]上递减， 所以f (x )min ＝f (1)＝a －2.综上所述，f (x )min ＝⎩⎪⎨⎪⎧a －2， a <1，－1a， a ≥1.指数与指数函数1. 若函数f (x )＝12x ＋1， 则该函数在(－∞，＋∞)上是(A)A ．单调递减无最小值B ．单调递减有最小值C ．单调递增无最大值D ．单调递增有最大值f (x )在R 上单调递减，又2x＋1>1，所以0<f (x )<1，无最大值也无最小值．2．若函数f (x )＝2x＋12x －a 是奇函数，则使f (x )>3成立的x 的取值范围为(C)A ．(－∞，－1)B ．(－1,0)C ．(0,1)D ．(1，＋∞)因为函数y ＝f (x )为奇函数，所以f (－x )＝－f (x )，即2－x＋12－x －a ＝－2x＋12x －a ，化简可得a ＝1， 则2x＋12x －1＞3，即2x＋12x －1－3＞0，即2x＋1－x－2x－1＞0，故不等式可化为2x－22x －1＜0，即1＜2x＜2，解得0＜x ＜1，故选C.3．函数y ＝|2x－1|在区间(k －1，k ＋1)内不单调，则k 的取值范围是(C) A ．(－1，＋∞) B．(－∞，1) C ．(－1,1) D ．(0,2)由于函数y ＝|2x－1|在(－∞，0)内单调递减，在(0，＋∞)内单调递增，而函数在区间(k －1，k ＋1)内不单调，所以有k －1<0<k ＋1，解得－1<k <1.4．已知函数f (x )＝|2x－1|，a <b <c ，且f (a )>f (c )>f (b )，则下列结论中，一定成立的是(D)A ．a <0，b <0，c <0B ．a <0，b ≥0，c >0C ．2－a<2c D ．2a ＋2c<2作出函数y ＝|2x－1|的图象，如下图．因为a <b <c ，且f (a )>f (c )>f (b )，结合图象知， 0<f (a )<1，a <0，c >0，所以0<2a<1. 所以f (a )＝|2a－1|＝1－2a<1，。

2020届高考理科数学一轮复习要点+题型解析导数及其应用一、导数的运算问题【要点解析】1.基本初等函数的导数公式表2.导数的四则运算法则设f(x)，g(x)是可导的，则(1)(f(x)±g(x))′＝f′(x)±g′(x)；(2)[f(x)g(x)]′＝f′(x)g(x)＋f(x)g′(x)；(3)'⎥⎦⎤⎢⎣⎡)()(xgxf＝g(x)f′(x)－f(x)g′(x)g2(x)(g(x)≠0)．(g(x)≠0)．3.复合函数的导数复合函数y＝f(g(x))的导数和函数y＝f(u)，u＝g(x)的导数间的关系为y x′＝y u′·u x′，即y 对x的导数等于y对u的导数与u对x的导数的乘积．【题型解析】【例1】．f (x )＝x (2 018＋ln x )，若f ′(x 0)＝2 019，则x 0等于( ) A ．e 2 B ．1 C ．ln 2D ．e解析：选B f ′(x )＝2 018＋ln x ＋x ×1x ＝2 019＋ln x ，故由f ′(x 0)＝2 019，得2 019＋ln x 0＝2 019，则ln x 0＝0，解得x 0＝1.【例2】．已知f ′(x )是函数f (x )的导数，f (x )＝f ′(1)·2x ＋x 2，则f ′(2)＝( ) A.12－8ln 21－2ln 2 B.21－2ln 2 C.41－2ln 2D ．－2【解析】：选C 因为f ′(x )＝f ′(1)·2x ln 2＋2x ，所以f ′(1)＝f ′(1)·2ln 2＋2，解得f ′(1)＝21－2ln 2，所以f ′(x )＝21－2ln 2·2x ln 2＋2x ，所以f ′(2)＝21－2ln 2×22ln 2＋2×2＝41－2ln 2.【例3】．若函数f (x )＝ax 4＋bx 2＋c 满足f ′(1)＝2，则f ′(－1)＝________. 【解析】：f ′(x )＝4ax 3＋2bx ， ∵f ′(x )为奇函数且f ′(1)＝2， ∴f ′(－1)＝－2. 【答案】：－2二、导数的几何意义【要点解析】函数f (x )在点x 0处的导数f ′(x 0)的几何意义是在曲线y ＝f (x )上点(x 0，f (x 0))处的切线的斜率．相应地，切线方程为y －f (x 0)＝f ′(x 0)(x －x 0)．（1）斜率：αtan )(0='=x f k（2）切点：())(00x f x '，在切线上，也在曲线上。

2020年高考理科数学一轮复习题型归纳与变式演练《抛物线及其性质》【题型一】：抛物线的标准方程 【题型二】：抛物线定义的理解 【题型三】：抛物线定义的应用 【题型四】：与抛物线有关的综合问题 【题型一】：抛物线的标准方程例1.求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程： （1）过点(3,2)-；（2）焦点在直线l ：240x y --=上【思路点拨】从方程形式看，求抛物线的标准方程仅需确定一次项系数；从实际分析，一般需结合图形确定开口方向和一次项系数两个条件，否则，应展开相应的讨论【解析】（1）∵点(3,2)-在第二象限，∴抛物线开口方向上或者向左当抛物线开口方向左时，设所求的抛物线方程为22y px =-（0p >）， ∵过点(3,2)-，∴222(3)p =-⋅-，∴23p =，∴243y x =-，当抛物线开口方向上时，设所求的抛物线方程为22x py =（0p >）， ∵过点(3,2)-，∴2322p =⨯，∴94p =，∴292x y =，∴所求的抛物线的方程为243y x =-或292x y =，对应的准线方程分别是13x =，98y =-.（2）令0x =得2y =-，令0y =得4x =，∴抛物线的焦点为(4,0)或(0,2)-当焦点为(4,0)时，42p=，∴8p =， 此时抛物线方程216y x =； 焦点为(0,2)-时，22p=，∴4p =， 此时抛物线方程为28x y =-∴所求的抛物线的方程为216y x =或28x y =-， 对应的准线方程分别是4x =-，2y =.【总结升华】这里易犯的错误就是缺少对开口方向的讨论，先入为主，设定一种形式的标准方程后求解，以致失去一解.求抛物线的标准方程关键是根据图象确定抛物线开口方向，选择适当的方程形式，准确求出焦参数P.举一反三：【变式1】分别求满足下列条件的抛物线的标准方程. （1）焦点为F(4,0)；（2）准线为1y 2=- ；（3）焦点到原点的距离为1； （4）过点（1，－2）； （5）焦点在直线x-3y+6=0上.【解析】（1）所求抛物线的方程为y 2=16x ； （2）所求抛物线的标准方程为x 2=2y ； （3）所求抛物线的方程y 2=±4x 或x 2=±4y ； （4）所求抛物线的方程为24y x =或212x y =-； （5）所求抛物线的标准方程为y 2=－24x 或x 2=8y.【变式2】已知抛物线的顶点在原点，焦点在x 轴负半轴上，过顶点且倾角为43π的弦长为22，求抛物线的方程.【解析】设抛物线方程为22y px =-(0p >)，又弦所在直线方程为y x =-由⎩⎨⎧-=-=x y px y 22，解得两交点坐标(0,0), (2,2)p p - ∴22(2)(2)22p p -+=，解得1p =.∴抛物线方程为22y x =-. 【题型二】：抛物线定义的理解【例2】已知点(),P x y 在以原点为圆心的单位圆上运动，则点(),Q x y xy +的轨迹是( ) A ．圆 B.抛物线 C.椭圆 D.双曲线 【答案】B【解析】设(),Q u v ，则u x yv xy=+⎧⎨=⎩221x y +=22221u v x y ∴-=+=∴点Q 的轨迹为抛物线.故选B.【变式训练】：【变式1】动圆C 经过点F(1,0),并且与直线x=-1相切，若动圆C 与直线221y x =++总有公共点，则圆C 的面积( )A.有最大值8πB.有最小值2πC.有最小值3πD.有最小值4π 【答案】D【解析】由题意可得：动圆圆心C(a,b)的方程为24y x =.即24b a = 动圆C 与直线221y x =++总有公共点，∴圆心C 到此直线的距离11d r a a ≤=+=+即22112a b a -++≤+又24b a = 化简整理得()()22144210b b -+-+≥解得2b ≥或()642b ≤-+当2b =时，a 取得最小值1，此时圆C 由最小面积4π.故选D.【变式2】抛物线y=4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是（ ） A ．1716 B ．1516 C ．78D ．0 【答案】B方法一：由题意抛物线为214x y =，则焦点为1(0,)16F ，准线为：116y =-； 由抛物线上的点M （x 0，y 0）到焦点的距离与到准线的距离相等，得01516y =， 即M 点的纵坐标为1516，故选择B 。

第十一节导数的应用知识点一利用导数研究函数的单调性函数y＝f(x)在区间(a，b)内可导，1．若f′(x)>0，则f(x)在这个区间内是单调递增函数；2．若f′(x)<0，则f(x)在这个区间内是单调递减函数；3．若恒有f′(x)＝0，则f(x)在这个区间内是常函数．1．判断下面结论是否正确(请在括号中打“√”或“×”)(1)若函数f(x)在(a，b)内单调递增，那么一定有f′(x)>0.(×)(2)如果函数f(x)在某个区间内恒有f′(x)＝0，则f(x)在此区间内没有单调性．(√)(3)在(a，b)内f′(x)≤0且f′(x)＝0的根有有限个，则f(x)在(a，b)内是减函数．(√)(4)开区间上的单调连续函数无最值．(√)2．如图所示是函数f(x)的导函数f′(x)的图象，则下列判断中正确的是(A)A．函数f(x)在区间(－3,0)上是减函数B．函数f(x)在区间(－3,2)上是减函数C．函数f(x)在区间(0,2)上是减函数D．函数f(x)在区间(－3,2)上是单调函数解析：当x∈(－3,0)时，f′(x)<0，则f(x)在(－3,0)上是减函数．其他判断均不正确．3．函数f(x)＝(x－3)e x的单调递增区间是(D)A．(－∞，2) B．(0,3)C．(1,4) D．(2，＋∞)解析：函数f(x)＝(x－3)e x的导数为f′(x)＝[(x－3)e x]′＝e x＋(x－3)e x ＝(x－2)e x.由函数导数与函数单调性的关系，得当f′(x)>0时，函数f(x)单调递增，此时由不等式f′(x)＝(x－2)e x>0，解得x>2.知识点二利用导数研究函数的极值函数极值的概念函数y＝f(x)在点x＝a处的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)<0，右侧f′(x)>0.类似地，函数y＝f(x)在点x＝b处的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)>0，右侧f′(x)<0.我们把点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值；点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．极大值点和极小值点统称为极值点，极大值和极小值统称为极值．4．(选修2—2P32A4改编)如图是f(x)的导函数f′(x)的图象，则f(x)的极小值点的个数为(A)A．1 B．2C ．3D ．4解析：由题意知在x ＝－1处f ′(－1)＝0，且其左右两侧导数符号为左负右正．5．函数f (x )＝ln x －ax 在x ＝1处有极值，则常数a ＝1.解析：∵f ′(x )＝1x －a ，∴f ′(1)＝1－a ＝0，∴a ＝1，经检验符合题意．知识点三 函数最值的求解步骤一般地，求函数y ＝f (x )在[a ，b ]上的最大值与最小值的步骤如下：(1)求函数y ＝f (x )在(a ，b )内的极值；(2)将函数y ＝f (x )的各极值与端点处的函数值f (a )，f (b )比较，其中最大的一个是最大值，最小的一个是最小值．6．函数f (x )＝13x 3－4x ＋4在[0,3]上的最大值与最小值分别为4，－43.解析：由f (x )＝13x 3－4x ＋4，得f ′(x )＝x 2－4＝(x －2)(x ＋2)，令f ′(x )>0，得x >2或x <－2；令f ′(x )<0，得－2<x <2.所以f (x )在(－∞，－2)，(2，＋∞)上单调递增；在(－2,2)上单调递减，而f (2)＝－43，f (0)＝4，f (3)＝1，故f (x )在[0,3]上的最大值是4，最小值是－43.1．在某区间内f ′(x )>0(f ′(x )<0)是函数f (x )在此区间上为增(减)函数的充分不必要条件．可导函数f (x )在(a ，b )上是增(减)函数的充要条件是对∀x ∈(a ，b )，都有f ′(x )≥0(f ′(x )≤0)且f ′(x )在(a ，b )上的任何子区间内都不恒为零．2．对于可导函数f (x )，f ′(x 0)＝0是函数f (x )在x ＝x 0处有极值的必要不充分条件．3．注意函数最值是个“整体”概念，而极值是个“局部”概念．(1)若函数在开区间(a ，b )内的极值点只有一个，则相应极值点为函数最值点．(2)若函数在闭区间[a ，b ]的最值点不是端点，则最值点亦为极值点．第1课时 导数与函数的单调性考向一 利用导数讨论函数的单调性【例1】 (1)(2019·开封调研)已知定义在区间(－π，π)上的函数f (x )＝x sin x ＋cos x ，则f (x )的单调递增区间是____________．(2)已知函数f (x )＝⎝ ⎛⎭⎪⎫k ＋4k ln x ＋4－x 2x ，其中常数k >0，讨论f (x )在(0,2)上的单调性．【解析】 (1)f ′(x )＝sin x ＋x cos x －sin x ＝x cos x .令f ′(x )＝x cos x >0，则其在区间(－π，π)上的解集为⎝⎛⎭⎪⎫－π，－π2∪⎝ ⎛⎭⎪⎫0，π2，即f (x )的单调递增区间为－π，－π2和⎝ ⎛⎭⎪⎫0，π2. (2)因为f ′(x )＝k ＋4k x －4x 2－1＝⎝ ⎛⎭⎪⎫k ＋4k x －4－x 2x 2＝－(x －k )⎝ ⎛⎭⎪⎫x －4k x 2(0<x <2，k >0)．①当0<k <2时，4k >k >0，且4k >2，所以x ∈(0，k )时，f ′(x )<0，x ∈(k,2)时，f ′(x )>0，所以函数f (x )在(0，k )上是减函数，在(k,2)上是增函数；②当k ＝2时，4k ＝k ＝2，f ′(x )<0在(0,2)上恒成立，所以f (x )在(0,2)上是减函数，③当k >2时，0<4k <2，k >4k ，所以x ∈⎝ ⎛⎭⎪⎫0，4k 时，f ′(x )<0，x ∈4k ，2时，f ′(x )>0，所以函数f (x )在⎝ ⎛⎭⎪⎫0，4k 上是减函数，在⎝ ⎛⎭⎪⎫4k ，2上是增函数． 【答案】 (1)⎝ ⎛⎭⎪⎫－π，－π2和⎝ ⎛⎭⎪⎫0，π2 (2)见解析在例1(2)中，将“(0,2)”改为“(0，＋∞)”，其他条件不变，求函数f (x )的单调区间．解：由例题知f ′(x )＝－(x －k )⎝ ⎛⎭⎪⎫x －4k x 2(x >0，k >0)． ①当0<k <2时，k <4k ，f (x )的单调减区间为(0，k )，⎝ ⎛⎭⎪⎫4k ，＋∞，增区间为⎝⎛⎭⎪⎫k ，4k . ②当k ＝2时，k ＝4k ＝2，f ′(x )<0，f (x )在(0，＋∞)上为减函数．③当k >2时，k >4k ，f (x )的单调减区间为⎝ ⎛⎭⎪⎫0，4k 和(k ，＋∞)，增区间为⎝ ⎛⎭⎪⎫4k ，k .1.确定函数单调区间的步骤(1)确定函数f (x )的定义域.(2)求f ′(x ).(3)解不等式f ′(x )>0，解集在定义域内的部分为单调递增区间.(4)解不等式f ′(x )<0，解集在定义域内的部分为单调递减区间.,2.研究含参数的函数的单调性，要依据参数对不等式解集的影响进行分类讨论.(1)函数y ＝4x 2＋1x 的单调增区间为( B ) A ．(0，＋∞) B.⎝ ⎛⎭⎪⎫12，＋∞C ．(－∞，－1)D.⎝ ⎛⎭⎪⎫－∞，－12 解析：由y ＝4x 2＋1x ，得y ′＝8x －1x 2，令y ′>0，即8x －1x 2>0，解得x >12，∴函数y ＝4x 2＋1x 的单调增区间为⎝ ⎛⎭⎪⎫12，＋∞.故选B. (2)设f (x )＝x ln x －ax 2＋(2a －1)x ，a ∈R ，令g (x )＝f ′(x )，求g (x )的单调区间．解：由f ′(x )＝ln x －2ax ＋2a ，得g (x )＝ln x －2ax ＋2a ，x ∈(0，＋∞)．则g ′(x )＝1x －2a ＝1－2ax x .若a ≤0，当x ∈(0，＋∞)时，g ′(x )>0，函数g (x )单调递增；若a >0，当x ∈⎝ ⎛⎭⎪⎫0，12a 时，g ′(x )>0，函数g (x )单调递增，当x ∈⎝ ⎛⎭⎪⎫12a ，＋∞时，g ′(x )<0，函数g (x )单调递减．所以当a ≤0时，g (x )的单调增区间为(0，＋∞)；当a >0时，g (x )的单调增区间为⎝ ⎛⎭⎪⎫0，12a ，单调减区间为⎝ ⎛⎭⎪⎫12a ，＋∞. 考向二 根据函数单调性求参数的范围【例2】 (1)若f (x )＝－12x 2＋b ln(x ＋2)在(－1，＋∞)内是减函数，则b的取值范围是________．(2)若函数f (x )＝x 2－e x －ax 在R 上存在单调递增区间，则实数a 的取值范围是________．【解析】 (1)(分离参数法)若f (x )＝－12x 2＋b ln(x ＋2)在(－1，＋∞)内是减函数，则对任意x ∈(－1，＋∞)，f ′(x )＝－x ＋b x ＋2≤0，只需b ≤x (x ＋2)在(－1，＋∞)内恒成立，令y ＝x (x ＋2)＝(x ＋1)2－1，则在(－1，＋∞)内y >－1，∴b 的取值范围是b ≤－1.(2)∵函数f (x )＝x 2－e x －ax ，∴f ′(x )＝2x －e x －a .∵函数f (x )＝x 2－e x －ax 在R 上存在单调递增区间，∴f ′(x )＝2x －e x －a >0有解，即a <2x －e x 有解．令g (x )＝2x －e x ，g ′(x )＝2－e x ＝0，x ＝ln2，g ′(x )＝2－e x >0，x <ln2，g ′(x )＝2－e x <0，x >ln2，∴当x ＝ln2时，g (x )max ＝2ln2－2.∴a <2ln2－2.故实数a 的取值范围是(－∞，2ln2－2)．【答案】 (1)b ≤－1 (2)(－∞，2ln2－2)1.已知函数的单调性，求参数的取值范围，应用条件f ′(x )≥0(或f ′(x )≤0)，x ∈(a ，b )恒成立，解出参数的取值范围(一般可用不等式恒成立的理论求解)，应注意参数的取值是f ′(x )不恒等于0的参数的范围.2.若函数y ＝f (x )在区间(a ，b )上不单调，则转化为f ′(x )＝0在(a ，b )上有解.(1)设函数f (x )＝ln x x 在区间(a ，a ＋2)内单调递增，则实数a 的取值范围是[0，e －2]．(2)已知函数g (x )＝kx 3－x －2在区间(1,2)内不单调，则实数k 的取值范围是⎩⎨⎧⎭⎬⎫k 112<k <13. 解析：(1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝1－ln x x 2，由f ′(x )＝1－ln xx 2>0，解得0<x <e ，即函数的递增区间为(0，e)．若函数f (x )在区间(a ，a ＋2)内单调递增，则⎩⎪⎨⎪⎧0≤a ，a ＋2≤e ，即0≤a ≤e －2. 故实数a 的取值范围是[0，e －2]．(2)依题意g ′(x )＝3kx 2－1.①当k ≤0时，g ′(x )＝3kx 2－1≤0，∴g (x )在(1,2)内单调递减，不满足题意；②当k >0时，g (x )在⎝ ⎛⎭⎪⎫0，13k 内单调递减，在⎝ ⎛⎭⎪⎫13k ，＋∞内单调递增．∵函数g (x )在区间(1,2)内不单调， ∴1<13k <2，解得112<k <13.综上所述，实数k 的取值范围是⎩⎨⎧⎭⎬⎫k 112<k <13. 考向三 函数单调性的简单应用方向1 比较大小【例3】 已知函数f (x )是定义在R 上的偶函数，设函数f (x )的导函数为f ′(x )，若对任意x >0都有2f (x )＋xf ′(x )>0成立，则( )A ．4f (－2)<9f (3)B ．4f (－2)>9f (3)C ．2f (3)>3f (－2)D ．3f (－3)<2f (－2)【解析】 根据题意，令g (x )＝x 2f (x )，其导数g ′(x )＝2xf (x )＋x 2f ′(x )，又对任意x >0都有2f (x )＋xf ′(x )>0成立，则当x >0时，有g ′(x )＝x (2f (x )＋xf ′(x ))>0恒成立，即函数g (x )在(0，＋∞)上为增函数，又由函数f (x )是定义在R 上的偶函数，则f (－x )＝f (x )，则有g (－x )＝(－x )2f (－x )＝x 2f (x )＝g (x )，即函数g (x )也为偶函数，则有g (－2)＝g (2)，且g (2)<g (3)，则有g (－2)<g (3)，即有4f (－2)<9f (3)．故选A.【答案】 A 方向2 解不等式【例4】 设f ′(x )是奇函数f (x )(x ∈R )的导函数，f (－2)＝0，当x >0时，xf ′(x )－f (x )>0，则使得f (x )>0成立的x 的取值范围是________．【解析】 令g (x )＝f (x )x ，则g ′(x )＝xf ′(x )－f (x )x 2>0，x ∈(0，＋∞)，所以函数g (x )在(0，＋∞)上单调递增．又g (－x )＝f (－x )－x ＝－f (x )－x＝f (x )x ＝g (x )，所以g (x )是偶函数，g (－2)＝0＝g (2)，所以f (x )＝xg (x )>0⇒⎩⎪⎨⎪⎧x >0，g (x )>0或⎩⎪⎨⎪⎧x <0，g (x )<0，解得x >2或－2<x <0，故不等式f (x )>0的解集为(－2，0)∪(2，＋∞)．【答案】 (－2,0)∪(2，＋∞)1．(方向1)已知f (x )是定义在区间(0，＋∞)内的函数，其导函数为f ′(x )，且不等式xf ′(x )<2f (x )恒成立，则( B )A ．4f (1)<f (2)B ．4f (1)>f (2)C ．f (1)<4f (2)D ．f (1)<4f ′(2)解析：设函数g (x )＝f (x )x 2(x >0)，则g ′(x )＝x 2f ′(x )－2xf (x )x 4＝xf ′(x )－2f (x )x 3<0，所以函数g (x )在(0，＋∞)内为减函数，所以g (1)>g (2)，即f (1)12>f (2)22，所以4f (1)>f (2)，故选B.2．(方向1)已知f (x )是定义在(－∞，＋∞)上的函数，导函数f ′(x )满足f ′(x )<f (x )对于x ∈R 恒成立，则( D )A ．f (2)>e 2f (0)，f (2 017)>e 2 017f (0)B ．f (2)<e 2f (0)，f (2 017)>e 2 017f (0)C ．f (2)>e 2f (0)，f (2 017)<e 2 017f (0)D ．f (2)<e 2f (0)，f (2 017)<e 2 017f (0) 解析：构造F (x )＝f (x )e x 形式，则F ′(x ) ＝e xf ′(x )－e x f (x )e 2x ＝f ′(x )－f (x )e x， 导函数f ′(x )满足f ′(x )<f (x )，则F ′(x )<0，F (x )在R 上单调递减，根据单调性可知选D.3．(方向2)已知函数f(x)的定义域为R，f(－2)＝2 021，对任意x∈R，都有f′(x)<2x成立，则不等式f(x)>x2＋2 017的解集为(C) A．(－2，＋∞) B．(－2,2)C．(－∞，－2) D．(－∞，＋∞)解析：令函数F(x)＝f(x)－x2－2 017，则F′(x)＝f′(x)－2x<0，则函数F(x)是减函数，且满足F(－2)＝f(－2)－4－2 017＝0，故不等式f(x)>x2＋2 017可化为F(x)>F(－2)，即原不等式f(x)>x2＋2 017的解集为{x|x<－2}．故选C.第2课时导数与函数的极值、最值考向一函数的极值方向1利用图象判断极值【例1】设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是()A．函数f(x)有极大值f(2)和极小值f(1)B．函数f(x)有极大值f(－2)和极小值f(1)C．函数f(x)有极大值f(2)和极小值f(－2)D．函数f(x)有极大值f(－2)和极小值f(2)【解析】由题图可知，当x<－2时，f′(x)>0；当－2<x<1时，f′(x)<0；当1<x<2时，f′(x)<0；当x>2时，f′(x)>0.由此可以得到函数f(x)在x＝－2处取得极大值，在x＝2处取得极小值．【答案】 D方向2求函数的极值【例2】(2019·深圳调研)设函数f(x)＝ln(x＋1)＋a(x2－x)，其中a∈R .讨论函数f (x )极值点的个数，并说明理由．【解】 f ′(x )＝1x ＋1＋a (2x －1)＝2ax 2＋ax －a ＋1x ＋1(x >－1)．令g (x )＝2ax 2＋ax －a ＋1，x ∈(－1，＋∞)． ①当a ＝0时，g (x )＝1，此时f ′(x )>0， 函数f (x )在(－1，＋∞)上单调递增，无极值点． ②当a >0时，Δ＝a 2－8a (1－a )＝a (9a －8)．a ．当0<a ≤89时，Δ≤0，g (x )≥0，f ′(x )≥0，函数f (x )在(－1，＋∞)上单调递增，无极值点．b ．当a >89时，Δ>0，设方程2ax 2＋ax －a ＋1＝0的两根为x 1，x 2(x 1<x 2)， 因为x 1＋x 2＝－12， 所以x 1<－14，x 2>－14. 由g (－1)＝1>0， 可得－1<x 1<－14.所以当x ∈(－1，x 1)时，g (x )>0，f ′(x )>0，函数f (x )单调递增；当x ∈(x 1，x 2)时，g (x )<0，f ′(x )<0，函数f (x )单调递减； 当x ∈(x 2，＋∞)时，g (x )>0，f ′(x )>0，函数f (x )单调递增． 因此函数有两个极值点．③当a <0时，Δ>0，由g (－1)＝1>0， 可得x 1<－1<x 2.当x ∈(－1，x 2)时，g (x )>0，f ′(x )>0，函数f (x )单调递增； 当x ∈(x 2，＋∞)时，g (x )<0，f ′(x )<0，函数f (x )单调递减． 所以函数有一个极值点．综上所述，当a <0时，函数f (x )有一个极值点； 当0≤a ≤89时，函数f (x )无极值点； 当a >89时，函数f (x )有两个极值点． 方向3 根据极值求参数【例3】 (2019·陕西质量检测)若函数f (x )＝ax －x 2－ln x 存在极值，且这些极值的和不小于4＋ln2，则a 的取值范围为( )A ．[2，＋∞)B ．[22，＋∞)C ．[23，＋∞)D ．[4，＋∞)【解析】 f ′(x )＝a －2x －1x ＝－2x 2－ax ＋1x ，因为f (x )存在极值，所以f ′(x )＝0在(0，＋∞)上有根，即2x 2－ax ＋1＝0在(0，＋∞)上有根，所以Δ＝a 2－8≥0，显然当Δ＝0时，f (x )无极值，不合题意，所以Δ＝a 2－8>0，即a >22或a <－2 2.记方程2x 2－ax ＋1＝0的两根为x 1，x 2，由根与系数的关系得x 1x 2＝12，x 1＋x 2＝a2，易知a >0，则f (x 1)，f (x 2)为f (x )的极值，所以f (x 1)＋f (x 2)＝(ax 1－x 21－ln x 1)＋(ax 2－x 22－ln x 2)＝a (x 1＋x 2)－(x 21＋x 22)－(ln x 1＋ln x 2)＝a 22－(a 24－1)＋ln2≥4＋ln2，所以a ≥2 3.综上，a 的取值范围为[23，＋∞)，故选C.【答案】 C函数极值的两类热点问题(1)求函数f (x )极值的一般解题步骤①确定函数的定义域；②求导数f ′(x )；③解方程f ′(x )＝0，求出函数定义域内的所有根；④列表检验f ′(x )在f ′(x )＝0的根x 0左右两侧值的符号．(2)根据函数极值情况求参数的两个要领①列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解．②验证：求解后验证根的合理性．1．(方向1)函数y ＝f (x )的导函数的图象如图所示，则下列说法错误的是( C )A ．(－1,3)为函数y ＝f (x )的单调递增区间B ．(3,5)为函数y ＝f (x )的单调递减区间C ．函数y ＝f (x )在x ＝0处取得极大值D ．函数y ＝f (x )在x ＝5处取得极小值解析：由函数y ＝f (x )的导函数的图象可知，当x <－1或3<x <5时，f ′(x )<0，y ＝f (x )单调递减；当x >5或－1<x <3时，f ′(x )>0，y ＝f (x )单调递增．所以函数y ＝f (x )的单调递减区间为(－∞，－1)，(3,5)，单调递增区间为(－1，3)，(5，＋∞)．函数y ＝f (x )在x ＝－1,5处取得极小值，在x ＝3处取得极大值，故选项C 错误，故选C.2．(方向2)(2019·山西太原模拟)设函数f (x )＝13x 3－x ＋m 的极大值为1，则函数f (x )的极小值为( A )A ．－13B ．－1C.13D ．1解析：f ′(x )＝x 2－1，由f ′(x )＝0得x 1＝－1，x 2＝1.所以f (x )在区间(－∞，－1)上单调递增，在区间(－1,1)上单调递减，在区间(1，＋∞)上单调递增，所以函数f (x )在x ＝－1处取得极大值，且f (－1)＝1，即m ＝13，函数f (x )在x ＝1处取得极小值，且f (1)＝13×13－1＋13＝－13.故选A.3．(方向3)(2019·江西八校联考)若函数f (x )＝x 2－x ＋a ln x 在[1，＋∞)上有极值点，则实数a 的取值范围为(－∞，－1]．解析：函数f (x )的定义域为(0，＋∞)，f ′(x )＝2x －1＋a x ＝2x 2－x ＋ax， 由题意知2x 2－x ＋a ＝0在R 上有两个不同的实数解，且在[1，＋∞)上有解，所以Δ＝1－8a >0，且2×12－1＋a ≤0， 所以a ∈(－∞，－1]． 考向二 函数的最值【例4】 已知函数f (x )＝x －m ln x －m －1x (m ∈R )，g (x )＝12x 2＋e x －x e x . (1)当x ∈[1，e]时，求f (x )的最小值；(2)当m ≤2时，若存在x 1∈[e ，e 2]，使得对任意x 2∈[－2,0]，f (x 1)≤g (x 2)成立，求实数m 的取值范围．【解】 (1)f (x )＝x －m ln x －m －1x (x >0)， ∴f ′(x )＝1－m x ＋m －1x 2 ＝(x －1)[x －(m －1)]x 2. 当m ≤2时，在[1，e]上有f ′(x )≥0，f (x )min ＝f (1)＝2－m ；当m ≥e ＋1时，在[1，e]上有f ′(x )≤0，f (x )min ＝f (e)＝e －m －m －1e ； 当2<m <e ＋1时，若x ∈[1，m －1]，则f ′(x )≤0，若x ∈[m －1，e]，则f ′(x )≥0，f (x )min ＝f (m －1)＝m －2－m ln(m －1)． 综上，f (x )min ＝⎩⎪⎨⎪⎧2－m ，m ≤2，m －2－m ln (m －1)，2<m <e ＋1，e －m －m －1e ，m ≥e ＋1.(2)由题知，条件等价于f (x 1)min ≤g (x 2)min . 由(1)知m ≤2时，在[e ，e 2]上有f ′(x )≥0， ∴f (x 1)min ＝f (e)＝e －m －m －1e .g ′(x )＝x ＋e x －(x ＋1)e x ＝x (1－e x )， 当x 2∈[－2,0]时，g ′(x 2)≤0，g (x 2)min ＝g (0)＝1.∴⎩⎨⎧m ≤2，e －m －m －1e ≤1，解得e 2－e ＋1e ＋1≤m ≤2.∴实数m 的取值范围是⎣⎢⎡⎦⎥⎤e 2－e ＋1e ＋1，2.(1)函数在闭区间上的最值在端点处或区间内的极值点处取得，上述值中最大的即为最大值、最小的即为最小值．如果函数在一个区间上(不论区间的类型)有唯一的极值点，则该点也是最值点．(2)注意把不等式恒成立问题转化为函数的最值问题．(2018·全国卷Ⅰ)已知函数f (x )＝2sin x ＋sin2x ，则f (x )的最小值是－332. 解析：解法1：因为f (x )＝2sin x ＋sin2x ，所以f ′(x )＝2cos x ＋2cos2x ＝4cos 2x ＋2cos x －2＝4(cos x －12)(cos x ＋1)，由f ′(x )≥0得12≤cos x ≤1，即2k π－π3≤x ≤2k π＋π3，k ∈Z ，由f ′(x )≤0得－1≤cos x ≤12，即2k π＋π≥x ≥2k π＋π3或2k π－π≤x ≤2k π－π3，k ∈Z ，所以当x ＝2k π－π3(k ∈Z )时，f (x )取得最小值，且f (x )min ＝f (2k π－π3)＝2sin(2k π－π3)＋sin2(2k π－π3)＝－332.解法2：因为f (x )＝2sin x ＋sin2x ＝2sin x (1＋cos x )，所以[f (x )]2＝4sin 2x (1＋cos x )2＝4(1－cos x )(1＋cos x )3，设cos x ＝t ，则y ＝4(1－t )(1＋t )3(－1≤t ≤1)，所以y ′＝4[－(1＋t )3＋3(1－t )(1＋t )2]＝4(1＋t )2(2－4t )，所以当－1<t <12时，y ′>0；当12<t <1时，y ′<0.所以函数y ＝4(1－t )(1＋t )3(－1≤t ≤1)在(－1，12)上单调递增，在(12，1)上单调递减，所以当t ＝12时，y max ＝274；当t ＝±1时，y min ＝0.所以0≤y ≤274，即0≤[f (x )]2≤274，所以－332≤f (x )≤332，所以f (x )的最小值为－332.第3课时 导数与不等式问题考向一 导数法证明不等式方向1 “单变量”型不等式证明【例1】 (2019·长春市质量检测)已知函数f (x )＝e x －a . (1)若函数f (x )的图象与直线l ：y ＝x －1相切，求a 的值； (2)若f (x )－ln x >0恒成立，求整数a 的最大值．【解】 (1)f ′(x )＝e x ，因为函数f (x )的图象与直线y ＝x －1相切，所以令f ′(x )＝1，即e x ＝1，得x ＝0，即f (0)＝－1，解得a ＝2.(2)现证明e x ≥x ＋1，设F (x )＝e x －x －1，则F ′(x )＝e x －1，令F ′(x )＝0，则x ＝0，当x ∈(0，＋∞)时，F ′(x )>0，当x ∈(－∞，0)时，F ′(x )<0，所以F (x )在(0，＋∞)上单调递增，在(－∞，0)上单调递减，所以F (x )min ＝F (0)＝0，即F (x )≥0恒成立，即e x ≥x ＋1，即e x －2≥x －1，同理可得ln x ≤x －1，所以e x －2>ln x ， 当a ≤2时，ln x <e x －2≤e x －a ， 即当a ≤2时，f (x )－ln x >0恒成立．当a ≥3时，存在x ，使e x －a <ln x ，即e x －a >ln x 不恒成立． 综上，整数a 的最大值为2. 方向2 “双变量”型不等式证明【例2】 (2018·全国卷Ⅰ)已知函数f (x )＝1x －x ＋a ln x . (1)讨论f (x )的单调性；(2)若f (x )存在两个极值点x 1，x 2，证明：f (x 1)－f (x 2)x 1－x 2<a －2.【解】 (1)f (x )的定义域为(0，＋∞)， f ′(x )＝－1x 2－1＋ax ＝－x 2－ax ＋1x 2. ①若a ≤2，则f ′(x )≤0，当且仅当a ＝2，x ＝1时，f ′(x )＝0，所以f (x )在(0，＋∞)单调递减．②若a >2，令f ′(x )＝0得， x ＝a －a 2－42或x ＝a ＋a 2－42. 当x ∈(0，a －a 2－42)∪(a ＋a 2－42，＋∞)时，f ′(x )<0；当x ∈(a －a 2－42，a ＋a 2－42)时，f ′(x )>0.所以f (x )在(0，a －a 2－42)，(a ＋a 2－42，＋∞)单调递减，在(a －a 2－42，a ＋a 2－42)单调递增． (2)证明：由(1)知，f (x )存在两个极值点时，当且仅当a >2.由于f (x )的两个极值点x 1，x 2满足x 2－ax ＋1＝0，所以x 1x 2＝1，不妨设x 1<x 2，则x 2>1.由于f (x 1)－f (x 2)x 1－x 2＝－1x 1x 2－1＋a ln x 1－ln x 2x 1－x 2＝－2＋a ln x 1－ln x 2x 1－x 2＝－2＋a －2ln x 21x 2－x 2，所以f (x 1)－f (x 2)x 1－x 2<a －2等价于1x 2－x 2＋2ln x 2<0.设函数g (x )＝1x －x ＋2ln x ，由(1)知，g (x )在(0，＋∞)单调递减，又g (1)＝0，从而当x ∈(1，＋∞)时，g (x )<0.所以1x 2－x 2＋2ln x 2<0，即f (x 1)－f (x 2)x 1－x 2<a －2.1.“单变量”型不等式的证明一般是通过构造差函数F (x )＝f (x )－g (x )解决，有时也可适当变形，再构造差函数．2．“双变量”型不等式的证明一般先通过题中关系找出两变量的关系(如例2)再转化为“单变量”型不等式解决．1．(方向1)已知函数f (x )＝ln x ＋(1－a )x 3＋bx ，g (x )＝x e x －b (a ，b ∈R ，e 为自然对数的底数)，且曲线y ＝f (x )在点(e ，f (e))处的切线方程为y ＝⎝ ⎛⎭⎪⎫1e ＋1x .(1)求实数a ，b 的值； (2)求证：f (x )≤g (x )．解：(1)∵f ′(x )＝1x ＋3(1－a )x 2＋b ， ∴f ′(e)＝1e ＋3(1－a )e 2＋b ， 且f (e)＝1＋(1－a )e 3＋b e ，又曲线y ＝f (x )在点(e ，f (e))处的切线方程为y ＝⎝⎛⎭⎪⎫1e ＋1x ，∴切点坐标为(e,1＋e)，∴⎩⎨⎧1e＋3(1－a )e 2＋b ＝1e ＋1，1＋(1－a )e 3＋b e ＝1＋e ，解得a ＝b ＝1.(2)证明：由(1)可知f (x )＝ln x ＋x ，g (x )＝x e x －1，且f (x )的定义域为(0，＋∞)，令F (x )＝f (x )－g (x )＝ln x ＋x －x e x ＋1，则F ′(x )＝1x ＋1－e x －x e x ＝1＋x x －(x ＋1)e x＝(x ＋1)⎝ ⎛⎭⎪⎫1x －e x .令G (x )＝1x －e x，可知G (x )在(0，＋∞)上为减函数，且G ⎝ ⎛⎭⎪⎫12＝2－e>0，G (1)＝1－e<0，∴存在x 0∈⎝ ⎛⎭⎪⎫12，1，使得G (x 0)＝0，即1x 0－e x 0＝0.当x ∈(0，x 0)时，G (x )>0， ∴F ′(x )>0，F (x )为增函数； 当x ∈(x 0，＋∞)时，G (x )<0， ∴F ′(x )<0，F (x )为减函数． ∴F (x )≤F (x 0)＝ln x 0＋x 0－x 0e x 0＋1， 又∵1x 0－e x 0＝0，∴1x 0＝e x 0，即ln x 0＝－x 0，∴F (x 0)＝0，即F (x )≤0，∴f (x )≤g (x )． 2．(方向2)已知函数f (x )＝ln x －x . (1)判断函数f (x )的单调性；(2)函数g (x )＝f (x )＋x ＋12x －m 有两个零点x 1，x 2，且x 1<x 2，求证：x 1＋x 2>1.解：(1)函数f (x )的定义域为(0，＋∞)． f ′(x )＝1x －1＝1－x x ，令f ′(x )＝1x －1＝1－x x >0，得0<x <1， 令f ′(x )＝1x －1＝1－x x <0，得x >1，所以函数f (x )的单调递增区间为(0,1)，函数f (x )的单调递减区间为(1，＋∞)．(2)证明：根据题意，g (x )＝ln x ＋12x －m (x >0)，因为x 1，x 2是函数g (x )＝ln x ＋12x －m 的两个零点，所以ln x 1＋12x 1－m ＝0，ln x 2＋12x 2－m ＝0.两式相减，可得ln x 1x 2＝12x 2－12x 1，即ln x 1x 2＝x 1－x 22x 2x 1，故x 1x 2＝x 1－x 22ln x 1x2. 那么x 1＝x 1x 2－12ln x 1x 2，x 2＝1－x 2x 12ln x 1x2.令t ＝x 1x 2，其中0<t <1，则x 1＋x 2＝t －12ln t ＋1－1t 2ln t ＝t －1t 2ln t . 构造函数h (t )＝t －1t －2ln t ， 则h ′(t )＝(t －1)2t 2.对于0<t <1，h ′(t )>0恒成立， 故h (t )<h (1)，即t －1t －2ln t <0. 可知t －1t2ln t >1，故x 1＋x 2>1. 考向二 不等式恒成立问题【例3】 (2019·陕西西北九校联考)已知函数f (x )＝－ln x ＋t (x －1)，t 为实数．(1)当t ＝1时，求函数f (x )的单调区间；(2)若当t ＝12时，k x －12－f (x )<0在(1，＋∞)上恒成立，求实数k 的取值范围．【解】 (1)当t ＝1时，f (x )＝－ln x ＋x －1，x >0， ∴f ′(x )＝－1x ＋1＝x －1x .由f ′(x )<0可得0<x <1， 由f ′(x )>0可得x >1，∴函数f (x )的单调递减区间为(0,1)，单调递增区间为(1，＋∞)． (2)当t ＝12时，f (x )＝－ln x ＋x 2－12，k x －12－f (x )＝k x －12－－ln x ＋x 2－12＝ln x －x 2＋k x ，当x >1时，k x －12－f (x )<0恒成立，等价于k <x 22－x ln x 在(1，＋∞)上恒成立．令g (x )＝x 22－x ln x ，则g ′(x )＝x －(ln x ＋1)＝x －1－ln x . 令h (x )＝x －1－ln x ， 则h ′(x )＝1－1x ＝x －1x .当x >1时，h ′(x )>0，函数h (x )＝x －1－ln x 在(1，＋∞)上单调递增，故h (x )>h (1)＝0，从而当x >1时，g ′(x )>g ′(1)＝0，即函数g (x )在(1，＋∞)上单调递增，故g (x )>g (1)＝12，因此当x >1时，若使k <x 22－x ln x 恒成立，必须k ≤12.∴实数k 的取值范围是⎝⎛⎦⎥⎤－∞，12.(1)f(x)>g(x)对一切x∈I恒成立⇔I是f(x)>g(x)解集的子集⇔[f(x)－g(x)]min>0(x∈I).(2)对∀x1，x2∈D使得f(x1)≤g(x2)⇔f(x)max≤g(x)min.(2019·山西八校联考)已知函数f(x)＝x－1－a ln x(a∈R)，g(x)＝1 x.(1)当a＝－2时，求曲线y＝f(x)在x＝1处的切线方程；(2)若a<0，且对任意x1，x2∈(0,1]，都有|f(x1)－f(x2)|<4×|g(x1)－g(x2)|，求实数a的取值范围．解：(1)当a＝－2时，f(x)＝x－1＋2ln x，f′(x)＝1＋2x，f(1)＝0，切线的斜率k＝f′(1)＝3，故曲线y＝f(x)在x＝1处的切线方程为3x－y－3＝0.(2)对x∈(0,1]，当a<0时，f′(x)＝1－ax>0，∴f(x)在(0,1]上单调递增，易知g(x)＝1x在(0,1]上单调递减，不妨设x1，x2∈(0,1]，且x1<x2，f(x1)<f(x2)，g(x1)>g(x2)，∴f(x2)－f(x1)<4×[g(x1)－g(x2)]，即f(x1)＋4x1>f(x2)＋4x2.令h(x)＝f(x)＋4x，则当x1<x2时，有h(x1)>h(x2)，∴h (x )在(0,1]上单调递减，∴h ′(x )＝1－a x －4x 2＝x 2－ax －4x 2≤0在(0,1]上恒成立， ∴x 2－ax －4≤0在(0,1]上恒成立，等价于a ≥x －4x 在(0,1]上恒成立， ∴只需a ≥(x －4x )max .∵y ＝x －4x 在(0,1]上单调递增，∴y max ＝－3，∴－3≤a <0，故实数a 的取值范围为[－3,0)．考向三 不等式存在性问题【例4】 已知函数f (x )＝x －(a ＋1)ln x －a x (a ∈R )，g (x )＝12x 2＋e x －x e x .(1)当x ∈[1，e]时，求f (x )的最小值；(2)当a <1时，若存在x 1∈[e ，e 2]，使得对任意的x 2∈[－2，0]，f (x 1)<g (x 2)恒成立，求a 的取值范围．【解】 (1)f (x )的定义域为(0，＋∞)，f ′(x )＝(x －1)(x －a )x 2. ①当a ≤1时，x ∈[1，e]，f ′(x )≥0，f (x )为增函数，f (x )min ＝f (1)＝1－a .②当1<a <e 时，x ∈[1，a ]时，f ′(x )≤0，f (x )为减函数；x ∈[a ，e]时，f ′(x )≥0，f (x )为增函数．所以f (x )min ＝f (a )＝a －(a ＋1)ln a －1.③当a ≥e 时，x ∈[1，e]时，f ′(x )≤0，f (x )在[1，e]上为减函数．f (x )min ＝f (e)＝e －(a ＋1)－a e .综上，当a ≤1时，f (x )min ＝1－a ；当1<a <e 时，f (x )min ＝a －(a ＋1)ln a －1；当a ≥e 时，f (x )min ＝e －(a ＋1)－a e .(2)由题意知f (x )(x ∈[e ，e 2])的最小值小于g (x )(x ∈[－2,0])的最小值．由(1)知当a <1时f (x )在[e ，e 2]上单调递增，f (x )min ＝f (e)＝e －(a ＋1)－a e .g ′(x )＝(1－e x )x .当x ∈[－2,0]时g ′(x )≤0，g (x )为减函数，g (x )min ＝g (0)＝1，所以e －(a ＋1)－a e <1，即a >e 2－2e e ＋1， 所以a 的取值范围为⎝ ⎛⎭⎪⎫e 2－2e e ＋1，1.存在型不等式恒成立问题的求解策略“恒成立”与“存在性”问题的求解是“互补”关系，即f (x )≥g (a )对于x ∈D 恒成立，应求f (x )的最小值；若存在x ∈D ，使得f (x )≥g (a )成立，应求f (x )的最大值，在具体问题中究竟是求最大值还是最小值，可以先联想“恒成立”是求最大值还是最小值，这样也就可以解决相应的“存在性”问题是求最大值还是最小值．特别需要关注等号是否成立问题，以免细节出错．(2019·河北五名校联考)已知a 为实数，函数f (x )＝a ln x ＋x 2－4x .(1)若x ＝3是函数f (x )的一个极值点，求实数a 的值；(2)设g (x )＝(a －2)x ，若存在x 0∈[1e ，e]，使得f (x 0)≤g (x 0)成立，求实数a 的取值范围．解：(1)函数f (x )的定义域为(0，＋∞)，f ′(x )＝a x ＋2x －4＝2x 2－4x ＋a x. ∵x ＝3是函数f (x )的一个极值点，∴f ′(3)＝0，解得a ＝－6.经检验，当a ＝－6时，x ＝3是函数f (x )的一个极小值点，符合题意，故a ＝－6.(2)由f (x 0)≤g (x 0)，得(x 0－ln x 0)a ≥x 20－2x 0，记F (x )＝x －ln x (x >0)，则f ′(x )＝x －1x (x >0)，∴当0<x <1时，f ′(x )<0，F (x )单调递减；当x >1时，f ′(x )>0，F (x )单调递增．∴F (x )>F (1)＝1>0，∴a ≥x 20－2x 0x 0－ln x 0. 记G (x )＝x 2－2x x －ln x，x ∈[1e ，e]， 则G ′(x )＝(2x －2)(x －ln x )－(x －2)(x －1)(x －ln x )2＝(x －1)(x －2ln x ＋2)(x －ln x )2. ∵x ∈[1e ，e]，∴2－2ln x ＝2(1－ln x )≥0，∴x －2ln x ＋2>0，∴当x ∈(1e ，1)时，G ′(x )<0，G (x )单调递减；当x ∈(1，e)时，G ′(x )>0，G (x )单调递增．∴G (x )min ＝G (1)＝－1，∴a≥G(x)min＝－1，故实数a的取值范围为[－1，＋∞)．解决e x，ln x与x的组合函数问题的二类技巧近几年高考压轴题常以x与e x，ln x组合的函数为基础来命制，将基本初等函数的概念、图象与性质糅合在一起，发挥导数的工具作用，应用导数研究函数性质、证明相关不等式(或比较大小)、求参数的取值范围(或最值)．预计今后高考试题除了延续往年的命题形式，还会更着眼于知识点的巧妙组合，注重对函数与方程、转化与化归、分类讨论和数形结合等思想的灵活运用，突出对数学思维能力和数学核心素养的考查．1．分离ln x与e x典例1设函数f(x)＝a＋ln xx，曲线y＝f(x)在点(e，f(e))处的切线与直线e2x－y＋e＝0垂直．(1)若f (x )在(m ，m ＋1)上存在极值，求实数m 的取值范围；(2)求证：当x >1时，不等式f (x )e ＋1>2e x －1(x ＋1)(x e x ＋1). 【思路点拨】 (1)求出f (x )的导数，求得切线的斜率，由两直线垂直的条件可得a ＝1，利用导数求出函数f (x )的单调区间和极值，列出不等式，解不等式即可得到m 的取值范围；(2)所证不等式中同时含有e x 与ln x ，结构复杂，可考虑构造新函数g (x )，h (x )，通过求导，利用其单调性进行证明．【解】 (1)因为f ′(x )＝1－a －ln x x 2，所以曲线y ＝f (x )在点(e ，f (e))处的切线斜率为－a e 2.又切线与直线e 2x －y ＋e ＝0垂直，可得f ′(e)＝－1e 2，所以－a e 2＝－1e 2，解得a ＝1，所以f (x )＝1＋ln x x ，f ′(x )＝－ln x x 2(x >0)，当0<x <1时，f ′(x )>0，f (x )为增函数；当x >1时，f ′(x )<0，f (x )为减函数，所以x ＝1是函数f (x )的极大值点．又f (x )在(m ，m ＋1)上存在极值，所以m <1<m ＋1，即0<m <1.综上所述，实数m 的取值范围是(0,1)．(2)将不等式f (x )e ＋1>2e x －1(x ＋1)(x e x ＋1)变形为1e ＋1·(x ＋1)(ln x ＋1)x >2e x －1x e x ＋1， 分别构建函数g (x )＝(x ＋1)(ln x ＋1)x 和函数h (x )＝2e x －1x e x ＋1. 则g ′(x )＝x －ln x x 2，令φ(x )＝x －ln x ，则φ′(x )＝1－1x ＝x －1x .因为x >1，所以φ′(x )>0，所以φ(x )在(1，＋∞)上是增函数，所以φ(x )>φ(1)＝1>0，所以g ′(x )>0，所以g (x )在(1，＋∞)上是增函数，所以x >1时，g (x )>g (1)＝2，故g (x )e ＋1>2e ＋1. h ′(x )＝2e x －1(1－e x )(x e x ＋1)2，因为x >1， 所以1－e x <0，所以h ′(x )<0，所以h (x )在(1，＋∞)上是减函数，所以x >1时，h (x )<h (1)＝2e ＋1. 综上所述，g (x )e ＋1>h (x )， 即f (x )e ＋1>2e x －1(x ＋1)(x e x ＋1). 【点评】 若不分离e x 与ln x ，则难以求导，因此，对于形式复杂的函数，往往需要合理分拆与变形．高考为体现选拔功能，在解答题中不会单一考查某一初等函数，而是将不同增长速度的函数综合在一起考查，这就需要我们把已经糅合在一起的不同增长速度的函数进行分离，转化为我们熟悉的利于用导数工具求解的函数模型．2．借助e x ≥x ＋1和ln x ≤x －1进行放缩典例2 (2019·山东、湖北部分重点中学模拟)已知函数f (x )＝mx 2＋nx －x ln x (m >0)，且f (x )≥0.(1)求n m 的最小值；(2)当nm取得最小值时，若方程ex－1＋(1－2a)x－af(x)＝0无实根，求实数a的取值范围．【思路点拨】(1)利用导数，借助单调性求最值；(2)分离参数，利用放缩法确定函数值域．【解】(1)令g(x)＝f(x)x＝mx＋n－ln x，则f(x)≥0⇔g(x)≥0(x>0)，令g′(x)＝mx－1x>0，则x>1m，所以g(x)在(0，1m)上单调递减，在(1m，＋∞)上单调递增．此时g(x)min＝g(1m)＝1＋n－ln 1m≥0⇒1m＋nm－1m ln 1m≥0，即nm≥1m ln1m－1m，令h(t)＝t ln t－t(t>0)，令h′(t)＝ln t>0，则t>1，所以h(t)在(0,1)上单调递减，在(1，＋∞)上单调递增，故h(t)min＝h(1)＝－1，则nm≥－1，即(nm)min＝－1.(2)由(1)知，当nm取得最小值－1时，t＝1m＝1，m＝1，n＝－1.e x－1＋(1－2a)x－af(x)＝0⇒a＝e x－1＋xx(x＋1－ln x)，记H(x)＝e x－1＋xx(x＋1－ln x)，则H′(x)＝(x－1)[(x－ln x)e x－1－x]x2(x＋1－ln x)2，由(1)知x－1－ln x≥0⇒ln x≤x－1，即e x－1≥x，则(x－ln x)e x－1－x≥e x－1－x≥0(当且仅当x＝1时取等号)，所以当x∈(0,1)时，H′(x)<0，所以H(x)在(0,1)上为减函数；当x ∈(1，＋∞)时，H ′(x )>0，所以H (x )在(1，＋∞)上为增函数．所以x ＝1时，H (x )取得最小值，为H (1)＝1.由ln x ≤x －1，自变量取1x 可得－ln x ≤1x －1⇒2≤x ＋1－ln x ≤x ＋1x ，即x (x ＋1－ln x )≤x 2＋1⇒1x (x ＋1－ln x )≥1x 2＋1， 由x －1≥ln x ，自变量取e x 3可得e x 3－1>x 3(x >0)，从而e x >(x ＋33)3，则可得e x －1>(x ＋2)327.当x >1时，H (x )＝e x －1＋x x (x ＋1－ln x )>(x ＋2)327(x 2＋1)>(x ＋1)327(x ＋1)2＝x ＋127，即H (x )无最大值，所以H (x )∈[1，＋∞)．故a <1时原方程无实根，即实数a 的取值范围为(－∞，1)．第4课时 导数与函数的零点问题考向一 求函数零点个数【例1】 设函数f (x )＝e x －ax ，a 是常数，讨论f (x )的零点的个数．【解】 当a >0时，f ′(x )＝e x －a ，由f ′(x )＝0得x ＝ln a .若x <ln a ，则f ′(x )<0；若x >ln a ，则f ′(x )>0.函数f (x )在区间(－∞，ln a )上单调递减，在区间(ln a，＋∞)上单调递增，f(x)的最小值为f(ln a)＝a(1－ln a)．①当0<a<e时，f(ln a)＝a(1－ln a)>0，f(x)无零点；②当a＝e时，f(ln a)＝a(1－ln a)＝0，f(x)只有一个零点；③当a>e时，f(ln a)＝a(1－ln a)<0，根据f(0)＝1>0与函数的单调性，可知f(x)在区间(－∞，ln a)和(ln a，＋∞)上各有一个零点，f(x)共有两个零点．当a＝0时，f(x)＝e x，f(x)无零点．当a<0时，由f(x)＝0，得e x＝ax，易知曲线y＝e x与直线y＝ax只有一个交点，所以f(x)只有一个零点．综上所述，当0≤a<e时，f(x)无零点；当a<0或a＝e时，f(x)有一个零点；当a>e时，f(x)有两个零点．根据参数确定函数零点的个数，解题的基本思想也是“数形结合”，即通过研究函数的性质(单调性、极值、函数值的极限位置等)，作出函数的大致图象，然后通过函数图象得出其与x 轴交点的个数，或者两个相关函数图象交点的个数，基本步骤是“先数后形”.已知函数f (x )＝ax 2e x (a ≠0)，h (x )＝x －1x .当a ＝1时，研究函数φ(x )＝f (x )－h (x )在(0，＋∞)上零点的个数．解：当a ＝1时，函数φ(x )＝f (x )－h (x )＝x 2e x －⎝ ⎛⎭⎪⎫x －1x ，φ′(x )＝x (2－x )e x －1－1x 2.当x ≥2时，φ′(x )<0恒成立，当0<x <2时，x (2－x )≤⎣⎢⎡⎦⎥⎤x ＋(2－x )22＝1， ∴φ′(x )＝x (2－x )e x －1－1x 2≤1e x －1－1x 2<1－1－1x 2<0， ∴φ′(x )<0在(0，＋∞)上恒成立， 故φ(x )在(0，＋∞)上单调递减． 又φ(1)＝1e >0，φ(2)＝4e 2－32<0，函数φ(x )＝f (x )－h (x )的图象在[1,2]上连续不间断，∴由函数零点存在性定理及φ(x )的单调性知，存在唯一的x 0∈(1,2)，使φ(x 0)＝0.所以，函数φ(x )＝f (x )－h (x )在(0，＋∞)上零点的个数为1.考向三 已知函数零点个数确定参数范围【例2】 已知函数f (x )＝－12ax 2＋(1＋a )x －ln x (a ∈R )． (1)当a >0时，求函数f (x )的单调递减区间；(2)当a ＝0时，设函数g (x )＝xf (x )－k (x ＋2)＋2.若函数g (x )在区间⎣⎢⎡⎭⎪⎫12，＋∞上有两个零点，求实数k 的取值范围． 【解】 (1)f (x )的定义域为(0，＋∞)， f (x )的导数为f ′(x )＝－ax ＋1＋a －1x ＝－(ax －1)(x －1)x (a >0)， ①当a ∈(0,1)时，1a >1.由f ′(x )<0，得x >1a 或x <1.所以f (x )的单调递减区间为(0,1)，⎝ ⎛⎭⎪⎫1a ，＋∞； ②当a ＝1时，恒有f ′(x )≤0， 所以f (x )的单调递减区间为(0，＋∞)； ③当a ∈(1，＋∞)时，1a <1.由f ′(x )<0，得x >1或x <1a .所以f (x )的单调递减区间为⎝ ⎛⎭⎪⎫0，1a ，(1，＋∞)． 综上，当a ∈(0,1)时，f (x )的单调递减区间为(0,1)，⎝ ⎛⎭⎪⎫1a ，＋∞；当a ＝1时，f (x )的单调递减区间为(0，＋∞)；当a ∈(1，＋∞)时，f (x )的单调递减区间为⎝⎛⎭⎪⎫0，1a ，(1，＋∞)．(2)g (x )＝x 2－x ln x －k (x ＋2)＋2在x ∈⎣⎢⎡⎭⎪⎫12，＋∞上有两个零点，即关于x的方程k ＝x 2－x ln x ＋2x ＋2在x ∈⎣⎢⎡⎭⎪⎫12，＋∞上有两个不相等的实数根．令函数h (x )＝x 2－x ln x ＋2x ＋2，x ∈12，＋∞，则h ′(x )＝x 2＋3x －2ln x －4(x ＋2)2，令函数p (x )＝x 2＋3x －2ln x －4，x ∈⎣⎢⎡⎭⎪⎫12，＋∞. 则p ′(x )＝(2x －1)(x ＋2)x在⎣⎢⎡⎭⎪⎫12，＋∞ 上有p ′(x )≥0，故p (x )在⎣⎢⎡⎭⎪⎫12，＋∞上单调递增． 因为p (1)＝0，所以当x ∈⎣⎢⎡⎭⎪⎫12，1时，有p (x )<0，即h ′(x )<0，所以h (x )单调递减；当x ∈(1，＋∞)时，有p (x )>0即h ′(x )>0，所以h (x )单调递增． 因为h ⎝ ⎛⎭⎪⎫12＝910＋ln25，h (1)＝1，h (10)＝102－10ln1012>h ⎝ ⎛⎭⎪⎫12， 所以k 的取值范围为⎝⎛⎦⎥⎤1，910＋ln25.通过函数的极值(最值)判断函数零点个数，主要是借助导数研究函数的单调性、极值，通过极值的正负、函数单调性判断函数图象走势，从而判断零点个数或者通过零点个数求参数范围.设函数f (x )＝x 2－a ln x ，g (x )＝(a －2)x . (1)求函数f (x )的单调区间；(2)若函数F (x )＝f (x )－g (x )有两个零点x 1，x 2，求满足条件的最小正整数a 的值．解：(1)f ′(x )＝2x －a x ＝2x 2－ax (x >0)．当a ≤0时，f ′(x )>0在(0，＋∞)上恒成立，所以函数f (x )的单调递增区间为(0，＋∞)，此时f (x )无单调递减区间．当a >0时，由f ′(x )>0，得x >2a 2，由f ′(x )<0，得0<x <2a2，所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫2a 2，＋∞，单调递减区间为⎝ ⎛⎭⎪⎫0，2a 2. (2)由题意知F (x )＝x 2－(a －2)x －a ln x ， ∴F ′(x )＝2x －(a －2)－a x＝2x 2－(a －2)x －a x ＝(2x －a )(x ＋1)x(x >0)． 因为函数F (x )有两个零点，所以a >0，此时函数F (x )在⎝ ⎛⎭⎪⎫a 2，＋∞上单调递增，在⎝ ⎛⎭⎪⎫0，a 2上单调递减．所以F (x )的最小值F ⎝ ⎛⎭⎪⎫a 2<0，即－a 2＋4a －4a ln a2<0. 因为a >0，所以a ＋4ln a2－4>0. 令h (a )＝a ＋4ln a2－4，显然h (a )在(0，＋∞)上为增函数，且h (2)＝－2<0，h (3)＝4ln 32－1＝ln 8116－1>0，所以存在a 0∈(2,3)，h (a 0)＝0.当a >a 0时，h (a )>0；当0<a <a 0时，h (a )<0. 所以满足条件的最小正整数a ＝3.又当a ＝3时，F (3)＝3(2－ln3)>0，F (1)＝0，所以a ＝3时，f (x )有两个零点．综上所述，满足条件的最小正整数a 的值为3.考向三 函数零点性质研究【例3】 (2019·福建龙岩质检)已知函数f (x )＝x 2＋mx －2ln x ，m ∈R . (1)求函数f (x )的单调区间；(2)若函数f (x )有两个极值点x 1，x 2，且x 1<x 2，证明：f (x 2)<x 2－1. 【解】 (1)由f (x )＝x ＋mx －2ln x ，m ∈R ，得f ′(x )＝1－m x 2－2x ＝x 2－2x －mx 2，x ∈(0，＋∞)． 设函数g (x )＝x 2－2x －m ，x ∈(0，＋∞)，当m ≤－1时，Δ＝4＋4m ≤0，则g (x )≥0，f ′(x )≥0， 所以函数f (x )在(0，＋∞)上单调递增． 当m >－1时，Δ＝4＋4m >0，令g (x )＝0得x 1＝1－1＋m ，x 2＝1＋1＋m ，x 1<x 2.当－1<m <0时，0<x 1<x 2，则在(0，x 1)∪(x 2，＋∞)上，g (x )>0，f ′(x )>0； 在(x 1，x 2)上，g (x )<0，f ′(x )<0.所以函数f (x )在(0，x 1)，(x 2，＋∞)上单调递增，在(x 1，x 2)上单调递减． 当m ≥0时，x 1≤0<x 2，则在(0，x 2)上，g (x )<0，f ′(x )<0； 在(x 2，＋∞)上，g (x )>0，f ′(x )>0.所以函数f (x )在(0，x 2)上单调递减，在(x 2，＋∞)上单调递增． 综上，当m ≤－1时，函数f (x )在(0，＋∞)上单调递增；当－1<m <0时，函数f (x )在(0,1－1＋m )，(1＋1＋m ，＋∞)上单调递增，在(1－1＋m ，1＋1＋m )上单调递减；当m ≥0时，函数f (x )在(0,1＋1＋m )上单调递减，在(1＋1＋m ，＋∞)上单调递增．(2)证明：因为函数f (x )有两个极值点x 1，x 2，且x 1<x 2, 所以g (x )＝x 2－2x －m ＝0有两个不同的正根x 1＝1－1＋m ，x 2＝1＋1＋m ，所以⎩⎪⎨⎪⎧x 1x 2＝－m >0，Δ＝4＋4m >0，解得－1<m <0.欲证明f (x 2)＝x 2＋m x 2－2ln x 2<x 2－1，只需证2ln x 2－m x 2>1.因为m ＝x 22－2x 2，所以证明2ln x 2－mx 2>1成立，等价于证明2ln x 2－x 2>－1成立．因为m ＝x 2(x 2－2)∈(－1,0)， 所以x 2＝1＋1＋m ∈(1,2)． 设函数h (x )＝2ln x －x ，x ∈(1,2)，求导可得h ′(x )＝2x －1.易知h ′(x )>0在(1,2)上恒成立，即h (x )在(1,2)上单调递增，。

第1节集合【选题明细表】基础巩固(时间:30分钟)1.(2018·全国Ⅰ卷)已知集合A={0,2},B={-2,-1,0,1,2},则A∩B等于( A )(A){0,2} (B){1,2}(C){0} (D){-2,-1,0,1,2}解析:A∩B={0,2}∩{-2,-1,0,1,2}={0,2}.故选A.2.已知集合A={x|lg x>0},B={x|x≤1},则( B )(A)A∩B≠∅(B)A∪B=R(C)B⊆A (D)A⊆B解析:由B={x|x≤1},且A={x|lg x>0}=(1,+∞),所以A∪B=R.3.(2018·西安一模改编)已知集合M={-1,0,1},N={x|x=ab,a,b∈M,且a≠b},则集合M与集合N的关系是( B )(A)M=N (B)N M(C)M⊆N (D)M∩N=∅解析:因为M={-1,0,1},N={x|x=ab,a,b∈M,且a≠b},所以N={-1,0},于是N M.4.若x∈A,则∈A,就称A是伙伴关系集合,集合M=｛-1,0,,2,3｝的所有非空子集中具有伙伴关系的集合的个数是( B )(A)1 (B)3 (C)7 (D)31解析:具有伙伴关系的元素组是-1,,2,所以具有伙伴关系的集合有3个:{-1},｛,2｝,｛-1,,2｝.5.(2018·石家庄模拟)设全集U={x|x∈N*,x<6},集合A={1,3},B= {3,5},则∁U(A∪B)等于( D )(A){1,4} (B){1,5}(C){2,5} (D){2,4}解析:由题意得A∪B={1,3}∪{3,5}={1,3,5}.又U={1,2,3,4,5},所以∁U(A∪B)={2,4}.6.试分别用描述法、列举法两种方法表示“所有不小于3,且不大于200的奇数”所构成的集合.(1)描述法 ;(2)列举法 . 答案:(1){x|x=2n+1,n∈N,1≤n<100}(2){3,5,7,9, (199)7.(2017·江苏卷)已知集合A={1,2},B={a,a2+3},若A∩B={1},则实数a的值为.解析:因为A∩B={1},A={1,2},所以1∈B且2∉B.若a=1,则a2+3=4,符合题意.又a2+3≥3≠1,故a=1.答案:18.(2018·成都检测)已知集合A={x|x2-2 018x-2 019≤0},B={x|x< m+1},若A⊆B,则实数m的取值范围是.解析:由x2-2 018x-2 019≤0,得A=[-1,2 019],又B={x|x<m+1},且A⊆B.所以m+1>2 019,则m>2 018.答案:(2 018,+∞)9.集合A={x|x<0},B={x|y=lg[x(x+1)]},若A-B={x|x∈A,且x∉B},则A-B= .解析:由x(x+1)>0,得x<-1或x>0.所以B=(-∞,-1)∪(0,+∞),所以A-B=[-1,0).答案:[-1,0)能力提升(时间:15分钟)10.(2016·全国Ⅲ卷改编)设集合S={x|(x-2)(x-3)≥0},T={x|x>0},则(∁R S)∩T等于( C )(A)[2,3](B)(-∞,-2)∪[3,+∞)(C)(2,3)(D)(0,+∞)解析:易知S=(-∞,2]∪[3,+∞),所以∁R S=(2,3),因此(∁R S)∩T= (2,3).11.设集合A={(x,y)|x+y=1},B={(x,y)|x-y=3},则满足M⊆(A∩B)的集合M的个数是( C )(A)0 (B)1 (C)2 (D)3解析:由得所以A∩B={(2,-1)}.由M⊆(A∩B),知M= 或M={(2,-1)}.12.(2018·江西省红色七校联考)如图,设全集U=R,集合A,B分别用椭圆内图形表示,若集合A={x|x2<2x},B={x|y=ln(1-x)},则阴影部分图形表示的集合为( D )(A){x|x≤1} (B){x|x≥1}(C){x|0<x≤1} (D){x|1≤x<2}解析:因为A={x|x2<2x}={x|0<x<2},B={x|y=ln(1-x)}={x|1-x>0}={x|x<1},所以∁U B={x|x≥1},则阴影部分为A∩(∁U B)={x|0<x<2}∩{x|x≥1}={x|1≤x<2}.故选D.13.若集合A={-1,1},B={x|mx=1},且A∪B=A,则m的值为( D )(A)1 (B)-1(C)1或-1 (D)1或-1或0解析:由A∪B=A,可知B A,故B={1}或{-1}或 ,此时m=1或-1或0.故选D.14.(2017·山东卷改编)设函数y=的定义域为A,函数y=ln(1-x)的定义域为B,全集U=R,则∁U(A∩B)= .解析:因为4-x2≥0,所以-2≤x≤2,所以A=[-2,2].因为1-x>0,所以x<1,所以B=(-∞,1),因此A∩B=[-2,1),于是∁U(A∩B)=(-∞,-2)∪[1,+∞).答案:(-∞,-2)∪[1,+∞)第2节命题及其关系、充分条件与必要条件【选题明细表】基础巩固(时间:30分钟)1.设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是( D )(A)若方程x2+x-m=0有实根,则m>0(B)若方程x2+x-m=0有实根,则m≤0(C)若方程x2+x-m=0没有实根,则m>0(D)若方程x2+x-m=0没有实根,则m≤0解析:根据逆否命题的定义,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是“若方程x2+x-m=0没有实根,则m≤0”.2.(2018·河南八市联考)命题“若a>b,则a+c>b+c”的否命题是( A )(A)若a≤b,则a+c≤b+c(B)若a+c≤b+c,则a≤b(C)若a+c>b+c,则a>b(D)若a>b,则a+c≤b+c解析:将条件、结论都否定.命题的否命题是“若a≤b,则a+c≤b+c”.3.(2018·山东省日照市模拟)命题p:sin 2x=1,命题q:tan x=1,则p 是q的( C )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件解析:由sin 2x=1,得2x=+2kπ,k∈Z,则x=+kπ,k∈Z,由tan x=1,得x=+kπ,k∈Z,所以p是q的充要条件.故选C.4.已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b 相交”是“平面α和平面β相交”的( A )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件解析:由题意知a⊂α,b⊂β,若a,b相交,则a,b有公共点,从而α,β有公共点,可得出α,β相交;反之,若α,β相交,则a,b的位置关系可能为平行、相交或异面.因此“直线a和直线b相交”是“平面α和平面β相交”的充分不必要条件.5.(2018·云南玉溪模拟)设a>0且a≠1,则“函数f(x)=a x在R上是减函数”是“函数g(x)=(2-a)x3在R上是增函数”的( A )(A)充分不必要条件(B)必要不充分条件(C)充分必要条件(D)既不充分也不必要条件解析:若函数f(x)=a x在R上是减函数,则a∈(0,1),若函数g(x)=(2-a)x3在R上是增函数,则a∈(0,2).则“函数f(x)=a x在R上是减函数”是“函数g(x)=(2-a)x3在R上是增函数”的充分不必要条件.6.(2018·江西九江十校联考)已知函数f(x)=则“x=0”是“f(x)=1”的( B )(A)充要条件(B)充分不必要条件(C)必要不充分条件(D)既不充分也不必要条件解析:若x=0,则f(0)=e0=1;若f(x)=1,则e x=1或ln(-x)=1,解得x=0或x=-e.故“x=0”是“f(x)=1”的充分不必要条件.故选B.7.(2018·北京卷)能说明“若a>b,则<”为假命题的一组a,b的值依次为.解析:只要保证a为正b为负即可满足要求.当a>0>b时,>0>.答案:1,-1(答案不唯一)8.有下列几个命题:①“若a>b,则a2>b2”的否命题;②“若x+y=0,则x,y互为相反数”的逆命题;③“若x2<4,则-2<x<2”的逆否命题.其中真命题的序号是.解析:①原命题的否命题为“若a≤b,则a2≤b2”,错误.②原命题的逆命题为“若x,y互为相反数,则x+y=0”,正确.③原命题的逆否命题为“若x≥2或x≤-2,则x2≥4”,正确.答案:②③9.直线x-y-k=0与圆(x-1)2+y2=2有两个不同交点的充要条件是.解析:直线x-y-k=0与圆(x-1)2+y2=2有两个不同交点等价于<,解之得-1<k<3.答案:-1<k<3能力提升(时间:15分钟)10.(2018·天津卷)设x∈R,则“|x-|<”是“x3<1”的( A )(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件解析:由“|x-|<”等价于0<x<1,而x3<1,即x<1,所以“|x-|<”是“x3<1”的充分而不必要条件.故选A.11.已知命题p:x2+2x-3>0;命题q:x>a,且﹁q的一个充分不必要条件是﹁p,则a的取值范围是( A )(A)[1,+∞) (B)(-∞,1](C)[-1,+∞) (D)(-∞,-3]解析:由x2+2x-3>0,得x<-3或x>1,由﹁q的一个充分不必要条件是﹁p,可知﹁p是﹁q的充分不必要条件,等价于q是p的充分不必要条件,故a≥1.12.函数f(x)=log a x-x+2(a>0且a≠1)有且仅有两个零点的充要条件是 .解析:若函数f(x)=log a x-x+2(a>0,且a≠1)有两个零点,即函数y=log a x的图象与直线y=x-2有两个交点,结合图象易知,此时a>1.可以检验,当a>1时,函数f(x)=log a x-x+2(a>0,且a≠1)有两个零点, 所以函数f(x)=log a x-x+2(a>0,且a≠1)有且仅有两个零点的充要条件是a>1.答案:a>113.(2018·湖南十校联考)已知数列{a n}的前n项和S n=Aq n+B(q≠0),则“A=-B”是“数列{a n}为等比数列”的条件.解析:若A=B=0,则S n=0,数列{a n}不是等比数列.如果{a n}是等比数列,由a1=S1=Aq+B得a2=S2-a1=Aq2-Aq,a3=S3-S2=Aq3-Aq2,由a1a3=,从而可得A=-B,故“A=-B”是“数列{a n}为等比数列”的必要不充分条件.答案:必要不充分14.(2018·山西五校联考)已知p:(x-m)2>3(x-m)是q:x2+3x-4<0的必要不充分条件,则实数m的取值范围为.解析:p对应的集合A={x|x<m或x>m+3},q对应的集合B={x|-4<x<1}.由p是q的必要不充分条件可知B A,所以m≥1或m+3≤-4,即m≥1或m≤-7.答案:(-∞,-7]∪[1,+∞)第3节简单的逻辑联结词、全称量词与存在量词【选题明细表】基础巩固(时间:30分钟)1.(2018·咸阳模拟)命题p:∀x<0,x2≥2x,则命题﹁p为( C )(A)∃x0<0,≥(B)∃x0≥0,<(C)∃x0<0,< (D)∃x0≥0,≥解析:全称命题的否定,应先改写量词,再否定结论,所以﹁p:∃x0<0,<.2.(2018·郑州调研)命题p:函数y=log2(x-2)的单调增区间是[1,+∞),命题q:函数y=的值域为(0,1).下列命题是真命题的为( B )(A)p∧q (B)p∨q(C)p∧(﹁q) (D)﹁q解析:由于y=log2(x-2)在(2,+∞)上是增函数,所以命题p是假命题.由3x>0,得3x+1>1,所以0<<1,所以函数y=的值域为(0,1),故命题q为真命题.所以p∧q为假命题,p∨q为真命题,p∧(﹁q)为假命题,﹁q为假命题.3.(2018·贵阳调研)下列命题中的假命题是( C )(A)∃x0∈R,lg x0=1 (B)∃x0∈R,sin x0=0(C)∀x∈R,x3>0 (D)∀x∈R,2x>0解析:当x=10时,lg 10=1,则A为真命题;当x=0时,sin 0=0,则B为真命题;当x<0时,x3<0,则C为假命题;由指数函数的性质知,∀x∈R,2x>0,则D为真命题.4.第十三届全运会于2017年8月27日在天津市隆重开幕,在体操预赛中,有甲、乙两位队员参加.设命题p是“甲落地站稳”,q是“乙落地站稳”,则命题“至少有一位队员落地没有站稳”可表示为( A ) (A)(﹁p)∨(﹁q) (B)p∨(﹁q)(C)(﹁p)∧(﹁q) (D)p∨q解析:命题“至少有一位队员落地没有站稳”包含以下三种情况:“甲、乙落地均没有站稳”“甲落地没站稳,乙落地站稳”“乙落地没有站稳,甲落地站稳”,故可表示为(﹁p)∨(﹁q).或者,命题“至少有一位队员落地没有站稳”等价于命题“甲、乙均落地站稳”的否定,即“p∧q”的否定.选A.5.(2018·河北省石家庄二中模拟)已知命题p:∃x0∈(0,+∞), ln x0=1-x0,则命题p的真假及﹁p依次为( B )(A)真;∃x0∈(0,+∞),ln x0≠1-x0(B)真;∀x∈(0,+∞),ln x≠1-x(C)假;∀x∈(0,+∞),ln x≠1-x(D)假;∃x0∈(0,+∞),ln x0≠1-x0解析:当x0=1时,ln x0=1-x0=0,故命题p为真命题;因为p:∃x0∈(0,+∞),ln x0=1-x0,所以﹁p:∀x∈(0,+∞),ln x≠1-x.6.命题p“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是( D )(A)∀x∈R,∃n∈N*,使得n<x2(B)∀x∈R,∀n∈N*,使得n<x2(C)∃x∈R,∃n∈N*,使得n<x2(D)∃x0∈R,∀n∈N*,使得n<解析:改变量词,否定结论.所以﹁p应为∃x0∈R,∀n∈N*,使得n<.7.(2018·河北“五个一”名校联考)命题“∃x0∈R,1<f(x0)≤2”的否定是.答案:∀x∈R,f(x)≤1或f(x)>28.若命题“∃x0∈R,使得+(a-1)x0+1<0”是真命题,则实数a的取值范围是.解析:因为“∃x0∈R,使得+(a-1)x0+1<0”是真命题,所以Δ=(a-1)2-4>0,即(a-1)2>4,所以a-1>2或a-1<-2,所以a>3或a<-1.答案:(-∞,-1)∪(3,+∞)9.已知命题p:x2+2x-3>0;命题q:>1,若“(﹁q)∧p”为真,则x的取值范围是.解析:因为“(﹁q)∧p”为真,即q假p真,又q为真命题时,<0,即2<x<3,所以q为假命题时,有x≥3或x≤2.p为真命题时,由x2+2x-3>0,解得x>1或x<-3.由得x≥3或1<x≤2或x<-3,所以x的取值范围是{x|x≥3或1<x≤2或x<-3}.答案:(-∞,-3)∪(1,2]∪[3,+∞)能力提升(时间:15分钟)10.下列命题中,真命题是( D )(A)∃x0∈R,使得≤0(B)sin2x+≥3(x≠kπ,k∈Z)(C)∀x∈R,2x>x2(D)a>1,b>1是ab>1的充分不必要条件解析:对∀x∈R都有e x>0,所以A错误;当x=-时,sin2x+=-1<3,所以B错误;当x=2时,2x=x2,所以C错误;a>1,b>1⇒ab>1,而当a=b=-2时,ab>1成立,a>1,b>1不成立,所以D 正确.11.(2018·北京朝阳区模拟)已知函数f(x)=a2x-2a+1.若命题“∀x∈(0,1),f(x)≠0”是假命题,则实数a的取值范围是( D ) (A)(,1) (B)(1,+∞)(C)(,+∞) (D)(,1)∪(1,+∞)解析:因为函数f(x)=a2x-2a+1,命题“∀x∈(0,1),f(x)≠0”是假命题,所以原命题的否定“∃x0∈(0,1),使f(x0)=0”是真命题,所以f(1)f(0)<0,即(a2-2a+1)(-2a+1)<0,所以(a-1)2(2a-1)>0,解得a>,且a≠1.所以实数a的取值范围是(,1)∪(1,+∞).12.(2018·江西红色七校联考)已知函数f(x)=给出下列两个命题:命题p:∃m∈(-∞,0),方程f(x)=0有解,命题q:若m=,则f(f(-1))=0.那么,下列命题为真命题的是( B )(A)p∧q (B)(﹁p)∧q(C)p∧(﹁q) (D)(﹁p)∧(﹁q)解析:因为3x>0,当m<0时,m-x2<0,所以命题p为假命题;当m=时,因为f(-1)=3-1=,所以f(f(-1))=f()=-()2=0,所以命题q为真命题,逐项检验可知,只有(﹁p)∧q为真命题.13.(2018·广东汕头一模)已知命题p:关于x的方程x2+ax+1=0没有实根;命题q:∀x>0,2x-a>0.若“﹁p”和“p∧q”都是假命题,则实数a的取值范围是( C )(A)(-∞,-2)∪(1,+∞) (B)(-2,1](C)(1,2) (D)(1,+∞)解析:因为“﹁p”和“p∧q”都是假命题,所以p真,q假.由p真,得Δ=a2-4<0,解之得-2<a<2.∀x>0,2x-a>0等价于a<2x恒成立,则a≤1.所以q假时,a>1.由得1<a<2,则a的取值范围是(1,2).14.(2018·郑州质量预测)已知函数f(x)=x+,g(x)=2x+a,若∀x1∈[,1],∃x2∈[2,3],使得f(x1)≤g(x2),则实数a的取值范围是.解析:依题意知f(x)max≤g(x)max.因为f(x)=x+在[,1]上是减函数,所以f(x)max=f()=.又g(x)=2x+a在[2,3]上是增函数,所以g(x)max=g(3)=8+a,因此≤8+a,则a≥.答案:[,+∞)第1节函数及其表示【选题明细表】基础巩固(时间:30分钟)1.函数g(x)=+log2(6-x)的定义域是( D )(A){x|x>6} (B){x|-3<x<6}(C){x|x>-3} (D){x|-3≤x<6}解析:由解得-3≤x<6,故函数的定义域为{x|-3≤x<6}.故选D.2.设f(x)=则f(f(-2))等于( C )(A)-1 (B) (C) (D)解析:因为-2<0,所以f(-2)=2-2=>0,所以f(f(-2))=f()=1-=1-=.故选C.3.如果f()=,则当x≠0且x≠1时,f(x)等于( B )(A)(x≠0且x≠1) (B)(x≠0且x≠1)(C)(x≠0且x≠1) (D)-1(x≠0且x≠1)解析:令t=,t≠0,则x=,则f()=可化为f(t)==(t≠1),所以f(x)=(x≠0,x≠1).故选B.4.(2016·全国Ⅱ卷)下列函数中,其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是( D )(A)y=x (B)y=lg x(C)y=2x(D)y=解析:由y=10lg x定义域值域均为(0,+∞),与D符合.故选D.5.下列函数中,与y=x相同的函数是( B )(A)y=(B)y=lg 10x(C)y=(D)y=()2+1解析:对于A,与函数y=x的对应关系不同;对于B,与函数y=x的定义域相同,对应关系也相同,是同一函数;对于C,与函数y=x的定义域不同;对于D,与函数y=x的定义域不同.故选B.6.(2018·西安联考)已知函数f(x)=-x2+4x,x∈[m,5]的值域是[-5,4],则实数m的取值范围是( C )(A)(-∞,-1) (B)(-1,2](C)[-1,2] (D)[2,5]解析:因为f(x)=-x2+4x=-(x-2)2+4,所以当x=2时,f(2)=4,由f(x)=-x2+4x=-5,解得x=5或x=-1,所以要使函数在[m,5]的值域是[-5,4],则-1≤m≤2,故选C.7.(2018·石家庄质检)设函数f(x)=若f(f())=2,则实数a为( D )(A)- (B)- (C)(D)解析:易得f（）=2×+a=+a.当+a<1时,f（f()）=f(+a)=3+3a,所以3+3a=2,a=-,不满足+a<1,舍去.当+a≥1,即a≥-时,f（f()）=log2(+a)=2,解得a=.故选D.8.(2018·西安铁中检测)已知函数f(2x)的定义域为[-1,1],则函数y=f(log2x)的定义域为.解析:由-1≤x≤1,知≤2x≤2,所以在函数y=f(log2x)中,有≤log2x≤2,因此≤x≤4,即y=f(log2x)的定义域为[,4].答案:[,4]能力提升(时间:15分钟)9.已知函数f(x)=且f(a)=-3,则f(6-a)等于( A )(A)- (B)- (C)- (D)-解析:当a≤1时,f(a)=2a-1-2=-3,即2a-1=-1,不成立,舍去;当a>1时,f(a)=-log2(a+1)=-3,即log2(a+1)=3,解得a=7,此时f(6-a)=f(-1)=2-2-2=-.故选A.10.已知函数f(x)=则f(x)的值域是( B )(A)[1,+∞) (B)[0,+∞)(C)(1,+∞) (D)[0,1)∪(1,+∞)解析:由f(x)=知当x≤1时,x2≥0;当x>1时,x+-3≥2-3=4-3=1,当且仅当x=,即x=2时取“=”,取并集得f(x)的值域是[0,+∞).故选B.11.已知f(x)是一次函数,且f[f(x)]=x+2,则 f(x)等于( A )(A)x+1 (B)2x-1(C)-x+1 (D)x+1或-x-1解析:设f(x)=kx+b(k≠0),又f[f(x)]=x+2,得k(kx+b)+b=x+2,即k2x+kb+b=x+2.所以k2=1,且kb+b=2,解得k=b=1,则f(x)=x+1.故选A.12.(2018·河南八市联合检测)设函数f(x)=若对任意的a∈R都有f(f(a))=2f(a)成立,则λ的取值范围是( C )(A)(0,2] (B)[0,2](C)[2,+∞) (D)(-∞,2)解析:当a≥1时,2a≥2,所以f(f(a))=f(2a)==2f(a)恒成立,当a<1时,f(f(a))=f(-a+λ)=2f(a)=2λ-a,所以λ-a≥1,即λ≥a+1恒成立,由题意,λ≥(a+1)max,λ≥2,综上,λ的取值范围是[2,+∞).故选C.13.(2018·江西上饶质检)已知函数f(x)=若a[f(a)- f(-a)]>0,则实数a的取值范围为( D )(A)(1,+∞)(B)(2,+∞)(C)(-∞,-1)∪(1,+∞)(D)(-∞,-2)∪(2,+∞)解析:当a>0时,不等式a[f(a)-f(-a)]>0可化为a2+a-3a>0,解得a>2,当a<0时,不等式a[f(a)-f(-a)]>0可化为-a2-2a<0,解得a<-2,综上所述,a的取值范围为(-∞,-2)∪(2,+∞).故选D.14.设函数f(x)=则使得f(x)≤2成立的x的取值范围是.解析:当x<1时,e x-1≤2,解得x≤1+ln 2,所以x<1.当x≥1时,≤2,解得x≤8,所以1≤x≤8.综上可知x的取值范围是(-∞,8].答案:(-∞,8]第2节函数的单调性与最值【选题明细表】基础巩固(时间:30分钟)1.(2018·湖北省高三调研)函数f(x)=log a(x2-4x-5)(a>1)的单调递增区间是( D )(A)(-∞,-2) (B)(-∞,-1)(C)(2,+∞) (D)(5,+∞)解析:由t=x2-4x-5>0,得x<-1或x>5,且函数t=x2-4x-5(x<-1或x>5)在区间(5,+∞)上单调递增,又函数y=log a t(a>1)为单调递增函数,故函数f(x)的单调递增区间是(5,+∞).故选D.2.(2018·郑州质检)下列函数中,在区间(-1,1)上为减函数的是( D )(A)y= (B)y=cos x(C)y=ln(x+1) (D)y=2-x解析:因为y=与y=ln(x+1)在(-1,1)上为增函数,且y=cos x在(-1,1)上不具备单调性,所以A,B,C不满足题意;只有y=2-x=（）x在(-1,1)上是减函数.故选D.3.(2018·湖师附中)如果f(x)=ax2-(2-a)x+1在区间（-∞,]上为减函数,则a的取值范围是( C )(A)(0,1] (B)[0,1) (C)[0,1] (D)(0,1)解析:a=0时,f(x)=-2x+1在区间(-∞,]上为减函数,符合题意;当a≠0时,如果f(x)=ax2-(2-a)x+1在区间(-∞,]上为减函数,必有解得0<a≤1.综上所述,a的取值范围是[0,1],故选C.4.(2018·唐山二模)函数y=,x∈(m,n]的最小值为0,则m的取值范围是( D )(A)(1,2) (B)(-1,2) (C)[1,2) (D)[-1,2)解析:函数y===-1在区间(-1,+∞)上是减函数,且f(2)=0,所以n=2,根据题意,x ∈(m,n]时,y min =0, 所以m 的取值范围是[-1,2).故选D. 5.设函数f(x)=若f(a+1)≥f(2a-1),则实数a 的取值范围是( B )(A)(-∞,1] (B)(-∞,2] (C)[2,6] (D)[2,+∞)解析:易知函数f(x)在定义域(-∞,+∞)上是增函数, 因为f(a+1)≥f(2a-1), 所以a+1≥2a-1,解得a ≤2.故实数a 的取值范围是(-∞,2].故选B. 6.已知f(x)=2x ,a=(),b=(),c=log 2,则 f(a),f(b),f(c)的大小顺序为( B )(A)f(b)<f(a)<f(c) (B)f(c)<f(b)<f(a) (C)f(c)<f(a)<f(b) (D)f(b)<f(c)<f(a) 解析:易知f(x)=2x 在(-∞,+∞)上是增函数, 又a=()=()>()=b>0,c=log 2<0,所以f(a)>f(b)>f(c).故选B.7.(2018·石家庄调研)函数f(x)=()x-log2(x+2)在区间[-1,1]上的最大值为.解析:由于y=()x在R上递减,y=log2(x+2)在[-1,1]上递增,所以f(x)在[-1,1]上单调递减,故f(x)在[-1,1]上的最大值为f(-1)=3.答案:38.设函数f(x)=g(x)=x2f(x-1),则函数g(x)的递减区间是.解析:由题意知g(x)=函数的图象为如图所示的实线部分,根据图象,g(x)的减区间是[0,1).答案:[0,1)9.对于任意实数a,b,定义min{a,b}=设函数f(x)=-x+3,g(x)=log2x,则函数h(x)=min{f(x),g(x)}的最大值是.解析:法一在同一坐标系中,作函数f(x),g(x)图象,依题意,h(x)的图象如图所示.易知点A(2,1)为图象的最高点,因此h(x)的最大值为h(2)=1.法二依题意,h(x)=当0<x≤2时,h(x)=log2x是增函数,当x>2时,h(x)=3-x是减函数.所以当x=2时,h(x)取最大值h(2)=1.答案:1能力提升(时间:15分钟)10.(2017·全国Ⅰ卷)函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( D ) (A)[-2,2] (B)[-1,1] (C)[0,4] (D)[1,3]解析:因为f(x)是奇函数,且f(1)=-1,所以f(-1)=-f(1)=1.所以f(1)≤f(x-2)≤f(-1).又因为f(x)在(-∞,+∞)上单调递减,所以-1≤x-2≤1.所以1≤x≤3.故选D.11.(2018·北京海淀期中)若函数f(x)=的值域为[-1,1],则实数a的取值范围是( A )(A)[1,+∞) (B)(-∞,-1](C)(0,1] (D)(-1,0)解析:当x≤a时,f(x)=cos x∈[-1,1],则当x>a时,-1≤≤1,即x≤-1或x≥1,所以a≥1.故选A.12.已知f(x)是定义在R上的偶函数,且在区间(-∞,0)上单调递增,若实数a满足f(2|a-1|)>f(-),则a的取值范围是.解析:因为f(x)在R上是偶函数,且在区间(-∞,0)上单调递增,所以f(x)在(0,+∞)上是减函数.则f(2|a-1|)>f(-)=f(),因此2|a-1|<=,又y=2x是增函数,所以|a-1|<,解得<a<.答案:(,)13.(2018·大理月考)已知f(x)是定义在[-1,1]上的奇函数且f(1)=1,当x1,x2∈[-1,1],且x1+x2≠0时,有>0,若f(x)≤m2-2am+1对所有x∈[-1,1],a∈[-1,1]恒成立,则实数m的取值范围是.解析:用-x2替换x2,得>0,由于f(x)是奇函数,所以>0,等价于函数f(x)是定义域上的增函数,所以f(x)max=f(1)=1.不等式f(x)≤m2-2am+1对所有x∈[-1,1]恒成立,即m2-2am+1≥1对任意a∈[-1,1]恒成立,即2ma-m2≤0对任意a∈[-1,1]恒成立,令g(a)=2ma-m2,则只要即可,解得m≤-2或者m≥2或者m=0.故所求的m的取值范围是(-∞,-2]∪{0}∪[2,+∞).答案:(-∞,-2]∪{0}∪[2,+∞)14.(2018·成都七中调研)已知函数f(x)=a-.(1)求f(0);(2)探究f(x)的单调性,并证明你的结论;(3)若f(x)为奇函数,求满足f(ax)<f(2)的x的范围.解:(1)f(0)=a-=a-1.(2)f(x)在R上单调递增.理由如下:因为f(x)的定义域为R,所以任取x1,x2∈R且x1<x2,则f(x1)-f(x2)=a--a+=, 因为y=2x在R上单调递增且x1<x2,所以0<<,所以-<0,+1>0,+1>0.所以f(x1)-f(x2)<0,即f(x1)<f(x2).所以f(x)在R上单调递增.(3)因为f(x)是奇函数,所以f(-x)=-f(x),则a-=-a+,解得a=1(或用f(0)=0去解).所以f(ax)<f(2)即 f(x)<f(2),又因为f(x)在R上单调递增,所以x<2.所以不等式的解集为(-∞,2).第3节函数的奇偶性与周期性【选题明细表】基础巩固(时间:30分钟)1.(2018·云南玉溪模拟)下列函数中,既是偶函数,又在(0,1)上单调递增的函数是( C )(A)y=|log3x| (B)y=x3(C)y=e|x| (D)y=cos |x|解析:对于A选项,函数定义域是(0,+∞),故是非奇非偶函数;对于B 选项,函数y=x3是一个奇函数,不正确;对于C选项,函数的定义域是R,是偶函数,且当x∈(0,+∞)时,函数是增函数,故在(0,1)上单调递增,选项C正确;对于D选项,函数y=cos |x|是偶函数,在(0,1)上单调递减,不正确.故选C.2.已知f(x)在R上是奇函数,且满足f(x+4)=f(x),当x∈(-2,0)时,f(x)=2x2,则f(2 019)等于( B )(A)-2 (B)2 (C)-98 (D)98解析:由f(x+4)=f(x)知,f(x)是周期为4的周期函数,f(2 019)=f(504×4+3)=f(3)=f(-1).由-1∈(-2,0)得f(-1)=2,所以f(2 019)=2.故选B.3.(2018·石家庄一模)已知f(x)为偶函数,且当x∈[0,2)时,f(x)=2sin x,当x∈[2,+∞)时,f(x)=log2x,则f(-)+f(4)等于( D )(A)-+2 (B)1(C)3 (D)+2解析:因为f(-)=f()=2sin =,f(4)=log24=2,所以f(-)+f(4)=+2.4.设函数f(x)=,则下列结论错误的是( D )(A)|f(x)|是偶函数(B)-f(x)是奇函数(C)f(x)·|f(x)|是奇函数(D)f(|x|)·f(x)是偶函数解析:f(-x)==-f(x),所以函数f(x)是奇函数,|f(-x)|=|f(x)|,函数|f(x)|是偶函数,-f(x)是奇函数,f(x)·|f(x)|为奇函数,f(|x|)是偶函数,所以f(|x|)·f(x)是奇函数,所以错的是D.故选D.5.(2018·河北“五个一”名校联盟二模)设函数f(x)是定义在R上的奇函数,且f(x)=则g(-8)等于( A )(A)-2 (B)-3 (C)2 (D)3解析:法一当x<0时,-x>0,且f(x)为奇函数,则f(-x)=log3(1-x),所以f(x)=-log3(1-x).因此g(x)=-log3(1-x),x<0,故g(-8)=-log39=-2.法二由题意知,g(-8)=f(-8)=-f(8)=-log39=-2.故选A.6.(2018·南昌模拟)若定义域为R的函数f(x)在(4,+∞)上为减函数,且函数y=f(x+4)为偶函数,则( D )(A)f(2)>f(3) (B)f(2)>f(5)(C)f(3)>f(5) (D)f(3)>f(6)解析:因为y=f(x+4)为偶函数,所以f(-x+4)=f(x+4),因此y=f(x)的图象关于直线x=4对称,所以f(2)=f(6),f(3)=f(5).又y=f(x)在(4,+∞)上为减函数,所以f(5)>f(6),所以f(3)>f(6).故选D.7.若f(x)=ln(e3x+1)+ax是偶函数,则a= .解析:由于f(-x)=f(x),所以ln(e-3x+1)-ax=ln(e3x+1)+ax,化简得2ax+3x=0(x∈R),则2a+3=0.所以a=-.答案:-8.已知f(x)是定义在R上的偶函数,且f(x+2)=-,当2≤x≤3时,f(x)=x,则f(105.5)= .解析:f(x+4)=f[(x+2)+2]=-=f(x).故函数的周期为4,所以f(105.5)=f(4×27-2.5)=f(-2.5)=f(2.5),因为2≤2.5≤3,由题意,得f(2.5)=2.5,所以f(105.5)=2.5.答案:2.59.设函数f(x)=ln(1+|x|)-,则使得f(x)>f(2x-1)成立的x的取值范围是.解析:由f(x)=ln(1+|x|)-,知f(x)为R上的偶函数,于是f(x)> f(2x-1),即为f(|x|)>f(|2x-1|).当x≥0时,f(x)=ln(1+x)-,所以f(x)为[0,+∞)上的增函数,则由f(|x|)>f(|2x-1|)得|x|>|2x-1|,两边平方,整理得3x2-4x+1<0,解得<x<1.答案:(,1)能力提升(时间:15分钟)10.(2018·吉林省实验中学模拟)已知f(x)是定义在R上的偶函数,且f(x+4)=f(x),当x∈[-2,0]时,f(x)=-2x,则f(1)+f(4)等于( D ) (A)(B)1 (C)-1 (D)-解析:因为f(x)是定义在R上的偶函数,且f(x+4)=f(x),所以f(x)是以4为周期的周期函数,又因为x∈[-2,0]时,f(x)=-2x,所以f(1)+f(4)=f(-1)+f(0)=-2-1-20=--1=-.故选D.11.(2018·山东、湖北部分重点中学模拟)已知定义在R上的函数f(x)在[1,+∞)上单调递减,且f(x+1)是偶函数,不等式f(m+2)≥f(x-1)对任意的x∈[-1,0]恒成立,则实数m的取值范围是( A )(A)[-3,1](B)[-4,2](C)(-∞,-3]∪[1,+∞)(D)(-∞,-4]∪[2,+∞)解析:f(x+1)是偶函数,所以f(-x+1)=f(x+1),所以f(x)的图象关于x=1对称,由f(m+2)≥f(x-1)得|(m+2)-1|≤|(x-1)-1|,所以|m+1|≤2,解得-3≤m≤1.故选A.12.(2017·安徽马鞍山三模)函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则f(5)等于( B )(A)-1 (B)0 (C)1 (D)5解析:因为函数f(x+1),f(x-1)都是奇函数,所以f(1)=f(-1)=0,函数f(x)既关于(1,0)对称,又关于(-1,0)对称, 即f(2-x)=-f(x),f(-2-x)=-f(x),那么f(2-x)=f(-2-x),即f(2+x)=f(-2+x),所以f(x)=f(x+4),因此函数的周期是4,f(5)=f(1)=0.故选B.13.已知奇函数f(x)=则f(-2)的值等于.解析:因为函数f(x)为奇函数,所以f(0)=0,则30-a=0,所以a=1,所以当x≥0时,f(x)=3x-1,则f(2)=32-1=8,因此f(-2)=-f(2)=-8.答案:-814.已知f(x)是R上最小正周期为2的周期函数,且当0≤x<2时,f(x)=x3-x,则函数y=f(x)的图象在区间[0,6]上与x轴的交点个数为.解析:因为当0≤x<2时,f(x)=x3-x,又f(x)是R上最小正周期为2的周期函数,且f(0)=0,则f(6)=f(4)=f(2)=f(0)=0.又f(1)=0,所以f(3)=f(5)=f(1)=0,故函数y=f(x)的图象在区间[0,6]上与x轴的交点有7个.答案:715.(2018·湖北荆州中学质检)若函数f(x)=为奇函数,g(x)=则不等式g(x)>1的解集为.解析:因为f(x)=为奇函数且定义域为R,所以f(0)=0,即=0,解得a=-1,所以g(x)=所以当x>0时,由-ln x>1,解得x∈(0,);当x≤0时,由e-x>1,解得x∈(-∞,0),所以不等式g(x)>1的解集为(-∞,0)∪(0,).答案:(-∞,0)∪(0,)第4节幂函数与二次函数【选题明细表】基础巩固(时间:30分钟)1.幂函数f(x)=(m2-4m+4)·在(0,+∞)上为增函数,则m的值为( B )(A)1或3 (B)1 (C)3 (D)2解析:由题意知解得m=1.2.(2018·山东济宁一中检测)下列命题正确的是( D )(A)y=x0的图象是一条直线(B)幂函数的图象都经过点(0,0),(1,1)(C)若幂函数y=x n是奇函数,则y=x n是增函数(D)幂函数的图象不可能出现在第四象限解析:A中,当α=0时,函数y=xα的定义域为{x|x≠0,x∈R},其图象为一条直线上挖去一点,A错;B中,y=x n,当n<0时,图象不过原点,B不正确.C中,当n<0,y=x n在(-∞,0),(0,+∞)上为减函数,C错误.幂函数图象一定过第一象限,一定不过第四象限,D正确.3.(2018·郑州检测)若函数f(x)=x2+ax+b的图象与x轴的交点为(1,0)和(3,0),则函数f(x)( A )(A)在(-∞,2]上递减,在[2,+∞)上递增(B)在(-∞,3)上递增(C)在[1,3]上递增(D)单调性不能确定解析:由已知可得该函数图象的对称轴为x=2,又二次项系数为1>0,所以f(x)在(-∞,2]上是递减的,在[2,+∞)上是递增的.4.设a=(),b=(),c=(),则a,b,c的大小关系是( B )(A)a<c<b (B)b<c<a(C)b<a<c (D)c<b<a解析:令函数f(x)=,易知函数f(x)=在(0,+∞)上为增函数,又>,所以a=()>()=c,令函数g(x)=()x,易知函数g(x)=()x在(0,+∞)上为减函数,又>,所以b=()<()=c.综上可知,b<c<a,故选B.5.如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出下面四个结论:①b2>4ac;②2a-b=1;③a-b+c=0;④5a<b.其中正确的是( B )(A)②④(B)①④(C)②③(D)①③解析:因为图象与x轴交于两点,所以b2-4ac>0,即b2>4ac,①正确;对称轴为x=-1,即-=-1,2a-b=0,②错误;结合图象,当x=-1时,y=a-b+c>0,③错误;由对称轴为x=-1知,b=2a,又函数图象开口向下,所以a<0,所以5a<2a,即5a<b,④正确.故选B.6.若关于x的不等式x2-4x-2-a>0在区间(1,4)内有解,则实数a的取值范围是( A )(A)(-∞,-2) (B)(-2,+∞)(C)(-6,+∞) (D)(-∞,-6)解析:不等式x2-4x-2-a>0在区间(1,4)内有解等价于a<(x2-4x-2)max, 令f(x)=x2-4x-2,x∈(1,4),f(x)<f(4)=-2,所以a<-2.7.二次函数f(x)=2x2+bx+c满足{x|f(x)=x}={1},则f(x)在区间[-2,2]上的最大值为( C )(A)4 (B)8 (C)16 (D)20解析:由题方程2x2+bx+c=x仅有一个根1,即2x2+(b-1)x+c=0仅有一个根.得b=-3,c=2.f(x)=2x2-3x+2,对称轴为x=,f(x)max=f(-2)=16.故选C.8.(2018·武汉模拟)若函数f(x)=(x+a)(bx+2a)(常数a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)= .解析:由f(x)是偶函数知f(x)的图象关于y轴对称,所以b=-2,所以f(x)=-2x2+2a2,又f(x)的值域为(-∞,4],所以2a2=4,故f(x)=-2x2+4.答案:-2x2+49.(2018·泉州质检)若二次函数f(x)=ax2-x+b(a≠0)的最小值为0,则a+4b的取值范围是.解析:依题意,知a>0,且Δ=1-4ab=0,所以4ab=1,且b>0.故a+4b≥2=2.当且仅当a=4b,即a=1,b=时等号成立.所以a+4b的取值范围是[2,+∞).答案:[2,+∞)能力提升(时间:15分钟)10.在同一坐标系内,函数y=x a(a≠0)和y=ax+的图象可能是( B )解析:若a<0,由y=x a的图象知排除C,D选项,由y=ax+的图象知选项B有可能;若a>0,由y=x a的图象知排除A,B选项,但y=ax+的图象均不适合.综上选B.11.(2018·秦皇岛模拟)已知函数f(x)=ax2+bx+c(a≠0),且2是f(x)的一个零点,-1是f(x)的一个极小值点,那么不等式f(x)>0的解集是( C )(A)(-4,2)(B)(-2,4)(C)(-∞,-4)∪(2,+∞)(D)(-∞,-2)∪(4,+∞)解析:依题意,f(x)是二次函数,其图象是抛物线,开口向上,对称轴为x=-1,方程ax2+bx+c=0的一个根是2,另一个根是-4.因此f(x)= a(x+4)(x-2)(a>0),于是f(x)>0,解得x>2或x<-4.12.(2018·浙江“超级全能生”模拟)已知在(-∞,1]上递减的函数f(x)=x2-2tx+1,且对任意的x1,x2∈[0,t+1],总有|f(x1)-f(x2)|≤2,则实数t的取值范围是( B )(A)[-,] (B)[1,](C)[2,3] (D)[1,2]解析:由于f(x)=x2-2tx+1的图象的对称轴为x=t.又y=f(x)在(-∞,1]上是减函数,所以t≥1.则在区间[0,t+1]上,f(x)max=f(0)=1,f(x)min=f(t)=t2-2t2+1=-t2+1,要使对任意的x1,x2∈[0,t+1],都有|f(x1)-f(x2)|≤2,只需1-(-t2+1)≤2,解得-≤t≤.又t≥1,所以1≤t≤.13.已知二次函数f(x)满足f(2+x)=f(2-x),且f(x)在[0,2]上是增函数,若f(a)≥f(0),则实数a的取值范围是.解析:由题意可知函数f(x)的图象开口向下,对称轴为x=2(如图),若f(a)≥f(0),从图象观察可知0≤a≤4.答案:[0,4]14.如果函数f(x)=ax2+2x-3在区间(-∞,4)上单调递增,则实数a的取值范围是.解析:当a=0时,f(x)=2x-3在(-∞,4)上单调递增.当a≠0时,若f(x)在(-∞,4)上单调递增.则解之得-≤a<0.综上可知,实数a的取值范围是[-,0].答案:[-,0]15.已知函数f(x)=ax2+bx+c(a>0,b,c∈R).(1)若函数f(x)的最小值是f(-1)=0,且c=1,F(x)=求F(2)+F(-2)的值;(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.解:(1)由已知c=1,a-b+c=0,且-=-1,解得a=1,b=2,所以f(x)=(x+1)2.所以F(x)=所以F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.(2)由a=1,c=0,得f(x)=x2+bx,从而|f(x)|≤1在区间(0,1]上恒成立等价于-1≤x2+bx≤1在区间(0,1]上恒成立,即b≤-x且b≥--x在(0,1]上恒成立.又-x的最小值为0,--x的最大值为-2.所以-2≤b≤0.故b的取值范围是[-2,0].第5节指数与指数函数【选题明细表】基础巩固(时间:30分钟)1.函数y=a x-(a>0,且a≠1)的图象可能是( D )解析:若a>1时,y=a x-是增函数;当x=0时,y=1-∈(0,1),A,B不满足;若0<a<1时,y=a x-在R上是减函数;当x=0时,y=1-<0,C错,D项满足.故选D.2.(2018·湖南永州第三次模拟)下列函数中,与函数y=2x-2-x的定义域、单调性与奇偶性均一致的是( B )(A)y=sin x (B)y=x3(C)y=()x (D)y=log2x解析:y=2x-2-x在(-∞,+∞)上是增函数且是奇函数,y=sin x不单调,y=log2x定义域为(0,+∞),y=()x是减函数,三者不满足,只有y=x3的定义域、单调性、奇偶性与之一致.3.函数f(x)=a x-1(a>0,a≠1)的图象恒过点A,下列函数中图象不经过点A的是( A )(A)y= (B)y=|x-2|(C)y=2x-1 (D)y=log2(2x)解析:由题意,得点A(1,1),将点A(1,1)代入四个选项,y=的图象不过点A(1,1).4.设x>0,且1<b x<a x,则( C )(A)0<b<a<1 (B)0<a<b<1(C)1<b<a (D)1<a<b解析:因为x>0时,1<b x,所以b>1.因为x>0时,b x<a x,所以x>0时,()x>1.所以>1,所以a>b.所以1<b<a.5.函数f(x)=a x-b的图象如图所示,其中a,b为常数,则下列结论正确的是( D )(A)a>1,b<0(B)a>1,b>0(C)0<a<1,b>0(D)0<a<1,b<0解析:由f(x)=a x-b的图象可以观察出,函数f(x)=a x-b在定义域上单调递减,所以0<a<1.函数f(x)=a x-b的图象是在f(x)=a x的基础上向左平移得到的,所以b<0.6.已知f(x)=2x+2-x,f(m)=3,且m>0,若a=f(2m),b=2f(m),c=f(m+2),则a,b,c的大小关系为( D )(A)c<b<a (B)a<c<b(C)a<b<c (D)b<a<c解析:因为f(m)=2m+2-m=3,m>0,所以2m=3-2-m>2,b=2f(m)=2×3=6,a=f(2m)=22m+2-2m=(2m+2-m)2-2=7,c=f(m+2)=2m+2+2-m-2=4·2m+·2-m>8,所以b<a<c.故选D.7.下列说法正确的序号是.①函数y=的值域是[0,4);②(a>0,b>0)化简结果是-24;③+的值是2π-9;④若x<0,则=-x.解析:由于y=≥0(当x=2时取等号),又因为4x>0,所以16-4x<16得y<,即y<4,所以①正确;②中原式====-24,正确;由于+=|π-4|+π-5=4-π+π-5=-1,所以③不正确.由于x<0,所以④正确.答案:①②④8.不等式<4的解集为.解析:因为<4,所以<22,所以x2-x<2,即x2-x-2<0,解得-1<x<2.答案:{x|-1<x<2}9.(2018·鸡西模拟)已知函数f(x)=a x+b(a>0,a≠1)的定义域和值域都是[-1,0],则a+b= .解析:若a>1,则f(x)=a x+b在[-1,0]上是增函数,所以则a-1=0,无解.当0<a<1时,则f(x)=a x+b在[-1,0]上是减函数,所以解得因此a+b=-.答案:-能力提升(时间:15分钟)10.若函数f(x)=a|2x-4|(a>0,且a≠1),满足f(1)=,则f(x)的单调递减区间是( B )(A)(-∞,2] (B)[2,+∞)(C)[-2,+∞) (D)(-∞,-2]解析:由f(1)=,得a2=,解得a=或a=-(舍去),即f(x)=()|2x-4|.由于y=|2x-4|在(-∞,2]上递减,在[2,+∞)上递增,所以f(x)在(-∞,2]上递增,在[2,+∞)上递减.11.(2018·湖南郴州第二次教学质量检测)已知函数f(x)=e x-,其中e是自然对数的底数,则关于x的不等式f(2x-1)+f(-x-1)>0的解集为( B )(A)(-∞,-)∪(2,+∞) (B)(2,+∞)(C)(-∞,)∪(2,+∞) (D)(-∞,2)解析:易知f(x)=e x-在R上是增函数,且f(-x)=e-x-=-(e x-)=-f(x),所以f(x)是奇函数.由f(2x-1)+f(-x-1)>0,得f(2x-1)>f(x+1),因此2x-1>x+1,所以x>2.12.(2018·衡阳三中模拟)当x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是( D )。

第5节指数与指数函数【选题明细表】知识点、方法题号指数幂运算6,7指数函数的图象1,3,5指数函数的性质2,4,8,9,10,12 指数函数的图象与性质的综合应用11,13,14,15根底稳固(时间:30分钟)1.函数y =a x -(a>0,且a≠1)的图象可能是( D )解析:假设a>1时,y =a x -是增函数;当x =0时,y =1 -∈(0,1),A,B不满足;假设0<a<1时,y =a x -在R上是减函数;当x =0时,y =1 -<0,C错,D项满足.应选D.2.(2021·湖南永州第三次模拟)以下函数中,与函数y =2x -2 -x的定义域、单调性与奇偶性均一致的是( B )(A)y =sin x (B)y =x3(C)y =()x (D)y =log2x解析:y =2x -2 -x在( -∞, +∞)上是增函数且是奇函数,y =sin x不单调,y =log2x定义域为(0, +∞),y =()x是减函数,三者不满足,只有y =x3的定义域、单调性、奇偶性与之一致.3.函数f(x) =a x -1(a>0,a≠1)的图象恒过点A,以下函数中图象不经过点A的是( A )(A)y = (B)y =|x -2|(C)y =2x -1 (D)y =log2(2x)解析:由题意,得点A(1,1),将点A(1,1)代入四个选项,y =的图象不过点A(1,1).4.设x>0,且1<b x<a x,那么( C )(A)0<b<a<1 (B)0<a<b<1(C)1<b<a (D)1<a<b解析:因为x>0时,1<b x,所以b>1.因为x>0时,b x<a x,所以x>0时,()x>1.所以>1,所以a>b.所以1<b<a.5.函数f(x) =a x -b的图象如下列图,其中a,b为常数,那么以下结论正确的选项是( D )(A)a>1,b<0(B)a>1,b>0(C)0<a<1,b>0(D)0<a<1,b<0解析:由f(x) =a x -b的图象可以观察出,函数f(x) =a x -b在定义域上单调递减,所以0<a<1.函数f(x) =a x -b的图象是在f(x) =a x的根底上向左平移得到的,所以b<0.6.f(x) =2x +2 -x,f(m) =3,且m>0,假设 a =f(2m),b =2f(m),c =f(m +2),那么a,b,c的大小关系为( D )(A)c<b<a (B)a<c<b(C)a<b<c (D)b<a<c解析:因为f(m) =2m +2 -m =3,m>0,所以2m =3 -2 -m>2,b =2f(m) =2×3 =6,a =f(2m) =22m +2 -2m =(2m +2 -m)2 -2 =7,c =f(m +2) =2m +2 +2 -m -2 =4·2m +·2 -m>8,所以b<a<c.应选D.7.以下说法正确的序号是.①函数y =的值域是[0,4);②(a>0,b>0)化简结果是 -24;③ +的值是2π -9;④假设x<0,那么 = -x.解析:由于y =≥0(当x =2时取等号),又因为4x>0,所以16 -4x<16得y<,即y<4,所以①正确;②中原式 = = = = -24,正确;由于 + =|π -4| +π -5 =4 -π +π-5 = -1,所以③不正确.由于x<0,所以④正确.答案:①②④8.不等式<4的解集为.解析:因为<4,所以<22,所以x2 -x<2,即x2 -x -2<0,解得 -1<x<2.答案:{x| -1<x<2}9.(2021·鸡西模拟)函数f(x) =a x +b(a>0,a≠1)的定义域和值域都是[ -1,0],那么a +b = .解析:假设a>1,那么f(x) =a x +b在[ -1,0]上是增函数,所以那么a -1 =0,无解.当0<a<1时,那么f(x) =a x +b在[ -1,0]上是减函数,所以解得因此a +b = -.答案: -能力提升(时间:15分钟)10.假设函数f(x) =a|2x -4|(a>0,且a≠1),满足f(1) =,那么f(x)的单调递减区间是( B )(A)( -∞,2] (B)[2, +∞)(C)[ -2, +∞) (D)( -∞, -2]解析:由f(1) =,得a2 =,解得a =或a = -(舍去),即f(x) =()|2x -4|.由于y =|2x -4|在( -∞,2]上递减,在[2, +∞)上递增,所以f(x)在( -∞,2]上递增,在[2, +∞)上递减.11.(2021·湖南郴州第二次教学质量检测)函数f(x) =e x -,其中e 是自然对数的底数,那么关于x的不等式f(2x -1) +f( -x -1)>0的解集为( B )(A)( -∞, -)∪(2, +∞) (B)(2, +∞)(C)( -∞,)∪(2, +∞) (D)( -∞,2)解析:易知f(x) =e x -在R上是增函数,且f( -x) =e -x - = -(e x -) = -f(x),所以f(x)是奇函数.由f(2x -1) +f( -x -1)>0,得f(2x -1)>f(x +1),因此2x -1>x +1,所以x>2.12.(2021·衡阳三中模拟)当x∈( -∞, -1]时,不等式(m2 -m)·4x -2x<0恒成立,那么实数m的取值范围是( D )(A)( -2,1) (B)( -4,3)(C)( -3,4) (D)( -1,2)解析:因为(m2 -m)·4x -2x<0在x∈( -∞, -1]上恒成立,所以(m2 -m)<在x∈( -∞, -1]上恒成立,由于f(x) =在x∈( -∞, -1]上单调递减,所以f(x)≥2,所以m2 -m<2,所以 -1<m<2.应选D.13.设偶函数g(x) =a|x +b|在(0, +∞)上单调递增,那么g(a)与g(b -1)的大小关系是.解析:由于g(x) =a|x +b|是偶函数,知b =0,又g(x) =a|x|在(0, +∞)上单调递增,得a>1.那么g(b -1) =g( -1) =g(1),故g(a)>g(1) =g(b -1).答案:g(a)>g(b -1)14.函数f(x) =a x(a>0,a≠1)在区间[ -1,2]上的最||大值为8,最||小值为m.假设函数g(x) =(3 -10m)是单调增函数,那么 a= .解析:根据题意,得3 -10m>0,解得m<;当a>1时,函数f(x) =a x在区间[ -1,2]上单调递增,最||大值为a2 =8,解得a =2,最||小值为m =a -1 = =>,不合题意,舍去;当0<a<1时,函数f(x) =a x在区间[ -1,2]上单调递减,最||大值为a -1 =8,解得a =,最||小值为m =a2 =<,满足题意.综上,a =. 答案:15.函数f(x) =x2 -bx +c满足f(x +1) =f(1 -x),且f(0) =3,那么f(b x)与f(c x)的大小关系是.解析:由f(x +1) =f(1 -x)知y =f(x)的图象关于x =1对称,所以b =2.又f(0) =3,得c =3.那么f(b x) =f(2x),f(c x) =f(3x).当x≥0时,3x≥2x≥1,且f(x)在[1, +∞)上是增函数,所以f(3x)≥f(2x).当x<0时,0<3x<2x<1,且f(x)在( -∞,1]上是减函数,所以f(3x)>f(2x),从而有f(c x)≥f(b x).答案:f(c x)≥f(b x)。