下载文档原格式
对某工程的静力弹塑性分析(push-over)的探讨摘要：本文简要介绍了静力弹塑性分析的原理和实施步骤，并通过工程实例进行相关的对比和讨论。
关键词：静力弹塑性分析；push-over；反应谱；结构抗震性能评价1 前言利用静力弹塑性分析(Pushover Analysis)进行结构分析的优点在于：既能对结构在多遇地震下的弹性设计进行校核，也能够确定结构在罕遇地震下潜在的破坏机制，找到最先破坏的薄弱环节，从而使设计者仅对局部薄弱环节进行修复和加强，不改变整体结构的性能，就能使整体结构达到预定的使用功能;而利用传统的弹性分析，对不能满足使用要求的结构，可能采取增加新的构件或增大原来构件的截面尺寸的办法，结果是增加了结构刚度，造成了一定程度的浪费，也可能存在新的薄弱环节和隐患。
对多遇地震的计算，可以与弹性分析的结果进行验证，看总侧移和层间位移角、各杆件是否满足弹性极限要求，各杆件是否处于弹性状态；对罕遇地震的计算，可以检验总侧移和层间位移角、各个杆件是否超过弹塑性极限状态，是否满足大震不倒的要求。
2 原理与实施步骤2.1 原理静力非线性分析方法是基于性能评估现有结构和设计新结构的一种方法。
它是将静力弹塑性分析和反应谱相结合进行图解的快速计算方法。
其原理是使结构分析模型受到一个沿结构高度为单调逐渐增加的侧向力或侧向位移，直至控制点达到目标位移或建筑物倾覆为止。
基于结构行为设计使用Pushover分析，包括形成结构近似需求曲线和能力曲线，并确定曲线交点。
需求曲线基于反应谱曲线，能力曲线基于静力非线性Pushover分析。
在Pushover分析中，结构受到逐渐增加的荷载作用，从而得到需求曲线和能力曲线的交点，即性能点。
由于性能点定义了结构的底部剪力和位移，因此通过结构在性能点的行为和现行规范进行比较，从而确定结构是否满足要求。
实施步骤准备工作：建立结构模型，包括几何尺寸、物理参数以及节点和构件的编号，并输入构件的实配钢筋以便求出各个构件的塑性承载力。
结构抗震静力弹塑性分析方法(Pushover)的研究与改进的开题报告一、研究背景随着建筑结构设计的发展，抗震设计成为其中的重点和难点。
为了保障建筑安全，结构的抗震能力得到了越来越广泛的重视。
在结构抗震设计中，抗震静力弹塑性分析方法（Pushover）已经成为全球广泛使用的一种分析方法。
该方法根据结构某一方向施加分布荷载，通过对结构力学性能的分析，评估结构抗震能力。
二、研究目的与意义随着现代建筑的不断发展，建筑的结构形式日益复杂。
在这种情况下，传统的计算方法已经不能满足抗震设计的需求。
因此，本研究旨在对抗震静力弹塑性分析方法进行研究和改进，扩充其适用范围，提高其计算精度和效率，以更准确地评估结构的抗震能力。
三、研究内容1. 国内外相关研究的调研和综述，对Pushover分析方法的基本原理和步骤进行总结和阐述。
2. 提出一种结构抗震静力弹塑性分析方法的改进方案，探讨在模型参数、荷载模拟、材料本构关系等方面的改进思路。
3. 基于实际工程，使用所提出的改进方法对不同类型的建筑结构进行抗震分析，评估其抗震能力。
4.设计和编写Pushover分析方法改进程序，验证改进方案的正确性和有效性。
四、预期成果和考核指标本研究旨在对抗震静力弹塑性分析方法进行改进研究。
主要的预期成果包括：1.提出一种结构抗震静力弹塑性分析方法的改进方案，改进方案应能够在某些方面比传统的方法更加准确和高效。
2.通过实际工程评估所提出的改进方法的优缺点，验证其适用性和实用性。
3.设计和编写Pushover分析方法改进程序，展示改进方案的正确性和有效性。
预计的考核指标包括：论文的质量、研究方法是否合理、研究成果是否能够达到预期目标、研究结果的可重复性和实用性。
五、研究步骤与进度安排1.查阅相关文献，了解国内外关于结构抗震静力弹塑性分析方法的研究现状和进展，设计改进方案。
预计用时2周。
2.对所提出的改进方案进行模拟，并对改进方案中涉及的各项参数进行详细分析研究。
浅谈静力弹塑性分析（Pushover ）的理解与应用摘要：本文首先介绍采用静力弹塑性分析（Pushover ）的主要理论基础和分析方法，以Midas/Gen 程序为例，采用计算实例进行具体说明弹塑性分析的步骤和过程，表明Pushover 是罕遇地震作用下结构分析的有效方法。
关键词：静力弹塑性 Pushover Midas/Gen 能力谱 需求谱 性能点一、基本理论静力弹塑性分析方法，也称Pushover 分析法，是基于性能评估现有结构和设计新结构的一种静力分析方法，在一定精度范围内对结构在罕遇地震作用下进行弹塑性变形分析。
简要地说，在结构计算模型上施加按某种规则分布的水平侧向力或侧向位移，单调加荷载（或位移）并逐级加大；一旦有构件开裂（或屈服）即修改其刚度（或使其退出工作），进而修改结构总刚度矩阵，进行下一步计算，依次循环直到控制点达到目标位移或建筑物倾覆为止，得到结构能力曲线，之后对照确定条件下的需求谱，并判断是否出现性能点，从而评价结构是否能满足目标性能要求。
Pushover 分析的基本要素是能力谱曲线和需求谱曲线，将两条曲线放在同一张图上，得出交会点的位移值，同位移容许值比较，检验是否满足特定地震作用下的弹塑性变形要求。
能力谱曲线由能力曲线（基底剪力-顶点位移曲线）转化而来（图1）。
与地震作用相应的结构基底剪力与结构加速度为正相关关系，顶点位移与谱位移为正相关关系，两种曲线形状一致。
其对应关系为：1/αG V S a =roofroof d X S ,11γ∆=，图1 基底剪力-顶点位移曲线转换为能力谱曲线其中1α、1γ、roof X ,1分别为第一阵型的质量系数，参与系数、顶点位移。
该曲线与主要建筑材料的本构关系曲线具有相似性，其实其物理意义亦有对应，在初始阶段作用力与变形为线性关系，随着作用力的增大，逐渐进入弹塑性阶段，变形显著增长，不论对于构件，还是结构整体，都是这个规律。
需求谱曲线由标准的加速度响应谱曲线转化而来。
浅谈结构非线性静力分析法之Pushover分析法摘要：结构抗震设计方法较多，静力非线性分析法是比较成熟的一种，我国已普遍采用，本人对Pushover分析法进行了详细的剖析。
关键字：抗震设计、静力非线性分析法、Pushover分析法Abstract: the seismic design method of structure is more, static nonlinear analysis method is a more mature, has been commonly used in our country, I for the Pushover method were analyzed in detail.Keywords: seismic design, non-linear static analysis method, Pushover analysis methodPushover 分析法在国外应用较早，上世纪80年代初期在一些重要的刊物上就有论文采用过这种方法。
进入90年代以后，国际抗震工程界提出了基于性能的抗震设计（PBSD）的新概念，这个概念的提出成为了工程抗震发展史上的一个重要的里程碑。
Pushover 分析法作为实现基于性能的抗震设计的重要方法，其研究逐渐深入，应用也逐渐得到推广。
该方法引入我国后，很快得到了大家的普遍重视与应用。
在我国《建筑抗震设计规范》的修订过程中，有些专家就提出了将Pushover 分析法引入规范的想法，只是最后在提法上明确没有采用这个词。
Pushover分析法的早期形式是“能力谱方法”(Capacity Spectrum Method CSM)，基于能量原理的一些研究成果，试图将实际结构的多自由度体系的弹塑性反应用单自由度体系的反应来表达，初衷是建立一种大震下结构抗震性能的快速评估方法。
从形式上看，这是一种将静力弹塑性分析与反应谱相结合、进行图解的快捷计算方法，它的结果具有直观、信息丰富的特点。
关于EPDA的静力弹塑性分析程序
(push-over)的探讨
陈辉（厦门市建筑设计院有限公司361004）
[提要] 本文简要介绍了静力弹塑性分析的原理和实施步骤，并通过工程实例进行相关的对比和讨论。
[关键词]静力弹塑性分析；push-over；反应谱；结构抗震性能评价
Some Discussion about Push-Over Analysis
Abstract：In this paper，the static push-over analysis,POA is briefly introduced，then some contrast and discussion are gived with practical cases.
Keywords：nonlinear static analysis，push-over，response spectrum，structural seismic capacity
1 引言
现行的《建筑抗震设计规范》（GB50011-2001）中，3.6.2条为：“……罕遇地震作用下的弹塑性变形分析。
此时，可根据结构特点采用静力弹塑性分析或弹塑性时程分析方法。
”这里的静力弹塑性分析，即静力非线性分析，除了指一般的与反应谱结合不密切的非线性静力分析外，也包括了push-over 方法。
《抗规》条文说明5.5.3明确提出“……较为精确的结构弹塑性分析方法，可以是三维的静力弹塑性（如push-over方法）……”。
因为弹塑性时程分析对计算机软硬件和分析人员要求较高，工作量也较大，在一段时期内不容易成为一种被广泛采用的方法。
因此逐步推广push-over这种较一般静力分析有许多改进而且相对简便易行的方法，在目前是一种可行的方向。
2 原理与实施步骤
2.1 原理
Push-over方法是近年来在国外得到广泛应用的一种结构抗震能力评价的新方法，其应用范围主要集中于对现有结构或设计方案进行抗震能力的估计。
这种方法从本质上说是一种静力非线性计算方法，与以往的抗震静力计算方法不同之处主要在于它将设计反应谱引入了计算过程和计算成果的工程解释。
这种方法的优点在于：水平力的大小是根据结构在不同工作阶段的周期由设计反应谱求得，而分布则根据结构的振型变化求得。
2.2实施步骤
（1）准备工作：建立结构模型，包括几何尺寸、物理参数以及节点和构件的编号，并输入构件的实配钢筋以便求出各个构件的塑性承载力。
（2）求出结构在竖向荷载作用下的内力。
这时还要求出结构的基本自振周期。
（3）施加一定量的水平荷载。
水平力大小的确定原则是：水平力产生的内力与第(2)步竖向荷载产生的内力叠加后，恰好能使一个或一批构件进入屈服。
（4）对在上一步进入屈服的构件的端部，设定塑性铰点变更结构的刚度，这样，相当于形成了一个新的结构。
求出这个“新”结构的自振周期，在其上再施加一定量的水平荷载，又使一个或一批构件恰好进入屈服。
（5）不断地重复第(4)步，直到结构的侧向位移达到预定的破坏极限。
记录每一次有新的塑性铰出现后结构的周期，累计每一次施加的荷载。
（6）成果整理：将每一个不同的结构自振周期及其对应的地震影响系数绘成曲线，也把相应场地的各条反应谱曲线绘在一起，如图1所示。
这样如果结构反应曲线能够穿过某条反应谱，就说明结构能够抵抗那条反应谱所对应的地震烈度。
还可以在
3 工程实例
以下两个工程为作者参与设计的工程，均用SATWE进行过振型分解法分析，现用EPDA进行
周期
图1 分析成果曲线
push-over 法的分析，判断结构的抗震性能，并与SATWE 程序的计算结果进行对比。
3.1 某大厦（框支－剪力墙）
某大厦为29层框支－剪力墙结构，三层高位转换。
0.1
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.01
0.65
1.15
1.65
2.15
2.65
3.15
3.65
4.15
4.65
5.15
5.65
6.15
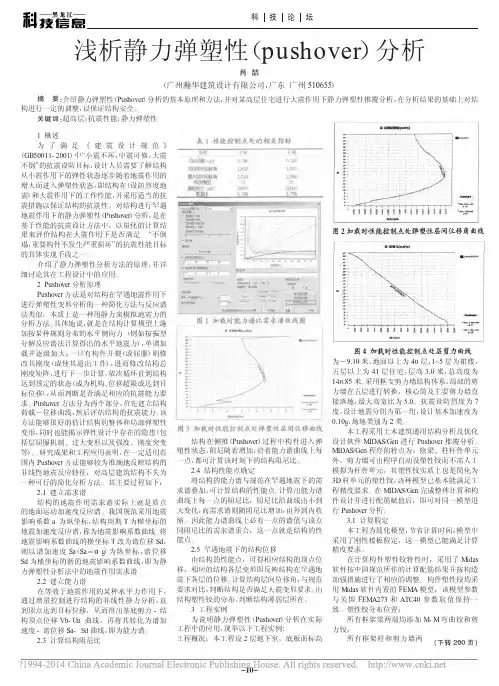
图2 某大厦X 向push-over 分析成果
图2中的结构反应曲线未能穿过罕遇地震（αmax=0.72）下的反应谱曲线，说明结构无法抵抗罕遇地震烈度，结构应做适当调整。
0.1
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.01
0.65
1.15
1.65
2.15
2.65
3.15
3.65
4.15
4.65
5.15
5.65
6.15
6.65
图3 某大厦Y 向push-over 分析成果
3.2 某办公楼（框架）
0.1
0.2 0.3 0.4 0.5
0.6 0.7 0.8 0.01
0.65
1.15
1.65
2.15
2.65
3.15
3.65
4.15
4.65
5.15
5.65
6.15
图4 某办公楼 push-over 分析成果
4 结论及问题讨论
4.1 楼板对梁刚度的影响
从以上2个工程实例与SATWE 的对比结果可以看出，在多遇地震下，当SATWE 的“中梁刚度增大系数”Bk=1时，结构的自振周期SATWE 与push-over 的结果基本一致，而当Bk=2时，SATWE 计算的自振周期比push-over 要短，说明了push-over 计算中并未考虑楼板对梁刚度的影响，程序中也没有提供相关的参数设置，建议程序对此作进一步改进。
4.2 周期折减系数Tc 的影响
从以上的对比中，还可以看出“周期折减系数”Tc 的影响，在多遇地震下，当Tc<1时，SATWE 计算的基底剪力和位移均大于push-over 的计算，只有当Tc=1时，两者的基底剪力和位移才较为接近。
Tc 在SATWE 中的作用是考虑填充墙的抗侧刚度对结构自振周期的影响，这个对比显示push-over 忽略了这项因素。
简单的修正方法是对求出来的周期乘上一个周期折减系数，然后在用于结果的整理。
周期折减系数的取值要注意的是当结构的侧向变形达到一定范围后，由于填充墙的逐渐破坏，周期折减系数要相应调整，以反映填充墙抗侧刚度的降低甚至消失。
4.3 混凝土本构关系模型的假定
文献[1]中计算实例（程序采用SCM-3D ）的自振周期-影响系数曲线，在结构尚未出现塑性铰，即结
表1 某大厦X 向多遇地震下结果
其中，Bk 为中梁刚度增大系数，Tc 为周期折减系数
表2 某大厦Y 向多遇地震下结果
其中，Bk 为中梁刚度增大系数，Tc 为周期折减系数
表3
某办公楼多遇地震下结果
其中，Bk 为中梁刚度增大系数，Tc 为周期折减系数
构处于弹性阶段内，结构的自振周期并不随影响系数的增大而发生变化，即曲线在此段内为一段垂直于X 轴的直线段。
而本文计算实例（程序采用EPDA ）的自振周期-影响系数曲线中（如图1、2、3），自振周期始终随影响系数的增大而增大。
根据结构的刚度矩阵与弹性模量E 的关系，推断这种差别的原因出在混凝土本构关系模型的假定上。
本文计算实例的push-over 法采用的混凝土应力应变关系模型为Saenz 曲线，如图5所示，在应变0~εc 范围内（即混凝土的弹性范围），应力应变的关系是非线性的，混凝土的弹性模量E （即图中曲线的切线斜率）随应变、应力的增大而减小。
结构的刚度随弹性模量E 的减小而减小。
自振周期随结构的刚度的减小而增大。
因此，自振周期随影响系数的增大而增大。
一般的弹塑性分析程序采用的混凝土应力应变关系模型如图6所示，其中应变0~εc 范围内（即混凝土的弹性范围），应力应变的关系是线性的，混凝
4.4 结论
虽然程序存在1、2所述问题，但由于结构在罕遇地震下进入弹塑性阶段后，楼板对梁刚度的影响已经大幅降低，填充墙已基本破坏并失去刚度，所以在罕遇地震下，EPDA 的push-over 分析程序的结果应该仍然具有一定的准确性。
参考文献
[1]叶燎原，潘文．结构静力弹塑性分析（push-over ）的原理和计算实例。
建筑结构学报[J]，2000，（1）
[2]杨溥，李英民等．结构静力弹塑性分析（Push-over ）方法的改进．建筑结构学报[J]，2000，（1）
[3]王理，王亚勇等，空间结构非线性静力分析的工程应用。
建筑结构学报[J]，2000，（1）
[4]吕西林等，《钢筋混凝土结构非线性有限元理论与应用》，同济大学出版社，1997
[5]建筑抗震设计规范，GB50011-2001,中国建筑工业出版社 [6]多层及高层建筑结构弹塑性动力、静力分析软件EPDA 用户手册及编制原理，中国建筑科学研究院PKPMCAD 工程部，2001
图5 混凝土模型（saenz ） 图6混凝土模型（线性）
（saenz ）。
