当前位置：文档之家 › 刚体定轴转动的动能定理

刚体定轴转动的动能定理

  • 格式：ppt
  • 大小：606.50 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

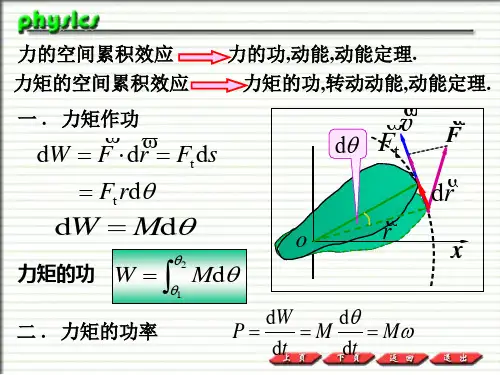
力矩的功刚体动能定理

力矩的功刚体动能定理

3.一根长l质量为m 的匀质细杆，其一端固定在光滑的 水平轴O，可以在竖直平面内转动。最初杆静止在水 平位置。求:杆由初始位置下摆 时的角速度?
θβ
解: 方法一用转动定律求解(略)
方法二用转动动能定理求解
杆处在β时,力矩 M mg l cos
杆转过d时, dA Md mg l cosd
2
2
A EK
k = 2.74×10-4 N·m·rad-2·s2. 求（2）吊扇由静止匀加
速的达到第二档转速经历的时间为 5s . 在此时间内阻力
矩做了多少功 ?
解: 吊扇由静止作匀角加速度运动
2
t5
t
阻力矩做功 W Mf 2d k3dt
W t k 3t3dt 1 k 3t 4
0
4
在 t ＝ 5s 时间内 W 84.8 J
EkA EpA EkB EpB
EkA EpA EkB EpB
o
m, l A
EkA EPA 0
m
EkB
1 2
J 2
J J1 J2
J 1 ml2 ml2 4 ml2
mg
B
mg
3
3
EpB
(mg
l 2
sin
mgl sin )
3 mgl sin
2
0 3 ml22 3 mgl sin 3 ( g sin )1 2
合外力矩对绕定轴转动的刚体所作的功等于刚 体转动动能的增量。
与质点运动类似，若刚体转动过程中，只有 保守力做功，同样刚体的机械能守恒。
3. 刚体的重力势能
y
N
N
mi yi
E p
mi gyi
i 1
Mg
i 1

刚体动能定理

刚体动能定理

人和杆：J = Jm+ JM， ω = 2.3 人和杆：
(1− cosθ )
人： J = JM
ω′ = 4.85 (1− cosθ )
∴ω′ ≈ 2ω
∆t ≈ 2∆t′
P17习题集： （一）5，7； （二）4，6
=θ时
m、L 、
θ
mg θ r2
M2 = r2mg sin θ L = mg sin θ ,⊗ 2
M2 3 g ∴α2 = = sin θ ,⊗ J 2L
杆在转动的过程中，仅有重力作功，故机械能守恒。 杆在转动的过程中，仅有重力作功，故机械能守恒。
θ = π/2 时 ，Ep1 =0，Ek1= 0 ， θ = θ 时， Ep2 = -mg（L/2）cos θ， （ ）
θ
mg
解：（1）水平位置 ：（ ）
∴M1 = r1mg sin
θ =π/2 π r r r r r M = r × mg M = Jα 1 1 π
2
m L
θ
mg
r1
L = r1mg = mg ⊗ 2
L M1 2 mg 3g ∴α1 = = = 1 2 2L J L 3
（2）当 θ ）
r r r M2 = r2 × mg
ri
刚体的 转动动能
1 2 2 Ek = ∑Eki = ∑( ∆mi ri ω ) 2 i i
1 1 2 2 = (∑∆mi ri )ω = Jω2 2 i 2
2.动能定理 动能定理
dω dW = Mdθ = J dθ = Jωdω dt
W =∫
ω2 ω1
1 1 2 2 Jωdω = Jω2 − Jω1 2 2
定理：刚体绕定轴转动时， 定理：刚体绕定轴转动时，合外力矩对刚体所 作的功，等于刚体转动动能的增量。 作的功，等于刚体转动动能的增量。

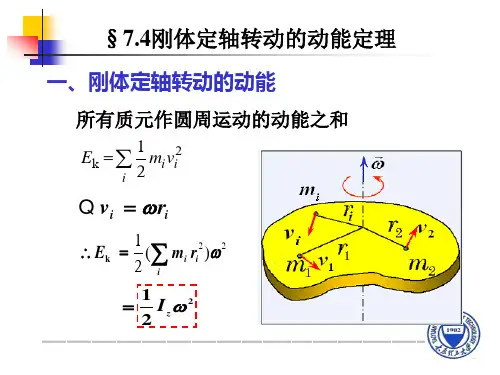
§7.4刚体定轴转动的动能定理

§7.4刚体定轴转动的动能定理

5mg 解得： N N n 2
小 结 刚体定轴转动
M I
质点直线运动
F ma
0
Mdt I I
功
Fdt mv mv
0
1 转动动能 Ek I 2 2 A Md 1 1 2 2 Md I I 0 2 2 重力势能 E p mghc
例2
解法二：刚体定轴转动的机械能守恒定律
[分析:以杆和地球为一系统,只有 mg 作功, 机械能守恒.] 选择水平位置为杆的势能零点，开始时 E0 0 1 2 l 至杆与水平线夹角为 时 E I mg sin 2 2 1 l 2 N I mg sin 0 2 2 O mg 3g sin 解得： l 1 mg vc 3 gl sin 2
mghc
决定于刚体重心距势能零点的高度。
五、刚体的机械能
1 2 E Ek E p I z mghc 2
刚体的机械能守恒定律：
若只有重力做功，则刚体机械能保持不变。
例1
已知：滑轮为匀质圆柱，质量为m1，半径为R质量 为m2的重物由静止下落h，求重物下落h后的速度。 解1：质点和刚体定轴转动的动能定理
外 k
k0
由于刚体内力作功的代数和为零
1 1 2 2 A外 2 I z 2 I z 0
内容: 刚体绕定轴转动时，转动动能的增量 等于刚体所受外力矩做功的代数和。
四、刚体的重力势能
E pi mi ghi mi gyi E p mi gyi
my mg m
i i i
m 2 gh v 2 m1 2m 2

例1
解2：质点系动能定理：

3-3 刚体定轴转动的动能定理

3-3 刚体定轴转动的动能定理
第3节
大学物理学(第4版) 1
一 转动动能 刚体绕定轴转动时的动能，称为转动动能．
Ek

n i 1
1 2
mi
ri2
2

1( n 2 i1
miri2 ) 2

1 2
J 2
刚体绕定轴转动时的转动动能等于刚体的转动惯量 与角速度平方乘积的一半.
第3章 刚体力学基础
第3节
二 力矩的功
解：棒受力如图
6 0
mg
l 2
cos d

1 2
J2

1 2
J02

1 2
J2
WG
6 0
mg
l cosd
2

l 4
mg

mg (hc末
hc初 )
第3章 刚体力学基础Fra bibliotek 第3节大学物理学(第4版) 6
Q WG

mg
l ，J 4

1 ml2 3
3g
2l
则中心点C和端点A的速度分别为
m oR
p v
以子弹和沙袋为系统 以子弹和杆为系统
动量守恒；
动量不守恒；
角动量守恒；
角动量守恒；
机械能不守恒 .
机械能不守恒 .
第3章 刚体力学基础
圆锥摆系统 动量不守恒； 角动量守恒； 机械能守恒 .
第3节
大学物理学(第4版) 5
例3.5 如图所示，一根质量为m，长为l的均匀细棒 OA，可绕固定点O在竖直平面内转动.今使棒从水平 位置开始自由下摆，求棒摆到与水平位置成30°角时 中心点C和端点A的速度.
dWi

vv Fidsi

刚体绕定轴转动的动能定理

刚体绕定轴转动的动能定理

刚体绕定轴转动的动能定理1. 引言刚体是指其内部各点之间的相对位置关系在运动过程中不会发生改变的物体。

刚体绕定轴转动是指刚体在固定轴线上做圆周运动的情况。

动能定理是物理学中的一条重要定理，描述了物体运动过程中动能的变化与外力做功之间的关系。

本文将对刚体绕定轴转动的动能定理进行全面详细、完整且深入的阐述。

2. 刚体绕定轴转动在刚体绕定轴转动的情况下，我们需要考虑刚体的转动惯量和角速度等因素。

转动惯量是描述刚体对转动运动抵抗程度的物理量，通常用符号I表示。

角速度是描述刚体旋转快慢程度的物理量，通常用符号ω表示。

根据牛顿第二定律和角动量守恒定律，我们可以得到刚体绕定轴转动时的基本方程：τ=Iα其中，τ表示作用于刚体上产生转矩（力矩）大小，α表示角加速度。

刚体绕定轴转动的运动规律与作用在刚体上的转矩和转动惯量有关。

3. 动能定理的推导根据刚体绕定轴转动的基本方程，我们可以推导出刚体绕定轴转动的动能定理。

我们来考虑刚体上某一质点的动能T。

由于刚体上各质点都在绕着同一个轴旋转，因此它们具有相同的角速度ω。

设某一质点到轴心的距离为r，则该质点具有的线速度v为v=rω。

该质点的动能T′可以表示为：T′=12mv2=12m(rω)2=12mr2ω2其中，m表示质点的质量。

由于刚体是由众多质点组成的，因此整个刚体的动能T 可以表示为所有质点动能之和：T=∑Tni=1′i其中，n表示刚体上质点的总数。

根据牛顿第二定律和角动量守恒定律，我们知道刚体绕定轴转动时转动惯量I和角加速度α之间存在关系τ=Iα。

将该关系代入动能的表达式中，得到：T=12Iω2其中，ω表示整个刚体的角速度。

刚体绕定轴转动的动能可以表示为12Iω2。

这就是刚体绕定轴转动的动能定理。

4. 动能定理的物理意义刚体绕定轴转动的动能定理描述了刚体在转动过程中动能的变化与外力做功之间的关系。

根据动能定理，我们可以得出以下物理结论：1.外力对刚体做功会改变刚体的动能。

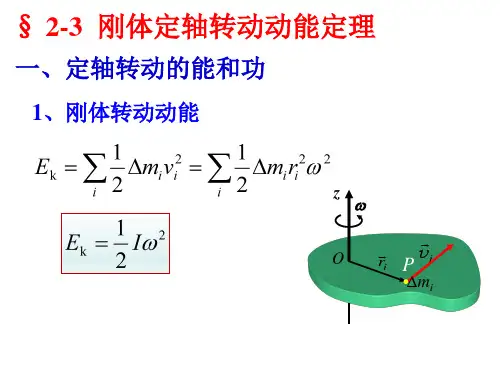
定轴转动动能定理

定轴转动动能定理

只有保守力做功时，含刚体的物体机械能守恒。
例 一质量为m ，长为 l 的均质细杆，转轴在O点， 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动，求：垂直位置时的角速度。
解：设水平位置为重力势能零点
初末机械能相同：
A
C
B
0 0 1 I2 1 mgl
O
2
6
1 1 ml22 1 mgl
29
6
返回 退出
作业：2.16、2.19、2.20
返回 退出
O
(1)水平位置
方向：
返回 退出
(2)解1：转动定律
A
C
B
O
返回 退出
(2)解2：转动动能定理
A
C
B
O
返回 退出
三、定轴转动刚体的机械能守恒
1、刚体的重力势能
以地面为势能零点，刚体和
z

地球系统的重力势能：
i O
刚体的重力势能： 与质量集中于质心处的质点重力势能相同
2、定轴转动刚体的机械能守恒
dt
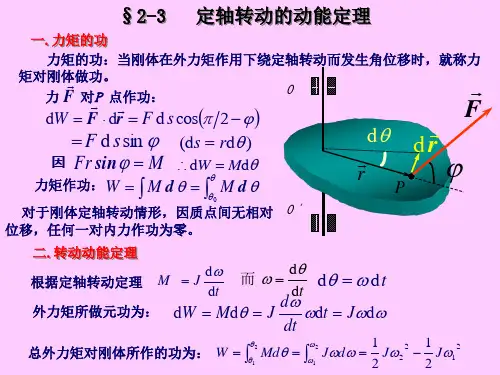
二、定轴转动的动能定理
刚体定轴转动的动能定理：总外力矩对刚体所做的功 等于刚体转动动能的增量。
讨论
子细 弹绳 击质 入量 沙不 袋计
o
v
角动量相对于转轴
以子弹和沙袋为系统 动量守恒； 角动量守恒； 机械能不守恒 .
子o
弹 击 入 杆
v
角动量相对于转轴
以子弹和杆为系统 动量不守恒； 角动量守恒； 机械能不守恒．
角动量相对于转轴
o'
圆 锥 摆
T
m oR
p v
圆锥摆系统 动量不守恒； 角动量守恒； 机械能守恒．

刚体定轴转动动能定理公式

刚体定轴转动动能定理公式

刚体定轴转动动能定理公式刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的物理定理。

在物理学中，刚体定轴转动动能定理是非常重要的定理之一，它能够帮助我们更好地理解物体在转动时的能量变化规律。

我们需要了解一下刚体的概念。

刚体是指在运动或者受力作用下不会发生形变的物体，也就是说，在运动或者受力作用下，刚体的形状和大小都不会发生任何改变。

我们可以将刚体分为两种类型，一种是平面刚体，另一种是空间刚体。

平面刚体指的是只有面积，没有厚度的物体，空间刚体指的是有一定大小和形状的物体。

接下来，我们来了解一下刚体定轴转动动能定理。

刚体定轴转动动能定理的表达式是：E = 1/2 * I * ω²，其中E表示刚体定轴转动的动能，I表示刚体对于轴的转动惯量，ω表示刚体绕轴的角速度。

从这个公式中，我们可以看出，刚体定轴转动动能与刚体的转动惯量和角速度的平方成正比。

那么，什么是转动惯量呢？转动惯量是描述物体转动惯性的物理量，它表示物体绕着某一轴旋转时所具有的旋转惯性。

不同形状的刚体，其转动惯量也是不同的。

例如，对于一个质量均匀分布的球体，其转动惯量为2/5 * m * r²，其中m表示球体的质量，r表示球体的半径。

刚体定轴转动动能定理的应用非常广泛。

例如，在机械制造和工程设计中，我们可以通过刚体定轴转动动能定理来计算物体旋转时所需要的能量和功率。

同时，在运动学和动力学研究中，刚体定轴转动动能定理也是非常重要的工具。

刚体定轴转动动能定理是描述刚体绕某一固定轴转动时动能变化的重要定理。

通过刚体定轴转动动能定理，我们可以更好地理解物体在转动时的能量变化规律，这对于物理学的研究和应用都具有非常重要的意义。

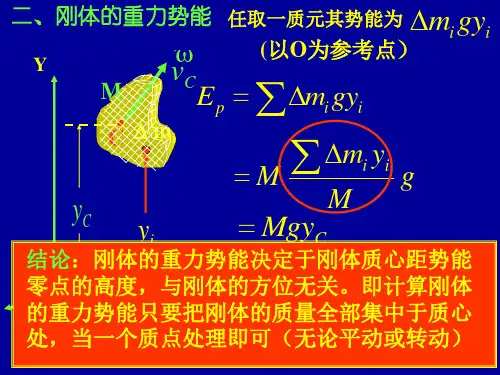
刚体的能量定轴转动的动能定理

刚体的能量定轴转动的动能定理

三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。
求： 当杆过铅直位置时的角速度：
N
YZ
XO
r
mg

定轴转动的动能定理

定轴转动的动能定理

例题2 一根质量为m、长为 l 的均匀细棒OA （如图），可绕通过其一
端的光滑轴O在竖直平面内转动，今使棒从水平位置开始自由下摆，求细棒
摆到竖直位置时其中点C和端点A的速度。
C
解 先对细棒OA 所受的力作一分析；重力G O
作用在棒的中心点C，方向竖直下；轴和棒之间没
A
有摩擦力，轴对棒作用的支承力 N 垂直于棒和 轴
的接触 面且通过O点，在棒的下摆过程中，此力
的方向和大小是随时改变的。
A
在棒的下摆过程中，对转轴O而言，支撑力N通
G
过O点，所以支撑力N的力矩等于零，重力G的力矩则
是变力矩，大小等于mg(l /2) cos ，棒转过一极小的角位移d 时，重力
矩所作的元功是
dW mg l cosd
2
在使棒从水平位置下摆到竖直位置过程中，重力矩所作的功是
度ω0=0,转动动能为0，重力势能为 mg（2l 选下摆到竖直位置hc=0），下摆到竖
直位置时角速度ω=ω,转动动能为
1 2
J重2 力势能为0。
mg l 1 J 2
22
由此得
3g l
mgl
J
所以细棒在竖直位置时，端点A和中心点C的速度分别为
vA l 3gl
vC
l
2
1 2
3gl
J2
2
1 2
J12
刚体定轴转动的动能定理：总外力矩对刚体所做的功等于刚体转动动能
的增量。
注：
1. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点的动能之和。
设刚体中第i个质点的质量为 mi ，速度为 vi
刚体做定轴转动时，各质点的角速度相同。
,则该质点的动能为

刚体定轴转动的动能定理

刚体定轴转动的动能定理

它的动能为 ΔEki
1 2
Δmi vi2
1 2
Δmi
ri 2 2
整个刚体的动能为全部质元的动能之和，即 Ek
1
2
n i 1
Δmi
ri2
2
1 2
J2
式即为刚体转动动能的表达式。
刚体定轴转动的动能定理
1.3 刚体定轴转动的动能定理
将式的转动定律代入可得 dW Md J d J d d Jd
式中 ds ——位移元 dr 对应的弧长，其与对应角位移 dθ 的关系为 ds rd
刚体定轴转动的动能定理
1.1 力矩的功
于是，式可写为 dW Fτrd Md
当刚体的角位置由1 变为2 时，外力矩所做功为W
2 Md
1
式中，M 若是合外力矩，则 W 就是合外力矩的功。
刚体定轴转动的动能定理 1.2 转动动能
大学物理
刚体定轴转动的动能定理 1.1 力矩的功
如图所示，一个绕固定轴 OO 转动的圆盘状刚体，在圆盘平面上有外力 F 作用于 A 点。外力 F 可分解 为切向分力 Fτ 和法向分力 Fn 。
刚体定轴转动的动能定理 1.1 力矩的功
由于法向分力 Fn 垂直于 A 点的角位移，不做功，因此，外力 F 所做的功等于切向分力 Fτ 所做的功，则 外力 F 所做的元功为 dW F dr Fτds
静止下降 h 距离时物体的速率 v。
【解】 由题意可知，以滑轮、物体和地球组成的系统机械能守恒。
取物体在 h 处时系统的重力势能为零，设物体下降到 h 处时滑轮的角速度为 ω，
则根据机械能守恒定律可得
m2 gh
1 2
J2
1 2
m2v2
根据表可知，滑轮的转动惯量为

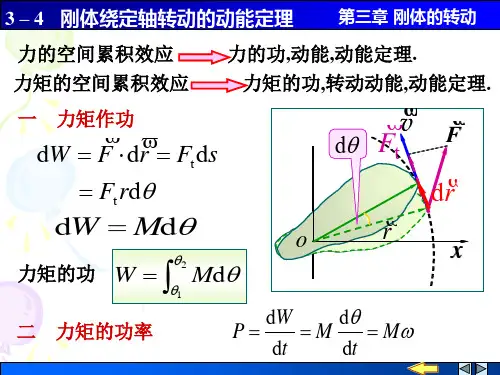
大学物理3_4 刚体绕定轴转动的动能定理

大学物理3_4 刚体绕定轴转动的动能定理
t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩

M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0

高二物理竞赛看：刚体定轴转动的机械能和力矩的功

高二物理竞赛看：刚体定轴转动的机械能和力矩的功

2
2
3
1 mgl 1 (1 ml 2 ) 2
2
23
m,l
mg
3g
l
刚体定轴转动的功能原理
2
1
M外
M重
d
1 2
J22
1 2
J12
2
1
M 外d
mgz
c
2
1 2
J22
mgz
c1
1 2
J12
2 1
M外d
E2
E1
若 M非重外 0 ，刚体的机械能守恒
E
1 2
J2
mghc
常量
m,l o
mg
Mz
dLz dt
当M z 0时
Lz 恒矢量
角动量守恒定律：刚体所受合外力矩为零，则刚体
的角动量保持不变。
J22 J11
对于刚体系统，角动量守恒定律可表示为
Jii C
需要多大的速度 才能滚上斜坡?
只有重力产生力矩，且重 力矩随摆角变化而变化。
N m,l o
l
2
M mg l sin mg l cos
mg
2
2
重力矩作功：
90
90
A重 0 Md
090 mg
l 2
cos d
1 mgl 2
始末两态动能： Ek0 0
Ek
1 2
J2
由动能定理： A Ek Ek0
o
1 mgl 1 J 2 0 J 1 ml 2
3.由定转轴动刚定体律的角M动 量J定理 J d
dJ
dL
dt
dt
dt
角动量定理微分式： dL M dt
Mdt 称为dt时间内刚体所受合外力矩的冲量矩。

4-4定轴转动的动能定理

4-4定轴转动的动能定理

三.定轴转动的动能定理
根据定轴转动定理 则物体在
dt时间内转过角位移 dθ = ω dt 时
d M = (Jω) dt
外力矩所做元功为： 外力矩所做元功为：
d dθ dA = Mdθ = ( Jω)dθ = Jdω = Jωdω dt dt
θ2 ω2
总外力矩对刚体所作的功为： 总外力矩对刚体所作的功为：
§4-4 定轴转动的动能定理 一.力矩的功
1.定义：当刚体在外力矩作用下绕定轴转动而发 定义： 定义 生角位移时，就称力矩对刚体做功。 生角位移时，就称力矩对刚体做功。 由于刚体内任意两质点 的相对位移为零， 的相对位移为零，所以 内力不做功； 内力不做功；平行于转 轴的的外力也不做功； 轴的的外力也不做功； r 只有垂直于转轴的力 F 才做功(即在图示中的 才做功 即在图示中的 r 就是在平面内的力) F 就是在平面内的力 0
r r
0‘
dθ
r dr
r F
ϕ
P
r 作用下， 在外力 F 作用下，刚体有一角位移 dθ ，对应线位移 r，则 为 dr r 点作功： 力 F 对 P点作功： 点作功
r r d A = ϕ)
0
= F ds sin ϕ = Fr dθ sinϕ
r r
0‘
dθ
r dr
1 2 ∆mivi 2
v = ωr
i i
因此整个刚体的动能 1 1 2 EK = ∑ ∆mivi = 2 2
(∑∆m r )ω
2 i i
2
刚体的转动动能
式中∑∆miri 2是刚体对转轴的转动惯量 所以上式写为
J
，
1 2 EK = Jω 2
上式中的动能是刚体因转动而具有的动能，因 上式中的动能是刚体因转动而具有的动能， 此叫刚体的转动动能。 此叫刚体的转动动能。

刚体的能量定轴转动的动能定理

刚体的能量定轴转动的动能定理

/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL
1 mL2
3g L
3
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
力 F 作的功：
ds rd
dA F ds F sin rd Md
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。

§5.3 绕定轴转动刚体的动能 动能定理

§5.3 绕定轴转动刚体的动能 动能定理


解一 机械能守恒( 以初始位置为0势能点)
1 2 0 0 = J mgh 2 l 1 2 h sin J ml 2 3 1 2 0 Md 2 J 0 1 M mgl cos 2

3g sin l
2
解二 定轴转动动能定理 m 动能的增量等于重力做的功
重力矩
3g sin l
2
例 本装置用于测量物体的转动惯量。待测物体A装在转动架上， 转轴Z上装一半径为r 的轻鼓轮，绳的一端缠在鼓轮上，另一 端绕过定滑轮悬挂一质量为 m 的重物。重物下落时，由绳带 动被测物体 A 绕 Z 轴转动。今测得重物由静止下落一段距离 h，所用时间为t。绳子、各轮质量及摩擦力忽略不计
一. 定轴转动刚体动能
第 i 个质点的动能

o
Eki
1 2 miv i 2
ri
v i ri
mi
刚体转动动能
1 1 1 2 2 2 Ek ( miv i ) ( mi ri ) 2 2 2

m r
2 i i
2
1 2 Ek J 2
转动惯量
J mi ri
1
说明 M —— 外力矩的代数和
外力矩M1、M2……、Mn所做元功之和
dA dAi M i d ( M i )d Md
i i i
三.定轴转动动能定理
dA Md
—— 力矩作功的效果
d M J dt 刚体从角坐标1 转到 2 , 刚体从角坐标1 转到 2
• 质点系动能定理
miv i2 A外 + A内 = Ek - Ek0 其中 Ek 2 一对内力所作元功之和等于一质点相对另一质

刚体定轴转动的动能定理

刚体定轴转动的动能定理

dm 积分遍及刚体体积V，
分几种情况：
dV , ( x, y, z )
1、刚体具有对称中心，对称中心就是质心；
2、若刚体无对称中心，但可以划分为几部分，而每一部 分都有对称中心，各部分的中心就是各部分的质心，这些质心 形成为分立的质点组，则刚体的质心就归结为这一质点组的质 心； 3、前二个条件都不具备，这时就必须求积分，计算刚体 的质心。
dri j r j ri rij (为什么?) dt dt r r ij j 2 2 d r j d ri i 2 2 即 v j v i , a j ai O ri dt dt
dr j
由于 i ，j 是任意两个质元，所以刚体上所有质元均有相同的速 度和加速度，各质元的运动轨迹的形状也相同。这里很自然想 到一个代表性的质元——质心。
二、刚体的转动
如果刚体上各质元都绕同一直线作圆周运动就称为刚体转 动，这条直线称为转轴，转轴固定于参考系的情况称为定轴转 动。例如机器上齿轮的运动，门窗等都是定轴转动。若转轴上 有一点静止于参考系，而转轴的方向在变动，这种转动称为定 点转动。例如玩具陀螺的转动就属于定点转动。
分析表明：刚体的任何复杂运动总可以分解为平动和转动（定 轴转动或定点转动）的叠加，例如车轮的滚动、螺帽的运动。 研究刚体绕定轴转动时，通常取任一垂直于定轴的平面作 为转动平面，如图所示，通过分析，转动平面内各个质点的运 动情况搞清楚了，整个刚体的运动情况就知道了。取任一质点 P，P在这一转动平面内绕O点作圆周运动，用矢径 r 与Ox 轴间
唯一确定。总之，为描述平面运动，必须给出
rB rB (t ) xB (t )i yB (t ) j, 或 xB xB (t ), yB yB (t )

转动动能定理

转动动能定理

转动动能定理引言转动动能定理是物理学中的一个重要定理，它描述了刚体绕固定轴旋转时转动动能的变化规律。

本文将对转动动能定理进行全面、详细、完整和深入的探讨。

转动动能定理的定义转动动能定理是指刚体绕固定轴旋转时，刚体的转动动能(简称为转动动能)随着时间的变化而改变的规律。

转动动能可以通过以下公式计算得到：ΔK=12Iω2其中，ΔK表示转动动能的变化量，I表示物体的转动惯量，ω表示物体的角速度。

转动动能定理的推导转动动能定理的推导过程如下：1.假设刚体在t1时刻的转动动能为K1，在t2时刻的转动动能为K2。

2.刚体在t1时刻的角速度为ω1，在t2时刻的角速度为ω2。

3.转动动能的变化量可以表示为ΔK=K2−K1。

4.根据定义可以得到K1=12I1ω12，K2=12I2ω22，其中I1和I2分别表示t1和t2时刻刚体的转动惯量。

5.将K1和K2代入ΔK=K2−K1中，得到ΔK=12I2ω22−12I1ω12。

6.化简上式，得到ΔK=12(I2ω22−I1ω12)。

7.根据角动量守恒定理，可以得到I1ω1=I2ω2。

8.将I1ω1代入上式，得到ΔK=12I1ω1(I2ω2I1ω1−1)=12I1ω1(I2I1−1)=12Iω2，其中I=I1。

因此，转动动能定理可以推导得到ΔK=12Iω2。

转动动能定理的应用转动动能定理在物体的转动运动中有广泛的应用。

下面介绍几个应用实例：应用实例1：旋转物体的动能变化当一个物体绕固定轴旋转时，它的转动动能会随着角速度的变化而改变。

转动动能定理可以帮助我们计算物体在不同角速度下的转动动能变化量，从而对物体的旋转运动进行分析。

应用实例2：转子动能的转换转动动能定理可以用来研究转子动能的转换。

例如，发电机中的转子通过机械能转换成电能，由于转子的转动惯量不变，转动动能定理可以帮助我们计算转子在转动过程中的动能转换效率。

应用实例3：转动惯量的测量转动动能定理可以通过测量物体的角速度和转动动能的变化量，间接计算出物体的转动惯量。

6 刚体的动能定理

6 刚体的动能定理

d
dr
F

P
3
力矩的功
因
Fr sin M
d A M d
力矩作功：
A M d M d
0

0
•对于刚体定轴转动情形， 因质点间无相对位移，任 何一对内力作功为零;
•另外只有在垂直于转轴平 面内的分力才作功，平行 于转轴的分力是不作功的 。
r
0‘
d
3g , l
0（合外力矩为零）
例题4-7
质量 m，长l 的均匀细杆，可绕水平轴在竖直平面内无 摩擦转动。转轴离杆一端l/3，设杆由水平位置自由转 下，求：(4)杆在竖直位置时对转轴的作用力。
(4)由质心运动定理：
2 vc 6m l N mg ma c m ( )2 l l 6 6
16
3g w l
3gl l v A wl 3gl , vC w 2 2
(2).由转动定理,得 M=I 在竖直位置 M=0
A C 0
17
若下垂角时， 情况怎样？
解法二
只有重力作功,因此机械能守恒.
1 1 2 mgl 0 mgl Iw 2 2
dA Md I d Id Id 所做的功等于刚体转动动能的增量。 dt dt
化的原因可以用力矩做 功的效果来解释。
总外力矩对刚体所作的功为：
A Md
122来自11 1 2 2 Id I 2 I1 2 2
5
3.刚体的重力势能
对于一个不太大的质量为 m 的物体，它的重力势 能应是组成刚体的各个质点的重力势能之和。
mg T ma
（2）．因为 v 2 2ah 所以物体的动能为

3-4刚体绕定轴转动的动能定理

3-4刚体绕定轴转动的动能定理

1 2 T h m v 根据 1 , 立即可以求得张力T1 1 2
1 2 1 T1 m1v 2 h
m1m 2 g m1 m 2
1 2
M
第3章 刚体力学
大学物理学 刘成林等编
1 2 根据 (m2 g T2 )h m2 v 或 T2 r T1 r J 2
可以立即算出张力T2
A M z 75 2.8 10 J 2.1 10 J
2
4
第3章 刚体力学 例 5：质量为 m1 的物体置于完全光滑的水平桌面 上 , 用一根不可伸长的细绳拉着 , 细绳跨过固定于 桌子边缘的定滑轮后，在下端悬挂一个质量为 m2 的 物体 , 如图所示。已知滑轮是一个质量为 M ,半径为r 的圆盘, 轴间的摩擦力忽略不计。求滑轮与 m1 之间 的绳子的张力 T1 、滑轮与 m2 之间的绳子的张力 T2 以 及物体运动的加速度 a 。
大学物理学 刘成林等编

N
闸瓦
解：为了求得飞轮从制 f 飞轮 动到停止所转过的角度 和摩擦力矩所作的功A, 必须先求得摩擦力、摩擦力矩 和飞轮的角加速度。
第3章 刚体力学 闸瓦对飞轮施加的摩擦力的大小等于摩擦系数与 正压力的乘积
大学物理学 刘成林等编
f N 0.50 500 N 2.5 10 N
i 1
n
2
代入动能公式中, 得到刚体转动动能的一般表达式
Ek
1 2 J 2
刚体转动动能与质点运动动能在表达形式上是 相似性的。
第3章 刚体力学 三、刚体定轴转动动能定理
大学物理学 刘成林等编
根据功能原理, 外力和非保守内力对系统作的 总功等于系统机械能的增量。对于刚体一切内力 所作的功都为零。对定轴转动的刚体 , 外力的功 即为外力矩所作的功; 系统的机械能为刚体的转 动动能。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
积累效应)
力矩作功的功率(power 作功的快慢):
P
dA dt
Md
dt
M
力矩的功： work done by torque
dA Mzd
2
A Mzd
1
A、 所谓力矩的功，实质上还是力的功，并无任何关于力
矩的功的新的定义，只是在刚体转动中，用力矩和角位移
的积来表示功更为方便而己。
B、对于定轴转动刚体，所有内力的功总和在任何过程 中均为零。（内力成对，大小相等方向相反，一对内力矩 的的功代数dA和为F零2 ；dr∴ 内相力对矩位的移功为总零和.）为零。另一角度，内力
m'l 2 3ma2
a m v m
3mva m'l 2 3ma2
o 30
射入竿后，以子弹、细杆和 地球为系统 ，机械能守恒 .
a m
1 (1 ml 2 ma2 ) 2
v m
2
3 mga(1
cos30)
mg
l 2
(1
cos30)
v g(2 3)(ml 2ma)(ml2 3ma2) 6 ma
dt d dt
d
2 Md
1
2 Id
1
1 2
I22
1 2
I12
Ek
1 2
I2
称为刚体的转动动能
A
Ek 2
Ek1
1 2
I22
1 2
I12
合外力矩对绕定轴转动的刚体做的功 = 刚体转动动能的增量
—— 刚体绕定轴转动的动能定理
刚体的重力势能：
刚体受保守力作用也有势能概念.
对于一个不太大的质量为 m 的物体，它的重
h
由刚体动能定理
FT R
1 2
I 2
1 4
m1R2 2
约束关系 R h v R
联立得
v 2 m2 gh m1 2m2
方法2. 利用质点系动能定理求解
将转动柱体、下落物体视作质点系
由质点系动能定理
m2 gh
1 2
m2v 2
1 2
I 2
1 2
m2v 2
1 2
(1 2
m1R2 ) 2
约束关系 R h v R
Fy
Fx mact 0
Fx O
Fy mg macn
c
Fy
mg
3 2
mg
5 2
mg.
解：（1）设小球新的角速度为ω
由于拉力通过转动轴中心，由角动量守恒得
mr020
m
r0 2
2
，
40
（2）由动能定理得，拉力所作的功为
A
1 2
[ I1 (40
)2
I
2
20
]
A 1 2
m(r0
2)2 1602 mr0202
(vi ri)
绕定轴转
动刚体的
Ek
i
Ei
n i 1
1 2mi
ri
2
2
1 2
n i1
mi ri2
2
总动能:
Ek
1 2
I
Z
2
二 刚体绕定轴转动的转动动能(kinetic energy)
Ek
i
Eki
i
1 2mi
vi2
1 2
(
i
mi ri2 )2
1 I2
2
刚体绕定轴转动的转动动能，等于刚体的转动惯 量与角速度二次方的乘积的一半。
1 2
I02
[例题]装置如图所示，均质圆柱体质量为m1，半径为R，重锤 质量为m2 ，最初静止，后将重锤释放下落并带动柱体旋转，求 重锤下落 h 高度时的速率v，不计阻力，不计绳的质量及伸长.
[解] 方法1. 利用质点和刚体转动的
R
动能定理求解.
m1
由质点动能定理
m2 gh
FTh
1 2
m2v 2
m2
3 2
mr0202
例 一长为 l , 质量为 m的竿可绕支点O自由
转动 . 一质量为 m、速率为 v 的子弹射入竿内距支 点为 a 处，使竿的偏转角为30º. 问子弹的初速率为
多少 ?
解 把子弹和竿看作一个系统 . 子弹射入竿的过程系统角动量守恒
o 30
mva (1 ml2 ma2 )
3 3mva
作 业：
7.4.2，7.5.4.
练 习：
7.5.1，7.5.2.
典型例题：
参见“刚体习题5”.
动而发生角位移时，就称力矩对刚体做功。
对于转动过程：
力矩的功 A 2 Md （力矩的空间积累效应） 1
对于恒力矩：
A M
一. 力矩的功
力矩的功：当刚体在外力矩作用下绕定轴转
动而发生角位移时，就称力矩对刚体做功。
v
dA
v F
drv
F
cos
drv
drv F
Ft rd
P
drv
dA Md
Z
x A 2 Md (力矩的空间
力的空间累积效应 力的功,动能,动能定理.
力矩的空间累积效应 力矩的功,转动动能,动能定理.
§7.4 定轴转动中的功能关系
v
F 一、力矩的功：
α
（设力F 在转动平面内）
d drvrv P
Z
x
rd
dA
v F
drv
F
drv
sin
rF
sin d
力矩的元功：dA Ftrd Md
力矩作功：当刚体在外力矩作用下绕定轴转
比较
Ek
1 2
mv2
Ek
1 I2
2
质点的动能与刚体绕定轴转动的转动动能，形式相似。
三、刚体绕定轴转动的动能定理(theorem of kinetic energy)
在合外力矩 M 的作用下，刚体绕定轴转动，由 1 转 到 2 ，则合外力矩 M 做的功为
Q M I I d I d d I d
联立得
v 2 m2 gh m1 2m2
[例题] 如图所示，一匀质细棒可绕水平轴 O 转动，已知棒长 为 l ，质量为 m ，开始时将棒置于水平状态，然后由静止摆下， 求棒摆到竖直的瞬间：
（1）棒的角速度；（2）棒的转动动能；
（3）质心的加速度（不计摩擦阻力）；
（4）轴对棒的作用力。
c
O
O
c
[解] （1）棒的角速度
I
l
（2）棒的转动动能
Ek
1 2
I 2
mg
l. 2
必须注意，在这里不能把棒的动能写成
1 2
mvc2
（3）质心的加速度
O
由线量和角量的关系可算出 c
acn
l 2
2
3 2
g.
又因棒在竖直位置时的角加速度 0（因此时合力矩为零）
0.
（4）可以由质心运动定理求出棒在竖直位置时，O 轴对棒的 反力 Fx 和 Fy：
力势能应是组成刚体的各个质点的重力势能之和。
C • mi
hc
EP 0
h Epi mi ghi i
Ep Epi mi ghi
i
i
mi hi
mg i m
EP mghc
（hc是刚体的质心位置坐标）
——一个不太大的刚体的重力势能等于质量集中在质心时 的重力势能.
三、定轴转动的功能原理：
质点系功能原理对刚体仍成立：
C、功率：
p dA M d M
dt
dt
当
M
与
同方向，A
和p
为正;
当
M
与
反方向， A
和
p 为负.
二 刚体绕定轴转动的转动动能
(kinetic energy)
质点运动的动能:
Ek
1 mv2 2
刚体是由许多质点组成的,
第 i 小块质元的质量 mi
Oi ri
vi
mi
其动能：
Eki
1 2
mi vi 2
细棒在下摆过程中，只有作用于棒的 O 重力做功，故细棒的机械能守恒。
设细棒在水平位置时的重力势能为
c
势能零点，则总机械能
E0 0
细棒摆到竖直位置时的角速度设为 ，则机械能
E 1 I 2 mg l ,
2
2
其中I
1 3
ml 2 .按机械能守恒有E
E0 , 所以得
1 I2 mg l 0
2
2
mgl 3g
A外 A内非 Ek2 EP2 Ek1 EP1 E2 E1
对于刚体，因其内部质点间无相对位移， 任何一对内力作功为零（对刚体的任何运动形式都 是成立的）。
若A外 A内非 0 E Ek EP 常量
则刚体系统的机械能守恒。
直线运动与定轴转动规律对照
质点的直线运动
v dx dt
dv d2 x a dt dt2
P mv F
EK
1 mv2 2
m
dA Fdx Fdt
F ma
F d t P P0
F
d
x
1 2
mv2
1 2
mv02
刚体的定轴转动
d
dt
d
dt
d2
dt2
L I
EK
1 2
I2
M
I
d A M d M dt
M I
M d t L L0
M
d
1 2
I2