最新定轴转动刚体的动能计算
- 格式：ppt
- 大小：415.00 KB
- 文档页数：7
下载文档原格式
合集下载
定轴转动刚体的动能计算
我们已知，定轴转动刚体的转动惯量I、角 速度ω分别与直线运动中刚体的质量M、速度v 对应，但教材上并未给出计算刚体旋转动能的 公式。我们猜想刚体的动能是否为
1 2 E k = Iω 2 下面来证明此公式：
设所有刚体均匀，密度为1，则质量和体积 在数值上相等。 考虑半径为Ｒ的圆环绕轴线转动：
I = mR 2 = 2πR 3 . 1 1 2 3 2 2 E k = ∫ •Rd θ • (Rω ) = πR ω = Iω . 2 2 0
若圆盘剖面如图，质量向轴集中，则使其转速达 到ω所需的能量就较少。将这种情况应用于吸尘器， 平动摩擦阻力f仍不变。故将底盘质量向轴集中也能节 省动能。 另外，我们可见，调整绕轴线转 动圆盘的质量分布，可以影响能量与 转速的对应关系。将动能（可由电能 转轴 转化而来，而电能容易控制）作输入， 转速作输出，同时对转子的质量分布加以调整；或者 反过来，以转速作输入，能量作输出；这种方法应是 有广阔的应用前景。
v f= µN. ωr
2
Ｃ Ｏ Ｃ’
v
ω
摩擦力集中在上半个月牙形内。
由于滑动摩擦力µN与接触面积无 2v 关，若切去盘中心O半径为 r − ω 的小圆盘，如图易知摩擦力增加
2v 2 ∆f = µN. ωr1
Ｐ
2
v
Ｃ Ｏ Ｃ’
Ｑ
ω
其中Δf是区域P、Q的摩擦力， P、Q的圆心分别是C和C’。
在吸尘器模型中，设吸尘器使用距离 为s，采用开孔的底盘，增加了摩擦力， 却减少了驱动底盘转动的能量。当
Ｐ
2 v
m小盘 2 2 1 2 µN • • s ≤ ω r1 ω r1 2 v
Ｃ Ｏ
Ｃ’
Ｑ
ω
时，即 了能量的。
3-3 力矩的功 刚体绕定轴转动的动能定理
1
3.3 力矩的空间累积效应
一 力矩作功 v v dW = F dr = Fτ ds
v v
dθ v
v F τ
v F
= Fτ rdθ
dW = Mdθ
力矩的功 W =
v dr
o
r
x
∫θ
θ2
1
M dθ
2
3.3 力矩的空间累积效应
dW dθ 力矩的功率 二 力矩的功率 P = =M = Mω dt dt v v v v 比较 W = F dr P = F v ∫
13
3.3 力矩的空间累积效应
解 (1) 如图取面 ) 积元ds 积元 = drdl，该面元 ， 所受的摩擦力为
v df
df =
mg
πR
2
o
r
dl dr
drdl
R
此力对点o的力矩为
rdf =
mg
πR
2
rd r d l
14
3.3 力矩的空间累积效应
于是，在宽为 的 于是，在宽为dr的 圆环上， 圆环上，唱片所受的摩 擦力矩为
3.3 力矩的空间累积效应
力的时间累积效应： 的时间累积效应： 冲量、动量、动量定理． 冲量、动量、动量定理． 力矩的时间累积效应 的时间累积效应： 力矩的时间累积效应： 角冲量、角动量、角动量定理． 角冲量、角动量、角动量定理． 力的空间累积效应： 力的空间累积效应： 效应 力的功、动能、动能定理． 力的功、动能、动能定理． 力矩的空间累积效应： 力矩的空间累积效应： 效应 力矩的功、转动动能、动能定理． 力矩的功、转动动能、动能定理．
m,l O
v FN
θ mg
10
3.3 力矩的空间累积效应
3.3 力矩的空间累积效应
一 力矩作功 v v dW = F dr = Fτ ds
v v
dθ v
v F τ
v F
= Fτ rdθ
dW = Mdθ
力矩的功 W =
v dr
o
r
x
∫θ
θ2
1
M dθ
2
3.3 力矩的空间累积效应
dW dθ 力矩的功率 二 力矩的功率 P = =M = Mω dt dt v v v v 比较 W = F dr P = F v ∫
13
3.3 力矩的空间累积效应
解 (1) 如图取面 ) 积元ds 积元 = drdl，该面元 ， 所受的摩擦力为
v df
df =
mg
πR
2
o
r
dl dr
drdl
R
此力对点o的力矩为
rdf =
mg
πR
2
rd r d l
14
3.3 力矩的空间累积效应
于是，在宽为 的 于是，在宽为dr的 圆环上， 圆环上，唱片所受的摩 擦力矩为
3.3 力矩的空间累积效应
力的时间累积效应： 的时间累积效应： 冲量、动量、动量定理． 冲量、动量、动量定理． 力矩的时间累积效应 的时间累积效应： 力矩的时间累积效应： 角冲量、角动量、角动量定理． 角冲量、角动量、角动量定理． 力的空间累积效应： 力的空间累积效应： 效应 力的功、动能、动能定理． 力的功、动能、动能定理． 力矩的空间累积效应： 力矩的空间累积效应： 效应 力矩的功、转动动能、动能定理． 力矩的功、转动动能、动能定理．
m,l O
v FN
θ mg
10
3.3 力矩的空间累积效应
3.3刚体定轴转动中的功与能
−1 1
解：以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳，绳的一端悬挂质量为m的物体 的物体。 动，滑轮上绕有轻绳，绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少？ 当物体从静止下降距离 时，物体速度是多少？ 以滑轮、 解：以滑轮、物体和地球组成系统为研究对 由于只有保守力做功，故机械能守恒。 象。由于只有保守力做功，故机械能守恒。 设终态时重力势能为零 初态：动能为零，重力势能为mgh 初态：动能为零，重力势能为 末态： 末态：动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
解：以 ω 和 ω 分别表示冲孔前后的飞轮的角速度
1 2
ω = (1 − 0 .2 )ω = 0.8ω
2 1
2
2
2πn ω = = 8πrad ⋅ s 60
1 1
−1
1
1 1 1 由转动动能定理 A = Jω − Jω = Jω (0 .8 − 1) 2 2 2 1 又 J = mr A = −5 .45 × 10 J 2
课后习题 3-8
θ1
θ2
二、刚体的转动动能和重力势能
1.绕定轴转动刚体的动能 绕定轴转动刚体的动能 绕定轴转动刚体的
∆ ,∆ ,⋅⋅⋅,∆ ,⋅⋅⋅,∆ m m m m r r r r r, r ,⋅⋅⋅, r ⋅⋅⋅, r r r r r v ,v ,⋅⋅⋅,v ,⋅⋅⋅,v
1 2 i
1 2 i, N
N
Q = rω v 1 E= ∆ v m 2
2 2 2
1 1
2
3
质量M的圆盘滑轮可绕通过盘心的水平轴转 例3-7半径R质量 的圆盘滑轮可绕通过盘心的水平轴转 半径 质量 滑轮上绕有轻绳，绳的一端悬挂质量为m的物体 的物体。 动，滑轮上绕有轻绳，绳的一端悬挂质量为 的物体。 当物体从静止下降距离h时 物体速度是多少？ 当物体从静止下降距离 时，物体速度是多少？ 以滑轮、 解：以滑轮、物体和地球组成系统为研究对 由于只有保守力做功，故机械能守恒。 象。由于只有保守力做功，故机械能守恒。 设终态时重力势能为零 初态：动能为零，重力势能为mgh 初态：动能为零，重力势能为 末态： 末态：动能包括滑轮转动动能和物体平动动能 由机械能守恒
i i
i i i
2
1
2
i
N
刚体的定轴转动定律
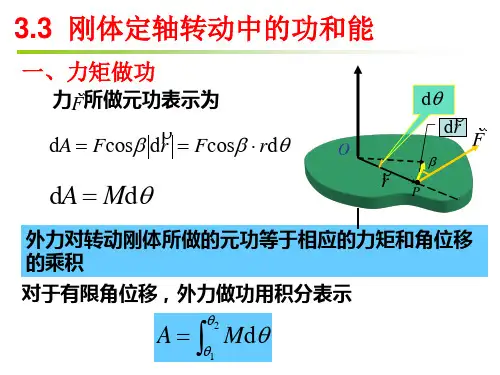
刚体的定轴转动定律1. 介绍刚体是物理学中的一个重要概念，它指的是在运动过程中形状和大小保持不变的物体。
刚体的定轴转动定律是描述刚体绕固定轴线转动的规律和性质，对于我们理解刚体的运动和应用相关物理问题具有重要意义。
2. 刚体的转动惯量2.1 定义刚体绕轴线转动时，其转动惯量是衡量刚体抵抗转动运动的特性。
转动惯量的大小取决于刚体的质量分布以及轴线的位置和方向。
2.2 转动惯量的计算方法转动惯量可以通过积分计算得到，对于一个质量为m的刚体，其转动惯量可以用以下公式表示： [ I = r^2 dm ] 其中，r是质量元dm到转轴的距离。
对于一些常见的简单形状的刚体，转动惯量可以通过一些公式直接计算得到，例如：- 细杆绕直线轴线转动：[ I = mL^2 ] - 球体绕直径轴线转动：[ I = MR^2 ] - 圆环绕直径轴线转动：[ I = MR^2 ]3. 定轴转动的角动量3.1 定义角动量是描述物体转动的物理量，刚体的角动量可以通过转动惯量和角速度的乘积得到。
3.2 角动量的守恒对于一个孤立系统，如果没有外力矩作用，刚体的角动量将保持不变，这就是角动量守恒定律的内容。
3.3 角动量定理角动量定理描述了外力矩对刚体角动量的影响，它可以表示为以下公式： [ = ] 其中，()是作用在刚体上的外力矩，(L)是刚体的角动量。
4. 牛顿第二定律与角加速度4.1 牛顿第二定律牛顿第二定律描述了刚体转动的加速度与作用力的关系，其公式为： [ = I] 其中，()是作用在刚体上的合外力矩，(I)是刚体的转动惯量，()是刚体的角加速度。
4.2 角加速度的计算对于旋转轴与力矩不垂直的情况，我们可以通过以下公式计算刚体的角加速度：[ = ] 其中，()是力矩与旋转轴之间的夹角。
5. 定轴转动的动能5.1 定义刚体的转动动能是由于其转动而具有的能量，它可以通过转动惯量和角速度的平方的乘积得到。
5.2 动能定理动能定理描述了外力对刚体转动动能的影响，它可以表示为以下公式： [ W = K ] 其中，(W)是作用在刚体上的合外力所做的功，(K)是刚体的转动动能。
3.刚体的定轴转动
a a n a
2 3 2
2
6.16 10
3
2
3.14 m / s
2
2
6.16 10 m / s
例3-2：一飞轮在时间t 内转过角度 at bt 3 ct 4式中a、b、c都 是常量。求它的角加速度。 解:飞轮上某点的角位置可用θ 表示为： at bt 3 ct 4 将此式对t 求导数，即得飞轮角速度的表达式为:
O
刚体定轴转动的描述
（1） 定轴转动的角量描述
角位置： (t )
角位移： (t ) (t 0 ) 角速度：
d dt d
dt d
2
角加速度：
dt
2
角速度和角加速度均为矢量，定轴转动中其方向沿转轴的
方向并满足右手螺旋定则。
说明：在刚体的定轴转动中加速度、角加速度和角位移通常用 代数量表示。通常规定：当刚体作逆时针转动时，这些角量均 取正值；反之，取负值。
观察圆盘O和圆盘上一点P的运动：
O点的运动：沿着直线向前移动 圆盘上其他点的运动：除向前移动外，还绕圆盘中心O且垂直于盘面的轴转动。
1.刚体的平动：在运动过程中，若刚体上任意一条直线在各个时 刻的位置始终彼此平行，则这种运动叫做平动。
特点：刚体内所有点具有相同的位移、速度和加速度。 －－刚体上任一点的运动规律即代表刚体的平动规律。
2
2
则整个刚体的转动动能为：
Ek
1 2
m i vi
2
1 2
m i ri
2
2
1 2
J
2
二、 力矩的功和功率
1.力矩的功
2 3 2
2
6.16 10
3
2
3.14 m / s
2
2
6.16 10 m / s
例3-2：一飞轮在时间t 内转过角度 at bt 3 ct 4式中a、b、c都 是常量。求它的角加速度。 解:飞轮上某点的角位置可用θ 表示为： at bt 3 ct 4 将此式对t 求导数，即得飞轮角速度的表达式为:
O
刚体定轴转动的描述
（1） 定轴转动的角量描述
角位置： (t )
角位移： (t ) (t 0 ) 角速度：
d dt d
dt d
2
角加速度：
dt
2
角速度和角加速度均为矢量，定轴转动中其方向沿转轴的
方向并满足右手螺旋定则。
说明：在刚体的定轴转动中加速度、角加速度和角位移通常用 代数量表示。通常规定：当刚体作逆时针转动时，这些角量均 取正值；反之，取负值。
观察圆盘O和圆盘上一点P的运动：
O点的运动：沿着直线向前移动 圆盘上其他点的运动：除向前移动外，还绕圆盘中心O且垂直于盘面的轴转动。
1.刚体的平动：在运动过程中，若刚体上任意一条直线在各个时 刻的位置始终彼此平行，则这种运动叫做平动。
特点：刚体内所有点具有相同的位移、速度和加速度。 －－刚体上任一点的运动规律即代表刚体的平动规律。
2
2
则整个刚体的转动动能为：
Ek
1 2
m i vi
2
1 2
m i ri
2
2
1 2
J
2
二、 力矩的功和功率
1.力矩的功
定轴转动刚体的动能计算
其中
包含刚体质心系中刚体的动能，这里不再推了。
成立。
这便证明了刚体定轴转动的动能 ω：8π(4Hz)
r1：0.
2．由
可知，既然能量是线性的，定轴转动的刚体的转动惯量也是线性的。
故将底盘质量向轴集中也能节省动能。
将动能（可由电能
公式。 转化而来，而电能容易控制）作输入，
转速作输出，同时对转子的质量分布加以调整； 《力学》，杨维纮，中国科学技术大学０４级理学院教材。
❖ 本幻灯片参考材料：
《力学》，杨维纮，中国科学技术大学０４级理 学院教材。
其他便没有了。限于客观原因，作者并没有准备 充分资源。日后若条件允许，也许能做出更有价 值的成果。
版权所有，商用付酬。
❖ 本文拟得出定轴转动下刚体 的动能表达式，并讨论教材例6.4 中电熨斗模型的改良及其他一些 简单应用。
参考系下“所有”的动能。若转轴亦运动， 这便证明了刚体定轴转动的动能公式。
若转轴亦运动，求刚体的总动能只需再加上刚体关于轴速度的动能，即
求刚体的总动能只需再加上刚体关于轴速 4中我们知半径r、自转角速度ω、平动速度v<< ω 、滑动摩擦系数μ、对地面压力N的圆盘受阻力
由于滑动摩擦力μN与接触面积无关，若切去盘中心O半径为 的小圆盘，如图易知摩擦力增加
体的动能为
E kB E kA 1 2M A 2B r2(rA是 BA距 B)离 .
4．由分析2及正交轴定理可求出刚体 作定点转动的动能公式：
E k O E k x E k y E k z 1 2 I xx 2 I yy 2 I zz 2 .
5．由分析1～4可得刚体作任意运动 的一般的动能公式：
度的动能，即 2．由
可知，既然能量是线性的，定轴转动的刚体的转动惯量也是线性的。
刚体定轴转动的功和能
2 3 R 0 转过的圈数： n 16g 2
(解毕 )
· 10 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
五、刚体的机械能守恒
当系统中只有保守力作功，系统的机械能守恒：
E0 E
其中 E
m ,l
l 2
1 mv 2 1 J 2 2 2
C
mgh 1 kx 2 2
滑轮(R, M)，m从静止开始下落，求下落 h 时物体的速 度及加速度。 系统 = 弹簧 + 滑轮 + 物体 + 地球： 提示： 机械能守恒
k
M ,R
2mgh kh 2 答案： v m M / 2
m
2(mg kh) a 2m M
ቤተ መጻሕፍቲ ባይዱ
减速、加速?
h
· 13 ·
Chapter 4. 刚体的转动
三、刚体绕定轴转动的动能定理
W Md
0
M J J d dt
d ω 0 J dt d 0 J d
·4 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
1 1 2 2 积分得： W J J 0 2 2
1 2 [定义] 刚体转动动能： E k J 2 1 1 2 2 W J J 0 E k E k 0 E k 2 2
mg
前例 已知：匀质细杆 (m，l )，光滑轴，从竖直位置静 止摆下，求细杆摆到θ 位置时的角速度。
· 11 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
解：以杆、地球为一系统，则系统机械能守恒：
(解毕 )
· 10 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
五、刚体的机械能守恒
当系统中只有保守力作功，系统的机械能守恒：
E0 E
其中 E
m ,l
l 2
1 mv 2 1 J 2 2 2
C
mgh 1 kx 2 2
滑轮(R, M)，m从静止开始下落，求下落 h 时物体的速 度及加速度。 系统 = 弹簧 + 滑轮 + 物体 + 地球： 提示： 机械能守恒
k
M ,R
2mgh kh 2 答案： v m M / 2
m
2(mg kh) a 2m M
ቤተ መጻሕፍቲ ባይዱ
减速、加速?
h
· 13 ·
Chapter 4. 刚体的转动
三、刚体绕定轴转动的动能定理
W Md
0
M J J d dt
d ω 0 J dt d 0 J d
·4 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
1 1 2 2 积分得： W J J 0 2 2
1 2 [定义] 刚体转动动能： E k J 2 1 1 2 2 W J J 0 E k E k 0 E k 2 2
mg
前例 已知：匀质细杆 (m，l )，光滑轴，从竖直位置静 止摆下，求细杆摆到θ 位置时的角速度。
· 11 ·
Chapter 4. 刚体的转动
§4. 5 刚体定轴转动的功和能
解：以杆、地球为一系统，则系统机械能守恒：
刚体的能量定轴转动的动能定理
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的
r i vi mi
M
质元 m1, m2 mi mn
r 任取一质元 mi 距转轴 i ，则该质元动能：
mivi2 / 2 mi (ri)2 / 2 miri22 / 2
故刚体的转动动能：
n
Ek Ek
在一微小过程中 力矩作的功
dA Md (1)
在一微小过程中
XX 力1矩O1作的2功2 M M
dA Md (1)
在考虑一个有限过程，设
在力矩作用下，刚体的角
位置由 功
1
2
则力矩的
A dA 2 Md (2) 1
力矩的功反映力矩对空间的积累作用，力矩越 大，在空间转过的角度越大，作的功就越大。 这种力矩对空间的积累作用的规律是什么呢？
/2 mg L cosd
0
2
mgL / 2
N
YZ
XO
r
mg
依动能定理
A力矩
1 2
J2
1 2
J02
A力矩
mg
L 2
mg
L 2
1 2
J
2
0
mgL J
mgL 1 mL2
3g L
3
XX
1
1 O
2
2
2 1
Md
1 2
J
2 2
1 2
J12
M
M
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。
求： 当杆过铅直位置时的角速度：
N
YZ
XO
r
mg
定轴转动的动能定理
例题2 一根质量为m、长为 l 的均匀细棒OA （如图），可绕通过其一
端的光滑轴O在竖直平面内转动，今使棒从水平位置开始自由下摆，求细棒
摆到竖直位置时其中点C和端点A的速度。
C
解 先对细棒OA 所受的力作一分析；重力G O
作用在棒的中心点C，方向竖直下；轴和棒之间没
A
有摩擦力，轴对棒作用的支承力 N 垂直于棒和 轴
的接触 面且通过O点，在棒的下摆过程中，此力
的方向和大小是随时改变的。
A
在棒的下摆过程中，对转轴O而言，支撑力N通
G
过O点，所以支撑力N的力矩等于零，重力G的力矩则
是变力矩，大小等于mg(l /2) cos ，棒转过一极小的角位移d 时，重力
矩所作的元功是
dW mg l cosd
2
在使棒从水平位置下摆到竖直位置过程中，重力矩所作的功是
度ω0=0,转动动能为0，重力势能为 mg（2l 选下摆到竖直位置hc=0），下摆到竖
直位置时角速度ω=ω,转动动能为
1 2
J重2 力势能为0。
mg l 1 J 2
22
由此得
3g l
mgl
J
所以细棒在竖直位置时，端点A和中心点C的速度分别为
vA l 3gl
vC
l
2
1 2
3gl
J2
2
1 2
J12
刚体定轴转动的动能定理：总外力矩对刚体所做的功等于刚体转动动能
的增量。
注：
1. 刚体的转动动能
刚体的转动动能应该是组成刚体的各个质点的动能之和。
设刚体中第i个质点的质量为 mi ，速度为 vi
刚体做定轴转动时，各质点的角速度相同。
,则该质点的动能为
刚体定轴转动的势能和机械能守恒_1446
m1l 2
12m2u
(m1 3m2 )l
u(m1 3m2)
m1 3m2
4.7 刚体定轴转动的势能和机械能守恒
4.7-4一长为l，质量为m1的棒可绕O点在竖直 平面内自由转动．一质量为m2，速度为v的子 弹射入棒内不复出，射入点距O点为a．若棒
偏转过的最大角度为60°，问子弹的初速度
联立解得 v Jg(m2a0.5m1l)
m2a
4.7 刚体定轴转动的势能和机械能守恒
水平面内绕通过其中心的竖直定轴转动，开
始细棒静止．质量为m2的小球，以水平速度 u与棒的端点作弹性碰撞．求：碰后小球弹
回的速度及棒的角速度
m2
解:不考虑摩擦力矩的作用,
O
u
弹性碰撞前后: 角动量守恒 m2u2l Jm22l 机械能守恒 12m2u212J212m22
m1 l
J
1 2
运动过程中只有保守内力做功，刚体 系统的机械能仍然守恒。
4.7 刚体定轴转动的势能和机械能守恒
4.7-1如图所示，一匀质细杆，质量为m1， 长为L，可绕通过其一端的水平光滑轴O在
铅直面内转动，另一端连接一质量为m2的小
球．现将杆抬至水平，静止后释放，求杆
摆至铅直位置时杆的角速度
解：杆摆下过程机械能守恒
刚体定轴转 动的势能和 机械能守恒
4.7 刚体定轴转动的势能和机械能守恒
刚体在重力、弹性力等保守力作用 下转动,刚体定轴转动的势能为：
E p m igh i( m ih i)gii刚体质心高度
m ihi
h c i m i
得 Ep mghc
i
刚体与地球系统的重力势能，等于刚体 的质量集中于质心时系统所具有的势能。
刚体定轴转动的动能定理
它的动能为 ΔEki
1 2
Δmi vi2
1 2
Δmi
ri 2 2
整个刚体的动能为全部质元的动能之和，即 Ek
1
2
n i 1
Δmi
ri2
2
1 2
J2
式即为刚体转动动能的表达式。
刚体定轴转动的动能定理
1.3 刚体定轴转动的动能定理
将式的转动定律代入可得 dW Md J d J d d Jd
式中 ds ——位移元 dr 对应的弧长，其与对应角位移 dθ 的关系为 ds rd
刚体定轴转动的动能定理
1.1 力矩的功
于是，式可写为 dW Fτrd Md
当刚体的角位置由1 变为2 时，外力矩所做功为W
2 Md
1
式中，M 若是合外力矩，则 W 就是合外力矩的功。
刚体定轴转动的动能定理 1.2 转动动能
大学物理
刚体定轴转动的动能定理 1.1 力矩的功
如图所示，一个绕固定轴 OO 转动的圆盘状刚体，在圆盘平面上有外力 F 作用于 A 点。外力 F 可分解 为切向分力 Fτ 和法向分力 Fn 。
刚体定轴转动的动能定理 1.1 力矩的功
由于法向分力 Fn 垂直于 A 点的角位移，不做功，因此，外力 F 所做的功等于切向分力 Fτ 所做的功，则 外力 F 所做的元功为 dW F dr Fτds
静止下降 h 距离时物体的速率 v。
【解】 由题意可知，以滑轮、物体和地球组成的系统机械能守恒。
取物体在 h 处时系统的重力势能为零，设物体下降到 h 处时滑轮的角速度为 ω，
则根据机械能守恒定律可得
m2 gh
1 2
J2
1 2
m2v2
根据表可知，滑轮的转动惯量为
大学物理3_4 刚体绕定轴转动的动能定理
t 3 3 3 5 3 2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
例3 留声机的转盘绕通过盘心垂直盘面的轴以角速度 作匀速转动.放上唱片后,唱片将在摩擦力作用下随转盘一 起转动.设唱片的半径为 R 、质量为 m ,它与转盘间的摩 擦系数为 .求(1)唱片与转盘间的摩擦力矩;(2)唱片达到 角速度 需要多长时间;(3)在这段时间内,转盘的驱动力 矩作了多少功? 解 (1)如图所示,在唱片上取长为 dl 宽为 dr 的面积元 dS dldr ,该面 积元所受的摩擦力为:
1 2 1 2 1 1 1 2 2 2 2 W J J0 mR 0 mR 2 2 2 2 4
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 例3-11 一长为 l , 质量为 m0 的均质细竿可绕支点O自 由转动 . 一质量为 m、速率为 v0 的子弹射入竿内一端， 使竿的偏转角为30º 问子弹的初速率为多少 ? .
加速度
力 质量
dr v dt dv a dt
F
d 角速度 dt d 角加速度 dt
力矩
M
m
转动惯量 J
动量
P mv
角动量
L J
r
dm
2
3–4
刚体绕定轴转动的动能定理
第三章 刚体的转动
质点运动规律与刚体定轴转动的规律对照 质点的平动 刚体的定轴转动
EPB EkB EPA EkA
3–4
第三章 刚体的转动 刚体绕定轴转动的动能定理 1 2 4 2 2 J J1 J 2 ml ml ml 3 3
取A点的重力势能为零,即 则有 而
EPA 0
大学物理 习题课(刚体)
J1r1r2 10 2 2 2 J1r2 J 2 r1
11、质量为m，长为 l的均匀棒，如图， 若用水平力打击在离轴下 y 处，作用时 Ry 间为t 求：轴反力
解：轴反力设为 Rx Ry d 由转动定律： yF J y dt yF t t 为作用时间 F 得到： J 由质心运动定理： l d l 2 切向： F Rx m 法向： R y mg m 2 dt 2 2 2 2 3y 9 F y (t ) R 于是得到： x (1 ) F R y m g 2l 2l 3 m
10
r1
r2
解： 受力分析： 无竖直方向上的运动
10
o1
N1
f
r1
N2
r2
N1 f m1 g N 2 f m2 g
以O1点为参考点， 计算系统的外力矩：
o2
f
m1 g
m2 g
M ( N2 m2 g )(r1 r2 )
f (r1 r2 ) 0
作用在系统上的外力矩不为0，故系统的角动量不守恒。 只能用转动定律做此题。
r
at r
在R处：
R
at R
（2）用一根绳连接两个或多个刚体
B
C
M 2 o2 R 2
o1R1 M1
D
A
m2
m1
• 同一根绳上各点的切向加速度相同；线速度也相同；
a t A a t B a t C a t D
A B C D
• 跨过有质量的圆盘两边的绳子中的张力不相等；
TA TB TD
但 TB TC
B
C
M 2 o2 R 2
o1R1 M1
刚体的能量,定轴转动的动能定理
yi
MgyC
M
g
mi
三、转动动能
刚体绕定轴以角速度旋转 刚体的动能应为各质元动能之 和为此将刚体分割成很多很小的 质元 m , m m m
1 2 i
2 i i 2
ri M
vi m
i
1 2 2 2 E mi ri J /2 k E k i 1 2 n 1 2 2 1 Ek lim mi ri ( r 2 dm) 2 m 0 2 2 mghC mvC J 2 2
四、力矩的功、定轴转动的动能定理 设有一外力 F 作用在 + d ds 刚体上，绕 O轴作定轴 转动（ F 在垂直于轴 O 的平面内）。 M M 在时间 内刚体角位移为 dt d 力 F 作的功：
F
r
ds rd dA F ds F sin rd Md
故刚体的转动动能：
n
i
m v / 2 mi (ri ) / 2 mi ri / 2
2 2
任取一质元 mi 距转轴 ri ，则该质元动能：
n
对既有平动又有转动的刚体的动能、机械能又 如何呢？
势能零点
1 2 2 Ek 1 mvC J m、J C 2 2 C vC
其平动动能应为各质元动能和。
二、刚体的重力势能 任取一质元其势能为 m gy i i (以O为参考点）
Y
M
vC
C mi
E p mi gyi
m y M
i
i
yC
结论：刚体的重力势能决定于刚体质心距势能 X 零点的高度，与刚体的方位无关。即计算刚体 O 的重力势能只要把刚体的质量全部集中于质心 处，当一个质点处理即可（无论平动或转动）
转动动能守恒定律
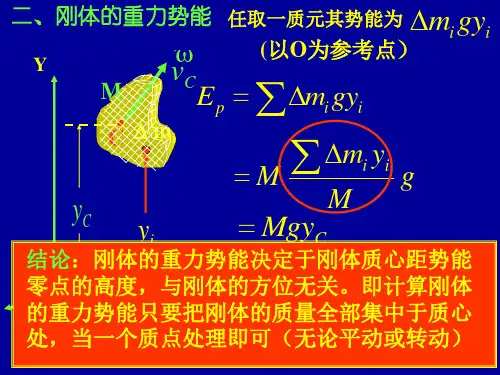
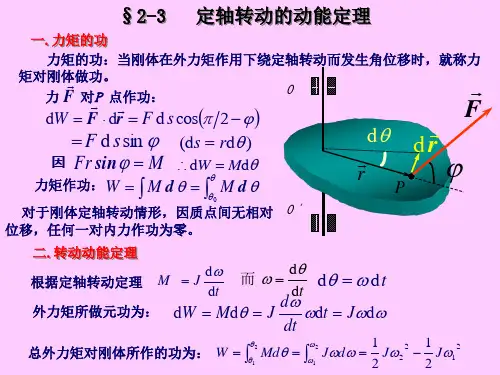
转动动能守恒定律
一、转动动能的概念
1. 对于一个绕固定轴转动的刚体，转动动能的表达式为E_{k}=(1)/(2)Iω^2，其中I是刚体对给定轴的转动惯量，ω是刚体转动的角速度。
- 转动惯量I取决于刚体的质量分布和转轴的位置。
对于一些简单形状的刚体，有特定的转动惯量计算公式。
例如，对于质量为m、半径为r的均匀圆盘，绕通过圆心垂直于盘面的轴转动时，转动惯量I = (1)/(2)mr^2；对于质量为m、长度为L的细棒，绕通过棒中心垂直于棒的轴转动时，转动惯量I=(1)/(12)mL^2。
2. 与平动动能类似，转动动能是描述刚体转动状态下具有的能量。
平动动能是(1)/(2)mv^2，这里的v是平动速度，而转动动能中的ω是角速度，反映了刚体转动的快慢。
1. 定律内容
- 如果一个刚体所受的合外力矩为零，即M = 0时，刚体的转动动能守恒，也就是(1)/(2)I_{1}ω_{1}^2=(1)/(2)I_{2}ω_{2}^2。
这意味着在转动过程中，虽然刚体的转动惯量I和角速度ω可能会发生变化，但它们的乘积Iω^2保持不变。
2. 适用条件
- 系统（刚体）所受的合外力矩为零。
这一条件类似于平动中的动量守恒定律（合外力为零）。
例如，在光滑的水平面上，一个圆盘绕中心轴转动，如果没有摩擦力矩等外力矩的作用，圆盘的转动动能守恒。
- 在一些实际问题中，需要准确分析系统的受力情况，判断是否满足合外力矩为零的条件。
例如，对于一个由多个刚体组成的系统，如果它们之间的内力矩不影响系统的总角动量（满足角动量守恒的条件下），并且系统没有受到外力矩作用，那么系统的转动动能也守恒。
3. 应用实例。
刚体力学_功 动能定理
m
.
N
R
m1
m2 解: 把m1、m2和m看作一系统 系统所受 m g 看作一系统,系统所受 看作一系统 1 m2 g 合外力有重力m 、 合外力有重力 1g、m2g,这两个力对轴 这两个力对轴 支撑力N通过转轴 的力矩分别为m 的力矩分别为 1gR、m2gR;支撑力 通过转轴 对轴的力 、 支撑力 通过转轴,对轴的力 矩为零.加上阻力矩 加上阻力矩M 系统所受合外力矩为 顺时针为正) 系统所受合外力矩为(顺时针为正 矩为零 加上阻力矩 f ,系统所受合外力矩为 顺时针为正 M=m2gR-m1gR-Mf 系统的总角动量为(顺时针为正 顺时针为正) 系统的角 m: Jω 系统的总角动量为 顺时针为正 动量包括 m1: Rm1v L=Jω+Rm1v+Rm2v m2: Rm2v
1 1 1 2 2 2 mv 0 = mv + Jω 2 2 2
的圆盘， 例 一质量为 m' 、半径为 R 的圆盘，可绕一垂 圆盘上绕有轻绳， 直通过盘心的无摩擦的水平轴转动 . 圆盘上绕有轻绳， 问物体由静止下落高度 一端挂质量为m 一端挂质量为 的物体 . 问物体由静止下落高度 h 时， 其速度的大小为多少? 其速度的大小为多少 设绳的质量忽略不计 . v 对圆盘做功， 解1 拉力 FT 对圆盘做功，由刚体绕定轴转动的动 v 能定理可得， 能定理可得，拉力 FT 的力矩所作的功为
o
圆 锥 摆
o
v θ T
'
m
v v
v p
o
v v
R
以子弹和杆为系统 守恒； 动量不守恒； 守恒； 角动量 守恒； 机械能 不守恒 .
圆锥摆系统 守恒； 动量不守恒； 对 O'O 轴角动量 守恒； 守恒； 机械能 守恒 .
定轴转动刚体的动能定理
它在水平位置
求 它由此下摆 角时的
解 定轴转动动能定理
重力矩的功 等于 直杆动能增量
Md 1 J 2 0
0
2
重力矩 M 1 mgl cos
2
O
ml
h
c
2 3g sin
l
例 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动，初始时
它在水平位置
求 它由此下摆 角时的
一. 定轴转动刚体动能
第 i 个质点的动能
Eki
1 2
mivi 2
刚体转动动能
vi ri
o ri mi
Ek
(1 2
mivi2 )
(
1 2
mi
ri22)1 2miri2 2
Ek
1 J 2
2
转动惯量 J miri2
说明
与质点动能比较 Ek
O
ml
解 机械能守恒( 以初始位置为0势能点)
h
00
=
1 J 2 mgh
2
h l sin
2
J 1 ml2 3
c
2 3g sin
l
dA dAi M id ( M i )d Md
i
i
i
三.定轴转动动能定理
• 刚体定轴转动
A外 = Ek - Ek0
A外 的力矩表示 Ek 的角量表示
A 2 Md 1
Ek
1 J 2
2
讨论 • 质点系动能变化取决于所有外力、内力做功； • 刚体的内力作功之和为零； • 刚体动能的增量，等于外力的功。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
下面是一些分析： 1．这个动能是刚体在视轴为静止的 参考系下“所有”的动能。若转轴亦运动， 求刚体的总动能只需再加上刚体关于轴速 度的动能，即
EkE定轴 1 2M 刚体 •v轴 2.
___________________________ _______________________
2．由
dEk
1 2
不规则的物体绕任意定轴转动：
dI dmd 2 .
ImNaoge dE
k
1 2
dm
•
v
2 dm
，
v
dm
d.
No
dE
k
1 2 • dmd 2
2.
Image 即
dE
k
1 2
dI
•
2.
成立。
___________________________ _______________________
这便证明了刚体定轴转动的动能 公式。
I2
可知，既然能量是线性
的，定轴转动的刚体的转动惯量也是线性
的。
3．若刚体在轴A的转动惯N量oIA已知， 由分析2及平行轴定理，将轴Im移a到gBe点时刚
体的动能为
E kB E kA 1 2M A 2Br2(rA是 BA距 B)离 .
___________________________ _______________________
2
1I2.
2
成立。
___________________________ _______________________
长为l的直细棒绕中垂线转动：
I 1 ml2 1 l3. 12 12
No
l
Image
ImNaoge Ek
2 l
1 •dl•l2
2
1 l32
24
1 I2.
2
2
成立。
___________________________ _______________________
Ｃ Ｏ
Image r1
2
1
Ｃ’
Ｑ
时，即 s m小盘 3r13 时整体来讲是节省 了能量的。 4vN
r1为小盘半径。
___________________________ _______________________
s m小盘 3r13
4vN
Ｃ
Ｏ
在实际生活中，各项数值如下：
Ｃ’
m小盘：2kg
考虑半径为Ｒ的圆环绕轴线转动：
Im2 R2R3.
Ek
21•Rd•R2
02
R32
1I2.
2
成立。
___________________________ _______________________
半径为R的圆盘绕轴线转动：
I1mR2 R4.
2
2
ImNaoge Ek
2R1•rdRd•r2
002
R42
Ｐ
2v
Ｃ’
Ｑ
其中Δf是区域P、Q的摩擦力， P、Q的圆心分别是C和C’。
___________________________ _______________________
在吸尘器模型中，设吸尘器使用距离
为s，采用开孔的底盘，增加了摩擦力，
却减少了驱动底盘转动的能量。当
No
Ｐ
2v
2vN•1•sm小盘 2r2
版权所有，商用付酬。
___________________________ _______________________
❖ 本文拟得出定轴转动下刚体 的动能表达式，并讨论教材例6.4 中电熨斗模型的改良及其他一些 简单应用。
___________________________ _______________________
Image 其中 EkxEkyEkz包含刚体质心系中刚体的动能，这里
不再推了。
___________________________ _______________________
在教材例6.4中我们知半径r、自 转角速度ω、平动速度v<< ω 、滑动 摩擦系数μ、对地面压力N的圆盘受阻 力
f v N. r
No ω：8π(4Hz)
r：0.3m
r1：0.25m v：0.2m/s
Image μ：0.3
N：5kg＊g＝50N．
Ｐ
2v
Ｑ
解得：s最大值是41.28m．这样的距离不用说 是家用吸尘器，除草都行了。因此，吸尘器底部
做成圆环更节能。
___________________________ _______________________
4．由分析2及正交轴定理可求出刚体 作定点转动的动能公式：
No E k O E k x E k y E k z 1 2 I xx 2 I yy 2 I zz 2 .
5．Im由a分ge析1～4可得刚体作任意运动
的一般的动能公式：
No E k E k x E k y E k z1 2 M v 轴 2x v 轴 2y v 轴 2z.
3
当转动周期、密度相同时，若 R 2r4 ，则I１＝I２，E１＝E２．亦即，半径ｒ的圆环与 半径Ｒ的圆柱如此旋转时有相同动能，但
定轴转动刚体的动能计算及一些 简单应用®
___________________________ _______________________
❖ 本幻灯片参考材料：
《力学》，杨维纮，中国科学技术大学０４级理 学院教材。
其他便没有了。限于客观原因，作者并没有准备 充分资源。日后若条件允许，也许能做出更有价 值的成果。
由本文前面特殊情况刚体动能公式，半径 为r，环壁厚为1(r＜＜1)的圆环与半径为R的圆 柱绕轴线转动的情况如下：
圆环I1： 2r3.E1 12I2.m1 2r1.
ImNaoge 圆柱 (盘)：I2 R 24.E2 12I2.m2 R2.
___________________________ _______________________
我们已知，定轴转动刚体的转动惯量I、角
速度ω分别与直线运动中刚体的质量M、速度v
对应，但教材上并未给出计算刚体旋转动能的
公式。我们猜想刚体的动能是否为
Ek
1 2
Iω
2
下面来证明此公式：
___________________________ _______________________
设所有刚体均匀，密度为1，则质量和体积 在数值上相等。
Ｃ Ｏ
2v
No
Ｃ’
Image
摩擦力集中在上半个月牙形内。
___________________________ _______________________
由于滑动摩擦力μN与接触面积无 关，若切去盘中心O半径为 r 2v 的小圆盘No，如图易知摩擦力增加
2fIm a2vgeN.
r1
Ｃ Ｏ
EkE定轴 1 2M 刚体 •v轴 2.
___________________________ _______________________
2．由
dEk
1 2
不规则的物体绕任意定轴转动：
dI dmd 2 .
ImNaoge dE
k
1 2
dm
•
v
2 dm
，
v
dm
d.
No
dE
k
1 2 • dmd 2
2.
Image 即
dE
k
1 2
dI
•
2.
成立。
___________________________ _______________________
这便证明了刚体定轴转动的动能 公式。
I2
可知，既然能量是线性
的，定轴转动的刚体的转动惯量也是线性
的。
3．若刚体在轴A的转动惯N量oIA已知， 由分析2及平行轴定理，将轴Im移a到gBe点时刚
体的动能为
E kB E kA 1 2M A 2Br2(rA是 BA距 B)离 .
___________________________ _______________________
2
1I2.
2
成立。
___________________________ _______________________
长为l的直细棒绕中垂线转动：
I 1 ml2 1 l3. 12 12
No
l
Image
ImNaoge Ek
2 l
1 •dl•l2
2
1 l32
24
1 I2.
2
2
成立。
___________________________ _______________________
Ｃ Ｏ
Image r1
2
1
Ｃ’
Ｑ
时，即 s m小盘 3r13 时整体来讲是节省 了能量的。 4vN
r1为小盘半径。
___________________________ _______________________
s m小盘 3r13
4vN
Ｃ
Ｏ
在实际生活中，各项数值如下：
Ｃ’
m小盘：2kg
考虑半径为Ｒ的圆环绕轴线转动：
Im2 R2R3.
Ek
21•Rd•R2
02
R32
1I2.
2
成立。
___________________________ _______________________
半径为R的圆盘绕轴线转动：
I1mR2 R4.
2
2
ImNaoge Ek
2R1•rdRd•r2
002
R42
Ｐ
2v
Ｃ’
Ｑ
其中Δf是区域P、Q的摩擦力， P、Q的圆心分别是C和C’。
___________________________ _______________________
在吸尘器模型中，设吸尘器使用距离
为s，采用开孔的底盘，增加了摩擦力，
却减少了驱动底盘转动的能量。当
No
Ｐ
2v
2vN•1•sm小盘 2r2
版权所有，商用付酬。
___________________________ _______________________
❖ 本文拟得出定轴转动下刚体 的动能表达式，并讨论教材例6.4 中电熨斗模型的改良及其他一些 简单应用。
___________________________ _______________________
Image 其中 EkxEkyEkz包含刚体质心系中刚体的动能，这里
不再推了。
___________________________ _______________________
在教材例6.4中我们知半径r、自 转角速度ω、平动速度v<< ω 、滑动 摩擦系数μ、对地面压力N的圆盘受阻 力
f v N. r
No ω：8π(4Hz)
r：0.3m
r1：0.25m v：0.2m/s
Image μ：0.3
N：5kg＊g＝50N．
Ｐ
2v
Ｑ
解得：s最大值是41.28m．这样的距离不用说 是家用吸尘器，除草都行了。因此，吸尘器底部
做成圆环更节能。
___________________________ _______________________
4．由分析2及正交轴定理可求出刚体 作定点转动的动能公式：
No E k O E k x E k y E k z 1 2 I xx 2 I yy 2 I zz 2 .
5．Im由a分ge析1～4可得刚体作任意运动
的一般的动能公式：
No E k E k x E k y E k z1 2 M v 轴 2x v 轴 2y v 轴 2z.
3
当转动周期、密度相同时，若 R 2r4 ，则I１＝I２，E１＝E２．亦即，半径ｒ的圆环与 半径Ｒ的圆柱如此旋转时有相同动能，但
定轴转动刚体的动能计算及一些 简单应用®
___________________________ _______________________
❖ 本幻灯片参考材料：
《力学》，杨维纮，中国科学技术大学０４级理 学院教材。
其他便没有了。限于客观原因，作者并没有准备 充分资源。日后若条件允许，也许能做出更有价 值的成果。
由本文前面特殊情况刚体动能公式，半径 为r，环壁厚为1(r＜＜1)的圆环与半径为R的圆 柱绕轴线转动的情况如下：
圆环I1： 2r3.E1 12I2.m1 2r1.
ImNaoge 圆柱 (盘)：I2 R 24.E2 12I2.m2 R2.
___________________________ _______________________
我们已知，定轴转动刚体的转动惯量I、角
速度ω分别与直线运动中刚体的质量M、速度v
对应，但教材上并未给出计算刚体旋转动能的
公式。我们猜想刚体的动能是否为
Ek
1 2
Iω
2
下面来证明此公式：
___________________________ _______________________
设所有刚体均匀，密度为1，则质量和体积 在数值上相等。
Ｃ Ｏ
2v
No
Ｃ’
Image
摩擦力集中在上半个月牙形内。
___________________________ _______________________
由于滑动摩擦力μN与接触面积无 关，若切去盘中心O半径为 r 2v 的小圆盘No，如图易知摩擦力增加
2fIm a2vgeN.
r1
Ｃ Ｏ