下载文档原格式
第七章面板数据模型的分析面板数据模型是一种广泛应用于计量经济学和实证研究领域的数据分析方法。
它的特点是利用了多个交叉时期和个体的数据来研究变量之间的关系，相比于截面数据模型和时间序列数据模型具有更为丰富的信息。
面板数据模型的分析可以从多个角度进行，以下是几种常见的分析方法：1.汇总统计分析：通过计算面板数据的平均值、标准差、最大值、最小值等统计量，可以对变量的总体特征进行汇总分析。
这种分析方法可以直观地了解变量的变化范围和分布情况。
2.横向分析：横向分析主要关注个体之间的差异，通过比较不同个体在同一时间点上的变量取值，可以研究个体特征、个体行为等方面的问题。
例如，可以比较不同公司在同一年份上的销售额，从而找出销售额较高或较低的公司有什么特点。
3.纵向分析：纵向分析主要关注个体随时间变化的特征，通过比较同一个体在不同时间点上的变量取值，可以研究个体的发展趋势、变化规律等方面的问题。
例如，可以比较同一家公司在不同年份上的销售额，分析销售额的增长趋势或变化原因。
4.固定效应模型：固定效应模型是面板数据模型中常用的一种建模方法。
它通过引入个体固定效应来控制个体特征对变量的影响，从而研究其他变量对个体的影响。
例如，可以研究公司规模对销售额的影响，控制掉公司固定效应后，观察销售额与公司规模的关系。
5.随机效应模型：随机效应模型是面板数据模型中另一种常用的建模方法。
它通过将个体固定效应视为随机变量，从而研究个体与时间的交互作用。
例如，可以研究公司规模对销售额的影响，同时考虑到不同公司的规模和销售额的随机波动。
6.固定效应与随机效应的比较：固定效应模型和随机效应模型分别考虑了个体固定效应和个体与时间的交互作用，它们各自有各自的优点和局限性。
通过比较两种模型的拟合优度、估计结果等指标，可以选择合适的模型来进行面板数据的分析。
7.动态面板数据模型：动态面板数据模型是对静态面板数据模型的扩展，它引入了变量的滞后项，来研究变量之间的动态关系。
回归分析RegressionAna1ysis一、课程基本信息课程编号：111093适用专业：统计学专业课程性质：专业必修开课单位：数学与数据科学学院学时：48（理论学时40；实验学时8）学分：3考核方式：考试（平时成绩占30%+考试成绩70%）中文简介：回归分析是应用统计学中一个重要的分支，在自然科学、管理科学和社会经济等领域应用十分广泛。
《回归分析》课程是统计学专业的学科专业必修课是学生掌握统计学的基本思想、理论和方法的主要课程，是培养学生熟练应用计算机软件处理统计数据的能力的基础课程。
通过本课程的学习，使学生掌握应用统计的一些基本理论与方法，初步掌握利用回归分析解决实际问题的能力。
二、教学目的与要求本课程的主要目的是学生在学习后，能够系统掌握回归分析的理论与方法，并在此基础上，掌握回归分析应用的艺术技巧，并利用其分析认识实际问题。
本课程注重回归分析的基本理论与方法，同时通过案例教学与实际应用来剖析回归分析的理论与方法所蕴含的统计思想及其应用艺术。
教学中在回归分析理论与方法的基础上结合社会、经济、自然学科学领域的研究实例，把回归分析方法与实际应用结合起来，注重定性分析与定量分析的紧密结合，强调每种方法的优缺点和实际运用中应注意的问题,研究与实践中应用回归分析的经验和体会融入其中，使学生充分体会到回归分析的应用艺术，并提高解决问题的能力。
通过本课程的学习，在理论教学过程中，可以结合国内外回归分析相关学者的研究经历和成果，传播科学研究所需要的实事求是、脚踏实地的精神，培养学生的科学素养。
在实践教学中，利用案例分析、软件仿真等方式培养学生的实践能力和创新思维，激发学生主动研究新问题和设计新方法的兴趣，让学生在实践中深刻体会科学研究的乐趣，也可以鼓励有突出能力的学生通过创新创业或成果转化为社会发展贡献年轻的力量。
三、教学方法与手段1.教学方法：课堂讲授中要重点对基本概念、基本方法和解题思路的讲解；采用启发式教学，培养学生思考问题、分析问题和解决问题的能力；引导和鼓励学生通过实践和自学获取知识，培养学生的自学能力和创新能力。
计量经济学+重点形式（3）计量经济学与经济统计学经济统计学：涉及经济数据的收集、处理、绘图、制表计量经济学：运用数据验证结论3、进行经济计量的分析步骤（P2-P3）（1）建立一个理论假说（2）收集数据（3）设定数学模型（4）设立统计或经济计量模型（5）估计经济计量模型参数（6）核查模型的适用性：模型设定检验（7）检验源自模型的假设（8）利用模型进行预测4、用于实证分析的三类数据（P3-P4）（1）时间序列数据：按时间跨度收集到的（定性数据、定量数据）；（2）截面数据：一个或多个变量在某一时点上的数据集合；（3）合并数据：包括时间序列数据和截面数据。
（一类特殊的合并数据—面板数据（纵向数据、微观面板数据）：同一个横截面单位的跨期调查数据）第二章线性回归的基本思想：双变量模型1、回归分析（P18）用于研究一个变量（称为被解释变量或应变量）与另一个或多个变量（称为解释变量或自变量）之间的关系2、回归分析的目的（P18-P19）（1）根据自变量的取值，估计应变量的均值；（2）检验（建立在经济理论基础上的）假设；（3）根据样本外自变量的取值，预测应变量的均值；（4）可同时进行上述各项分析。
3、总体回归函数（PRF）（P19-P22）（1）概念：反映了被解释变量的均值同一个或多个解释变量之间的关系（2）表达式：）①确定/非随机总体回归函数：E（Y|Xi=B1+B2XiB1：截距；B2：斜率从总体上表明了单个Y同解释变量和随机干扰项之间的关系②随机/统计总体回归函数：Yi =B1+B2Xi+μiμi：随机扰动项（随机误差项、噪声）B1+B2Xi：系统/确定性部分μi：非系统/随机部分4、随机误差项（P22）（1）定义：代表了与被解释变量Y有关但未被纳入模型变量的影响。
每一个随机误差项对于Y 的影响是非常小的，且是随机的。
随机误差项的均值为0（2）性质①误差项代表了未纳入模型变量的影响；②反映人类行为的内在随机性；③代表了度量误差；④反映了模型的次要因素，使得模型描述尽可能简单。
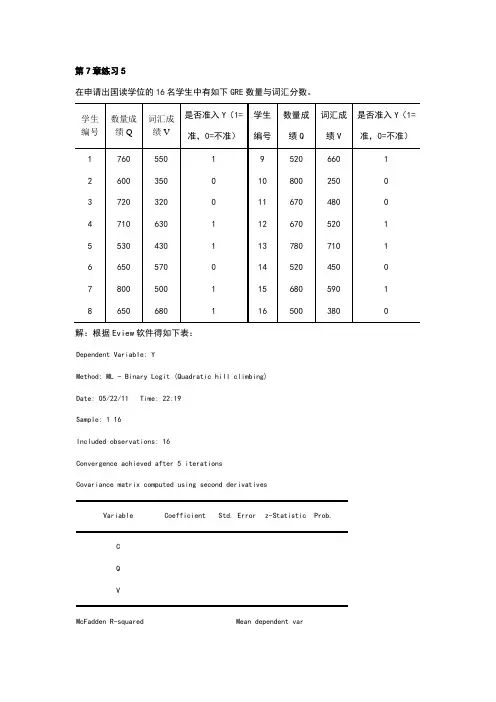
第7章练习5在申请出国读学位的16名学生中有如下GRE数量与词汇分数。
解：根据Eview软件得如下表：Dependent Variable: YMethod: ML - Binary Logit (Quadratic hill climbing)Date: 05/22/11 Time: 22:19Sample: 1 16Included observations: 16Convergence achieved after 5 iterationsCovariance matrix computed using second derivativesVariable Coefficient Std. Error z-Statistic Prob.CQVMcFadden R-squared Mean dependent var. dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterionLog likelihoodHannan-Quinn criter. Restr. loglikelihoodLR statistic Avg. log likelihoodProb(LR statistic)Obs with Dep=0 7 Total obs 16Obs with Dep=19于是，我们可得到Logit 模型为：V Q i0177.0004.0107.11Y ˆ++-= （） （） （）685.40R 2MCF = ， LR(2)=如果在Binary estination 这一栏中选择Probit 估计方法，可得到如下表：Dependent Variable: YMethod: ML - Binary Probit (Quadratic hill climbing) Date: 05/22/11 Time: 22:25 Sample: 1 16Included observations: 16Convergence achieved after 5 iterationsCovariance matrix computed using second derivativesVariable Coefficient Std. Error z-Statistic Prob.C QVMcFadden R-squared Mean dependent var . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterionLog likelihoodHannan-Quinn criter. Restr. loglikelihoodLR statistic Avg. log likelihoodProb(LR statistic)Obs with Dep=0 7 Total obs 16Obs with Dep=19于是，我们可得到Probit 模型为：V Q i0105.00024.035.66Y ˆ++-= （） （） （）763.40R 2MCF = ， LR(2)=第7章练习6下表列出了美国、加拿大、英国在1980~1999年的失业率Y 以及对制造业的补偿X 的相关数据资料。
