弦切角的性质

知能达标演练
课后习题解答
【考题2】 (2012·辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于 C， D两点，连结 DB并延长交 ⊙O于点E.
证明
(1)AC·BD＝AD·AB； (2)AC＝AE.
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
证明
(1)由 AC 与圆 O′相切于点 A， 得∠CAB＝∠ADB；
课前探究学习 课堂讲练互动 知能达标演练 课后习题解答
反思感悟
(1)弦切角是很重要的与圆相交的角．其主要功能是协
调与圆相关的各种角，如圆心角、圆周角等，是连接圆与三角形
全等、三角形相似及与圆相关的各种直线位置关系的桥梁．
(2)弦切角定理经常作为工具，进行三角形相似的证明，然后利用 三角形相似进一步确定相应边之间的关系，在圆中证明比例式或 等积式，常常需要借助于三角形相似处理． (3)弦切角定理有时还与圆周角定理等知识综合运用，它们不但在
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
解
如图所示，连接 BD.
∵AC 为⊙O 的切线，∴∠ADE＝∠ABD. ∵∠A＝∠A，∴△ADE∽△ABD， AD BD BD 2 DE 1 ∴ AE ＝DE，即DE＝1，∴BD＝2. DE 1 ∵BE 为⊙O 的直径，∴∠BDE＝90° ，∴tan∠ABD＝BD＝2. ∵∠F＋∠BEF＝90° ，∠ABD＋∠BEF＝90° ， 1 ∴∠ABD＝∠F，∴tan∠F＝tan∠ABD＝ . 2
②一边和圆相切(一边所在直线为圆的切线)；
③一边和圆相交(一边为圆的过切点的弦)． 三者缺一不可，例如图中，∠CAD很像弦切角，但它不是弦切 角，因为 AD 与圆相交， ∠ BAE 也不一定是弦切角，只有已知 AE切圆于点A，才能确定它是弦切角．

弦切角的性质
1．弦切角的定义 顶点在圆上，一边和圆相交、另一边和圆相切的角叫 做弦切角． 温馨提示 弦切角具备的三个条件：(1)顶点在圆上 (顶点为切线的切点)；(2)一边和圆相切(一边所在的直线 为圆的切线)；(3)一边和圆相交(一边为圆的过切点的弦)．
2．弦切角的性质定理 弦切角等于它所夹的弧所对的圆周角．
类型 2 利用定理求线段的长度、证明线段相等
[典例 2] 如图所示，P 是⊙O 外一点，PA 是切线， A 为切点，割线 PBC 与⊙O 相交与点 B，C，PC＝2PA， D 为 PC 的中点，AD 与延长线交⊙O 于点 E.
证明：BE＝EC.
证明：连接 AB，AC(如图)．
由题设知 PA＝PD. 故∠PAD＝∠PDA. 因为∠PDA＝∠DAC＋∠DCA， ∠PAD＝∠BAD＋解题的第一步是要准确找到 弦切角．弦切角的特点是：(1)顶点在圆上；(2)一边是圆 的弦；(3)一边与圆相切．第二步是要准确地找到弦切角 所夹的弧，再看这段弧所对的圆周角或圆心角．再结合弦 切角定理、圆周角定理进行推理证明．
2．利用弦切角解决与角有关的问题的步骤：(1)根据 图形及弦切角的定义找出与题目有关的弦切角；(2)利用 弦切角定理找出与其相等的角；(3)综合运用相关的知识 进行角的求解．
∠DCA＝∠PAB， 所以∠DAC＝∠BAD，从而B︵E＝E︵C， 因此 BE＝EC.
归纳升华 1．利用弦切角定理证明线段相等的技巧． 利用弦切角定理证明线段相等时，常常通过弦切角定 理获得角相等，然后再转化为线段相等的关系，从而解决 问题．
2．比例式(或等积式)的证明方法． 证明比例式(或等积式)成立，往往与相似三角形有 关，若存在切线，常要寻找弦切角．确定三角形相似，有 时需要添加辅助线创造条件．

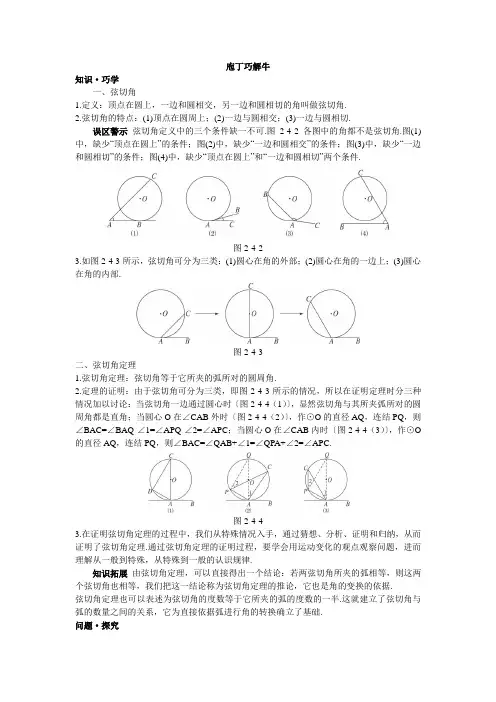
庖丁巧解牛知识·巧学一、弦切角1.定义：顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角.2.弦切角的特点：(1)顶点在圆周上；(2)一边与圆相交；(3)一边与圆相切.误区警示弦切角定义中的三个条件缺一不可.图2-4-2各图中的角都不是弦切角.图(1)中，缺少“顶点在圆上”的条件；图(2)中，缺少“一边和圆相交”的条件；图(3)中，缺少“一边和圆相切”的条件；图(4)中，缺少“顶点在圆上”和“一边和圆相切”两个条件.图2-4-23.如图2-4-3所示，弦切角可分为三类：(1)圆心在角的外部；(2)圆心在角的一边上；(3)圆心在角的内部.图2-4-3二、弦切角定理1.弦切角定理：弦切角等于它所夹的弧所对的圆周角.2.定理的证明：由于弦切角可分为三类，即图2-4-3所示的情况，所以在证明定理时分三种情况加以讨论：当弦切角一边通过圆心时〔图2-4-4（1）〕，显然弦切角与其所夹弧所对的圆周角都是直角；当圆心O在∠CAB外时〔图2-4-4（2）〕，作⊙O的直径AQ，连结PQ，则∠BAC=∠BAQ-∠1=∠APQ-∠2=∠APC；当圆心O在∠CAB内时〔图2-4-4（3）〕，作⊙O 的直径AQ，连结PQ，则∠BAC=∠QAB+∠1=∠QPA+∠2=∠APC.图2-4-43.在证明弦切角定理的过程中，我们从特殊情况入手，通过猜想、分析、证明和归纳，从而证明了弦切角定理.通过弦切角定理的证明过程，要学会用运动变化的观点观察问题，进而理解从一般到特殊，从特殊到一般的认识规律.知识拓展由弦切角定理，可以直接得出一个结论：若两弦切角所夹的弧相等，则这两个弦切角也相等，我们把这一结论称为弦切角定理的推论，它也是角的变换的依据.弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半.这就建立了弦切角与弧的数量之间的关系，它为直接依据弧进行角的转换确立了基础.问题·探究问题到目前为止，对于圆中有关的角我们已学过圆心角、圆周角、弦切角，它们各自有定义、定理及和它所对的弧的度数关系，这三种角在证明题和计算题中经常用到，它们是几何综合题中不可缺少的知识点.它们相互之间有哪些联系和区别？如何把握这些联系和区别？思路:从理解圆心角、圆周角、弦切角的定义、定理及与所对、所夹的弧的关系入手思考.探究:圆心角、圆周角、弦切角是圆中三类重要的角，准确理解它们的定义、定理及与所对、所夹的弧的关系，对于我们在圆中的计算、证明，起着举足轻重的作用，将这些知识总结对比列表如下，的度数典题·热题例1如图2-4-5，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB 与⊙O相交于点E，AE平分∠CAB，且AE=2，求△ABC各边的长.J图2-4-5思路分析：∠BAE为弦切角，于是∠BAE=∠C，再由AE平分∠CAB和△ABC是直角三角形可得∠C的度数，进而解直角三角形即可.解：∵AD为⊙O的切线，∴∠BAE=∠C.∵AE平分∠CAB，∴∠BAC=2∠BAE.又∵∠C+∠BAC=90°，∴∠BAE=∠C=30°.2.则有BE=1，AB=3，BC=3，AC=3深化升华本题应用弦切角、解直角三角形的知识,为基础题型，求解此类题时，要注意弦切角在角的转换中的作用，本题正是由于这一条件，沟通了角之间的数量关系.例2如图2-4-6，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F.求证：EF∥BC.图2-4-6思路分析：连结DF，构造弦切角，于是∠FDC=∠DAC，根据AD是△ABC中∠BAC的平分线,得∠BAD=∠DAC，而∠BAD与∠EFD对着同一段弧，所以相等，由此建立∠EFD与∠FDC的相等关系，根据内错角相等，可以断定两直线平行.证明：连结DF.∵AD是∠BAC的平分线，∴∠BAD=∠DAC.∵∠EFD=∠BAD，∴∠EFD=∠DAC.∵⊙O切BC于D，∴∠FDC=∠DAC.∴∠EFD=∠FDC.∴EF∥BC.方法归纳证明两条直线平行的方法有：（1）内错角相等，两直线平行；（2）同位角相等，两直线平行；（3）同旁内角互补，两直线平行等.证题时可以根据图形与已知合理选择.本题由于有切线，所以考虑弦切角和它所对的圆周角.例3如图2-4-7，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，弦BD∥XY，AC、BD相交于点E.图2-4-7（1）求证：△ABE≌△ACD；（2）若AB=6 cm，BC=4 cm，求AE的长.思路分析：第（1）问中的全等已经具备了AB=AC，再利用弦切角定理与圆周角定理可以得角的相等关系；对于（2），则利用△BCE∽△ACB建立比例式，解方程获得AE的长.（1）证明：∵XY 是⊙O 的切线，∴∠1=∠2. ∵BD ∥XY ，∴∠1=∠3.∴∠2=∠3. ∵∠3=∠4，∴∠2=∠4.∵∠ABD=∠ACD ，又∵AB=AC ，∴△ABE ≌△ACD.（2）解：∵∠3=∠2，∠BCE=∠ACB ，∴△BCE ∽△ACB. ∴CBCEAC BC . ∴AC·CE=BC 2，即AC·(AC-AE)=BC 2. ∵AB=AC=6，BC=4，∴6(6-AE)=16. ∴AE=310（cm ）. 深化升华 本题利用平行线、弦切角、圆周角等进行了角的转换，利用相似建立方程求线段的长度，综合应用时，必须非常熟悉图形中的各个量，盯准要求的数值，向图形和已知索取条件.。

结合(1)的结论知，AC＝AE.
【名师点评】 比例式(或乘积式)的证明方法： 证明乘积式成立，往往与相似三角形有关，若存在切线，常
要寻找弦切角，确定三角形相似的条件，有时需要添加辅助
线创造条件． 注意：直接证明比例式或乘积式有困难时，可考虑把它分解 成两个比例式的形式．
即 BC2＝BE·CD.
考点二 利用弦切角定理证明乘积式 例2 如图，⊙O 和⊙O′相交于 A，B 两点，过 A 作两圆的切 线分别交两圆于 C，D 两点，连接 DB 并延长交⊙O 于点 E. 证明：
(1)AC·BD＝AD ·AB ； (2)AC＝AE .
【证明】 (1)由 AC 与⊙O′相切于 A，得∠CAB＝∠ADB， 同理∠ACB＝∠DAB， 所以△ACB∽△DAB.从而AACD＝BADB， 即 AC·BD＝AD·AB. (2)由 AD 与⊙O 相切于 A，得∠AED＝∠BAD. 又∠ADE＝∠BDA， 得△EAD∽△ABD.从而AAEB＝ABDD， 即 AE·BD＝AD·AB.
弦切角的性质
1．弦切角 顶点在圆上，一边和圆_相__交__，另一边和圆_相__切__的角叫做弦
切角．
2．弦切角定理 弦切角等于它___所__夹__的__弧__所__对__的__圆__周__角___．
考点突破
考点一 弦切角性质的简单应用
例1
︵︵ 如图，已知圆上的弧 AC＝BD，过 C 点的圆的切线与 BA
的延长线交ቤተ መጻሕፍቲ ባይዱ E 点，证明：
(1)∠ACE＝∠BCD；
(2)BC2＝BE·CD.
︵︵ 【证明】 (1)因为 AC＝BD， 所以∠BCD＝∠ABC. 又因为 EC 与圆相切于点 C，故∠ACE＝∠ABC， 所以∠ACE＝∠BCD. (2)因为∠CDB＝∠ECB， ∠BCD＝∠EBC， 所以△BDC∽△ECB，故BBCE＝CBDC，

∵AB为☉O的直径,∴∠ADB=90°.
∴∠E=∠ADB,

∴△ADE∽△BAD, ∴ = ,
∴AD2=AB·DE.
∵CD∥AB,∴∠1=∠2,∠3=∠4.
∵∠2=∠4,∴∠1=∠3,
∴ = ,
∴AD=BC,∴BC2=AB·DE.
题型一
题型二
题型三
题型三
易错辨析
易错点:忽视弦切角的一边是切线致错
【例3】 如图,△ABC内接于☉O,AD⊥AC,∠C=32°,∠B=110°,
则∠BAD=
.
错解:∵AD⊥AC,
∴∠BAD是弦切角.
∴∠BAD=∠C.
又∠C=32°,∴∠BAD=32°.
错因分析:错解Βιβλιοθήκη ,误认为∠BAD是弦切角.虽然AD⊥AC,但AD不
是切线.
题型一
题型二
题型三
正解:∵∠C+∠B+∠BAC=180°,
和圆周角定理得到角相等,再通过三角形相似得到成比例线段.
题型一
题型二
题型三
【变式训练2】 如图,AB为☉O的直径,弦CD∥AB,AE切☉O于点A,
交CD的延长线于点E.求证:BC2=AB·DE.
证明:如图,连接BD,OD,OC.
∵AE切☉O于点A,∴∠EAD=∠ABD,
且AE⊥AB.又AB∥CD,∴AE⊥CE,∴∠E=90°.
∴∠BAC=180°-∠C-∠B=38°.
又AD⊥AC,∴∠BAC+∠BAD=90°.
∴∠BAD=90°-∠BAC=90°-38°=52°.
答案:52°
反思在利用弦切角定理解决问题时,要注意所涉及的角是不是弦
切角,即弦切角的三个条件缺一不可.

D 化归 A
B
A C
弦切角
E
C
E
∵∠DAC=∠DCE=90° 且 ∠DAB=∠DCB ∴∠BAC= 90°+ ∠DAB = 90°+ ∠DCB = ∠BCE ∴∠BAC = ∠BCE
弦切角性质定理：
弦切角等于它所夹的弧 对的圆周角．
例题分析
例1：如图，已知AB是⊙O的直径，AC是弦，直线 CE和⊙O切于点C，AD⊥CE，垂足为D. 求证： AC平分∠BAD． 分析： 要证AC平分∠BAD 即证∠1＝∠2 可证这两角所在的直角三 角形相似。 于是连结BC，得Rt△ACB
2.4弦切角的性质
复习回顾
下图圆中的∠BAC和∠BOC分别是什么角？
圆周角
圆周角定理 : 圆上一条弧所 对的圆周角等于其所对圆心 角的一半.
A
圆心角
O B
C
p
B
A
p
B A
p
B
A
p
B
A
p
B
A
p B
A
p
B
A
概念解读：
顶点在圆上，一边与圆相交，另一边与圆相切的 p 角叫做弦切角。(如∠BPA)
B O 1
∟
2
A D
E
C
由弦切角性质 ∠ACD＝∠B ，故结论得证
解：连结BC ∵ AD⊥CE， AB是⊙O的 直径 ∴∠BCA=∠ADC=90°
B O 1 2 D A
又∵CD与圆相切
由弦切角性质∠ACD=∠ABC ∴RT△ACB ~ RT△ADB
E
C
∴∠1=∠2
∴AC平分∠BAD
思路二： 连结OC
B O
3

两边都和圆相交
的 关 系
交
一边和圆相交
2.与弦切角定理有关的结论
(1)弦切角的度数等于它所夹的弧的度数的一半.
(2)弦切角的度数等于它所夹的弧所对的圆心角度数的一半.
(3)如果两个弦切角所夹的弧相等,那么这两个弦切角也相等.
【做一做2】 如图,正三角形ABC内接于圆O,CP是圆O的切线,则
∠ACP=(
错用弦切角定理致误
【典例】 如图,以△ABD的边AB为直径,作半圆O交AD于C,过点C
的切线CE和BD互相垂直,垂足为E,延长EC到F.求证:AB=BD.
错解:如图,连接BC,OC.
∵CE是半圆O的切线,
∴∠DCE=∠CBE,OC⊥CE.
又BD⊥CE,∴OC∥BD,
∴∠CBE=∠BCO,
∴∠DCE=∠BCO.
弦切角的性质
1.弦切角的概念
定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切
角.
如图,∠ACD和∠BCD都是弦切角.
名师点拨1.弦切角的分类:
(1)圆心在角的一边上(如图a);(2)圆心在角的内部(如图b);(3)圆心
在角的外部(如图c).
2.弦切角的条件:
(1)顶点在圆上(顶点为圆切线的切点);(2)一边和圆相切(一边所
∵AB为半圆O的直径,∴AD⊥BC,
∴∠BAC=90°-∠CBA.
又BD⊥CE,∴∠D=90°-∠DCE,
∴∠D=∠BAC,∴AB=BD.
纠错心得弦切角是顶点在圆上,一边与圆相交,另一边与圆相切
的角,其中弦切角的顶点是圆的一条切线与圆的切点,一边是过切
点的圆的一条弦所在的射线,另一边是过切点的圆的一条切线.本
于弦CD可证.
证明:如图,连接BC.

弦切角弦切角是指一个角的两边分别与弦和切线相交的情况。

在几何学中，弦切角有着重要的应用。

本文将讨论弦切角的定义、性质以及一些常见的应用。

定义在一个圆上，将一个角的两边分别与圆的弦和切线相交，这个角就被称为弦切角。

弦切角的定义可以用以下形式表示：设圆上一点O，P是圆上点O的切点，A 是圆上点O的一个切点外的点，如果线段OP是圆的弦，并且∠APO是一个角，则∠APO就是弦切角。

性质弦切角具有一些重要的性质，下面将介绍其中的几个性质。

性质1：弦切角等于其对向的圆心角如果一条弦切角的顶点不在圆上，则这个弦切角的度数等于其对向的圆心角的度数。

这是因为在圆上，切线和切点相切的性质使得切线和弦的夹角与切线和切点的夹角相等。

性质2：弦切角的度数不随弦的长度改变当弦的两个端点固定时，弦切角的度数不会随弦的长度的变化而改变。

这可以通过角度保持不变的定义来解释，即角∠APO保持不变。

性质3：切线与弦切角的夹角等于弦与切线的夹角的补角如果∠APO是一个弦切角，切线AO与弦AP的夹角是α，那么切线AO与弦AP的夹角的补角与弦切角的度数相等。

这可以通过证明∠APO和∠AOB为补角来得到，其中∠AOB是切线和弦的夹角。

应用弦切角在几何学中有着重要的应用。

下面将介绍几个常见的应用。

应用1：求解弦的长度已知弦切角和圆的半径，可以利用三角函数求解弦的长度。

设弦的长度为x，半径为r，弦切角的度数为θ，则有以下关系：sin(θ/2) = x / (2 * r)通过解这个方程，可以求得弦的长度x。

应用2：计算圆心角的度数已知一个弦切角的度数和弦的长度，可以通过利用角度保持不变的性质计算圆心角的度数。

设弦切角的度数为θ，弦的长度为x，圆心角的度数为α，则有以下关系：2 * α = θ通过解这个方程，可以求得圆心角的度数α。

应用3：应用于三角函数的证明在三角函数的证明中，经常会用到圆的弦切角。

通过引入弦切角，可以推导出各种三角函数的等式和性质。

︵
连接 EF 并延长交⊙O 于点 A，求证：点 A 是BC 的中点．
[思路点拨] (1)由切线的性质定理，知△PCF 是等腰直角 三角形，因此求出 CF 的长，进而求出半径；
(2)中，利用弦切角定理，可以求出两个三角形中，有一组
︵︵
角相等，然后利用相似三角形的判定及性质，可证出AC 与AB
︵
所对的圆周角相等，从而证出点 A 是BC 的中点．
如图所示，因为∠BDE 与∠BED 所夹的弧是同一个弧，所
以∠BDE＝∠BED；
︵
︵
如 果 EM ＝ DM
__∠__C_E_M__＝__∠__A_D__M___.
，也可以得出
利用弦切角解决与角有关的问题
如 图 甲 ， 在 △ABC 中 ， ∠B ＝ 90° ， O 是 AB 上 一 点，以O为圆心，OB为半径的圆与AB交于点E，与AC切于点 D，直线ED交BC的延长线于F.若AD∶AE＝2∶1，求tan∠F.
[思路点拨]
[解题过程] 如图乙所示，连接 BD．
∵AC 为⊙O 的切线，∴∠1＝∠2. ∵∠A＝∠A，∴△ADE∽△ABD， ∴AADE＝BDDE，即BDDE＝21，∴DBDE＝12. ∵BE 为⊙O 的直径，∴∠BDE＝90°，∴tan∠2＝DBDE＝12. ∵∠F＋∠BEF＝90°，∠2＋∠BEF＝90°， ∴∠2＝∠F，∴tan∠F＝tan∠2＝12.
3．弦切角定理 (1)文字语言叙述 弦切角等于它_所__夹__的__弧___所对的圆周角． (2)图形语言叙述
如图，AB与⊙O切于A点，则∠BAC＝__∠__D___．
4．与弦切角定理有关的结论 (1)弦切角的度数等于它__所__夹__的__弧__的__度__数__的__一__半__． (2)弦切角的度数等于它__所__夹__的__弧__所__对__的__圆__心__角__度__数__的___ _一__半_____． (3) 如 果 两 个 弦 切 角 所 夹 的 __弧__相__等____ ， 那 么 这 两 个 __弦__切__角__也__相__等____．

优化教学：弦切角数学教案第一章：弦切角的定义与性质1.1 弦切角的定义引入圆的弦和切线的概念解释弦切角的定义：从圆上某点引出一条切线，圆上与此切线相交的弦所对的圆心角称为弦切角1.2 弦切角的性质演示弦切角的性质：弦切角等于其所对圆弧的一半解释弦切角的度数与圆的半径和弦的长度有关第二章：弦切角的计算2.1 基本弦切角公式介绍弦切角的基本计算公式：弦切角= 圆心角的一半解释弦切角的大小与圆的半径和弦的长度有关2.2 应用弦切角公式解题举例说明如何使用弦切角公式计算不同情况下的弦切角练习题目：给出圆的半径和弦的长度，求解弦切角的大小第三章：弦切角的应用3.1 弦切角与圆的切割解释弦切角在圆的切割中的应用：通过弦切角可以确定切割线的位置和方向演示如何利用弦切角计算圆的切割线长度和切割角度3.2 弦切角与圆的对称性介绍弦切角与圆的对称性：弦切角关于圆心对称解释弦切角在圆的对称性中的应用：通过弦切角可以确定圆的对称轴和对应角第四章：弦切角与圆的相交4.1 弦切角与圆相交的性质解释弦切角与圆相交的性质：弦切角等于相交弦所对圆心角的一半演示弦切角与圆相交的性质，并给出证明4.2 弦切角与圆相交的应用举例说明如何利用弦切角与圆相交的性质解决几何问题练习题目：给出弦和圆的位置关系，求解弦切角的大小第五章：弦切角的综合应用5.1 弦切角在几何证明中的应用介绍弦切角在几何证明中的应用：利用弦切角的性质和计算公式证明几何定理演示如何使用弦切角证明几何定理，并给出示例5.2 弦切角在实际问题中的应用解释弦切角在实际问题中的应用：通过弦切角可以解决圆的切割、对称性和相交等问题举例说明如何利用弦切角解决实际问题，并提供练习题目供学生练习第六章：弦切角与圆的相交弦6.1 弦切角与相交弦的关系解释弦切角与相交弦的关系：弦切角等于相交弦所对圆心角的一半演示弦切角与相交弦的位置关系，并给出证明6.2 应用弦切角与相交弦解决几何问题举例说明如何利用弦切角与相交弦的关系解决几何问题练习题目：给出弦和相交弦的位置关系，求解弦切角的大小第七章：弦切角与圆的割线7.1 弦切角与割线的关系解释弦切角与割线的关系：弦切角等于割线与圆的切点所对圆心角的一半演示弦切角与割线的位置关系，并给出证明7.2 应用弦切角与割线解决几何问题举例说明如何利用弦切角与割线的关系解决几何问题练习题目：给出割线与圆的切点，求解弦切角的大小第八章：弦切角与圆的切线8.1 弦切角与切线的关系解释弦切角与切线的关系：弦切角等于切线与圆的切点所对圆心角的一半演示弦切角与切线的位置关系，并给出证明8.2 应用弦切角与切线解决几何问题举例说明如何利用弦切角与切线的关系解决几何问题练习题目：给出切线与圆的切点，求解弦切角的大小第九章：弦切角与圆的割线和切线的综合应用9.1 弦切角与割线和切线的综合应用解释弦切角在割线和切线中的综合应用：通过弦切角可以解决割线和切线与圆的位置关系问题演示如何利用弦切角解决割线和切线与圆的综合问题，并给出示例9.2 应用弦切角解决实际问题解释弦切角在实际问题中的应用：通过弦切角可以解决圆的切割、对称性和相交等问题举例说明如何利用弦切角解决实际问题，并提供练习题目供学生练习第十章：弦切角的复习与拓展10.1 弦切角的复习复习弦切角的定义、性质、计算和应用给出复习题目，帮助学生巩固弦切角的知识10.2 弦切角的拓展介绍弦切角的拓展知识：弦切角与其他几何概念的关系，如圆心角、相交弦、割线和切线等给出拓展题目，引导学生深入研究弦切角的相关知识重点和难点解析一、弦切角的定义与性质环节解析：理解弦切角的基本概念是学习弦切角计算和应用的基础。

提示：弦切角等于它所夹的弧所对的圆心角的一半．
[研一题] [例1] 如图，AB、CB分别切⊙O于D、
E，试写出图中所有的弦切角． 分析：本题考查弦切角的定义．解答本 题需要明确构成弦切角的三个条件，然后依
据定义作出判断．
解：由弦切角的定义可知， ∠ADE、∠BDE、∠BED、∠CED都是弦切角．
[悟一法]
∴∠EFB＝90°.
连接BC，则∠ECB＝90°， ∴E、F、B、C四点共圆．
∴AE· AC＝AF· AB.①
同理A、D、E、F四点共圆． ∴BE· BD＝BF· AB.②
将①、②两式相加得
AF· AB＋BF· AB＝AE· AC＋BE· BD＝AB2.
弦切角定理在几何证明中有广泛的应用，高考中 常与三角形相似、圆的切线等问题结合考查.2012年辽 宁高考以解答题的形式将弦切角定理与相似三角形的 判定及应用相结合考查，是高考命题的一个新亮点．
[考题印证] (2012· 辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于C，D两点，连结DB并延长
交⊙O于点E.证明：
(1)AC· BD＝AD· AB； (2)AC＝AE.
[命题立意]
本题主要考查弦切角定理，考查学生综合
运用所学知识，分析问题并解决问题的能力．
证明：(1)由 AC 与⊙O′相切于 A， 得∠CAB＝∠ADB， 同理∠ACB＝∠DAB， 所以△ACB∽△DAB. AC AB 从而AD＝BD， 即 AC· BD＝AD· AB. (2)由 AD 与⊙O 相切于 A，得∠AED＝∠BAD， 又∠ADE＝∠BDA，得 AE AD △EAD∽△ABD.从而AB＝BD， 即 AE· BD＝AD· AB. 结合(1)的结论，AC＝AE.

E
C
D
当堂检测： 课本P34，习题2.4：1.
课后作业： 课本P34，习题2.4：2
创设情景 以旧探新
问题1：
在前面我们共同研究过与圆有关的哪两种角？
圆心角和圆周角 问题2：
什么是圆心角和圆周角？同弧所对的圆心角和圆 周角之间有什么关系？
B
1 ∠BAC= ∠BOC 2
A
C O
弦切角
弦切角定义：顶点在圆上,一边与圆相交、另一边
与圆相切的角叫弦切角.
B C O A O O B B
C
⊙O的切线，则∠BCE= ∠ A.
C O Ａ

Ｅ
C O
Ｅ
C O
Ｅ
Ｂ
Ａ
Ｂ
Ａ Ｂ
分析：延用从特殊到一般的思路。先分析△ ABC 为直角三角形时的情形，再将锐角三角形和钝角 三角形的情形化归为直角三角形的情形。
2.弦切角定理
弦切角等于它所夹的弧所对的圆周角。
D Ｃ
Ｏ
Ａ
m
Ｂ
几何语言:
BA切⊙O于A
AC是圆O的弦
∠BAC= ∠ADC
练一练
已知AB是⊙O的切线,A为切点，由图填空：
30º
O
70ºO2O8º31A
B
25º
4
A
B
A
B
∠1= 30º ；∠2= 70º ；∠3= 65º ；∠4= 40º 。
例1.如图已知AB是⊙O的直径,AC是弦, 直线CE和⊙O切于点C,AD⊥CE,垂足为D. 求证:AC平分∠BAD.
(C A E ) ∠BAE的特征：(1) 顶点在圆上； (2) 一边和圆相交； A (3) 另一边和圆相切。
观察

1．把证明线段相等转化为证明角的相等是弦切角定理 应用的常见题目．
2．利用弦切角定理进行计算、证明，要特别注意弦切 角所夹弧所对的圆周角，有时与圆的直径所对的圆周角结合 运用，同时要注意根据题目的需要可添加辅助线构成所需要 的弦切角．
如图 2－4－4，PA、PB 是⊙O 的切线，点 C 在 AB 上，CD⊥AB，CE⊥PA，CF⊥PB，垂足分别为 D、E、F， 求证：CD2＝CE·CF.
弦切角的性质
1．弦切角 顶点在 圆 上，一边和圆相交 、另一边和圆 相切 的角 叫做弦切角． 2．弦切角定理 (1)文字语言叙述： 弦切角等于它 所夹的弧 所对的圆周角．
(2)图形语言叙述： 如图 2－4－1，AB 与⊙O 切于 A 点，则∠BAC＝∠D .
图 2－4－1
如图 2－4－2，AB 是半圆 O 的直径，C 是圆周上一点(异 于 A、B)，过 C 作圆 O 的切线 l，过 A 作直线 l 的垂线 AD， 垂足为 D，AD 交半圆】 解答本题的关键是运用弦切角定理与圆 周角定理的有关知识，进行角度的等量替换．
【自主解答】 连接 AC，BE，在 DC 延长线上取一点 F，因为 AB 是半 圆 O 的直径，C 为圆周上一点， 所以∠ACB＝90°，即∠BCF＋∠ACD＝90° 又因为 AD⊥l，所以∠DAC＋∠ACD＝90° 所以∠BCF＝∠DAC 又因为直线 l 是圆 O 的切线，所以∠CEB＝∠BCF， 又∠DAC＝∠CBE，所以∠CBE＝∠CEB，∴CB＝CE.
图 2－4－4
【思路探究】
【自主解答】 连接 CA、CB. ∵PA、PB 是⊙O 的切线． ∴∠CAP＝∠CBA，∠CBP＝∠CAB. 又 CD⊥AB，CE⊥PA，CF⊥PB， ∴Rt△CAE∽Rt△CBD， Rt△CBF∽Rt△CAD， ∴CCAB＝CCDE ，CCBA＝CCDF ， ∴CCDE＝CCDF，即 CD2＝CE·CF.

弦切角(一)引言在几何学中，弦切角是指一个角落在圆的内部，其两边分别与圆的弦和切线相交。

弦切角在解决与圆相关的几何问题时经常出现。

本文将介绍弦切角的定义、性质以及应用。

弦切角的定义弦切角的定义是一个角，其两边分别与圆的弦和切线相交。

具体来说，如果角ABC是一个弦切角，那么点A和点C位于圆上，点B位于圆的圆周上的一点，线段AC是圆上的一条弦，而线段BC是与圆相切的切线。

弦切角的性质对于弦切角，有以下几个重要性质：1.弦切角的两边互补，即角ABC和角CBA的和为180度。

2.弧角定理适用于弦切角，即弦切角的一半等于它所对应的圆弧的一半。

即角ABC的一半等于圆弧AC的一半。

3.弦切角的顶点处于圆上，弦切角的两边与弦和切线相交于圆上的两点。

4.弦切角的两边及其对应的圆心角相等，即角ABC与其所对应的圆心角OAC 相等。

弦切角的应用弦切角在几何学中有着广泛的应用。

下面介绍一些弦切角的常见应用场景：1. 弦长的计算在计算圆上弦的长度时，可以利用弦切角的概念。

通过已知弦长和对应的弦切角，可以使用正弦函数来计算弦的长度。

具体的计算公式如下：弦长 = 2 * 半径 * sin(弦切角/2)2. 圆内接多边形的角度关系当一个多边形的顶点位于圆上，并且多边形边的某一边是圆的切线时，可以利用弦切角来计算多边形的各个角度。

通过弦切角的性质，可以得到多边形顶点对应的圆心角的度数，从而计算出多边形的各个角度。

3. 圆上弦的角度关系当一条弦与圆的直径垂直时，可以利用弦切角的性质计算该弦与圆的直径之间的夹角。

通过弦切角的性质，可以得到该夹角的度数，从而计算出圆弧与圆的直径之间的夹角。

结论弦切角是解决与圆相关几何问题时常用的概念。

通过弦切角的定义和性质，我们可以计算弦的长度，求解圆内接多边形的角度关系，以及计算圆上弦的角度关系。

在实际应用中，弦切角可以帮助我们更好地理解和解决与圆相关的几何问题。

注意：本文为纯文本格式，无法显示图片和网址。

四弦切角的性质[对应学生用书P28]弦切角定理(1)文字语言叙述：弦切角等于它所夹的弧所对的圆周角．(2)图形语言叙述：如图，AB与⊙O切于A点，则∠BAC＝∠D.[说明]弦切角的度数等于它所夹弧度数的一半，圆周角的度数等于它所对的弧的度数的一半，圆心角的度数等于它所对弧的度数．[对应学生用书P29]弦切角定理[例1](2010·新课标全国卷)如图，已知圆上的弧AC＝BD，过C点的圆的切线与BA的延长线交于E点，证明：(1)∠ACE＝∠BCD；(2)BC2＝BE·CD.[思路点拨]利用弦切角定理．[证明](1)因为AC＝BD，所以∠BCD＝∠ABC.又因为EC与圆相切于点C，故∠ACE＝∠ABC，所以∠ACE＝∠BCD.(2)因为∠ECB＝∠CDB，∠EBC＝∠BCD，所以△BDC∽△ECB.故BCBE＝CDBC，即BC2＝BE·CD.利用弦切角定理进行计算、证明，要特别注意弦切角所夹弧所对的圆周角，有时与圆的直径所对的圆周角结合运用，同时要注意根据题目的需要可添加辅助线构成所需要的弦切角．1．如图，AB为⊙O的直径，直线EF切⊙O于C，若∠BAC＝56°，则∠ECA＝________.解析：连接BC，∵AB为⊙O的直径，∴∠ACB＝90°.∴∠B＝90°－∠BAC＝90°－56°＝34°.又∵EF与⊙O相切于点C，由弦切角定理，有∠ECA＝∠B＝34°.答案：34°2.如图，AB是⊙O的弦，CD是经过⊙O上的点M的切线，求证：(1)如果AB∥CD，那么AM＝MB；(2)如果AM＝BM，那么AB∥CD.证明：(1)∵CD切⊙O于M点，∴∠DMB＝∠A，∠CMA＝∠B.∵AB∥CD，∴∠CMA＝∠A.∴∠A＝∠B，故AM＝MB.(2)∵AM＝BM，∴∠A＝∠B.∵CD切⊙O于M点，∠CMA＝∠B，∴∠CMA＝∠A.∴AB∥CD.3．如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB.(1)求证：AD⊥CD；(2)若AD＝2，AC＝5，求AB的长．解：(1)证明：如图，连接BC.∵直线CD与⊙O相切于点C，∴∠DCA＝∠B.∵AC平分∠DAB，∴∠DAC＝∠CAB.∴∠ADC＝∠ACB.∵AB为⊙O的直径，∴∠ACB＝90°.∴∠ADC＝90°，即AD⊥CD.(2)∵∠DCA ＝∠B ，∠DAC ＝∠CAB ， ∴△ADC ∽△ACB . ∴AD AC ＝AC AB， ∴AC 2＝AD ·AB .∵AD ＝2，AC ＝5，∴AB ＝52.运用弦切角定理证明比例式或乘积式[例2] 如图，P A ，PB 是⊙O 的切线，点C 在AB 上，CD ⊥AB ，CE ⊥P A ，CF ⊥PB ，垂足分别为D ，E ，F .求证：CD 2＝CE ·CF . [思路点拨]连接CA 、CB ，∠CAP ＝∠CBA 、∠CBP ＝∠CAB→Rt △CAE ∽Rt △CBD Rt △CBF ∽Rt △CAD→CE CD ＝CDCF→结论 [证明] 连接CA 、CB . ∵P A 、PB 是⊙O 的切线， ∴∠CAP ＝∠CBA ， ∠CBP ＝∠CAB .又CD ⊥AB ，CE ⊥P A ，CF ⊥PB ， ∴Rt △CAE ∽Rt △CBD ， Rt △CBF ∽Rt △CAD ， ∴CA CB ＝CE CD ，CB CA ＝CFCD ， ∴CE CD ＝CDCF，即CD 2＝CE ·CF .证明乘积式成立，往往与相似三角形有关，若存在切线，常要寻找弦切角，确定三角形相似的条件，有时需要添加辅助线创造条件．4．如图，已知MN 是⊙O 的切线，A 为切点，MN 平行于弦CD ，弦AB 交CD 于E .求证：AC 2＝AE ·AB .证明：连接BC .⎭⎪⎬⎪⎫MN ∥CD ⇒∠MAC ＝∠ACD MN 切⊙O 于A ⇒∠MAC ＝∠B⎭⎪⎬⎪⎫⇒∠ACD ＝∠B ∠CAE ＝∠CAB ⇒△ACE ∽△ABC⇒AC AB ＝AEAC⇒AC 2＝AB ·AE .5．如图，AD 是△ABC 的角平分线，经过点A 、D 的⊙O 和BC 切于D ，且AB 、AC 与⊙O 相交于点E 、F ，连接DF ，EF .(1)求证：EF ∥BC ； (2)求证：DF 2＝AF ·BE . 证明：(1)∵⊙O 切BC 于D ， ∴∠CAD ＝∠CDF .∵AD 是△ABC 的角平分线， ∴∠BAD ＝∠CAD . 又∵∠BAD ＝∠EFD ， ∴∠EFD ＝∠CDF . ∴EF ∥BC . (2)连接DE ，∵⊙O 切BC 于D ， ∴∠BAD ＝∠BDE . 由(1)可得∠BDE ＝∠F AD ， 又∵⊙O 内接四边形AEDF ， ∴∠BED ＝∠DF A . ∴△BED ∽△DF A . ∴DE AF ＝BEDF. 又∵∠BAD ＝∠CAD ， ∴DE ＝DF .∴DF 2＝AF ·BE .[对应学生用书P30]一、选择题1．P 在⊙O 外，PM 切⊙O 于C ，P AB 交⊙O 于A 、B ，则( ) A ．∠MCB ＝∠B B ．∠P AC ＝∠P C ．∠PCA ＝∠BD ．∠P AC ＝∠BCA解析：由弦切角定理知∠PCA ＝∠B .答案：C2．如图，△ABC 内接于⊙O ，EC 切⊙O 于点C .若∠BOC ＝76°，则∠BCE 等于( )A ．14°B ．38°C ．52°D ．76°解析：∵EC 为⊙O 的切线， ∴∠BCE ＝∠BAC ＝12∠BOC ＝38°.答案：B3．如图，AB 是⊙O 的直径，EF 切⊙O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 的长为( )A ．2B ．3C ．2 3D ．4解析：连接BC ，则∠ACB ＝90°， 又AD ⊥EF ，∴∠ADC ＝90°， 即∠ADC ＝∠ACB ， 又∵∠ACD ＝∠ABC ， ∴△ABC ∽△ACD ， ∴AC 2＝AD ·AB ＝12， 即AC ＝2 3. 答案：C4．如图，AB 是⊙O 直径，P 在AB 的延长线上，PD 切⊙O 于C 点，连接AC ，若AC ＝PC ，PB ＝1，则⊙O 的半径为( )A ．1B ．2C ．3D ．4解析：连接BC .∵AC ＝PC ，∴∠A ＝∠P . ∵∠BCP ＝∠A ，∴∠BCP ＝∠P .∴BC ＝BP ＝1.由△BCP ∽△CAP 得 PC 2＝PB ·P A ， 即AC 2＝PB ·P A . 而AC 2＝AB 2－BC 2， 设⊙O 半径为r ，则4r 2－12＝1·(1＋2r )，解得r ＝1. 答案：A 二、填空题为14圆周长，则∠5.如图，已知AB 与⊙O 相切于点M ，且MC ＝MD ，且MC ，MD AMC ＝________，∠BMC ＝________，∠MDC ＝________，∠MOC ＝________. 解析：弦切角等于所夹弧所对的圆周角，等于所夹弦所对圆心角度数的一半．答案：45° 135° 45° 90°6．如图，AB 是⊙O 的直径，PB ，PE 分别切⊙O 于B ，C ，若∠ACE ＝40°，则∠P ＝________.解析：连接BC ， ∵AB 是⊙O 的直径， ∴∠ACB ＝90°. 又∠ACE ＝40°，∴∠PCB ＝∠PBC ＝50°.∴∠P ＝80°. 答案：80°7.如图，点P 在圆O 直径AB 的延长线上，且PB ＝OB ＝2，PC 切圆O 于C 点，CD ⊥AB 于D 点，则CD ＝________.解析：连接OC ， ∵PC 切⊙O 于C 点， ∴OC ⊥PC .∵PB ＝OB ＝2，OC ＝2. ∴PC ＝2 3. ∵OC ·PC ＝OP ·CD ， ∴CD ＝2×234＝ 3.答案： 3 三、解答题8.如图所示，⊙O1与⊙O 2交于 A 、B 两点，过⊙O 1上一点P 作直线P A 、PB 分别交⊙O 2于点C 和点D ，EF 切⊙O 1于点P .求证：EF ∥CD . 证明：如图，连接AB ， ∵EF 是⊙O 切线，∴∠FP A ＝∠PBA .又在⊙O 2中，ABCD 为⊙O 内接四边形， ∴∠C ＝∠ABP .∴∠FP A ＝∠C . ∴EF ∥CD .9.如图所示，△ABC 内接于⊙O ，AB ＝AC ，直线XY 切⊙O 于点C ，弦BD ∥XY ，AC 、BD 相交于E .(1)求证：△ABE ≌△ACD ； (2)若AB ＝6 cm ，BC ＝4 cm ， 求AE 的长．解：(1)证明：因为XY 是⊙O 的切线， 所以∠1＝∠2.因为BD ∥XY ，所以∠1＝∠3，所以∠2＝∠3. 因为∠3＝∠4，所以∠2＝∠4.因为∠ABD ＝∠ACD ，又因为AB ＝AC ， 所以△ABE ≌△ACD .(2)因为∠3＝∠2，∠ABC ＝∠ACB ， 所以△BCE ∽△ACB ，BC AC ＝CECB ，AC ·CE ＝BC 2.因为AB ＝AC ＝6 cm ，BC ＝4 cm ， 所以6·(6－AE )＝16. 所以AE ＝103cm.10.如图，△ABC 内接于圆O ，AD 平分∠BAC 交圆O 于点D ，过点B 作圆O 的切线交直线AD 于点E .(1)求证：∠EBD ＝∠CBD ； (2)求证：AB ·BE ＝AE ·DC . 证明：(1)∵BE 为圆O 的切线， ∴∠EBD ＝∠BAD ，又∵AD 平分∠BAC ，∴∠BAD ＝∠CAD ， ∴∠EBD ＝∠CAD ， 又∵∠CBD ＝∠CAD ， ∴∠EBD ＝∠CBD .(2)在△EBD和△EAB中，∠E＝∠E，∠EBD＝∠EAB，∴△EBD∽△EAB，∴BEAE＝BDAB，∴AB·BE＝AE·BD，又∵AD平分∠BAC, ∴BD＝DC，故AB·BE＝AE·DC.。

形相似证比例中项，这样的类型题较常见．
题型二 性质定理用于计算
例2 如图所示，过圆O外一点P分别作圆O的切线 和割线交圆于A，B，且PB＝7，C是圆上一点使 得BC＝5，∠BAC＝∠APB，则AB＝________．
【命题立意】本题主要考查弦切角定理，相似三角形判定和性质的应用． 解析：∵PA 是圆 O 的切线， ∴∠BAP＝∠BCA， 又∵∠BAC＝∠APB，∴△BAP∽△BCA. ∴ACBB＝APBB，∴AB2＝PB·CB＝7×5＝35， ∴AB＝ 35.故填 35. 答案： 35 点评：进行三角形相似的证明时，经常用到弦切角定理，然后利用相似 三角形的性质进一步确定相应线段之间的关系．在圆中证明比例式或等 积式成立时，常常需要借助三角形相似来处理．
弦切角的性质
题型一 性质定理用于证明
例1 已知MN是⊙O的切线，点A为切点， MN平行于弦CD，弦AB交CD于点E.求证： AC2＝AE·AB.
证明：如图，连接 BC.
MN∥CD⇒∠MAC＝∠ACD
MN切⊙O于点A⇒∠MAC＝∠B
⇒∠∠CAAEC＝D∠＝C∠ABB⇒△ACE∽△ABC⇒
AACB＝AAEC⇒AC2＝AB·AE. 点评：此题主要是利用弦切角的性质去证明两个角相等，再利用三角
︵ 例3 已知四边形 ABCD 内接于⊙O，点 D 是AC的中点，BC 和 AD 的 延长线相交于点 E，DH 切⊙O 于点 D.求证：DH 平分∠CDE.
证明：如图，连接BD.
︵ ∵点 D 是AC的中点， ∴∠ABD＝∠CBD. ∵DH 切⊙O 又∠CDE＝∠ABC， ∴∠HDE＝∠ABD， ∴∠CDH＝∠HDE， ∴DH 平分∠CDE.
︵︵ 2．若 AB 切⊙O 于 A，AC、AD 为⊙O 的弦，且AC＝AD， 则∠C 与∠CAB 的关系是_∠__C__＝__∠__C_．AB

Rt△CAE∽Rt△CBD CE CD → ＝ → 结论 Rt△CBF∽Rt△CAD CD CF
[证明]
连接CA、CB.
∵PA、PB是⊙O的切线， ∴∠CAP＝∠CBA， ∠CBP＝∠CAB. 又CD⊥AB，CE⊥PA，CF⊥PB， ∴Rt△CAE∽Rt△CBD， Rt△CBF∽Rt△CAD， CA CE CB CF ∴CB＝CD，CA＝CD， CE CD ∴CD＝ CF，即CD2＝CE· CF.
5．如图，AD是△ABC的角平分线，
经过于点E、F， 连接DF，EF. (1)求证：EF∥BC； (2)求证：DF2＝AF· BE.
证明：(1)∵⊙O切BC于D，
∴∠CAD＝∠CDF.
∵AD是△ABC的角平分线， ∴∠BAD＝∠CAD. 又∵∠BAD＝∠EFD， ∴∠EFD＝∠CDF. ∴EF∥BC.
证明乘积式成立，往往与相似三角形有关，若
存在切线，常要寻找弦切角，确定三角形相似的条
件，有时需要添加辅助线创造条件．
4．如图，已知MN是⊙O的切线，A为切点，MN平行于弦 CD，弦AB交CD于E.求证：AC2＝AE· AB.
证明：连接BC. MN∥CD⇒∠MAC＝∠ACD MN切⊙O于A⇒∠MAC＝∠B ⇒∠ACD＝∠B ⇒△ACE∽△ABC ∠CAE＝∠CAB AC AE ⇒AB＝AC⇒AC2＝AB· AE.
1. 弦切角定理
(1)文字语言叙述： 弦切角等于它 所夹的弧 所对的圆周角． (2)图形语言叙述： 如图，AB与⊙O切于A点，则∠BAC＝ ∠D .
[说明]
弦切角的度数等于它所夹弧度数的一半，
圆周角的度数等于它所对的弧的度数的一半，圆心
角的度数等于它所对弧的度数．
[例 1]