数字电子技术基础逻辑代数和逻辑函数化简详解
- 格式:ppt
- 大小:2.59 MB
- 文档页数:80



《数字电子技术基础》读书笔记02 逻辑代数基础2.1从布尔代数到逻辑代数1849年英国数学家乔治布尔(George Boole)提出布尔代数,使用数学方法进行逻辑运算。
把布尔代数应用到二值逻辑电路中,即为逻辑代数。
2.2逻辑代数中的运算(想想初等代数中的加减乘除)2.2.1三种基本运算与(AND):逻辑乘,Y=A B或(OR):逻辑加,Y=A+B非(NOT):逻辑求反,Y=Aˊ简单逻辑运算(与、或、非)的两套图形符号,均为IEEE(国际电气与电子工程师协会)和IEC(国际电工协会)认定。
上排为国外教材和EDA软件中普遍使用的特定外形符号;下排为矩形符号。
2.2.2复合逻辑运算(都可以表示为与、或、非的组合)与非(NAND):先与后非,与的反运算,Y=(A B)ˊ或非(NOR):先或后非,非的反运算,Y=(A+B)ˊ与或非(AND-NOR):先与再或再非,Y=(A B+C D)ˊ异或(Exclusive OR):Y=A⊕B=A Bˊ+AˊB A和B不同,Y为1;A和B相同,Y为0。
当A与B相反时,A Bˊ和AˊB,肯定有一个结果为1,则Y为1。
同或(Exclusive NOR):Y=A⊙B=A B+AˊBˊA和B相同,Y为1;A和B不同,Y为0。
当A与B相同时,A B和AˊBˊ,肯定有一个结果为1,则Y为1。
同或与同或互为反运算,即两组运算,只要输入相同,一定结果相反。
A⊕B=(A⊙B)ˊA⊙B=(A⊕B)ˊ复合逻辑运算的图像符号和运算符号。
2.3逻辑代数的基本公式和常用公式2.3.1基本公式(见对偶定理)2.3.2若干常用公式(见逻辑函数化简方法之公式化简法)2.4逻辑代数的基本定理2.4.1代入定理(相当于初等代数中的换元)任何一个包含逻辑变量A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式依然成立。
2.4.2反演定理对于任意一个逻辑式Y,若将其中所有的""换成"+","+"换成"","0"换成"1","1"换成"0",原变量换成反变量,反变量换成原变量,则得到的结果就是Yˊ。



一文看懂,数电中逻辑函数的,代数,化简法常用公式
1.交换律: A+B=B+A;---@1 AB=BA;---@2
2.结合律:(A+B)+C=A+(B+C);---@3 (AB)C=A(BC);---@4
3.分配律: A(B+C)=AB+BC;---@5 A+BC=(A+B)(A+C);---@6
4.吸收率: A+AB=A;---@7 A(A+B)=A;---@8
5.其他常用:A+!AB=A+B;---@9 A(!A+B)=AB@10
以上逻辑运算基本定律中,恒等式大多是成对出现的,且具有对偶性。
用完全归纳法可以证明所列等式的正确性,方法是:列出等式的左边函数与右边函数的真值表,如果等式两边的真值表相同,说明等式成立。
但此方法较为笨拙,下面以代数方法证明其中几个较难证明的公式。
@7式证明:A+AB=A(1+B)=A;
@8式证明:A(A+B)=AA+AB=A+AB=A;由七式易得;
@6式证明:
A+BC=(A+AB)+BC;此处由@7式可得A=A+AB;
=A+AB+BC=A+B(A+C);此处由@5式可得AB+BC=B(A+C);
=A+AC+B(A+C);此处由@7式可得A=A+AC;
=A(A+C)+B(A+C);
=(A+B)(A+C); 得证。
@9式证明: A+!AB=A(1+B)+!AB;
=A+AB+!AB;
=A+B(A+!A);
=A+B;得证。




Word -可编辑3.3.4 逻辑函数的最小项和最大项及标准与或式一个逻辑函数可以由多种等效的表达式,但其标准形式是唯一的,逻辑函数有两种标准形式,即标准与或式(最小项表达式)和标准或与式(最大项表达式)。
一、最小项(标准与或式)1.最小项的概念:n 个变量的逻辑函数中,包括所有n 个变量的乘积项(每个变量必须而且只能以原变量或反变量的形式浮上一次)。
n 个变量有2n 个最小项,记作m i 。
编号i :各输入变量取值看成二进制数,对应十进制数。
3个变量有23(8)个最小项。
【例12】写出 F AB AC BC =++ 的最小项标准与或表达式。
解:()()()()F AB AC BC AB C C AC B B BC A AABC ABC ABC ABC ABC ABC ABC ABC ABC ABC m m m m m ,,,∑=++=+++++=+++++=+++=+++=35673567(2)最小项的性质:随意一组变量取值:惟独一个最小项的值为1。
同一组变量取值:随意两个不同最小项的乘积为0,即m i m j =0 (i ≠j )。
所有最小项之和为1,即具有相邻性的两个最小项之和可合并成一项并消去一对因子。
2.最大项:(1)概念:n 个变量的逻辑函数中,包括所有n 个变量的和项(每个变量必须而且只能C B A BC A C B A CB AC AB ABCmmmmmm01011 100101 11111234567∑-==1201n i im千里之行,始于足下以原变量或反变量的形式浮上一次)。
n 个变量有2n 个最大项,记作i 。
3个变量有23(8)个最大项。
(2)最大项的性质:随意一组变量取值:惟独一个最大项的值为0。
同一组变量取值:随意两个不同最大项的和为1,即M i +M j =1 ( i ≠j )。
所有最大项之积为0,即惟独一个变量不同的两个最大项的乘积等于各相同变量之和。
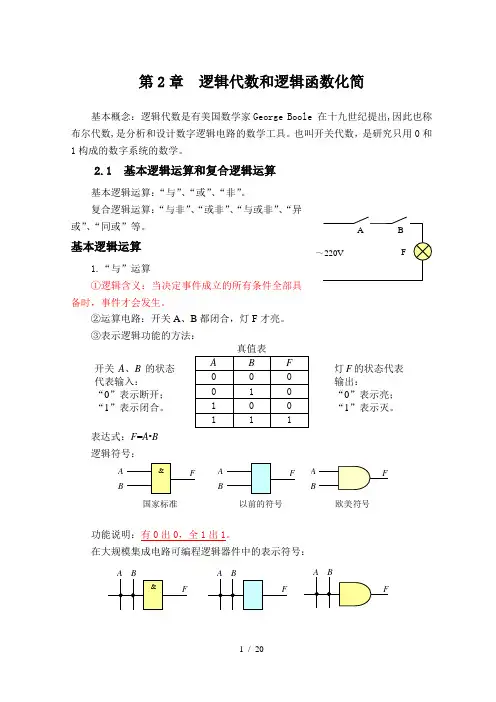
第2章 逻辑代数和逻辑函数化简基本概念:逻辑代数是有美国数学家George Boole 在十九世纪提出,因此也称布尔代数,是分析和设计数字逻辑电路的数学工具。
也叫开关代数,是研究只用0和1构成的数字系统的数学。
2.1 基本逻辑运算和复合逻辑运算基本逻辑运算:“与”、“或”、“非”。
复合逻辑运算:“与非”、“或非”、“与或非”、“异或”、“同或”等。
基本逻辑运算1.“与”运算①逻辑含义:当决定事件成立的所有条件全部具备时,事件才会发生。
②运算电路:开关A 、B 都闭合,灯F 才亮。
③表示逻辑功能的方法:表达式:F =A •B 逻辑符号:功能说明:有0出0,全1出1。
在大规模集成电路可编程逻辑器件中的表示符号:A B国家标准 A B以前的符号A B欧美符号开关A 、B 的状态代表输入:“0”表示断开; “1”表示闭合。
灯F 的状态代表输出:“0”表示亮; “1”表示灭。
通过“•”接入到此线上的输入信号都是该与门的一个输入端。
推广:当有n 个变量时:F =A 1A 2A 3∙∙∙A n “与”运算的几个等式: 0•0=0,0•1=0,1•1=1A •0=0(0-1律),A •1=A (自等律),A •A =A (同一律),A •A •A =A (同一律)。
2.“或”运算①逻辑含义:在决定事件成立的所有条件中,只要具备一个,事件就会发生。
②运算电路:开关A 、B 只要闭合一个,灯F 就亮。
③表示逻辑功能的方法: 逻辑功能:有1出1,全0出0。
真值表:(略) 表达式:F =A +B 逻辑符号:推广:当有n 个变量时:F =A 1+A 2+A 3+∙∙∙+A n“或”运算的几个等式: 0+0=0,0+1=1,1+1=1A +0=A (自等律)A +1=1(0-1律),A +A =A (同一律)。
上次课小结:与、或的功能、表达式等,几个等式。
3.“非”运算①逻辑含义:当决定事件的条件具备时,事件不发生;当条件不具备时,事件反而发生了。