角的计算专项练习题

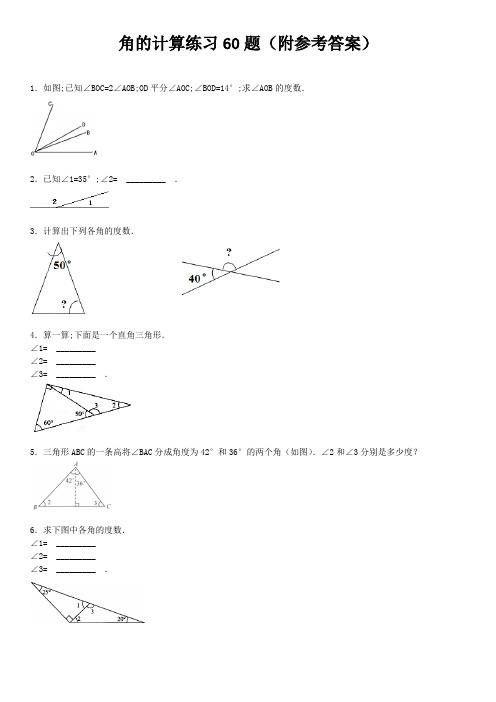
角的计算练习60题（附参考答案）1．如图;已知∠BOC=2∠AOB;OD平分∠AOC;∠BOD=14°;求∠AOB的度数．2．已知∠1=35°;∠2= _________ ．3．计算出下列各角的度数．4．算一算;下面是一个直角三角形．∠1= _________∠2= _________∠3= _________ ．5．三角形ABC的一条高将∠BAC分成角度为42°和36°的两个角（如图）．∠2和∠3分别是多少度？6．求下图中各角的度数．∠1= _________∠2= _________∠3= _________ ．7．如图中;已知∠1=30°;∠2= _________ ;∠3= _________ ．8．如图;∠1= _________ ;∠2= _________ ;∠3= _________ ．9．求下面各个三角形中∠A的度数10．如图中;已知∠1=43°;∠2= _________ ;∠3= _________ ．11．计算三角形中角的度数．∠1= _________ ;∠2= _________ ;∠3= _________ ．12．算一算：∠1= _________ ;∠2= _________ ;∠3= _________ ．13．算一算;这些角各是多少度．已知∠2=40°求得：∠1= _________ °;∠3= _________ °;∠4= _________ °．14．求出如图所示各角的度数．15．如图;已知∠l=20°;∠2=46°;求∠3的度数．16．如图所示;∠BOC=110°;∠AOB=∠DOC;∠AOB是几度？17．如图：∠1=48°;∠2= _________ ．18．算一算．已知∠1=65°;求出：∠2、∠3、∠4的度数．19．求下面各角的度数．图1;∠1= _________ ∠2= _________图2;∠1= _________ ．20．求下面各角的度数．已知∠1=30°;∠2=90°．∠3= _________ ;∠4= _________ ;∠5= _________ ．21．∠1=32゜;∠2=36゜;∠3= _________ ．22．如图已知∠1=35°;∠2= _________ ;∠3= _________ ;∠4= _________ ．23．如图所示;已知∠1=30°．求：∠2、∠3和∠4的度数．24．已知∠1=25°;∠2= _________ °;∠3= _________ °;∠4= _________ °．25．算一算：∠1= _________ ;∠2= _________ ;∠3= _________ ．26．角的计算（1）如图1所示;已知：∠1=72°;∠2=45°;求：∠AOB= _________ ？（2）如图2所示;已知：∠1=35°;求∠2= _________ ？27．用量角器量出图中∠2的度数;再求∠1、∠3和∠4的度数．28．如图;已知∠1=130°;求∠2、∠3的度数．29．如图中;∠AOB=14°;∠COB=∠COD;求∠COD．30．在直角∠AOB内有射线OC、OD．∠AOC=∠BOD=60°;求∠COD的大小．31．求下面各角的度数．∠A= _________ ∠B= _________ ∠B=∠C= _________ ∠C= _________ ．32．（1）如图1;已知：∠1=45°;求：∠2（2）如图2;已知：∠1=90°;∠2=30°求：∠3等于多少度？（3）如图3;已知：∠1=135°求：∠2、∠3、∠4各等于多少度？33．如图;已知∠1=70°;∠2=25°;∠3=50°;求∠5=？34．如图是一张长方形纸折起来以后的图形;已知么∠2是 65°;∠1是多少度？35．已知∠1=28°求∠2、∠3、∠4和∠5各是多少度？36．算一算∠1=65°∠2= _________ ∠3= _________ ∠4= _________ ∠1+∠2+∠3+∠4= _________ ．37．求角的度数．（1）AB=AC（如图1）∠1= _________∠2= _________（2）三角形ABC是等腰三角形（如图2）∠1= _________∠2= _________ ．38．如图中∠1=30°;∠2= _________ ;∠3= _________ ;∠4= _________ ;∠5= _________ ．39．如图所示;∠1=55．;请分别求出∠2、∠3、∠4的度数．40．图中;已知∠1=37°∠2= _________ ;∠3= _________ ;∠4= _________ ．41．如图;已知∠1=40°;∠2= _________ ;∠3= _________ ;∠4= _________ ;∠3+∠4= _________ 42．图中∠1= _________ ;∠2= _________ ;∠3= _________ ;∠1+∠2= _________ ．43．已知∠1=50°;求∠2=？∠3=？44．算一算．已知∠1=36°;∠2= _________ ;∠3= _________ ;∠4= _________ ;∠5= _________ ．45．图中;∠1=55°;∠2是直角;你能求∠3、∠4、∠5各是多少度吗？46．先量一量;再填空．①∠1= _________ ;是_________ 角;∠2= _________ ;是_________ 角;∠3= _________ ;是_________ 角．②画出∠1;使∠1=75°．47．算一算如图：已知∠1=35°∠3= _________ ∠4= _________∠2= _________ ∠1+∠2+∠3= _________ ．48．如图1;已知∠1=40°;∠2= _________ ;∠3= _________ ;∠4= _________ ．如图2;已知∠1=30°;∠2= _________ ;∠3= _________ ;∠4= _________ ;∠5=_________ ．49．求各个角的度数．（1）图1中：已知∠1=60°∠2= _________∠3= _________∠4= _________∠5= _________（2）图2中：已知∠1=75°∠2= _________∠3= _________∠4= _________ ．50．分别量出图中4个角的度数;再求出这4个角的和．∠1= _________ ;∠2= _________ ;∠3= _________ ;∠4= _________ ;∠1+∠2+∠3+∠4= _________ ．51．∠1= _________ ;∠2= _________ ;∠3= _________ ．52．∠1= _________ ;∠2= _________ ;∠3= _________ ．53．已知∠1=90°;∠2=50°;求∠3、∠4和∠5的度数．54．如图;求∠1和∠2的度数．55．已知：∠1=∠3;∠2=40°求：∠ADE=？56．在下面三角形中;∠1=38°;∠2+∠3=90°;求∠3和∠4各是多少度？57．在三角形ABC中;∠l=60°;∠3=50°;求∠2、∠4的度数．58．如图;已知：∠2=30°;∠3是直角;则∠2+∠3= _________ ;∠1+∠2+∠4= _________ ;∠1+∠2+∠3+∠4= _________ ．59．求图中各角的度数．图1：∠2= _________ ∠3= _________ 图2：∠1= _________ ∠2= _________ ∠3= _________ ．60．看图填数．①如图一;已知∠1=75°;那么∠2= _________ ∠3= _________ ∠4= _________ ．②如图二;∠1= _________ ∠2= _________ ∠3= _________ ．角的计算参考答案：1．设∠AOB=x;∠BOC=2x．则∠AOC=3x．又OD平分∠AOC;因为∠AOD=x．所以∠BOD=∠AOD﹣∠AOB=x﹣x=14°因为x=28°即∠AOB=28°．答：∠AOB的度数是28°2．∠2=180°﹣∠1;∠2=180°﹣35°;∠2=145°．故答案为：145°．3．（1）（180°﹣50°）÷2;=130°÷2;=65°．答：角的度数是65°．（2）180°﹣40°=140°．答：角的度数是140°4．∠2=90°﹣60°=30°;∠3=180°﹣50°=130°;∠1=180°﹣∠2﹣∠3=180°﹣30°﹣130°=20°．故答案为：20°;30°;130°5．在直角三角形ABD中;因为∠ADB=90°;所以∠2=180°﹣90°﹣42°;∠2=48°;在直角三角形ADC中;∠ADC=90°;所以∠3=180°﹣90°﹣36°;∠3=54°答：∠2和∠3分别是48°和54°．6．（1）∠1=180°﹣90°﹣25°=65°;（2）180°﹣25°﹣20°=135°;∠2=135°﹣90°=45°;（3）∠3=180°﹣∠1=180°﹣65°=115°．故答案为：65°;45°;115°7．∠1与∠2组成了一个平角;所以∠2=180°﹣30°=150°;∠1与∠3组成一个直角;所以∠3=90°﹣30°=60°; 故答案为：150°;60°8．根据题干分析可得：∠1=180﹣90﹣45=45（度）; ∠3=180﹣45=135（度）; ∠2=180﹣135=45（度）;故答案为：45°;45°;135°9．∠ABC=90°;∠ACB=60°．所以;∠BAC=90°﹣∠BAC=90°﹣60°=30°;∠A=180°﹣∠B﹣∠C=180°﹣135°﹣20°=25°10．（1）∠2=90°﹣∠1=90°﹣43°=47°; （2）∠3=180°﹣∠2=180°﹣47°=133°．故答案为：47°;133°11．（1）根据题干分析可得：∠2=65°;则∠1=180°﹣65°﹣65°=50°;（2）∠3=90°﹣41°=49°;故答案为：50°;65°;49°12．∠1=180°﹣45°﹣90°=45°;∠2=180°﹣45°=135°;∠3=180°﹣135°=45°．故答案为：45°;135°;45°．13．根据题干分析可得：∠1=90°﹣40°=50°;∠3=180°﹣40°=140°;∠4=180°﹣140°=40°;故答案为：50;140;40．14．∠A=180°﹣40°﹣85°=55°;∠B=180°﹣90°﹣35°=55°;∠C=180°﹣20°﹣47°=113°．如图所示：故答案为：55°、55°、113°15．∠4=180°﹣∠1﹣∠2;=180°﹣20°﹣46°;=114°;∠3=180°﹣∠4;=180°﹣114°;=66°．答：∠3是66°16．根据题干分析可得：（180﹣110）÷2;=70÷2;=35（度）;答：∠AOB的度数是35度．17．∠2=90°﹣48°=42°;故答案为：42°18．∠1与∠3是对顶角;所以∠3也是65°;因为∠1与∠2组成了一个平角;∠2与∠4又是对顶角; 所以∠2=∠4=180°﹣65°=115°;答：∠2=115°;∠3=65°;∠4=115°．19．（1）∠1=∠2=（180°﹣120°）÷2=30°;（2）90°﹣40°=50°;所以∠1=50°;故答案为：30°;30°;50°20．∠1和∠5组成了一个直角;所以∠5=90﹣30=60（度）;∠5与∠4组成了一个平角;所以∠4=180﹣60=120（度）; 因为∠5与∠3是一组对顶角;所以∠3=∠5=60（度）; 故答案为：60°;120°;60°21．180°﹣32°﹣36°=112°;故答案为：112°22．∠2=90°﹣∠1=90°﹣35°=55°;∠3=180°﹣∠2=180°﹣55°=125°;∠4=180°﹣∠3=180°﹣125°=55°;故答案为：55°;125°;55°．23．∠2=90°﹣30°=60°;∠3=180°﹣60°=120°;∠4=180°﹣120°=60°．答：∠2的度数是60°;∠3的度数是120°;∠4的度数是60°24．∠2=180°﹣∠1=155°;∠3=180°﹣∠2=25°;∠4=180°﹣∠1=155°．故答案为：155;25;155．25．∠1=180°﹣35°=145°;∠2=180°﹣90°=90°;∠3=180°﹣125°=55°．故答案为：145°;90°;55°26．（1）∠AOB=∠1+∠2=72°+45°=117°;（2）∠2=180°﹣90°﹣∠1=55°．故答案为：117°;55°．27．经测量可得∠2=35°;则∠1=90°﹣35°=55°;∠3=180°﹣35°=145°;∠4=180°﹣145°=35°．答：∠1的度数是55°;∠3的度数是145°;∠4的度数是35°28．∠2=180°﹣∠1=180°﹣130°=50°;∠3=90°﹣∠2=90°﹣50°=40°;答：∠2是50度;∠3是40度．29.（90°﹣14°）÷2;=76°÷2;=38°;答：∠COD=38°30．∠COD=∠AOC+∠BOD﹣∠AOB;=60°+60°﹣90°; =30°．答：∠COD的大小是30°．31．（1）∠A=90°﹣34°=56°;（2）∠C=180°﹣90°﹣18°=72°;∠B=180°﹣60°﹣72°=48°;（3）∠B=∠C=（180°﹣48°）÷2=66°;（4）∠A=180°﹣119°=61°;∠C=90°﹣61°=29°．故答案为：56°;48°;66°;29°32．（1）∠2=180°﹣∠1=180°﹣45°=135°．（2）∠3=180°﹣∠1﹣∠2=180﹣90°﹣30°=60°．（3）∠3=180°﹣∠1=180°﹣135°=45°;∠4=180°﹣∠1=180°﹣135°=45°;∠2=180°﹣∠3=180°﹣45°=135°33．在小三角形里最大的角=180°﹣∠2﹣∠3=105°; ∠4=180°﹣105°=75°;∠5=180°﹣∠1﹣∠4;=180°﹣70°﹣75°;=35°．答：∠5是35°34．180°﹣65°×2=180°﹣130°=50°．答：∠1是50度．35．∠4=90°;∠5=90°﹣∠1=90°﹣28°=62°;∠2=180°﹣∠1=180°﹣28°=152°;∠3=180°﹣∠2=180°﹣152°=28°;答：∠2=152°;∠3=28°;∠4=90°;∠5=62°．36．（1））∠2=90°﹣∠1;=90°﹣65°;=25°;（2））∠3=180°﹣∠2;=180°﹣25°;=155°;（3））∠4=180°﹣∠3;=180°﹣155°;=25°;（4））∠1+∠2+∠3+∠4=360°﹣90°;=270°．或∠1+∠2+∠3+∠4=65°+25°+155°+25°=270°．故答案为：25°;155°;25°;270°37．（1）∠C=180°﹣120°=60°;∠1=90°﹣∠C=90°﹣60°=30°;∠2=180°﹣60°×2=60°;（2）∠1=90°﹣60°=30°;∠2=180°﹣∠1×2﹣90°;=180°﹣30°×2﹣90°;=30°．故答案为：（1）30°;60°;（2）30°;30°38．根据题干分析可得：∠3=90°;∠2=90°﹣30°=60°;∠4=∠1=30°;∠5=180°﹣30°=150°;故答案为：60°;90°;30°;15039．如图：∠4=90°﹣∠1;=90°﹣55°;=35°;∠3=180°﹣∠4﹣∠5;=180°﹣35°﹣90°;=55°;∠2=180°﹣∠3;=180°﹣55°;=125°;答：∠2是125°、∠3是55°、∠4是35°40．∠2=90°﹣∠1=90°﹣37°=53°;∠3=180°﹣∠2=180°﹣53°=127°;∠4=180°﹣∠3=180°﹣127°=53°故答案为：53°;127°;53°41．∠2=∠4=180°﹣40°=140°;∠3=180°﹣∠2=40°;∠3+∠4=180°．故答案为：140°;40°;140°;180°42．∠1=90﹣50=40（度）;∠2=90﹣40=50（度）;∠3=180﹣50=130（度）;∠1+∠2=90（度）;故答案为：40°;50°;130°;90°43．∠2=180°﹣50°=130°;∠3=180°﹣90°=90°．答：∠2=130°;∠3=90°．44．根据题干分析可得：∠3是直角;是90°;∠2=90°﹣36°=54°;∠4=90°﹣54°=36°;∠5=180°﹣36°=144°;故答案为：54°;90°;36°;144°45．∠3=90°﹣55°=35°;∠5=180°﹣55°=125°;∠4=180°﹣125°=55°．答：∠3=35°、∠4=55°、∠5=125°46．（1）经过测量可知∠1=50°;是锐角;∠2=40°;是锐角;∠3=120°;是钝角;（2）根据分析画图如下：故答案为：50°;锐;4°;锐;120°;钝47．∠2=180°﹣∠1=180°﹣35°=145°;∠3=180°﹣∠2=180°﹣145°=35°;∠4=90°;∠1+∠2+∠3=35°+145°+35°=215°．故答案为：35°;90°;145°;215°48．图一：因为;∠1=40°．所以;∠2=180°﹣40°=140°;∠3=180°﹣140°=40°;∠4=180°﹣40°=140°;图二：因为;∠1=30°．所以;∠2=90°﹣30°=60°;∠3=90°;∠4=180°﹣60°﹣90°=30°;∠5=180°﹣30°=150°;故答案为：140°;40°;140°;60°;90°;30°;150°49．（1）因为∠2=90°;平角=180°;所以;∠3=180°﹣∠1﹣∠2=180°﹣90°﹣60°=30°;∠5=180°﹣∠1=180°﹣60°=120°;∠4=180°﹣∠5=180°﹣120°=60°;（2）因为∠1=75°;平角=180°;所以;∠2=180°﹣∠1=180°﹣75°=105°;∠4=180°﹣∠1=180°﹣75°=105°;∠3=180°﹣∠4=180°﹣105°=75°;故答案为：90°;30°;60°;120°;105°;75°;105°50．测量可得图中∠1=90°;∠2=45°;∠3=90°;∠4=135°．∠1+∠2+∠3+∠4=90°+45°+90°+135°=360°．故答案为：90°;45°;90°;135°．360°51．观察图形可知：∠3=90°;∠1=180﹣35=145（度）;∠2=90﹣30=60（度）;故答案为：145°;60°;90°52．因为∠1是等腰直角三角形底角;所以∠1=90°÷2=45°;因为正方形的两条对角线互相垂直;所以∠2=∠3=90°．故答案为：45°;90°;90°53．（1）∠3=180°﹣∠2=180°﹣50°=130°; （2）∠4=180°﹣∠3=180°﹣130°=50°;（3）∠5=180°﹣∠1﹣∠2=180°﹣90°﹣50°=40°．故答案为：∠3=130°;∠4=50°;∠5=40°54．∠1=180°﹣90°﹣65°=25°;∠2=180°﹣120°=60°．答：∠1的度数是25°;∠2的度数是60°．55．∠ADE=（180°﹣40°）÷2+40°;=140°÷2+40°;=70°+40°;=110°．答：∠ADE是110°．56．∠4=180°﹣∠1﹣（∠2+∠3）;∠4=180°﹣38°﹣90°;∠4=52°;∠3=180°﹣90°﹣∠4;∠3=180°﹣90°﹣52°;∠3=38°．答：∠3是38°;∠4是52°57．因为∠1+∠3+∠4=180°;∠l=60°;∠3=50°;所以∠4=180°﹣60°﹣50°=70°;因为∠6=90°;所以∠2=90°﹣∠3;=90°﹣50°;=40°58．∠2+∠3=30°+90°=120°;∠1+∠2+∠3+∠4=360°;∠1+∠2+∠4=360°﹣90°=270°．故答案为：120°;270°;360°．59.（1）∠2=90°=50°=40°;∠3=180°﹣（40°+30°）=110°; （2）∠1=180°﹣120°=60°;∠2=180°﹣（60°+45°）;=180°﹣105°;=75°;∠3=180°﹣75°=105°．故答案为：40°、110°;60°、75°、60．因为∠1+∠2=180°;∠1=75°;所以75°+∠2=180°;75°﹣75°+∠2=180°﹣75°;∠2=105°;因为∠1与∠3;∠2与∠4;分别是对顶角; 所以∠1=∠3=75°;∠2=∠4=105°; （2）因为∠1+35°=180°;∠1+35°﹣35°=180°﹣35°;∠1=145°;因为∠2+30°=90°;∠2+30°﹣30°=90°﹣30°;∠2=60°;因为∠3是一个直角;所以∠3=90°;故答案为：（1）105°;75°;105°．（2）145°;60°;90°．。

第四章复习卷三（角的计算）几何语言：一、选择题（本大题共13小题，共45.0分。

在每小题列出的选项中，选出符合题目的一项）1. 如图，OC 平分∠AOB ，下列结论错误的是( )A. ∠AOB =2∠AOCB. ∠AOC =∠BOCC. ∠AOC =12∠AOBD. ∠BOC =∠AOB2. 如图，∠AOC 和∠DOB 都是直角，如果∠AOB =150∘，则∠DOC 的度数为( )A. 30∘B. 40∘C. 50∘D. 60∘3. 将一副直角三角尺如图放置，若∠AOD =16°，则∠BOC 的大小为A. 174°B. 164°C. 154°D. 144°4. 已知∠AOB =40°，∠BOC =20°，则∠AOC 的度数为( )A. 60°B. 20°C. 40°D. 20°或60°5. 有两个角，它们的比为7︰3，它们的差为36°，则这两个角的关系是A. 和为90度B. 和为180度C. 相等D. 以上答案都不对6. 如图，∠AOB =20°，∠AOC =90°，点B 、O 、D 在同一直线上，则∠COD 的度数为( )从一个角的顶点出发的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.角平分线的定义A. 100°B. 105°C. 110°D. 115°7.如图，∠AOB=90∘，∠AOC为∠AOB外的一个锐角，且∠AOC=40∘，射线OM平分∠BOC，ON平分∠AOC.则∠MON的度数为( )A. 45°B. 65°C. 50°D. 25°8.如图，OB是∠AOC的角平分线，OD是∠COE的角平分线，如果∠AOB=40°，∠COE=60°，则∠BOD的度数为( )A. 50°B. 60°C. 70°D. 80°9.已知α、β都是钝角，甲、乙、丙、丁四人计算1(α+β)的结果依次是50°，26°，72°，90°，6那么结果正确的可能是( )A. 甲B. 乙C. 丙D. 丁10.一个角的的余角是50°，则这个角的补角为A. 40°B. 50°C. 130°D. 140°11.一个角的补角比这个角的余角3倍还多10°，则这个角的度数为A. 40°B. 50°C. 130°D. 140°12.用一副三角板不能画出下列哪组角( )A. 45°，30°，90°B. 75°，15°，135°C. 60°，105°，150°D. 45°，80°，120°13.如图，把一张长方形的纸按图那样折叠后，B、C两点落在B′、C′点处，若得∠AOB′=70°，则∠B′OG的度数为( )A. 60°B. 40°C. 65°D. 55°二、计算题（本大题共1小题，共8.0分）14.如图，已知∠COB=2∠AOC，OD平分∠AOB，且∠COD=25°，求∠AOB的度数．三、解答题（本大题共4小题，共35.0分。

计算角的度数<练习题>1.如图6—10，已知△ABC中，∠A=58°，∠1=∠2，∠3=∠4，求∠BOC的度数．2．如图6—11，已知∠C=90°，∠1=∠2，∠3=∠4，求∠D的度数．3．如图6—12，已知六边形有六个内角，求它们的和是多少度？4．如图6—13，△ABC是等腰三角形，AB=AC，求∠A的度数．5．相同大小的8个等边三角形排列成如图6—14的形状，求∠1的度数．6．如图6—15，已知正方形ABCD的边BC上有一点E，边CD上有一点F，且∠1=∠2=15°，证明△AEF是等边三角形．7．如图6—16，D在△ABC的边BC上，且BD=DA=AC，∠BAC=63°，求∠DAC 的度数．8．设正方形ABCD对半折叠后，折线为EF，如图6—17，将B点移到直线EF上，折线为AP，求∠1、∠2的度数．答案仅供参考：1．在△ABC中，因为∠1=∠2，∠3=∠4，所以∠B+∠C=2∠2+2∠3=180°-∠A=180°-58°2（∠2+∠3）=122°∠2＋∠3=61°在△BOC中，∠BOC=180°-∠2-∠3=180°-61°=119°．2．因为∠1＋∠2＋∠ABC=180°∠3+∠4＋∠BAC=180°又因为∠C=90°，所以∠ABC＋∠BAC＝90°．∠1+∠2+∠3＋∠4＝360°-（∠ABC+∠BAC）∠1+∠2+∠3＋∠4＝360°-90°=270°因为∠1=∠2，∠3=∠4所以2∠1＋2∠3=270°∠1＋∠3=270°÷2=135°∠D=180°－∠1-∠3=180°-135°=45°3．将图6—12分割成图6—1’形状，六边形的六个内角和恰好等于这四个三角形的内角和，而每个三角形的内角和等于180°，所以六边形的六个内角和4×180°=720°．4．因为△ABC是等腰三角形，AB=AC，所以∠B=∠ACB=180°-110°=70°，因此∠A=180°-∠B-∠ACB=180°—70°-70°=40°．5．将四个等边三角形组成的水平的平行四边形绕∠1的顶点按顺时针旋转60°，与另外四个等边三角形组成的斜的平行四边形重合，所以∠1=60°．6．以对角线AC为折线折叠后，B与D重合，∠1与∠2重合，直线AE与AF重合，因此AE=AF，所以∠AEF=∠AFE．在△AEF中，∠EAF=90°-∠1-∠2=90°-15°-15°=60°，所以∠AEF=∠AFE=（180°-∠EAF）÷2=（180°-60°）÷2=60°．故△AEF是等边三角形．7．如图6—2’，因为BD=AD，所以∠1=∠2，又因为AD=AC，所以∠3=∠4，而∠3=∠1+∠2，所以∠4=∠3=2∠2在△ABC中，∠BAC＋∠B＋∠C=180°，63°＋∠2＋2∠2＝180°3∠2=180°-63°=117°∠2＝39°∠DAC=∠5=∠BAC-∠2=63°-39°=24°8．如图6—3’，以AP为折线折叠后，B与M重合，则AB=AM，∠3=∠4，以EF为折线折叠后，A与D重合，则AM=MD，又因为AM=AB，而AB=AD，所以AM=MD=AD，即△AMD是等边三角形，则∠1=60°．因为∠1+∠3+∠4=90°，∠3=∠4，所以∠4=（90°－∠1）÷2＝（90°-60°）÷2=15°∠2＝90°-∠4=90°-15°=75°。

求角的度数练习题在数学中，角度是一个非常重要的概念。

它是用来度量两条射线之间的旋转程度的单位。

我们可以通过练习题来加深对角度的理解和应用。

下面，我将给大家提供一些有关角度的练习题，希望能帮助大家更好地掌握这个概念。

1. 请计算以下角的度数：a) 直角的度数是多少？b) 一个锐角的度数是多少？c) 一个钝角的度数是多少？解答：a) 直角的度数是90度。

b) 一个锐角的度数小于90度。

c) 一个钝角的度数大于90度，但小于180度。

2. 请计算以下角的度数：a) 30度和60度的和是多少？b) 120度和240度的差是多少？解答：a) 30度和60度的和是90度。

b) 120度和240度的差是120度。

3. 请计算以下角的度数：a) 一个角的度数是它的补角度数的3倍，那么这个角的度数是多少？b) 一个角的度数是它的补角度数的一半，那么这个角的度数是多少？解答：a) 设这个角的度数为x，则它的补角度数为90度-x。

根据题意，有x = 3(90度-x)，解方程可得x = 67.5度。

b) 设这个角的度数为x，则它的补角度数为90度-x。

根据题意，有x = 0.5(90度-x)，解方程可得x = 30度。

4. 请计算以下角的度数：a) 一个角的度数是它的补角度数的5倍加上30度，那么这个角的度数是多少？b) 一个角的度数是它的补角度数的2倍减去45度，那么这个角的度数是多少？解答：a) 设这个角的度数为x，则它的补角度数为90度-x。

根据题意，有x = 5(90度-x) + 30度，解方程可得x = 72度。

b) 设这个角的度数为x，则它的补角度数为90度-x。

根据题意，有x = 2(90度-x) - 45度，解方程可得x = 45度。

5. 请计算以下角的度数：a) 一个角的度数是它的补角度数的3倍减去60度，那么这个角的度数是多少？b) 一个角的度数是它的补角度数的一半加上15度，那么这个角的度数是多少？解答：a) 设这个角的度数为x，则它的补角度数为90度-x。

角的计算专项练习60题(有答案)ok角的计算练习60题（附参考答案）1．如图，已知∠BOC=2∠AOB，OD平分∠AOC，∠BOD=14°，求∠AOB的度数．2．已知∠1=35°，∠2= _________ ．3．计算出下列各角的度数．4．算一算，下面是一个直角三角形．∠1= _________∠2= _________∠3= _________ ．9．求下面各个三角形中∠A的度数10．如图中，已知∠1=43°，∠2= _________ ，∠3= _________ ．11．计算三角形中角的度数．∠1= _________ ，∠2= _________ ，∠3=_________ ．12．算一算：∠1= _________ ；∠2= _________ ；∠3=_________ ．13．算一算，这些角各是多少度．已知∠2=40°求得：∠1= _________ °，∠3= _________ °，∠4= _________ °．14．求出如图所示各角的度数．15．如图，已知∠l=20°，∠2=46°，求∠3的度数．16．如图所示，∠BOC=110°，∠AOB=∠DOC，∠AOB是几度？17．如图：∠1=48°；∠2= _________ ．18．算一算．已知∠1=65°，求出：∠2、∠3、∠4的度数．19．求下面各角的度数．图1，∠1= _________ ∠2= _________图2，∠1= _________ ．20．求下面各角的度数．已知∠1=30°，∠2=90°．∠3= _________ ；∠4= _________ ；∠5= _________ ．21．∠1=32゜，∠2=36゜，∠3= _________ ．22．如图已知∠1=35°，∠2= _________ ，∠3=_________ ，∠4= _________ ．23．如图所示，已知∠1=30°．求：∠2、∠3和∠4的度数．24．已知∠1=25°，∠2= _________ °，∠3= _________ °，∠4= _________ °．25．算一算：∠1= _________ ；∠2= _________ ；∠3=_________ ．26．角的计算（1）如图1所示，已知：∠1=72°，∠2=45°，求：∠AOB= _________ ？（2）如图2所示，已知：∠1=35°，求∠2= _________ ？27．用量角器量出图中∠2的度数，再求∠1、∠3和∠4的度数．28．如图，已知∠1=130°，求∠2、∠3的度数．29．如图中，∠AOB=14°，∠COB=∠COD，求∠COD．30．在直角∠AOB内有射线OC、OD．∠AOC=∠BOD=60°，求∠COD的大小．31．求下面各角的度数．∠A= _________ ∠B= _________ ∠B=∠C=_________ ∠C= _________ ．32．（1）如图1，已知：∠1=45°，求：∠2（2）如图2，已知：∠1=90°，∠2=30°求：∠3等于多少度？（3）如图3，已知：∠1=135°求：∠2、∠3、∠4各等于多少度？33．如图，已知∠1=70°，∠2=25°，∠3=50°，求∠5=？34．如图是一张长方形纸折起来以后的图形，已知么∠2是65°，∠1是多少度？35．已知∠1=28°求∠2、∠3、∠4和∠5各是多少度？36．算一算∠1=65°∠2= _________ ∠3= _________ ∠4=_________ ∠1+∠2+∠3+∠4= _________ ．37．求角的度数．（1）AB=AC（如图1）∠1= _________∠2= _________（2）三角形ABC是等腰三角形（如图2）∠1= _________∠2= _________ ．38．如图中∠1=30°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠5= _________ ．39．如图所示，∠1=55．，请分别求出∠2、∠3、∠4的度数．40．图中，已知∠1=37°∠2= _________ ；∠3= _________ ；∠4=_________ ．41．如图，已知∠1=40°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠3+∠4= _________42．图中∠1= _________ ，∠2= _________ ，∠3= _________ ，∠1+∠2= _________ ．43．已知∠1=50°，求∠2=？∠3=？44．算一算．已知∠1=36°；∠2= _________ ；∠3= _________ ；∠4= _________ ；∠5= _________ ．45．图中，∠1=55°，∠2是直角，你能求∠3、∠4、∠5各是多少度吗？46．先量一量，再填空．①∠1= _________ ，是_________ 角；∠2=_________ ，是_________ 角；∠3= _________ ，是_________ 角．②画出∠1，使∠1=75°．47．算一算如图：已知∠1=35°∠3= _________ ∠4= _________∠2= _________ ∠1+∠2+∠3= _________ ．48．如图1，已知∠1=40°，∠2= _________ ，∠3= _________ ，∠4= _________ ．如图2，已知∠1=30°，∠2= _________ ，∠3=_________ ，∠4= _________ ，∠5=_________ ．49．求各个角的度数．（1）图1中：已知∠1=60°∠2= _________∠3= _________∠4= _________∠5= _________（2）图2中：已知∠1=75°∠2= _________∠3= _________∠4= _________ ．50．分别量出图中4个角的度数，再求出这4个角的和．∠1= _________ ；∠2= _________ ；∠3=_________ ；∠4= _________ ；∠1+∠2+∠3+∠4= _________ ．51．∠1= _________ ；∠2= _________ ；∠3=_________ ．52．∠1= _________ ；∠2= _________ ；∠3=_________ ．53．已知∠1=90°，∠2=50°，求∠3、∠4和∠5的度数．54．如图，求∠1和∠2的度数．55．已知：∠1=∠3，∠2=40°求：∠ADE=？56．在下面三角形中，∠1=38°，∠2+∠3=90°，求∠3和∠4各是多少度？57．在三角形ABC中，∠l=60°，∠3=50°，求∠2、∠4的度数．58．如图，已知：∠2=30°，∠3是直角，则∠2+∠3=_________ ，∠1+∠2+∠4= _________ ，∠1+∠2+∠3+∠4= _________ ．59．求图中各角的度数．图1：∠2= _________ ∠3= _________ 图2：∠1= _________ ∠2= _________ ∠3= _________ ．60．看图填数．①如图一，已知∠1=75°，那么∠2= _________ ∠3= _________ ∠4= _________ ．②如图二，∠1= _________ ∠2= _________ ∠3= _________ ．角的计算参考答案：1．设∠AOB=x，∠BOC=2x．则∠AOC=3x．又OD平分∠AOC，因为∠AOD=x．所以∠BOD=∠AOD﹣∠AOB=x ﹣x=14°因为x=28°即∠AOB=28°．答：∠AOB的度数是28°2．∠2=180°﹣∠1，∠2=180°﹣35°，∠2=145°．故答案为：145°．3．（1）（180°﹣50°）÷2，=130°÷2，=65°．答：角的度数是65°．（2）180°﹣40°=140°．答：角的度数是140°4．∠2=90°﹣60°=30°；∠3=180°﹣50°=130°；∠1=180°﹣∠2﹣∠3=180°﹣30°﹣130°=20°．故答案为：20°；30°；130°5．在直角三角形ABD中，因为∠ADB=90°，所以∠2=180°﹣90°﹣42°，∠2=48°；在直角三角形ADC中，∠ADC=90°，所以∠3=180°﹣90°﹣36°，∠3=54°答：∠2和∠3分别是48°和54°．6．（1）∠1=180°﹣90°﹣25°=65°；（2）180°﹣25°﹣20°=135°；∠2=135°﹣90°=45°；（3）∠3=180°﹣∠1=180°﹣65°=115°．故答案为：65°，45°，115°7．∠1与∠2组成了一个平角，所以∠2=180°﹣30°=150°；∠1与∠3组成一个直角，所以∠3=90°﹣30°=60°；故答案为：150°；60°8．根据题干分析可得：∠1=180﹣90﹣45=45（度），∠3=180﹣45=135（度），∠2=180﹣135=45（度），故答案为：45°，45°，135°9．∠ABC=90°，∠ACB=60°．所以，∠BAC=90°﹣∠BAC=90°﹣60°=30°；∠A=180°﹣∠B﹣∠C=180°﹣135°﹣20°=25°10．（1）∠2=90°﹣∠1=90°﹣43°=47°；（2）∠3=180°﹣∠2=180°﹣47°=133°．故答案为：47°，133°11．（1）根据题干分析可得：∠2=65°；则∠1=180°﹣65°﹣65°=50°；（2）∠3=90°﹣41°=49°；故答案为：50°；65°；49°12．∠1=180°﹣45°﹣90°=45°；∠2=180°﹣45°=135°；∠3=180°﹣135°=45°．故答案为：45°；135°；45°．13．根据题干分析可得：∠1=90°﹣40°=50°；∠3=180°﹣40°=140°；∠4=180°﹣140°=40°；故答案为：50；140；40．14．∠A=180°﹣40°﹣85°=55°；∠B=180°﹣90°﹣35°=55°；∠C=180°﹣20°﹣47°=113°．如图所示：故答案为：55°、55°、113°15．∠4=180°﹣∠1﹣∠2，=180°﹣20°﹣46°，=114°，∠3=180°﹣∠4，=180°﹣114°，=66°．答：∠3是66°16．根据题干分析可得：（180﹣110）÷2，=70÷2，=35（度），答：∠AOB的度数是35度．17．∠2=90°﹣48°=42°，故答案为：42°18．∠1与∠3是对顶角，所以∠3也是65°；因为∠1与∠2组成了一个平角，∠2与∠4又是对顶角，所以∠2=∠4=180°﹣65°=115°，答：∠2=115°，∠3=65°，∠4=115°．19．（1）∠1=∠2=（180°﹣120°）÷2=30°；（2）90°﹣40°=50°；所以∠1=50°；故答案为：30°；30°；50°20．∠1和∠5组成了一个直角，所以∠5=90﹣30=60（度），∠5与∠4组成了一个平角，所以∠4=180﹣60=120（度）；因为∠5与∠3是一组对顶角，所以∠3=∠5=60（度），故答案为：60°；120°；60°21．180°﹣32°﹣36°=112°；故答案为：112°22．∠2=90°﹣∠1=90°﹣35°=55°，∠3=180°﹣∠2=180°﹣55°=125°，∠4=180°﹣∠3=180°﹣125°=55°，故答案为：55°，125°，55°．23．∠2=90°﹣30°=60°，∠3=180°﹣60°=120°，∠4=180°﹣120°=60°．答：∠2的度数是60°，∠3的度数是120°，∠4的度数是60°24．∠2=180°﹣∠1=155°，∠3=180°﹣∠2=25°，∠4=180°﹣∠1=155°．故答案为：155，25，155．25．∠1=180°﹣35°=145°；∠2=180°﹣90°=90°；∠3=180°﹣125°=55°．故答案为：145°；90°；55°26．（1）∠AOB=∠1+∠2=72°+45°=117°；（2）∠2=180°﹣90°﹣∠1=55°．故答案为：117°；55°．27．经测量可得∠2=35°，则∠1=90°﹣35°=55°，∠3=180°﹣35°=145°，∠4=180°﹣145°=35°．答：∠1的度数是55°，∠3的度数是145°，∠4的度数是35°28．∠2=180°﹣∠1=180°﹣130°=50°；∠3=90°﹣∠2=90°﹣50°=40°；答：∠2是50度，∠3是40度．29.（90°﹣14°）÷2，=76°÷2，=38°；答：∠COD=38°30．∠COD=∠AOC+∠BOD﹣∠AOB，=60°+60°﹣90°，=30°．答：∠COD的大小是30°．31．（1）∠A=90°﹣34°=56°；（2）∠C=180°﹣90°﹣18°=72°，∠B=180°﹣60°﹣72°=48°；（3）∠B=∠C=（180°﹣48°）÷2=66°；（4）∠A=180°﹣119°=61°，∠C=90°﹣61°=29°．故答案为：56°；48°；66°；29°32．（1）∠2=180°﹣∠1=180°﹣45°=135°．（2）∠3=180°﹣∠1﹣∠2=180﹣90°﹣30°=60°．（3）∠3=180°﹣∠1=180°﹣135°=45°，∠4=180°﹣∠1=180°﹣135°=45°，∠2=180°﹣∠3=180°﹣45°=135°33．在小三角形里最大的角=180°﹣∠2﹣∠3=105°，∠4=180°﹣105°=75°，∠5=180°﹣∠1﹣∠4，=180°﹣70°﹣75°，=35°．答：∠5是35°34．180°﹣65°×2=180°﹣130°=50°．答：∠1是50度．35．∠4=90°，∠5=90°﹣∠1=90°﹣28°=62°，∠2=180°﹣∠1=180°﹣28°=152°，∠3=180°﹣∠2=180°﹣152°=28°；答：∠2=152°，∠3=28°，∠4=90°，∠5=62°．36．（1））∠2=90°﹣∠1，=90°﹣65°，=25°；（2））∠3=180°﹣∠2，=180°﹣25°，=155°；（3））∠4=180°﹣∠3，=180°﹣155°，=25°；（4））∠1+∠2+∠3+∠4=360°﹣90°，=270°．或∠1+∠2+∠3+∠4=65°+25°+155°+25°=270°．故答案为：25°；155°；25°；270°37．（1）∠C=180°﹣120°=60°，∠1=90°﹣∠C=90°﹣60°=30°；∠2=180°﹣60°×2=60°；（2）∠1=90°﹣60°=30°；∠2=180°﹣∠1×2﹣90°，=180°﹣30°×2﹣90°，=30°．故答案为：（1）30°，60°；（2）30°，30°38．根据题干分析可得：∠3=90°；∠2=90°﹣30°=60°；∠4=∠1=30°；∠5=180°﹣30°=150°；故答案为：60°；90°；30°；15039．如图：∠4=90°﹣∠1，=90°﹣55°，=35°，∠3=180°﹣∠4﹣∠5，=180°﹣35°﹣90°，=55°，∠2=180°﹣∠3，=180°﹣55°，=125°，答：∠2是125°、∠3是55°、∠4是35°40．∠2=90°﹣∠1=90°﹣37°=53°，∠3=180°﹣∠2=180°﹣53°=127°，∠4=180°﹣∠3=180°﹣127°=53°故答案为：53°，127°，53°41．∠2=∠4=180°﹣40°=140°，∠3=180°﹣∠2=40°，∠3+∠4=180°．故答案为：140°，40°，140°，180°42．∠1=90﹣50=40（度）；∠2=90﹣40=50（度）；∠3=180﹣50=130（度）；∠1+∠2=90（度）；故答案为：40°；50°；130°；90°43．∠2=180°﹣50°=130°，∠3=180°﹣90°=90°．答：∠2=130°，∠3=90°．44．根据题干分析可得：∠3是直角，是90°；∠2=90°﹣36°=54°；∠4=90°﹣54°=36°；∠5=180°﹣36°=144°，故答案为：54°；90°；36°；144°45．∠3=90°﹣55°=35°，∠5=180°﹣55°=125°，∠4=180°﹣125°=55°．答：∠3=35°、∠4=55°、∠5=125°46．（1）经过测量可知∠1=50°，是锐角，∠2=40°，是锐角，∠3=120°，是钝角；（2）根据分析画图如下：故答案为：50°；锐；4°；锐；120°；钝47．∠2=180°﹣∠1=180°﹣35°=145°，∠3=180°﹣∠2=180°﹣145°=35°，∠4=90°，∠1+∠2+∠3=35°+145°+35°=215°．故答案为：35°，90°，145°，215°48．图一：因为，∠1=40°．所以，∠2=180°﹣40°=140°；∠3=180°﹣140°=40°；∠4=180°﹣40°=140°；图二：因为，∠1=30°．所以，∠2=90°﹣30°=60°；∠3=90°；∠4=180°﹣60°﹣90°=30°；∠5=180°﹣30°=150°；故答案为：140°，40°，140°，60°，90°，30°，150°49．（1）因为∠2=90°，平角=180°，所以，∠3=180°﹣∠1﹣∠2=180°﹣90°﹣60°=30°；∠5=180°﹣∠1=180°﹣60°=120°；∠4=180°﹣∠5=180°﹣120°=60°；（2）因为∠1=75°，平角=180°，所以，∠2=180°﹣∠1=180°﹣75°=105°；∠4=180°﹣∠1=180°﹣75°=105°；∠3=180°﹣∠4=180°﹣105°=75°；故答案为：90°，30°，60°，120°，105°，75°，105°50．测量可得图中∠1=90°，∠2=45°，∠3=90°，∠4=135°．∠1+∠2+∠3+∠4=90°+45°+90°+135°=360°．故答案为：90°，45°，90°，135°．360°51．观察图形可知：∠3=90°；∠1=180﹣35=145（度）；∠2=90﹣30=60（度）；故答案为：145°；60°；90°52．因为∠1是等腰直角三角形底角，所以∠1=90°÷2=45°；因为正方形的两条对角线互相垂直，所以∠2=∠3=90°．故答案为：45°；90°；90°53．（1）∠3=180°﹣∠2=180°﹣50°=130°；（2）∠4=180°﹣∠3=180°﹣130°=50°；（3）∠5=180°﹣∠1﹣∠2=180°﹣90°﹣50°=40°．故答案为：∠3=130°，∠4=50°，∠5=40°54．∠1=180°﹣90°﹣65°=25°；∠2=180°﹣120°=60°．答：∠1的度数是25°；∠2的度数是60°．55．∠ADE=（180°﹣40°）÷2+40°，=140°÷2+40°，=70°+40°，=110°．答：∠ADE是110°．56．∠4=180°﹣∠1﹣（∠2+∠3），∠4=180°﹣38°﹣90°，∠4=52°；∠3=180°﹣90°﹣∠4，∠3=180°﹣90°﹣52°，∠3=38°．答：∠3是38°，∠4是52°57．因为∠1+∠3+∠4=180°，∠l=60°，∠3=50°，所以∠4=180°﹣60°﹣50°=70°；因为∠6=90°，所以∠2=90°﹣∠3，=90°﹣50°，=40°58．∠2+∠3=30°+90°=120°；∠1+∠2+∠3+∠4=360°；∠1+∠2+∠4=360°﹣90°=270°．故答案为：120°，270°，360°．59.（1）∠2=90°=50°=40°；∠3=180°﹣（40°+30°）=110°；（2）∠1=180°﹣120°=60°；∠2=180°﹣（60°+45°），=180°﹣105°，=75°；∠3=180°﹣75°=105°．故答案为：40°、110°；60°、75°、60．因为∠1+∠2=180°，∠1=75°，所以75°+∠2=180°，75°﹣75°+∠2=180°﹣75°，∠2=105°；因为∠1与∠3，∠2与∠4，分别是对顶角，所以∠1=∠3=75°，∠2=∠4=105°；（2）因为∠1+35°=180°，∠1+35°﹣35°=180°﹣35°，∠1=145°；因为∠2+30°=90°，∠2+30°﹣30°=90°﹣30°，∠2=60°；因为∠3是一个直角，所以∠3=90°；故答案为：（1）105°，75°，105°．（2）145°，60°，90°．。

小学二年级数学角的练习题
1. 计算下列角度的度数:
a) 直角
b) 钝角
c) 锐角
d) 平角
2. 判断下列角度是否是锐角:
a) 35度
b) 90度
c) 120度
d) 180度
3. 在下列各组角中，找出每组中度数最大的角:
a) 30度, 45度, 60度
b) 75度, 90度, 105度
c) 120度, 135度, 150度
d) 170度, 180度, 185度
4. 用直尺、铅笔和量角器绘制下列角度:
a) 50度
b) 90度
c) 135度
d) 160度
5. 判断下列两个角度是否互补角或补角:
a) 60度, 120度
b) 45度, 135度
c) 30度, 150度
d) 75度, 105度
6. 两个角的度数之和为180度，这两个角是什么关系?举一个例子来说明。

7. 在下列四幅图中，哪些图中包含锐角?哪些图中包含钝角?哪些图中包含直角?
8. 凸多边形（凸四边形、凸五边形等）中，每个角度的和等于多少度?
9. 画一个锐角、一个钝角和一个直角。

对每个角度进行标记，并计算它们的度数。

10. 如果一个角的度数是60度，它的补角和余角各是多少度?
以上是一些小学二年级数学角的练习题，希望能够帮助学生巩固和理解角度的概念和计算方法。

通过这些练习题，学生可以提高自己对角度的感知能力，并且加深对锐角、钝角、直角和平角的认识。

通过手工绘画和计算，学生可以更好地理解角度的度数，并且掌握角度的测量技巧。

希望同学们能够认真完成这些练习题，并且善于思考和总结，提高数学学习的效果。

小学求角度10题
以下是10道适合小学生练习的角度计算题目，这些题目旨在帮助学生理解角度的基本概念，掌握角度的计算方法。

基本角度认识：
一个完整的圆是多少度？
直角判断：
一个角是90°，它是什么角？
锐角和钝角判断：
一个角比90°小，它是什么角？一个角比90°大但比180°小，它是什么角？
计算两角之和：
一个角是30°，另一个角是60°，这两个角的和是多少度？
计算补角：
如果一个角的度数是45°，那么它的补角是多少度？
利用三角形内角和：
一个三角形有两个角分别是50°和60°，求第三个角的度数。

平角计算：
一个角的补角是130°，求这个角的度数。

利用钟表计算角度：
时钟上，3时整时针和分针之间的夹角是多少度？
多角度之和：
有三个角，分别是35°、45°和70°，求这三个角的和。

多角度计算综合：
四边形ABCD中，已知∠A=60°，∠B=90°，∠C=120°，求∠D的度数。

这些题目旨在通过不同的角度计算情境，帮助学生理解角度的概念，掌握角度的加、减以及补角、内角和等知识点，从而提高学生的空间观念和数学运算能力。

2023-2024学年四年级数学上册典型例题系列第二单元：角度计算问题“拓展型”专项练习（解析版）一、填空题。

1．图中∠1＝70°，那么∠2＝( )°。

【答案】40【分析】由图可知，∠1、∠2和∠3构成了一个平角，根据折叠的特性可知，∠1与∠3的度数相等，用平角的度数减去∠1和∠3的度数，即可算出∠2的度数。

据此解答。

如图：【详解】180°－70°－70°＝110°－70°＝40°图中∠1＝70°，那么∠2＝40°。

【点睛】本题主要考查学生对平角的认识，掌握折叠后角大小不变这一特性是解决此题的关键。

2．看图计算。

如图，已知∠1＝50°，那么∠2＝( )。

【答案】80°【分析】在图中添加∠3；如图：∠1是∠3折上去的，∠1与∠3相等，且∠1＋∠2＋∠3＝平角＝180°，已知∠1的度数，只要用180°－∠1－∠3＝∠2，据此解答。

【详解】因为∠1＝∠3＝50°，∠1＋∠2＋∠3＝180°，所以∠2＝180°－50°－50°＝130°－50°＝80°。

如图，已知∠1＝50°，那么∠2＝（80°）。

【点睛】本题主要考查了学生对折叠角的求法，关键是清楚哪些角的度数和是180°。

3．将长方形的一个角按下图所示的方式折叠。

已知140∠=︒，那么2∠=( )°。

【答案】10【分析】长方形中有四个直角，因此∠1＋∠1＋∠2＝90°，由此可知，用90°减2个∠1的度数即可，依此计算。

【详解】90°–40°－40°＝50°–40°＝10°，即∠2＝10°。

【点睛】解答此题的关键是应熟练掌握直角的特点，以及图形的折叠特点。

四年级算角练习题1. 计算下列各式中的角度，并判断该角度是锐角、直角还是钝角。

a) 45°b) 90°c) 30°d) 120°e) 60°f) 150°2. 在下图中，找出各个角度并判断它们是锐角、直角还是钝角。

[插入一张有几个角度的图]3. 根据下面的问题，作答并计算所需角度。

a) 一张纸平铺在桌子上，两边分别与桌子的边缘平行。

如果一次使用一支直尺，你能有几种办法画出一个钝角？b) 两根长度相同的线段相交，它们最多能形成几个角度？c) 某个多边形的内角和是540度，这个多边形有几个角？4. 直角、钝角和锐角可以进一步分为哪些类型？请列举并解释。

5. 用非常简单的方式解释下面的几个术语：a) 角度b) 直角c) 锐角d) 钝角6. 在自己的生活中找到至少三个每天都会遇到的角度，并解释它们在日常生活中的重要性。

7. 在建筑或设计中，角度应用得非常广泛。

举例说明在以下情境中为什么需要仔细考虑和使用正确的角度：a) 建造房屋b) 设计桥梁c) 绘画和设计d) 制造家具8. 角度测量的工具有哪些？请简要说明它们的用途。

9. 通过以下问题，加深对角度的理解：a) 画一个锐角和一个钝角。

b) 将一个直角划分为两个锐角。

c) 如何判断两条线是平行的？d) 如果一个三角形的两个角是45°和90°，第三个角是多少度？10. 如果一个锐角的度数是x，它的补角是多少度？而它的余角呢？11. 通过解决实际问题，进一步巩固对角度的理解：a) 一个钟上的时针和分针形成一个锐角，那么它们之间的度数差是多少？b) 一条边与水平线成30°的角，另一条边与竖直线成60°的角，这个角的度数是多少？c) 影子的长度是物体长度的3倍，那么太阳高度角度数是多少？12. 总结本次练习题所学的知识，并总结角度的定义、类型和计算方法。

通过以上练习题，相信你对四年级的算角有了更深入的理解。

小学数学《角度的计算》练习题(含答案) 知识要点：角的分类：小于9°的角叫做锐角。

直角等于90°。

大于90°而小于180°的角叫钝角。

平角等于180°。

三角形的特点：三角形内角和是180°。

一个三角形中最多有一个钝角，最多有一个直角，可以有三个锐角。

直角三角形的两个锐角的度数和是90°。

四边形的特点：平行四边形、梯形、正方形、长方形的内角和都是360°。

角的关系：解题指导1：例1】求下图中∠a的度数。

思路点拨】三角形的内角和是180°，根据图形可以看出，180°-（∠a+57°）=180°-142°，也就是∠a+57°=142°，就可以求出∠a的度数。

解题过程】180°-57°-142°=38°答：∠a是38°。

解题指导2：例2】在下面的图中，∠1=∠2=∠3，在这个图中所有锐角的和是15°。

∠AOB是多少度？思路点拨】图中所有锐角的和是15°，图中一共有几个锐角呢，观察图形可知，除了∠1，∠2，∠3外，还有∠1+∠2，∠2+∠3，和∠AOB三个锐角。

因此有∠1+∠2+∠3+（∠1+∠2）+（∠2+∠3）+∠AOB=15°，根据∠1=∠2=∠3，就可以求出∠AOB的度数。

解题过程】___∠1+∠2+∠3，∠1=∠2=∠3AOB=15°×3=45°答：∠AOB=45°。

解题指导3：例3】六边形有六个内角，它们的和是多少度？五边形的内角和是多少度？解答：五边形可以分成三个三角形，每个三角形的内角和是180°，所以五边形的内角和是3个三角形的内角和，即180°×3=540°。

基础巩固】1、求下图中∠2的度数。