用Excel快速制作直方图、柏拉图[1]
- 格式:doc
- 大小:44.01 KB
- 文档页数:6


柏拉图,直方图,管制图绘制方法目录第一章柏拉图制作方法 (3)1.1、制作方法 (3)1.2、举例说明 (3)第二章直方图制作方法 (7)2.1、直方图的制作步骤 (7)2.2、举例说明 (7)第三章管制图制作说明 (11)3.1、各个管制图界限一览表 (11)3.2、符号说明 (11)3.3、绘制管制图的步骤 (12)3.4、管制图使用时之注意事项 (12)3.5、举例说明 (13)第一章柏拉图制作方法1.1、制作方法1、收集制作柏拉图需要的数据,分类输入表格。
2、将数据按照由小到大的顺序排列3、以此计算出这些数据的累积数目和累积百分率。
4、选择需要的数据生成柱状图。
5、选择累积百分比,将图表类型变为折线形式。
6、更改两个纵坐标值将累积百分比的的最大值改为1;将发生数据的最大值改为发生数据的累计最大值,或大于等于累计最大值。
7、调整图之间的间隙,美化图形生成柏拉图。
1.2、举例说明第一步:收集整理数据。
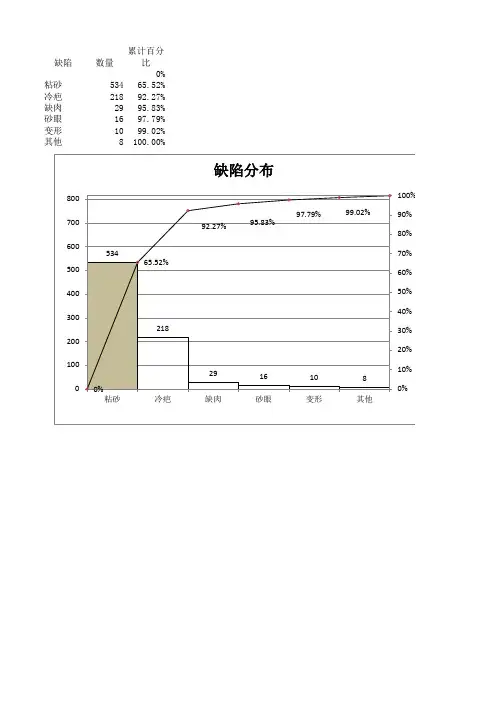
收集不良数量,以此计算累计不良数,百分比,累计百分比。
第二步:选择项目,不良数量,累计百分比生成柱状图。
第三步:在图上选择累计百分比图形,点击鼠标右键,选择更改图标类型,以此选择带标记的折线图。
将累计百分比的柱状图变为折线图。
第四步:更改成折线图后,选中折线图,在右键里面选择“设置数据系列格式”随后选择“次坐标轴”得到如下图像。
第五步:选择累积百分比的坐标轴,点击右键选择“设置坐标轴格式”。
在里面将最大值改为1,最小值为0,其他可按照需求或选择默认设置。
选择数量坐标轴,点击右键选择“设置坐标轴格式”在里面将最大值设置为大于或等于累计不良数的最大值。
最小值和间隔可按照需要选择。
得到如下图形。
第六步:选中图形点击右键选择“设置数据系列格式”在里面将“分类间隔”调整为零。
双击每个柱子选择不同的颜色可以改变每个柱子的颜色。
最后调整后得到如下图形。
第七步:如果要清晰的表达数据,可点击右键在图形上面添加数据标签。

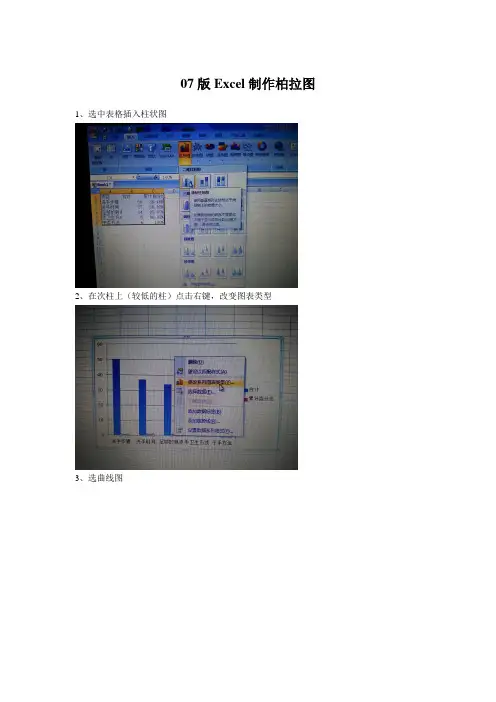
07版Excel制作柏拉图1、选中表格插入柱状图
2、在次柱上(较低的柱)点击右键,改变图表类型
3、选曲线图
4、选中曲线右击---设置格式
5、选“次坐标轴”
6、设置y轴,选中左侧数字点右键—设置格式
7、最大值、最小值选“固定”最大值改130(五个项目总数是130)
8、设置右侧数值,选中右击—设置格式,
最大值、最小值选固定----最大值改成1,右侧数值就会成为100%
9、点布局---坐标轴---次要坐标横轴----显示从左向右坐标轴,次坐标轴就会出现
10、选中次坐标轴,右击设置格式
11、选中---在刻度线上。
(这一步是为了让曲线起点落在y轴上)
把坐标轴标签---改为“无”(这一步是为了再次隐藏次坐标轴,我给忘了,嘻嘻)
12、在表格上添加一行,输入(这一步是为了让曲线起点落在0点上)
13、点击曲线,左侧表格就会出现蓝框框,
14、把累计百分比的蓝框框扩大至0%上
15、选中柱状图右击---设置
16曲线间距划到0%(这一步为了缩小柱状的间距)
17、成了!!!。
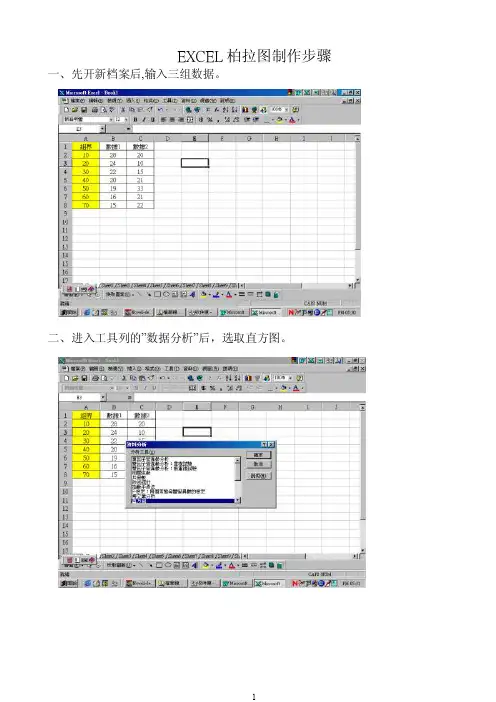
EXCEL柏拉图制作步骤一、先开新档案后,输入三组数据。
二、进入工具列的”数据分析”后,选取直方图。
三、选择数据范围,如下图所示。
四、选择完成后按确认,会出现图表、累计百分率及柏拉图,如下图。
五、依以下步骤删除不必要储存格。
六、删除储存格
七、删除以下三栏储存格。
八、得到下列结果。
九、更改自己所要之表头项目,如下例。
十、选取数据范围后依需求作计算。
十一、选取储存格数据范围后按鼠标右键,选取数据范围
十二、将累计%中的数值消除,重新输入累加百分率公式。
十三、如下图。
十四、输入完成后如下。
十五、依个人喜好调整柏拉图刻度。
十七、如下例。
十八、调整后如下。
十九、订正坐标轴名称。
二十、更改数列宽度。
二十一、调整间距。
二十二、完成后可依需要输入实验名称、日期时间、作业者等,或做改善前后比较。
11。

ExceL中柏拉图制作方法分析ExceL中柏拉图制作方法一、柏拉图——质量数据处理七大工具之一柏拉图统计是QC里常用的统计管理方法之一,就是所谓的品管七大手法中的一项——圆柱折线排列图的另称。
圆柱折线排列图是分析和寻找影响质量主原因素的一种工具,其形式是一条分类轴,两条数值轴的坐标图:1.左边纵坐标表示频数(如件数、价值等),右边纵坐标表示频率(百分比率);2.折线表示百分率,准确的说是累积百分率;(作图关键,一定要理解。
有的资料没有注意到,只是一笔带过)3.横坐标表示影响质量的各项因素,按影响程度的大小(即出现频数多少)从左向右排列。
二、收集基础数据注意事项1.归纳决定数据分类项目,分类项目必须合乎问题的焦点,应先从结果上着手,便于洞察问题。
2.横轴按项目类别降序排列,“其它”项目排在末位。
3.如果问题焦点少的项目多时,就归纳到“其它”项。
4.前2~3项累计影响度应在70%以上。
三、制做方法步骤(一)最终效果,如图1“数据表”、图2“最后效果”。
——看到下面表格了吗?最后一项:累计百分率(知道怎么算吗?按照顺序由最高的不良率依次累计下面的,这样才能累计到100%啊!很简单吧!)图1 数据表图2 最后效果(二)方法步骤1.先建数据表如图3数据源。
图3数据源2.图表向导4-步骤之1-图表类型”对话窗,点“自定义类型”标签,在“图标类型”标签下拉框中选择“两轴线-柱图”,然后点“完成”后如图4选择类型后。
图4 选择类型后3.对Y轴刻度进行设置。
——对左边Y轴刻度设置如图5;对右边Y轴刻度如图6图5 左边Y轴设置图6 右边Y轴刻度设置——左右Y轴设置设置后如图7图7 左右Y轴设置设置后4.最后格式化最后对图表表达要素对标题、数轴名称、数据表等进行格式化设置,完成后如图8完成图。
柏拉图的制作1.柏拉图的意义及用途1.1 意义柏拉图系意大利十七世纪的经济学家,在研究当时的社会贫富现象时所发明的,特取其名称之为柏拉图,在中国又称为排列图,又称ABC图,亦可称重点分析图。
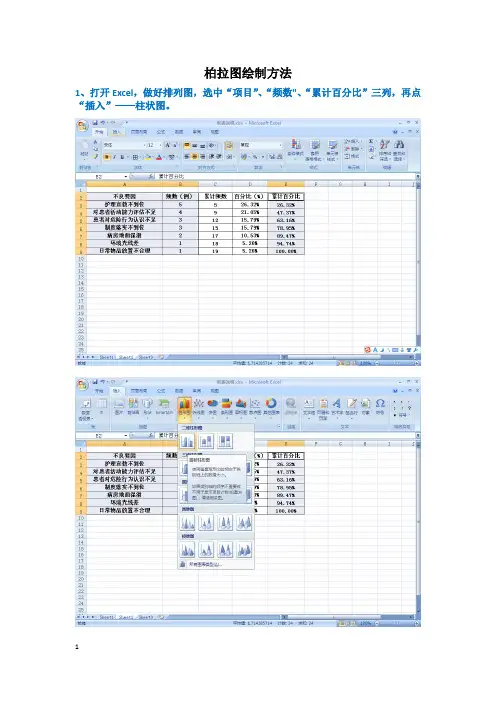
柏拉图绘制方法1、打开Excel,做好排列图,选中“项目”、“频数"、“累计百分比”三列,再点“插入”——柱状图。
2、左键点中“累计百分比”项柱状图,即砖红色柱状部分;右键单击,选择“更改系列图表类型"。
3、在弹出的新窗口中选择“折线图”,便出现下面第二张图里砖红色曲线。
砖红色柱状图变成了红色折线图4、左键点中“累计百分比”项折线图,即砖红色折线部分,单击右键,选择“设置数据系列格式”5、在弹出的新窗口中选择“系列选项"中的“次坐标轴"选项(若为2003版Excel,则在新窗口中点“坐标轴"—“次坐标轴”),之后关闭窗口。
6、下图为初步完成的图,还需要继续绘制(加油!)7、左键点中蓝色柱状图,单击右键,选择“设置数据系列格式",在新窗口中的“分类间距"中调至“无间距”,便出现第三张图所示的柱状图。
这时,我们发现,折线图的起点还不在坐标轴的0点上,所以要进行以下的调整:8、左键再次点中红色折线图,排列图中会出现各种颜色的框框,将代表“累计百分比”的框框(即蓝色箭头所指部分)往上拉一格,折线的起点就会回到横坐标轴(x轴)的0点,如第二张图红色箭头所示.上图看到折线起点与x轴重合,那么以下这两步,要将起点调至左y轴0点.9、点中柏拉图,选择图表工具中的“布局”选项,再点中“坐标轴”--“次要横坐标轴”-—“显示从左到右坐标轴”,得到图3图1图2图310、再次点中“坐标轴”——“次要横坐标轴”——“其它次要横坐标轴选项”,得到下图:11、在弹出的新窗口中选择“在刻度线上”,得到下图:12、左键单击上方横坐标轴,右键选择“设置坐标轴格式”,在弹出的窗口当中,将“主要刻度线类型”及“坐标轴标签"都设为“无”(如箭头所指),得到图2:图1图2从上图我们看到折线的起点和终点都在x轴和y轴上,但是还需要更改主y轴和次y轴的标签,其中左y轴的最大值设为不良要因累计频数的总和,右y轴最大值设为1.13、左键点中左y轴标签,右键选择“设置坐标轴格式”,如下图:14、在弹出的新窗口中将“最小值”设为“0";“最大值"设为不良要因累计频数值,在本例中,即设为“19”;“主要刻度单位"和“次要刻度单位”根据频数的大小设置合理的间距,本例设为“5”,如下图:15、同样方法,设置右y轴的最小值为“0”,最大值为“1"(即100%),得到下图:16、调整各柱状图的颜色方便区分。


excel2020制作柏拉图的方法
制作柏拉图步骤2:选中“不良描述”,"不良数量","累积不良率"三列数据,选择插入---直方图--平面直方图里的群组直方图,得到如下初版图
制作柏拉图步骤3:①右键点击累积不良率棕色直方图
②点击弹出菜单里的【变更图表类型】如下图
制作柏拉图步骤4:在弹出的对话框选择折线图如下图一,得到如下图二
制作柏拉图步骤5:①右键点击刚生成的折线图的折线
②选择弹出菜单里的【资料数列格式】
制作柏拉图步骤6:选择--副坐标轴--确定后得到如下第二图
制作柏拉图步骤7:调整下图表颜色,并加上数据标签,得到最后的柏拉图,看是不是很简单
猜你喜欢:。
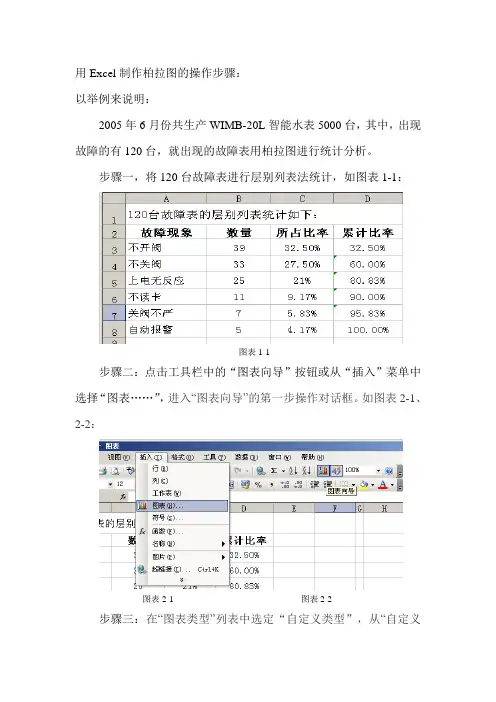
用Excel制作柏拉图的操作步骤:以举例来说明:2005年6月份共生产WIMB-20L智能水表5000台,其中,出现故障的有120台,就出现的故障表用柏拉图进行统计分析。
步骤一,将120台故障表进行层别列表法统计,如图表1-1:图表1-1步骤二:点击工具栏中的“图表向导”按钮或从“插入”菜单中选择“图表……”,进入“图表向导”的第一步操作对话框。
如图表2-1、2-2:图表2-1 图表2-2步骤三:在“图表类型”列表中选定“自定义类型”,从“自定义类型”选项中选择“线—柱图”,接着单击“下一步”按钮。
步骤四:将出现“图表源数据”对话框,如下图表4-1;点击“系列”选项,将出现图表4-2界面;在系列选框中,1、点击“添加”按钮,将自动添加“系列一”,弹出图表4-3界面,在“名称(N)”栏中录入“数量”,点击“值(V)”栏后的红色箭头,选择数据区域,如:下表4-4,点击“分类(X)轴标志(T)”栏后的红色箭头,选择X轴的标志,如下表4-5,选取完整后将出现图4-6界面,在预览框内显示图表样式。
2、点击“添加”,自动添加系列二,在名称栏中录入“累积比率”,“值(V)”的选取参照系列一,分类(X)轴标志不变,操作完成后,界面如图4-7,点击“下一步”图表4-1图表4-2图表4-3图表4-4图表4-5图4-6图表4-7步骤五:图标选项中,录入所需内容:如下表5-1,在“坐标轴”选项中,点击“次坐标轴数值Y轴”前的小方框,在预览框中将看到次Y轴坐标显示数值,如下表5-2,在“数据标志”栏中点击“值”前面的小方框,则预览框中的图表显示出相应的数值,如下表5-3,点击“下一步”,将出现5-4对话框,点击“完成”,图表将自动插入到Excel文档中。
(其他的选项则根据自己的需求选取)图表5-1图表5-2图表5-3图表5-4图表5-5步骤六:点击图表移动到合适位置,双击“数值Y轴”将弹出“坐标轴格式”,选择“刻度”,将“自动设置”的值按需求设置,最大值为数量的和120,其他的选项按自己的需求设置;同样双击“次Y轴数值”,对Y轴数值进行重新设置,注意:次Y轴的数值与Y轴的数值是相对应的,当Y轴的最大值为不合格数量的总量时,则与之对应的此Y轴的最大值应为100%。
用EXCEL划柏拉图陈锦河老师提供一、依據課堂案例在ecxel上完成此統計表二、繪製柏拉圖雛形1. 用左手按住Ctrl+Al t,右手操作滑鼠以下籃色區塊Mark起來2. 選取圖表精靈(出現對話框)3. 點選自訂類型\ 雙軸直線圖加直條圖3. 按完成,出現如下圖表4. 選取圖表,按滑鼠右鍵出現選單,選擇圖表選項\標題,輸入圖表、類別X軸、數值Y 軸、次要數值Y軸標題5. 按確定後得到下圖三、調整數值Y軸與次要數值Y軸,使對應刻度一致。
1. 選取Y軸,按滑鼠右鍵,選取座標軸格式2. 出現下圖3. 選取刻度4. 將最大值改為250(同累計不良數)、主要刻度改為50,如此可將數值Y軸劃分為五個區間(如下圖)5. 選取次要數值Y軸,按滑鼠右鍵,選取座標軸格式\刻度,將最大值改為1(同累計不良率100%)、主要刻度改為0.2,如此可將次要數值Y軸劃分為五個區間(如下圖)四、消除柱與柱之間的間隔1. 選取柱狀圖,按滑鼠右鍵,選取資料數列格式\選項,修改類別間距為0,2. 按確定,得到下圖五、在圖面上清楚標註相關數據1. 在柱狀圖上標示出各不良項目的不良數,選取柱狀圖,按滑鼠右鍵,選取資料數列格式\資料標籤,勾選資料包含內容2. 按確定,得到下圖3. 在推移圖上標示出各不良項目的累計不良率,選取推移圖,按滑鼠右鍵,選取資料數列格式\資料標籤,勾選資料包含內容,按確定,得到下圖六、想辦法把累計不良率的資料點移至柱狀圖的右上角1. 在統計表內增加一個0,如下圖2. 於累計不良率的資料來源中包含此欄,選取圖表,按滑鼠右鍵,點選來源資料\數列\,點選數列中的累計不良率,如下圖3. 將滑鼠移至數值(V),重新定義資料來源,使資料來源包含“F2”(用左手按住Ctrl+Al t,右手操作滑鼠)5. 選取圖表,按滑鼠右鍵,點選圖表選項\座標軸\,勾選X次座標軸,如下圖7. 選取累計不良率推移圖,按滑鼠右鍵,點選資料數列格式\選項,勾選漲跌線定,得到下圖(達到目的了,很神奇吧!!)七、多出次分類X軸,怪怪的,得想辦法把它去掉~1. 取圖表,按滑鼠右鍵,點選來源資料\數列\,數列選擇不良數,重新定義第二類別X軸標籤範圍,選取空白區域,2. 按確定,得到下圖3. 調整第二數值座標軸格式為“百分比”,此時推移圖與第二數值座標軸的百分比數值(100%)重疊,請手動微調位置。
Excel不会制作柏拉图?简单快速一分钟搞定
1.建立需要使用的数据。
2.选择数据建立图表。
先选择柱状图即可
3.建立图表后,选择“累计占比”数据,右键点击,然后左键单击“设置数据系列格式”。
选中“累计占比“数据”
选择“数据系列格式”
4.添加次要坐标轴:直接在选项内选一下就行啦。
5.再次选中“累计占比”数据,右键单击,选择“更改系列图表类型”,选择折线图。
右键单击“累计占比”数据,更改图表类型
6.选择“迟到人数”项,右键单击,选择“设置数据系列格式”,将“分类间距”调整为0.
右键点击“迟到人数”设置柱状图间隔
7.选中图表,在布局中依次添加标题、单位。
并按照自我喜好美化就可以啦。
添加标题及单位
PS:小编每周至少发文五篇,主要对象是0基础Office教程,关注小编不迷路。
品质管理工具如何用EXCEL绘制柏拉图品质管理工具如何用EXCEL绘制柏拉图一、什么是柏拉图1.起源意大利经济学家柏拉图(Vilfredo.Pareto)在分析社会财富分配时设计出的一种统计图,美国品管大师Joseph Juran将之发展并应用到了质量管理中。
柏拉图能够充分反映出“少数关键、多数次要”的规律,也就是说柏拉图是一种寻找主要因素、抓住主要矛盾的手法。
例如:少数用户占有大部分销售额、设备故障停顿时间大部分由少数故障引起,不合格品中大多数由少数人员造成等。
2.定义根据收集的数据,以不良原因、不良状况、不良发生的位置分类;计算各项目所占的比例按大小顺序排列,再加上累积值的图形。
按照累计的百分数可以将各项分成三类:0~80%为A类,显然是主要问题点;80~90%为B类,是次要因素;90~100%为C类,是一般因素。
二、如何用EXCEL绘制柏拉图1.先搜集数据;如在本例中,对110PCS的工具剪产品品质进行检验,分别按不良项目统计各项不良的具体数量。
如剪刀开口34PCS,手柄错位26PCS,刀片生锈19PCS等等。
具体数据的收集方式可以使用QC七大手法里面的查检表。
如以下表1。
表12. 用EXCEL作出分项统计表(按原因、人员、工序、不良项目等);a) 把分类项目按频数大小从大到小进行排列,至于“其他”项,不论其频数大小均放在最后;b) 计算各项目在全体项目中所占比率(在本例中即指不良率);c) 计算累计比率(即累计不良率),相关数据可经EXCEL公式自动生成。
(见如下表二)表二3.作好以上数据表格后,我们就可以用EXCEL根据以上数据自动生成柏拉图的要件了。
a) 先生成柱状图;在数据表中,我们先选择代码和不良品数两列的数据区域;如下图1图1b) 然后调出EXCEL的图表工具栏,点击图表类型图标旁边的下拉箭头,选取柱形图按扭;这时在选中的数据区域附近就会自动成生一份柱形图,如下图2。
图2c) 这样我们所要绘制的柏拉图柱形图的部分已经出来了,但是我们要清除不需要的部分并稍作调整;i. 由于我们生成柱形图时选择的两列数据,所以EXCEL生成了两组柱形图,我们要将按代码生成的那一组柱形图(即浅蓝色的那一组)清除掉。
EXCEL柏拉圖製作步驟一、先開新檔案後,輸入三組數據。
二、進入工具列的”資料分析”後,選取直方圖。
三、選擇資料範圍,如下圖所示。
四、選擇完成後按確認,會出現圖表、累計百分率及柏拉圖,如下圖。
五、依以下步驟刪除不必要儲存格。
六、刪除儲存格
七、刪除以下三欄儲存格。
八、得到下列結果。
九、更改自己所要之表頭項目,如下例。
十、選取資料範圍後依需求作計算。
十一、選取儲存格資料範圍後按滑鼠右鍵,選取資料範圍
十二、將累計%中的數值消除,重新輸入累加百分率公式。
十三、如下圖。
十四、輸入完成後如下。
十五、依個人喜好調整柏拉圖刻度。
十七、如下例。
十八、調整後如下。
十九、訂正座標軸名稱。
二十、更改數列寬度。
二十一、調整間距。
較。
11。
方法是先要加载分析工具库!打开<工具>下拉菜单,看看有没有<数据分析>选项?如果没有的话,按下面的方法操作加载分析工具库!打开<工具>下拉菜单,点击<加载宏>!在“分析工具库” 前的复选框打上“ √ ” 并确定!呵呵,安装完以后,在打看<工具>下拉菜单,看看有什么新发现?是不是多了<数据分析>这一栏?呵呵,就是他!用处可大了!打开数据分析,看看有什么新发现?看到了吧,你要的东东都在里面!还有其他好多东东!navyxu2006-03-17 10:34 可以用呀,office 2003 上的有好多中类:方差分析方差分析工具提供了几种方差分析工具。
具体使用哪一种工具则根据因素的个数以及待检验样本总体中所含样本的个数而定。
方差分析:单因素此工具可对两个或更多样本的数据执行简单的方差分析。
此分析可提供一种假设测试,该假设的内容是:每个样本都取自相同基础概率分布,而不是对所有样本来说基础概率分布都不相同。
如果只有两个样本,则工作表函数TTEST 可被平等使用。
如果有两个以上样本,则没有合适的TTEST 归纳和“单因素方差分析”模型可被调用。
方差分析:包含重复的双因素此分析工具可用于当数据按照二维进行分类时的情况。
例如,在测量植物高度的实验中,植物可能使用不同品牌的化肥(例如A、B 和C),并且也可能放在不同温度的环境中(例如高和低)。
对于这 6 对可能的组合{化肥,温度},我们有相同数量的植物高度观察值。
使用此方差分析工具,我们可检验:使用不同品牌化肥的植物的高度是否取自相同的基础总体;在此分析中,温度可以被忽略。
不同温度下的植物的高度是否取自相同的基础总体;在此分析中,化肥可以被忽略。
是否考虑到在第 1 步中发现的不同品牌化肥之间的差异以及第 2 步中不同温度之间差异的影响,代表所有{化肥,温度} 值的 6 个样本取自相同的样本总体。
另一种假设是仅基于化肥或温度来说,这些差异会对特定的{化肥,温度} 值有影响。
方差分析:无重复的双因素此分析工具可用于当数据按照二维进行分类且包含重复的双因素的情况。
但是,对于此工具,假设每一对值只有一个观察值(例如,在上面的示例中的{化肥,温度} 值)。
使用此工具我们可以应用方差分析的第 1 和 2 步检验:包含重复的双因素情况,但没有足够的数据应用第 3 步的数据。
相关系数CORREL 和PEARSON 工作表函数可计算两组不同测量值变量之间的相关系数,条件是当每种变量的测量值都是对N 个对象进行观测所得到的。
(任何对象的任何丢失的观测值都会引起在分析中忽略该对象。
)系数分析工具特别适合于当N 个对象中的每个对象都有多于两个测量值变量的情况。
它可提供输出表和相关矩阵,并显示应用于每种可能的测量值变量对的CORREL(或PEARSON)值。
与协方差一样,相关系数是描述两个测量值变量之间的离散程度的指标。
与协方差的不同之处在于,相关系数是成比例的,因此它的值独立于这两种测量值变量的表示单位。
(例如,如果两个测量值变量为重量和高度,如果重量单位从磅换算成千克,则相关系数的值不改变)。
任何相关系数的值必须介于-1 和+1 之间。
可以使用相关分析工具来检验每对测量值变量,以便确定两个测量值变量的变化是否相关,即,一个变量的较大值是否与另一个变量的较大值相关联(正相关);或者一个变量的较小值是否与另一个变量的较大值相关联(负相关);还是两个变量中的值互不关联(相关系数近似于零)。
协方差“相关”和“协方差”工具可在相同设置下使用,当您对一组个体进行观测而获得了N 个不同的测量值变量。
“相关”和“协方差”工具都可返回一个输出表和一个矩阵,分别表示每对测量值变量之间的相关系数和协方差。
不同之处在于相关系数的取值在-1 和+1 之间,而协方差没有限定的取值范围。
相关系数和协方差都是描述两个变量离散程度的指标。
“协方差”工具为每对测量值变量计算工作表函数COVAR 的值。
(当只有两个测量值变量,即N=2 时,可直接使用函数COVAR,而不是协方差工具)在协方差工具的输出表中的第i 行、第j 列的对角线上的输入值就是第i 个测量值变量与其自身的协方差;这就是用工作表函数VARP 计算得出的变量的总体方差。
可以使用协方差工具来检验每对测量值变量,以便确定两个测量值变量的变化是否相关,即,一个变量的较大值是否与另一个变量的较大值相关联(正相关);或者一个变量的较小值是否与另一个变量的较大值相关联(负相关);还是两个变量中的值互不关联(协方差近似于零)。
描述统计“描述统计”分析工具用于生成数据源区域中数据的单变量统计分析报表,提供有关数据趋中性和易变性的信息。
指数平滑“指数平滑”分析工具基于前期预测值导出相应的新预测值,并修正前期预测值的误差。
此工具将使用平滑常数a,其大小决定了本次预测对前期预测误差的修正程度。
注释0.2 到0.3 之间的数值可作为合理的平滑常数。
这些数值表明本次预测应将前期预测值的误差调整20% 到30%。
大一些的常数导致快一些的响应但会生成不可靠的预测。
小一些的常数会导致预测值长期的延迟。
F-检验双样本方差“F-检验双样本方差”分析工具通过双样本F-检验,对两个样本总体的方差进行比较。
例如,您可在一次游泳比赛中对每两个队的时间样本使用F-检验工具。
该工具提供空值假设的检验结果,该假设的内容是:这两个样本来自具有相同方差的分布,而不是方差在基础分布中不相等。
该工具计算F-统计(或F-比值)的 F 值。
F 值接近于1 说明基础总体方差是相等的。
在输出表中,如果 F < 1,则当总体方差相等且根据所选择的显著水平“F 单尾临界值”返回小于1 的临界值时,“P(F <= f) 单尾”返回F-统计的观察值小于F 的概率Alpha。
如果F > 1,则当总体方差相等且根据所选择的显著水平,“F 单尾临界值”返回大于1 的临界值时,“P(F <= f) 单尾”返回F-统计的观察值大于 F 的概率Alpha。
傅立叶分析“傅立叶分析”分析工具可以解决线性系统问题,并能通过快速傅立叶变换(FFT) 进行数据变换来分析周期性的数据。
此工具也支持逆变换,即通过对变换后的数据的逆变换返回初始数据。
直方图“直方图”分析工具可计算数据单元格区域和数据接收区间的单个和累积频率。
此工具可用于统计数据集中某个数值出现的次数。
例如,在一个有20 名学生的班里,可按字母评分的分类来确定成绩的分布情况。
直方图表可给出字母评分的边界,以及在最低边界和当前边界之间分数出现的次数。
出现频率最多的分数即为数据集中的众数。
移动平均“移动平均”分析工具可以基于特定的过去某段时期中变量的平均值,对未来值进行预测。
移动平均值提供了由所有历史数据的简单的平均值所代表的趋势信息。
使用此工具可以预测销售量、库存或其他趋势。
预测值的计算公式如下:式中:N 为进行移动平均计算的过去期间的个数Aj 为期间j 的实际值Fj 为期间j 的预测值随机数发生器“随机数发生器”分析工具可用几个分布中的一个产生的独立随机数来填充某个区域。
可以通过概率分布来表示总体中的主体特征。
例如,可以使用正态分布来表示人体身高的总体特征,或者使用双值输出的伯努利分布来表示掷币实验结果的总体特征。
排位与百分比排位“排位与百分比排位”分析工具可以产生一个数据表,在其中包含数据集中各个数值的顺序排位和百分比排位。
该工具用来分析数据集中各数值间的相对位置关系。
该工具使用工作表函数RANK 和PERCENTRANK。
RANK 不考虑重复值。
如果希望考虑重复值,请在使用工作表函数RANK 的同时,使用帮助文件中所建议的函数RANK 的修正因素。
回归分析回归分析工具通过对一组观察值使用“最小二乘法”直线拟合来执行线性回归分析。
本工具可用来分析单个因变量是如何受一个或几个自变量影响的。
例如,观察某个运动员的运动成绩与一系列统计因素的关系,如年龄、身高和体重等。
可以基于一组已知的成绩统计数据,确定这三个因素分别在运动成绩测试中所占的比重,使用该结果对尚未进行过测试的运动员的表现作出预测。
回归工具使用工作表函数LINEST。
抽样分析抽样分析工具以数据源区域为总体,从而为其创建一个样本。
当总体太大而不能进行处理或绘制时,可以选用具有代表性的样本。
如果确认数据源区域中的数据是周期性的,还可以对一个周期中特定时间段中的数值进行采样。
例如,如果数据源区域包含季度销售量数据,则以四为周期进行取样,将在输出区域中生成与数据源区域中相同季度的数值。
t-检验“双样本t-检验”分析工具基于每个样本检验样本总体平均值是否相等。
这三个工具分别使用不同的假设:样本总体方差相等;样本总体方差不相等;两个样本代表处理前后同一对象上的观察值。
对于以下所有三个工具,t-统计值t 被计算并在输出表中显示为“t Stat”。
数据决定了t 是负值还是非负值。
假设基于相等的基础总体平均值,如果t < 0,则“P(T <= t) 单尾”返回t-统计的观察值比t 更趋向负值的概率。
如果t >=0,则“P(T <= t) 单尾”返回t-统计的观察值比t 更趋向正值的概率。
“t 单尾临界值”返回截止值,这样,t-统计的观察值将大于或等于“t 单尾临界值”的概率就为Alpha。
“P(T <= t) 双尾”返回将被观察的t-统计的绝对值大于t 的概率。
“P 双尾临界值”返回截止值,这样,被观察的t-统计的绝对值大于“P 双尾临界值”的概率就为Alpha。
t-检验:双样本等方差假设本分析工具可进行双样本学生t-检验。
此t-检验窗体先假设两个数据集取自具有相同方差的分布,故也称作同方差t-检验。
可以使用此t-检验来确定两个样本是否来自具有相同总体平均值的分布。
t-检验:双样本异方差假设本分析工具可进行双样本学生t-检验。
此t-检验窗体先假设两个数据集取自具有不同方差的分布,故也称作异方差t-检验。
如同上面的“等方差”情况,可以使用此t-检验来确定两个样本是否来自具有相同总体平均值的分布。
当两个样本中有截然不同的对象时,可使用此检验。
当对于每个对象具有唯一一组对象以及代表每个对象在处理前后的测量值的两个样本时,则应使用下面所描述的成对检验。
用于确定统计值t 的公式如下:下列公式可用于计算自由度df。
因为计算结果一般不是整数,所以df 的值被舍入为最接近的整数以便从t 表中获得临界值。
因为有可能为TTEST 计算出一个带有非整数df 的。