(完整版)双星系统

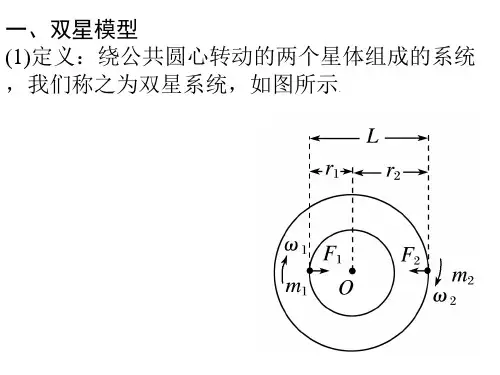
双星系统的形成和演化双星系统是宇宙中常见的一种天体系统，由两颗恒星相互绕转而成。

本文将探讨双星系统的形成和演化过程。

一、形成过程在宇宙的演化过程中，恒星的形成是通过分子云坍缩所产生的。

当分子云的质心坍缩形成一个原恒星时，由于吸积物质的非均匀性分布，可能会导致分子云中心的质量团块与外部质量较小的物质吸积体之间的角动量不同。

这种非均匀性分布导致了质心的不稳定性，从而在分子云中心形成了两个或多个质量团块，最终发展为双星系统。

二、演化过程1. 原初阶段在形成后的双星系统中，两颗恒星间的距离通常很近，它们之间的相互作用力非常强烈。

由于双星系统质量团块之间具有固有的旋转动量，这些旋转动量会影响系统的演化。

2. 潮汐相互作用由于双星系统内部存在着引力相互作用，较大质量的恒星会通过引力作用导致其表面形变，并使两颗恒星之间产生潮汐作用。

这种潮汐力会逐渐追赶较小质量的恒星，从而引起双星系统间的能量损失。

潮汐作用还可以使恒星轨道逐渐缩小，使双星系统的距离变得更加紧密。

3. 能量交换恒星在运动过程中会释放能量，并通过辐射传递到周围空间。

在双星系统中，恒星之间的引力作用会导致能量的交换。

这种能量交换可以改变恒星轨道的形状和大小，进而影响双星系统的演化。

4. 质量转移在一些双星系统中，恒星之间可能发生质量的传输现象。

当其中一颗恒星膨胀成为红巨星时，其外层物质可能被吸引到另一颗恒星上，导致质量的转移。

这种质量转移会改变双星系统的质量比例，进而影响它们的演化路径。

5. 演化终阶在双星系统的演化过程中，由于质量的转移和能量的损失，较大质量的恒星可能会进一步发展成为红巨星，而较小质量的恒星可能会逐渐燃烧耗尽内部的氢融合燃料。

最终，较大质量的恒星可能会发生超新星爆炸，而较小质量的恒星可能会形成白矮星或中子星。

综上所述，双星系统的形成和演化是一个复杂的过程，涉及到重力相互作用、潮汐力、质量转移等多个因素的影响。

只有通过不断观测和研究，我们才能更好地理解宇宙中双星系统的丰富多样性及其对宇宙演化的重要作用。

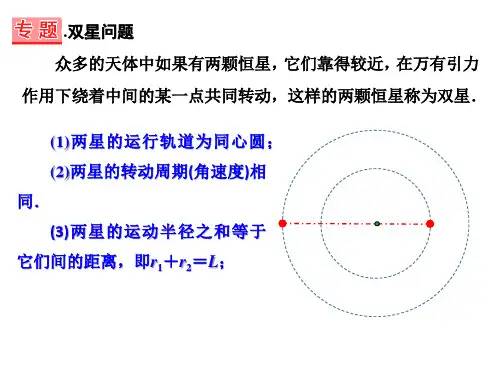
双星模型、三星模型、四星模型天体物理中的双星，三星，四星，多星系统是自然的天文现象，天体之间的相互作用遵循万有引力的规律，他们的运动规律也同样遵循开普勒行星运动的三条基本规律。

双星、三星系统的等效质量的计算，运行周期的计算等都是以万有引力提供向心力为出发点的。

双星系统的引力作用遵循牛顿第三定律：F F ='，作用力的方向在双星间的连线上，角速度相等，ωωω==21。

【例题1】天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星。

双星系统在银河系中很普遍。

利用双星系统中两颗恒星的运动特征可推算出它们的总质量。

已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动，周期均为T ，两颗恒星之间的距离为r ，试推算这个双星系统的总质量。

（引力常量为G ）【解析】：设两颗恒星的质量分别为m 1、m 2，做圆周运动的半径分别为r 1、r 2，角速度分别为ω1、ω2。

根据题意有21ωω=①r r r =+21②根据万有引力定律和牛顿定律，有G1211221r w m rm m = ③G1221221r w m rm m =④联立以上各式解得2121m m rm r +=⑤根据解速度与周期的关系知Tπωω221== ⑥联立③⑤⑥式解得322214r GT m m π=+【例题2】神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时，发现了LMCX3双星系统，它由可见星A 和不可见的暗星B 构成，两星视为质点，不考虑其他天体的影响.A 、B 围绕两者连线上的O 点做匀速圆周运动，它们之间的距离保持不变，如图4-2所示.引力常量为G ，由观测能够得到可见星A 的速率v 和运行周期T.(1)可见星A 所受暗星B 的引力F a 可等效为位于O 点处质量为m′的星体(视为质点)对它的引力，设A 和B 的质量分别为m 1、m 2，试求m′(用m 1、m 2表示).(2)求暗星B 的质量m 2与可见星A 的速率v 、运行周期T 和质量m 1之间的关系式；(3)恒星演化到末期，如果其质量大于太阳质量m s 的2倍，它将有可能成为黑洞.若可见星A 的速率v=2.7×105 m/s ，运行周期T=4.7π×104 s ，质量m 1=6m s ，试通过估算来判断暗星B 有可能是黑洞吗？ （G=6.67×10-11 N·m 2/kg 2，m s =2.0×1030 kg ）解析：设A 、B 的圆轨道半径分别为，由题意知，A 、B 做匀速圆周运动的角速度相同，设其为。

专题：“双星”及“三星”问题【前置性学习】1.甲、乙两名滑冰运动员 m甲=70kg, m乙=36 kg，当面拉着弹簧秤做圆周运动的滑冰表演（如图1），两人相距0.9 m，弹簧秤的示数为21 N，以下判断正确的选项是（）A．两人的线速度同样，约为 1 m/sB．两人的角速度同样，为 1 rad/sC．两人的运动半径同样，为0.45 m图 1 D．两人的运动半径不一样，甲为0.6 m, 乙为 0.3 m★学习目标1.★ 新知研究一、“双星”问题：两颗质量能够对比的恒星互相绕着旋转的现象，叫双星。

双星问题是万有引力定律在天文学上的应用的一个重要内容，现就这种问题的办理作简要剖析。

1.要明确双星中两颗子星做匀速圆周运动的向心力根源双星中两颗子星互相绕着旋转可看作匀速圆周运动，其向心力由两恒星间的万有引力提供。

因为力的作用是互相的，因此两子星做圆周运动的向心力大小是相等的，利用万有引力定律能够求得其大小。

2.要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动，因此它们的运动周期是相等的，角速度也是相等的，因此线速度与两子星的轨道半径成正比。

（因为在双星运动问题中，忽视其余星体引力的状况下向心力由双星相互间万有引力供给，可理解为一对作使劲与反作使劲）轨道半径之比与双星质量之比相反：（由向心力同样推导）r 1： r 2=m： m2122mω r =mω r2112m1r 1=m2r 2r 1:r 2=m2:m1线速度之比与质量比相反：（由半径之比推导）V1:V 2=m2:m1V1=ω r 1V2=ωr 2V1:V 2=r 1:r 2=m2:m1二、“三星”问题有两种状况：第一种三颗星连在同向来线上，两颗星环绕中央的星（静止不动）在同一半径为R的圆轨道上运转，周期同样；第二种三颗星位于等边三角形的三个极点上，并沿外接于等边三角形的外接圆轨道运转，三星运转周期同样。

3.要明确两子星圆周运动的动力学关系。

“双星”问题及天体的追及相遇问题一、双星问题1.模型构建：在天体运动中，将两颗彼此相距较近，且在相互之间万有引力作用下绕两者连线上的某点做角速度、周期相同的匀速圆周运动的恒星称为双星。

2．模型条件：（1)两颗星彼此相距较近.(2)两颗星靠相互之间的万有引力提供向心力做匀速圆周运动。

(3）两颗星绕同一圆心做圆周运动。

3．模型特点: (1)“向心力等大反向"——两颗星做匀速圆周运动的向心力由它们之间的万有引力提供.(2)“周期、角速度相同”—-两颗恒星做匀速圆周运动的周期、角速度相等。

（3)三个反比关系：m1r1＝m2r2；m1v1＝m2v2;m1a1＝m2a2推导：根据两球的向心力大小相等可得，m1ω2r1＝m2ω2r2,即m1r1＝m2r2；等式m1r1＝m2r2两边同乘以角速度ω,得m1r1ω＝m2r2ω，即m1v1＝m2v2；由m1ω2r1＝m2ω2r2直接可得，m1a1＝m2a2。

（4）巧妙求质量和：错误!＝m1ω2r1①错误!＝m2ω2r2②由①＋②得：错误!＝ω2L ∴m1＋m2＝错误!4. 解答双星问题应注意“两等"“两不等"(1）“两等”: ①它们的角速度相等.②双星做匀速圆周运动向心力由它们之间的万有引力提供，即它们受到的向心力大小总是相等。

（2)“两不等"：①双星做匀速圆周运动的圆心是它们连线上的一点，所以双星做匀速圆周运动的半径与双星间的距离是不相等的，它们的轨道半径之和才等于它们间的距离。

②由m1ω2r1＝m2ω2r2知由于m1与m2一般不相等，故r1与r2一般也不相等。

二、多星模型（1）定义:所研究星体的万有引力的合力提供做圆周运动的向心力，除中央星体外,各星体的角速度或周期相同．（2)三星模型：①三颗星位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上运行(如图甲所示)．②三颗质量均为m的星体位于等边三角形的三个顶点上(如图乙所示）．（3）四星模型：①其中一种是四颗质量相等的恒星位于正方形的四个顶点上，沿着外接于正方形的圆形轨道做匀速圆周运动(如图丙）．②另一种是三颗恒星始终位于正三角形的三个顶点上,另一颗位于中心O，外围三颗星绕O做匀速圆周运动（如图丁所示）．三、卫星的追及相遇问题1、某星体的两颗卫星从相距最近到再次相距最近遵从的规律：内轨道卫星所转过的圆心角与外轨道卫星所转过的圆心角之差为2π的整数倍。

双星系统高中物理
双星系统高中物理
双星系统是由两个恒星组成的天体系统。

其中一颗恒星的质量比另一颗恒星的质量大得多，因此被称为主恒星，而另一颗恒星被称为伴恒星。

双星系统的运行受到两个恒星之间的引力而动态稳定的控制，当两个恒星的引力力不平衡时，它们将开始运动。

高中物理中，双星系统是理解物体运动的重要理论。

双星系统不仅仅是人们理解物体运动的一种简单模型，它还被广泛应用于实际情况，如太阳系中太阳和行星之间的运动、卫星中卫星和地球之间的运动等。

此外，双星系统还可以帮助人们探索太空环境中的科学问题，如星系结构、太阳系中物理过程等。

专题：“双星”及“三星”问题【前置性学习】1. 甲、乙两名溜冰运动员m 甲=70kg,m 乙=36 kg ，面对面拉着弹簧秤做圆周运动的溜冰表演（如图1），两人相距0.9 m ，弹簧秤的示数为21 N ，下列判断正确的是（ ）A ．两人的线速度相同，约为1 m/sB ．两人的角速度相同，为1 rad/sC ．两人的运动半径相同，为0.45 mD ．两人的运动半径不同，甲为0.6 m,乙为0.3 m ★学习目标 1.★新知探究一、 “双星”问题：两颗质量可以相比的恒星相互绕着旋转的现象，叫双星。

双星问题是万有引力定律在天文学上的应用的一个重要内容，现就这类问题的处理作简要分析。

1.要明确双星中两颗子星做匀速圆周运动的向心力来源双星中两颗子星相互绕着旋转可看作匀速圆周运动，其向心力由两恒星间的万有引力提 供。

由于力的作用是相互的，所以两子星做圆周运动的向心力大小是相等的，利用万有引力定律可以求得其大小。

2.要明确双星中两颗子星匀速圆周运动的运动参量的关系两子星绕着连线上的一点做圆周运动，所以它们的运动周期是相等的，角速度也是相等 的，所以线速度与两子星的轨道半径成正比。

3.要明确两子星圆周运动的动力学关系。

设双星的两子星的质量分别为M 1和M 2，相距L ，M 1和M 2的线速度分别为v 1和v 2，角 速度分别为ω1和ω2，由万有引力定律和牛顿第二定律得：M 1： 22121111121M M v G M M r Lr ω==M 2： 22122222222M M v G M M r Lr ω== 在这里要特别注意的是在求两子星间的万有引力时两子星间的距离不能代成了两子星做圆周运动的轨道半径。

4.“双星”问题的分析思路 质量m 1，m 2；球心间距离L ；轨道半径 r 1 ，r 2 ；周期T 1，T 2 ；角速度ω1，ω2 线速度V 1 V 2；周期相同：（参考同轴转动问题） T 1=T 2 角速度相同：（参考同轴转动问题）ω1 =ω2 向心力相同：Fn 1=Fn 2（由于在双星运动问题中，忽略其他星体引力的情况下向心力由双星彼此间万有引力提供，可理解为一对作用力与反作用力） 轨道半径之比与双星质量之比相反：（由向心力相同推导）r 1：r 2=m 2：m 1m 1ω2r 1=m 2ω2r 2m 1r 1=m 2r 2 r 1:r 2=m 2:m 1 线速度之比与质量比相反：（由半径之比推导） V 1:V 2=m 2:m 1V 1=ωr 1 V 2=ωr 2M 1 M 2 ω1 ω2L r 1r 2图1V1:V2=r1:r2=m2:m1二、“三星”问题有两种情况：第一种三颗星连在同一直线上，两颗星围绕中央的星（静止不动）在同一半径为R 的圆轨道上运行，周期相同；第二种三颗星位于等边三角形的三个顶点上，并沿外接于等边三角形的外接圆轨道运行，三星运行周期相同。