双星系统

物理双星问题三个公式物理中的双星问题，可是个有趣又有点烧脑的知识点。

咱们今儿就来好好唠唠其中的三个关键公式。

先来说说双星系统的定义哈。

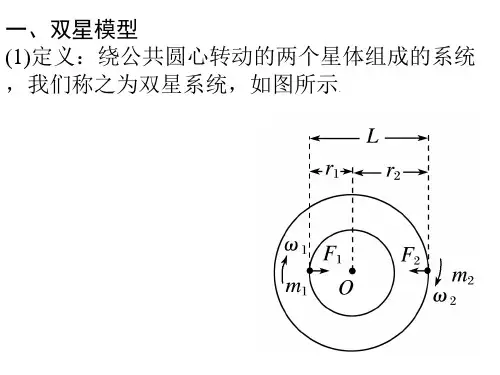
双星，简单说就是两颗恒星在彼此引力作用下，绕着共同的中心做圆周运动。

这就像两个人手拉手在转圈跳舞，彼此的引力就是那只拉住他们的“无形的手”。

咱们来看看第一个公式，线速度与半径的关系公式：$v_1r_1 =v_2r_2$ 。

这里的$v_1$、$v_2$ 分别是两颗星的线速度，$r_1$、$r_2$ 是它们各自做圆周运动的半径。

给您举个例子吧。

有一次我在公园里散步，看到两个小孩在玩那种用绳子拴着的小球甩圈游戏。

其中一个小孩力气大，甩动的速度快，绳子也长，就相当于线速度大、半径大；另一个小孩力气小，速度慢，绳子短，就类似线速度小、半径小。

但是不管怎样，他们转一圈所用的时间是一样的，这就和双星系统里线速度和半径的关系有点像。

再来说第二个公式，角速度相同公式：$\omega_1 = \omega_2$ 。

这个很好理解，双星就像在一个锅里搅和的两个勺子，它们转动的快慢是一样的。

记得有一次我在厨房搅拌鸡蛋，我用两根筷子，就像是双星一样，一起在蛋液里转动，它们的角速度肯定是相同的呀。

最后是第三个公式，向心力公式：$F = m\omega^2r$ 。

这个公式告诉我们，向心力的大小和质量、角速度以及半径都有关系。

就像我骑自行车，轮子的质量越大，我蹬得越快（角速度大），轮子的半径越大，我蹬起来就越费劲，需要的力就越大。

总之，这三个公式在双星问题中可是起着关键作用。

只要咱们理解透彻，再遇到双星相关的题目，那都不在话下。

您瞧，物理其实没那么可怕，只要多观察生活中的现象，很多抽象的知识就能变得清晰易懂。

希望您在学习物理的道路上越走越顺，加油！。

一、双星模型 (1)定义：绕公共圆心转动的两个星体组成的系统 ，我们称之为双星系统，如图所示．
(2)特点： ①各自所需的向心力由彼此间的万有引力相互提供 ②两颗星的周期及角速度都相同 ③两颗星的半径与它们之间的距离关系为 (3)两颗星到圆心的距离与星体质量成反比，与星体 运动的线速度成反比．
拓展： 1．若在双星模型中，图中L、m1、m2、G为已知量， 双星运动的周期如何表示？ 2．若双星运动的周期为T，双星之间的距离为L，G 已知，双星的总质量如何表示？
球的影响，可以将月球和地球看成 上述星球A和B，月球绕其轨道中 心运行的周期记为T1ቤተ መጻሕፍቲ ባይዱ但在近似处 理问题时，常常认为月球是绕地心
做圆周运动的，这样算得的运行周 期为T2。已知地球和月球的质量分 别为5.98×1024 kg和7.35×1022 kg 。求T2与T1两者的平方之比。(结果 保留3位小数)
[典例2] (多选)宇宙间存在一些离其他恒星较远的三星 系统，其中有一种三星系统如图所示，三颗质量均为m 的星位于等边三角形的三个顶点，三角形边长为R，忽略
其他星体对它们的引力作用，三星在同一平面内绕三角 形中心O做匀速圆周运动，万有引力常量为G，则
（1）每颗星做圆周运动的线速度？ （2）每颗星做圆周运动的角速度？ （3）每颗星做圆周运动的周期？
(二)宇宙三星模型 (1)定义：所研究星体的万有引力的合力提供做圆周运 动的向心力，除中央星体外，各星体的角速度或周期 相同． (2)三星模型： ①三颗星位于同一直线上，两颗环绕
星围绕中央星在同一半径 为R的圆形轨道上运行 ②三颗质量均为m的星体位 于等边三角形的三个顶点 上(如图乙所示)．
(三)宇宙四星模型
万有引力的合力提供做圆周运动的向心力，除中央 星体外，各星体的角速度或周期相同．

宇宙隐秘;双星系统的现代传说宇宙，是人类探索的永恒之谜，充满无尽的奥秘和未知。

在这无垠的星空中，隐藏着许多令人惊叹的奇观和传奇故事。

而双星系统，则是其中一个备受关注的话题，它们的存在和运行方式引发了人们无尽的遐想和想象。

双星系统是指两颗恒星彼此紧密相连，它们共同围绕着它们的质心旋转。

这种系统在宇宙中并不罕见，据科学家的研究，大约有一半以上的恒星都存在于双星系统之中。

但是，即便科学家们对双星系统有着相对全面的了解，但它们带来的神秘和传奇永远不会减少。

双星系统的现代传说，源自于人们对它们的浪漫化想象和探索。

在许多文化中，双星系统被赋予了各种神话传说和浪漫情怀。

例如，在古代希腊神话中，双星系统被认为是爱神维纳斯和战神玛尔斯的象征，它们的轨迹被解释为两位神明的热烈爱情。

而在许多古老的传说中，双星系统也被视为不可分割的伴侣，它们共同舞动在星空中，象征着永恒的爱情和忠诚。

除了浪漫的传说之外，双星系统也给科学家们带来了无数的挑战和谜团。

它们的运行方式和相互作用机制，常常让人们感到震惊和困惑。

一些双星系统呈现出复杂多变的轨迹和周期，有些甚至会发生黑洞合并或超新星爆炸等壮观事件。

这些奇特的现象，成为了天文学家们深入研究的对象，也为人们带来了更多关于宇宙奥秘的发现和推测。

随着科技的不断进步，人类对双星系统的探索也在不断深入。

通过望远镜和卫星等设备，科学家们能够观测到更多细微的现象和变化，从而加深对双星系统的理解。

同时，一些天文学家还尝试利用双星系统来寻找外星生命的线索，因为这些系统可能会孕育出适宜生命存在的行星。

总的来说，双星系统的现代传说是一个充满未知和想象的故事。

它们以神秘的方式影响着人类文化和科学探索，成为了宇宙中不可或缺的一部分。

无论是浪漫的传说还是科学的探索，双星系统都将继续激发人们对宇宙的好奇心和向往，引领着我们不断前行，探寻宇宙的无尽奥秘。

双星系统在天文学中的未来应用
天体演化研究
利用双星系统研究恒星演化过程和物理特性，深入理 解恒星的起源、演化和结局。
宇宙尺度结构研究
通过双星系统观测和研究宇宙尺度上的物质分布、星 系形成和演化等重要问题。
天体物理学实验验证
利用双星系统验证天体物理学的理论和模型，推动天 文学的发展和进步。
THANKS
银河系中心是一个高密度的恒星区域，其中存在大量的双星系统。这些 双星系统对于研究银河系中心的结构和演化具有重要的意义。
03
星系核
在一些星系的中心，存在超大质量的黑洞，周围环绕着大量的恒星。在
这些恒星中，有些会形成双星系统。这些双星系统对于研究星系核的演
化具有重要的意义。
03
双星系统的物理效应
双星系统的引力效应
双星系统专题
目 录
• 双星系统的定义与特性 • 双星系统的观测与发现 • 双星系统的物理效应 • 双星系统在天文学中的应用 • 双星系统的未来研究展望
01
双星系统的定义与特 性
双星系统的定义
总结词
双星系统是由两颗恒星绕共同质心旋转的系统。
详细描述
双星系统是由两颗恒星组成的系统，它们通过相互之间的引力作用相互绕转， 形成一个稳定的系统。双星系统可以是密近双星，也可以是分居双星。
恒星物理参数
双星系统中的恒星由于相互引力作用 ，其物理参数（如质量、半径、温度 等）会发生变化，通过对这些参数的 测量和研究，有助于深入了解恒星的 物理性质和演化规律。
双星系统在星系演化研究中的应用
星系结构
通过对双星系统的观测和研究，可以了解星系的结构和分布，探究星系的形成和演化过程。
星系动力学
双星系统中的恒星运动轨迹受到相互引力的影响，通过对这些运动轨迹的研究，可以深入了解星系的 动力学特征和演化机制。

双星系统的运动学与动力学特性双星系统是宇宙中一种常见的天体系统，由两颗恒星围绕共同的质心进行运动。

这种系统的运动学和动力学特性对于我们理解恒星演化、星际物质的形成和星系的演化等诸多天体物理现象具有重要意义。

本文将探讨双星系统的运动学和动力学特性，以及它们对宇宙中的各种现象的影响。

首先，让我们来了解双星系统的运动学特性。

在一个双星系统中，两颗恒星相互围绕着共同的质心进行旋转运动。

这种旋转运动可以分为两种类型：椭圆轨道和环形轨道。

在椭圆轨道中，两颗恒星的距离会随着时间的推移而发生变化，而在环形轨道中，两颗恒星的距离保持不变。

这些运动学特性的研究可以帮助我们了解双星系统的形成和演化过程。

另外，双星系统的动力学特性也是非常重要的。

动力学研究主要关注双星系统的力学性质，包括引力相互作用、角动量守恒以及轨道演化等。

在双星系统中，两颗恒星之间的引力相互作用是导致它们围绕质心旋转的原因。

根据牛顿第二定律，两颗恒星的质量越大，它们之间的引力也就越大。

这种引力相互作用将影响双星系统的轨道形状和运动速度。

此外，角动量守恒也是双星系统的一个重要特性。

根据角动量守恒定律，一个物体的角动量在没有外力作用下保持不变。

在双星系统中，两颗恒星围绕质心旋转时，它们的角动量也是守恒的。

这意味着当一颗恒星靠近质心时，它的转速会加快，而当另一颗恒星靠近质心时，它的转速会减慢。

这种角动量守恒的特性对于我们理解恒星演化和星系的形成有着重要的意义。

最后，双星系统的轨道演化也是一个重要的研究领域。

在双星系统中，由于引力相互作用和其他外部因素的影响，它们的轨道形状和大小会随着时间的推移而发生变化。

这种轨道演化可能导致双星系统的合并或者分离，从而影响它们的演化轨迹。

对于理解星系和星际物质的形成过程以及恒星演化的理论模型的建立，轨道演化的研究具有重要的意义。

总结起来，双星系统的运动学和动力学特性对于我们理解宇宙中各种天体物理现象具有重要意义。

通过研究双星系统的运动学特性，我们可以了解它们的形成和演化过程。

双星系统高中物理
双星系统是由两个恒星组成的天体系统。

其中一颗恒星的质量比另一颗恒星的质量大得多，因此被称为主恒星，而另一颗恒星被称为伴恒星。

双星系统的运行受到两个恒星之间的引力而动态稳定的控制，当两个恒星的引力力不平衡时，它们将开始运动。

高中物理中，双星系统是理解物体运动的重要理论。

双星系统不仅仅是人们理解物体运动的一种简单模型，它还被广泛应用于实际情况，如太阳系中太阳和行星之间的运动、卫星中卫星和地球之间的运动等。

此外，双星系统还可以帮助人们探索太空环境中的科学问题，如星系结构、太阳系中物理过程等。

双星系统的角速度公式双星系统是由两颗星体相互围绕质心运动的天体系统。

在该系统中，每个星体都对另一个星体施加引力作用，使两个星体的运动状态相互影响。

角速度是描述旋转或转动的速度的物理量，在双星系统中也有其相应的角速度公式。

首先，我们需要了解双星系统的质心和规约角速度的概念。

质心是指双星系统中两颗星体质量加权平均后的位置，规约角速度是指双星系统围绕质心旋转的角速度。

质心公式可以表示为：\[ r = \frac {m_1 \cdot r_1 + m_2 \cdot r_2}{m_1 + m_2} \]其中，m1和m2分别是两颗星体的质量，r1和r2分别是它们相对于质心的位置矢量。

而规约角速度公式可表示为：\[ \omega = \sqrt{\frac {G \cdot (m_1 + m_2)}{r^3}} \]其中，G为引力常数。

这个公式的推导可以从牛顿运动定律出发。

根据牛顿定律，两个星体的引力相互作用可写为：\[ F = \frac {G \cdot m_1 \cdot m_2}{r^2} \]其中，F为引力大小，m1和m2为星体的质量，r为星体之间的距离。

另一方面，质心受到的合外力为0，所以在两个星体之间的引力产生的合外力为0. 由此可得：\[ m_1 \cdot a_1 + m_2 \cdot a_2 = 0 \]其中，a1和a2分别为两个星体的加速度。

在双星系统中，质心和星体之间的力无外力 torque，并且绕质心的合力矩为0。

所以我们可以得出：\[ m_1 \cdot a_1 \times r_1 + m_2 \cdot a_2 \times r_2 = 0 \]其中，×表示向量叉乘。

由于等式左侧可以表示为角动量L，即：\[ L = m_1 \cdot a_1 \times r_1 + m_2 \cdot a_2 \times r_2 \]通过代入质心公式，可得：\[ L = (m_1 \cdot r_1 + m_2 \cdot r_2) \times (m_1 \cdot v_1 +m_2 \cdot v_2) \]其中，v1和v2分别为两个星体相对于质心的速度。

添加副标题
双星系统专题课件
汇报人：PPT
目录
PART One
添加目录标题
PART Three
双星系统的观测与 发现
PART Five
双星系统的研究意 义与价值
PART Two
双星系统的基本概 念
PART Four
双星系统的分类与 演化
PART Six
双星系统的观测技 术与数据处理
单击添加章节标题
双星系统的形 成和演化过程， 可以为我们提 供关于恒星形 成和演化的重
要信息。
双星系统的相 互作用和演化， 可以帮助我们 理解宇宙中的 引力、电磁力 和物质相互作 用等基本物理
规律。
双星系统的研 究，还可以帮 助我们更好地 理解宇宙中的 暗物质和暗能
量等问题。
双星系统在其他学科领域的应用价值
天文学：研究双 星系统的演化和 相互作用，有助 于理解宇宙的起 源和演化
双星系统的演 化：双星系统 中的两颗恒系统的合 并：在某些情 况下，双星系 统中的两颗恒 星可能会合并， 形成一颗新的
恒星
双星系统的解 体：在某些情 况下，双星系 统中的两颗恒 星可能会解体， 形成两个独立
的恒星系统
双星系统的演化结果
双星系统的演化过程：从形成到演 化，再到最终解体
双星系统研究的前沿问题与方向
双星系统 的形成和 演化机制
双星系统 的相互作 用和动力 学特性
双星系统 中的物质 交换和能 量传输
双星系统 对周围环 境的影响 和作用
双星系统 在宇宙学 和天体物 理学中的 地位和意 义
双星系统 的未来观 测和研究 计划
双星系统研究的未来发展趋势
观测技术的进步：提高观测精度和分辨率，发现更多双星系统

（3） 7 a （4）T π a3
4
Gm
【解析】（1）由万有引力定律，A 星体所受 B、C 星体引力大小为
关于引力常量，下列说法正确的是（ ）
A．在国际单位制中，引力2常量在数值上等于两个质量是1kg的质点相距1m时万有引力的大小
Gm m 2m A B
B．在不同的单位制中，引力常量的数值是相同的
F G F BA
【参考答案】A
课堂练习
【练习2】（多选）2021年5月，基于俗称“中国天眼”的500米口径球面射电望远镜（FAST）
的观测，国家天文台李菂、朱炜玮研究团组姚菊枚博士等首次研究发现脉冲星三维速度与自
转轴共线的证据。之前的2020年3月，我国天文学家通过FAST，在武仙座球状星团（M13）中
发现个脉冲双星系统。如图所示，假设在太空中有恒星A、B双星系统绕点O做顺时针匀速圆
主讲老师：XXXX 2023.02.09
目录
01 双星系统 02 三星系统 03 四星系统 04 暗物质
问题与思考
它们
宇宙中，有两颗星
的运 动有
在一起组成的稳定旋转
什么
系统，有三颗星的，也
特点 和规
有更多颗星体组成的稳
律呢
定旋转系统。它们除相
？让
互吸引外，几乎不受外
我们 一起
界其他星体的干扰。
探索
2 C．计算不同2物体间相CA互作用的万有引力时，引力常量的值是不同的
r a D．著名的“月—地检验”是在已知引力常量的数值后才进行的
则合力大小为
FA 2
3G m2 a2
课堂练习
（2）同上，B 星体所受 A、C 星体引力大小分别为
FAB
G

【答案】 2 (1) a 2
2a . 4＋ 2Gm
m (2)G 2 R (3)2πa 2a 4＋ 2Gm
【解析】
(1)两星球围绕同一点O做匀速圆周运动，其角
速度相同，周期也相同，其所需向心力由两者间的万有引力提 供，则 Mm 4π2 对于星球B：G 2 ＝M 2 r1， L T Mm 4π2 对于星球A：G 2 ＝m 2 r2， L T 其中r1＋r2＝L， 由以上三式可得： T＝2π L3 . GM＋m
【解析】
(1)由星体均围绕正方形对角线的交点做匀速圆
2 周运动可知，星体做匀速圆周运动的轨道半径r＝ a. 2 mm′ (2)由万有引力定律可知G ＝m′g，则星体表面的重 R2 m 力加速度g＝G 2. R
(3)星体在其他三个星体的万有引力作用下围绕正方形对角 线的交点做匀速圆周运动，由万有引力定律和向心力公式得： m2 m2 2 4π2 G ＋2G 2 cos 45° ＝m· a· 2 ， a 2 T 2a2 解得周期T＝2πa
【答案】 (1)2π L3 GM＋m (2)1.012
宇宙中存在一些质量相等且离其他恒星较远的四 颗星组成的四星系统，通常可忽略其他星体对它们的引力作 用，设每个星体的质量均为m，四颗星稳定地分布在边长为a的 正方形的四个顶点上，已知这四颗星均围绕正方形对角线的交 点做匀速圆周运动，引力常量为G. (1)求星体做匀速圆周运动的轨道半径； (2)若实验观测得到星体的半径为R，求星体表面的重力加 速度； (3)求星体做匀速圆周运动的周期．
图 61
双星系统的特点 1．双星绕它们共同的圆心做匀速圆周运动，它们之间的距 离保持不变； 2．两星之间的万有引力提供各自需要的向心力； 3．双星系统中每颗星的角速度相等； 4．两星的轨道半径之和等于两星间的距离．

双星的重力场线是指由双星系统所产生的重力场在空间中的分布形态。

双星系统由两个星体组成，它们互相围绕着彼此旋转。

由于每个星体都具有质量，它们之间会相互吸引，形成一个共同的重力场。

在双星系统中，重力场线通常呈现出以下特点：
1. 中心重力井：双星系统的中心点是两个星体之间的质心，也是重力场的最强区域。

在这个区域附近，重力场线会向中心点集中，形成一个类似于井口的形态。

2. 重力势能槽：在双星系统中，两个星体之间的距离会随着它们的运动而变化。

当两个星体靠近时，它们之间的重力势能会增加，重力场线会变得更加密集。

而当两个星体远离时，重力势能减小，重力场线则会变得稀疏。

3. 重力潮汐：在双星系统中，两个星体的引力会产生潮汐力。

这种潮汐力会导致星体表面的形变，同时也会影响周围空间的重力场线。

在潮汐力作用下，重力场线会呈现出一种扭曲的形态。

总的来说，双星系统的重力场线是由两个星体之间的相互作用所决定的。

这些重力场线的分布形态可以通过数学模型和计算机模拟来研究和描述。

双星系统角速度推导过程在浩瀚的宇宙中，双星系统就像是两颗璀璨的明珠，相互依偎着旋转。

想象一下，这两个星星就像是一对舞者，手拉手，优雅地旋转着，仿佛在宇宙的舞台上演绎一场精彩的表演。

说到角速度，这可不是简单的数学问题，而是揭示它们互动的奥秘。

在这个过程中，我们不妨先聊聊这双星的体重。

嘿，你知道吗？星星也有体重，只不过是以质量来衡量的。

就像我们上称时的斤两，双星的质量决定了它们在宇宙中的“重量级”。

当我们提到角速度，首先得明确，角速度就是星星转动的快慢程度。

想象一下，一个疯狂转圈的孩子，转得快得让人眼花缭乱；再想想，那些慢慢转悠的老年人，稳稳当当的感觉。

双星系统的角速度也有点类似，取决于它们的质量和彼此的距离。

我们常常用牛顿的万有引力定律来解说这个关系，毕竟，重的东西会把轻的东西吸引得紧紧的。

就像在班级里，班长总是吸引所有人的目光一样。

这个吸引力越大，旋转得就越快。

有趣的是，双星的运动轨迹并不是完全对称的。

两颗星星就像是两个性格迥异的朋友，一个爱热闹，另一个偏安静。

他们的旋转方式各有千秋，影响着角速度的变化。

如果一颗星星比另一颗重，它会影响到另一颗的旋转速度。

可以想象，重的那颗就像个“大胖子”，总是要牵着轻的那颗绕圈。

这样一来，它们的角速度就变得不那么简单。

就像在玩“老鹰抓小鸡”的游戏，老鹰总是想尽办法去抓小鸡，小鸡则得快速闪避，真是妙趣横生。

再说说角速度的计算。

它就像一根魔法棒，轻轻一挥，就能揭开双星运动的秘密。

我们用公式来描述这种关系，虽然看上去有些复杂，但实际上，它是宇宙间的简约之美。

通过这个公式，我们能得到双星的角速度，只要知道它们的质量和距离。

就像做一道菜，只要掌握了材料和火候，便能烹饪出美味佳肴。

看，这个公式就像那神秘的食谱，让人既期待又兴奋。

再讲讲双星系统的“家族关系”。

这些星星之间的互动，不仅仅是转圈那么简单，它们会在引力的作用下产生潮汐效应。

哦，你听说过潮汐吗？没错，海洋的涨潮和退潮就是因为月球的引力。

双星系统的形成与演化过程分析在宇宙的浩瀚中，有着无数个圆圈中亮点的星系。

这些星系中，单星系是比较常见的。

然而，双星系统也经常出现。

那么，双星系统是如何形成的？它们的演化过程是怎样的呢？一、双星系统的形成双星系统的形成主要有两种方式，分别是原始分裂和聚积。

原始分裂是指恒星形成前的分裂过程。

在星云中，由于潮汐力、自转力等因素的作用，星云会发生不均匀收缩，产生一些密度较高的区域。

当这些区域的密度足够大时，巨大的引力会使得这些区域分裂为两个或多个原恒星。

这些原始分裂的区域最终会形成双星系统。

聚积是指恒星形成后的聚集过程。

在某些星际云中，密度可能不够高，无法引发原始分裂。

但随着整个星际云的坍缩，云中的恒星会逐渐靠近。

当它们的距离接近到一定程度时，引力会开始起作用，使得这些恒星相互聚拢形成双星系统。

二、双星系统的演化过程一对双星系统的演化过程取决于初始条件、质量和距离等因素。

根据这些因素的不同组合，双星系统的演化可以分为三个阶段：起始阶段、主序星阶段和终结阶段。

在起始阶段，双星系统中的两颗恒星都处于非常接近的距离，并以高速旋转。

它们会相互交换物质，并形成一个星周盘，这个盘中的物质会不断减少，最终形成行星。

随着时间的推移，双星系统中较大质量的恒星会进入主序星阶段，而较小质量的恒星可能仍然是红矮星。

在主序星阶段，较大质量的恒星通过核聚变反应维持能量产生，同时辐射出大量的光和热。

这个阶段可能会持续几十亿年。

而红矮星则通过核融合反应较慢地燃烧氢，并持续产生能量。

最终，双星系统的终结阶段会是两颗恒星的演化趋势的总和。

较大质量的恒星会首先变成红巨星，它的半径会急剧膨胀。

这个过程中，恒星的质量会逐渐流失。

而红矮星则逐渐变成白矮星，体积变得非常小，但质量非常密集。

当较大质量的恒星耗尽燃料时，它会发生超新星爆发。

而这个过程中，红矮星可能会被引力吸引到较大质量恒星的附近。

三、双星系统的意义双星系统的研究对于我们理解宇宙的演化和恒星物理过程具有重要意义。

恒星的双星系统与恒星多重系统的形成机制恒星是宇宙中最常见的天体之一，它们具有各种形态和性质。

在宇宙中，恒星的双星系统和恒星多重系统占据了相当比例。

本文将探讨恒星的双星系统和恒星多重系统的形成机制。

一、恒星的双星系统恒星的双星系统是由两颗恒星组成的系统，它们围绕共同的质心进行旋转。

双星系统在宇宙中非常常见，大约有70％的恒星属于双星系统。

那么恒星双星系统是如何形成的呢？1.捕获理论根据捕获理论，恒星双星系统的形成是由于原本独立存在的恒星之间相互吸引，进而相互捕获形成的。

当两颗恒星经过足够接近的距离时，它们之间的引力相互作用将使它们开始绕着共同的质心旋转。

2.共同形成另一种可能的情况是恒星在形成过程中同时产生，它们保持了一定的距离并保持在一起形成了双星系统。

这种共同形成的情况可以通过观测新生恒星和星云的形态来证实。

3.演化过程中的分离恒星双星系统在演化过程中也可能发生分离。

当一个恒星演化为红巨星时，其外层气体膨胀并可能超出其洛希球，这时另一颗恒星可以被弹出系统。

这种分离过程被认为是一种可行的方式。

二、恒星的多重系统除了双星系统，恒星之间还存在一些更大规模的多重系统。

这些系统由三颗或更多恒星组成，其形成机制可以通过以下方式解释。

1.分裂形成多重系统的形成可以通过原本的恒星分裂而来。

当一个恒星失去稳定平衡时，可能会发生分裂形成两颗或更多的恒星，并形成多重系统。

2.碰撞合并在恒星聚集的密集区域，恒星之间可能会发生碰撞合并的情况。

这样的碰撞合并可能会形成更大规模的多重系统，包括三颗或更多恒星。

3.动力不稳定性动力不稳定性是另一种可能导致多重系统形成的机制。

当多个恒星在一个紧凑的空间范围内密集存在时，它们之间的相互作用可能导致它们形成一个相对稳定的多重系统。

总结：恒星的双星系统和恒星多重系统是宇宙中普遍存在的天体组合形式。

它们的形成机制可以通过捕获理论、共同形成、演化过程中的分离等方式解释。

恒星多重系统的形成可能涉及到分裂形成、碰撞合并和动力不稳定性等因素。

双星系统的形成与演化机制分析双星系统是宇宙中一种常见而又神秘的天体结构，它由两颗恒星以一定的轨道相互环绕而成。

在这个广袤的宇宙世界中，双星系统的形成和演化机制一直是天文学家们关注的焦点。

本文将深入探讨双星系统形成的几种可能机制以及它们的演化过程。

首先，我们来分析双星系统形成的最主要机制之一：共同形成。

这种机制是指两颗恒星同时在同一星云中形成，并通过引力相互吸引而形成一个双星系统。

星云是由气体和尘埃组成的，当星云内部密度较高时，它会发生塌缩，形成恒星。

如果恒星的形成过程几乎同时发生，它们就有可能形成一个双星系统。

这种机制通常发生在密度较高的星云中，因此在星系中心附近或星际云团中会比较常见。

其次，我们来讨论另一种双星系统形成的机制：捕获。

这种机制是指一个孤立行星或恒星与另一颗恒星相遇，通过引力相互吸引而形成一个双星系统。

在这个过程中，双方之间需要足够接近，以便克服它们各自的逃逸速度，从而让它们陷入相对稳定的轨道运动。

捕获机制通常发生在星际空间中，当恒星或行星在星系中穿越时，它们有可能与其他恒星相撞，从而形成一个双星系统。

除了共同形成和捕获机制外，还存在一种双星系统形成的机制：分离。

这种机制是指最初是一个单独的恒星系统，在某个阶段发生了分离，形成了两颗相对独立的恒星。

分离机制通常发生在双星系统中的一颗恒星进化到红巨星或超巨星阶段时。

在这个阶段，恒星的尺度会变大，往往超过了它们的Roche叶面，而Roche叶面是指两颗恒星的引力平衡面。

当其中一颗恒星尺度增大时，它会传递一部分物质给另一颗恒星，从而打破原来的引力平衡，导致恒星系统发生分离。

无论是共同形成、捕获还是分离机制，双星系统的演化过程都是一个复杂而长久的过程。

在初始形成后，双星系统会经历各种动态过程，如轨道共振、互相干扰等。

这些过程会导致双星系统的轨道参数发生变化，甚至可能导致它们的相对位置发生变化或成为一个单独的恒星。

而双星系统的演化过程也会受到外部因素的影响，比如邻近天体的引力作用或星际介质的摩擦力等。

两恒星之间分别提供了两恒星运动恒星质量轨道半径旋转中心靠匀速圆周运动相等相等相等相等和和万有引力万有引力向心力向心力作用力作用力反作用力反作用力越大越大越小越小质量大的物体质量大的物体13重点难点小结重点难点小结度与半径成与质量成6
教学补充：
“双星”问题探 究
学习目标：
1、了解双星模型。
2、理解双星模型的特点及其运动规律。
3、会用万有引力定律及相关公式解双星 问题。
教学重点与难点
• 重点：
•
用万有引力定律及相关公式解决双星问题
• 难点：
•
区分万有引力公式中的(R)与圆周运动轨道半径(r)
哈柏太空望远镜 拍摄的天狼星双 星系统，在左下 方可以清楚的看 见天狼伴星(天 狼 B)。
双星模型
所谓的“双星”就是指两颗 恒星相在互的万有引力 作用下，绕 两颗星连线的某点做匀速圆周运动 的系统。
重点、难点小结
* 5.两颗恒星的轨道半径与恒星质量成 反比 ，线速 度与半径成 正比 与质量成 反比 。
* 6.两子星圆周运动的动力学关系。
物体1：
G M1M2 L2

M1
v12 r1
M1r112
物体2：
G
M1M 2 L2
M2
v22 r2
M 2r222
例：两个星球组成双星，它们在相互之间的万有引力作用下， 绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距
离为R，其运动周期为T，求两星的总质量。（引力常量为G）
作业
• 必做题：大本：P41 典例
•
P42 4
•
小本：P115 8
• 选做题：大本：P42 5
谢谢！
• 5.两颗恒星间的距离和各自做圆周运动的轨道 半径是否相同？找出对应的轨道半径与两者间 距离的关系？

微专题4双星系统和卫星变轨问题类型一对双星系统的理解1．双星模型如图所示，宇宙中有相距较近、质量可以相比的两个星球，它们离其他星球都较远，因此其他星球对它们的万有引力可以忽略不计．在这种情况下，它们将围绕它们连线上的某一固定点做周期相同的匀速圆周运动，这种结构叫作“双星”．2．双星模型的特点(1)两星的运行轨道为同心圆，圆心是它们之间连线上的某一点．(2)两星的向心力大小相等，由它们间的万有引力提供．(3)两星的运动周期、角速度都相同．(4)两星的运动轨道半径之和等于它们之间的距离，即r1＋r2＝L.【例1】(多选)图甲是一对相互环绕旋转的质量不等的双黑洞系统，其示意图如图乙所示．双黑洞A、B在相互之间的万有引力的作用下，绕其连线上的O点做匀速圆周运动，若双黑洞的质量之比m A∶m B＝n∶1，则()A．黑洞A、B做圆周运动的角速度之比为1∶1B．黑洞A、B做圆周运动的向心力大小之比为n2∶1C．黑洞A、B做圆周运动的半径之比为1∶nD．黑洞A、B做圆周运动的线速度之比为1∶n2[解析]由于二者绕连线上同一点做匀速圆周运动，二者角速度相等，又由彼此间的万有引力提供向心力，二者做圆周运动的向心力之比为1∶1，故有m A r A ω2＝m B r B ω2，解得r A r B ＝m B m A ＝1n ，故A 、C 正确，B 错误；由线速度与角速度的关系可知，当角速度相同时，二者做圆周运动的线速度与半径成正比，故二者线速度之比为1∶n ，故D 错误．[答案] AC【例2】 如图所示，质量分别为m 和M 的两个星球A和B 在引力作用下都绕O 点做匀速圆周运动，星球A 和B 两者中心之间距离为L .已知A 、B 的中心和O 三点始终共线，A和B 分别在O 的两侧，引力常量为G .(1)求A 星球做圆周运动的半径R 和B 星球做圆周运动的半径r ；(2)求两星球做圆周运动的周期；(3)如果把星球A 质量的12搬运到B 星球上，并保持A 和B 两者中心之间距离仍为L .则组成新的稳定双星后星球A 半径和周期如何变化？[解析] (1)令A 星的轨道半径为R ，B 星的轨道半径为r ，则由题意有L ＝r ＋R两星做圆周运动时的向心力由万有引力提供，则有G mM L 2＝mR 4π2T 2G mM L 2＝Mr 4π2T 2，可得R r ＝M m ，又因为L ＝R ＋r所以可以解得R ＝M M ＋m L ，r ＝m M ＋mL ； (2)根据(1)可以得到G mM L 2＝m 4π2T 2R ，R ＝M M ＋mL 两式联立解得T ＝4π2L 3（M ＋m ）G ＝2π L 3G （M ＋m ）； (3)根据R ＝M M ＋m L ，知M 变大，R 变大 根据T ＝ 4π2L 3（M ＋m ）G ＝2π L 3G （m ＋M ），知周期不变． [答案] (1)M M ＋m L m M ＋mL(2)2πL3G（M＋m）(3)半径变大周期不变[针对训练1]宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用互相绕转，称之为双星系统．设某双星系统中A、B两星绕其连线上的O点做匀速圆周运动，如图所示．若A星轨道半径较大，则() A．星球A的质量大于B的质量B．星球A的线速度大于B的线速度C．星球A的角速度大于B的角速度D．星球A的周期大于B的周期解析：选B.根据万有引力提供向心力有m Aω2r A＝m Bω2r B，因为r A＞r B，所以m A＜m B，即A的质量一定小于B的质量，故A错误；双星角速度相等，则周期相等，根据v＝ωr可知，v A＞v B，故B正确，C、D错误．[针对训练2](多选)经长期观测，人们在宇宙中已经发现了“双星系统”，“双星系统”由两颗相距较近的恒星组成，每个恒星的大小远小于两个星体之间的距离，而且双星系统一般远离其他天体．两颗星球组成的双星A、B，A、B 的质量分别为m1、m2，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L，质量之比为m1∶m2＝3∶2.则可知()A．A与B做圆周运动的角速度之比为2∶3B．A与B做圆周运动的线速度之比为2∶3C．A做圆周运动的半径为2 5LD．B做圆周运动的半径为2 5L解析：选BC.双星靠相互间的万有引力提供向心力，相等的时间内转过相同的角度，则角速度相等，故A错误；向心力大小相等，有：m1ω2r1＝m2ω2r2，即m1r1＝m2r2，因为质量之比为m1∶m2＝3∶2，则轨道半径之比r1∶r2＝2∶3，所以A做圆周运动的半径为25L，B做圆周运动的半径为35L，故C正确，D错误；根据v＝ωr，角速度相等，双星的线速度比等于半径比为2∶3，故B正确．类型二卫星变轨问题卫星在运动中的“变轨”有两种情况：离心运动和向心运动．当万有引力恰好提供卫星所需的向心力，即G Mm r 2＝m v 2r 时，卫星做匀速圆周运动；当某时刻速度发生突变，所需的向心力也会发生突变，而突变瞬间万有引力不变．(1)制动变轨：卫星的速率变小时，使得万有引力大于所需向心力，即G Mm r 2>m v 2r ，卫星做近心运动，轨道半径将变小．所以要使卫星的轨道半径变小，需开动反冲发动机使卫星做减速运动．(2)加速变轨：卫星的速率变大时，使得万有引力小于所需向心力，即G Mm r 2<m v 2r，卫星做离心运动，轨道半径将变大．所以要使卫星的轨道半径变大，需开动反冲发动机使卫星做加速运动．【例3】 北京时间2022年5月10日01时56分，搭载天舟四号货运飞船的长征七号遥五运载火箭，在我国文昌航天发射场点火发射，约10 min 后，飞船与火箭成功分离，进入预定轨道.2时23分，飞船的太阳能帆板顺利展开工作，发射取得圆满成功．后续，天舟四号货运飞船与在轨运行的空间站组合体进行交会对接．若对接前两者在同一轨道上运动，下列说法正确的是( )A ．对接前天舟四号的运行速率大于空间站组合体的运行速率B ．对接前天舟四号的向心加速度小于空间站组合体的向心加速度C ．天舟四号通过加速可实现与空间站组合体在原轨道上对接D ．天舟四号先减速后加速可实现与空间站组合体在原轨道上对接[解析] 对接前两者在同一轨道上运动，由万有引力提供向心力可知G Mm r 2＝m v 2r ＝ma ，解得v ＝G M r ，a ＝G M r 2 ，同一轨道，运行速率、向心加速度相等，A 、B 错误；飞船与空间站组合体在同一轨道上，此时飞船受到的万有引力等于向心力，若让飞船加速，则所需要的向心力变大，万有引力不变，所以飞船做离心运动，不能实现对接，C 错误；天舟四号先减速做近心运动，进入较低的轨道，后加速做离心运动，轨道半径变大，可以实现对接，D 正确．[答案] D【例4】 (多选)2022年3月23日，“天宫课堂”进行了第二次授课活动．授课过程中信号顺畅不卡顿，主要是利用天链系列地球同步轨道卫星进行数据中继来实现的．如图所示，天链卫星的发射过程可以简化如下：卫星先在近地圆形轨道Ⅰ上运动，到达轨道的A 点时点火变轨进入椭圆轨道Ⅱ，到达轨道的远地点B 时，再次点火进入圆形同步轨道Ⅲ绕地球做匀速圆周运动．设地球半径为R ，地球表面的重力加速度为g 0，卫星质量保持不变，则下列说法正确的是( )A ．卫星在轨道Ⅰ和轨道Ⅲ运动的周期均与地球自转周期相同B ．卫星在轨道Ⅱ和轨道Ⅲ运动经过B 点的加速度大小相同C ．卫星在轨道Ⅲ上的运行速率小于g 0RD ．卫星在轨道Ⅰ向轨道Ⅱ变轨时，火箭需在A 点点火向前喷气[解析] 同步轨道Ⅲ属于同步卫星轨道，与地球自转周期保持相同，轨道Ⅰ属于近地卫星轨道，与地球自转周期不相同，A 错误；根据万有引力充当合外力可知G Mm r 2 ＝ma ，所以卫星在轨道Ⅱ和轨道Ⅲ运动经过B 点的加速度相同，B正确；在地面上，则有G Mm R 2 ＝mg 0，对于轨道卫星，则有G Mm r 2 ＝m v 2r ，可解得v ＝g 0R 2r ，C 正确；卫星在轨道Ⅰ向轨道Ⅱ变轨时做离心运动，需要加速，故火箭需在A 点点火向后喷气，D 错误．[答案] BC[针对训练3] 一人造卫星绕地球做匀速圆周运动，假如该卫星变轨后仍做匀速圆周运动，速度大小减小为原来的12 ，则变轨前后卫星的( ) A ．周期之比为1∶8B ．角速度大小之比为2∶1C ．向心加速度大小之比为4∶1D ．轨道半径之比为1∶2解析：选A.根据万有引力充当卫星绕地球运动的向心力：G Mm r 2 ＝m v 2r ，卫星的线速度v ＝ GM r ，由题知，速度大小减小为原来的12 ，则轨道半径增大到原来的4倍，即变轨前后轨道半径之比为1∶4；卫星的角速度ω＝v r ＝GMr 3 ，可得变轨前后角速度大小之比为8∶1；卫星的向心加速度a ＝v 2r ＝GM r 2 ，可得变轨前后向心加速度大小之比为16∶1；卫星的周期T ＝2πω ，可得变轨前后周期之比为1∶8，故B 、C 、D 错误，A 正确．[针对训练4] 如图所示，一颗人造卫星原来在椭圆轨道1绕地球运行，在P 点变轨后进入轨道2做匀速圆周运动．下列说法正确的是( )A ．不论在轨道1还是在轨道2运行，卫星在P 点的速度都相同B ．不论在轨道1还是在轨道2运行，卫星在P 点的加速度都相同C ．卫星在轨道1的任何位置都具有相同加速度D ．卫星在轨道2的任何位置都具有相同速度解析：选B.从轨道1变轨到轨道2，需要加速做离心运动，A 错误；根据公式G Mm R 2 ＝ma 可得a ＝G M R 2 ，故只要到地心距离相同，加速度大小就相同，由于卫星在椭圆轨道1运动，到地心距离、引力的方向均在变化，所以运行过程的加速度在变，B 正确，C 错误；卫星在轨道2做匀速圆周运动，过程中的速度方向时刻在变，所以不同位置处速度不同，D 错误．[A 级——合格考达标练]1．如图所示，一颗人造卫星原来在椭圆轨道1绕地球运行，在P 点变轨后进入轨道2做匀速圆周运动．下列说法正确的是( )A ．不论在轨道1还是在轨道2运行，卫星在P 点的速度都相同B ．不论在轨道1还是在轨道2运行，卫星在P 点的加速度都相同C ．卫星在轨道1的任何位置都具有相同加速度D ．卫星在轨道2的任何位置都具有相同速度解析：选B.从轨道1变轨到2，需要加速逃逸，A 错误；根据公式G Mm R 2＝ma 可得a ＝G M R 2，故只要到地心距离相同，加速度则相同，由于卫星在轨道1做椭圆运动，到地心距离、引力的方向均在变化，所以运行过程的加速度在变，B 正确，C 错误；卫星在轨道2做匀速圆周运动，过程中的速度方向时刻在变，所以不同位置处速度不同，D 错误．2．如图所示，a 、b 、c 是在地球大气层外圆形轨道上运行的3颗人造卫星，下列说法正确的是( )A ．b 、c 的线速度大小相等，且大于a 的线速度B ．a 卫星由于某种原因，轨道半径缓慢减小，其线速度将变大C ．c 加速可以追上同一轨道上的b ，b 减速可以等候同一轨道上的cD ．b 、c 向心加速度相等，且大于a 的向心加速度解析：选 B.人造卫星绕地球做匀速圆周运动，根据万有引力提供向心力，设卫星的质量为m 、轨道半径为r 、地球质量为M ，有G Mm r 2＝m v 2r ＝ma ，解得卫星线速度v ＝GMr ，由图可知，r a ＜r b ＝r c ，则b 、c 的线速度大小相等，且小于a 的线速度，故A 错误；由v ＝GMr 知，a 卫星由于某种原因，轨道半径缓慢减小，其线速度将变大，故B 正确；c 加速要做离心运动，不可以追上同一轨道上的b ；b 减速要做近心运动，不可以等候同一轨道上的c ，故C 错误；由向心加速度a ＝GM r 2知，b 、c 的向心加速度大小相等，且小于a 的向心加速度，故D 错误．3．(多选)图为两颗人造卫星绕地球运动的轨道示意图，Ⅰ为圆轨道，Ⅱ为椭圆轨道，AB 为椭圆的长轴，两轨道和地心都在同一平面内，C 、D 为两轨道交点．已知轨道Ⅱ上的卫星运动到C 点时速度方向与AB 平行，则下列说法正确的是( )A ．两颗卫星的运动周期相同B ．卫星在Ⅰ轨道的速率为v 0，卫星在Ⅱ轨道B 点的速率为v B ，则v 0<v BC ．两个轨道上的卫星运动到C 点时的加速度相同D ．两个轨道上的卫星运动到C 点时的向心加速度大小相等解析：选AC.由轨道Ⅱ上的卫星运动到C 点时速度方向与AB 平行可知CD 为椭圆短轴的两个端点，由于圆的圆心与椭圆的左焦点重合，则由几何关系可知圆的半径与椭圆的半长轴相等，故由开普勒第三定律可知两卫星运行周期相等，A 正确；设有一个与椭圆相切于B 点、以地球为圆心的圆轨道Ⅲ，卫星在轨道Ⅱ上从B 点进入该圆轨道Ⅲ则需要加速，而由v ＝ GMr 可知卫星在轨道Ⅲ的速度必小于在轨道Ⅰ上的速度，故v 0>v B ，B 错误；卫星在C 点时的加速度(不是向心加速度)由牛顿第二定律有G Mm r 2＝ma ，即加速度a ＝G M r 2与卫星质量无关、与轨道形状无关，C 正确；卫星在轨道Ⅰ上做匀速圆周运动，加速度即为向心加速度；卫星在椭圆轨道Ⅱ上运动，在C点，其加速度沿垂直于速度方向上的分量才是向心加速度，故卫星在轨道Ⅱ上C点的向心加速度小于卫星在轨道Ⅰ上C 点的向心加速度，D错误．4．如图所示，在赤道发射场发射地球同步卫星的过程中，卫星首先进入椭圆轨道Ⅰ，然后在Q点通过改变卫星速度，让卫星进入地球同步轨道Ⅱ，则()A．该卫星在P点的速度大于11.2 km/sB．卫星在轨道Ⅱ上的运行速度大于7.9 km/sC．卫星在Q点需要适当加速，才能够由轨道Ⅰ进入轨道ⅡD．卫星在轨道Ⅱ上经过Q点时的加速度大于在轨道Ⅰ上经过Q点时的加速度解析：选C.11.2 km/s是卫星脱离地球束缚的最小发射速度，由于同步卫星仍然绕地球运动，则在P点的速度小于11.2 km/s，故A错误；7.9 km/s是卫星在地球表面飞行的环绕速度，根据万有引力提供向心力，由GMmr2＝mv2r可知v＝GMr，卫星在轨道Ⅱ上，半径变大，则运行速度小于7.9 km/s，故B错误；卫星需要加速，让卫星做离心运动，才能由轨道Ⅰ进入轨道Ⅱ，故C正确；根据GMm r2＝ma可知a＝GMr2，则卫星在轨道Ⅱ上经过Q点时的加速度等于在轨道Ⅰ上经过Q点时的加速度，故D错误．5．宇宙中两颗相距较近的天体称为“双星”，它们以二者连线上的某一点为圆心做匀速圆周运动，而不至因为万有引力的作用而吸引到一起．如图所示，某双星系统中A、B两颗天体绕O点做匀速圆周运动，它们的轨道半径之比r A∶r B ＝1∶2，则两颗天体的()A ．质量之比m A ∶mB ＝2∶1B ．角速度之比ωA ∶ωB ＝1∶2C ．线速度大小之比v A ∶v B ＝2∶1D ．向心力大小之比F A ∶F B ＝2∶1解析：选 A.双星绕连线上的一点做匀速圆周运动，其角速度相同，周期相同，两者之间的万有引力提供向心力，有F ＝m A ω2r A ＝m B ω2r B ，所以m A ∶m B ＝2∶1，B 、D 错误，A 正确；由v ＝ωr 可知，线速度大小之比v A ∶v B ＝1∶2，C 错误．6．宇宙中，两颗靠得比较近的恒星，只受到彼此之间的万有引力作用而互相绕转，称之为双星系统．设某双星系统中的A 、B 两星球绕其连线上的某固定点O 做匀速圆周运动，如图所示．现测得两星球球心之间的距离为L ，运动周期为T ，已知引力常量为G ，若R A >R B ，则( )A ．两星球的总质量等于4π2L 3GT 3B ．星球A 的向心力大于星球B 的向心力C ．星球A 的线速度一定小于星球B 的线速度D ．双星的质量一定，双星之间的距离减小，其转动周期减小解析：选D.由题可知，双星的角速度相等，根据v ＝ωr ，且R A >R B ，则v A >v B ，C 错误；双星靠相互间的万有引力提供向心力，根据牛顿第三定律知它们的向心力大小相等，B 错误；根据万有引力提供向心力，对A 有G M A M B L 2＝M A ⎝ ⎛⎭⎪⎫2πT 2R A ，对B 有G M A M B L 2＝M B ⎝ ⎛⎭⎪⎫2πT 2R B ，其中L ＝R A ＋R B ，解得T ＝4π2L 3G ()M A ＋M B ，M A ＋M B ＝4π2L 3GT 2，故当双星的质量一定，双星之间的距离减小时，其转动周期减小，D 正确，A 错误．[B 级——等级考增分练]7．如图所示，半径为r 的圆形轨道Ⅰ为空间站运行轨道，半长轴为a 的椭圆轨道Ⅱ为载人飞船的运行轨道，飞船在两个轨道相切点A 与空间站交会对接，已知飞船与空间站均绕地球运动，引力常量为G ，地球质量为M ，下列说法中正确的是( )A.空间站的运行速度大于第一宇宙速度 B ．在A 点对接时飞船应沿运行速度方向喷气 C ．飞船与空间站运行周期之比为r 3a 3D ．飞船在轨道Ⅱ经过A 点，喷气变轨前一刻的速度小于GM r解析：选 D.第一宇宙速度是物体绕地球做圆周运动的最大速度，所以空间站的运行速度不可能大于第一宇宙速度，故A 错误；载人飞船与空间站对接需向高轨道做离心运动，则需要向后点火加速，即飞船应沿运行速度相反方向喷气，故B 错误；设飞船的运行周期为T 1，空间站的运动周期为T 2，根据开普勒第三定律得a 3T 21 ＝r 3T 22 ，则T 1T 2＝a 3r 3，故C 错误；以r 为半径做圆周运动的物体，根据万有引力提供向心力得G mMr 2 ＝m v 2r ，得以r 为半径做圆周运动的物体的速度为v ＝GMr ，飞船在轨道Ⅱ经过A 点后做近心运动，喷气变轨前一刻的速度小于GMr ，故D 正确．8．北斗导航系统又被称为“双星定位系统”，具有导航、定位等功能．“北斗”系统中两颗工作卫星均绕地心O 做匀速圆周运动，轨道半径为r ，某时刻两颗工作卫星分别位于轨道上的A 、B 两位置(如图所示).若卫星均顺时针运行，地球表面处的重力加速度为g ，地球半径为R .不计卫星间的相互作用力，则以下判断正确的是( )A.这两颗卫星的加速度大小相等，均为Rgr B ．卫星1向后喷气就一定能追上卫星2C.卫星1由位置A 运动到位置B 所需的时间为πr3R r gD ．卫星1中物体的速度为gr解析：选C.由GMm r 2 ＝ma 、GMm R 2 ＝mg ，得 a ＝gR 2r 2 ，A 错误；卫星1向后喷气时速度增大，所需的向心力增大，万有引力不足以提供其所需的向心力而做离心运动，与卫星2不处于同一轨道上了，B 错误；卫星1由位置A 运动到位置B 的过程，由t ＝θ360° T ＝16 T 、GMm r 2 ＝mr (2πT )2、GMm R 2 ＝mg 可得，t ＝πr 3R r g ，C 正确；由GMmr 2 ＝m v 2r 、GMm R 2 ＝mg 可得，卫星1中物体的速度v ＝ gR 2r ，D 错误．9．(多选)双星的运动是产生引力波的来源之一，假设宇宙中有一双星系统由a 、b 两颗星体组成，这两颗星绕它们连线的某一点在万有引力作用下做匀速圆周运动，测得a 星的周期为T ，a 、b 两颗星的距离为l ，a 、b 两颗星的轨道半径之差为Δr (a 星的轨道半径大于b 星的)，则( )A ．b 星的周期为l －Δrl ＋ΔrT B ．a 星的线速度大小为π（l ＋Δr ）TC ．a 、b 两颗星的轨道半径之比为l l ＋ΔrD ．a 、b 两颗星的质量之比为l －Δrl ＋Δr解析：选BD.由于双星系统是在相互间万有引力作用下绕连线上同一点做圆周运动，故二者连线始终过圆心，则二者在任意相同时间内转过的圆心角相等，故二者的转动周期相同，A 错误；由r a ＋r b ＝l 及r a －r b ＝Δr 得r a ＝l ＋Δr2 ，r b ＝l －Δr 2 ，故a 星的线速度大小为v a ＝2πr aT ＝π（l ＋Δr ）T ，B 正确；a 、b 两颗星的轨道半径之比为r a r b ＝l ＋Δr l －Δr ，C 错误；由F 引＝m a r a ⎝ ⎛⎭⎪⎫2πT 2 ＝m b r b ⎝ ⎛⎭⎪⎫2πT 2 有m a m b＝r b r a ＝l －Δrl ＋Δr，D 正确．。