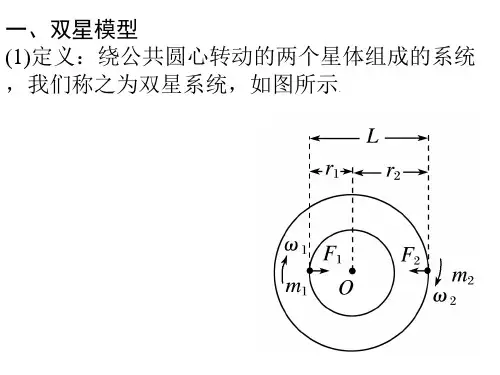
第17点双星系统中的三个特点
- 格式:docx
- 大小:88.74 KB
- 文档页数:2



2023-2024学年北京市第四中学高一下学期期中物理试卷一、选择题:本大题共14小题,共56分。
1.万有引力定律的发现者是( )A. 开普勒B. 伽利略C. 牛顿D. 卡文迪许2.如图所示,质量为m1和m2的两个物体,在大小相等的两个力F1和F2的作用下分别沿水平方向移动了相同的距离,F1和F2与水平方向的夹角相同。
若两物体与地面间的动摩擦因数分别为μ1,μ2,且μ1≤μ2,m1<m2,则F1做功W1与F2做功W2的关系是( )A. W1>W2B. W1<W2C. W1=W2D. 条件不足,无法确定3.一个学生用100N的力,将静止在球场的质量为0.5kg的足球,以10m/s的速度踢出20m远,则该学生对足球做的功为( )A. 25JB. 50JC. 500JD. 2000J4.名宇航员来到某星上,此星的密度为地球的一半,半径也为地球的一半,则他受到的“重力”为在地球上所受重力的( )A. 1/4B. 1/2C. 2倍D. 4倍5.2017年6月15日上午,我国在酒泉卫星发射中心成功发射首颗X射线调制望远镜卫星“慧眼”。
它的总质量约2.5吨,在距离地面550公里的轨道上运行,其运动轨道可近似看成圆轨道。
已知地球半径约为6400公里,根据上述信息可知该卫星( )A. 运行速度大于7.9km/sB. 轨道平面可能不通过地心C. 周期小于更低轨道近地卫星的周期D. 向心加速度小于地球表面重力加速度值6.如图所示,质量相同的两物体从同一高度由静止开始运动,沿着固定在地面上的光滑斜面下滑,做自由落体运动,两物体分别到达地面,下列说法正确的是( )A. 运动过程中重力的平均功率P A>P BB. 运动过程中重力的平均功率P A=P BC. 到达地面时重力的瞬时功率P A<P BD. 到达地面时重力的瞬时功率P A=P B7.如图所示,把一个带弹簧但质量未知的签字笔笔尖朝上,沿竖直方向压缩到底,无初速释放后笔上升的最大高度为ℎ;再把笔水平放置在桌面上,沿水平方向压缩到底,无初速释放后,笔在桌面上滑行的最大距离为s,忽略空气阻力,则由上述物理量可估算出( )A. 弹簧的弹性势能的最大值B. 上升过程中重力所做的功C. 水平滑行过程中摩擦力所做的功D. 笔与桌面间的动摩擦因数8.如图所示,质量m=1kg的物块,以速度v0=4m/s滑上正沿顺时针转动的水平传送带,传送带上A、B 两点间的距离L=6m,已知传送带的速度v=6m/s,物块与传送带间的动摩擦因数µ=0.2,重力加速度g 取10m/s2。

人造卫星宇宙速度素养目标:1.会比较卫星运行的各物理量之间的关系。
2.理解三种宇宙速度,并会求解第一宇宙速度的大小。
3.会分析天体的“追及”问题。
1.北京时间2024年5月3日17时27分,长征五号遥五运载火箭在我国文昌航天发射场点火升空,嫦娥六号顺利发射。
如图所示,嫦娥六号探测器进行多次变轨修正之后,“着陆器、上升器组合体”降落月球表面,下列关于嫦娥六号探测器的说法正确的是( )A.在地球上的发射速度一定大于第二宇宙速度B.在P点由轨道1进入轨道2需要加速C.在轨道1与轨道2上经过P点时,机械能相同D.在轨道2上运行时经过P点时的速度小于经过Q点时的速度【答案】D【解析】A.嫦娥六号发射出去后绕地球做椭圆运动,没有离开地球束缚,故嫦娥六号的发射速度大于第一宇宙速度7.9km/s,小于第二宇宙速度11.2km/s。
故A错误;BC.嫦娥六号在轨道1上的P点处减速,使万有引力大于向心力做近心运动,才能进入轨道2,嫦娥六号的机械能减小,则在轨道1与轨道2上经过P点时,机械能不相等。
故BC 错误;D.由开普勒第二定律可知,在轨道2上运行经过P点时的速度小于经过Q点时的速度。
故D正确。
故选D。
考点一 卫星运行参量的分析1.基本公式(1)线速度大小:由G Mmr 2=m v 2r得v(2)角速度:由GMm r 2=mω2r 得ω(3)周期:由G Mmr 2=m (2πT )2r 得T =(4)向心加速度:由GMm r 2=ma n 得a n =GM r 2。
结论:同一中心天体的不同卫星,轨道半径r 越大,v 、ω、a n 越小,T 越大,即越高越慢。
2.“黄金代换式”的应用忽略中心天体自转影响,则有mg =G Mm R 2,整理可得GM =gR 2。
在引力常量G 和中心天体质量M 未知时,可用gR 2替换GM 。
3.人造卫星卫星运行的轨道平面一定通过地心,一般分为赤道轨道、极地轨道和其他轨道,同步卫星中的静止卫星的轨道是赤道轨道。


双星系统双星系统:宇宙中两颗靠得比较近的横行称为双星,它们绕其连线上某点做匀速圆周运动,其特点是两者的周期和角速度相等,也称为物理双星;近年来天文学家们发现,大部分已知恒星都存在于双星甚至多星系统中。
双星对于天体物理尤其重要,因为两颗星的质量可从通过观测旋转轨道确定。
这样,很多独立星体的质量也可以推算出来。
在银河系中,双星的数量非常多,估计不少于单星。
研究双星,不但对于了解恒星形成和演化过程的多样性有重要的意义,而且对于了解银河系的形成和演化,也是一个不可缺少的方面。
例1:宇宙中两颗相距较近的天体均为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动,而不至因为万有引力的作用而吸引到一起。
设两者的质量分别为m1和m2,两者相距L,求:(1)双星的轨道半径之比;(2)双星的线速度之比;(3)双星的角速度。
例2:(01北京.08宁夏卷)两个星球组成双星,它们在相互之间的万有引力作用下,绕连线上某点做周期相同的匀速圆周运动。
现测得两星中心距离为R,其运动周期为T,求两星的总质量。
(引力常量为G)例3:(06广东))宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统,通常可忽略其它星体对它们的引力作用。
已观测到稳定的三星系统存在两种基本的构成形式:一种是三颗星位于同一直线上,两颗星围绕中央星在同一半径为R的圆轨道上运行;另一种形式是三颗星位于等边三角形的三个项点上,并沿外接于等边三角形的圆形轨道运行。
设每个星体的质量均为m。
⑴试求第一种形式下,星体运动的线速度和周期。
⑵假设两种形式星体的运动周期相同,第二种形式下星体之间的距离应为多少?(2010全国卷1)例4:如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。
已知A、B的中心和O三点始终共线,A和B分别在O的两侧。
引力常数为G。
⑴求两星球做圆周运动的周期。
⑵在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。

高中物理双星系统在浩瀚的宇宙中,有一种天体系统,简直就是“天作之合”,那就是双星系统。
你是不是觉得挺浪漫的?像两颗不舍得分开的星星,永远在一起,环绕着对方不停地转圈圈。
其实双星系统的魅力,远不止于此,它不仅仅是个美丽的天文现象,还给咱们带来了不少惊奇的发现。
好比两颗星星像情侣一样相互吸引,却又始终保持着某种微妙的平衡,这让人不禁想要探究它们之间到底有什么“隐秘的关系”呢。
先来说说啥是双星系统吧。
顾名思义,就是由两颗星星组成的系统。
它们彼此间靠得很近,像是亲密无间的朋友,或者说是“如胶似漆”的情侣。
在这个系统中,两个天体的引力相互作用,它们绕着共同的中心点转动。
这个过程看起来简单,可其实不简单,得靠精确的天文计算来理解。
比如你想想,如果一颗星星比另一颗大,那么它的引力就会更强,可能就会把另一颗小星星拉得更近;而这两颗星星如果太近了,又可能因为彼此的引力作用而碰撞,或者因为质量差异太大,形成某种不稳定的关系。
所以说,双星系统的稳定性和复杂性,简直堪比一段“理智又疯狂”的爱情故事。
有意思的是,双星系统不仅仅是天文爱好者的乐趣。
它其实对科学界的贡献也可大了。
比如通过观测双星的运动轨迹,科学家能够更准确地推算出星体的质量、大小,甚至连它们的年龄都能推算出来!想象一下,咱们在地球上用肉眼看着这些遥远的星星,竟然能推算出它们的种种秘密,简直就像是破解了宇宙的密码。
对了,这个过程叫做“天体力学”,其实就是研究天体如何相互作用、如何运动的一门学问。
你知道吗?在这双星的舞蹈中,有一个叫做“光变”的现象,特别有趣。
光变就是指由于双星系统中两颗星星的运动,造成它们的亮度变化。
简单来说,就是星星们互相绕着走,它们的位置一变化,咱们地球上的观察者就能看到亮度有高有低,就像是星星“在闪烁”一样。
这种变化其实是非常有规律的,有时候甚至能预测到星星什么时候“亮”和“暗”。
你觉得它是不是像个星星版的“灯泡开关”?每当两颗星互相掩蔽时,光线就变弱,给人一种星星在玩捉迷藏的感觉。


第17点双星系统中的三个特点宇宙中两个靠得比较近的天体,它们以两者连线上的某一点为圆心做匀速圆周运动而不至因为万有引力的作用吸引到一起,从而使它们间的距离不变,这样的系统称为双星系统,双星系统距离其他星体很远,可以当作孤立的系统处理.双星系统具有的三个特点:(1)两颗子星的向心力大小相等由于圆心O处无物体存在,所以这两颗行星做圆周运动所需的向心力只能由它们之间的万有引力互相提供——m2给m1的引力F1使m1做圆周运动;m1给m2的引力F2使m2做圆周运动.根据牛顿第三定律可知F1=F2,且方向相反,分别作用在m1、m2两颗星上.(2)两颗子星的圆心相同,且两轨道半径之和等于两星间距如图1所示,由于F1和F2提供向心力,所以它们都必须永远指向圆心O,又因两颗星的距离总是L,所以两颗星的连线必须始终通过圆心O,于是r1+r2=L.图1(3)两颗子星的运行周期相同两颗子星之间的距离总是恒定不变,且圆心总是在两星连线上,两星好像用一根无形的杆连着,所以这两颗星的运行周期必须相等,即T1=T2.对点例题在天体运动中,将两颗彼此相距较近的星体称为双星.它们在相互的万有引力作用下间距保持不变,并沿半径不同的同心圆轨道做匀速圆周运动.如果双星间距为L,质量分别为M1和M2,引力常量为G,试计算:(1)双星的轨道半径R1、R2;(2)双星的运行周期T;(3)双星的线速度v1、v2.解题指导因为双星受到同样大小的万有引力作用,且保持距离不变,绕同一圆心做匀速圆周运动,所以具有周期、转速和角速度均相同,而轨道半径和线速度不同的特点.(1)根据万有引力定律F=M1ω2R1=M2ω2R2及L=R1+R2可得:R1=M2M1+M2L,R2=M 1M 1+M 2L . (2)同理,G M 1M 2L 2=M 1⎝⎛⎭⎫2πT 2R 1=M 2⎝⎛⎭⎫2πT 2R 2 所以,周期T =4π2L 2R 1GM 2=4π2L 2R 2GM 1=2πL L G (M 1+M 2). (3)根据线速度公式有,v 1=2πR 1T =M 2 G L (M 1+M 2),v 2=2πR 2T =M 1 G L (M 1+M 2). 答案 (1)M 2M 1+M 2L M 1M 1+M 2L (2)2πLL G (M 1+M 2) (3)M 2 G L (M 1+M 2) M 1 G L (M 1+M 2)宇宙中距离较近的两个星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则( )A .双星相互间的万有引力增大B .双星圆周运动的角速度增大C .双星圆周运动的周期增大D .双星圆周运动的半径减小答案 C。
一、选择题1.2020年12月17日,嫦娥五号成功返回地球,创造了我国到月球取土的伟大历史。
如图所示,嫦娥五号取土后,在P点处由圆形轨道Ⅰ变轨到椭圆轨道Ⅱ,以便返回地球。
已知嫦娥五号在圆形轨道Ⅰ的运行周期为T1,轨道半径为R;椭圆轨道Ⅱ的半长轴为a,经过P点的速率为v,运行周期为T2。
已知月球的质量为M,万有引力常量为G,则()A.3132TTaR=B.GMva=C.GMvR=D.23214πRMGT=2.据报道,我国将在2022年前后完成空间站建造并开始运营,建成后空间站轨道距地面高度约h=4.0×102km。
已知地球的半径R=6.4×103km,第一宇宙速度为7.9km/s。
则该空间站的运行速度约为()A.7.7km/s B.8.0km/s C.7.0km/s D.3.1km/s3.已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述中正确的是()A.卫星的运行速度可能等于第一宇宙速度B2 324 GMTπC.卫星运行的向心加速度小于地球表面的重力加速度D.卫星运行的向心加速度等于地球赤道表面物体的向心加速度4.2019年12月16日,我国的西昌卫星发射中心又一次完美发射两颗北斗卫星,标志着“北斗三号”全球系统核心星座部署完成。
若北斗卫星A与B运行时都绕地心做匀速圆周运动,轨道半径之比为2:3,且两者动能相等,则下列说法正确的是()A.A、B两颗卫星的运行速度都大于7.9km/sB.A、B卫星所受到的万有引力大小之比是3:2C.A、B两颗卫星环绕地球的周期之比是2:3D.A、B两颗卫星的运行速度大小之比是2:35.我国即将展开深空探测,计划在2020年通过一次发射,实现火星环绕探测和软着陆巡视探测,已知太阳的质量为M,地球、火星绕太阳做匀速圆周运动的轨道半径分别为R1和R2,速率分别为v1和v2,地球绕太阳的周期为T。
当质量为m的探测器被发射到以地球轨道上的A点为近日点,火星轨道上的B点为远日点的轨道上围绕太阳运行时(如图),只考虑太阳对探测器的作用,则()A .探测器在A 点加速度的值大于211v RB .探测器在B 点的加速度小于22GMRC .探测地在B 点的加速度222v RD .探测器沿椭圆轨道从A 飞行到B 的时间为312211()2R R T R 6.我国首次火星探测任务被命名为“天问一号”,图为探测任务的标识。
双星系统演化以及行星形成过程解析在宇宙的浩瀚星空中,有许多恒星不是孤单地存在,而是以双星系统的形式存在。
双星系统是指两颗恒星以引力相互束缚在一起,共同绕着质心运动。
这种系统的演化过程和行星形成过程有着紧密的关联,为了更好地理解双星系统演化和行星形成的奥秘,我们需要从恒星的形成开始探寻。
恒星的形成始于分子云的坍缩。
当分子云中的物质密度达到一定程度时,引力开始主导,并使分子云内的物质向中心聚集。
这一过程称为原恒星形成过程。
在聚集过程中,初始条件的微小差异会导致最终物质聚集成多个星团。
如果这些星团足够靠近,它们的引力作用会使它们逐渐合并,形成双星系统。
因此,双星系统的形成可以视为恒星形成过程中的一个可能结果。
一旦双星系统形成,它们将共同经历一系列复杂的演化过程。
最常见的一种演化方式是通过星际云层的相互作用而发生的。
在云层中,双星系统可能受到其他恒星或浮游行星的干扰。
这种干扰会改变双星系统的运动轨迹,使其轨道变得更加离心或相对更加稳定。
这种干扰也可能导致双星系统的轨道融合,从而形成更大质量的恒星或聚星团。
这种演化过程可能会持续几百万年甚至几十亿年。
双星系统中的恒星演化过程也会对行星的形成产生重要影响。
在恒星形成的初始阶段,盘状结构会围绕恒星形成。
这个被称为原行星盘的结构是行星形成的理想环境。
在原行星盘中,尘埃和气体开始聚集,并在引力的作用下逐渐形成行星。
然而,双星系统中的恒星发出的强大引力将会干扰行星形成的过程。
它们可能会破坏尘埃环,使行星的形成变得困难。
此外,在双星系统中,行星的形成可能受到双星的重力共振的影响。
这种重力共振可能会导致行星轨道变得不稳定,甚至行星被抛出系统。
然而,随着时间的推移,双星系统的演化和行星形成的关系变得更加复杂。
研究表明,在一些双星系统中,行星的形成仍然可能发生。
当双星系统的轨道足够宽阔,它们不会对行星形成的初始阶段产生明显影响。
此外,如果尘埃和气体在双星系统中足够稳定,它们仍然可以通过重力相互作用和碰撞逐渐形成行星。
双星系统高中物理
双星系统高中物理
双星系统是由两个恒星组成的天体系统。
其中一颗恒星的质量比另一颗恒星的质量大得多,因此被称为主恒星,而另一颗恒星被称为伴恒星。
双星系统的运行受到两个恒星之间的引力而动态稳定的控制,当两个恒星的引力力不平衡时,它们将开始运动。
高中物理中,双星系统是理解物体运动的重要理论。
双星系统不仅仅是人们理解物体运动的一种简单模型,它还被广泛应用于实际情况,如太阳系中太阳和行星之间的运动、卫星中卫星和地球之间的运动等。
此外,双星系统还可以帮助人们探索太空环境中的科学问题,如星系结构、太阳系中物理过程等。
北斗卫星导航系统简介与概述2013年08月17日⁄北斗导航资讯⁄共1511字⁄字号小中大⁄暂无评论一、概述北斗卫星导航系统﹝BeiDou(COMPASS)Navigation Satellite System﹞是中国正在实施的自主发展、独立运行的全球卫星导航系统。
系统建设目标是:建成独立自主、开放兼容、技术先进、稳定可靠的覆盖全球的北斗卫星导航系统,促进卫星导航产业链形成,形成完善的国家卫星导航应用产业支撑、推广和保障体系,推动卫星导航在国民经济社会各行业的广泛应用。
北斗卫星导航系统由空间段、地面段和用户段三部分组成,空间段包括5颗静止轨道卫星和30颗非静止轨道卫星,地面段包括主控站、注入站和监测站等若干个地面站,用户段包括北斗用户终端以及与其他卫星导航系统兼容二、发展历程卫星导航系统是重要的空间信息基础设施。
中国高度重视卫星导航系统的建设,一直在努力探索和发展拥有自主知识产权的卫星导航系统。
2000年,首先建成北斗导航试验系统,使我国成为继美、俄之后的世界上第三个拥有自主卫星导航系统的国家。
该系统已成功应用于测绘、电信、水利、渔业、交通运输、森林防火、减灾救灾和公共安全等诸多领域,产生显著的经济效益和社会效益。
特别是在2008年北京奥运会、汶川抗震救灾中发挥了重要作用。
为更好地服务于国家建设与发展,满足全球应用需求,我国启动实施了北斗卫星导航系统建设(一)北斗双星定位系统:2003年5月建成;三颗地球同步轨道卫星36,000km;卫星寿命5年;主动式定位,有源定位下行S波段,上行L波段;二维定位、授时、短报文服务、广域增强军民两用系统;被动式定位,无源定位。
特点:具有定位、授时、短报文通信多种功能;可用于发布广域差分信息;军民两用系统。
局限性:二维定位,高程要用气压计或DEM数字地面模型;中心站定位,不利于用户自主导航,安全性差;定位速度受到限制;用户量受限制。
(二)中国北斗导航定位系统(三)我国开始建设拥有自主知识产权的全球卫星导航系统――北斗卫星导航系统,这也是我国自主建立的第一代卫星导航定位系统。
双星系统引力平衡点
双星系统的引力平衡点是指在双星系统中,两颗恒星的引力相互作用下,存在着一个使得第三个质点能够与两颗恒星保持相对静止的点。
这个点被称为拉格朗日点,通常用L1、L2、L3、L4和L5来表示。
首先,让我们来看L1点。
L1点位于两颗恒星之间的直线上,距离较近的一颗恒星的前方。
在L1点,第三个质点受到两颗恒星的引力,恰好与两颗恒星的引力平衡,保持相对静止。
L1点在太空任务中有着重要的应用,例如太空望远镜常常被放置在L1点,这样可以保持与地球的相对位置,从而更好地观测宇宙。
接下来是L2点,位于两颗恒星之间的直线上,距离较远的一颗恒星的后方。
在L2点,第三个质点同样受到两颗恒星的引力,恰好与两颗恒星的引力平衡,保持相对静止。
L2点也被用于太空任务,例如“雅典娜”和“詹姆斯·韦伯”太空望远镜就被计划放置在L2点。
然后是L3点,位于两颗恒星之间的直线上,与L1点相对。
在L3点,第三个质点同样受到两颗恒星的引力,保持相对静止。
L3点
也可能被用于太空任务,但由于其位置相对不稳定,使用较少。
L4和L5点则位于两颗恒星构成的等边三角形的顶点,相对于两颗恒星来说,这两个点是稳定的。
在这两个点上,第三个质点同样受到两颗恒星的引力,保持相对静止。
L4和L5点被称为“特洛伊安点”,在太阳系中的木星和土星的特洛伊安小行星就是位于这两个点上的。
总的来说,双星系统的引力平衡点是由两颗恒星的引力共同作用形成的特殊位置,这些点在太空科学和太空任务中有着重要的应用价值。
第17点双星系统中的三个特点
宇宙中两个靠得比较近的天体,它们以两者连线上的某一点为圆心做匀速圆周运动而不至因为万有引力的作用吸引到一起,从而使它们间的距离不变,这样的系统称为双星系统,双星系统距离其他星体很远,可以当作孤立的系统处理.
双星系统具有的三个特点:
(1)两颗子星的向心力大小相等
由于圆心O处无物体存在,所以这两颗行星做圆周运动所需的向心力只能由它们之间的万有引力互相提供——m2给m1的引力F1使m1做圆周运动;m1给m2的引力F2使m2做圆周运动.根据牛顿第三定律可知F1=F2,且方向相反,分别作用在m1、m2两颗星上.(2)两颗子星的圆心相同,且两轨道半径之和等于两星间距
如图1所示,由于F1和F2提供向心力,所以它们都必须永远指向圆心O,又因两颗星的距离总是L,所以两颗星的连线必须始终通过圆心O,于是r1+r2=L.
图1
(3)两颗子星的运行周期相同
两颗子星之间的距离总是恒定不变,且圆心总是在两星连线上,两星好像用一根无形的杆连着,所以这两颗星的运行周期必须相等,即T1=T2.
对点例题在天体运动中,将两颗彼此相距较近的星体称为双星.它们在相互的万有引力作用下间距保持不变,并沿半径不同的同心圆轨道做匀速圆周运动.如果双星间距为L,质量分别为M1和M2,引力常量为G,试计算:
(1)双星的轨道半径R1、R2;(2)双星的运行周期T;(3)双星的线速度v1、v2.
解题指导因为双星受到同样大小的万有引力作用,且保持距离不变,绕同一圆心做匀速圆周运动,所以具有周期、转速和角速度均相同,而轨道半径和线速度不同的特点.
(1)根据万有引力定律F=M1ω2R1=M2ω2R2及L=R1+R2可得:R1=
M2
M1+M2
L,R2=
M 1M 1+M 2
L .
(2)同理,G M 1M 2L 2=M 1⎝⎛⎭⎫2πT 2R 1=M 2⎝⎛⎭⎫2πT 2R 2 所以,周期T =
4π2L 2R 1
GM 2
=4π2L 2R 2
GM 1
=2πL L
G (M 1+M 2)
.
(3)根据线速度公式有,v 1=
2πR 1
T
=M 2 G
L (M 1+M 2)
,v 2=2πR 2
T =M 1
G
L (M 1+M 2)
.
答案 (1)M 2M 1+M 2L M 1
M 1+M 2L
(2)2πL L
G (M 1+M 2)
(3)M 2
G
L (M 1+M 2)
M 1
G
L (M 1+M 2)
宇宙中距离较近的两个星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动,则( ) A .双星相互间的万有引力增大 B .双星圆周运动的角速度增大 C .双星圆周运动的周期增大 D .双星圆周运动的半径减小 答案 C。