阵列信号处理作业

阵列信号处理（Array Signal Processing）1. 简介阵列信号处理是一种利用多个传感器或微phones接收到的信号进行处理的技术。

这些传感器通常以阵列的形式排列在一起，可以在空间上对信号进行采样。

阵列信号处理技术可以用于各种应用，包括无线通信、雷达、声音定位和语音增强等领域。

在阵列信号处理中，经常会使用到点扩散函数（Point Spread Function，PSF）和反卷积（Deconvolution）等概念。

本文将详细介绍这些特定函数的定义、用途和工作方式。

2. 点扩散函数（Point Spread Function，PSF）2.1 定义点扩散函数（PSF）是指在观察到一个点源时，系统输出的响应。

点源可以是一个理想的点光源、点声源或点热源等。

PSF描述了系统对于一个点源的感知能力，可以用于评估系统的分辨率和信号传输特性。

2.2 用途PSF在阵列信号处理中具有广泛的应用，主要用于以下几个方面：2.2.1 分辨率评估PSF可以用于评估系统的分辨率，即系统能够分辨并显示的最小特征尺寸。

通过分析PSF的形状和尺寸，可以确定系统的分辨率限制，进而优化系统设计和参数设置。

2.2.2 反卷积PSF还可以用于图像或信号的反卷积处理。

在实际应用中，由于传感器和系统的限制，观测到的信号往往受到模糊和失真的影响。

通过将观测到的信号与PSF进行卷积运算的逆过程，可以恢复出原始信号的更清晰的图像或声音。

2.2.3 信号重构PSF在阵列信号处理中也可以用于信号重构。

通过对多个传感器接收到的信号进行处理和分析，可以利用PSF将信号的不同成分分离出来，从而实现信号的重构和定位。

2.3 工作方式PSF的工作方式可以通过以下几个步骤来理解：2.3.1 系统建模首先，需要对阵列系统进行建模。

这包括确定阵列的几何结构、传感器的位置和响应特性等。

通过建模，可以得到系统的传递函数，即系统对于输入信号的响应。

2.3.2 点源输入接下来，将一个点源输入到系统中，观察系统的输出。

宽带信号中的三种二维平面阵DOA估计宽带信号中的三种二维平面阵DOA 估计一． 背景目前关于阵列窄带信号的高分辨算法已比较成熟，但是随着信号处理技术的发展，信号环境日趋复杂，信号形式多样，信号密度日渐增大，窄带阵列探测系统的确定逐渐显示出来。

由于宽带信号具有目标回波携带的信息量大，有利于目标探测、参量估计和目标特征提取等特点，在有源探测系统中越来越多地得到应用。

而在无源探测系统中，利用目标辐射的宽带连续谱进行目标检测是有效发现目标的一种重要手段。

ISM 方法把宽带信号在频域分解为J 个窄带分量，然后在每一个子带上直接进行窄带处理。

因为信号为调频信号，所以信号在时域的分段实际上就是频域的分段。

将信号分解为窄带信号后，我们就可以利用窄带算法进行处理，最后将各个结果进行加权综合，即可得到最终的结果。

二维DOA 估计是阵列信号处理中的重要内容，通过二维DOA 估计可以得到信号源在平面中的角度信息。

一般采用L 型、面阵和平行阵或矢量传感器实现二维参数的估计，多数有效的二维DOA 估计算法是在一维DOA 估计的基础上，直接针对空间二维谱提出的，如二维MUSIC 算法以及二维CAPON 算法等。

这两种算法可以产生渐进无偏估计，但要在二维参数空间搜索谱峰，计算量相当大。

而采用二维ROOT MUSIC 算法可以减小计算量，但是需要付出精度下降的代价。

本次报告将结合宽带信号和二维DOA 估计算法，进行相关的算法介绍和仿真。

二． 算法介绍1. 接收信号模型：图 1 平面阵列示意图如图1所示，设平面阵元数为M ×N ，信源数为K 。

信源的波达方向为11(,),,(,)k k θφθφ ，第i 个阵元与参考阵元之间的波程差为：2(cos sin sin sin cos )/i i i x y z βπφθφθθλ=++设子阵1沿x 轴的方向矩阵为x A ，而子阵2的每个阵元相对于参考阵元的波程差就等于子阵1的阵元的波程差加上2sin sin /d πφθλ，所以接收信号为121()()()y x y x y M x A D A A D A X S N A D A -⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎣⎦协方差矩阵为H H H s s s n n n R XX E D E E D E ==+其中，s D 代表由最大的K 个特征值构成的一个K ×K 对角阵，n D 代表由MN-k 个较小的特征值构成的对角矩阵, s E 和n E 分别代表由s D 和n D 对应的特征值构成的特征矢量。

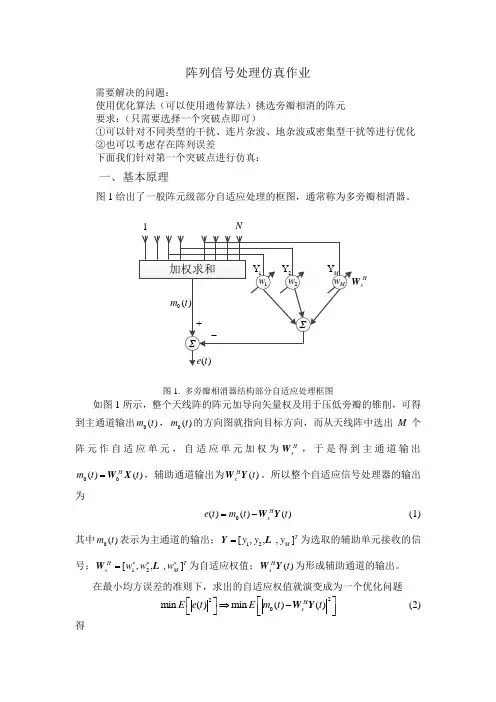
阵列信号处理仿真作业需要解决的问题：使用优化算法（可以使用遗传算法）挑选旁瓣相消的阵元 要求：（只需要选择一个突破点即可）①可以针对不同类型的干扰、连片杂波、地杂波或密集型干扰等进行优化 ②也可以考虑存在阵列误差下面我们针对第一个突破点进行仿真：一、基本原理图1给出了一般阵元级部分自适应处理的框图，通常称为多旁瓣相消器。

1NHx图1. 多旁瓣相消器结构部分自适应处理框图如图1所示，整个天线阵的阵元加导向矢量权及用于压低旁瓣的锥削，可得到主通道输出0()m t ，0()m t 的方向图就指向目标方向，而从天线阵中选出M 个阵元作自适应单元，自适应单元加权为H x W ，于是得到主通道输出00()()H m t t =W X ，辅助通道输出为()H x t W Y 。

所以整个自适应信号处理器的输出为0()()()H x e t m t t =-W Y(1)其中0()m t 表示为主通道的输出；12[,,,]T M y y y =Y L 为选取的辅助单元接收的信号；12[,,,]H Tx M w w w ***=W L 为自适应权值；()H x t W Y 为形成辅助通道的输出。

在最小均方误差的准则下，求出的自适应权值就演变成为一个优化问题220min ()min ()()H x E e t E m t t ⎡⎤⎡⎤⇒-⎢⎥⎣⎦⎣⎦W Y (2)得10()()()()H H xE t t E t m t -*⎡⎤⎡⎤=⎣⎦⎣⎦WY Y Y(3)为了保证目标信号不损失，应对自适应权作约束，约束条件是在目标信号的方向上，阵列自适应处理的增益为一常数。

即在权值调整过程中，无论权x W 怎样变化，对有用信号的增益不变。

这样在使自适应阵输出()e t 的均方值2()E e t ⎡⎤⎣⎦最小时，能最大限度地抑制干扰且不损失有用信号能量。

图1中应用式( 2) 的无约束优化方程显然不合理，它不能保证有用信号增益不变。

阵列接收信号处理流程一、信号接收阵列接收信号处理的第一步是信号接收。

在阵列中，有多个接收器同时接收信号。

这些接收器可以是天线、传感器或其他接收设备。

每个接收器都可以独立地接收到信号，并将信号传输到后续的信号处理单元。

二、信号预处理接收到的信号可能会受到噪声、干扰或其他不完美因素的影响，因此需要进行信号预处理。

信号预处理的目的是提高信号的质量和准确性。

常见的信号预处理方法包括滤波、增益控制、噪声消除和时序校正等。

滤波是信号预处理的一种常用方法。

通过滤波可以去除信号中的噪声和干扰，提高信号的清晰度和可辨识度。

常见的滤波方法有低通滤波、高通滤波和带通滤波等。

增益控制是调整信号强度的方法。

通过增益控制可以使信号的强度达到最佳状态，避免信号过强或过弱的问题。

噪声消除是去除信号中噪声成分的方法。

噪声是信号中的不完美因素，可能会干扰信号的质量和准确性。

通过噪声消除可以提高信号的清晰度和准确性。

时序校正是调整信号的时序关系的方法。

在多个接收器同时接收信号时，由于信号传输路径的不同，信号到达各个接收器的时间可能存在微小的差异。

通过时序校正可以使信号的时序关系达到一致，提高信号的同步性和准确性。

三、信号合并经过信号预处理后，接收到的信号可以进行合并。

信号合并是将多个接收器接收到的信号进行综合和整合的过程。

通过信号合并可以提高信号的强度和准确性，增加信号的可靠性和鲁棒性。

常见的信号合并方法有加权平均法、最大比例合并法和最大比例合并法等。

加权平均法是将每个接收器接收到的信号按照一定的权重进行加权平均，得到综合的信号。

最大比例合并法是选择接收到信号强度最大的接收器的信号作为综合的信号。

最大比例合并法是根据接收到信号的强度比例进行综合，提高信号的强度和准确性。

四、信号解调和解码信号合并后，接下来需要进行信号的解调和解码。

信号解调是将调制信号转化为原始信号的过程。

常见的调制方式有频率调制、相位调制和振幅调制等。

通过信号解调可以恢复出原始信号的特征和信息。

作业一 在球坐标系下推导平面波表达式球面波波动方程：22222222()E E x y z tεμ∂∂∂∂++=∂∂∂∂ 将直角坐标与球坐标的关系带入得到：22222222221111()(sin )sin sin s s sr r r r r r c tθθθθθϕ∂∂∂∂∂∂++=∂∂∂∂∂∂ 应用球面波方程一般都是球对称的，简化为：2222211()s sr r r r c t∂∂∂=∂∂∂ 经过变化，可得：222221rs rsr c t ∂∂=∂∂ 该方程的一个解为：exp[()As j t kr rω=- 同样有如下关系：/k c ω=根据平面波的定义，在球坐标系下，单频平面波的表达式为：(,)exp[()]As r t j t k r rω=-⋅作业二对于有限孔径的感应器，某一感应器接收的信号可以表示为：(,)()(,)z x t w x f x t =其中()w x 为窗函数。

通过空间傅立叶变换可得：()()exp()W k w x jk x dx ∞-∞=⋅⎰(,)(,)exp[()F k f x t j t k x dxdt ωω∞∞-∞-∞=--⋅⎰⎰对接收信号(,)z x t 进行傅立叶变换：()()()()[]()()()(){}()(),,exp[(),exp exp ,exp ,exp exp ,exp exp o Z k z x t j t k x dxdtw x f x t j t jk x dxdtw x F x jk x dxw x F l jl x dl jk x dx w x F l jl x jk ωωωωωω∞∞-∞-∞∞∞-∞-∞∞-∞∞∞-∞-∞∞∞-∞-∞=--⋅⎡⎤=-⋅⎣⎦⎡⎤=⋅⎣⎦⎡⎤⎡⎤=-⋅⋅⎣⎦⎣⎦⎡⎤=-⋅⋅⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰⎰()()(){}()(),exp ,x dldxF l w x j k l x dx dlW k l F l dlωω∞∞-∞-∞∞-∞⎡⎤⎣⎦⎡⎤=-⋅⎣⎦=-⎰⎰⎰ 其中，()()[],,exp o F x f x t j t dt ωω∞-∞=-⎰。