下载文档原格式
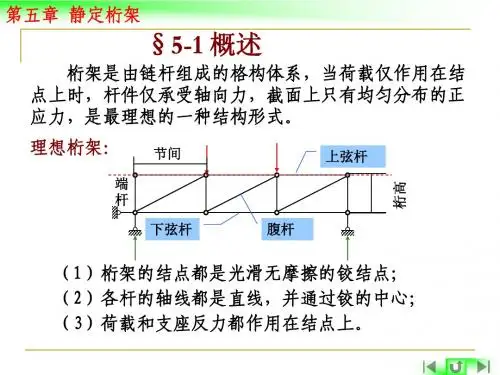
§3-5 一.桁架的特点和组成静定桁架§3-5弦杆 下弦杆 上弦杆静定桁架斜杆 竖杆 腹杆 桁高 d 节间跨度 • 抽象简化成杆轴交于一点、且只受结点荷载作 用的直杆铰结体系 • 特性：只有轴力，没有弯矩和剪力。
§3-5静定桁架二.桁架的简化和假定<1> 桁架的结点为光滑的铰结点。
<2> 各杆的轴线均为直线且通过铰心。
<3> 荷载和支座反力都作用在结点上。
理想桁架各杆只受轴力 ——主内力 截面上应力分布均匀 ——主应力 次内力—— 实际内力与主内力的差值 理想桁架§3-5静定桁架三.桁架结构的分类 简单桁架 — 由基础或一个基本铰接三角形开始， 依次增加二元体所组成的桁架。
§3-5静定桁架 联合桁架 — 由几个简单桁架按照两刚片或 三刚片规则组成的桁架§3-5静定桁架四、计算桁架内力的方法求桁架的轴力：截取桁架的一部分为隔离体， 考虑隔离体的平衡，建立平衡方程，由平衡方 程解出杆的轴力。
§3-5静定桁架1、结点法 ——截取的隔离体为一个结点yFN 1FN 3FN 2Fx平衡方程： ∑ Fx = 0∑Fy=0——可求两个未知力要求：截取的结点上不超过二个未知内力 结点法：为分析桁架的基本方法之一，适合简单桁架A BC DE对于简单桁架，若与组成顺序相反依次截取结点， 可顺利地求出全部杆件的轴力。
§3-5静定桁架2、求各杆内力8kN【例】 试求桁架的内力图8kN 8kN 6kN 8kN 8kN 0.5mA BAαCEG F1.5mβD0.75m 0.75mFAy = 19 KN1.5mFBy = 19 KNFAy = 19 KNyFNAC FNAD∑F=019 − 8 − FNAD sin α = 0解： 1、 求支座反力FNAD = 34.8kN∑ F = 0，F ∑ M = 0，F ∑ F = 0，Fx A yAx=0 = 19kN (↑) = 19kN (↑)∑Fx=0FNAC + FNAD cos α = 0ByFNAC = −33kNAy§3-5【例】 试求桁架的内力图8kN 8kN 6kN 8kN 8kN静定桁架8kN 33kNCFNCE0.5mAαCEG F1.5mBFNCDβD0.75m 0.75mFAy = 19 KN1.5mFBy = 19 KN∑F ∑Fx y= 0， FNCE = − 33 kN = 0， FNCD = − 8 kNFNDEβ8kN⎧ FNAC = −33kN ⎨ ⎩ FNAD = 34.8kN34.8kNDFNDF∑F∑Fxy= 0， FNDE sin β − 8 + 34.8 sin α = 0FNDE = −5.4kN FNDF = 37.5kN= 0， FNDE cos β + FNDF − 34.8 cos α = 0§3-5静定桁架3、 绘制内力图A -3334.8【例】 试求桁架的内力图8kN 8kN 6kN 8kN 8kN 0.5mAαCEG F1.5mBβD0.75m 0.75mFAy = 19 KN1.5mFBy = 19 KNE G -33 -33 -33 -8 -5.4 -5.4 -8 34.8 D 37.5 FCBFN图（kN )利用结构的对称性得所有杆的内力⎧ FNAC = −33kN ⎨ ⎩ FNAD = 34.8kNFNCE = − 33 kN FNCD = − 8 kN⎧ FNDE = −5.4kN ⎨ ⎩ FNDF = 37.5kN零杆的判别：轴力为零 1、两杆结点上无荷载作用，则两杆内力＝0FN 1FN 1 = FN 2 = 0L形结点FN 22、三杆结点上无荷载作用，若其中两杆在一条 直线上，则另一杆必为零杆。
