bayes判别分析案例及结果

bayes法计算遗传例子(一)Bayes法计算遗传Bayes法是一种常用的概率统计方法，用于计算遗传学中的各种概率问题。

下面列举了一些应用Bayes法计算遗传的例子，并详细讲解每个例子的计算步骤。

例子1: 遗传病携带者概率假设某种遗传病是由一对隐性基因引起的，该基因阻碍了患者体内产生特定的酶。

现在有一对夫妇，二者都没有表现出遗传病的症状，但知道自己的父母中有人患有该病。

他们打算要一个孩子，现在想知道他们的孩子患有该病的概率。

计算步骤： 1. 假设该夫妇都是基因携带者的概率为P(A) = 1/4，其中A代表该夫妇都是基因携带者。

2. 由于该病是由隐性基因引起的，在一对隐性基因携带者夫妇的子女中，每个子女的患病概率为1/4。

3. 因此，该夫妇的孩子患有该病的概率为P(B|A) = 1/4。

例子2: 遗传病与基因检测某种遗传病的表现型只有基因型为Aa或AA的个体才会患病。

现有一家三口，父亲和母亲的基因型均为Aa，他们的孩子患病的概率是多少？计算步骤： 1. 父亲和母亲的基因型为Aa，即每个人都有一个A基因和一个a基因。

2. 孩子患病的概率可以通过计算父亲和母亲之间产生不同基因型子代的概率来得到。

在这种情况下，父亲和母亲之间共有以下四种基因组合：AA、Aa、aA、aa，每种组合的概率均为1/4。

3. 只有基因型为Aa或AA的个体才会患病，因此只有前三种基因组合的孩子有可能患病。

这三种组合中，有两种携带基因A的组合(AA和Aa)，因此孩子患病的概率为P(B) = 2/4 = 1/2。

例子3: 利用先验概率计算遗传性状某种遗传性状受一个隐性基因和一个显性基因共同决定。

现有一对夫妇，其中丈夫是显性基因型，妻子是隐性基因型。

他们的孩子有多大概率是显性基因型？计算步骤： 1. 根据题目所给的信息，丈夫的基因型是显性，即AA或Aa；妻子的基因型是隐性，即aa。

2. 在这种情况下，通过计算丈夫和妻子之间产生不同基因型子代的概率，来确定孩子是显性基因型的概率。

贝叶斯判别、费希尔判别法的计算机操作及结果分析一、实验内容、目标及要求（一）实验内容选取140家上市公司作为样本，其中70家为由于“财务状况异常”而被交易所对其股票实行特别处理（Special Treatment，简称ST）的公司，另外70家为财务正常的公司。

为了研究上市公司发生财务困境的可能性，以“是否被ST”为分组变量，选择资产负债率、总资产周转率和总资产利润率几个财务指标作为判别分析变量，这三个指标分别从上市公司的偿债能力、资产管理能力和获利能力三个不同的角度反映了企业的财务状况。

（二）实验目标贝叶斯判别、费希尔判别法的计算机操作及结果分析。

（三）实验要求要求学生能熟练应用计算机软件进行判别分析并对结果进行分析，培养实际应用能力。

二、实验准备（一）运行环境说明电脑操作系统为Windows XP及以上版本，所需软件为SPSS 16.0。

（二）基础数据设置说明将数据正确导入SPSS，设置相应的变量值。

三、实验基本操作流程及说明（一）系统界面及说明同实验一。

（二）操作步骤1. 选择菜单项Analyze→Classify→Discriminate，打开Discriminate Analysis对话框，如图4-1。

将分组变量st移入Grouping V ariable列表框中，将自变量x1－x3选入Independents 列表框中。

选择Enter independents together单选按钮，即使用所有自变量进行判别分析。

若选择了Use stepwise method单选按钮，则可以根据不同自变量对判别贡献的大小进行变量筛选，此时，对话框下方的Method按钮被激活，可以通过点击该按钮设置变量筛选的方法及变量筛选的标准。

图4-1 Discriminate Analysis对话框2. 单击Define Range按钮，在打开的Define Range子对话框中定义分组变量的取值范围。

本例中分类变量的取值范围为0到1，所以在Minimum和Maximum输入框中分别输入0和1。

我们来看一个简单的例子：例：高射炮向敌机发射三发炮弹，每弹击中与否相互独立且每发炮弹击中的概率均为0.3，又知敌机若中一弹，坠毁的概率为0.2，若中两弹，坠毁的概率为0.6，若中三弹，敌机必坠毁。

求敌机坠毁的概率。

解：设事件B=“敌机坠毁”；Ai=“敌机中弹”；i=0,1,2,3 实际上我们从题目知道应该是A0,A1,A2,A3构成完备事件组，但是敌机坠毁只和A1,A2,A3有关，即则我们可用如下公式则贝叶斯准则例题P(B|A) 在A的情况下B发生的概率P（A|B）在B的情况下A发生的概率贝叶斯公式：贝叶斯定理公式：P(A|B)=P(B|A)*P(A)/P(B)如上公式也可变形为：P(B|A)=P(A|B)*P(B)/P(A)1、例如：一座别墅在过去的 20 年里一共发生过 2 次被盗，别墅的主人有一条狗，狗平均每周晚上叫 3 次，在盗贼入侵时狗叫的概率被估计为0.9，问题是：在狗叫的时候发生入侵的概率是多少？我们假设 A 事件为狗在晚上叫，B 为盗贼入侵，则 P(A) = 3 / 7，P(B)=2/(20·365)=2/7300，P(A | B) = 0.9（窃贼入室盗窃狗叫概率），按照公式很容易得出结果：P(B|A)=0.9*(2/7300)*(7/3)=0.000582、另一个例子，现分别有 A，B 两个容器，在容器 A 里分别有 7 个红球和 3 个白球，在容器 B 里有 1 个红球和 9 个白球，现已知从这两个容器里任意抽出了一个球，且是红球，问这个红球是来自容器 A 的概率是多少?假设已经抽出红球为事件 B，从容器 A 里抽出球为事件 A，则有：P(B) = 8 / 20，P(A) = 1 / 2，P(B | A) = 7 / 10（容器A中抽到红球的概率），按照公式，则有：P(A|B)=(7 / 10)*(1 / 2)*(20/8)=7/8。

实验十一Bayes判别实验目的和要求掌握Bayes判别分析的理论与方法、模型的建立与误差率估计；掌握利用判别分析的SAS过程解决有关实际问题.实验要求:编写程序，结果分析．实验内容：5.4 5.5 选一题data examp5_4。

input group $ x1-x7 @@。

cards。

G1 6.6 39 1.0 6.0 6 0.12 20G1 6.6 39 1.0 6.0 12 0.12 20G1 6.1 47 1.0 6.0 6 0.08 12G1 6.1 47 1.0 6.0 12 0.08 12G1 8.4 32 2.0 7.5 19 0.35 75G1 7.2 6 1.0 7.0 28 0.30 30G1 8.4 113 3.5 6.0 18 0.15 75G1 7.5 52 1.0 6.0 12 0.16 40G1 7.5 52 3.5 7.5 6 0.16 40G1 8.3 113 0.0 7.5 35 0.12 180G1 7.8 172 1.0 3.5 14 0.21 45G1 7.8 172 1.5 3.0 15 0.21 45G2 8.4 32 2.0 9.0 10 0.35 75 G2 8.4 32 2.5 4.0 10 0.35 75 G2 6.3 11 4.5 7.5 3 0.20 15 G2 7.0 8 4.5 4.5 9 0.25 30 G2 7.0 8 6.0 7.5 4 0.25 30 G2 7.0 8 1.5 6.0 1 0.25 30 G2 8.3 161 1.5 4.0 4 0.08 70 G2 8.3 161 0.5 2.5 1 0.08 70 G2 7.2 6 3.5 4.0 12 0.30 30 G2 7.2 6 1.0 3.0 3 0.30 30 G2 7.2 6 1.0 6.0 5 0.30 30 G2 5.5 6 2.5 3.0 7 0.18 18 G2 8.4 113 3.5 4.5 6 0.15 75 G2 8.4 113 3.5 4.5 8 0.15 75 G2 7.5 52 1.0 6.0 6 0.16 40 G2 7.5 52 1.0 7.5 8 0.16 40 G2 8.3 97 0.0 6.0 5 0.15 180 G2 8.3 97 2.5 6.0 5 0.15 180 G2 8.3 89 0.0 6.0 10 0.16 180 G2 8.3 56 1.5 6.0 13 0.25 180 G2 7.8 172 1.0 3.5 6 0.21 45run。

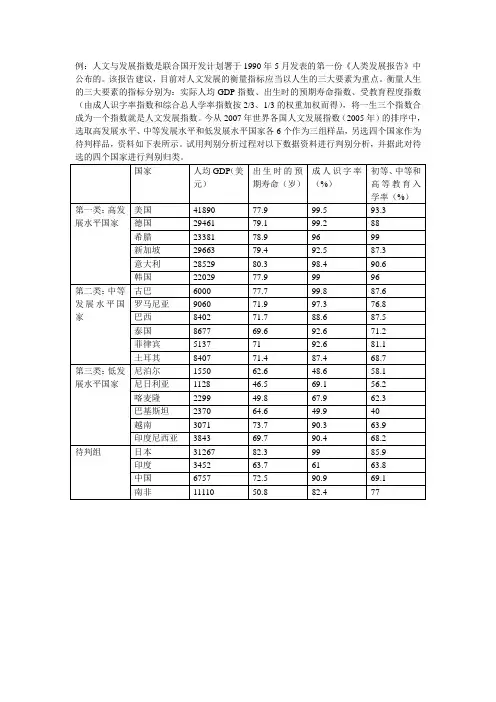
例：人文与发展指数是联合国开发计划署于1990年5月发表的第一份《人类发展报告》中公布的。

该报告建议，目前对人文发展的衡量指标应当以人生的三大要素为重点。

衡量人生的三大要素的指标分别为：实际人均GDP指数、出生时的预期寿命指数、受教育程度指数（由成人识字率指数和综合总人学率指数按2/3、1/3的权重加权而得），将一生三个指数合成为一个指数就是人文发展指数。

今从2007年世界各国人文发展指数（2005年）的排序中，选取高发展水平、中等发展水平和低发展水平国家各6个作为三组样品，另选四个国家作为待判样品，资料如下表所示。

试用判别分析过程对以下数据资料进行判别分析，并据此对待data develop;input type gdp life rate zhrate@@;cards;1 41890 77.9 99.5 93.31 29461 79.1 99.2 881 23381 78.9 96 991 29663 79.4 92.5 87.31 28529 80.3 98.4 90.61 22029 77.9 99 962 6000 77.7 99.8 87.62 9060 71.9 97.3 76.82 8402 71.7 88.6 87.52 8677 69.6 92.6 71.22 5137 71 92.6 81.12 8407 71.4 87.4 68.73 1550 62.6 48.6 58.13 1128 46.5 69.1 56.23 2299 49.8 67.9 62.33 2370 64.6 49.9 403 3071 73.7 90.3 63.93 3843 69.7 90.4 68.2. 31267 82.3 99 85.9. 3452 63.7 61 63.8. 6757 72.5 90.9 69.1. 11110 50.8 82.4 77;proc discrim simple wcov distance list;/*simple:要求技术各类样品的简单描述统计量；选项WCOV要求计算类内协方差阵；选项DISTANCE要求计算马氏距离；选项LIST要求输出重复替换归类结果。