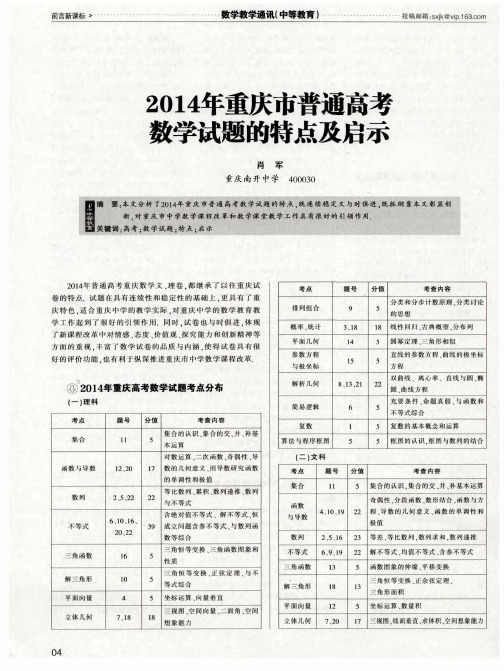
2014长庆高考数学(文)试卷

2014年重庆市高考数学试卷（文科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的．3．（5分）（2014•重庆）某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则解：分层抽样的抽取比例为，×5．（5分）（2014•重庆）执行如图所示的程序框图，则输出s的值为（）6．（5分）（2014•重庆）已知命题：p：对任意x∈R，总有|x|≥0，q：x=1是方程x+2=0的根；7．（5分）（2014•重庆）某几何体的三视图如图所示，则该几何体的体积为（）V=×﹣×8．（5分）（2014•重庆）设F1，F2分别为双曲线﹣=1（a＞0，b＞0）的左、右焦点，22B===+2+2＞2∴a+b=a+=a+=a+3++7+7a=4+210．（5分）（2014•重庆）已知函数f（x）=，且g（x）（﹣，﹣]（﹣]（﹣]（﹣]，x=﹣＜，二、填空题：本大题共5小题，每小题5分，把答案填写在答题卡相应的位置上．11．（5分）（2014•重庆）已知集合A={3，4，5，12，13}，B={2，3，5，8，13}，则A∩B= {3，5，13}．12．（5分）（2014•重庆）已知向量与的夹角为60°，且=（﹣2，﹣6），||=，则•=10．解：∵=∴∴13．（5分）（2014•重庆）将函数f（x）=sin（ωx+φ）（ω＞0，﹣≤φ＜）图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移个单位长度得到y=sinx的图象，则f（）=．ωω（，﹣）图象上每一点的横坐标缩短为个单位长度得到函数﹣ω﹣（x+（（）=sin=故答案为：14．（5分）（2014•重庆）已知直线x﹣y+a=0与圆心为C的圆x2+y2+2x﹣4y﹣4=0相交于A、B两点，且AC⊥BC，则实数a的值为0或6．=15．（5分）（2014•重庆）某校早上8：00开始上课，假设该校学生小张与小王在早上7：30～7：50之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早5分钟到校的概率为（用数字作答）．，联立得，联立得×，故答案为：．三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16．（13分）（2014•重庆）已知{a n}是首项为1，公差为2的等差数列，S n表示{a n}的前n 项和．（Ⅰ）求a n及S n；（Ⅱ）设{b n}是首项为2的等比数列，公比为q满足q2﹣（a4+1）q+S4=0．求{b n}的通项公式及其前n项和T n．∴17．（13分）（2014•重庆）20名学生某次数学考试成绩（单位：分）的频率分布直方图如图：（Ⅰ）求频率分布直方图中a的值；（Ⅱ）分别求出成绩落在[50，60）与[60，70）中的学生人数；（Ⅲ）从成绩在[50，70）的学生任选2人，求此2人的成绩都在[60，70）中的概率．P=18．（13分）（2014•重庆）在△ABC中，内角A、B、C所对的边分别是a、b、c，且a+b+c=8．（Ⅰ）若a=2，b=，求cosC的值；（Ⅱ）若sinAcos2+sinBcos2=2sinC，且△ABC的面积S=sinC，求a和b的值．求出sinC，且，cosC==；22=2sinCabsinC=sinC19．（12分）（2014•重庆）已知函数f（x）=+﹣lnx﹣，其中a∈R，且曲线y=f（x）在点（1，f（1））处的切线垂直于直线y=x．（Ⅰ）求a的值；（Ⅱ）求函数f（x）的单调区间与极值．y=+﹣﹣，x﹣a=+﹣﹣﹣=20．（12分）（2014•重庆）如图，四棱锥P﹣ABCD中，底面是以O为中心的菱形，PO⊥底面ABCD，AB=2，∠BAD=，M为BC上一点，且BM=．（Ⅰ）证明：BC⊥平面POM；（Ⅱ）若MP⊥AP，求四棱锥P﹣ABMO的体积．BAD=，BM=，结合菱形的性质，余弦定理，勾股定理，可得BAD=，（BM=OBM=（，，=，=，，即PO==•OM=S PO=21．（12分）（2014•重庆）如图，设椭圆+=1（a＞b＞0）的左右焦点分别为F1，F2，点D在椭圆上，DF1⊥F1F2，=2，△DF1F2的面积为．（Ⅰ）求该椭圆的标准方程；（Ⅱ）是否存在圆心在y轴上的圆，使圆在x轴的上方与椭圆有两个交点，且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点？若存在，求出圆的方程；若不存在，请说明理由．|=，于是可求得椭圆的标准方程；与椭圆﹣=2，得==，得，，因此，所求椭圆的标准方程为与椭圆，所以+﹣，即3﹣﹣得+1|=，==。

2014年高考（重庆卷）及参考答案高三2014-06-09 11:322014年普通高等学校招生全国统一考试（重庆卷）及参考答案语文试题卷语文试题卷共8页。

考试时间150分钟。

第1至6题、第8至10题为选抒題，27分；第7 题、第11至22题为非选择题，123分。

满分150分。

一、（本大题共4小题，毎小题3分，共12分）1.下列词语中,字形和加点字的读音全都正确的一组是A.屋檐下绿草如茵刀把子bà相机行事xiàngB.势利眼卑躬屈膝撒大网sǎ博闻强识zhìC.一溜烟通货膨胀狙击手jū蓦然回首mùD.辨证法中流砥柱沏茶喝qī杀一儆百jǐng2.依次填人下列横线处的词语，最恰当的一组是①再全面的维生者补充剂对健康的弥补作用也不能______膳食结构不合理带来的损害。

想要保持健康,更重要的是维持饮食的平衡以及适度运动。

②在自然环境中怎样才能______病虫害的侵袭呢？与松树共生,就是杨树通过长期自然演化选择的一种自我保护方式。

③有些人严重缺乏安全感，他们把说谎作为一种自我______手段,总是下意识地保护自己，不愿自己的任何行为和心思被人知道。

④现实生活中没有法外之地，互联网同样没有。

查处淫秽网站，______网格暴力,是净化网络环境的需要,更是建立法治社会的需要。

A.抵制抵消防御抵御B.抵消抵御防御抵制C.抵制防御抵御抵消D.抵消抵制抵御防御3.依次填入下边一段话中横线处的语句，与上下文衔接最恰当的一组是乐观的人看见问题后面的机会, ______。

机会从来不会主动敲响你的门，无论你等待多少年，______。

朝着既定目标前进______。

①悲观的人则看见机会后面的问题②悲观的人只看见机会后面的问题③它只如一阵风拂面而过，需要你有反应能力和追随速度④需要你有反应能力和追随速度，它只如一阵风拂而而过⑤你就会发现机会的存在，充分发挥你的潜能⑥尽量发挥你的潜能，你就会发现机会的存在A. ①④⑥B. ②④⑤C. ①③⑤D. ②③⑥4.下列选项中,标点符号使用不正确的一项是A.中国重庆______德国杜伊斯堡，2011年开通的渝新欧铁路,横跨欧亚6国，为建立新丝绸之路经济带打下了基础。

2014年普通高等学校招生考试（重庆卷）数学文科试题答案及解析一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个备选项中，只有一项是符合题目要求的.1.实部为-2，虚部为1的复数所对应的点位于复平面的（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】B 【解析】实部为横坐标，虚部为纵坐标。

2.在等差数列{}n a 中，1352,10a a a =+=,则7______a =A.5 B.8 C.10 D.14【答案】B 【解析】将条件全部化成1a d 和:112410a d a d +++=,解得1d =,于是7168a a d =+=.3.某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n 的样本。

已知从高中生中抽取70人，则n 为（）A.100B.150C.200D.250【答案】A 【解析】高中生在总体中所占的比例，与样本中所占的比例相等，也就是有：3500701005000n n=⇒=。

考察分层抽样的简单计算.4.下列函数为偶函数的是（）A.()1f x x =-B.()2f x x x =+C.()22x x f x -=-D.()22x xf x -=+【答案】D 【解析】利用奇偶性的判断法则：()()()()()()f x f x f x f x f x f x -=-⇒-=⇒为奇函数为偶函数。

即可得到答案为D 。

考察最简单的奇偶性判断.5.执行如题（5）图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是（A）12s >（B）35s >（C）710s >（D）45s >【答案】：C【解析】：按照循环步骤：9871,9,8,7,6101010s k s k s k s k ==⇒==⇒==⇒==，此时需要不满足条件输出，则输出条件应为710s >。

6.已知命题p ：对任意x R ∈，总有20x >；q ：“1x >”是“2x >”的充分不必要条件，则下列倒是为真命题的是（A）p q ∧（B）p q ⌝∧⌝（C）p q ⌝∧（D）p q∧⌝【答案】：D【解析】：根据复合命题的判断关系可知，命题p 为真，命题q 为假，所以只有p q ∧⌝为真。

2014·重庆卷(课标语文)一、(本大题共4小题，毎小题3分,共12分)1．［2014·重庆卷］下列词语中，字形和加点字的读音全都正确的一组是（）A．屋檐下绿草如茵刀把．子(bà）相．机行事（xiàng)B．势利眼卑躬屈膝撒．大网(sǎ)博闻强识．(zhì）C．一溜烟通货膨胀狙．击手(jū)蓦．然回首(mù)D．辨证法中流砥柱沏．茶喝（qī)杀一儆．百（jǐng）1．A[解析] 本题考查识记现代汉语普通话常用字的字音和识记并正确书写现代常用规范汉字的能力。

B.撒．大网(sā)；C。

蓦．然（mò);D。

辩证法.2．[2014·重庆卷］依次填入下列横线处的词语,最恰当的一组是（)①再全面的维生素补充剂对健康的弥补作用也不能________膳食结构不合理带来的损害。

想要保持健康，更重要的是维持饮食的平衡以及适度运动。

②在自然环境中怎样才能________病虫害的侵袭呢？与松树共生,就是杨树通过长期自然演化选择的一种自我保护方式.③有些人严重缺乏安全感，他们把说谎作为一种自我________手段，总是下意识地保护自己，不愿自己的任何行为和心思被人知道。

④现实生活中没有法外之地，互联网同样没有。

查处淫秽网站，________网络暴力，是净化网络环境的需要,更是建立法治社会的需要。

A．抵制抵消防御抵御B．抵消抵御防御抵制C．抵制防御抵御抵消D．抵消抵制抵御防御2．B［解析］本题考查正确使用词语(包括熟语)的能力,注意辨析近义词，弄清各个词语的意思。

抵制：阻止某些事物，使不能侵入或发生作用.抵消:两种事物的作用因相反而互相消除。

抵御：抵挡，抵抗。

防御:抗击敌人的进攻。

3．［2014·重庆卷] 依次填入下边一段话中横线处的语句,与上下文衔接最恰当的一组是()乐观的人看见问题后面的机会，________。

机会从来不会主动敲响你的门,无论你等待多少年，________.朝着既定目标前进，________.①悲观的人则看见机会后面的问题②悲观的人只看见机会后面的问题③它只如一阵风拂面而过，需要你有反应能力和追随速度④需要你有反应能力和追随速度，它只如一阵风拂面而过⑤你就会发现机会的存在,充分发挥你的潜能⑥尽量发挥你的潜能，你就会发现机会的存在A．①④⑥B．②④⑤C．①③⑤D．②③⑥3．D［解析] 本题考查语言表达连贯的能力，做题时要结合语境，注意句子的前后关系。

2014年重庆高考数学试题（理）一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在复平面内表示复数(12)i i -的点位于（ ）.A 第一象限 .B 第二象限.C 第三象限 .D 第四象限2.对任意等比数列{}n a ,下列说法一定正确的是（ ）139.,,A a a a 成等比数列 236.,,B a a a 成等比数列248.,,C a a a 成等比数列 D a 3,a 6,a 9成等比数列 3.已知变量x 与y 正相关，且由观测数据算得样本的平均数 2.5x =， 3.5y =，则由观测的数据得线性回归方程可能为（ ）.0.4 2.3A y x =+ .2 2.4B y x =-.29.5C y x =-+ .0.3 4.4C y x =-+4.已知向量(,3),(1,4),(2,1)a k b c ===，且（2a -3b ）⊥c , 则实数k ＝（ ）9.2A - .0B .C 3 D 215 5. 5. 执行如图（5）所示的程序框图，若输出k 的值为6，则判断框内可填入的条件（ ）A s ＞21 B s ＞53 C s ＞107 D s ＞54 6.已知命题 :p 对任意x R ∈，总有20x >；:"1"q x >是"2"x >的充分不必要条件 则下列命题为真命题的是（ ）.A p q ∧ .B p q ⌝∧⌝ .C p q ⌝∧ .D p q ∧⌝7.某几何体的三视图如图所示，则该几何体的表面积为（ ）A.54B.60C.66D.72 8.设21F F ，分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点，双曲线上存在一点P 使得,49||||,3||||2121ab PF PF b PF PF =⋅=+则该双曲线的离心率为（ ） A.34 B.35 C.49 D.3 9.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法种数是（ ）A.72B.120C.144D.310.已知ABC ∆的内角21)sin()sin(2sin ,+--=+-+B A C C B A A C B A 满足，，面积满足C B A c b a S ,,,,21分别为，记≤≤所对的边，则下列不等式成立的是（ ）A.8)(>+c b bcB.)(c a ac +C.126≤≤abcD.12≤abc ≤24二、填空题11.设全集=⋂==≤≤∈=B A C B A n N n U U )(},9,7,5,3,1{},8,5,3,2,1{},101|{则______.12.函数)2(log log )(2x x x f ⋅=的最小值为_________.13. 已知直线02=-+y ax 与圆心为C 的圆()()4122=-+-a y x 相交于B A ，两点，且ABC ∆为等边三角形，则实数=a _________.考生注意：14、15、16三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分.14. 过圆外一点P 作圆的切线PA （A 为切点），再作割线PB ，PC 分别交圆于B ，C ，若6=PA ，AC =8，BC =9，则AB =________.15. 已知直线l 的参数方程为⎩⎨⎧+=+=ty t x 32（t 为参数），以坐标原点为极点，x 正半轴为极轴建立坐标系，曲线C 的极坐标方程，ρsin 2θ-4sin θ=0 (ρ≥0，0≤θ＜ 2∏ )则直线l 与曲线C 的公共点的极经=ρ________.16. 若不等式2212122++≥++-a a x x 对任意实数x 恒成立，则实数a 的取值范围是 ____________.三、解答题：本大题共6小题，共75分.解答应写出文字说明，证明过程或演算过程.17. （本小题13分，（I ）小问5分，（II ）小问8分）已知函数()()⎪⎭⎫ ⎝⎛<≤->+=220sin 3πϕπωϕω，x x f 的图像关于直线3π=x 对称，且图像上相邻两个最高点的距离为π.（I ）求ω和ϕ的值；（II ）若⎪⎭⎫ ⎝⎛<<=⎪⎭⎫⎝⎛326432παπαf ，求⎪⎭⎫ ⎝⎛+23cos πα的值.18.（本小题满分13分）一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3，从盒中任取3张卡片.（1）求所取3张卡片上的数字完全相同的概率;（2）X 表示所取3张卡片上的数字的中位数，求X 的分布列（注：若三个数c b a ,,满足c b a ≤≤，则称b 为这三个数的中位数）.19.（本小题满分12分）如图（19），四棱锥ABCD P -，底面是以O 为中心的菱形，⊥PO 底面ABCD ，3,2π=∠=BAD AB ，M 为BC 上一点，且AP MP BM ⊥=,21. （1）求PO 的长；（2）求二面角C PM A --的正弦值。

2014年重庆高考数学试题（文）一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．实部为-2，虚部为1的复数所对应的点位于复平面的（ ）.A 第一象限 .B 第二象限 .C 第三象限 .D 第四象限 2．在等差数列{}n a 中,1352,10a a a =+=，则7a =（ ）.5A .8B .10C .14D3．某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n 的样本，已知从高中生中抽取70人，则n 为（ ） .100A .150B .200C .250C 4．下列函数为偶函数的是（ ）.()1A f x x =- 3.()B f x x x =+ .()22x x C f x -=- .()22x xD f x -=+s 为（ ）.19C D ．366．已知命题 :p 对任意x R ∈，总有||0x ≥；:1q x =是方程20x +=的根 则下列命题为真命题的是（ ） .A p q ∧⌝ .B p q ⌝∧ .C p q ⌝∧ .D p q ∧A ．8．设21F F ，分别为双曲线)0,0(12222>>=-b a by a x 的左．右焦点，双曲线上存在一点P 使得,3|)||(|2221ab b PF PF -=+则该双曲线的离心率为（ ）A.2 B ．15 C ．4 D ．17 9．若b a ab b a +=+则）（,log 43log 24的最小值是（ ）A.326+ B ．327+ C ．346+ D ．347+10．已知函数13,(1,0](),1,(0,1]x f x x x x ⎧-∈-⎪=+⎨⎪∈⎩且()()g x f x mx m =--在(]1,1-内有且仅有两个不同的零点，则实数m 的取值范围是（ ）A ．]21,0(]2,49(⋃--B ．]21,0(]2,411(⋃--C ．]32,0(]2,49(⋃--D ．]32,0(]2,411(⋃--二．填空题11．已知集合=⋂==B A B A 则},13,8,5,3,1{},8,5,3,2,1{______．12．已知向量a 与b 的夹角为60，且(2,6),||10a b =--=，则a b ⋅=_________． 13．将函数()()⎪⎭⎫⎝⎛<≤->+=220sin πϕπωϕω，x x f 图像上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移6π的单位长度得到x y sin =的图像，则=⎪⎭⎫⎝⎛6πf ______． 14．已知直线0=+-a y x 与圆心为C 的圆222440x y x y ++--=相交于B A ，两点，且 BC AC ⊥，则实数a 的值为_________．15．某校早上8：00上课，假设该校学生小张与小王在早上7:30—7:50之间到校，且每人在该时间段的任何时间到校是等可能的，则小张比小王至少早5分钟到校的概率为_____（用数字作答） 三．解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16.（本小题满分13分．（I ）小问6分，（II ）小问5分）已知{}n a 是首相为1，公差为2的等差数列，n S 表示{}n a 的前n 项和． （I ）求n a 及n S ；（II ）设{}n b 是首相为2的等比数列，公比q满足()01442=++-S q a q ，求{}n b 的通项公式及其前n 项和n T ．17．（本小题满分13分．（I ）小问4分，（II ）小问4分，（III ）小问5分）20名学生某次数学考试成绩（单位：分）的频数分布直方图如下：（I ）求频数直方图中a 的值；（II ）分别球出成绩落在[)6050，与[)7060，中的学生人数；（III ）从成绩在[)7050，的学生中人选2人， 求次2人的成绩都在[)7060，中的概率． 18．（本小题满分12分）在ABC ∆中，内角C B A ,,所对的边分别为c b a ,,，且8=++c b a （1）若25,2==b a ，求C cos 的值; （2）若C AB B A sin 22cos sin 2cossin 22=+，且ABC ∆的面积C S sin 29=，求a和b 的值． 19．（本小题满分12分） 已知函数23ln 4)(--+=x x a x x f ，其中R a ∈，且曲线)(x f y =在点))1(,1(f 处的切 线垂直于x y 21=（1）求a 的值；（2）求函数)(x f 的单调区间和极值。

【母题来源】2014重庆卷文-15【母题原题】某校早上8：00开始上课，假设该校学生小张与小王在早上7:30—7:50之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早5分钟到校的概率为_____（用数字作答）所以()1151592202032 DEFABCDSP AS ∆⨯⨯===⨯正方形所以答案应填：932．【命题意图】本题考查不等式表示的平面区域、几何概型等知识，意在考查数形结合思想、转化与化归思想，同时考查考生运算能力.【方法技巧】将实际问题转化为几何概型中的长度、角度、面积、体积等常见几何概型的求解问题，构造出随机事件A对应的几何图形，利用几何图形的度量来求随机事件的概率，根据实际问题的具体情况，合理设置参数，建立适当的坐标系，在此基础上将试验的每一个结果一一对应于该坐标系的点，便可构造出度量区域．1．【2014高考陕西卷文第6题】从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离小于该正方形边长的概率为（ ）1.5A2.5B3.5C4.5D2．【2014高考湖北卷文第5题】随机投掷两枚均匀的投骰子，他们向上的点数之和不超过5的概率为1P ，点数之和大于5的概率为2P ，点数之和为偶数的概率为3P ，则（ ） A ． 321P P P << B ． 312P P P << C ． 231P P P << D ． 213P P P <<3．【2014高考湖南卷文第3题】对一个容量为N 的总体抽取容量为n 的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为123,,p p p ，则（ ）123.A p p p =< 231.B p p p =< 132.C p p p =< 123.D p p p ==4．【2014高考湖南卷文第5题】在区间[2,3]-上随机选取一个数X ，则1X ≤的概率为（ ）4.5A 3.5B 2.5C 1.5D5．【2014高考江西卷文3第题】掷两颗均匀的骰子，则点数之和为5的概率等于（ ）1.18A 1.9B 1.6C 1.12D6．【2014高考辽宁卷文第6题】若将一个质点随机投入如图所示的长方形ABCD 中，其中AB=2，BC=1，则质点落在以AB 为直径的半圆内的概率是（ ） A ．2πB ．4πC ．6πD ．8π7．【2014高考广东卷文第12题】从字母a 、b 、c 、d 、e 中任取两个不同的字母，则取到字母a 的概率为 ． 【答案】【解析】所有的基本事件有(),a b 、(),a c 、(),a d 、(),a e 、(),b c 、(),b d 、(),b e 、(),c d 、(),c e 、(),d e ，8．【2014高考浙江卷文第14题】在三张奖劵中有一、二等各一张，另有一张无奖，甲乙两人各抽取一张，两人都中奖的概率为 ．9．【2014高考上海卷文第13题】为强化安全意识，某商场拟在未来的连续10天中随机选择3天进行紧急疏散演练，则选择的3天恰好为连续3天的概率 是 （结构用最简分数表示）．10．【2014高考全国1卷文第13题】将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为________．11．【2014高考全国2卷文第13题】甲，乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种，则他们选择相同颜色运动服的概率为_______．12．【2014高考江苏卷第4题】 从1，2，3，6这四个数中一次随机地取2个数，则所取两个数的乘积为6的概率为 ．13．【山东省德州市2014届高三上学期期末考试】如图，设D 是边长为l 的正方形区域，E 是D 内函数y x =与2y x =所构成(阴影部分)的区域，在D 中任取一点，则该点在E 中的概率是（ ）14.【山东省济南外国语学校2014届高三上学期期中考试】已知}02,0,4|),{(},0,0,6|),{(≥-≥≤=≥≥≤+=Ωy x y x y x A y x y x y x ，若向区域Ω上随机投一点P ，则点P 落入区域A 的概率为 （ ）A ．92 B ．32 C ．31 D ．9115.【辽宁省铁岭市第一高级中学2013—2014学年高三上学期期中考试试题理】连续抛掷两次骰子，得到的点数分别为m,n ，记向量()(),,1,1a m n b →→==-的夹角为θ，则0,2πθ⎛⎤∈ ⎥⎝⎦的概率是（ ） A.512 B. 12 C. 712 D. 5616．【2014高考福建卷文第13题】如图，在边长为1的正方形中，随机撒1000粒豆子，有180粒落到阴影部分，据此估计阴影部分的面积为___________．17．【2014高考山东文第16题】海关对同时从C B A ,,三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如右表所示，工作人员用分层抽样的方法从这些商品中共抽取6件进行检测．（1）求这6件样品中来自C B A ,,各地区商品的数量；（2）若在这6件样品中随机抽取2件送往甲机构进一步检测，求这2件商品来自相同地区的概率．地区 ABC数量5015010018．【2014高考陕西文第19题】某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：赔付金额（元）0 1000 2000 3000 4000车辆数（辆）500 130 100 150 120（1）若每辆车的投保金额均为2800元，估计赔付金额大于投保金额的概率；（2）在样本车辆中，车主是新司机的占10%，在赔付金额为4000元的样本车辆中，车主是新司机的占20%，估计在已投保车辆中，新司机获赔金额为4000元的概率．19．【2014高考四川文第16题】一个盒子里装有三张卡片，分别标记有数字1，2，3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a，b，c．+=”的概率；（Ⅰ）求“抽取的卡片上的数字满足a b c（Ⅱ）求“抽取的卡片上的数字a，b，c不完全相同”的概率．20．【2014高考天津文第15题】某校夏令营有3名男同学C B A ,,和3名女同学Z Y X ,,，其年级情况如下表： 一年级 二年级 三年级 男同学A B C 女同学X Y Z现从这6名同学中随机选出2人参加知识竞赛（每人被选到的可能性相同）（1）用表中字母列举出所有可能的结果（2）设M 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”，求事件M 发生的概率．21．【2014高考重庆文第17题】20名学生某次数学考试成绩（单位：分）的频数分布直方图如下：（I ）求频率分布直方图中a 的值；（II ）分别球出成绩落在[)6050，与[)7060，中的学生人数； （III ）从成绩在[)7050，的学生中人选2人，求此2人的成绩都在[)7060，中的概率． 【答案】（I ）0.005a =；（II ）2，3；（III ）310． 【解析】。

2014年普通高等学校招生全国统一考试(重庆卷)数学试题卷(文史类)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个备选项中，只有一项是符合题目要求的．1．(2014重庆，文1)实部为－2，虚部为1的复数所对应的点位于复平面的()．A．第一象限B．第二象限C．第三象限D．第四象限答案：B解析：由题意知，该复数在复平面内对应的点为(－2,1)，所以该点位于复平面的第二象限．故选B.2．(2014重庆，文2)在等差数列{a n}中，a1＝2，a3＋a5＝10，则a7＝()．A．5 B．8 C．10 D．14答案：B解析：由等差数列的性质，可知a1＋a7＝a3＋a5.因为a1＝2，a3＋a5＝10，所以a7＝8.故选B.3．(2014重庆，文3)某中学有高中生3 500人，初中生1 500人．为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则n为()．A．100 B．150 C．200 D．250答案：A解析：由题意知，抽样比为701= 350050，所以1=3500150050n，即n＝100.故选A.4．(2014重庆，文4)下列函数为偶函数的是()．A．f(x)＝x－1 B．f(x)＝x2＋xC．f(x)＝2x－2－x D．f(x)＝2x＋2－x答案：D解析：由题意知，所给四个函数其定义域均为R，关于原点对称．由偶函数的定义知，选项A，B，C中函数均不满足f(－x)＝f(x)．而D选项中，f(－x)＝2－x＋2x＝f(x)，显然为偶函数，故选D.5．(2014重庆，文5)执行如图所示的程序框图，则输出s的值为()．A．10 B．17 C．19 D．36答案：C解析：执行过程如下：k＝2，s＝0；经判断执行“是”，此时s＝0＋2＝2，k＝3；经判断执行“是”，此时s＝2＋3＝5，k＝5；经判断执行“是”，此时s＝5＋5＝10，k＝9；经判断执行“是”，此时s ＝10＋9＝19，k ＝17；经判断执行“否”，此时输出s ＝19.故选C.6．(2014重庆，文6)已知命题 p ：对任意x ∈R ，总有|x |≥0； q ：x ＝1是方程x ＋2＝0的根． 则下列命题为真命题的是( )． A ．p ∧q B ．p ∧q C ．p ∧q D ．p ∧q 答案：A解析：由题意知，命题p 为真命题，命题q 为假命题，所以p 为假，q 为真．所以p ∧q 为真，p ∧q 为假，p ∧q 为假，p ∧q 为假．故选A.7．(2014重庆，文7)某几何体的三视图如图所示，则该几何体的体积为( )．A ．12B ．18C ．24D ．30 答案：C解析：由三视图可知，该几何体的直观图如图所示，为直三棱柱ABC －A 1B 1C 1截掉了三棱锥D －A 1B 1C 1，所以其体积V ＝VABC －A 1B 1C 1－VD －A 1B 1C 1＝12×3×4×5－1132⨯×3×4×3＝24.8．(2014重庆，文8)设F 1，F 2分别为双曲线2222=1x y a b-(a ＞0，b ＞0)的左、右焦点，双曲线上存在一点P 使得(|PF |－|PF 2|)2＝b 2－3ab ，则该双曲线的离心率为( )．A B C ．4 D 答案：D解析：由双曲线的定义知，(|PF 1|－|PF 2|)2＝4a 2，所以4a 2＝b 2－3ab ，即223=4b ba a-⋅，解得=4ba(－1舍去)．因为双曲线的离心率c e a ==所以e =.故选D.9．(2014重庆，文9)若4log (34)log a b =＋a ＋b 的最小值是( )． A． B．C． D．答案：D解析：由4log (34)log a b =＋2211log (34)log ()22a b ab =＋，所以3a ＋4b ＝ab ，即34=1b a+.所以3434()+77a ba b a b b a ba ⎛⎫=+=+≥⎪⎝⎭＋＋，当且仅当34a b b a +，即4a =，3b =+ D.10．(2014重庆，文10)已知函数()13,(1,0],1,(0,1],x f x x x x ⎧-∈-⎪=+⎨⎪∈⎩且g (x )＝f (x )－mx －m 在(－1,1]内有且仅有两个不同的零点，则实数m 的取值范围是( )．A ．91,20,42⎛⎤⎛⎤-- ⎥⎥⎝⎦⎝⎦ B ．111,20,42⎛⎤⎛⎤-- ⎥⎥⎝⎦⎝⎦ C ．92,20,43⎛⎤⎛⎤-- ⎥⎥⎝⎦⎝⎦ D ．112,20,43⎛⎤⎛⎤--⎥⎥⎝⎦⎝⎦答案：A解析：由题意画出f (x )的图象，如图所示．令g (x )＝f (x )－mx －m ＝0，得f (x )＝m (x ＋1)，所以g (x )＝f (x )－mx －m 在(－1,1]内有且仅有两个不同的零点，可转化为y ＝f (x )与y ＝m (x ＋1)的图象在(－1,1]上有且仅有两个不同的交点．y ＝m (x ＋1)是过定点(－1,0)的一条直线，m 是其斜率．由数形结合知，符合题意的直线位于l 1(x 轴)与l 2之间和l 3与l 4(切线)之间． 因为l 4与y ＝f (x )相切，所以13(1)1m x x -=+＋有两个相等的实根，即m (x ＋1)2＋3(x ＋1)－1＝0有两个相等的实根，即Δ＝9＋4m ＝0，解得94m =-. 设直线l 1，l 2，l 3的斜率分别为k 1，k 2，k 3，易求k 1＝0，212k =，k 3＝－2， 所以91,20,42m ⎛⎤⎛⎤∈-- ⎥⎥⎝⎦⎝⎦.二、填空题：本大题共5小题，每小题5分，共25分．把答案填写在答题卡相应位置上．11．(2014重庆，文11)已知集合A ＝{3,4,5,12,13}，B ＝{2,3,5,8,13}，则A ∩B ＝__________. 答案：{3,5,13}解析：由已知条件，结合交集运算，可得A ∩B ＝{3,5,13}．12．(2014重庆，文12)已知向量a 与b 的夹角为60°，且a ＝(－2，－6)，||=b 则a ·b ＝__________.答案：10解析：由题意得||=a所以ab ＝|a||b|cos 〈a ，b 〉＝1102=. 13．(2014重庆，文13)将函数f (x )＝sin(ωx ＋φ)ππ(0,)22ωϕ>-≤<图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移π6个单位长度得到y ＝sin x 的图象，则π()6f ＝__________.答案：2解析：本题可逆推，由y ＝sin x 的图象推f (x )＝sin(ωx ＋φ)的图象．将y ＝sin x 的图象向左平移π6个单位长度得到πsin()6y x +＝的图象，再保持纵坐标不变，横坐标伸长为原来的两倍，得到()1πsin()26f x x =+的图象．所以ππππsin sin 612642f ⎛⎫⎛⎫=+==⎪ ⎪⎝⎭⎝⎭. 14．(2014重庆，文14)已知直线x －y ＋a ＝0与圆心为C 的圆x 2＋y 2＋2x －4y －4＝0相交于A ，B 两点，且AC ⊥BC ，则实数a 的值为__________．答案：0或6解析：由题意，得圆心C 的坐标为(－1,2)，半径r ＝3.因为AC ⊥BC ，所以圆心C 到直线x －y ＋a ＝0的距离d ===|－3＋a |＝3，所以a ＝0或a ＝6. 15．(2014重庆，文15)某校早上8：00开始上课，假设该校学生小张与小王在早上7：30～7：50之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早5分钟到校的概率为__________．(用数字作答)答案：932解析：用x 轴表示小张到校时刻，用y 轴表示小王到校时刻，建立如图直角坐标系．设小张到校的时刻为x ，小王到校的时刻为y ，则x －y ≥5.由题意，知0≤x ≤20,0≤y ≤20，可得可行域如图所示，其中，阴影部分表示小张比小王至少早5分钟到校．由5,20x y x -=⎧⎨=⎩得A (20,15)．易知B (20,20)，C (5,0)，D (20,0)． 由几何概型概率公式，得所求概率1151592=202032ACD ODBES P S ∆⨯⨯==⨯正方形.三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．(本小题满分13分，(1)小问6分，(2)小问7分)(2014重庆，文16)已知{a n }是首项为1，公差为2的等差数列，S n 表示{a n }的前n 项和．(1)求a n 及S n ；(2)设{b n }是首项为2的等比数列，公比q 满足q 2－(a 4＋1)q ＋S 4＝0.求{b n }的通项公式及其前n 项和T n .分析：通过已知条件，借助等差数列的通项公式以及前n 项和公式，即可求出a n 和S n ；在第(2)问充分利用第(1)问的结论，求出a 4，S 4并代入方程，求出q ，然后利用等比数列通项公式及前n 项和公式可求出结果．解：(1)因为{a n }是首项a 1＝1，公差d ＝2的等差数列， 所以a n ＝a 1＋(n －1)d ＝2n －1.故S n ＝1＋3＋…＋(2n －1)＝1()(121)22n n a a n n ++-=＝n 2. (2)由(1)得a 4＝7，S 4＝16.因为q 2－(a 4＋1)q ＋S 4＝0， 即q 2－8q ＋16＝0，所以(q －4)2＝0，从而q ＝4.又因b 1＝2，{b n }是公比q ＝4的等比数列，所以b n ＝b 1q n －1＝2·4n －1＝22n －1.从而{b n }的前n 项和112(41)13n n n b q T q (-)==--．17．(本小题满分13分，(1)小问4分，(2)小问4分，(3)小问5分)(2014重庆，文17)20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：(1)求频率分布直方图中a 的值；(2)分别求出成绩落在[50,60)与[60,70)中的学生人数；(3)从成绩在[50,70)的学生中任选2人，求此2人的成绩都在[60,70)中的概率．分析：由频率分布直方图各小矩形面积和为1，可列出关于a 的方程，然后解方程求出a 的值；在第(2)问中，利用第(1)问的结果，分别计算得出[50,60)与[60,70)的频率，然后根据频率公式求出频数；在第(3)问中，利用第(2)问的结果得出成绩在[50,70)的人数，然后分别用字母来表示来自[50,60)，[60,70)的人，并列出所有基本事件，再利用古典概型的概率公式求出概率．解：(1)据直方图知组距＝10，由(2a ＋3a ＋6a ＋7a ＋2a )×10＝1，解得10.005200a ==. (2)成绩落在[50,60)中的学生人数为2×0.005×10×20＝2. 成绩落在[60,70)中的学生人数为3×0.005×10×20＝3.(3)记成绩落在[50,60)中的2人为A 1，A 2，成绩落在[60,70)中的3人为B 1，B 2，B 3，则从成绩在[50,70)的学生中任选2人的基本事件共有10个：(A 1，A 2)，(A 1，B 1)，(A 1，B 2)，(A 1，B 3)，(A 2，B 1)，(A 2，B 2)，(A 2，B 3)，(B 1，B 2)，(B 1，B 3)，(B 2，B 3)．其中2人的成绩都在[60,70)中的基本事件有3个：(B 1，B 2)，(B 1，B 3)，(B 2，B 3)，故所求概率为310p =. 18．(本小题满分13分，(1)小问5分，(2)小问8分)(2014重庆，文18)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＋b ＋c ＝8，(1)若a ＝2，52b =，求cos C 的值； (2)若22sin cos sin cos 2sin 22B A A B C ==，且△ABC 的面积9sin C 2S =，求a 和b 的值．分析：先通过已知条件，求出c ，然后借助余弦定理求出cos C 的值；在第(2)问中，利用已知条件中的关系式，根据二倍角公式，得到sin A ，sin B ，sin C 之间的关系，然后借助正弦定理转化为边的关系，再结合已知条件列出关于a ，b 的方程组，求出a ，b 的值．解：(1)由题意可知：c ＝8－(a ＋b )＝72. 由余弦定理得，222222572122cos 525222a b c C ab ⎛⎫⎛⎫+- ⎪ ⎪+-⎝⎭⎝⎭===-⨯⨯.(2)由22sin cos+sin cos 2sin 22B A A BC =可得： 1cos 1cos sin sin 2sin 22B A A BC ++⋅+⋅=，化简得sin A ＋sin A cos B ＋sin B ＋sin B cos A ＝4sin C .因为sin A cos B ＋cos A sin B ＝sin(A ＋B )＝sin C ， 所以sin A ＋sin B ＝3sin C . 由正弦定理可知：a ＋b ＝3c . 又因a ＋b ＋c ＝8，故a ＋b ＝6. 由于19sin sin 22S ab C C ==，所以ab ＝9， 从而a 2－6a ＋9＝0，解得a ＝3，b ＝3.19．(本小题满分12分，(1)小问5分，(2)小问7分)(2014重庆，文19)已知函数3()ln 42x a f x x x =+--，其中a ∈R ，且曲线y ＝f (x )在点(1，f (1))处的切线垂直于直线12y x =.(1)求a 的值；(2)求函数f (x )的单调区间与极值．分析：利用已知条件得切线的斜率为－2，然后求出f (x )在x ＝1处的导数，列出关于a 的方程，求出a 的值；在第(2)问中，充分利用导数判断函数单调性与极值的方法，求导后转化为求方程f ′(x )＝0，然后判断f ′(x )在每个区间的符号，在求解过程中要注意函数的定义域．解：(1)对f (x )求导得()2114a f x x x'=--，由f (x )在点(1，f (1))处的切线垂直于直线12y x =，知()3124f a '=--=-，解得54a =.(2)由(1)知53()ln 442x f x x x =+--， 则()22454x x f x x--'=， 令f ′(x )＝0，解得x ＝－1或x ＝5.因x ＝－1不在f (x )的定义域(0，＋∞)内，故舍去． 当x ∈(0,5)时，f ′(x )＜0，故f (x )在(0,5)内为减函数；当x ∈(5，＋∞)时，f ′(x )＞0，故f (x )在(5，＋∞)内为增函数． 由此知函数f (x )在x ＝5时取得极小值f (5)＝－ln 5.20．(本小题满分12分，(1)小问4分，(2)小问8分)(2014重庆，文20)如图，四棱锥P －ABCD 中，底面是以O 为中心的菱形，PO ⊥底面ABCD ，AB ＝2，π3BAD ∠=，M 为BC 上一点，且12BM =.(1)证明：BC ⊥平面POM ；(2)若MP ⊥AP ，求四棱锥P －ABMO 的体积．分析：先利用平面几何的方法，求出OB ，然后在△OBM 中，借助余弦定理求出OM 的值，运用勾股定理的逆定理，得出线线垂直，再结合已知条件，利用线面垂直的判定定理，得出BC ⊥平面POM ；在第(2)问中，充分利用第(1)问的结论，得到OA 的长度，然后分别在△POM ，△ABM ，△POA 中借助余弦定理得到关于PO 的方程，求出PO 的长度，再分别计算△AOB 与△OMB 的面积得出四边形ABMO 的面积，最后根据棱锥的体积公式求出四棱锥P －ABMO 的体积．(1)证明：如图，因ABCD 为菱形，O 为菱形中心，连结OB ，则AO ⊥OB .因π3BAD ∠=，故OB ＝AB ·sin ∠OAB ＝π2sin6＝1， 又因12BM =，且π3OBM ∠=，在△OBM 中，OM 2＝OB 2＋BM 2－2OB ·BM ·cos ∠OBM＝2211π31()21cos 2234+-⋅⋅⋅=.所以OB 2＝OM 2＋BM 2，故OM ⊥BM . 又PO ⊥底面ABCD ，所以PO ⊥BC .从而BC 与平面POM 内两条相交直线OM ，PO 都垂直，所以BC ⊥平面POM .(2)解：由(1)可得，OA ＝AB ·cos ∠OAB ＝π2cos6⋅=. 设PO ＝a ，由PO ⊥底面ABCD 知，△POA 为直角三角形， 故P A 2＝PO 2＋OA 2＝a 2＋3.由△POM 也是直角三角形，故PM 2＝PO 2＋OM 2＝234a +. 连结AM ，在△ABM 中，AM 2＝AB 2＋BM 2－2AB ·BM ·cos ∠ABM ＝22112π212()22cos 2234+-⋅⋅⋅=.由已知MP ⊥AP ，故△APM 为直角三角形， 则P A 2＋PM 2＝AM 2，即22321344a a +=++，得2a =2a =(舍去)，即PO =. 此时S ABMO ＝S △AOB ＋S △OMB＝1122AO OB BM OM ⋅⋅+⋅⋅＝1111222+⨯=.所以四棱锥P －ABMO 的体积115·3316P ABMO ABMO V S PO -=⋅==. 21．(本小题满分12分，(1)小问5分，(2)小问7分)(2014重庆，文21)如图，设椭圆22221x y a b +=(a ＞b ＞0)的左、右焦点分别为F 1，F 2，点D 在椭圆上，DF 1⊥F 1F 2，121||F F DF =△DF 1F 2的面积为2.(1)求该椭圆的标准方程；(2)是否存在圆心在y 轴上的圆，使圆在x 轴的上方与椭圆有两个交点，且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点？若存在，求出圆的方程；若不存在，请说明理由．分析：先通过已知条件，借助a ，b ，c 之间的关系，转化为关于a ，b ，c 的方程，然后利用a ，b ，c 的几何意义，求出a ，b ，c 的值，从而得到椭圆的标准方程；在第(2)问中，充分利用数形结合的思想方法，首先设出交点P 1，P 2的坐标，然后写出向量11F P ，22F P ，再由F 1P 1⊥F 2P 2列出关于x 1的方程求出x 1，得到圆心坐标，最后利用两点间的距离公式求出半径得到圆的方程．解：(1)设F 1(－c,0)，F 2(c,0)，其中c 2＝a 2－b 2.由121||2F F DF =得1||DF ==.从而1221121222DF F S DF F F ∆===，故c ＝1.从而1||2DF =，由DF 1⊥F 1F 2得|DF 2|2＝|DF 1|2＋|F 1F 2|2＝92，因此2||2DF =.所以2a ＝|DF 1|＋|DF 2|＝a =b 2＝a 2－c 2＝1.因此，所求椭圆的标准方程为2212x y +=. (2)如图，设圆心在y 轴上的圆C 与椭圆2212x y +=相交，P 1(x 1，y 1)，P 2(x 2，y 2)是两个交点，y 1＞0，y 2＞0，F 1P 1，F 2P 2是圆C 的切线，且F 1P 1⊥F 2P 2.由圆和椭圆的对称性，易知，x 2＝－x 1，y 1＝y 2. 由(1)知F 1(－1,0)，F 2(1,0)，所以11F P ＝(x 1＋1，y 1)，22F P ＝(－x 1－1，y 1)． 再由F 1P 1⊥F 2P 2得－(x 1＋1)2＋21y ＝0.由椭圆方程得22111(1)2x x -=＋， 即211340x x +=.解得143x =-或x 1＝0.当x 1＝0时，P 1，P 2重合，题设要求的圆不存在．当143x =-时，过P 1，P 2分别与F 1P 1，F 2P 2垂直的直线的交点即为圆心C . 设C (0，y 0)，由CP 1⊥F 1P 1，得1011111y y y x x -⋅=-+.而y 1＝|x 1＋1|＝13，故053y =.圆C 的半径1||3CP ==. 综上，存在满足题设条件的圆，其方程为2253239x y ⎛⎫+-= ⎪⎝⎭.。

2014年重庆高考数学试题（文）一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.实部为-2，虚部为1 的复数所对应的点位于复平面的（ ）.A 第一象限 .B 第二象限.C 第三象限 .D 第四象限2.在等差数列{}n a 中,1352,10a a a =+=，则7a =（ ）.5A .8B .10C .14D3.某中学有高中生3500人，初中生1500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n 的样本，已知从高中生中抽取70人，则n 为（ ）.100A .150B .200C .250C4.下列函数为偶函数的是（ ）.()1A f x x =- 3.()B f x x x =+ .()22x x C f x -=- .()22x x D f x -=+5.执行如题（5）图所示的程序框图，则输出，的值为.10A .17B .19C .36C6.已知命题:p 对任意x R ∈，总有||0x ≥；:"1"q x =是方程"20"x +=的根 则下列命题为真命题的是（ ）.A p q ∧⌝ .B p q ⌝∧ .C p q ⌝∧ .D p q ∧7.某几何体的三视图如图所示，则该几何体的体积为（ ）A.12B.18C.24D.308.设21F F ，分别为双曲线)0,0(12222>>=-b a b y a x 的左、右焦点， 双曲线上存在一点P 使得,3|)||(|2221ab b PF PF -=+则该双曲线的离心率为（ ） 1.2 B.15 C.4 D.17I.若b a ab b a +=+则）（,log 43log 24的最小值是（ ） 1.326+ B.327+ C.346+ D.347+J.已知函数]1,1)()(,]1,0(,]0,1(,311)(---=⎪⎩⎪⎨⎧∈-∈-+=在（且m mx x f x g x x x x x f 内有且仅有两个不同的零点，则实数m 的取值范围是（ ）A.]21,0(]2,49(⋃-- B.]21,0(]2,411(⋃-- C.]32,0(]2,49(⋃-- D.]32,0(]2,411(⋃-- 二、填空题11.已 知集合=⋂==B A B A 则},13,8,5,3,1{},8,5,3,2,1{______. 12.已知向量=⋅=--=b a b a b a 则，且的夹角为与,10||),6,2(60_________.13. 将函数()()⎪⎭⎫ ⎝⎛<≤->+=220sin πϕπωϕω，x x f 图像上每一点的横坐标缩短为原来的 一半，纵坐标不变，再向右平移6π的单位长度得到x y sin =的图像，则=⎪⎭⎫ ⎝⎛6πf ______.。