2019年高考数学一轮复习导学案71坐标系理北师大版

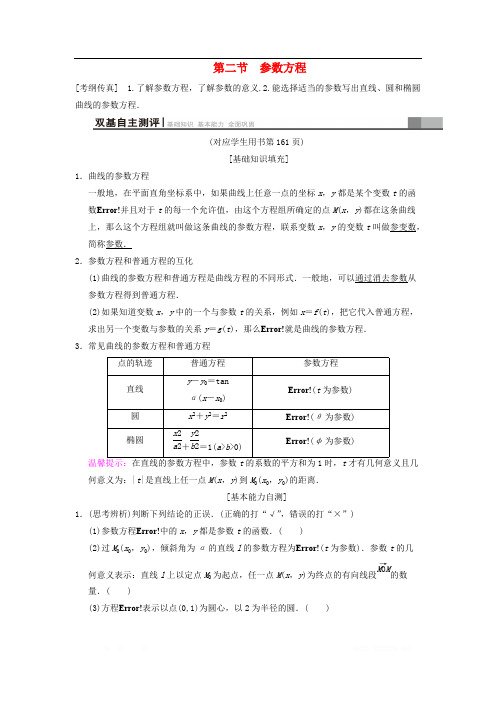
第二节　参数方程[考纲传真]　1.了解参数方程，了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第161页)[基础知识填充]1．曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数Error!并且对于t 的每一个允许值，由这个方程组所确定的点M (x ，y )都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数．2．参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数从参数方程得到普通方程．(2)如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通方程，求出另一个变数与参数的关系y ＝g (t )，那么Error!就是曲线的参数方程．3．常见曲线的参数方程和普通方程点的轨迹普通方程参数方程直线y －y 0＝tan α(x －x 0)Error!(t 为参数)圆x 2＋y 2＝r 2Error!(θ为参数)椭圆＋＝1(a >b >0)x 2a 2y 2b 2Error!(φ为参数)温馨提示：在直线的参数方程中，参数t 的系数的平方和为1时，t 才有几何意义且几何意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程Error!中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为Error!(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段的数M 0M→量．( )(3)方程Error!表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程Error!(t 为参数)，点M 在椭圆上，对应参数t ＝，点O 为原π3点，则直线OM .( )3[答案]　(1)√　(2)√　(3)√　(4)×2．(教材改编)曲线Error!(θ为参数)的对称中心( )A ．在直线y ＝2x 上B ．在直线y ＝－2x 上C ．在直线y ＝x －1上D ．在直线y ＝x ＋1上B [由Error!得Error!所以(x ＋1)2＋(y －2)2＝1.曲线是以(－1,2)为圆心，1为半径的圆，所以对称中心为(－1,2)，在直线y ＝－2x 上．]3．(教材改编)在平面直角坐标系中，曲线C ：Error!(t 为参数)的普通方程为________．x －y －1＝0　[由x ＝2＋t ，且y ＝1＋t ，2222消去t ，得x －y ＝1，即x －y －1＝0.]4．在平面直角坐标系xOy 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．曲线C 1的极坐标方程为ρ(cos θ＋sin θ)＝－2，曲线C 2的参数方程为Error!(t 为参数)，则C 1与C 2交点的直角坐标为________．(2，－4)　[由ρ(cos θ＋sin θ)＝－2，得x ＋y ＝－2.①由Error!消去t 得y 2＝8x .②联立①②得Error!即交点坐标为(2，－4)．]5．(2016·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为Error!(t 为参数)，椭圆C 的参数方程为Error!(θ为参数)．设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长. 【导学号：00090372】[解]　椭圆C 的普通方程为x 2＋＝1.2分y 24将直线l 的参数方程Error!代入x 2＋＝1，得2＋＝1，即7t 2＋16t ＝0，y 24(1＋12t)(32t )24解得t 1＝0，t 2＝－，所以AB ＝|t 1－t 2|＝.10分167167(对应学生用书第162页)参数方程与普通方程的互化　已知直线l 的参数方程为Error!(t 为参数)，圆C 的参数方程为Error!(θ为参数)．(1)求直线l 和圆C 的普通方程；(2)若直线l 与圆C 有公共点，求实数a 的取值范围．[解]　(1)直线l 的普通方程为2x －y －2a ＝0，2分圆C 的普通方程为x 2＋y 2＝16.4分(2)因为直线l 与圆C 有公共点，故圆C 的圆心到直线l 的距离d ＝≤4，8分|－2a |5解得－2≤a ≤2.10分55[规律方法]　1.将参数方程化为普通方程，消参数常用代入法、加减消元法、三角恒等变换消去参数．2．把参数方程化为普通方程时，要注意哪一个量是参数，并且要注意参数的取值对普通方程中x 及y 的取值范围的影响，要保持同解变形．[变式训练1]　在平面直角坐标系xOy 中，若直线l ：Error!(t 为参数)过椭圆C ：Error!(φ为参数)的右顶点，求常数a 的值．[解]　直线l 的普通方程为x －y －a ＝0，椭圆C 的普通方程为＋＝1，4分x 29y 24所以椭圆C 的右顶点坐标为(3,0)，若直线l 过椭圆的右顶点(3,0)，则3－0－a ＝0，所以a ＝3.10分参数方程的应用　(2018·合肥模拟)已知曲线C ：＋＝1，直线l ：Error!(t 为参数)．x 24y 29(1)写出曲线C 的参数方程，直线l 的普通方程；(2)过曲线C 上任意一点P 作与l 夹角为30°的直线，交l 于点A ，求|PA |的最大值与最小值．[解]　(1)曲线C 的参数方程为Error!(θ为参数)．直线l 的普通方程为2x ＋y －6＝0.4分(2)曲线C 上任意一点P (2cosθ，3sin θ)到l 的距离为d ＝|4cos θ＋3sin55θ－6|，则|PA |＝＝|5sin(θ＋α)－6|，其中α为锐角，且tan α＝.8分d sin 30°25543当sin(θ＋α)＝－1时，|PA |取得最大值，最大值为.2255当sin(θ＋α)＝1时，|PA |取得最小值，最小值为.10分255[规律方法]　1.解决直线与圆的参数方程的应用问题时，一般是先化为普通方程，再根据直线与圆的位置关系来解决问题．2．对于形如Error!(t 为参数)，当a 2＋b 2≠1时，应先化为标准形式后才能利用t 的几何意义解题．[变式训练2]　(2017·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为Error!(θ为参数)，直线l 经过点P (1,2)，倾斜角α＝.π6(1)写出圆C 的普通方程和直线l 的参数方程；(2)设直线l 与圆C 相交于A ，B 两点，求|PA |·|PB |的值. 【导学号：00090373】[解]　(1)由Error!消去θ，得圆C 的普通方程为x 2＋y 2＝16.2分又直线l 过点P (1,2)且倾斜角α＝，π6所以l 的参数方程为Error!即Error!(t 为参数).4分(2)把直线l 的参数方程Error!代入x 2＋y 2＝16，得2＋2＝16，t 2＋(＋2)t －11＝0，(1＋32t)(2＋12t )3所以t 1t 2＝－11，8分由参数方程的几何意义，|PA |·|PB |＝|t 1t 2|＝11.10分参数方程与极坐标方程的综合应用　(2017·全国卷Ⅲ)在直角坐标系xOy 中，直线l 1的参数方程为Error!(t 为参数)，直线l 2的参数方程为Error!(m 为参数)．设l 1与l 2的交点为P ，当k 变化时，P 的轨迹为曲线C ．(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－＝0，M 为l 3与C 的交点，求M 的极径．2[解]　(1)消去参数t 得l 1的普通方程l 1：y ＝k (x －2)；1分消去参数m 得l 2的普通方程l 2：y ＝(x ＋2).2分1k 设P (x ，y )，由题设得Error!消去k 得x 2－y 2＝4(y ≠0)．所以C 的普通方程为x 2－y 2＝4(y ≠0).4分(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0<θ<2π，θ≠π).5分联立Error!得cos θ－sin θ＝2(cos θ＋sin θ).6分故tan θ＝－，从而cos 2θ＝，sin 2θ＝.8分13910110代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5，所以交点M 的极径为.10分5[规律方法]　1.参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．2．数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，可化繁为简．[变式训练3]　(2016·全国卷Ⅲ)在直角坐标系xOy 中，曲线C 1的参数方程为Error!(α为参数)．以坐标原点为极点，以x 轴的正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为ρsin＝2.(θ＋π4)2(1)写出C 1的普通方程和C 2的直角坐标方程；(2)设点P 在C 1上，点Q 在C 2上，求|PQ |的最小值及此时P 的直角坐标．[解]　(1)C 1的普通方程为＋y 2＝1，2分x 23由于曲线C 2的方程为ρsin＝2，(θ＋π4)2所以ρsin θ＋ρcos θ＝4，因此曲线C 2的直角坐标方程为x ＋y －4＝0.4分(2)由题意，可设点P 的直角坐标为(cos α，sin α)．3因为C 2是直线，所以|PQ |的最小值即为P 到C 2的距离d (α)的最小值，8分又d (α)＝＝，|3cos α＋sin α－4|22|s in (α＋π3)－2|当且仅当α＝2k π＋(k ∈Z )时，d (α)取得最小值，最小值为，此时P 的直角坐标π62为.10分(32，12)。

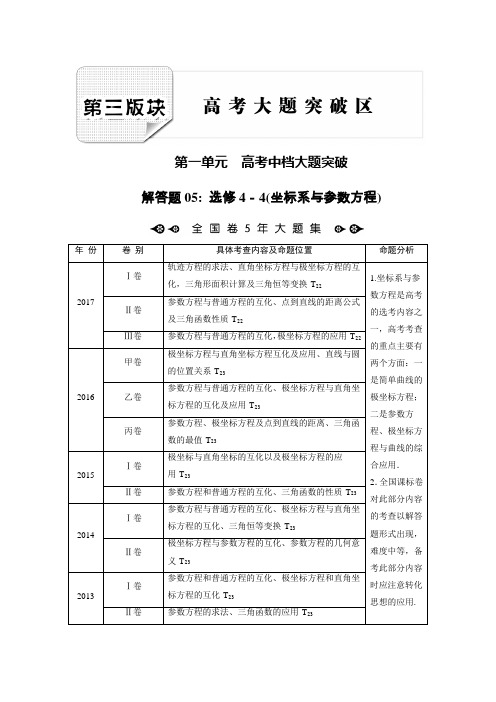
第一单元高考中档大题突破解答题05: 选修4－4(坐标系与参数方程)年份卷别具体考查内容及命题位置命题分析2017 Ⅰ卷轨迹方程的求法、直角坐标方程与极坐标方程的互化，三角形面积计算及三角恒等变换·T221.坐标系与参数方程是高考的选考内容之一，高考考查的重点主要有两个方面：一是简单曲线的极坐标方程；二是参数方程、极坐标方程与曲线的综合应用．2．全国课标卷对此部分内容的考查以解答题形式出现，难度中等，备考此部分内容时应注意转化思想的应用. Ⅱ卷参数方程与普通方程的互化、点到直线的距离公式及三角函数性质·T22Ⅲ卷参数方程与普通方程的互化，极坐标方程的应用·T222016 甲卷极坐标方程与直角坐标方程互化及应用、直线与圆的位置关系·T23乙卷参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化及应用·T23丙卷参数方程、极坐标方程及点到直线的距离、三角函数的最值·T232015 Ⅰ卷极坐标与直角坐标的互化以及极坐标方程的应用·T23Ⅱ卷参数方程和普通方程的互化、三角函数的性质·T232014 Ⅰ卷参数方程与普通方程的互化、极坐标方程与直角坐标方程的互化、三角恒等变换·T23Ⅱ卷极坐标方程与参数方程的互化、参数方程的几何意义·T232013 Ⅰ卷参数方程和普通方程的互化、极坐标方程和直角坐标方程的互化·T23Ⅱ卷参数方程的求法、三角函数的应用·T23基本考点——极坐标方程1．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r ，则圆的方程为：ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0. 几个特殊位置的圆的极坐标方程： (1)当圆心位于极点，半径为r ：ρ＝r ； (2)当圆心位于M (a,0)，半径为a ：ρ＝2a cos θ； (3)当圆心位于M (a, π2)，半径为a ：ρ＝2a sin θ.2．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴与此直线所成的角为α， 则它的方程为：ρsin(θ－α)＝ρ0sin(θ0－α)． 几个特殊位置的直线的极坐标方程： (1)直线过极点：θ＝θ0和θ＝π＋θ0；(2)直线过点M (a,0)且垂直于极轴：ρcos θ＝a ； (3)直线过M (b, π2)且平行于极轴：ρsin θ＝b .1．(2017·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．解：(1)设P 的极坐标为(ρ，θ)(ρ>0)，M 的极坐标为(ρ1，θ)(ρ1>0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ. 由|OM |·|OP |＝16得C 2的极坐标方程为ρ＝4cos θ(ρ>0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB >0)．由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积S ＝12|OA |·ρB ·sin ∠AOB ＝4cos α·⎪⎪⎪⎪sin α－π3 ＝2⎪⎪⎪⎪sin2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.2．(2016·全国乙卷)在直角坐标系xOy 中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t ，(t 为参数，a >0)，在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求a .解：(1)消去参数t 得到C 1的普通方程x 2＋(y －1)2＝a 2，则C 1是以(0,1)为圆心，a 为半径的圆．将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ.若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0， 由已知tan θ＝2，可得16cos 2θ－8sin θcos θ＝0， 从而1－a 2＝0，解得a ＝－1(舍去)，a ＝1.当a ＝1时，极点也为C 1，C 2的公共点，在C 3上． 所以a ＝1.极坐标方程与普通方程的互化技巧(1)巧用极坐标方程两边同乘以ρ或同时平方技巧，将极坐标方程构造成含有ρcos θ，ρsin θ，ρ2的形式，然后利用公式代入化简得到普通方程．(2)巧借两角和差公式，转化ρsin(θ±α)或ρcos(θ±α)的结构形式，进而利用互化公式得到普通方程．(3)将直角坐标方程中的x 转化为ρcos θ，将y 换成ρsin θ，即可得到其极坐标方程．常考热点——参数方程与极坐标的综合几种常见曲线的参数方程(1)圆：以O ′(a ，b )为圆心，r 为半径的圆的参数方程是⎩⎪⎨⎪⎧x ＝a ＋r cos α，y ＝b ＋r sin α，其中α是参数．当圆心在(0,0)时，方程为⎩⎪⎨⎪⎧x ＝r cos α，y ＝r sin α，其中α是参数．(2)椭圆：椭圆x 2a 2＋y 2b 2＝1(a >b >0)的参数方程是⎩⎪⎨⎪⎧x ＝a cos φ，y ＝b sin φ，其中φ是参数．椭圆x 2b 2＋y 2a 2＝1(a >b >0)的参数方程是⎩⎪⎨⎪⎧x ＝b cos φ，y ＝a sin φ，其中φ是参数．(3)直线：经过点P 0(x 0，y 0)，倾斜角为α的直线的参数方程是⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α，其中t是参数．1．(2017·全国卷Ⅰ)选修4－4：坐标系与参数方程在直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t (t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . 解：(1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎨⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点 (3cos θ，sin θ )到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917. 由题设得a ＋917＝17，所以a ＝8；当a <－4时，d 的最大值为－a ＋117.由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.2．(2017·大庆二模)在直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－35t ＋2y ＝45t(t 为参数)，以原点O 为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝a sin θ.(1)若a ＝2，求圆C 的直角坐标方程与直线l 的普通方程； (2)设直线l 截圆C 的弦长等于圆C 的半径长的3倍，求a 的值． 解：(1)当a ＝2时，ρ＝a sin θ转化为ρ＝2sin θ， 整理成直角坐标方程为：x 2＋(y －1)2＝1，直线l 的参数方程⎩⎨⎧x ＝－35t ＋2y ＝45t(t 为参数)．转化成直角坐标方程为4x ＋3y －8＝0.(2)圆C 的极坐标方程转化成直角坐标方程为x 2＋⎝⎛⎭⎫y －a 22＝a 24， 直线l 截圆C 的弦长等于圆C 的半径长的3倍， 所以：d ＝|3a2－8|5＝12·|a |2，2|3a －16|＝5|a |，利用平方法解得：a ＝32或3211.1．(2017·全国卷Ⅲ)在直角坐标系xOy 中，直线l 1的参数方程为⎩⎪⎨⎪⎧x ＝2＋t ，y ＝kt (t 为参数)，直线l 2的参数方程为⎩⎪⎨⎪⎧x ＝－2＋m ，y ＝m k ，(m 为参数)．设l 1与l 2的交点为P ，当 变化时，P 的轨迹为曲线C .(1)写出C 的普通方程；(2)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，设l 3：ρ(cos θ＋sin θ)－2＝0，M 为l 3与C 的交点，求M 的极径．解：(1)消去参数t 得l 1的普通方程l 1：y ＝ (x －2)； 消去参数m 得l 2的普通方程l 2：y ＝1k(x ＋2)．设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝k (x －2)，y ＝1k (x ＋2)，消去 得x 2－y 2＝4(y ≠0)，所以C 的普通方程为x 2－y 2＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0<θ<2π，θ≠π)，联立⎩⎪⎨⎪⎧ρ2(cos 2θ－sin 2θ)＝4，ρ(cos θ＋sin θ)－2＝0得cos θ－sin θ＝2(cos θ＋sin θ)． 故tan θ＝－13，从而cos 2θ＝910，sin 2θ＝110.代入ρ2(cos 2θ－sin 2θ)＝4得ρ2＝5， 所以交点M 的极径为 5.2．(2017·承德二模)在直角坐标系xOy 中，圆的参数方程为⎩⎨⎧x ＝2cos θy ＝2sin θ(θ为参数)，直线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1＋ty ＝2＋t (t 为参数)．(1)若直线C 1与圆O 相交于A ，B ，求弦长|AB |；(2)以该直角坐标系的原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，圆C 2的极坐标方程为ρ＝2cos θ＋23sin θ，圆O 和圆C 2的交点为P ，Q ，求弦PQ 所在直线的直角坐标方程．解：(1)由直线C 1的参数方程为⎩⎪⎨⎪⎧x ＝1＋ty ＝2＋t(t 为参数)消去参数t ，可得：x －y ＋1＝0，即直线C 1的普通方程为x －y ＋1＝0.圆O 的参数方程为⎩⎪⎨⎪⎧x ＝2cos θy ＝2sin θ(θ为参数)，根据sin 2θ＋cos 2θ＝1消去参数θ，可得：x 2＋y 2＝2.那么圆心到直线的距离d ＝12＝22， 故得弦长|AB |＝2r 2－d 2＝ 6.(2)圆C 2的极坐标方程为ρ＝2cos θ＋23sin θ，利用ρ2＝x 2＋y 2，ρcos θ＝x ，ρsin θ＝y ，可得圆C 2的普通方程为x 2＋y 2＝2x ＋23y . ∵圆O 为：x 2＋y 2＝2.∴弦PQ 所在直线的直角坐标方程为2＝2x ＋23y ，即x ＋3y －1＝0.3．(2017·河南六市一模)在直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－5＋22ty ＝5－22t (t 为参数)若以O 点为极点，x 轴正半轴为极轴建立极坐标系，则曲线C 的极坐标方程为ρ＝4cos θ.(1)求曲线C 的直角坐标方程及直线l 的普通方程；(2)将曲线C 上各点的横坐标缩短为原来的12，再将所得曲线向左平移1个单位，得到曲线C 1，求曲线C 1上的点到直线l 的距离的最小值．解：(1)由ρ＝4cos θ，得出ρ2＝4ρcos θ，化为直角坐标方程x 2＋y 2＝4x ， 即曲线C 的方程为(x －2)2＋y 2＝4，直线l 的方程是：x ＋y ＝0.(2)将曲线C 横坐标缩短为原来的12，再向左平移1个单位，得到曲线C 1的方程为4x 2＋y 2＝4，设曲线C 1上的任意点(cos θ，2sin θ)，到直线l 距离d ＝|cos θ＋2sin θ|2＝5|sin (θ＋α)|2.当sin(θ＋α)＝0时，到直线l 距离的最小值为0.4．(2017·南阳二模)在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝12ty ＝1－32t (t为参数)．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，圆C 的极坐标方程为ρ＝2sin θ.(1)判断直线l 与圆C 的交点个数；(2)若圆C 与直线l 交于A ，B 两点，求线段AB 的长度．解：(1)∵直线l 的参数方程为⎩⎨⎧x ＝12t y ＝1－32t (t 为参数)．∴消去参数t 得直线l 的普通方程为3x ＋y －1＝0， ∵圆C 的极坐标方程为ρ＝2sin θ，即ρ2＝2ρsin θ，∴由ρ2＝x 2＋y 2，ρsin θ＝y ，得圆C 的直角坐标方程为x 2＋y 2－2y ＝0. ∵圆心(0,1)在直线l 上， ∴直线l 与圆C 的交点个数为2. (2)由(1)知圆心(0,1)在直线l 上， ∴AB 为圆C 的直径，∵圆C 的直角坐标方程为x 2＋y 2－2y ＝0. ∴圆C 的半径r ＝12×4＝1，∴圆C 的直径为2，∴|AB |＝2.5．(2017·厦门二模)在平面直角坐标系中，以原点为极点，x 轴正半轴为极轴建立极坐标系，并在两坐标系中取相同的长度单位．已知曲线C 的极坐标方程为ρ＝2cos θ，直线l的参数方程为⎩⎪⎨⎪⎧x ＝－1＋t cos αy ＝t sin α(t 为参数，α为直线的倾斜角)．(1)写出直线l 的普通方程和曲线C 的直角坐标方程； (2)若直线l 与曲线C 有唯一的公共点，求角α的大小． 解：(1)当α＝π2时，直线l 的普通方程为x ＝－1；当α≠π2时，直线l 的普通方程为y ＝tan α·(x ＋1)．由ρ＝2cos θ，得ρ2＝2ρcos θ，所以x 2＋y 2＝2x ，即为曲线C 的直角坐标方程．(2)把x ＝－1＋t cos α，y ＝t sin α代入x 2＋y 2＝2x ，整理得t 2－4t cos α＋3＝0.当α＝π2时，方程化为：t 2＋3＝0，方程不成立，当α≠π2时，由Δ＝16cos 2α－12＝0，得cos 2α＝34，所以cos α＝32或cos α＝－32， 故直线l 倾斜角α为π6或5π6.6．(2017·梅州二模)已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝－2＋2cos θy ＝2sin θ(θ为参数)，以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程是ρ＝4sin θ.(1)求曲线C 1与C 2交点的平面直角坐标；(2)A ，B 两点分别在曲线C 1与C 2上，当|AB |最大时，求△OAB 的面积(O 为坐标原点)．解：(1)∵曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝－2＋2cos θy ＝2sin θ(θ为参数)，∴曲线C 1的平面直角坐标方程为(x ＋2)2＋y 2＝4. 又由曲线C 2的极坐标方程是ρ＝4sin θ， 得ρ2＝4ρsin θ，∴x 2＋y 2＝4y ，把两式作差，得y ＝－x ，代入x 2＋y 2＝4y ，得2x 2＋4x ＝0，解得⎩⎪⎨⎪⎧ x ＝0y ＝0或⎩⎪⎨⎪⎧x ＝－2y ＝2，∴曲线C 1与C 2交点的平面直角坐标为(0,0)，(－2,2)．(2)如图，由平面几何知识可知：当A ，C 1，C 2，B 依次排列且共线时，|AB |最大，此时|AB |＝22＋4，O 到AB 的距离为2，∴△OAB 的面积为S ＝12(22＋4)·2＝2＋2 2.。

第二节 参数方程[考纲传真] (教师用书独具)1.了解参数方程，了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第201页)[基础知识填充]1．曲线的参数方程(1)一般地，在取定的坐标系中，如果曲线上任意一点的坐标(x ，y )都是某个变数t 的函数⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )，并且对于t 取的每一个允许值，由方程组所确定的点P (x ，y )都在这条曲线上，那么方程组就叫作这条曲线的参数方程，联系x ，y 之间关系的变数t 叫作参变数，简称参数．相对于参数方程，我们直接用坐标(x ，y )表示的曲线方程f (x ，y )＝0叫作曲线的普通方程．(2)曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数，从参数方程得到普通方程．2．常见曲线的参数方程和普通方程[意义为：|t |是直线上任一点M (x ，y )到M 0(x 0，y 0)的距离．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)参数方程⎩⎪⎨⎪⎧x ＝f (t )，y ＝g (t )中的x ，y 都是参数t 的函数．( )(2)过M 0(x 0，y 0)，倾斜角为α的直线l 的参数方程为⎩⎪⎨⎪⎧x ＝x 0＋t cos α，y ＝y 0＋t sin α(t 为参数)．参数t 的几何意义表示：直线l 上以定点M 0为起点，任一点M (x ，y )为终点的有向线段M 0M →的数量．( ) (3)方程⎩⎪⎨⎪⎧x ＝2cos θ，y ＝1＋2sin θ表示以点(0,1)为圆心，以2为半径的圆．( )(4)已知椭圆的参数方程⎩⎪⎨⎪⎧x ＝2cos t ，y ＝4sin t(t 为参数)，点M 在椭圆上，对应参数t＝π3，点O 为原点，则直线OM 的斜率为 3.( ) [答案] (1)√ (2)√ (3)√ (4)×2．(教材改编)曲线⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ(θ为参数)的对称中心( ) A ．在直线y ＝2x 上 B ．在直线y ＝－2x 上 C ．在直线y ＝x －1上D ．在直线y ＝x ＋1上B [由⎩⎪⎨⎪⎧x ＝－1＋cos θ，y ＝2＋sin θ，得⎩⎪⎨⎪⎧cos θ＝x ＋1，sin θ＝y －2，所以(x ＋1)2＋(y －2)2＝1.曲线是以(－1,2)为圆心，1为半径的圆， 所以对称中心为(－1,2)，在直线y ＝－2x 上．] 3．(教材改编)在平面直角坐标系中，曲线C ：⎩⎪⎨⎪⎧x ＝2＋22t ，y ＝1＋22t (t 为参数)的普通方程为________．x －y －1＝0 [由x ＝2＋22t ，且y ＝1＋22t ， 消去t ，得x －y ＝1，即x －y －1＝0.] 4．椭圆C 的参数方程为⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，过左焦点F 1的直线l 与C 相交于A ，B ，则|AB |min ＝________.185 [由⎩⎪⎨⎪⎧x ＝5cos φ，y ＝3sin φ(φ为参数)，消去参数φ得x 225＋y 29＝1，当AB ⊥x 轴时，|AB |有最小值． 所以|AB |min ＝2×95＝185.]5．(2017·江苏高考)在平面直角坐标系xOy 中，已知直线l 的参数方程为⎩⎪⎨⎪⎧x ＝－8＋t ，y ＝t2(t 为参数)，曲线C 的参数方程为⎩⎨⎧x ＝2s 2，y ＝22s(s 为参数)．设P 为曲线C 上的动点，求点P 到直线l 的距离的最小值．[解] 直线l 的普通方程为x －2y ＋8＝0. 因为点P 在曲线C 上，设P (2s 2,22s )， 从而点P 到直线l 的距离d ＝|2s 2－42s ＋8|12＋(－2)2＝2(s －2)2＋45. 当s ＝2时，d min ＝455.因此当点P 的坐标为(4,4)时，曲线C 上的点P 到直线l 的距离取到最小值455.(对应学生用书第202页)(1)求直线⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t(t 为参数)与曲线⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α(α为参数)的交点个数．(2)在平面直角坐标系xOy中，若直线l ：⎩⎪⎨⎪⎧x ＝t ，y ＝t －a (t 为参数)过椭圆C ：⎩⎪⎨⎪⎧x ＝3cos φ，y ＝2sin φ(φ为参数)的右顶点，求常数a 的值.【导学号：79140389】[解] (1)将⎩⎪⎨⎪⎧x ＝2＋t ，y ＝－1－t消去参数t 得直线x ＋y －1＝0；将⎩⎪⎨⎪⎧x ＝3cos α，y ＝3sin α消去参数α得圆x 2＋y 2＝9.又圆心(0,0)到直线x ＋y －1＝0的距离d ＝22<3.因此直线与圆相交，故直线与曲线有2个交点． (2)直线l 的普通方程为x －y －a ＝0， 椭圆C 的普通方程为x 29＋y 24＝1，所以椭圆C 的右顶点坐标为(3,0)，若直线l 过(3,0)， 则3－a ＝0，∴a ＝3.法、加减消去法、恒等式三角的或代数的消去法普通方程化为参数方程时，先分清普通方程所表示的曲线类型，图2[解] 圆的半径为12，记圆心为C ⎝ ⎛⎭⎪⎫12，0，连接CP ， 则∠PCx ＝2θ，故x P ＝12＋12cos 2θ＝cos 2θ，y P ＝12sin 2θ＝sin θcos θ(θ为参数)．所以圆的参数方程为⎩⎪⎨⎪⎧x ＝cos 2θ，y ＝sin θcos θ(θ为参数)．(2017·石家庄质检)在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ(θ为参数)，直线l 经过点P (1,2)，倾斜角α＝π6.(1)写出圆C 的普通方程和直线l 的参数方程；(2)设直线l 与圆C 相交于A ，B 两点，求|PA |·|PB |的值．[解] (1)由⎩⎪⎨⎪⎧x ＝4cos θ，y ＝4sin θ，消去θ，得圆C 的普通方程为x 2＋y 2＝16. 又直线l 过点P (1,2)且倾斜角α＝π6，所以l 的参数方程为⎩⎪⎨⎪⎧x ＝1＋t cos π6，y ＝2＋t sin π6，即⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t (t 为参数)．(2)把直线l 的参数方程⎩⎪⎨⎪⎧x ＝1＋32t ，y ＝2＋12t代入x 2＋y 2＝16，得⎝⎛⎭⎪⎫1＋32t 2＋⎝ ⎛⎭⎪⎫2＋12t 2＝16，t 2＋(3＋2)t －11＝0，所以t 1t 2＝－11，由参数方程的几何意义，|PA |·|PB |＝|t 1t 2|＝11. 解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有关的问题，如最值、2根据直线的参数方程的标准式中过定点M ①弦长l⎩⎪⎨⎪⎧x ＝3cos θ，y ＝sin θ(θ为参数)，直线l 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋4t ，y ＝1－t(t 为参数)．(1)若a ＝－1，求C 与l 的交点坐标； (2)若C 上的点到l 距离的最大值为17，求a . [解] (1)曲线C 的普通方程为x 29＋y 2＝1.当a ＝－1时，直线l 的普通方程为x ＋4y －3＝0.由⎩⎪⎨⎪⎧x ＋4y －3＝0，x 29＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝3，y ＝0或⎩⎪⎨⎪⎧x ＝－2125，y ＝2425.从而C 与l 的交点坐标为(3,0)，⎝ ⎛⎭⎪⎫－2125，2425.(2)直线l 的普通方程为x ＋4y －a －4＝0，故C 上的点(3cos θ，sin θ)到l 的距离为d ＝|3cos θ＋4sin θ－a －4|17.当a ≥－4时，d 的最大值为a ＋917.由题设得a ＋917＝17，所以a ＝8;当a ＜－4时，d 的最大值为－a ＋117. 由题设得－a ＋117＝17，所以a ＝－16.综上，a ＝8或a ＝－16.(2018·石家庄质检(二))在平面直角坐标系xOy 中，曲线C 的参数方程为⎩⎪⎨⎪⎧x ＝a ＋a cos β，y ＝a sin β(a >0，β为参数)．以O 为极点，x 轴的正半轴为极轴，建立极坐标系，直线l 的极坐标方程ρcos ⎝⎛⎭⎪⎫θ－π3＝32.(1)若曲线C 与l 只有一个公共点，求a 的值；(2)A ，B 为曲线C 上的两点，且∠AOB ＝π3，求△OAB 的面积最大值．[解] (1)曲线C 是以(a,0)为圆心，以a 为半径的圆， 直线l 的直角坐标方程为x ＋3y －3＝0.由直线l 与圆C 只有一个公共点，则可得|a －3|2＝a ，解得a ＝－3(舍)，a ＝1. 所以a ＝1.(2)法一：曲线C 的极坐标方程为ρ＝2a cos θ(a >0)， 设A 的极角为θ，B 的极角为θ＋π3，则S △OAB ＝12|OA |·|OB |sin π3＝34|2a cos θ|·⎪⎪⎪⎪⎪⎪2a cos ⎝⎛⎭⎪⎫θ＋π3＝3a 2⎪⎪⎪⎪⎪⎪cos θcos ⎝⎛⎭⎪⎫θ＋π3，∵cos θcos ⎝ ⎛⎭⎪⎫θ＋π3＝12cos 2θ－32sin θcos θ ＝12·cos 2θ＋12－34sin 2θ ＝12⎝ ⎛⎭⎪⎫12cos 2θ－32sin 2θ＋14 ＝12cos ⎝⎛⎭⎪⎫2θ＋π3＋14，所以当θ＝－π6时，12cos ⎝ ⎛⎭⎪⎫2θ＋π3＋14取得最大值34.△OAB 的面积最大值为33a24.法二：因为曲线C 是以(a,0)为圆心，以a 为半径的圆，且∠AOB ＝π3，由正弦定理得|AB |sinπ3＝2a ，所以|AB |＝3a .由余弦定理得|AB |2＝3a 2＝|OA |2＋|OB |2－|OA |·|OB | ≥|OA |·|OB |，所以S △OAB ＝12|OA |·|OB |sin π3≤12×3a 2×32＝33a 24， 所以△OAB 的面积最大值为33a 24.1涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解2数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用意义，直接求解，能达到化繁为简的解题目的[跟踪训练1⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ(其中φ为参数)．以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 2的极坐标方程是ρ(tan α·cos θ－sin θ)＝1(α是常数，0<α<π，且α≠π2)，点A ，B (A 在x 轴的下方)是曲线C 1与C 2的两个不同交点．(1)求曲线C 1的普通方程和C 2的直角坐标方程； (2)求|AB |的最大值及此时点B 的坐标.【导学号：79140390】[解] (1)∵⎩⎪⎨⎪⎧x ＝2cos φ，y ＝sin φ，∴x 24＋y 2＝1，由⎩⎪⎨⎪⎧x ＝ρcos θ，y ＝ρsin θ得曲线C 2的直角坐标方程为y ＝tan α·x －1.(2)由(1)得曲线C 2的参数方程为⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α(t 是参数)，设A (t 1cos α，－1＋t 1sin α)，B (t 2cos α，－1＋t 2sin α)，将C 2：⎩⎪⎨⎪⎧x ＝t cos α，y ＝－1＋t sin α，代入x 24＋y 2＝1，整理得t 2(1＋3sin 2α)－8t sin α＝0， ∴t 1＝0，t 2＝8sin α1＋3sin α， ∴|AB |＝|t 1－t 2|＝8|sin α|1＋3sin 2α ＝83|sin α|＋1|sin α|≤823＝433(当且仅当sin α＝33取等号)， 当sin α＝33时，∴0<α<π，且α≠π2， ∴cos α＝±63， ∴B ⎝ ⎛⎭⎪⎫±423，13， ∴|AB |的最大值为433，此时点B 的坐标为⎝ ⎛⎭⎪⎫±423，13.。

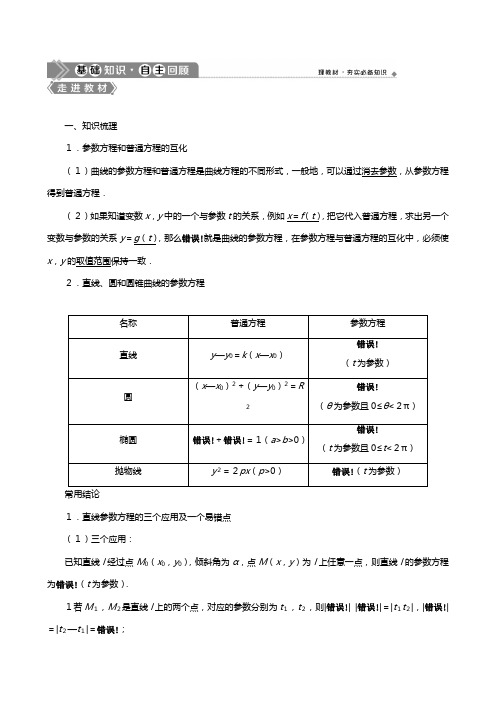
一、知识梳理１．参数方程和普通方程的互化（１）曲线的参数方程和普通方程是曲线方程的不同形式，一般地，可以通过消去参数，从参数方程得到普通方程．（２）如果知道变数x，y中的一个与参数t的关系，例如x＝f（t），把它代入普通方程，求出另一个变数与参数的关系y＝g（t），那么错误!就是曲线的参数方程，在参数方程与普通方程的互化中，必须使x，y的取值范围保持一致．２．直线、圆和圆锥曲线的参数方程名称普通方程参数方程直线y—y0＝k（x—x0）错误!（t为参数）圆（x—x0）２＋（y—y0）２＝R２错误!（θ为参数且0≤θ<２π）椭圆错误!＋错误!＝１（a>b>0）错误!（t为参数且0≤t<２π）抛物线y２＝２px（p>0）错误!（t为参数）１．直线参数方程的三个应用及一个易错点（１）三个应用：已知直线l经过点M0（x0，y0），倾斜角为α，点M（x，y）为l上任意一点，则直线l的参数方程为错误!（t为参数）．１若M１，M２是直线l上的两个点，对应的参数分别为t１，t２，则|错误!| |错误!|＝|t１t２|，|错误!|＝|t２—t１|＝错误!；２若线段M１M２的中点为M３，点M１，M２，M３对应的参数分别为t１，t２，t３，则t３＝错误!；３若直线l上的线段M１M２的中点为M0（x0，y0），则t１＋t２＝0，t１t２<0．（２）一个易错点：在使用直线参数方程的几何意义时，要注意参数前面的系数应该是该直线倾斜角的正余弦值．否则参数不具备该几何含义．２．掌握圆的参数方程的两种应用（１）解决与圆上的动点有关的距离取值范围以及最大值和最小值问题，通常可以转化为点与圆、直线与圆的位置关系．（２）求距离的问题，通过设圆的参数方程，就转化为求三角函数的值域问题．二、教材衍化１．曲线错误!（θ为参数）的对称中心（）Ａ．在直线y＝２x上Ｂ．在直线y＝—２x上Ｃ．在直线y＝x—１上Ｄ．在直线y＝x＋１上解析：选Ｂ．由错误!得错误!所以（x＋１）２＋（y—２）２＝１．曲线是以（—１，２）为圆心，１为半径的圆，所以对称中心为（—１，２），在直线y＝—２x上．２．在平面直角坐标系xOy中，若直线l：错误!（t为参数）过椭圆C：错误!（φ为参数）的右顶点，则常数a的值为________．解析：直线l的普通方程为x—y—a＝0，椭圆C的普通方程为错误!＋错误!＝１，所以椭圆C的右顶点坐标为（３，0），若直线l过点（３，0），则３—a＝0，所以a＝３．答案：３一、思考辨析判断正误（正确的打“√”，错误的打“×”）（１）参数方程错误!中的x，y都是参数t的函数．（）（２）过M0（x0，y0），倾斜角为α错误!的直线l的参数方程为错误!（t为参数）．参数t的几何意义表示：直线l上以定点M0为起点，任一点M（x，y）为终点的有向线段M0M的数量．（）（３）方程错误!（θ为参数）表示以点（0，１）为圆心，以２为半径的圆．（）（４）已知椭圆的参数方程错误!（t为参数），点M在椭圆上，对应参数t＝错误!，点O为原点，则直线OM的斜率为错误!.（）答案：（１）√（２）√（３）√（４）×二、易错纠偏错误!错误!（１）不注意互化的等价性致误；（２）直线参数方程中参数t的几何意义不清致误；（３）交点坐标计算出错致错．１．若曲线C的参数方程为错误!（θ为参数），则曲线C上的点的轨迹是（）Ａ．直线x＋２y—２＝0Ｂ．以（２，0）为端点的射线Ｃ．圆（x—１）２＋y２＝１Ｄ．以（２，0）和（0，１）为端点的线段解析：选Ｄ．将曲线C的参数方程化为普通方程得x＋２y—２＝0（0≤x≤２，0≤y≤１）．故选Ｄ．２．已知直线错误!（t为参数）上两点A，B对应的参数值是t１，t２，则|AB|＝（）Ａ．|t１＋t２| Ｂ．|t１—t２|Ｃ．错误!|t１—t２| Ｄ．错误!解析：选Ｃ．依题意，A（x0＋at１，y0＋bt１），B（x0＋at２，y0＋bt２），则|AB|＝错误!＝错误!|t１—t２|.故选Ｃ．３．在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴建立极坐标系．曲线C１的极坐标方程为ρ（cos θ＋sin θ）＝—２，曲线C２的参数方程为错误!（t为参数），则C１与C２交点的直角坐标为________．解析：由ρ（cos θ＋sin θ）＝—２，得x＋y＝—２１．又错误!消去t，得y２＝8x２．联立１２得错误!即交点坐标为（２，—４）．答案：（２，—４）参数方程与普通方程的互化（自主练透）１．将下列参数方程化为普通方程．（１）错误!（t为参数）；（２）错误!（θ为参数）．解：（１）由t２—１≥0⇒t≥１或t≤—１⇒0<x≤１或—１≤x<0．由错误!１式代入２式得x２＋y２＝１．其中错误!或错误!（２）由x＝２＋sin２θ，0≤sin２θ≤１⇒２≤２＋sin２θ≤３⇒２≤x≤３，错误!⇒错误!⇒错误!⇒２x＋y—４＝0（２≤x≤３）．２．已知曲线C１：错误!（t为参数），曲线C２：错误!（θ为参数）．化C１，C２的方程为普通方程，并说明它们分别表示什么曲线．解：曲线C１：（x＋４）２＋（y—３）２＝１，曲线C２：错误!＋错误!＝１，所以曲线C１是以（—４，３）为圆心，１为半径的圆；曲线C２是中心为坐标原点，焦点在x轴上，长半轴长是8，短半轴长是３的椭圆．错误!将参数方程化为普通方程的方法（１）将参数方程化为普通方程，需要根据参数方程的结构特征，选取适当的消参方法．常见的消参方法有：代入消参法、加减消参法、平方消参法等．对于含三角函数的参数方程，常利用同角三角函数关系式消参，如sin２θ＋cos２θ＝１等．（２）将参数方程化为普通方程时，要注意两种方程的等价性，不要增解．参数方程的应用（师生共研）（２0２0·安徽宣城模拟）在直角坐标系xOy中，圆O的参数方程为错误!（θ为参数），直线l的参数方程为错误!（t为参数）．（１）若直线l与圆O相交于A，B两点，求弦长|AB|，若点P（２，４），求|PA|·|PB|的值；（２）以该直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ＝２cos θ＋２错误!sin θ，圆O和圆C的交点为P，Q，求弦PQ所在直线的直角坐标方程．【解】（１）由直线l的参数方程错误!（t为参数），消去参数t可得x—y＋２＝0，即直线l的普通方程为x—y＋２＝0．圆O的参数方程为错误!（θ为参数），根据sin２θ＋cos２θ＝１消去参数θ，可得x２＋y２＝４，所以圆心O到直线l的距离d＝错误!＝错误!，故弦长|AB|＝２错误!＝２错误!.把直线l的参数方程标准化可得错误!将其代入圆O的方程x２＋y２＝４得t２＋6错误!t＋１6＝0，设A，B两点对应的参数分别为t１，t２，所以|PA|·|PB|＝|t１t２|＝１6．（２）圆C的极坐标方程为ρ＝２cos θ＋２错误!sin θ，利用ρ２＝x２＋y２，ρcos θ＝x，ρsin θ＝y，可得圆C的普通方程为x２＋y２＝２x＋２错误!y.因为圆O的直角坐标方程为x２＋y２＝４，所以弦PQ所在直线的直角坐标方程为４＝２x＋２错误!y，即x＋错误!y—２＝0．错误!（１）解决与圆、圆锥曲线的参数方程有关的综合问题时，要注意普通方程与参数方程的互化公式，主要是通过互化解决与圆、圆锥曲线上与动点有关的问题，如最值、范围等．（２）根据直线的参数方程的标准式中t的几何意义，有如下常用结论：过定点M0的直线与圆锥曲线相交，交点为M１，M２，所对应的参数分别为t１，t２.１弦长l＝|t１—t２|；２弦M１M２的中点⇒t１＋t２＝0；３|M0M１||M0M２|＝|t１t２|.１．（２0２0·日照模拟）在平面直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．已知曲线C的极坐标方程为ρ＝４cos错误!，直线l过点P（0，—错误!）且倾斜角为错误!.（１）求曲线C的直角坐标方程和直线l的参数方程；（２）设直线l与曲线C交于A，B两点，求|PA|＋|PB|的值．解：（１）曲线C：ρ＝４cos错误!⇒ρ＝４cos θcos 错误!＋４sin θsin 错误!，所以ρ２＝２ρcos θ＋２错误!ρsin θ，即x２＋y２＝２x＋２错误!y，得曲线C的直角坐标方程为（x—１）２＋（y—错误!）２＝４．直线l的参数方程为错误!（t为参数）．（２）将错误!（t为参数）代入曲线C的直角坐标方程，得错误!错误!＋错误!错误!＝４，整理得t２—7t＋9＝0，设点A，B对应的参数分别为t１，t２，则t１＋t２＝7，t１t２＝9，所以t１>0，t２>0，所以|PA|＋|PB|＝t１＋t２＝7．２．在直角坐标系xOy中，曲线C的参数方程为错误!（θ为参数），直线l的参数方程为错误!（t 为参数）．（１）若a＝—１，求C与l的交点坐标；（２）若C上的点到l距离的最大值为错误!，求a.解：（１）曲线C的普通方程为错误!＋y２＝１．当a＝—１时，直线l的普通方程为x＋４y—３＝0．由错误!解得错误!或错误!从而C与l的交点坐标为（３，0），错误!.（２）直线l的普通方程为x＋４y—a—４＝0，故C上的点（３cos θ，sin θ）到l的距离为d＝错误!＝错误!，φ满足tan φ＝错误!.当—a—４≤0，即a≥—４时，d的最大值为错误! .由题设得错误!＝错误!，所以a＝8；当—a—４>0，即a<—４时，d的最大值为错误!，由题设得错误!＝错误!，所以a＝—１6．综上，a＝8或a＝—１6．参数方程与极坐标方程的综合应用（师生共研）（２0２0·淄博模拟）在平面直角坐标系xOy中，设倾斜角为α的直线l的参数方程为错误!（α为参数）．在以坐标原点O为极点，以x轴正半轴为极轴建立的极坐标系中，曲线C的极坐标方程为ρ＝错误!，直线l与曲线C相交于不同的两点A，B.（１）若α＝错误!，求直线l的普通方程和曲线C的直角坐标方程；（２）若|OP|为|PA|与|PB|的等比中项，其中P（错误!，２），求直线l的斜率．【解】（１）因为α＝错误!，所以直线l的参数方程为错误!（t为参数）．消t可得直线l的普通方程为x—错误!y＋错误!＝0．因为曲线C的极坐标方程ρ＝错误!可化为ρ２（１＋３cos２θ）＝４，所以曲线C的直角坐标方程为４x２＋y２＝４．（２）设直线l上两点A，B对应的参数分别为t１，t２，将错误!代入曲线C的直角坐标方程４x２＋y２＝４可得４（错误!＋t cos α）２＋（２＋t sin α）２＝４，化简得（４cos２α＋sin２α）t２＋（8错误!cos α＋４sin α）t＋１２＝0，因为|PA|·|PB|＝|t１t２|＝错误!，|OP|２＝7，所以错误!＝7，解得tan２α＝错误!.因为Δ＝（8错误!cos α＋４sin α）２—４8（４cos２α＋sin２α）>0即２sin α（２错误!cos α—sin α）>0，可知tan α>0，解得tan α＝错误!，所以直线l的斜率为错误!.错误!（１）涉及参数方程和极坐标方程的综合题，求解的一般方法是分别化为普通方程和直角坐标方程后求解．当然，还要结合题目本身特点，确定选择何种方程．（２）数形结合的应用，即充分利用参数方程中参数的几何意义，或者利用ρ和θ的几何意义，直接求解，能达到化繁为简的解题目的．１．（２0２0·河南省第五次测评）在直角坐标系xOy中，曲线C１：错误!（α为参数）．以原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C２：ρ２＝４ρcos θ—３．（１）求C１的普通方程和C２的直角坐标方程；（２）若曲线C１与C２交于A，B两点，A，B的中点为M，点P（0，—１），求|PM|·|AB|的值．解：（１）曲线C１的普通方程为x２＋（y—２）２＝５．由ρ２＝x２＋y２，ρcos θ＝x，得曲线C２的直角坐标方程为x２＋y２—４x＋３＝0．（２）将两圆的方程x２＋（y—２）２＝５与x２＋y２—４x＋３＝0作差得直线AB的方程为x—y—１＝0．点P（0，—１）在直线AB上，设直线AB的参数方程为错误!（t为参数），代入x２＋y２—４x＋３＝0化简得t２—３错误!t＋４＝0，所以t１＋t２＝３错误!，t１t２＝４．因为点M对应的参数为错误!＝错误!，所以|PM|·|AB|＝错误!·|t１—t２|＝错误!×错误!＝错误!×错误!＝３．２．（２0１9·高考全国卷Ⅰ）在直角坐标系xOy中，曲线C的参数方程为错误!（t为参数）．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为２ρcos θ＋错误!ρsin θ＋１１＝0．（１）求C和l的直角坐标方程；（２）求C上的点到l距离的最小值．解：（１）因为—１＜错误!≤１，且x２＋错误!错误!＝错误!错误!＋错误!＝１，所以C的直角坐标方程为x２＋错误!＝１（x≠—１）．l的直角坐标方程为２x＋错误!y＋１１＝0．（２）由（１）可设C的参数方程为错误!（α为参数，—π＜α＜π）．C上的点到l的距离为错误!＝错误!.当α＝—错误!时，４cos错误!＋１１取得最小值7，故C上的点到l距离的最小值为错误!.[基础题组练]１．（２0２0·安徽巢湖模拟）在平面直角坐标系xOy中，已知直线l：错误!（t为参数）．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ＝４sin（θ＋错误!）．（１）求曲线C的直角坐标方程．（２）设点M的直角坐标为（0，３），直线l与曲线C的交点为A，B，求|MA|＋|MB|的值．解：（１）把ρ＝４sin错误!，展开得ρ＝２sin θ＋２错误!cos θ，两边同乘ρ得ρ２＝２ρsin θ＋２错误!ρcos θ１．将ρ２＝x２＋y２，ρcos θ＝x，ρsin θ＝y代入１，即得曲线C的直角坐标方程为x２＋y２—２错误!x—２y＝0 ２．（２）将错误!代入２式，得t２＋３错误!t＋３＝0，点M的直角坐标为（0，３）．设这个方程的两个实数根分别为t１，t２，则t１＋t２＝—３错误!，t１·t２＝３，所以t１<0，t２<0．则由参数t的几何意义即得|MA|＋|MB|＝|t１＋t２|＝３错误!.２．（２0２0·太原模拟）在直角坐标系中，圆C的参数方程为：错误!（α为参数），以坐标原点为极点，以x轴的正半轴为极轴建立极坐标系，且长度单位相同．（１）求圆C的极坐标方程；（２）若直线l：错误!（t为参数）被圆C截得的弦长为２错误!，求直线l的倾斜角．解：（１）圆C：错误!消去参数α得（x—１）２＋（y—错误!）２＝４，即x２＋y２—２x—２错误!y＝0，因为ρ２＝x２＋y２，x＝ρcos θ，y＝ρsin θ.所以ρ２—２ρcos θ—２错误!ρsin θ＝0，ρ＝４cos错误!.（２）因为直线l：错误!的极坐标方程为θ＝φ，当θ＝φ时ρ＝４cos错误!＝２错误!.即cos 错误!＝错误!，所以φ—错误!＝错误!或φ—错误!＝—错误!.所以φ＝错误!或φ＝错误!，所以直线l的倾斜角为错误!或错误!.３．在平面直角坐标系xOy中，曲线C１的参数方程为错误!（t为参数），以坐标原点O为极点，x 轴的正半轴为极轴建立极坐标系，曲线C２的极坐标方程为ρ＝错误!.（１）求曲线C２的直角坐标方程；（２）设M１是曲线C１上的点，M２是曲线C２上的点，求|M１M２|的最小值．解：（１）因为ρ＝错误!，所以ρ—ρcos θ＝２，即ρ＝ρcos θ＋２．因为x＝ρcos θ，ρ２＝x２＋y２，所以x２＋y２＝（x＋２）２，化简得y２—４x—４＝0．所以曲线C２的直角坐标方程为y２—４x—４＝0．（２）因为错误!所以２x＋y＋４＝0．所以曲线C１的普通方程为２x＋y＋４＝0．因为M１是曲线C１上的点，M２是曲线C２上的点，所以|M１M２|的最小值等于点M２到直线２x＋y＋４＝0的距离的最小值．不妨设M２（r２—１，２r），点M２到直线２x＋y＋４＝0的距离为d，则d＝错误!＝错误!≥错误!＝错误!，当且仅当r＝—错误!时取等号．所以|M１M２|的最小值为错误!.４．在直角坐标系中，曲线C的参数方程为错误!（α为参数），以原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线D的极坐标方程为ρ＝４sin错误!.（１）写出曲线C的极坐标方程以及曲线D的直角坐标方程；（２）若过点A错误!（极坐标）且倾斜角为错误!的直线l与曲线C交于M，N两点，弦MN的中点为P，求错误!的值．解：（１）由题意可得曲线C的普通方程为错误!＋错误!＝１，将错误!代入曲线C的普通方程可得，曲线C的极坐标方程为错误!＋错误!＝１．因为曲线D的极坐标方程为ρ＝４sin错误!，所以ρ２＝４ρsin错误!＝４ρ错误!，又ρ２＝x２＋y２，x＝ρcos θ，y＝ρsin θ，所以x２＋y２＝２错误!y—２x，所以曲线C的极坐标方程为错误!＋错误!＝１；曲线D的直角坐标方程为x２＋y２＋２x—２错误!y ＝0．（２）点A错误!，则错误!所以A（２，２）．因为直线l过点A（２，２）且倾斜角为错误!，所以直线l的参数方程为错误!（t为参数），代入错误!＋错误!＝１中可得，错误!t２＋（8＋１8错误!）t＋１6＝0，设M，N对应的参数分别为t１，t２，由一元二次方程根与系数的关系得，t１＋t２＝—错误!，t１t２＝错误!，所以错误!＝错误!＝错误!.[综合题组练]１．（２0２0·广州模拟）在直角坐标系xOy中，曲线C１：错误!（α为参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，曲线C２的极坐标方程为ρ＝8cos θ，直线l的极坐标方程为θ＝错误!（ρ∈R）．（１）求曲线C１的极坐标方程与直线l的直角坐标方程；（２）若直线l与曲线C１，C２在第一象限分别交于A，B两点，P为曲线C２上的动点，求△PAB面积的最大值．解：（１）依题意得，曲线C１的普通方程为（x—２）２＋y２＝7，曲线C１的极坐标方程为ρ２—４ρcos θ—３＝0．直线l的直角坐标方程为y＝错误!x.（２）曲线C２的直角坐标方程为（x—４）２＋y２＝１6，设A错误!，B错误!，则ρ错误!—４ρ１cos 错误!—３＝0，即ρ错误!—２ρ１—３＝0，得ρ１＝３或ρ１＝—１（舍），又ρ２＝8cos 错误!＝４，则|AB|＝|ρ２—ρ１|＝１．C２（４，0）到l的距离d＝错误!＝２错误!，以AB为底边的△PAB的高的最大值为４＋２错误!，则△PAB的面积的最大值为错误!×１×（４＋２错误!）＝２＋错误!.２．（２0２0·南昌模拟）在直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρcos θ—ρsin θ＝２，曲线C的极坐标方程为ρsin２θ＝２P cos θ（P>0）．（１）求直线l过点（—２，—４）的参数方程；（２）已知直线l与曲线C交于N，Q两点，M（—２，—４），且|NQ|２＝|MN|·|MQ|，求实数P 的值．解：（１）将x＝ρcos θ，y＝ρsin θ代入直线l的极坐标方程，得直线l的直角坐标方程为x—y—２＝0．所以直线l过点（—２，—４）的参数方程为错误!（t为参数）．（２）由ρsin２θ＝２P cos θ（P>0），得（ρsin θ）２＝２Pρcos θ（P>0），将ρcos θ＝x，ρsin θ＝y代入，得y２＝２Px（P>0）．将直线l的参数方程与曲线C的直角坐标方程联立，得t２—２错误!（４＋P）t＋8（４＋P）＝0，（*）Δ＝8P（４＋P）>0．设点N，Q分别对应参数t１，t２，恰好为上述方程的根，则|MN|＝t１，|MQ|＝t２，|NQ|＝|t１—t２|.由题设得（t１—t２）２＝|t１t２|，即（t１＋t２）２—４t１t２＝|t１t２|.由（*）得t１＋t２＝２错误!（４＋P），t１t２＝8（４＋P）>0，则有（４＋P）２—５（４＋P）＝0，得P＝１或P＝—４．因为P>0，所以P＝１．３．（２0２0·栖霞模拟）在平面直角坐标系xOy中，曲线C的参数方程为错误!（t为参数，a>0），以坐标原点O为极点，x轴的非负半轴为极轴，建立极坐标系，直线l的极坐标方程为ρcos错误!＝—４错误!.（１）设P是曲线C上的一个动点，当a＝２错误!时，求点P到直线l的距离的最小值；（２）若曲线C上所有的点都在直线l的右下方，求实数a的取值范围．解：（１）由ρcos错误!＝—４错误!，得到ρ（cos θ—sin θ）＝—8，因为ρcos θ＝x，ρsin θ＝y，所以直线l的普通方程为x—y＋8＝0．设P（２错误!cos t，２sin t），则点P到直线l的距离d＝错误!＝错误!＝２错误!|sin错误!—２|，当sin错误!＝１时，d min＝２错误!，所以点P到直线l的距离的最小值为２错误!.（２）设曲线C上任意点P（a cos t，２sin t），由于曲线C上所有的点都在直线l的右下方，所以a cos t—２sin t＋8>0对任意t∈R恒成立．错误!sin（t—φ）<8，其中cos φ＝错误!，sin φ＝错误!.从而错误!<8．由于a>0，解得0<a<２错误!.即a∈（0，２错误!）．４．在平面直角坐标系xOy中，圆C的参数方程为错误!（t为参数），在以原点O为极点，x轴的非负半轴为极轴建立的极坐标系中，直线l的极坐标方程为ρcos（θ＋错误!）＝—错误!.（１）求圆C的普通方程和直线l的直角坐标方程；（２）设直线l与x轴，y轴分别交于A，B两点，点P是圆C上任意一点，求A，B两点的极坐标和△PAB面积的最小值．解：（１）由错误!消去参数t，得（x＋５）２＋（y—３）２＝２，所以圆C的普通方程为（x＋５）２＋（y—３）２＝２．由ρcos （θ＋错误!）＝—错误!，得ρcos θ—ρsin θ＝—２，所以直线l的直角坐标方程为x—y＋２＝0．（２）直线l与x轴，y轴的交点分别为A（—２，0），B（0，２），化为极坐标为A（２，π），B错误!，设点P的坐标为（—５＋错误!cos t，３＋错误!sin t），则点P到直线l的距离为d＝错误!＝错误!.所以d min＝错误!＝２错误!，又|AB|＝２错误!.所以△PAB面积的最小值是S＝错误!×２错误!×２错误!＝４．。

第一节 坐标系[考纲传真] 1.理解坐标系的作用，了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.2.了解极坐标的基本概念，会在极坐标系中用极坐标刻画点的位置，能进行极坐标和直角坐标的互化.3.能在极坐标系中给出简单图形表示的极坐标方程．(对应学生用书第158页)[基础知识填充]1．平面直角坐标系中的坐标伸缩变换设点P (x ，y )是平面直角坐标系中的任意一点，在变换φ：⎩⎪⎨⎪⎧x ′＝λx ，λ＞0，y ′＝μy ，μ＞0的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换． 2．极坐标系(1)极坐标与极坐标系的概念在平面内取一个定点O ，叫作极点，从O 点引一条射线Ox ，叫作极轴，选定一个单位长度和角的正方向(通常取逆时针方向)．这样就确定了一个平面极坐标系，简称为极坐标系．对于平面内任意一点M ，用ρ表示线段OM 的长，θ表示以Ox 为始边、OM 为终边的角度，ρ叫作点M 的极径，θ叫作点M 的极角，有序实数对(ρ，θ)叫做点M 的极坐标，记作M (ρ，θ)．当点M 在极点时，它的极径ρ＝0，极角θ可以取任意值．图­­(2)极坐标与直角坐标的互化设M 为平面内的一点，它的直角坐标为(x ，y )，极坐标为(ρ，θ)．由图可知下面关系式成立：⎩⎪⎨⎪⎧x ＝ρcos θy ＝ρsin θ或⎩⎪⎨⎪⎧ρ2＝x 2＋y 2tan θ＝y x x图­­3．常用简单曲线的极坐标方程1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面直角坐标系内的点与坐标能建立一一对应关系，在极坐标系中点与坐标也是一一对应关系．( )(2)若点P 的直角坐标为(1，－3)，则点P 的一个极坐标是⎝ ⎛⎭⎪⎫2，－π3.( )(3)在极坐标系中，曲线的极坐标方程不是唯一的．( ) (4)极坐标方程θ＝π(ρ≥0)表示的曲线是一条直线．( ) [答案] (1)× (2)√ (3)√ (4)×2．(教材改编)若以直角坐标系的原点为极点，x 轴的非负半轴为极轴建立极坐标系，则线段y ＝1－x (0≤x ≤1)的极坐标方程为( ) A ．ρ＝1cos θ＋sin θ，0≤θ≤π2B ．ρ＝1cos θ＋sin θ，0≤θ≤π4C ．ρ＝cos θ＋sin θ，0≤θ≤π2D ．ρ＝cos θ＋sin θ，0≤θ≤π4A [∵y ＝1－x (0≤x ≤1)，∴ρsin θ＝1－ρcos θ(0≤ρcos θ≤1)， ∴ρ＝1sin θ＋cos θ⎝ ⎛⎭⎪⎫0≤θ≤π2.]3．(教材改编)在直角坐标系xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系．若曲线C 的极坐标方程为ρ＝2sin θ，则曲线C 的直角坐标方程为________．x 2＋y 2－2y ＝0 [由ρ＝2sin θ，得ρ2＝2ρsin θ.所以曲线C 的直角坐标方程为x 2＋y 2－2y ＝0.]4．已知直线l 的极坐标方程为2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝2，点A 的极坐标为A ⎝⎛⎭⎪⎫22，7π4，则点A 到直线l 的距离为________．522 [由2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝2，得2ρ⎝⎛⎭⎪⎫22sin θ－22cos θ＝2，∴y －x ＝1.由A ⎝ ⎛⎭⎪⎫22，7π4，得点A 的直角坐标为(2，－2)． ∴点A 到直线l 的距离d ＝|2＋2＋1|2＝522.]5．已知圆C 的极坐标方程为ρ2＋22ρ·sin ⎝⎛⎭⎪⎫θ－π4－4＝0，求圆C 的半径.【导学号：00090368】[解] 以极坐标系的极点为平面直角坐标系的原点O ，以极轴为x 轴的正半轴，建立直角坐标系xOy .圆C 的极坐标方程可化为ρ2＋22ρ⎝⎛⎭⎪⎫22sin θ－22cos θ－4＝0，化简，得ρ2＋2ρsin θ－2ρcos θ－4＝0. 则圆C 的直角坐标方程为x 2＋y 2－2x ＋2y －4＝0，即(x －1)2＋(y ＋1)2＝6， 所以圆C 的半径为 6.(对应学生用书第159页)将圆C ．(1)求曲线C 的方程；(2)设直线l ：2x ＋y －2＝0与C 的交点为P 1，P 2，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求过线段P 1P 2的中点且与l 垂直的直线的极坐标方程．[解] (1)设(x 1，y 1)为圆上的点，在已知变换下变为曲线C 上的点(x ，y )，依题意，得⎩⎪⎨⎪⎧x ＝x 1，y ＝2y 1.2分由x 21＋y 21＝1得x 2＋⎝ ⎛⎭⎪⎫y 22＝1，故曲线C 的方程为x 2＋y 24＝1.5分(2)由⎩⎪⎨⎪⎧x 2＋y 24＝1，2x ＋y －2＝0，解得⎩⎪⎨⎪⎧x ＝1，y ＝0或⎩⎪⎨⎪⎧x ＝0，y ＝2.6分不妨设P 1(1,0)，P 2(0,2)，则线段P 1P 2的中点坐标为⎝ ⎛⎭⎪⎫12，1，所求直线斜率为k ＝12，于是所求直线方程为y －1＝12⎝ ⎛⎭⎪⎫x －12，化为极坐标方程，并整理得2ρcos θ－4ρsin θ＝－3， 故所求直线的极坐标方程为ρ＝34sin θ－2cos θ.10分[规律方法] 1.解答该类问题应明确两点：一是根据平面直角坐标系中的伸缩变换公式的意义与作用；二是明确变换前的点P (x ，y )与变换后的点P ′(x ′，y ′)的坐标关系，利用方程思想求解．2．求交点坐标，得直线方程，最后化为极坐标方程，其实质是将x ＝ρcos θ，y ＝ρsin θ代入转化．[变式训练1] 在平面直角坐标系中，已知伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y .(1)求点A ⎝ ⎛⎭⎪⎫13，－2经过φ变换所得点A ′的坐标；(2)求直线l ：y ＝6x 经过φ变换后所得直线l ′的方程． [解] (1)设点A ′(x ′，y ′)，由伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，得⎩⎪⎨⎪⎧x ′＝3x ，y ′＝y 2，∴x ′＝13×3＝1，y ′＝－22＝－1.∴点A ′的坐标为(1，－1)．(2)设P ′(x ′，y ′)是直线l ′上任意一点．由伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，得⎩⎪⎨⎪⎧x ＝x ′3，y ＝2y ′，代入y ＝6x ，得2y ′＝6·x ′3＝2x ′，∴y ′＝x ′为所求直线l ′的方程．立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为⎝⎛⎭⎪⎫2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．[解] (1)设点P 的极坐标为(ρ，θ)(ρ>0)，点M 的极坐标为(ρ1，θ)(ρ1>0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16得C 2的极坐标方程ρ＝4cos θ(ρ＞0). 2分 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0). 4分(2)设点B 的极坐标为(ρB ，α)(ρB >0)．由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积S ＝12|OA |·ρB ·sin∠AOB6分＝4cos α·⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3 ＝2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2α－π3－32≤2＋ 3.8分当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.10分[规律方法] 1.进行极坐标方程与直角坐标方程互化的关键是灵活应用互化公式：x ＝ρcos θ，y ＝ρsin θ，ρ2＝x 2＋y 2，tan θ＝y x(x ≠0)．2．进行极坐标方程与直角坐标方程互化时，要注意ρ，θ的取值范围及其影响；要善于对方程进行合理变形，并重视公式的逆向与变形使用；要灵活运用代入法和平方法等方法． [变式训练2] (2016·北京高考改编)在极坐标系中，已知极坐标方程C 1：ρcos θ－3ρsin θ－1＝0，C 2：ρ＝2cos θ.(1)求曲线C 1，C 2的直角坐标方程，并判断两曲线的形状； (2)若曲线C 1，C 2交于A ，B 两点，求两交点间的距离． [解] (1)由C 1：ρcos θ－3ρsin θ－1＝0， ∴x －3y －1＝0，表示一条直线． 由C 2：ρ＝2cos θ，得ρ2＝2ρcos θ， ∴x 2＋y 2＝2x ，则(x －1)2＋y 2＝1. ∴C 2是圆心为(1,0)，半径r ＝1的圆． (2)由(1)知点(1,0)在直线x －3y －1＝0上， 因此直线C 1过圆C 2的圆心．∴两交点A ，B 的连线段是圆C 2的直径． 因此两交点A ，B 间的距离|AB |＝2r ＝2.(2016·全国卷Ⅰ)在直角坐标系xOy中，曲线C 1的参数方程为⎩⎪⎨⎪⎧x ＝a cos t ，y ＝1＋a sin t (t为参数，a >0)．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ＝4cos θ.(1)说明C 1是哪一种曲线，并将C 1的方程化为极坐标方程；(2)直线C 3的极坐标方程为θ＝α0，其中α0满足tan α0＝2，若曲线C 1与C 2的公共点都在C 3上，求A ．[解] (1)消去参数t 得到C 1的普通方程为x 2＋(y －1)2＝a 2，则C 1是以(0,1)为圆心，a 为半径的圆.2分将x ＝ρcos θ，y ＝ρsin θ代入C 1的普通方程中，得到C 1的极坐标方程为ρ2－2ρsin θ＋1－a 2＝0.4分(2)曲线C 1，C 2的公共点的极坐标满足方程组⎩⎪⎨⎪⎧ρ2－2ρsin θ＋1－a 2＝0，ρ＝4cos θ.若ρ≠0，由方程组得16cos 2θ－8sin θcos θ＋1－a 2＝0， 由已知tan θ＝2，得16cos 2θ－8sin θcos θ＝0， 8分从而1－a 2＝0，解得a ＝－1(舍去)或a ＝1.当a ＝1时，极点也为C 1，C 2的公共点，且在C 3上． 所以a ＝1.10分[规律方法] 1.第(1)问将曲线C 1的参数方程先化为普通方程，再化为极坐标方程，考查学生的化归与转化能力．第(2)问中关键是理解极坐标方程，有意识地将问题简单化，进而求解．2．由极坐标方程求曲线交点、距离等几何问题时，如果不能直接用极坐标方程解决，可先转化为直角坐标方程，然后求解．[变式训练3] (2018·石家庄模拟)已知曲线C 1：x ＋3y ＝3和C 2：⎩⎨⎧x ＝6cos φ，y ＝2sin φ(φ为参数)．以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，且两种坐标系中取相同的长度单位．(1)把曲线C 1和C 2的方程化为极坐标方程；(2)设C 1与x ，y 轴交于M ，N 两点，且线段MN 的中点为P .若射线OP 与C 1，C 2交于P ，Q 两点，求P ，Q 两点间的距离．[解] (1)曲线C 1化为ρcos θ＋3ρsin θ＝ 3. ∴ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32.2分曲线C 2化为x 26＋y 22＝1.(*) 将x ＝ρcos θ，y ＝ρsin θ代入(*)式得ρ26cos 2θ＋ρ22sin 2θ＝1，即ρ2(cos 2θ＋3sin 2θ)＝6.∴曲线C 2的极坐标方程为ρ2＝61＋2sin 2θ. 4分(2)∵M (3，0)，N (0,1)，∴P ⎝⎛⎭⎪⎫32，12， ∴OP 的极坐标方程为θ＝π6，6分把θ＝π6代入ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32得ρ1＝1，P ⎝ ⎛⎭⎪⎫1，π6. 把θ＝π6代入ρ2＝61＋2sin 2θ得ρ2＝2，Q ⎝ ⎛⎭⎪⎫2，π6. 8分 ∴|PQ |＝|ρ2－ρ1|＝1，即P ，Q 两点间的距离为1.10分。

第一节 坐标系[考纲传真] (教师用书独具)1.理解坐标系的作用，了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.2.了解极坐标的基本概念，会在极坐标系中用极坐标刻画点的位置，能进行极坐标和直角坐标的互化.3.能在极坐标系中给出简单图形表示的极坐标方程．(对应学生用书第198页)[基础知识填充]1．平面直角坐标系中的坐标伸缩变换设点P (x ，y )是平面直角坐标系中的任意一点，在变换φ：⎩⎪⎨⎪⎧x ′＝λx ，λ＞0，y ′＝μy ，μ＞0的作用下，点P (x ，y )对应到点P ′(x ′，y ′)，称φ为平面直角坐标系中的坐标伸缩变换． 2．极坐标与极坐标系的概念图1在平面内取一个定点O ，叫作极点，从O 点引一条射线Ox ，叫作极轴，选定一个单位长度和角的正方向(通常取逆时针方向)．这样就确定了一个平面极坐标系，简称为极坐标系．对于平面内任意一点M ，用ρ表示线段OM 的长，θ表示以Ox 为始边、OM 为终边的角度，ρ叫作点M 的极径，θ叫作点M 的极角，有序实数对(ρ，θ)叫作点M 的极坐标，记作M (ρ，θ)．当点M 在极点时，它的极径ρ＝0，极角θ可以取任意值． 3．极坐标与直角坐标的互化4.5.(1)直线l 过极点，且极轴到此直线的角为α，则直线l 的极坐标方程是θ＝α(ρ∈R )．(2)直线l 过点M (a,0)且垂直于极轴，则直线l 的极坐标方程为ρcos θ＝a ⎝⎛⎭⎪⎫－π2＜θ＜π2.(3)直线过M ⎝⎛⎭⎪⎫b ，π2且平行于极轴，则直线l 的极坐标方程为ρsin θ＝b (0＜θ＜π)．[基本能力自测]1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)(1)平面直角坐标系内的点与坐标能建立一一对应关系，在极坐标系中点与坐标也是一一对应关系．( )(2)若点P 的直角坐标为(1，－3)，则点P 的一个极坐标是⎝ ⎛⎭⎪⎫2，－π3.( )(3)在极坐标系中，曲线的极坐标方程不是唯一的．( ) (4)极坐标方程θ＝π(ρ≥0)表示的曲线是一条直线．( ) [答案] (1)× (2)√ (3)√ (4)×2．(教材改编)若以直角坐标系的原点为极点，x 轴的非负半轴为极轴建立极坐标系，则线段y ＝1－x (0≤x ≤1)的极坐标方程为( ) A ．ρ＝1cos θ＋sin θ，0≤θ≤π2B ．ρ＝1cos θ＋sin θ，0≤θ≤π4C ．ρ＝cos θ＋sin θ，0≤θ≤π2D ．ρ＝cos θ＋sin θ，0≤θ≤π4A [∵y ＝1－x (0≤x ≤1)，∴ρsin θ＝1－ρcos θ(0≤ρcos θ≤1)， ∴ρ＝1sin θ＋cos θ⎝ ⎛⎭⎪⎫0≤θ≤π2.]3．(2017·北京高考)在极坐标系中，点A 在圆ρ2－2ρcos θ－4ρsin θ＋4＝0上，点P 的坐标为(1,0)，则|AP |的最小值为________．1 [由ρ2－2ρcos θ－4ρsin θ＋4＝0，得x 2＋y 2－2x －4y ＋4＝0，即(x －1)2＋(y －2)2＝1， 圆心坐标为C (1,2)，半径长为1. ∵点P 的坐标为(1,0)，∴点P 在圆C 外．又∵点A 在圆C 上，∴|AP |min ＝|PC |－1＝2－1＝1.]4．已知直线l 的极坐标方程为2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝2，点A 的极坐标为A ⎝⎛⎭⎪⎫22，7π4，则点A 到直线l 的距离为______．522 [由2ρsin ⎝ ⎛⎭⎪⎫θ－π4＝2，得2ρ⎝⎛⎭⎪⎫22sin θ－22cos θ＝2，∴y －x ＝1.由A ⎝ ⎛⎭⎪⎫22，7π4，得点A 的直角坐标为(2，－2)． ∴点A 到直线l 的距离d ＝|2＋2＋1|2＝522.]5．已知圆C 的极坐标方程为ρ2＋22ρ·sin ⎝⎛⎭⎪⎫θ－π4－4＝0，求圆C 的半径．[解] 以极坐标系的极点为平面直角坐标系的原点O ，以极轴为x 轴的正半轴，建立直角坐标系xOy . 圆C 的极坐标方程可化为 ρ2＋22ρ⎝⎛⎭⎪⎫22sin θ－22cos θ－4＝0，化简，得ρ2＋2ρsin θ－2ρcos θ－4＝0. 则圆C 的直角坐标方程为x 2＋y 2－2x ＋2y －4＝0，即(x －1)2＋(y ＋1)2＝6， 所以圆C 的半径为 6.(对应学生用书第199页)在平面直角坐标系中，已知伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y .(1)求点A ⎝ ⎛⎭⎪⎫13，－2经过φ变换所得点A ′的坐标；(2)求直线l ：y ＝6x 经过φ变换后所得直线l ′的方程． [解] (1)设点A ′(x ′，y ′)，由伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，得⎩⎪⎨⎪⎧x ′＝3x ，y ′＝y 2，∴x ′＝13×3＝1，y ′＝－22＝－1.∴点A ′的坐标为(1，－1)．(2)设P ′(x ′，y ′)是直线l ′上任意一点． 由伸缩变换φ：⎩⎪⎨⎪⎧x ′＝3x ，2y ′＝y ，得⎩⎪⎨⎪⎧x ＝x ′3，y ＝2y ′，代入y ＝6x ，得2y ′＝6·x ′3＝2x ′，∴y ＝x 即为所求直线l ′的方程．x 在变代入y x ，h x，即为所求变换之后的方程要分清变换前的点的坐标x ，与变换后的点的坐标x ′，y[跟踪训练] 求椭圆x 24＋y 2＝1，经过伸缩变换⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y后的曲线方程.【导学号：79140385】[解] 由⎩⎪⎨⎪⎧x ′＝12x ，y ′＝y ，得⎩⎪⎨⎪⎧x ＝2x ′，y ＝y ′.①将①代入x 24＋y 2＝1，得4x ′24＋y ′2＝1，即x ′2＋y ′2＝1.因此椭圆x 24＋y 2＝1经过伸缩变换后得到的曲线方程是x 2＋y 2＝1.(2016·全国卷Ⅱ)在直角坐标系xOy 中，圆C 的方程为(x ＋6)2＋y 2＝25. (1)以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程；(2)直线l 的参数方程是⎩⎪⎨⎪⎧x ＝t cos α，y ＝t sin α(t 为参数)，l 与C 交于A ，B 两点，|AB |＝10，求l 的斜率．[解] (1)由x ＝ρcos θ，y ＝ρsin θ可得圆C 的极坐标方程为ρ2＋12ρcos θ＋11＝0.(2)在(1)中建立的极坐标系中，直线l 的极坐标方程为θ＝α(ρ∈R )． 设A ，B 所对应的极径分别为ρ1，ρ2，将l 的极坐标方程代入C 的极坐标方程得ρ2＋12ρcos α＋11＝0，于是ρ1＋ρ2＝－12cos α，ρ1ρ2＝11. |AB |＝|ρ1－ρ2|＝(ρ1＋ρ2)2－4ρ1ρ2 ＝144cos 2α－44.由|AB |＝10得cos 2α＝38，tan α＝±153.所以l 的斜率为153或－153.[为极轴建立极坐标系，圆C 的极坐标方程为ρ＝4cos θ.(1)求出圆C 的直角坐标方程；(2)已知圆C 与x 轴相交于A ，B 两点，直线l ：y ＝2x 关于点M (0，m )(m ≠0)对称的直线为l ′.若直线l ′上存在点P 使得∠APB ＝90°，求实数m 的最大值． [解] (1)由ρ＝4cos θ得ρ2＝4ρcos θ，即x 2＋y 2－4x ＝0， 即圆C 的标准方程为(x －2)2＋y 2＝4.(2)直线l ：y ＝2x 关于点M (0，m )的对称直线l ′的方程为y ＝2x ＋2m ，而AB 为圆C 的直径，故直线l ′上存在点P 使得∠APB ＝90°的充要条件是直线l ′与圆C 有公共点， 故|4＋2m |5≤2，解得－2－5≤m ≤5－2， 所以实数m 的最大值为5－2.(2017·全国卷Ⅱ)在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 1的极坐标方程为ρcos θ＝4.(1)M 为曲线C 1上的动点，点P 在线段OM 上，且满足|OM |·|OP |＝16，求点P 的轨迹C 2的直角坐标方程；(2)设点A 的极坐标为⎝⎛⎭⎪⎫2，π3，点B 在曲线C 2上，求△OAB 面积的最大值．[解] (1)设P 的极坐标为(ρ，θ)(ρ>0)，M 的极坐标为(ρ1，θ)(ρ1>0)． 由题设知|OP |＝ρ，|OM |＝ρ1＝4cos θ.由|OM |·|OP |＝16得C 2的极坐标方程为ρ＝4cos θ(ρ＞0)． 因此C 2的直角坐标方程为(x －2)2＋y 2＝4(x ≠0)． (2)设点B 的极坐标为(ρB ，α)(ρB >0)．由题设知|OA |＝2，ρB ＝4cos α，于是△OAB 的面积 S ＝12|OA |·ρB ·sin∠AOB ＝4cos α·⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α－π3 ＝2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2α－π3－32≤2＋ 3.当α＝－π12时，S 取得最大值2＋ 3.所以△OAB 面积的最大值为2＋ 3.[跟踪训练] (2017·太原市质检)已知曲线C 1：x ＋3y ＝3和C 2：⎩⎨⎧x ＝6cos φ，y ＝2sin φ(φ为参数)．以原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，且两种坐标系中取相同的长度单位．(1)把曲线C 1和C 2的方程化为极坐标方程；(2)设C 1与x ，y 轴交于M ，N 两点，且线段MN 的中点为P .若射线OP 与C 1，C 2交于P ，Q 两点，求P ，Q 两点间的距离.【导学号：79140386】[解] (1)曲线C 1化为ρcos θ＋3ρsin θ＝ 3. ∴ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32.曲线C 2化为x 26＋y 22＝1.(*) 将x ＝ρcos θ，y ＝ρsin θ代入(*)式得ρ26cos 2θ＋ρ22sin 2θ＝1，即ρ2(cos 2θ＋3sin 2θ)＝6. ∴曲线C 2的极坐标方程为ρ2＝61＋2sin 2θ. (2)∵M (3，0)，N (0,1)，∴P ⎝ ⎛⎭⎪⎫32，12， ∴OP 的极坐标方程为θ＝π6，把θ＝π6代入ρsin ⎝ ⎛⎭⎪⎫θ＋π6＝32得ρ1＝1，P ⎝⎛⎭⎪⎫1，π6.把θ＝π6代入ρ2＝61＋2sin 2θ得ρ2＝2，Q ⎝⎛⎭⎪⎫2，π6. ∴|PQ |＝|ρ2－ρ1|＝1，即P ，Q 两点间的距离为1.。

课时分层训练(十六) 导数与函数的综合问题A 组 基础达标一、选择题1．方程x 3－6x 2＋9x －10＝0的实根个数是( )A ．3B ．2C ．1D ．0C [设f (x )＝x 3－6x 2＋9x －10，f ′(x )＝3x 2－12x ＋9＝3(x －1)(x －3)，由此可知函数的极大值为f (1)＝－6＜0，极小值为f (3)＝－10＜0，所以方程x 3－6x 2＋9x －10＝0的实根个数为1.]2．若存在正数x 使2x(x －a )＜1成立，则实数a 的取值范围是( )【导学号：79140088】A ．(－∞，＋∞)B ．(－2，＋∞)C ．(0，＋∞)D ．(－1，＋∞)D [∵2x(x －a )＜1，∴a ＞x －12x .令f (x )＝x －12x ，∴f ′(x )＝1＋2－xln 2＞0.∴f (x )在(0，＋∞)上单调递增， ∴f (x )＞f (0)＝0－1＝－1， ∴实数a 的取值范围为(－1，＋∞)．]3．已知y ＝f (x )为R 上的连续可导函数，且xf ′(x )＋f (x )＞0，则函数g (x )＝xf (x )＋1(x ＞0)的零点个数为( ) A ．0 B ．1 C ．0或1D ．无数个 A [因为g (x )＝xf (x )＋1(x ＞0)，g ′(x )＝xf ′(x )＋f (x )＞0，所以g (x )在(0，＋∞)上单调递增，因为g (0)＝1，y ＝f (x )为R 上的连续可导函数，所以g (x )为(0，＋∞)上的连续可导函数，g (x )＞g (0)＝1，所以g (x )在(0，＋∞)上无零点．] 4．(2017·郑州市第一次质量预测)已知函数f (x )＝x ＋4x ，g (x )＝2x ＋a ，若任意x 1∈⎣⎢⎡⎦⎥⎤12，1，存在x 2∈[2,3]，使得f (x 1)≥g (x 2)，则实数a 的取值范围是( ) A ．a ≤1 B ．a ≥1 C ．a ≤2D ．a ≥2A [由题意知f (x )min ⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤12，1≥g (x )min (x ∈[2,3])，因为f (x )min ＝5，g (x )min ＝4＋a ，所以5≥4＋a ，即a ≤1，故选A.]5．做一个无盖的圆柱形水桶，若要使其体积是27π，且用料最省，则圆柱的底面半径为( ) A ．3 B ．4 C ．6D ．5A [设圆柱的底面半径为R ，母线长为l ，则V ＝πR 2l ＝27π，∴l ＝27R2，要使用料最省，只需使圆柱的侧面积与下底面面积之和S 最小． 由题意，S ＝πR 2＋2πRl ＝πR 2＋2π·27R.∴S ′＝2πR －54πR2，令S ′＝0，得R ＝3，则当R ＝3时，S 最小．故选A.]二、填空题6．若函数e xf (x )(e ＝2.718 28…是自然对数的底数)在f (x )的定义域上单调递增，则称函数f (x )具有M 性质．下列函数中所有具有M 性质的函数的序号为________． ①f (x )＝2－x；②f (x )＝3－x；③f (x )＝x 3； ④f (x )＝x 2＋2.①④ [设g (x )＝e xf (x )． 对于①，g (x )＝e x·2－x(x ∈R )，g ′(x )＝e x ·2－x －e x ·2－x ·ln 2＝(1－ln 2)·e x ·2－x >0，∴函数g (x )在R 上单调递增，故①中f (x )具有M 性质． 对于②，g (x )＝e x·3－x(x ∈R )，g ′(x )＝e x ·3－x －e x ·3－x ·ln 3＝(1－ln 3)·e x ·3－x <0，∴函数g (x )在R 上单调递减，故②中f (x )不具有M 性质． 对于③，g (x )＝e x·x 3(x ∈R )，g ′(x )＝e x ·x 3＋e x ·3x 2＝(x ＋3)·e x ·x 2，当x <－3时，g ′(x )<0，g (x )单调递减，故③中f (x )不具有M 性质． 对于④，g (x )＝e x·(x 2＋2)(x ∈R )，g ′(x )＝e x ·(x 2＋2)＋e x ·2x ＝(x 2＋2x ＋2)·e x＝[(x ＋1)2＋1]·e x>0，∴函数g (x )在R 上单调递增，故④中f (x )具有M 性质． 综上，具有M 性质的函数的序号为①④.]7．(2017·江苏高考)已知函数f (x )＝x 3－2x ＋e x－1ex ，其中e 是自然对数的底数．若f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________.【导学号：79140089】⎣⎢⎡⎦⎥⎤－1，12 [因为f (－x )＝(－x )3－2(－x )＋e －x －1e －x＝－x 3＋2x －e x＋1e x ＝－f (x )，所以f (x )＝x 3－2x ＋e x－1e x 是奇函数．因为f (a －1)＋f (2a 2)≤0，所以f (2a 2)≤－f (a －1)，即f (2a 2)≤f (1－a )．因为f ′(x )＝3x 2－2＋e x ＋e －x ≥3x 2－2＋2e x ·e －x ＝3x 2≥0， 所以f (x )在R 上单调递增， 所以2a 2≤1－a ，即2a 2＋a －1≤0， 所以－1≤a ≤12.]8．若函数f (x )＝2x ＋sin x 对任意的m ∈[－2,2]，f (mx －3)＋f (x )＜0恒成立，则x 的取值范围是________．(－3,1) [因为f (x )是R 上的奇函数，f ′(x )＝2＋cos x ＞0，则f (x )在定义域内为增函数，所以f (mx －3)＋f (x )＜0可变形为f (mx －3)＜f (－x )， 所以mx －3＜－x ，将其看作关于m 的一次函数， 则g (m )＝x ·m －3＋x ，m ∈[－2,2]， 可得若m ∈[－2,2]时，g (m )＜0恒成立． 则g (2)＜0，g (－2)＜0，解得－3＜x ＜1.]三、解答题9．已知函数f (x )＝e x＋ax －a (a ∈R 且a ≠0)．(1)若f (0)＝2，求实数a 的值，并求此时f (x )在[－2,1]上的最小值； (2)若函数f (x )不存在零点，求实数a 的取值范围．[解] (1)由f (0)＝1－a ＝2，得a ＝－1.易知f (x )在[－2,0)上单调递减，在(0,1]上单调递增，所以当x ＝0时，f (x )在[－2,1]上取得最小值2. (2)f ′(x )＝e x＋a ，由于e x＞0. ①当a ＞0时，f ′(x )＞0，f (x )是增函数， 当x ＞1时，f (x )＝e x ＋a (x －1)＞0.当x ＜0时，取x ＝－1a，则f ⎝ ⎛⎭⎪⎫－1a ＜1＋a ⎝ ⎛⎭⎪⎫－1a －1＝－a ＜0.所以函数f (x )存在零点，不满足题意． ②当a ＜0时，f ′(x )＝e x＋a ， 令f ′(x )＝0，得x ＝ln(－a )．在(－∞，ln(－a ))上，f ′(x )＜0，f (x )单调递减， 在(ln(－a )，＋∞)上，f ′(x )＞0，f (x )单调递增， 所以当x ＝ln(－a )时，f (x )取最小值． 函数f (x )不存在零点，等价于f (ln(－a ))＝e ln(－a )＋a ln(－a )－a ＝－2a ＋a ln(－a )＞0，解得－e 2＜a ＜0.综上所述，所求实数a 的取值范围是－e 2＜a ＜0. 10．(2018·合肥一检)已知函数f (x )＝2a －x2ex (a ∈R )．(1)求函数f (x )的单调区间；(2)若任意x ∈[1，＋∞)，不等式f (x )＞－1恒成立，求实数a 的取值范围． [解] (1)f ′(x )＝x 2－2x －2aex，当a ≤－12时，x 2－2x －2a ≥0，故f ′(x )≥0，∴函数f (x )在(－∞，＋∞)上单调递增，∴当a ≤－12时，函数f (x )的单调递增区间为(－∞，＋∞)，无单调递减区间．当a ＞－12时，令x 2－2x －2a ＝0⇒x 1＝1－2a ＋1，x 2＝1＋2a ＋1，列表由表可知，当a ＞－2时，函数f (x )的单调递增区间为(－∞，1－2a ＋1)和(1＋2a ＋1，＋∞)，单调递减区间为(1－2a ＋1，1＋2a ＋1)．(2)∵f (x )＞－1⇔2a －x 2ex ＞－1⇔2a ＞x 2－e x，∴由条件2a ＞x 2－e x，对任意x ≥1成立． 令g (x )＝x 2－e x ，h (x )＝g ′(x )＝2x －e x， ∴h ′(x )＝2－e x，当x ∈[1，＋∞)时，h ′(x )＝2－e x≤2－e ＜0， ∴h (x )＝g ′(x )＝2x －e x在[1，＋∞)上单调递减， ∴h (x )＝2x －e x≤2－e ＜0，即g ′(x )＜0， ∴g (x )＝x 2－e x在[1，＋∞)上单调递减， ∴g (x )＝x 2－e x≤g (1)＝1－e ，故f (x )＞－1在[1，＋∞)上恒成立，只需2a ＞g (x )max ＝1－e ， ∴a ＞1－e 2，即实数a 的取值范围是⎝ ⎛⎭⎪⎫1－e 2，＋∞. B 组 能力提升11．(2018·山东省实验中学诊断)若函数f (x )在R 上可导，且满足f (x )－xf ′(x )＞0，则( )A ．3f (1)＜f (3)B ．3f (1)＞f (3)C ．3f (1)＝f (3)D ．f (1)＝f (3)B [由于f (x )＞xf ′(x )，则⎣⎢⎡⎦⎥⎤f (x )x ′＝xf ′(x )－f (x )x 2＜0恒成立，因此f (x )x 在R 上是单调递减函数， 所以f (3)3＜f (1)1，即3f (1)＞f (3)．]12．方程f (x )＝f ′(x )的实数根x 0叫作函数f (x )的“新驻点”，如果函数g (x )＝ln x 的“新驻点”为a ，那么a 满足( ) A ．a ＝1 B ．0＜a ＜1 C ．2＜a ＜3D ．1＜a ＜2D [∵g ′(x )＝1x ，∴ln x ＝1x.设h (x )＝ln x －1x，则h (x )在(0，＋∞)上为增函数．又∵h (1)＝－1＜0，h (2)＝ln 2－12＝ln 2－ln e ＞0，∴h (x )在(1,2)上有零点，∴1＜a ＜2.]13．已知函数f (x )＝ax 3－3x 2＋1，若f (x )存在唯一的零点x 0，且x 0＞0，则a 的取值范围是________.【导学号：79140090】(－∞，－2) [当a ＝0时，显然f (x )有两个零点，不符合题意． 当a ≠0时，f ′(x )＝3ax 2－6x ，令f ′(x )＝0，解得x 1＝0，x 2＝2a.当a ＞0时，2a＞0，所以函数f (x )＝ax 3－3x 2＋1在(－∞，0)和⎝ ⎛⎭⎪⎫2a ，＋∞上为增函数，在⎝⎛⎭⎪⎫0，2a 上为减函数，因为f (x )存在唯一零点x 0，且x 0＞0，则f (0)＜0，即1＜0，不成立．当a ＜0时，2a＜0，所以函数f (x )＝ax 3－3x 2＋1在⎝ ⎛⎭⎪⎫－∞，2a 和(0，＋∞)上为减函数，在⎝ ⎛⎭⎪⎫2a，0上为增函数，因为f (x )存在唯一零点x 0，且x 0＞0，则f ⎝ ⎛⎭⎪⎫2a ＞0，即a ·8a 3－3·4a 2＋1＞0，解得a ＞2或a ＜－2，又因为a ＜0，故a 的取值范围为(－∞，－2)．]14．已知函数f (x )＝ex －m－x ，其中m 为常数．(1)若对任意x ∈R 有f (x )≥0恒成立，求m 的取值范围； (2)当m ＞1时，判断f (x )在[0,2m ]上零点的个数，并说明理由． [解] (1)依题意，可知f ′(x )＝e x －m－1，令f ′(x )＝0，得x ＝m . 故当x ∈(－∞，m )时，e x －m＜1，f ′(x )＜0，f (x )单调递减；当x ∈(m ，＋∞)时，ex －m＞1，f ′(x )＞0，f (x )单调递增．故当x ＝m 时，f (m )为极小值也是最小值． 令f (m )＝1－m ≥0，得m ≤1，即对任意x ∈R ，f (x )≥0恒成立时，m 的取值范围是(－∞，1]． (2)f (x )在[0,2m ]上有两个零点，理由如下： 当m ＞1时，f (m )＝1－m ＜0.∵f (0)＝e －m＞0，f (0)·f (m )＜0，且f (x )在(0，m )上单调递减． ∴f (x )在(0，m )上有一个零点． 又f (2m )＝e m－2m ，令g (m )＝e m－2m ，则g ′(m )＝e m－2，∵当m ＞1时，g ′(m )＝e m－2＞0， ∴g (m )在(1，＋∞)上单调递增．∴g (m )＞g (1)＝e －2＞0，即f (2m )＞0. ∴f (m )·f (2m )＜0，∴f (x )在(m,2m )上有一个零点．故f(x)在[0,2m]上有两个零点．。

课时作业71坐标系［授课提示：对应学生用书第284页］将①代入.^+/= 1,2因此椭圆亍+尹=1经伸缩变换后得到的曲线方程是X+y2=］.2. (2018-邯郸调研)在极坐标系中，已知直线/过点力(1,0),且其向上的方向与极轴的正方向所成的最小正角为令求:(1) 直线的极坐标方程；(2) 极点到该直线的距离.解析：(1)如图，由正弦定理得・•・所求直线的极坐标方程为ps 硝一0=爭(2)作OHU,垂足为H,兀71在△OH4 中,OA = l f ZOHA = y AOAH=y 则 O//=CMsin 彳=¥，即极点到该直线的距离等于罗.3・(2018-沈阳市教学质量检测(一))在直角坐标系妝万中，直线厶圆— 1 +cos° C . (°为参数)，以坐标原点为极点，X 轴的正半轴为极轴建立极 —2 十sm°C经过伸缩变换＜x f 192后的曲线方程=尹仪=2*得到,①4x , 2得 \ +/ 2-1即"2+；/ 2=1.1 =尹,=y1.求椭圆才+于=1,7U即 “sin 身_“ = sin¥=¥坐标系.(1) 求直线Z 与圆C 的极坐标方程；(2) 设直线/与圆C 的交点为M, N,求△CMN 的面积.解析：⑴将C 的参数方程化为普通方程，得(x+l)2 + (y+2)2=l,jr•：x=pcosO, y=psinO,・••直线/的极坐标方程为〃=才(/?丘只)，圆C 的极坐标方程为才+ 2#cos0+4/?sin0+4 = O.(2)将 0=¥代入 p 2+2pcos3+4psin0+4=0,得 p 2+ 3^/2/?+4=0,解得 p\ — 一2迈，p 2=—yf2, \MN\ = |/91 —P2I = V2,•・•圆C 的半径为1, :./XCMN 的面积为*X 迈XIXsi 请=*.4. (2018-成都模拟)在直角坐标系xO 尹中，半圆C 的直角坐标方程为(x-1)2+b=i(0WyWl)・以O 为极点，x 轴的非负半轴为极轴建立极坐标系.(1) 求仑的极坐标方程；(2) 直线/的极坐标方程是#(sin0+羽cos0) = 5羽，射线OM ： 0=扌与半圆C 的交点为O, P,与直线/的交点为0,求线段P0的长.解析：(1)由x=pcos3, y=psm0,所以半圆C 的极坐标方程是#=2cos&, 0W 0,申.为点0的极坐标，〃2(sin&2+羽 cos%) = 5 羽, 02老 "2 = 5, 解得’/)〃2=亍，由于0\ = ()2，所以|P0| = bi —021=4,所以线段PQ 的长为4.5. (2018•广州五校联考)在极坐标系中，圆C 是以点C (2, 一却为圆心，2 为半径的圆.(1) 求圆C 的极坐标方程；(2) 求圆C 被直线/： &=—誥(“CR)所截得的弦长.解析：法一：⑴设所求圆上任意一点M(p, 0),如图,p\ =2cos&], ⑵设S1，0|)为点F 的极坐标，则有｛ 7T &1=亍，解得 0 = 1,&1=务 设(P2,弘)jr在Rt/\OAM中，ZOMA = yTtZAOM=2n-e-^ \OA\=4. 因为COS ZAOM=^^^9所以|OM = |Q4|・cosZ/OM,验证可知，极点O与力(4, 一劭的极坐标也满足方程，故“=4cos@+扌)为所求.(2)设人0=—譬(“GR)交圆C于点P,JT在Rt A OAP中，ZOPA=y易得Z/OP斗，所以|0 鬥= |O/|cosZ/OP=2 寸17T法二：(1)0 C是将圆p=4cos&绕极点按顺时针方向旋转彳而得到的圆，所以圆C的极坐标方程是p=4cos(0+g|.(2)将0=—普代入圆C的极坐标方程p=4cos@+g), 得p=2y[2,所以圆C被直线厶0=—詩(pWR)所截得的弦长为2迈.[能力挑战]6.(2018-成都市第二次诊断性检测)在直角坐标系兀Oy中，曲线C的参数方[x=2cosa x=y[i—^-t—S为参数)，育•线/的参数方程为彳, (/为参数)•在ly = 2十2sinc(亠,1尸3+歹以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，过极点O的射线与曲线C相交于不同于极点的点且点/的极坐标为(2羽，0),其屮“丘曾，4(1)求〃的值；(2)若射线OA与直线I相交于点B,求|M|的值.解析：(1)由题意知，曲线C的普通方程为x2+(y-2)2=4,Vx=pcos0, y=psind,曲线C 的极坐标方程为G9Cos0)2 + (psin0-2)2=4, 即“=4sin0.2兀T(2)由题，易知直线/的普通方程为x+3心一4羽=0, 程为/>cos&+羽psin〃一4羽=0.2兀又射线OA的极坐标方程为0=了3上0),・••直线I的极坐标方联立, 2兀得戸心)”cos&+羽#sin0—4羽=0解得卩=4书.・••点B的极坐标为（4萌，y）,••- \AB\ = \p B~P A\=4^/3 — 2羽=2 羽.。

第二节参数方程[考纲传真] .了解参数方程，了解参数的意义.能选择适当的参数写出直线、圆和椭圆曲线的参数方程．(对应学生用书第页)[基础知识填充]．曲线的参数方程一般地，在平面直角坐标系中，如果曲线上任意一点的坐标，都是某个变数的函数(\\(＝，＝))并且对于的每一个允许值，由这个方程组所确定的点(，)都在这条曲线上，那么这个方程组就叫做这条曲线的参数方程，联系变数，的变数叫做参变数，简称参数．．参数方程和普通方程的互化()曲线的参数方程和普通方程是曲线方程的不同形式．一般地，可以通过消去参数从参数方程得到普通方程．()如果知道变数，中的一个与参数的关系，例如＝()，把它代入普通方程，求出另一个变数与参数的关系＝()，那么(\\(＝，＝))就是曲线的参数方程．．常见曲线的参数方程和普通方程是直线上任一点(，)到(，)的距离．[基本能力自测]．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)()参数方程(\\(＝，＝))中的，都是参数的函数．( )()过(，)，倾斜角为α的直线的参数方程为(\\(＝＋α，＝＋α))(为参数)．参数的几何意义表示：直线上以定点为起点，任一点(，)为终点的有向线段的数量．( ) ()方程(\\(＝θ，＝＋θ))表示以点()为圆心，以为半径的圆．( )()已知椭圆的参数方程(\\(＝，＝ ))(为参数)，点在椭圆上，对应参数＝，点为原点，则直线的斜率为.( )[答案]()√()√()√()×．(教材改编)曲线(\\(＝－＋θ，＝＋θ))(θ为参数)的对称中心( )．在直线＝上．在直线＝－上．在直线＝－上．在直线＝＋上[由(\\(＝－＋θ，＝＋θ，))得(\\( θ＝＋，θ＝－，))所以(＋)＋(－)＝.曲线是以(－)为圆心，为半径的圆，所以对称中心为(－)，在直线＝－上．]．(教材改编)在平面直角坐标系中，曲线：(\\(＝＋(())，＝＋(())))(为参数)的普通方程为．－－＝[由＝＋，且＝＋，消去，得－＝，即－－＝.]．在平面直角坐标系中，以原点为极点，轴的正半轴为极轴建立极坐标系．曲线的极坐标方程为ρ( θ＋θ)＝－，曲线的参数方程为(\\(＝，＝()))(为参数)，则与交点的直角坐标为．(，－)[由ρ( θ＋θ)＝－，得＋＝－.①由(\\(＝，＝()，))消去得＝.②联立①②得(\\(＝，＝－，))即交点坐标为(，－)．]．(·江苏高考)在平面直角坐标系中，已知直线的参数方程为(\\(＝＋()，＝(())))(为参数)，椭圆的参数方程为(\\(＝θ，＝θ))(θ为参数)．设直线与椭圆相交于，两点，求线段的长. 【导学号：】[解]椭圆的普通方程为＋＝分将直线的参数方程(\\(＝＋()，＝(())))代入＋＝，得＋＝，即＋＝，分解得＝，＝－，所以＝－＝分(对应学生用书第页)(\\(＝θ，＝θ))(θ为参数)．()求直线和圆的普通方程；。