平面几何选讲(4)

复 数 与 平 面 几 何 证 明 选 讲一、知识要点1．复数的概念：形如(,)a bi a b R +∈的数叫复数，a 叫复数的实部，b 叫复数的虚部复数集，用字母C 表示 复数通常用字母z 表示，即(,)z a bi a b R =+∈（其中21i =-）3．两个复数相等：,()a bi c di a b c d R ++∈、、、相等的充要条件是=a c b d =且.4．复平面：建立直角坐标系来表示复数的平面叫做复平面，横轴为实轴，竖轴除去原点为虚轴.5．复数的模：复数z a bi =+可以用复平面内的点Z(,)a b 表示，向量OZ 的模叫做复数z a bi =+的模，表示为：||||z a bi =+=6．共轭复数：两个复数的实部相等，虚部互为相反数时，这两个复数叫做共轭复数。

若z a bi =+则z a bi =- 7．复数的四则运算（1）加减运算：()()()()a bi c di a c b d i +±+=±++； （2）乘法运算：()()()()a bi c di ac bd ad bc i +⋅+=-++； （3）除法运算：2222()()()()(0)ac bd bc ad a bi c di i c di c d c d +-+÷+=++≠++；（4）i 的幂运算：41ni=，41n i i +=，421n i +=-，43n i i +=-.()n Z ∈8．共轭复数的性质：（1）实数的共轭复数仍然是它本身（2）22||||z z z z ==（3）两个共轭复数对应的点关于实轴对称9．复数的两种几何意义：10．几个常用结论：（1）()i i 212=+，（2）()i i 212-=-（3）ii -=1，（4） i ii =-+11 （5） i i i-=+-11 点),(b a Z向量OZ一一对应一一对应一一对应复数()R b a bia Z ∈+=,一、选择题1．复数=z i i m 212+-（i R m ,∈为虚数单位）在复平面上对应的点不可能位于（ ）A.第一象限B.第二象限C.第三象限D.第四象限 2．使复数为实数的充分而不必要条件是由 ( )A ．z z -= B ．z z = C ．2z 为实数 D ．z z -+为实数3．设456124561212,,z i i i i z i i i i =+++++⋅⋅⋅⋅则12,z z 的关系是( )A ．12z z =B ．12z z =-C ．121z z =+D ．无法确定 4． 2020(1)(1)i i +--的值是( )A ．1024-B ．1024C ．0D ．1024i 5．已知复数=1z 3+4i ，i t z +=2，且12z z ⋅是实数，则实数=t （ ）A ．43 B ．34 C ．-34 D ．-436212i i-+++的值是( ). A ．0 B ．1 C ．i D ．2i7．若复数z 满足)1z z i +=,则2z z +的值等于( )A ．1B ．0C ．1-D ．122i -+8．已知3()z -=-,那么复数z 在平面内对应的点位于( )A ．第一象限B ． 第二象限C ．第三象限D ．第四象限 9．已知12121z z z z ==-=,则12z z +等于( )A ．1BC ．10．若12ω=-,则等于421ωω++=( )A ．1B ．0C ．3+D ．1-+ 11．给出下列命题(1)实数的共轭复数一定是实数; (2)满足2z i z i -++=的复数z 的轨迹是椭圆; (3)若2,1m Z i ∈=-,则1230;mm m m i ii i ++++++= 其中正确命题的序号是( )A.(1)B.(2)(3)C.(1)(3)D.(1)(4)12．若22(1)(32)x x x i -+++是纯虚数，则实数x 的值是（ ） A ．1 B ．1- C ． 1± D ．以上都不对13．221(1)(4),.z m m m m i m R =++++-∈232.z i =-则1m =是12z z =的（ ）条件A ．充分不必要B ．必要不充分C ．充要D ．既不充分又不必要 14．设i z 431-=，i z 322+-=，则21z z +在复平面内对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 15．设z 的共轭复数是z ，且z +z =4，z ·z ＝8，则zz等于（ ） A.1 B.-i C.±1 D.±i 16．设1z i =+（i 是虚数单位），则22z z+= ( ) A ．1i -- B ．1i -+ C ．1i - D ． 1i +17．已知i iz+=+21,则复数=z （ ）（A ）-1+3i (B)1-3i (C)3+i (D)3-i 18． 已知复数12z i =-，那么1z=（ ）A ．- C.1255i + D.1255i - 19．复数11212i i+-+-的虚部是（ ） A ．15i B ．15 C ．15i -D ．15-20．下面是关于复数21z i=-+的四个命题：其中的真命题为（ ）1:2p z = 22:2p z i = 3:p z 的共轭复数为1i + 4:p z 的虚部为1-()A 23,p p ()B 12,p p （C ）,p p 24 ()D ,p p 3421．复数2311i i i i -++=-（ ） （A ）1122i -- (B) 1122i -+ (C)1122i - (D) 1122i + 22．复数22iz i-=+(i 为虚数单位)在复平面内对应的点所在象限为 （A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限23．已知),(2R b a i b iia ∈+=+，则=+b a （ ） （A ）-1 （B ）1 （C ）2 （D ）3 24．设a,b 为实数，若复数11+2ii a bi=++，则（ ）（A ）31,22a b == (B) 3,1a b == (C) 13,22a b == (D) 1,3a b == 25．已知复数z =，z 是z 的共轭复数，则z z ∙=（ ）A. 14 B.12 C.1 D.2二、填空题1．如果(,,0)z a bi a b R a =+∈≠且是虚数，则222,,,,,,,,z z z z z z z z z z -=--⋅中是虚数的有 _______个，是实数的有 个，相等的有 组.2．已知3(2),z i =-则z z -⋅= . 3．复数234z i i i i =+++的值是___________。

2015年第56届国际奥林匹克数学竞赛（2015年7月10-11日，泰国清迈）试题选讲【分析】AO是O的弦FG的中垂线，要证明X在AO上，只要证明XF XG∠=∠。

=或者XFG XGF（下面只是证明本题最关键的步骤，略去了大量的文字阐述和引用的常用中间结论，这在正式竞赛中是不允许的。

所以，同学们如果要自己动手做一做、练一练，一定要把过程写详细、写清楚!) Array【证一】∵AFX AFK FKB FAB FDB FCB DFC∠=∠=∠-∠=∠-∠=∠，AGX AGL CLG CAG CEG CBG EBG∠=∠=∠-∠=∠-∠=∠，∴F N M G，，，四点共圆，可得NFM NGM DFC EGB∠=∠⇒∠=∠，∴AFX AGX∠=∠。

而AF AG AFG AGF∠=∠。

，，则XFG XGF=∠=∠这样，A X，两点都在弦FG的中垂线上。

而弦FG的中垂线必过圆心O，可知A X O，，三点共线。

【证二】【另证F N M G，，，四点共圆】=∠。

FMG【本题剖析，及拓展】如图，可以证明以下诸多结论：（1）JHF KIG ∆∆——JHF JBF ABF KIG KCG ACG JHF KIG F G A AF AG A F B C G O ∠=∠=∠⎧⎪∠=∠=∠⎪⇒∠=∠⎨=⎪⎪⎩，在上，，，，，在上； AFX AFJ FJB FAB FDB FCB DFC LFM AFX AFJ FJB FAB FDB FGB FGE FGB BGE LGM AFX AFJ FHB FGB HBG AGX AGK GKC GAC GIC GFC FCI AGX AGK GKC GAC GEC GBC EGB LGM AGX AGK ∠=∠=∠-∠=∠-∠=∠=∠∠=∠=∠-∠=∠-∠=∠-∠=∠=∠∠=∠=∠-∠=∠∠=∠=∠-∠=∠-∠=∠∠=∠=∠-∠=∠-∠=∠=∠∠=∠=∠或或或或AFX AGX GKC GAC GEC GFC GFD GFC DFC LFM⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⇒∠=∠⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪-∠=∠-∠⎪=∠-∠=∠=∠⎪⎩；而AF AG AFG AGF =⇒∠=∠，可知JFH KGI ∠=∠，FJH GKI ∠=∠。

2015年第56届国际奥林匹克数学竞赛（2015年7月10-11日，泰国清迈）试题选讲【分析】AO是O的弦FG的中垂线，要证明X在AO上，只要证明XF XG∠=∠。

=或者XFG XGF（下面只是证明本题最关键的步骤，略去了大量的文字阐述和引用的常用中间结论，这在正式竞赛中是不允许的。

所以，同学们如果要自己动手做一做、练一练，一定要把过程写详细、写清楚!) Array【证一】∵AFX AFK FKB FAB FDB FCB DFC∠=∠=∠-∠=∠-∠=∠，AGX AGL CLG CAG CEG CBG EBG∠=∠=∠-∠=∠-∠=∠，∴F N M G，，，四点共圆，可得NFM NGM DFC EGB∠=∠⇒∠=∠，∴AFX AGX∠=∠。

而AF AG AFG AGF∠=∠。

，，则XFG XGF=∠=∠这样，A X，两点都在弦FG的中垂线上。

而弦FG的中垂线必过圆心O，可知A X O，，三点共线。

【证二】【另证F N M G，，，四点共圆】=∠。

FMG【本题剖析，及拓展】如图，可以证明以下诸多结论：（1）JHF KIG ∆∆——JHF JBF ABF KIG KCG ACG JHF KIG F G A AF AG A F B C G O ∠=∠=∠⎧⎪∠=∠=∠⎪⇒∠=∠⎨=⎪⎪⎩，在上，，，，，在上； AFX AFJ FJB FAB FDB FCB DFC LFM AFX AFJ FJB FAB FDB FGB FGE FGB BGE LGM AFX AFJ FHB FGB HBG AGX AGK GKC GAC GIC GFC FCI AGX AGK GKC GAC GEC GBC EGB LGM AGX AGK ∠=∠=∠-∠=∠-∠=∠=∠∠=∠=∠-∠=∠-∠=∠-∠=∠=∠∠=∠=∠-∠=∠∠=∠=∠-∠=∠-∠=∠∠=∠=∠-∠=∠-∠=∠=∠∠=∠=∠或或或或AFX AGX GKC GAC GEC GFC GFD GFC DFC LFM⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⇒∠=∠⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪-∠=∠-∠⎪=∠-∠=∠=∠⎪⎩；而AF AG AFG AGF =⇒∠=∠，可知JFH KGI ∠=∠，FJH GKI ∠=∠。

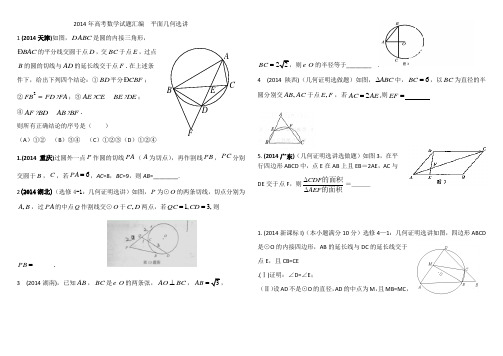
FED CBA 2014年高考数学试题汇编 平面几何选讲1 (2014天津)如图，ABC D 是圆的内接三角形，BAC Ð的平分线交圆于点D ，交BC 于点E ，过点B 的圆的切线与AD 的延长线交于点F .在上述条件下，给出下列四个结论：①BD 平分CBF Ð；②2FB FD FA = ；③AE CE BE DE ? ；④AF BDAB BF ? .则所有正确结论的序号是（ ）（A ）①② （B ）③④ （C ）①②③（D ）①②④1.(2014重庆)过圆外一点P 作圆的切线PA （A 为切点），再作割线PB ，PC 分别交圆于B ，C ，若6=PA ，AC =8，BC =9，则AB =________.2(2014湖北)（选修4-1：几何证明选讲）如图，P 为⊙O 的两条切线，切点分别为B A ,，过PA 的中点Q 作割线交⊙O 于DC ,两点，若,3,1==CD QC 则_____=PB .3 (2014湖南)，已知AB ，BC 是O 的两条弦，AO BC ⊥，AB =BC =O 的半径等于________ .4 (2014陕西)（几何证明选做题）如图，ABC ∆中，6BC =，以BC 为直径的半圆分别交,AB AC 于点,E F ，若2AC AE =,则EF =5. (2014广东)（几何证明选讲选做题）如图3，在平行四边形ABCD 中，点E 在AB 上且EB ＝2AE ，AC 与DE 交于点F ，则CDF AEF ∆∆的面积的面积＝＿＿＿1. (2014新课标I)（本小题满分10分）选修4—1：几何证明选讲如图，四边形ABCD 是⊙O 的内接四边形，AB 的延长线与DC 的延长线交于点E ，且CB=CE .(Ⅰ)证明：∠D=∠E ；（Ⅱ）设AD 不是⊙O 的直径，AD 的中点为M ，且MB=MC ，- 2 -2. (2014新课标II)（本小题满分10）选修4—1：几何证明选讲。

2021-2022学年安徽省安庆市高三（上）摸底数学试卷（文科）一、选择题1．已知A={x|﹣2＜x＜4}，B={x|x＞3}，则A∩B=( )A．{x|﹣2＜x＜4} B．{x|x＞3} C．{x|3＜x＜4} D．{x|﹣2＜x＜3}2．若i（x+yi）=3+4i，x，y∈R，则复数x+yi的模是( )A．2 B．3 C．4 D．53．下列函数中，在（0，+∞）上单调递减，并且是偶函数的是( )A．y=x2 B．y=﹣x3C．y=﹣lg|x| D．y=2x4．已知{a n}各项为正的等比数列，其前n项和为Sn，若a3=4，S3=7，则公比q等于( )A ．B ．C．2 D．35．在样本颇率分布直方图中，共有9个小长方形，若中间一个小长方形的面积等于它8个长方形的面积和的，且样本容量为140，则中间一组的频数为( )A．28 B．40 C．56 D．606．在△ABC中，sinA=，，则△ABC的面积为( )A．3 B．4 C．6 D ．7．设a，b是平面α内两条不同的直线，l是平面α外的一条直线，则“l⊥a，l⊥b”是“l⊥α”的( )A．充要条件 B．充分而不必要的条件C．必要而不充分的条件D．既不充分也不必要的条件8．已知f（x）=2cos2x﹣6sinxcosx，则函数f（x）的最大值是( )A．3 B ． C ．+1 D ．﹣19．下列说法中正确的有（1）命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠l，则x2﹣3x+2≠0”；（2）“x＞2”是“x2﹣3x+2＞0”的充分不必要条件；（3）对于命题p：∃x∈R，x2+x+1＜0，则￢p：∀x∈R，x2+x+1≥0（4）若P∧q为假命题，则P、q均为假命题．( )A．1个B．2个C．3个D．4个10．一个几何体的三视图如图所示，则该几何体的表面积是( ) A．4+2B．4+C．4+2D．4+11．已知抛物线y2=2px（p＞0）与双曲线=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的一个交点，且AF⊥x轴，则双曲线的离心率为( )A ．+2B ．+1C ．+1D ．+112．已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=6，BC=2，则棱锥O﹣ABCD的侧面积为( )A．20+8B．44 C．20D．46二、填空题13．若tan（θ+）=，则tanθ=__________．14．若函数f（x）=4x﹣2x﹣a，x∈[﹣1，1]有零点，则实数a的取值范围是__________．15．已知程序框图如图，若a=0.62，b=30.5，c=log0.55，则输出的数是__________16．在边长为2的正方形ABCD中有一个不规章的图形M，用随机模拟方法来估量不规章图形的面积．若在正方形ABCD中随机产生了10000个点，落在不规章图形M内的点数恰有2000个，则在这次模拟中，不规章图形M 的面积的估量值为__________．三、解答题17．己知等差数列{a n}满足a1=1，a4=7．（Ⅰ）求数列{an}的通项公式；（Ⅱ）设c n=，数列{c n}的前n项和为T n，证明：≤T n．18．某中学作为蓝色海洋训练特色学校，随机抽取100名同学，进行一次海洋学问测试，按测试成果分组如下：第一组[65，70），其次组[70，75），第三组[75，80），第四组[80，85），第五组[85，90）（假设考试成果均在[65，90）内），得到频率分布直方图如图：（1）求测试成果在[80，85）内的频率；（2）从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋学问宣讲小组，定期在校内进行义务宣讲，并在这6名同学中随机选取2名参与市组织的蓝色海洋训练义务宣讲队，求第四组至少有一名同学被抽中的概率．19．如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，其中PA=PD=AD=2，∠BAD=60°，Q 为AD的中点．（1）求证：AD⊥平面PQB；（2）若平面PAD⊥平面ABCD，且，求四棱锥M﹣ABCD的体积．20．己知椭圆C：+=1（a＞b＞0）的两个焦点和短轴的两个端点都圆x2+y2=1上．（Ⅰ）求椭圆C的方程；（Ⅱ）若斜率为k的直线经过点M（2，0），且与椭圆C相交于A，B两点，摸索讨k为何值时，OA⊥OB．21．已知函数，其中k∈R且k≠0．（1）求函数f（x）的单调区间；（2）当k=1时，若存在x＞0，使1nf（x）＞ax成立，求实数a的取值范围．平面几何选讲22．已知AB为半圆O的直径，AB=4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE=1．（Ⅰ）求证：AC平分∠BAD；（Ⅱ）求BC的长．坐标系与参数方程23．已知曲线C的参数方程为（θ为参数），在同一平面直角坐标系中，将曲线C上的点按坐标变换得到曲线C′．（1）求曲线C′的一般方程；（2）若点A在曲线C′上，点B（3，0），当点A在曲线C′上运动时，求AB中点P的轨迹方程．不等式选讲24．函数f（x）=．（Ⅰ）若a=5，求函数f（x）的定义域A；（Ⅱ）设a，b∈（﹣1，1），证明：＜|1+|．2021-2022学年安徽省安庆市高三（上）摸底数学试卷（文科）一、选择题1．已知A={x|﹣2＜x＜4}，B={x|x＞3}，则A∩B=( )A．{x|﹣2＜x＜4} B．{x|x＞3} C．{x|3＜x＜4} D．{x|﹣2＜x＜3}【考点】交集及其运算．【专题】计算题．【分析】直接利用交集的概念求解．【解答】解：由A={x|﹣2＜x＜4}，B={x|x＞3}，则A∩B={x|﹣2＜x＜4}∩{x|x＞3}={x|3＜x＜4}．故选C．【点评】本题考查了交集及其运算，是基础的概念题．2．若i（x+yi）=3+4i，x，y∈R，则复数x+yi的模是( )A．2 B．3 C．4 D．5【考点】复数求模；复数相等的充要条件．【专题】数系的扩充和复数．【分析】利用复数的运算法则把i（x+yi）可化为3+4i，利用复数相等即可得出x=4，y=﹣3．再利用模的计算公式可得|x+yi|=|4﹣3i|==5．【解答】解：∵i（x+yi）=xi﹣y=3+4i，x，y∈R，∴x=4，﹣y=3，即x=4，y=﹣3．∴|x+yi|=|4﹣3i|==5．故选D．【点评】娴熟把握复数的运算法则和模的计算公式是解题的关键．3．下列函数中，在（0，+∞）上单调递减，并且是偶函数的是( )A．y=x2 B．y=﹣x3C．y=﹣lg|x| D．y=2x【考点】函数单调性的推断与证明；函数奇偶性的推断．【专题】函数的性质及应用．【分析】依据函数的奇偶性和单调性加以判定．【解答】解：四个函数中，A，C是偶函数，B是奇函数，D是非奇非偶函数，又A，y=x2在（0，+∞）内单调递增，故选：C．【点评】本题主要考查函数的奇偶性和单调性，属于基础题．4．已知{a n}各项为正的等比数列，其前n项和为Sn，若a3=4，S3=7，则公比q等于( )A ．B ．C．2 D．3【考点】等比数列的通项公式．【专题】等差数列与等比数列．【分析】利用等比数列的通项公式及其前n项和公式即可得出．【解答】解：设等比数列{a n}的公比为q＞0，由已知可得：q≠1．∵a3=4，S3=7，∴，简洁a1=1，q=2．故选：C．【点评】本题考查了等比数列的通项公式及其前n项和公式，考查了推理力量与计算力量，属于中档题．5．在样本颇率分布直方图中，共有9个小长方形，若中间一个小长方形的面积等于它8个长方形的面积和的，且样本容量为140，则中间一组的频数为( )A．28 B．40 C．56 D．60【考点】频率分布直方图．【专题】概率与统计．【分析】设中间一组的频数为x，利用中间一个小长方形的面积等于它8个长方形的面积和的，建立方程，即可求x．【解答】解：设中间一组的频数为x，由于中间一个小长方形的面积等于它8个长方形的面积和的，所以其他8组的频数和为，由x+=140，解得x=40．故选B．【点评】本题主要考查频率直方图的应用，比较基础．6．在△ABC中，sinA=，，则△ABC的面积为( )A．3 B．4 C．6 D ．【考点】平面对量数量积的运算．【专题】平面对量及应用．【分析】由题意结合数量积的运算可得，而△ABC的面积S=，代入数据计算可得．【解答】解：由题意可得，又sinA=，故可得cosA=，故=10故△ABC的面积S===3故选A【点评】本题考查平面对量的数量积的运算，涉及三角形的面积公式，属中档题．7．设a，b是平面α内两条不同的直线，l是平面α外的一条直线，则“l⊥a，l⊥b”是“l⊥α”的( )A．充要条件 B．充分而不必要的条件C．必要而不充分的条件D．既不充分也不必要的条件【考点】必要条件、充分条件与充要条件的推断．【专题】常规题型．【分析】由题意a，b是平面α内两条不同的直线，l是平面α外的一条直线，若a∥b，l与a垂直，且斜交，推不出l肯定垂直平面α，利用此对命题进行推断；【解答】解：∵a、b是平面α内两条不同的直线，l是平面α外的一条直线，“∵l⊥a，l⊥b”，若a∥b，l可以与平面α斜交，推不出l⊥α，若“l⊥α，∵a，b是平面α内两条不同的直线，l是平面α外的一条直线，∴l⊥a，l⊥b，∴“l⊥a，l⊥b”是“l⊥α”的必要而不充分的条件，故选C．【点评】此题以平面立体几何为载体，考查了线线垂直和线面垂直的判定定了，还考查了必要条件和充分条件的定义，是一道基础题．8．已知f（x）=2cos2x﹣6sinxcosx，则函数f（x）的最大值是( )A．3 B ． C ．+1 D ．﹣1【考点】两角和与差的正弦函数；二倍角的正弦；二倍角的余弦；正弦函数的定义域和值域．【专题】三角函数的图像与性质．【分析】f（x）解析式利用二倍角的正弦、余弦函数公式化简，整理后再利用两角和与差的余弦函数公式化为一个角的余弦函数，依据余弦函数的值域即可确定出最大值．【解答】解：f（x）=2cos2x﹣6sinxcosx=1+cos2x﹣3sin2x=（cos2x ﹣sin2x）+1=cos（2x+α）（其中cosα=，sinα=），∵cos（2x+α）∈[﹣1，1]，即cos（2x+α）∈[﹣，]，∴f（x ）的最大值为+1．故选C．【点评】此题考查了两角和与差的余弦函数公式，二倍角的正弦、余弦函数公式，以及余弦函数的定义域与值域，娴熟把握公式是解本题的关键．9．下列说法中正确的有（1）命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠l，则x2﹣3x+2≠0”；（2）“x＞2”是“x2﹣3x+2＞0”的充分不必要条件；（3）对于命题p：∃x∈R，x2+x+1＜0，则￢p：∀x∈R，x2+x+1≥0 （4）若P∧q为假命题，则P、q均为假命题．( )A．1个B．2个C．3个D．4个【考点】命题的真假推断与应用．【专题】简易规律．【分析】（1）由逆否命题的意义即可推断出正误；（2）由x2﹣3x+2＞0解得x＞2或x＜1，即可推断出结论；（3）由￢p的定义即可推断出正误；（4）若P∧q为假命题，则P、q至少有一个为假命题，即可推断出正误．【解答】解：（1）命题“若x2﹣3x+2=0，则x=1”，由逆否命题的意义可得：其逆否命题为“若x≠l，则x2﹣3x+2≠0”，正确；（2）由x2﹣3x+2＞0解得x＞2或x＜1，∴“x＞2”是“x2﹣3x+2＞0”的充分不必要条件，正确；（3）对于命题p：∃x∈R，x2+x+1＜0，由￢p的定义可知￢p：∀x∈R，x2+x+1≥0，正确；（4）若P∧q为假命题，则P、q至少有一个为假命题，因此不正确．综上可得：正确命题的个数为3．故选：C．【点评】本题考查了简易规律的判定方法，考查了推理力量与计算力量，属于中档题．10．一个几何体的三视图如图所示，则该几何体的表面积是( )A．4+2B．4+C．4+2D．4+【考点】由三视图求面积、体积．【专题】空间位置关系与距离．【分析】由三视图可知：该几何体是如图所示的三棱锥，其中侧面SAC⊥面ABC，△SAC，△ABC都是底边长为2，高为2的等腰三角形．据此可计算出表面积．【解答】解：由三视图可知：该几何体是如图所示的三棱锥，其中侧面SAC⊥面ABC，△SAC，△ABC都是底边长为2，高为2的等腰三角形，过D作AB的垂线交AB于E，连SE，则SE⊥AB，在直角三角形ABD中，DE==，在直角三角形SDE中，SE===，于是此几何体的表面积S=S△SAC+S△ABC+2S△SAB =×2×2+×2×2+2×××=4+2．故选A．【点评】由三视图正确恢复原几何体是解决问题的关键，属于基础题．11．已知抛物线y2=2px（p＞0）与双曲线=1（a＞0，b＞0）有相同的焦点F，点A是两曲线的一个交点，且AF⊥x轴，则双曲线的离心率为( )A ．+2B ．+1C ．+1D ．+1【考点】抛物线的简洁性质；双曲线的简洁性质．【专题】圆锥曲线的定义、性质与方程．【分析】求出抛物线与双曲线的焦点坐标，将其代入双曲线方程求出A的坐标，将A代入抛物线方程求出双曲线的三参数a，b，c的关系，则双曲线的渐近线的斜率可求．【解答】解：抛物线的焦点坐标为（，0）；双曲线的焦点坐标为（c，0），∴p=2c，∵点A 是两曲线的一个交点，且AF⊥x轴，将x=c代入双曲线方程得到A（c ，），将A 的坐标代入抛物线方程得到=2pc，即4a4+4a2b2﹣b4=0．解得，∴，解得：．故选：D．【点评】本题考查由圆锥曲线的方程求焦点坐标、考查双曲线中三参数的关系及由双曲线方程求双曲线的离心率，是中档题．12．已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=6，BC=2，则棱锥O﹣ABCD的侧面积为( )A．20+8B．44 C．20D．46【考点】球内接多面体；棱柱、棱锥、棱台的体积．【专题】计算题；空间位置关系与距离．【分析】由题意求出矩形的对角线的长，结合球的半径，球心到矩形的距离，满足勾股定理，求出棱锥的高，即可求出棱锥的体积．【解答】解：由题意可知四棱锥O﹣ABCD的侧棱长为：5．所以侧面中底面边长为6和2，它们的斜高为：4和2，所以棱锥O﹣ABCD的侧面积为：S=4×6+2=44．故选B．【点评】本题是基础题，考查球内几何体的体积的计算，考查计算力量，空间想象力量，常考题型．二、填空题13．若tan（θ+）=，则tanθ=．【考点】两角和与差的正切函数．【专题】三角函数的求值．【分析】利用两角和的正切函数公式及特殊角的三角函数值即可得解．【解答】解：∵tan（θ+）===，∴解得：tan．故答案为：．【点评】本题主要考查了两角和的正切函数公式及特殊角的三角函数值在化简求值中的应用，娴熟把握公式是解题的关键，属于基础题．14．若函数f（x）=4x﹣2x﹣a，x∈[﹣1，1]有零点，则实数a 的取值范围是．【考点】根的存在性及根的个数推断．【专题】计算题；函数的性质及应用．【分析】由题意可得方程4x﹣2x﹣a=0在[﹣1，1]上有解，从而化为求函数a=4x﹣2x=（2x ﹣）2﹣，x∈[﹣1，1]上的值域．【解答】解：∵函数f（x）=4x﹣2x﹣a，x∈[﹣1，1]有零点，∴方程4x﹣2x﹣a=0在[﹣1，1]上有解，即a=4x﹣2x=（2x ﹣）2﹣，∵x∈[﹣1，1]，∴2x∈[，2]，∴（2x ﹣）2﹣∈；故答案为：．【点评】本题考查了函数的零点与方程的根的关系应用及函数的值域的求法．15．已知程序框图如图，若a=0.62，b=30.5，c=log0.55，则输出的数是【考点】程序框图．【专题】算法和程序框图．【分析】分析程序中各变量、各语句的作用，再依据流程图所示的挨次，可知：该程序的作用是输出a，b，c 中最大的数，结合指数运算和对数运算的性质，a，b，c与1，0比较后易得到答案．【解答】解：分析程序中各变量、各语句的作用，再依据流程图所示的挨次，可知：该程序的作用是：输出a，b，c中最大的数，∵a=0.62=0.36＜1，0＜b=30.5=＞1，c=log0.55=﹣＜0，∴输出的数为．故答案为：．【点评】依据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，属于基础题．16．在边长为2的正方形ABCD中有一个不规章的图形M，用随机模拟方法来估量不规章图形的面积．若在正方形ABCD中随机产生了10000个点，落在不规章图形M内的点数恰有2000个，则在这次模拟中，不规章图形M 的面积的估量值为．【考点】模拟方法估量概率．【专题】概率与统计．【分析】先利用古典概型的概率公式求概率，再求不规章图形M的面积的估量值．【解答】解：由题意，∵在正方形ABCD中随机产生了10000个点，落在不规章图形M内的点数恰有2000个，∴概率P==，∵边长为2的正方形ABCD的面积为4，∴不规章图形M 的面积的估量值为=．故答案为：【点评】本题考查古典概型概率公式，考查同学的计算力量，属于中档题．三、解答题17．己知等差数列{a n}满足a1=1，a4=7．（Ⅰ）求数列{an}的通项公式；（Ⅱ）设c n =，数列{c n}的前n项和为T n ，证明：≤T n．【考点】数列的求和；等差数列的通项公式．【专题】等差数列与等比数列．【分析】（I）利用等差数列的通项公式即可得出；（II ），利用“裂项求和”即可证明右边；利用单调性即可证明左边．【解答】解：（I）设{a n}的公差为d，a1=1，b4=1+3d=7，∴d=2．∴a n=1+（n﹣1）×2=2n﹣1．（II ），∴，∵n∈N*，∴；，∴数列{T n}是一个递增数列，∴．综上所述，．【点评】本题考查了等差数列的通项公式、“裂项求和”、数列的单调性，考查了推理力量与计算力量，属于中档题．18．某中学作为蓝色海洋训练特色学校，随机抽取100名同学，进行一次海洋学问测试，按测试成果分组如下：第一组[65，70），其次组[70，75），第三组[75，80），第四组[80，85），第五组[85，90）（假设考试成果均在[65，90）内），得到频率分布直方图如图：（1）求测试成果在[80，85）内的频率；（2）从第三、四、五组同学中用分层抽样的方法抽取6名同学组成海洋学问宣讲小组，定期在校内进行义务宣讲，并在这6名同学中随机选取2名参与市组织的蓝色海洋训练义务宣讲队，求第四组至少有一名同学被抽中的概率．【考点】列举法计算基本大事数及大事发生的概率；频率分布直方图．【专题】概率与统计．【分析】（1）设测试成果在[80，85）内的频率为x，依据全部直方图的面积之和等于1求得x的值．（2）先求得抽取的这6名同学中，第三、四、五组同学的数量分别为3，2，1．在这6名同学中随机选取2名参与市组织的蓝色海洋训练义务宣讲队，全部的抽法共有种，而第四组至少有一名同学被抽中的抽法有•+=9种，由此求得第四组至少有一名同学被抽中的概率．【解答】解：（1）设测试成果在[80，85）内的频率为x，依据所给的频率分布直方图可得，0.01×5+0.07×5+0.06×5+x+0.02×5=1，解得x=0.2．（2）第三、四、五组同学的数量之比为0.3：0.2：0.1=3：2：1，故抽取的这6名同学中，第三、四、五组同学的数量分别为3，2，1．在这6名同学中随机选取2名参与市组织的蓝色海洋训练义务宣讲队，全部的抽法共有=15种，而第四组至少有一名同学被抽中的抽法有•+=9种，第四组至少有一名同学被抽中的概率为=．【点评】本题主要考查频率分步直方图的性质，分层抽样的定义和方法，古典概率及其计算公式，属于基础题．19．如图，在四棱锥P﹣ABCD中，底面ABCD为菱形，其中PA=PD=AD=2，∠BAD=60°，Q为AD的中点．（1）求证：AD⊥平面PQB；（2）若平面PAD⊥平面ABCD ，且，求四棱锥M﹣ABCD的体积．【考点】平面与平面垂直的性质；直线与平面垂直的判定．【专题】计算题；空间位置关系与距离．【分析】（1）连接BD，等边三角形PAD中，中线PQ⊥AD；由于菱形ABCD中∠BAD=60°，所以AD⊥BQ，最终由线面垂直的判定定理即可证出AD⊥平面PQB；（2）连接QC，作MH⊥QC于H．由于平面PAD⊥平面ABCD，PQ⊥AD，结合面面垂直性质定理证出PQ⊥平面ABCD．而平面PQC中，PQ∥MH，可得MH⊥平面ABCD，即MH就是四棱锥M﹣ABCD的高线．最终利用锥体体积公式结合题中数据即可算出四棱锥M﹣ABCD的体积．【解答】解：（1）连接BD∵PA=PD=AD=2，Q为AD的中点，∴PQ⊥AD又∵∠BAD=60°，底面ABCD为菱形，∴△ABD是等边三角形，∵Q为AD的中点，∴AD⊥BQ∵PQ、BQ是平面PQB内的相交直线，∴AD⊥平面PQB．（2）连接QC，作MH⊥QC于H．∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD=AD，PQ⊥AD∴PQ⊥平面ABCD，结合QC⊂平面ABCD，可得PQ⊥QC∵平面PQC中，MH⊥QC且PQ⊥QC，∴PQ∥MH，可得MH⊥平面ABCD，即MH就是四棱锥M﹣ABCD的高线∵，可得，∴四棱锥M﹣ABCD的体积为V M﹣ABCD ==．【点评】本题给出特殊四棱锥，求证线面垂直并求锥体体积，着重考查了直线与平面垂直的判定、平面与平面垂直的性质和体积公式等学问，属于中档题．20．己知椭圆C ：+=1（a＞b＞0）的两个焦点和短轴的两个端点都圆x2+y2=1上．（Ⅰ）求椭圆C的方程；（Ⅱ）若斜率为k的直线经过点M（2，0），且与椭圆C相交于A，B两点，摸索讨k为何值时，OA⊥OB．【考点】椭圆的简洁性质．【专题】方程思想；待定系数法；直线与圆；圆锥曲线的定义、性质与方程．【分析】（Ⅰ）由题意可得焦点为（±1，0），短轴的端点为（0，±1），可得b=c=1，求得a，进而得到椭圆方程；（II）设A（x1，y1），B（x2，y2），直线AB的方程为：y=k（x﹣2），代入椭圆方程，消去y，可得x的方程，运用韦达定理和两直线垂直的条件：斜率之积为﹣1，化简计算即可得到所求k的值．【解答】解：（I）依题意椭圆的两个焦点和短轴的两个端点都圆x2+y2=1上，可得b=1，c=1所以a2=2，所以椭圆C 的方程；；（II）设A（x1，y1），B（x2，y2），直线AB的方程为：y=k（x﹣2），由消去y得：（1+2k2）x2﹣8k2x+8k2﹣2=0，所以，由于OA⊥OB ，所以，即x1x2+y1y2=0，而，所以，所以，解得：，此时△＞0，所以．【点评】本题考查椭圆的方程的求法，考查直线方程和椭圆方程联立，运用韦达定理和两直线垂直的条件，考查运算力量，属于中档题．21．已知函数，其中k∈R且k≠0．（1）求函数f（x）的单调区间；（2）当k=1时，若存在x＞0，使1nf（x）＞ax成立，求实数a的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数争辩函数的单调性．【专题】综合题；导数的综合应用．【分析】（1）求导函数，对k争辩，利用导数的正负，可得函数的单调区间；（2）分别参数，构造新函数，g（x）=（x＞0），存在x＞0，使1nf（x）＞ax成立，等价于a＜g（x）max，由此可求实数a的取值范围．【解答】解：（1）函数的定义域为R，求导函数可得f′（x）=当k＜0时，令f′（x）＞0，可得x＜0或x＞2；令f′（x）＜0，可得0＜x＜2∴函数f（x）的单调增区间为（﹣∞，0），（2，+∞），单调减区间为（0，2）；当k＞0时，令f′（x）＜0，可得x＜0或x＞2；令f′（x）＞0，可得0＜x＜2∴函数f（x）的单调增区间为（0，2），单调减区间为（﹣∞，0），（2，+∞）；（2）当k=1时，，x＞0，1nf（x）＞ax成立，等价于a ＜设g（x）=（x＞0）存在x＞0，使1nf（x）＞ax成立，等价于a＜g（x）max，，当0＜x＜e时，g′（x）＞0；当x＞e时，g′（x）＜0∴g（x）在（0，e）上单调递增，在（e，+∞）上单调递减∴g（x）max=g（e）=∴a ＜．【点评】本题考查导数学问的运用，考查函数的单调性与最值，考查存在性问题，考查分类争辩的数学思想，属于中档题．平面几何选讲22．已知AB为半圆O的直径，AB=4，C为半圆上一点，过点C作半圆的切线CD，过点A作AD⊥CD于D，交半圆于点E，DE=1．（Ⅰ）求证：AC平分∠BAD；（Ⅱ）求BC的长．【考点】圆的切线的性质定理的证明；圆內接多边形的性质与判定．【专题】综合题．【分析】（Ⅰ）连接OC，由于OA=OC，所以∠OAC=∠OCA，再证明OC∥AD，即可证得AC平分∠BAD．（Ⅱ）由（Ⅰ）知，从而BC=CE，利用ABCE四点共圆，可得∠B=∠CED ，从而有，故可求BC的长．【解答】（Ⅰ）证明：连接OC，由于OA=OC，所以∠OAC=∠OCA，由于CD为半圆的切线，所以OC⊥CD，又由于AD⊥CD，所以OC∥AD，所以∠OCA=∠CAD，∠OAC=∠CAD，所以AC平分∠BAD．（Ⅱ）解：由（Ⅰ）知，∴BC=CE，连接CE，由于ABCE四点共圆，∠B=∠CED，所以cosB=cos∠CED，所以，所以BC=2．【点评】本题考查圆的切线，考查圆内接四边形，解题的关键是正确运用圆的切线性质及圆内接四边形的性质．坐标系与参数方程23．已知曲线C 的参数方程为（θ为参数），在同一平面直角坐标系中，将曲线C上的点按坐标变换得到曲线C′．（1）求曲线C′的一般方程；（2）若点A在曲线C′上，点B（3，0），当点A在曲线C′上运动时，求AB中点P的轨迹方程．【考点】参数方程化成一般方程．【专题】坐标系和参数方程．【分析】（1）利用坐标转移，代入参数方程，消去参数即可求曲线C′的一般方程；（2）设P（x，y），A（x0，y0），点A在曲线C′上，点B（3，0），点A在曲线C′上，列出方程组，即可求AB中点P的轨迹方程．【解答】解：（1）将代入，得C'的参数方程为∴曲线C'的一般方程为x2+y2=1．…（2）设P（x，y），A（x0，y0），又B（3，0），且AB中点为P所以有：又点A在曲线C'上，∴代入C'的一般方程得（2x﹣3）2+（2y）2=1∴动点P 的轨迹方程为．…【点评】本题考查参数方程和直角坐标的互化，利用直角坐标方程与参数方程间的关系，点到直线的距离公式的应用，考查计算力量．不等式选讲24．函数f（x）=．（Ⅰ）若a=5，求函数f（x）的定义域A；（Ⅱ）设a，b∈（﹣1，1），证明：＜|1+|．【考点】函数的定义域及其求法．【专题】函数的性质及应用；不等式的解法及应用．【分析】（Ⅰ）把a=5代入，然后由根式内部的代数式大于等于0，求解确定值的不等式得答案；（Ⅱ）把要证的不等式转化为2|a+b|＜|4+ab|，然后利用平方作差证得答案．【解答】（Ⅰ）解：由|x+1|+|x+2|﹣5≥0，得x≤﹣4或x≥1．∴A={x|x≤﹣4或x≥1}；（Ⅱ）证明：∵，而4（a+b）2﹣（4+ab）2=4（a2+2ab+b2）﹣（16+8ab+a2b2）=4a2+4b2﹣a2b2﹣16=a2（4﹣b2）+4（b2﹣4）=（b2﹣4）（4﹣a2），又∵a，b∈（﹣1，1），∴（b2﹣4）（4﹣a2）＜0，∴4（a+b）2＜（4+ab）2，故．【点评】本题考查函数的定义域及其求法，考查了确定值不等式的解法，训练了利用作差法证明不等式，是中档题．。

2012版数学一轮精品复习学案：选修系列第三部分几何证明选讲【高考目标导航】一、相似三角形的判定及有关性质1．考纲点击（1）了解平行线分线段成比例定理。

（2）会证明并应用直角三角形射影定理。

2．热点提示（1）利用平行线等分线段定理和平行级分线段成比例定理进行相关推理和计算。

（2）相似三角形的判定及有关性质，直角三角形的射影定理的应用。

二、直线与圆的位置关系1．考纲点击（1）会证明并应用圆周定理、圆的切线的判定定理及性质定理。

（2）会证明并应用相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理。

2．热点提示（1）应用圆心角、圆周角、弦切角定理说明角之间的关系。

（2）应用圆内接四边形的性质进行推理。

（3）利用圆的切线的性质和判定进行推理和证明。

（4）利用圆中的比例线段进行计算和推理。

【考纲知识梳理】一、相似三角形的判定及有关性质1．平行线等分线段定理及其推论（1）定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等。

（2）推论：①经过三角形一边的中点与另一边平行的直线必平分第三边。

②经过梯形一腰的中点，且与底边平行的直线平分另一腰。

2．平行线分线段成比例定理及推论（1）定理：三条平行线截两条直线，所得的对应线段成比例。

（2）推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例。

如图，若123////l l l ，则有：,,.AD AE AD AE DB ECAB AC DB EC AB AC=== 注：把推论中的题设和结论交换之后，命题仍然成立。

3．相似三角形的判定及性质 （1）相似三角形的定义对应角相等，对应边成比例的两个三角形叫做相似三角形，相似三角形对应边的比值叫做相似比（或相似系数）。

（2）相似三角形的判定①预备定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。

如图，若EF//BC ，则⊿AEF ∽⊿ABC 。

平面几何四讲主讲人：著名平面几何专家黄全福第一讲：值得关注的几个问题例1． 点I 为ABC ∆的内心，射线AI 、BI 、CI 交ABC ∆外接圆于'''A B C 、、，求证：'''AI BI CI I I I A B C ⋅⋅≤⋅⋅.例2． 1O 圆交2O 圆于A 、B 两点，PM 切1O 圆于M 、PN 切2O 圆于N ，若PM ＝PN ，则P 、B 、A 三点共线.例3． ABC ∆中，A 90︒∠＜，AM 为中线，过B 、C 分别作ABC ∆外接圆的切线得交点P ，求证：BAM PAC ∠∠＝，若A 90︒∠＞，本题结论有何变化？例4． 延长圆外切四边形ABCD 的AB 、DC 得交点Q ，延长AD 、BC得交点P.E 、F 、M 、N 分别是AB 、DC 、AD 、BC 上的切点.若：P 、F 、E 三点共线，则：Q 、N 、M 三点共线.例5． C D 为Rt ABC ∆斜边AB 上的高，1O 、2O 分别是D AC ∆、DBC ∆的内心，12O O 交CD 于K ，求证：111AC BC CK＋＝. 例6． 正六边形ABCDEF 边长为a ，动点M 、N 分别在BC 、DE 上，满足MAN 60︒∠＝，求证：AM AN BM DN ⋅⋅－是一个定值.例7． 1O 圆、2O 圆交于X 、Y ，它们同时与大圆O 圆内切，E 、F 为两个切点，直线XY 交O 圆于A 、B ，OP AB ⊥于P ，求证：BPE BPF ∠∠＝.例8． ABC 为锐角三角形，外心O 到三边距离之和为1d ，重心G到三边距离之和为2d ，垂心H 到三边距离之和为3d ，证明：123d d d ≥≥.例9． 锐角ABC ∆中，O 为外心，OM BC ⊥于M ，R 、r 分别为其外接圆、内切圆半径，BE 、CF 为两高，若EF ＝BF ＋CE ，则OM 为R 、r 的等差中项.例10． ABC 中，C 0︒∠＝9，O 圆为内切圆，E 、F 是AC 、BC 上的切点，射线AO 、BO 交直线EF 于N 、M.求证：S 1154OMN ABC S ∆∆<<.想想练练：1. AD 、BE 、CF 为锐角ABC ∆的三高，O 为外心，OM BC ⊥于M ，若：BF+CE ＝BC ，则1111AD BE CF OM ＋＋＝. 2. ABC ∆中，AB ＝AC ，P 在射线CB 上，E 在AB 上，PE 延长线交AC 于F ，求证：PE PF=PB PC BE CF ⋅⋅+⋅.3. CD 是Rt ABC ∆斜边AB 上的高，1O 、2O 分别是D AC ∆、D BC ∆的内心，直线12O O 交AC 、BC 于M 、N ，证明：2ABC CMN S S ∆∆≥⋅.4. PA 、PB 切圆于A 、B 两点，割线PCD 交圆于C 、D 两点，点Q 在弦CD 上，若DAQ PBC ∠∠＝，则DBQ PAC ∠∠＝.5. 两小圆相交于A 、B 两点，它们同时与大圆O 圆内切，M 、N 是两个切点，若：OA B A ⊥，则M 、B 、N 三点共线.6. H 点为锐角ABC ∆之垂心，求证：HB HC HC HA HA HB R HA HB HC⋅+⋅+⋅≤++.（式中R 为ABC ∆外接圆半径）第二讲：两种有用的证题方法甲、“四点共圆” 乙、“面积法”例1． 锐角ABC ∆的AB>BC CA >，1AA 、1BB 、1CC 是三高．以1AA 为直径的圆交AB 、AC 于E 、F 点，作2AA EF ⊥．类似地有2BB 、2CC ，求证：222BB CC AA 、、三线共点.例2． 锐角ABC ∆中，CA>C B ．以AB 为直径的圆O 交CA 、CB 于E 、F 点．EOF ∠与ECF ∠的平分线交于点S ，求证：△AES 、△BFS 外接圆的另一交点在AB 上.例3． 锐角ABC ∆中，H 为垂心．以BC 为直径作O 圆，AM 、AN 切O 圆于M 、N 点，求证：M 、H 、N 三点共线.例4． CD 为Rt ABC ∆斜边上的高，1O 圆、2O 圆分别为△ACD 、△BCD 的内切圆，两圆的另一条公切线交AC 、BC 与P 、Q 两点，求证：2CA CP CB CQ CD PQ ⋅+⋅=⋅⋅．例5． 点P 在ABC ∆内部，已知：BPC BAC ∠-∠＝CPA CBA ∠-∠＝APB ACB ∠-∠.求证：AP BC BP CA CP AB ⋅=⋅=⋅．例6． 在凸四边形ABC D 中，AC BD P =，M 、N 各是AB 、CD 的中点，当M 、P 、N 三点共线时，AB 与DC 平行吗？例7． 在凸四边形ABC D 中，延长AD 、BC 得交点P ，AC BD Q =，直线PQ 交AB 、DC 于E 、F 点，求证：PE QE PF QF=． 例8． AD 、BE 、CF 为锐角ABC ∆的三高，求证：ABC ∆的周长2DEF ≥⋅∆的周长.例9． ABC ∆为锐角三角形，证明：3cosA cosB cosC 22cos()cos()cos()B C C A A B ≤---++<.想想练练：1. ABC ∆中，BC 为大边，E 、F 两点都在BC 上，D 点在形外．已知：BE ＝BA 、CF ＝CA 、DE AB 、DF AC ，证明：ABF ∆、ACE ∆、DEF ∆的外接圆共点．2. ABC ∆中，AB ＞AC ，AD 、BE 、CF 是三条内角平分线，I 为内心．已知：AD 的中垂线交BE 、CF 于M 、N 两点，求证：I 为DMN ∆的垂心.3. 锐角ABC ∆中，AB ＞AC ，AD 是高．半圆O 与AB 、AC 相切于M 、N 点，O 在BC 上，证明：AD 、BN 、CM 三线共点.4. FBA 、FCD 是圆的两条割线，过A 、B 作圆的切线行交点P ，AC BD Q =、PQ AB E =．求证：AE AF EB FB=. 5. ABC ∆中，AB ＞AC ，AD 为中线，P 点在ADC ∆内部，满足BAD PAC ∠=∠．1O 、2O 、O 分别是ABP ∆、ACP ∆、ABC ∆的外心．求证：AO 平分1O 2O .6. 在正五边形ABCDE 中，AH CD ⊥于H 点，形内的动点P 到AB 、BC 、CD 、DE 、EA 之距离为a 、b 、c 、d 、e ．证明：a b c d e AH++++是一个定值.第三讲：分析图形特点，探索多种证法例1． ABC ∆中，I 点为内心，AB AC ≠，射线BI 、CI 交ABC ∆外接圆于''B C 、，若''BB =CC ，则IBC ∆与ABC ∆的外接圆相等． 例2． ABC ∆为锐角三角形，点H 为垂心，证明：BC CA AB BC CA AB AH BH CH AH BH CH⋅⋅++=⋅⋅. 例3． ABC ∆的AB 、BC 、CA 成等差数列，点Q 是它的旁心（在BAC∠的内部），证明：BC 平分线段AQ ．例4． ABC ∆为锐角三角形，O 点为外心，OD BC ⊥于D 、OE CA ⊥于E 、OF B A ⊥于F ， R 、r 为ABC ∆外接圆及内切圆的半径．证明：OD ＋OE ＋OF ＝R ＋r.例5． PA 、PB 切圆于A 、B ，圆的两弦AD BC=S ，射线AC 、BD交于Q 点，求证：P 、S 、Q 三点共线．例6． ⊙1O 、⊙2O 交于P 、Q ，它们同时内切于大圆⊙O ，C 、D为切点，PQ 交⊙O 于A 、B ．求证：AC BD ⋅⋅＝AD BC .例7． 锐角三角形ABC ∆中，AE 是高，AF 是内角平分线，R 、r 分别为其外接圆及内切圆半径，求证：AE AF ≥条件下，上式取等号？例8． ABC ∆为锐角三角形，a 、b 、c 为三边的长， R 为ABC ∆外接圆半径．求证：222228R <a +b +c 9R ≤.例9． O 圆半径＝R ，直线l 与O 圆相离，OA l ⊥于A 且OA ＝a ，动点P 在l 上，PC 、PD 切O 圆于C 、D ，AE C P ⊥于E 、AF PD ⊥于F ，证明：直线EF 恒过某一个定点.例10． 点P 在ABC ∆内部，PAB ∠＝PBC ∠＝PCA ∠＝θ．证明：30θ︒≤．问：当30θ︒=时，ABC 具有什么特征？想想练练：1. G 点是ABC ∆重心，若AG BG CG BC CA AB==，则：ABC 是正三角形． 2. 点P 在ABC ∆的内部，已知：ABC ∠＝BPC ∠90︒=、AB ＝BC 、PB:PC=1:2．求： S :S :S PAB PBC PCA ∆∆∆.3. I 为ABC ∆的内心，射线BI 交AC 于D ，当111I B I C I D +=时，?A ∠= 4. AD 、BE 、CF 为锐角ABC ∆之三高，H 为垂心，O 为AH 中点，EO AB=P 、BH =Q DF ，求证：PQ BC ⊥．5. ABC ∆中，AB ＝AC ，D 在BC 上．ABD ∆、ADC ∆的外心是P 、Q ．证明：S S =S S PAC QAB PBC QBC ∆∆∆∆++.6. P 为ABC ∆的内心．已知：AB 、BC 、CA 成等差数列，PB 、PA 、PC 成等比数列，问：ABC ∆具有怎样的形状特征？证明你的判断．第四讲：互逆命题的求解策略甲：“你来我往”型；乙：“殊途同归”型例1． 点P 在凸四边形ABC D 内部，已知：PBC ABD ∠=∠、PDC ADB ∠=∠，求证：A 、B 、C 、D 四点共圆的充分必要条件是PA ＝PC ．例2． ABC ∆中，A B A C ≠，G 点是重心、I 是内心，求证：3GI BC AB AC BC ⊥⇔+=⋅．例3． ABC DEF 为圆内接六边形，求证：AD 、BE 、CF 三线共点⇔AB CD EF BC DE FA ⋅⋅=⋅⋅．例4． ABC ∆中，AB AC ≠、I 为内心，M 、N 为AB 、AC 之中点，射线NI AB=P 、射线MI AC=Q ．求证：60APQ ABC A S S ︒∆∆∠=⇔= 例5． 梯形ABCD 中，DC AB 、AC =P BD ，△PAB 、△PBC 、△PCD 、△PDA 的内切圆半径分别为1r 、2r 、3r 、4r ，求证：AB ＋CD ＝AD ＋BC 12341111r r r r ⇔+=+． 例6． ABC ∆中，A B A C ≠、D 点在BC 上，求证：AD 平分BAC ∠2A D A B A C B D DC ⇔=⋅-⋅．例7． 点Q 在ABC ∆内部，证明：Q 为ABC ∆内心的充分必要条件是222a QA b QB c QC a b c ⋅+⋅+⋅=⋅⋅．例8． ABC ∆是锐角三角形，AD 、BE 、CF 是三高．求证：直线EF 平分ABC ∆面积的充分必要条件是：2222DE DF EF BC ++=．例9． ABC ∆中，D 、E 、F 三点分别在BC 、CA 、AB 上（B D D C >、CE ＞EA 、AF ＞FB ），AD 、BE 、CF 两两相交于P 、Q 、R ，求证：APE BQF CRD PQR S S S S ∆∆∆∆===的充分必要条件是D 、E 、F为各边的黄金分割点.想想练练：1. P 为ABC ∆的内心，射线AP 交ABC ∆外接圆于D 点，求证：AB 、BC 、CA 成等差数列的充分必要条件是PBC DBC S S ∆∆=．2. ABC ∆内切圆O 切AB 、AC 于E 、F ，射线BO 、CO 交直线EF于N 、M ，D 为BC 中点，求证：DMN ∆为正三角形60A ︒⇔∠=．3. 锐角三角形ABC ∆中，AD 为中线，O 为外心，H 为垂心，求证：OH AD ⊥⇔2AB 、2BC 、2CA 成等差数列.4. 锐角三角形ABC ∆中，AH 是高，AE 为内角平分线，R 、r 分别为外接圆半径、内切圆半径，证明：AB ＋AC ＝2BC ⋅AH AE ⇔= 5. 在凸四边形ABC D 中，BA ＝AD ＝DC 、AC BD ≠、AC =P BD ，求证：120ABC DCB PB PC ︒∠+∠=⇔=．6. 锐角ABC ∆中，AB ＜AC ，AD 是高，P 在形内且在AD 上．PE C A ⊥、PF B A ⊥，1O 、2O 分别是BDF ∆、CDE ∆之外心，求证：1O 、2O 、E 、F 四点共圆的充分必要条件是P 点为ABC ∆之垂心．。

焦作市高三期末考试数学试题分析一、试题评价1、关于试卷命题科学性的分析：本试题就所考查的目标来说比较合理、明确，考查内容比较准确、适度，基本符合高中数学教学大纲和高考新大纲的具体要求。

题目文字表述规范、简洁，原理设计较为合理，容量适中。

整个试题对于高中数学主要知识的覆盖比较广泛、全面，应用题及其他题型在有关材料的选取和组合上比较严谨、巧妙，较好的贯彻和体现了数学简洁、严谨、全面、细致的学科特点。

试题的设计具有一定的梯度和区分度，真正起到了检测、区分学生对有关数学知识掌握程度和数学思维能力水平的作用。

2、关于命题知识和考点的分析：从整个试题的设计来看，由于本试题仍然围绕高考应试模式进行命题与考核，所以，对于有关素质教育所提倡的教育三维目标来说，本试题还是比较注重考查学生对相关数学知识掌握和运用的熟练程度以及运用知识解决实际问题的能力，也注意到了对于有关高中数学重要方法和思想的考查，注意对学生数学思维能力的考查。

但是，对于学习研究过程的培养与体验却几乎没有涉及，在这一点上跟新课标的要求还有一定的距离。

当然，这也和近几年高考题型设计的模式、考试的方式等都有着很大的关系。

如何不仅在教学过程而且在考试中渗透、落实素质教育的三维目标仍旧是一个值得探讨和尝试的问题。

本试题的立意主要在于通过这种方式检测学生对于中学数学基本知识掌握的熟练程度和运用的灵活程度，考查的重点紧紧围绕高考的目标与要求，不仅考查学生的数学基础知识和基本技能，而且注意考查学生对于重要数学思想、方法和技巧的掌握程度，注重对学生逻辑思维能力、归纳分析能力、空间想象能力和运用知识解决实际问题能力的考查。

相关考点的分布情况也较为科学、合理。

3、对试卷题型、卷面的分析：本试题基本按照新课标高考真题题型的格式与模式进行设计，整个卷面分为客观题和主观题两部分。

其中客观题分为选择题12道，每题5分，填空题4道每题5分，共计80分。

主观题5道，每道各12分，第23题为选讲选做题，10分，理科考生可在两道题中任选一道作答，如果多选，则按所做的第一题评阅计分，文科考生只有一个选作题。

高二数学几何选讲试题答案及解析于点，过点作两1.如图，已知⊙与⊙相交于、两点，过点A作⊙的切线交⊙O2圆的割线，分别交⊙、⊙于点、，与相交于点.（1）求证：；（2）若是⊙的切线，且，，求的长．【答案】（1）证明见解析；（2）【解析】（1）圆的切线的性质定理圆的切线垂直于过切点的半径，推论1经过圆心且垂直于切线的直线必过切点，推论2经过切点且垂直于切线的直线必过圆心；（2）圆的切线的性质定理经过半径的外端并且垂直于这条半径的直径是圆的切线；若已知条件中直线与圆的公共点不明确，则应过圆心作直线的垂线，得到垂线段，设法证明这条垂线段的长等于圆的半径；（3）掌握与圆有关的比例线段，如相交弦定理，割线定理，切割线定理，切线长定理.试题解析：解：（I）∵AC是⊙O的切线，∴∠BAC＝∠D，1又∵∠BAC＝∠E，∴∠D＝∠E，∴AD∥EC. 5分（II）设BP＝x，PE＝y，∵PA＝6，PC＝2，∴＝12 ①∵AD∥EC，∴，∴②由①、②解得（∵x>0，y>0）∴DE＝9＋x＋y＝16，∵AD是⊙O的切线，∴AD2＝DB·DE＝9×16，∴AD＝12. 11分2【考点】（1）证明直线与直线平行；（2）求切线长.2.如图，在△ABC中，AB=8，AC=7，BC=6，D是AB的中点，∠ADE=∠ACB，则DE=_________．【答案】.【解析】首先由知，∽，所以.然后因为AB=8，D是AB的中点，所以.又AC=7，BC=6，所以，即.【考点】相似三角形的性质.3.如图，AC为⊙O的直径，OB⊥AC，弦BN交AC于点M．若OC=，OM=1，则MN=_________．【答案】1.【解析】因为AC为⊙O的直径，OB⊥AC，且OC=，OM=1，所以，. 设，由相交弦定理知，即，所以，即.【考点】与圆有关的比例线段.4.如图，四边形是圆的内接四边形，延长和相交于点，若，，则的值为（）A．B．C．D．【答案】B【解析】四边形是圆的内接四边形，它的两对对角互补，进而得到∽，因而有，故选择B.【考点】平面几何中的圆与四边形.5.如图在△中,∥,,交于点,则图中相似三角形的对数为( ).A．1B．2C．3D．4【答案】B【解析】,;又,,故选B.【考点】相似三角形.6.如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】（1）见解析；（2）.【解析】（1）欲证三角形全等，需牢牢掌握这种证明方法和所需要的条件.本小题,(已知)，下寻找另外的边和角，考虑到这里有圆，所以运用同弧所对应的圆周角相等可得(弧所对)，接着证明(其他角和边不好证，同时这里有弦切角可以利用).（2）欲求,因,则可转化为求,考虑到，需将联系起来就得考虑三角形相似.注意到,.试题解析：(1)证明因为XY是⊙O的切线，所以.因为，所以，∴. 2分因为，所以. 4分因为，又因为，所以. 5分(2)解因为，，所以， 7分所以，即 8分因为，，所以.所以AE. 10分【考点】（1）三角形全等的证明；（2）三角形相似的证明与应用；（3）圆性质的应用.7.如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF＝，AF∶FB∶BE＝4∶2∶1，若CE与圆相切，求线段CE的长.【答案】【解析】利用相交弦定理可得到的等量关系，并结合已知条件可计算出,利用切割线定理可得到的等量关系，并结合前面所得可得结果.试题解析：由相交弦定理得，由于，可解得，所以.由切割线定理得，即.【考点】相交弦定理，切割线定理.8.若一个直角三角形的一条直角边为3 cm，斜边上的高为2.4 cm，则这个直角三角形的面积为A．7.2 cm2B．6 cm2C．12 cm2D．24 cm2【答案】B【解析】长为3 cm的直角边在斜边上的射影为＝1.8 (cm)，故由射影定理知斜边长为＝5 (cm)，∴三角形的面积为×5×2.4＝6 (cm2)．9.如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝，点E，F分别为线段AB，AD的中点，则EF＝________.【答案】【解析】连接BD、DE，由题意可知DE⊥AB，DE＝a，即BC＝DE＝a，∴BD＝＝a，∴EF＝BD＝.10.如图所示，圆内的两条弦AB、CD相交于圆内一点P，已知PA＝PB＝4，PC＝PD.求CD 的长．【答案】10【解析】解设CD＝x，则PD＝x，PC＝x.由相交弦定理，得PA·PB＝PC·PD，∴4×4＝x·x，x＝10.∴CD＝10.11.如图所示，PA是⊙O的切线，切点为A，PA＝2.AC是⊙O的直径，PC与⊙O交于点B，PB＝1，则⊙O的半径r＝________.【答案】【解析】依题意，△PBA∽△ABC，所以＝，即r＝＝＝.12.如图所示，P、Q分别在BC和AC上，BP∶CP＝2∶5，CQ∶QA＝3∶4，则等于A．3∶14B．14∶3C．17∶3D．17∶14【答案】B【解析】过Q点作QM∥AP交BC于M，则＝＝，又∵＝，∴＝.又＝＝，＝＝，∴＝，∴＝.13.如图所示，点D、E分别在AB、AC上，下列条件能判定△ADE与△ACB相似的有①∠AED＝∠B②＝③＝④DE∥BCA．1个 B．2个 C．3个 D．4个【答案】C【解析】由判定定理1知①正确，由判定定理2知②正确，由预备定理1知④正确，③不符合相似三角形的判定定理，故不正确，从而选C.14.如图所示，在直角梯形ABCD中，AB＝7，AD＝2，BC＝3.设边AB上的一点P，使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似，那么这样的点P有A．1个 B．2个C．3个 D．4个【答案】C【解析】设AP＝x，则PB＝7－x.(1)若△PAD∽△PBC，则＝，即＝，得x＝<7，符合条件．(2)若△PAD∽△CBP，即＝，x2－7x＋6＝0，解得x1＝1，x2＝6也符合条件，故满足条件的点P 有3个．15. 在四边形ABCD 中，∠A ＝135°，∠B ＝∠D ＝90°，BC ＝2，AD ＝2，则四边形ABCD 的面积是______． 【答案】4【解析】因∠B ＝∠D ＝90°，于是设想构造直角三角形，延长BA 与CD 的延长线交于E ，则得到Rt △BCE 和Rt △ADE ，由题目条件知，△ADE 为等腰直角三角形，所以DE ＝AD ＝2，所以S △ADE ＝×2×2＝2. 又可证Rt △EBC ∽Rt △EDA ， 所以＝2＝2＝3.∴S △EBC ＝3S △EDA ，∴S 四边形ABCD ＝S △EBC －S △ADE ＝4.16. 如图所示，D 为△ABC 中BC 边上的一点，∠CAD ＝∠B ，若AD ＝6，AB ＝8，BD ＝7，求DC 的长．【答案】9【解析】解 ∵∠CAD ＝∠B ，∠C ＝∠C ， ∴△CAD ∽△CBA.∴＝＝.∴AC ＝，AC ＝.∴＝.设CD ＝x ， 则＝，解得x ＝9.故DC ＝9.17. 如图所示，已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ，且AB ＝4，DE ＝CE ＋3，则CD 的长为________．【答案】5【解析】由相交弦定理知 EA·EB ＝EC·ED. (*)又∵E 为AB 中点，AB ＝4，DE ＝CE ＋3， ∴(*)式可化为22＝EC(CE ＋3)＝CE 2＋3CE ， ∴CE ＝－4(舍去)或CE ＝1.∴CD ＝DE ＋CE ＝2CE ＋3＝2＋3＝5.18. 如图所示，已知BC 是⊙O 的弦，P 是BC 延长线上一点，PA 与⊙O 相切于点A ，∠ABC ＝25°，∠ACB＝80°，求∠P的度数．【答案】55°【解析】解因为PA与⊙O相切于点A，所以∠PAC＝∠ABP＝25°.又因为∠ACB＝80°，所以∠ACP＝100°.又因为∠PAC＋∠PCA＋∠P＝180°，所以∠P＝180°－100°－25°＝55°.19.(拓展深化)如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】(1)见解析 (2)cm【解析】(1)证明因为XY是⊙O的切线，所以∠1＝∠2.因为BD∥XY，所以∠1＝∠3，∴∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD＝∠ACD，又因为AB＝AC，所以△ABE≌△ACD.(2)解因为∠3＝∠2，∠ABC＝∠ACB，所以△BCE∽△ACB，＝，AC·CE＝BC2.因为AB＝AC＝6 cm，BC＝4 cm，所以6·(6－AE)＝16.所以AE＝cm.20.如图所示，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，以BC上一点O为圆心作⊙O与AB相切于E，与AC相切于C，又⊙O与BC的另一个交点为D，则线段BD的长为A．1B．C．D．【答案】C【解析】⊙O与AC相切于C，则∠ACB＝90°，又AC＝4，BC＝3，∴AB＝5，连接OE，且设⊙O的半径为R，则由△OEB∽△ACB，∴OB＝＝R，∴BC＝OC＋OB＝R＋R＝R＝3，∴R＝，∴BD＝BC－2R＝3－＝.21.若两条直线(a＋2)x＋(1－a)y－3＝0，(a－1)x＋(2a＋3)y＋2＝0与两坐标轴围成的四边形有一个外接圆，则实数a＝________.【答案】1或－1【解析】由圆内接四边形的性质，知(a＋2)(a－1)＋(1－a)·(2a＋3)＝0，整理得a2＝1，∴a＝±1. 22.(拓展深化)如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.(1)证明：B、D、H、E四点共圆；(2)证明：CE平分∠DEF.【答案】见解析【解析】证明(1)在△ABC中，因为∠B＝60°，所以∠BAC＋∠BCA＝120°.因为AD，CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°.于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．(2)连接BH，则BH为∠ABC的平分线，得∠HBD＝30°.由(1)知B、D、H、E四点共圆．所以∠CED＝∠HBD＝30°.又∵∠AHE＝∠EBD＝60°，由已知可得EF⊥AD，可得∠CEF＝30°，所以CE平分∠DEF.23.如图，点A、B、C是圆O上的点，且AB＝4，∠ACB＝30°，则圆O的面积等于A．4π B．8πC．12π D．16π【答案】D【解析】连接OA、OB，∵∠ACB＝30°，∴∠AOB＝60°，又∵OA＝OB，∴△AOB为等边三角形，又AB＝4，∴OA＝OB＝4，∴S＝π·42＝16π.⊙O24.在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.若BC＝m，∠B＝α，则AD的长为A．m sin2α B．m cos2αC．m sin αcos α D．m sin αtan α【答案】C【解析】由射影定理，得AB2＝BD·BC，AC2＝CD·BC，即m2cos2α＝BD·m，m2sin2α＝CD·m，即BD＝mcos2α，CD＝msin2α.又∵AD2＝BD·DC＝m2cos2αsin2α，∴AD＝mcos αsin α.故选C.25.如图，在正方形ABCD中，E为AB的中点，AF⊥DE于点O，则等于________．【答案】【解析】在Rt△DAO及Rt△DEA中，∠ADO为公共角，∴Rt△DAO∽Rt△DEA，∴＝，即＝.∵E为AB的中点，∴＝＝，∴＝.26. (拓展深化)如图，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α.且DM交AC于F，ME交BC于G，(1)写出图中三对相似三角形，并证明其中的一对；(2)连接FG，如果α＝45°，AB＝4，AF＝3，求FG的长．【答案】(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM，证明见解析 (2)【解析】解(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM.以下证明：△AMF∽△BGM.∵∠AFM＝∠DME＋∠E＝∠A＋∠E＝∠BMG，∠A＝∠B，∴△AMF∽△BGM.(2)当α＝45°时，可得AC⊥BC且AC＝BC.∵M为AB的中点，∴AM＝BM＝2.又∵△AMF∽△BGM，∴＝∴BG＝＝＝.又AC＝BC＝4×sin 45°＝4，∴CG＝4－＝.∵CF＝4－3＝1，∴FG＝＝＝.27.如图所示，已知DE∥BC，BF∶EF＝3∶2，则AC∶AE＝________，AD∶DB＝________.【答案】3∶22∶1【解析】∵DE∥BC，∴＝＝.∵BF∶EF＝3∶2，∴＝＝.∴AC∶AE＝3∶2.又DE∥BC，得AB∶AD＝3∶2，即＝.∴＝.即＝＝2，即＝2.∴AD∶BD＝2∶1.28.如图，以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED，DC的延长线交BE于点F，求证：EF＝BF.【答案】见解析【解析】证明如图所示，连接AE交DC于O.∵四边形ACED是平行四边形．∴O是AE的中点．∵在梯形ABCD中，DC∥AB，在△EAB中，OF∥AB，又∵O是AE的中点，∴F是EB的中点，∴EF＝BF.29.如图甲,四边形是等腰梯形,.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形中度数为 ( )A．B．C．D．【答案】C【解析】由于上底和两腰长已知，故要求梯形面积，关键是要找出底边上和高，由于图形中无法再分析出边与边的关系，所以我们可以从角的方向入手，求梯形的内角。