R案例分析_异方差

异方差检验案例那我就来给你讲个异方差检验的案例哈。

咱们就说有个超级好奇的经济学家，他想研究一下不同城市居民的消费和收入之间的关系。

这个经济学家啊，从各个城市收集了好多家庭的数据，比如说每个家庭的月收入，还有他们每个月的消费金额。

他就想着啊，用一个线性回归模型来看看收入和消费到底有啥联系。

于是他就开始噼里啪啦地在电脑上一顿操作，得出了一个初步的回归方程。

但是呢，这个经济学家可没那么容易就满足。

他就琢磨啊，这里面会不会有个捣蛋鬼叫异方差呢？啥是异方差呢？就好比每个城市的家庭，他们在消费这个事儿上的波动情况可能不一样，不是那种规规矩矩都一样的波动。

那他怎么去检验有没有异方差呢？他就用了怀特（White）检验。

这怀特检验啊，就像是给数据来个全面的体检。

他把各种可能影响消费和收入关系的变量都组合在一起，搞出了一些新的统计量。

比如说，他把家庭人数、城市的物价水平这些因素都考虑进去了。

然后计算这个怀特检验的统计量。

如果这个统计量的值很大很大，那就像是敲响了警钟，告诉他：“老兄，这里面很可能有异方差哦！”就像有个城市呢，是那种超大型的商业城市，里面有很多高收入人群，他们的消费可能就特别多样化。

今天去买个超级贵的限量版包包，明天又去参加个豪华游艇派对，消费的波动超级大。

而另外一个小县城呢，大家收入都差不多，消费也比较固定，就每天买买菜、偶尔添置个新衣服啥的，消费波动就小得多。

这种不同城市之间消费波动的差别，就可能导致异方差的出现。

如果这个经济学家发现真的有异方差，那他之前做的那个简单的线性回归模型可能就不太靠谱啦。

他就得想办法去调整，比如说用加权最小二乘法，给那些波动大的数据一些特殊的“照顾”，让模型更准确地反映收入和消费之间的关系。

这样呢，他就能更好地给政府出谋划策，告诉政府不同城市在消费和收入方面的真实情况，政府就能制定出更合适的经济政策啦。

怎么样，这个案例是不是还挺好理解的呀？。

例4.1.1： 在截面资料下研究居民家庭的储蓄行为 Yi=0+1Xi+i
Yi和Xi分别为第i个家庭的储蓄额和可支配收入。
在该模型中，i的同方差假定往往不符合实际情况。对高收 入家庭来说，储蓄的差异较大；低收入家庭的储蓄则更有规律 性（如为某一特定目的而储蓄），差异较小。
因此，i的方差往往随Xi的增加而增加，呈单调递增型变化 。
– 在选项中，EViews提供了包含交叉项的怀特检验“White Heteroskedasticity（cross terms）”和没有交叉项的怀特检 验“White Heteroskedasticity（no cross terms）” 这样两个 选择。
• 软件输出结果：最上方显示两个检验统计量：F统计 量和White统计量nR2；下方则显示以OLS的残差平 方为被解释变量的辅助回归方程的回归结果。
随机误差项具有不同的方差，那么： 检验异方差性，也就是检验随机误差项的方差与解
释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
路漫漫其修远兮, 吾将上下而求索
问题在于：用什么来表示随机误差项的方差？ 一般的处理方法：
路漫漫其修远兮, 吾将上下而求索
2.图示检验法
路漫漫其修远兮, 吾将上下而求索
3.模型的预测失效
一方面，由于上述后果，使得模型不具有良好的统计性质；
【书上这句话有点问题】
其中 所以，当模型出现异方差性时，Y预测区间的建立将发生困 难，它的预测功能失效。
路漫漫其修远兮, 吾将上下而求索
三、异方差性的检验（教材P111）
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值，
（注意：其中的2完全可以是1）

r语言多元回归异方差检验并处理以下是关于r语言多元回归异方差检验并处理的文章：1. 引言在统计学中，多元回归分析是一种常用的技术，用于研究自变量对因变量的影响。

然而，在实际应用中，数据可能存在异方差的问题，即误差方差与自变量之间存在相关性。

本文将介绍如何使用R语言进行多元回归异方差检验并处理。

2. 异方差的概念异方差是指在多元回归分析中，误差项的方差不是恒定的，而是与自变量之间的差异有关。

这可能导致参数估计的不准确性，从而影响对因变量的预测和解释。

3. 多元回归异方差检验在R语言中，我们可以使用许多方法来检验多元回归模型中是否存在异方差。

其中最常用的方法是利用residuals()函数来获取模型的残差，然后使用对应的统计检验方法来检验残差的异方差性。

4. 处理异方差的方法一旦检测到存在异方差，就需要采取相应的处理方法。

在R语言中，可以使用诸如加权最小二乘法（WLS）或广义最小二乘法（GLS）等方法来处理异方差。

5. 个人观点与理解对于多元回归异方差检验并处理，我个人认为这是一个非常重要的统计问题。

在实际应用中，数据往往不满足经典统计假设，因此需要我们针对具体情况进行检验和处理，以确保模型的合理性和准确性。

6. 总结通过本文的介绍，我们了解了R语言中多元回归异方差检验并处理的基本方法和步骤。

在实际应用中，我们需要仔细对待数据的异方差问题，以确保多元回归模型的有效性和稳健性。

通过以上内容，我希望你能对r语言多元回归异方差检验并处理有更深入的了解和掌握。

如果还有任何问题或需要进一步解释，请随时与我联系。

多元回归分析是一种应用广泛的统计技术，它可以用来研究多个自变量对一个因变量的影响。

然而，在实际应用中，我们常常会遇到异方差的问题，即误差项的方差不是恒定的，而是与自变量之间的差异有关。

这可能会对参数估计和模型的预测产生影响。

在R语言中，我们可以使用许多方法来检验多元回归模型中是否存在异方差。

其中最常用的方法是利用residuals()函数来获取模型的残差，然后使用对应的统计检验方法来检验残差的异方差性。

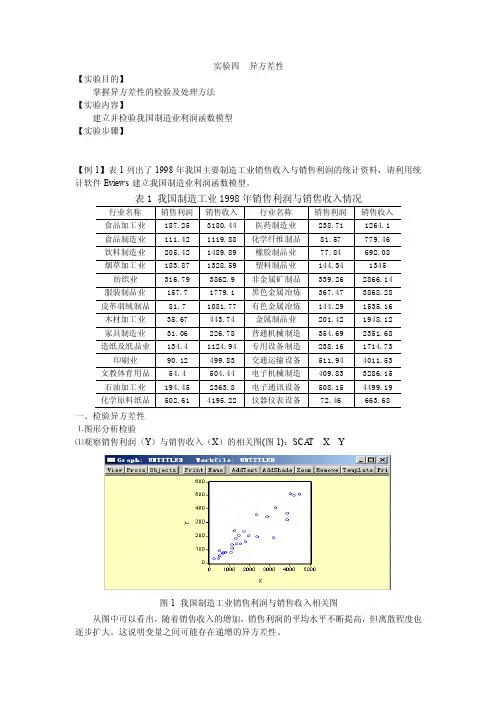
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料，请利用统计软件Eviews建立我国制造业利润函数模型。

一、检验异方差性⒈图形分析检验⑴观察销售利润（Y）与销售收入（X）的相关图(图1)：SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出，随着销售收入的增加，销售利润的平均水平不断提高，但离散程度也逐步扩大。

这说明变量之间可能存在递增的异方差性。

⑵残差分析首先将数据排序（命令格式为：SORT 解释变量），然后建立回归方程。

在方程窗口中点击Resids按钮就可以得到模型的残差分布图（或建立方程后在Eviews工作文件窗口中点击resid对象来观察）。

图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势，即表明存在异方差性。

⒉Goldfeld-Quant检验⑴将样本按解释变量排序（SORT X）并分成两部分（分别有1到10共11个样本合19到28共10个样本）⑵利用样本1建立回归模型1（回归结果如图3），其残差平方和为2579.587。

SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2（回归结果如图4），其残差平方和为63769.67。

SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量：12/RSS RSS F =＝63769.67/2579.59=24.72，21RSS RSS 和分别是模型1和模型2的残差平方和。

取05.0=α时，查F 分布表得44.3)1110,1110(05.0=----F ，而44.372.2405.0=>=F F ，所以存在异方差性⒊White 检验⑴建立回归模型：LS Y C X ，回归结果如图5。

图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。

ei 0 1 x ji i
ei 0 1x i2 i
ei 0 1 x ji i
ei 0 1 1 i x ji
对本例进行Glezser test

异方差的诊断
2、正规的检验 （2）戈德菲尔德-匡特检验（GlodfeldQuandt test） 先给原始数据进行排序，然后。。。
戈德菲尔德-匡特检验（GlodfeldQuandt test）
3/8个样本
24,000 22,000
¼ 个样本
两个回归 可以产生 两个残差 平方和
20,000 18,000
CONS
16,000 14,000 12,000
同方差时， 两个残差 平方和应 该差不多！
10,000 8,000 12,000
1,200
ABRE
800 400
0 12,000
16,000
20,000
24,000
28,000
32,000
INC
案例：用截面数据估计消费函数

直观感受：
存在异方差 （heteroskedasticity）
Homoskedasticity （同方差）
Heteroskedasticity（异方差）
异方差的诊断
2、正规的检验 （3）怀特检验：
③ 由上述辅助方程的R2构成的统计量 nR2服从X2 (p)分布，可进行卡方检验； 大于临界值时，拒绝同方差假设 当然，也可以应用F检验。
案例：纽约的租金和收入
案例：纽约的租金和收入
因变量：RENT（n=108）
变量
C Income
系数
5455.48 0.06
所以，可进行F检验。

R案例分析_异方差异方差是指在统计分析中，随着自变量的不同取值，因变量的方差也随之发生变化的现象。

异方差问题在实际数据分析中经常遇到，其存在会对统计模型的准确性和效果产生重要影响。

本文将以一个实际案例为例，分析异方差问题及其解决办法。

假设我们是一家电商公司的数据分析师，负责分析产品销售情况。

在进行销售数据分析时，我们发现在不同的销售渠道下，产品的销售量存在差异。

为了更准确地分析销售情况，我们希望解决异方差问题。

首先，我们需要通过数据分析手段来确认异方差的存在。

我们可以绘制销售量和销售渠道的散点图，观察销售量在不同渠道下的分布情况。

如果不同渠道下的散点图呈现出不同的方差大小，则可以初步判断存在异方差问题。

确定存在异方差问题后，我们需要采取措施来解决。

以下是几种常见的异方差处理方法：1.数据变换：可以通过对因变量进行一些数学变换，如开方、取对数等。

这样可以将异方差问题转化为方差齐性问题，便于后续的数据分析。

但需要注意的是，变换后的数据在解释上可能会有所改变。

2. 加权最小二乘法（Weighted Least Squares, WLS）：WLS是一种适用于异方差数据的回归分析方法。

其基本思想是根据异方差结构，对不同的观测值赋予不同的权重，从而修正回归模型的误差项。

3.方差分析（ANOVA）：如果我们可以找到一些能够解释异方差的因素，可以通过方差分析来进行处理。

对于不同的因子水平，通过统计方法比较其差异性，进而确定是否存在异方差问题。

4. 偏最小二乘回归（Partial Least Squares Regression, PLS）：PLS是一种非参数化的回归分析方法，可以在一定程度上克服异方差问题。

PLS通过找到主成分来降低变量间的相关性，从而改善模型的准确性。

在实际应用中，我们可以尝试使用上述方法中的一个或多个来解决异方差问题。

需要注意的是，不同的方法适用于不同的数据情况，选择合适的方法需要基于实际情况和数据分析的目的进行综合考虑。

异方差的例子异方差指的是在统计分析中，不同观测值的方差不相等。

这种情况下，使用传统的线性回归模型可能会导致结果的偏差和误差。

因此，为了得到更准确的结果，需要采取一些方法来处理异方差性。

下面将列举一些常见的异方差的例子，并介绍相应的处理方法。

1. 股票价格波动：股票价格的波动通常呈现出非常明显的异方差性。

在股票市场中，有些股票的价格非常波动，而有些股票的价格相对稳定。

这种情况下，可以使用加权最小二乘法来处理异方差。

2. 学生考试成绩：学生考试成绩的方差通常也会存在异方差性。

一些学生的考试成绩波动较大，而一些学生的考试成绩相对稳定。

在分析学生的考试成绩时，可以考虑使用方差齐性检验来确定是否存在异方差，并选择相应的处理方法。

3. 经济增长率：经济增长率在不同的时间段和地区通常也会呈现出异方差性。

一些地区的经济增长率波动较大，而一些地区的经济增长率相对稳定。

在分析经济增长率时，可以使用异方差稳健标准误来处理异方差。

4. 气温变化：气温在不同的季节和地区通常也会呈现出异方差性。

一些地区的气温波动较大，而一些地区的气温相对稳定。

在分析气温变化时，可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。

5. 金融市场波动：金融市场的波动性也会导致异方差的问题。

一些金融资产的价格波动较大，而一些金融资产的价格相对稳定。

在分析金融市场波动时，可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。

6. 人口增长率：人口增长率在不同的国家和地区也会呈现出异方差性。

一些国家的人口增长率波动较大，而一些国家的人口增长率相对稳定。

在分析人口增长率时，可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。

7. 网络流量：网络流量在不同的时间段和地区也会呈现出异方差性。

一些地区的网络流量波动较大，而一些地区的网络流量相对稳定。

在分析网络流量时，可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。

8. 土地价格：土地价格在不同的地区和时间段也会呈现出异方差性。

（一）残差序列分析 （二）戈德菲尔德-夸特检验 （三）戈里瑟检验 （四）怀特检验



（一）残差序列分析
(a)
e
i
X k
(b)
eห้องสมุดไป่ตู้
i
X k
(c)
e
i
X k
(d)
e
i
X k
(e)
e
i
X k
(f)
e
i
X k
（二）戈德菲尔德-夸特检验


戈德菲尔德-夸特检验是最常用的异方差专门检 验方法之一。这种方法适合于检验样本容量较大 的线性回归模型的递增或递减型异方差性。 对于存在递增异方差模型，步骤：首先将样本按 X值的大小顺序将观测值排列，然后略去居中的C 个观测值，并将其余的(n-C)个观测值分成两组， 每组(n-C)/2个，分别对两个子样本进行回归， 并分别获得残差平方和，自由度都为（n-C)/2K-1。


普遍性：两类数据都有，横截面数据更多。 原因：
1.按照边错边改学习模型，人们在学习过程中，其行为误 2 差随时间而减少。在这种情形下，方差 i 会逐渐变小。 例如，随着打字练习小时数的增加，不仅平时打错的个 数而且打错的方差都有所下降。 2.随着收入的增长，人们有更多的备用收入，从而如何支 配他们的收入有更大的选择范围。因此，在作出储蓄对 收入的回归时，很可能发现，由于人们对其储蓄行为有 更多的选择， i2 与收入俱增。因此，以增长为导向的公 司比之于已发展定型的公司在红利支付方面也可能表现 更多的变异。
（二）戈德菲尔德-夸特检验
计算统计量：
F e
i2 2 i2
2 e i1 i1

14异方差案例分析异方差（heteroscedasticity）是指随着自变量的变化，因变量的方差也发生变化的一种情况。

在统计分析中，当异方差存在时，会影响到参数估计的准确性和统计检验的可靠性，因此需要进行异方差的诊断和处理。

下面通过一个案例来分析异方差的问题。

假设有一家电子产品公司，想要研究其产品销售量与广告投入的关系。

公司从10个城市中随机选择了200家零售店作为样本，并分别统计了广告投入金额（自变量）和产品销售量（因变量）。

数据如下：店铺编号，广告投入金额（万元），产品销售量（千件）---------，-----------------，-----------------1，1.2，102，1.8，113，1.5，94，2.3，155，2.0，86，1.6，107，1.9，128，1.1，99，2.5，1610，2.2，14...，...，...200，3.4，18```pythonimport matplotlib.pyplot as pltadvertising = [1.2, 1.8, 1.5, 2.3, 2.0, 1.6, 1.9, 1.1, 2.5, 2.2, ...]sales = [10, 11, 9, 15, 8, 10, 12, 9, 16, 14, ...]plt.scatter(advertising, sales)plt.xlabel("Advertising Investment (million yuan)")plt.ylabel("Product Sales (thousand units)")plt.show```从散点图中我们可以看出，随着广告投入的增加，产品销售量并没有呈现出明显的线性增长趋势，同时也可以看到在销售量较低和高投入时，方差较大的情况。

为了进一步确定是否存在异方差的问题，我们可以进行异方差的诊断检验，最常用的方法是利用残差图。

下面克服异方差
• ⑴ 取对数 • 得两个新变量Lnyt 和Lnxt。用Lnyt 对 Lnxt 回归，得 • Lnyt = - 4.1801 + 0.9625 Lnxt . (16.9) R2 = 0.91, F = 285.6, (t = 1, …, 29)
6 LOG(Y)
1.0 RES2 0.5 0.0 -0.5
5
4
3
2 LOG(X) 5 6 7 8 9 10
-1.0 0 10 20 T 30
1
图： Ln yt和 Ln xt
图 ：残差图
经White检验也不存在异方差
ˆ u ˆ utt
• (2) 用Glejser法检验异方差 • 用 (5.18) 式, yt = -5.6610 + 0.0123 xt, 的残差的绝 对值对xt回归 ˆt u|| = 0.0024 xt (8.0) R^2 = 0.22 可见误差项的异方差形式是 Var(ut) = E(ut)^2 = （5.76×10-6） xt^2 克服异方差的方法是用xt分别除(5.18) 式两侧， 变换变量yt* = yt / xt，xt* = 1 / xt 用yt* 对xt* 回归，得： yt* = 0.0113 + 0.8239 xt* (13.8) (0.8)
300 Y
60 40 20 0
• 15000
X 20000
RES
-60 0 10 20
T 30
无论是从yt和xt观测值的散点图，还是模型的残差图都可以发现数据中存在异方 差。
• 用White方法检验是否存在异方差。在上式回归的基础上， 做White。检验输出结果中的概率是指 χ2 (2) 统计量取值 大于8.02的概率为0.018。

规律
• 一般经验告诉人们：对于采用截面数据作样本 的计量经济学问题，由于在不同样本点（即不 同空间）上解释变量以外的其他因素的差异较 大，所以往往存在异方差性。
二、异方差性的后果
1.参数估计量非有效
• 当计量经济学模型出现异方差性时，其普通最小二乘法参 数估计量仍然具有无偏性，但不具有有效性。而且，在大样 本情况下，参数估计量仍然不具有渐近有效性。
一般的处理方法：
首先采用 OLS 法估计模型，以求得随机误差项的
估计量（注意，该估计量是不严格的），我们称之为“近
似估计量”，用e~i 表示。于是有
e~ Y (Yˆ )
ii
i 0ls
Var(i ) E(i2 ) e~i2
即用e~2 来表示随机误差项的方差。
i
2.图示检验法
（1）用X-Y的散点图进行判断（李子奈P108）
怀特(White)检验的基本思想与步骤
• 下面，以二元回归为例，说明怀特检验的基本思想与步骤：
设回归模型为：
Yi 0 1X1i 2 X 2i i
首先，对该模型做普通最小二乘回归，记残差为：
e~ Y (Yˆ )
ii
i 0ls
然后，以上述残差的平方为被解释变量，以原模型中各解释
变量的水平项、平方项（还可以有更高次项）、交叉项等各
种组合为解释变量，做如下的辅助回归：
e~i2
0
1 X1i
2 X 2i
3
X
2 1i
4
X
2 2i
5 X1i X 2i
i
则在同方差性假设下【也即H0：1=…= 5=0 】，该辅助回归 方程的可决系数R2与样本容量n的乘积渐近地服从自由度=辅
助回归方程中解释变量个数【该例= 5】的2分布：

异方差性案例分析异方差性是统计学中一种常见的问题，指的是随机变量具有不同的方差或者方差不稳定的情况。

当异方差性存在时，会影响到统计模型的效果和结果的可信度。

本文将通过一个实际案例来分析异方差性的问题，并探讨如何解决这一问题。

假设我们进行了一项研究，调查了一批学生的学业成绩和上网时间的关系。

我们收集了60位学生的数据，其中包括学习时间（以小时为单位）和平均每周上网时间（以小时为单位）。

我们的研究目的是确定学生的学习时间与上网时间是否存在相关性，并且构建一个合适的回归模型来预测学生成绩。

首先，我们绘制了学习时间和上网时间的散点图，以探索两个变量之间的关系。

从散点图中，我们可以看到数据的分布情况和可能的相关性。

接下来，我们使用线性回归模型来分析学习时间和上网时间的关系。

我们假设学习时间是因变量，上网时间是自变量。

模型的形式为：学习时间=β0+β1*上网时间+ε其中，β0和β1是回归系数，ε是误差项。

我们利用最小二乘法估计出回归系数，进而得到回归模型。

然而，在进行异方差性检验时，我们发现了一个令人担忧的问题：残差的方差并不是恒定的。

简单说，残差并不是随机地围绕着回归线分布，而是变动的。

异方差性的存在会导致参数估计的不准确性，进而使统计结果产生偏差和误导性。

因此，解决异方差性问题是非常重要的。

为了解决这个问题，我们可以尝试使用加权最小二乘法，即引入一个权重系数来重新估计回归系数。

权重系数的选择与残差的方差相关，即越大的权重用于较小方差的观测值，越小的权重用于较大方差的观测值。

为了确定权重系数，我们可以进行一些统计方法的变换，例如对残差进行平方根、对数转换等。

我们还可以使用一些专门用于解决异方差性的模型，如加权最小二乘法（WLS）、广义最小二乘法（GLS）等。

在我们的案例中，我们尝试了通过对残差进行平方根转换来解决异方差性问题。

具体来说，我们计算了残差的平方根，并重新估计了回归系数。

经过尝试和比较，我们发现使用平方根转换的模型的残差方差相对于未加权的模型有了显著的改善。

第五章案例分析一、问题的提出和模型设定为了分析不同省份或城市的交通和通讯支出的规划提供依据，支配收入的关系，建立交通和通讯支出与可支配收入的回归模型。

支配收入满足线性约束，则理论模型设定为得到如下数据注：见数据文件 cumexp_income.csv利用最小二乘法估计模型(1 )的参数:mydata .lm <- lm(cumexp ~ in come) summary(mydata .Im) R 软件输出的结果为： Call:lm(formula = cumexp ~ in come) -97.465 -19.986 -5.111 15.532 184.115cum iin come i u i(1)其中cum i 表示交通和通讯支出,income i 表示可支配收入。

由1999年《中国统计年鉴》分析交通和通讯支出与可 假定交通和通讯支出与可f t . 可丸配收入 地 &t Ie宁n.尚議总江 内薫古 卅 中 北 南4009. 6] MSC 73 4112+ 41 4206. 61 421P. 42 4220.24 4240,13 4251. A2 4258. 50 4353.02 4&65+ 39 4617. 24 4770.47 4826, 36 ^852. 87159. 60137.11 231.51 172.65 bl 65 19】，76 197. 04 176.39 1S5. 7S 20«. 91 227. 2]201, &7237. lfi 2H. 37 265,朋册 河广t ；£云5000. 795084+ 64 5127,08 53S0. 085412. 24 5434.26 51G6. 57 6017, 85 6042. 78 £485.637110.54 7B36. 76 847 L 98 8773.10B839. 6Bcum212. 30270, Q9212,46 255.53 252.37255. 79 337. 83吳娠来画：中耳施计卑蓦，申M 皱计出蚤社卿参数估计Residuals:Min 1Q Median 3Q MaxI 单位=元｝*4. I丈逋釦诞iff,支出incumJi &哥jt 配收人|交遇和道酬JI 出 ”- 一卜inCoefficie nts:Estimate Std. Error t value Pr(>|t|)(In tercept) -56.91798 36.20624 -1.5720.127in come 0.058080.006488.962 1.02e-09 ***Signif. codes: 0' *** ' 0.001' ** ' 0.01'* ' 1 0.05'. ' 0.1Residual sta ndard error: 50.48 on 28 degrees of freedom Multiple R-squared: 0.7415, Adjusted R-squared: 0.7323 F-statistic: 80.32 on 1 and 28 DF, p-value: 1.021e-09估计结果为：cuifl 56.92 0.06i ncome (36.21) (0.01)R 2 0.74 s.e. 5048 F 80.32括号内为标准差。

10.5 一个更完整的例子让我们来看一个更完整的基于横殿面的异方差的例子。

20世纪70年代中期，美国能源部门试图基于各地过去的汽油消耗量和人口变动情况以及其他一些因素给各地区、各州甚至各零售点直接分配汽油。

实现这种分配必须将大量因素作为各州（各地区）的燃油消耗量(应变量)的函数而建立模型。

而对于这样的横截面模型，即使是估计的模型,也很可能会具有异方差问题。

在模型中，应变量为各州的燃油消耗量，可能的解释变量包括：与各州规模大小相关的变量（例如公路里程数、注册的机动车数量和人口），以及与各州规模大小无关的变量（例如燃油税率和最高限速）。

因为在模型中反映各州规模大小的变量不应多于一个（如果包含过多变量容易导致多重共线性），因为有许多州的最高限速相同（但在时间序列模型中，它将是一个有用的变量）。

因此，一个合理的模型为：012(,)i i i i i PCON f REG TAX REG TAX εβββε+-=+=+++ （10-20）式中 i PCON ——第i 个州的燃油消耗量（百万BTU ）， i REG ——第i 个州的注册机动车数量（千辆）， i TAX ——第i 个州的燃油税率（美分/加仑）， i ε——经典误差项。

我们可以认为一个州注册的汽车数量越多，该州所消耗的燃油也越多；而一个州的燃油税率越高则该州的燃油消耗量越小1。

我们搜集那一时期的数据（见表10-1）用于估计方程（10-20），得到：i i i TAX REG PCON 59.531861.07.551-+=∧（10-21）（0.0117） （16.86）15.88t = 3.18-20.861R =50N =表10-1 燃油消费例子中的数据PCON UHM TAX REG POP e state270 2.2 9 743 1136 62.335 Maine 122 2.4 14 774 948 176.52 New Hampshire58 0.7 11 351 520 30.481 Vermont 82120.69.937505750101.87Massachusetts1在方程中我们也可用*TAX REG 或者*TAX PO P （iPOP 代表第i 个州的人口）取代TAX 作为方程的解释变量。

r语言残差项标准误异方差R语言是一种用于统计分析和数据可视化的编程语言，它具有强大的数据处理能力和丰富的统计函数库。

在进行数据分析和回归分析时，我们经常需要评估残差项的标准误以及处理异方差的方法，这对于确保分析结果的准确性和可靠性至关重要。

在回归分析中，残差项扮演着至关重要的角色。

它表示了因变量的实际观测值与回归方程所估计的值之间的差异，即误差项。

残差项的标准误是衡量残差项变异程度的指标，它能够帮助我们评估回归模型对数据的拟合程度，从而判断模型是否足够准确。

在R语言中，我们可以使用相关函数来计算残差项的标准误，并据此对回归模型进行评估和比较。

然而，在实际的数据分析中，我们常常会面临异方差的问题。

异方差指的是因变量的方差在自变量的不同取值下不相等，这可能会导致回归分析中的标准误估计不准确，进而影响参数估计的显著性和置信区间的准确性。

针对异方差问题，我们需要采取相应的处理方法，如异方差稳健标准误的计算、加权最小二乘回归等，以确保回归分析结果的稳健性和可靠性。

从简到繁，我们可以先从残差项的基本概念和计算方法开始，逐步深入讨论残差项标准误的意义和计算方式。

我们可以介绍异方差的概念及其对回归分析的影响，进而探讨处理异方差的常见方法和在R语言中的实现。

通过这种逐步深入的方式，我能更好地理解残差项标准误和异方差的重要性以及在实际数据分析中的应用。

总结回顾：残差项标准误和异方差是回归分析中至关重要的概念和问题。

准确评估残差项的标准误和处理异方差对于确保回归模型的准确性和稳健性至关重要。

在使用R语言进行数据分析时，我们可以充分利用其强大的统计函数库和数据处理能力，对残差项的标准误进行评估和处理异方差，从而得到可靠的回归分析结果。

个人观点：在实际的数据分析工作中，残差项标准误和异方差问题常常会遇到，对于数据分析工作者来说，掌握如何正确评估残差项的标准误并处理异方差是非常重要的。

R语言作为一种功能强大的统计分析工具，为我们提供了丰富的函数库和工具，能够帮助我们有效地处理残差项标准误和异方差问题，从而确保我们的数据分析结果的准确性和可靠性。

r语言异方差检验方法
在R语言中，进行异方差检验可以使用lmtest包中的函数het.test()。

具体步骤如下：
1. 导入数据并建立线性回归模型。

例如，使用以下代码建立回归模型：
r
model <- lm(y ~ x1 + x2, data = mydata)
其中，y表示因变量，x1和x2表示自变量，mydata表示数据集。

2. 安装和导入lmtest包。

使用以下代码安装lmtest包：
r
install.packages("lmtest")
使用以下代码导入lmtest包：
r
library(lmtest)
3. 进行异方差检验。

使用以下代码进行异方差检验：
r
het.test(model)
其中，model为前面建立的回归模型。

执行以上代码后，会输出检验结果。

4. 解读异方差检验结果。

异方差检验输出结果包括三个统计量：LM统计量、LM对数似然比统计量和LM 方差比统计量。

如果LM统计量的p值小于0.05，则说明存在异方差。

通过上述步骤，就可以在R语言中进行异方差检验了。

第二章：异方差及其处理
单击此处添加副标题
案例：用截面数据估计消费函数
上机实验：利用31个省市自治区的人均收入与人均消费数据估计消费函数。 Consumption = 0.7042*Income t=(83.0652) R2=0.9289
案例：用截面数据估计消费函数
观察残差图（取残差绝对值）：
案例：用截面数据估计消费函数
-1.58
Income
1200.58
2.42
Income2
-0.01
-1.87
案例：纽约的租金和收入
怀特统计量=108*0.082=8.87， 自由度为2的卡方统计量=5.99 拒绝“没有异方差”的原假设！
案例：纽约的租金和收入
点点滴滴：
EVIEWS设计的一个缺陷：
如果在进行怀特检验时，选择“不包括交叉项”； 如果你的原始回归本身不带常数项； 在上述两种情况下，white检验的辅助回归方程中都不会出现“解释变量的水平值”，只有其平方项。
异方差的诊断
正规的检验 戈里瑟检验(Glezser test) ： 回归的形式通常为如下几种：
对本例进行Glezser test
异方差的诊断
2、正规的检验
戈德菲尔德-匡特检验（Glodfeld- Quandt test） 先给原始数据进行排序，然后。。。
¼个样本
3/8个样本
两个回归可以产生两个残差平方和
估计消费函数时，对异方差的处理
i
i
异方差的处理
可行的广义最小二乘（Feasible GLS） 但通常di与Xi之间的关系并不能确定！ 假设： 那么h就是一个未知数！ 如何知道h的大小呢？
v
a
r
(
e