异方差案例分析
- 格式:doc
- 大小:366.00 KB
- 文档页数:11
异方差案例分析中国农村居民人均消费支出主要由人均纯收入来决定.农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入等。
为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,可使用如下双对数模型:1122ln ln ln Y X X βββμ0=+++其中,Y 表示农村家庭人均消费支出,X 1表示从事农业经营的收入,X 2表示其他收入。
下表列出了中国2001年各地区农村居民家庭人均纯收入及消费支出的相关数据。
中国2001年各地区农村居民家庭人均纯收入与消费支出安徽 1412.4 1013。
1 1006。
9 甘肃 1127.37 621。
6 887 福建 2503。
11053 2327。
7 青海 1330。
45 803.8 753。
5 江西 1720 1027。
8 1203。
8 宁夏 1388。
79 859.6 963.4 山东 19051293 1511。
6 新疆1350.231300.1410。
3河南1375.6 1083。
8 1014。
1资料来源:《中国农村住户调查年鉴》(2002)、《中国统计年鉴》(2002)。
我们不妨假设该线性回归模型满足基本假定,采用OLS 估计法,估计结果如下:12ˆln 1.6550.3166ln 0.5084ln YX X =++ (1。
87) (3。
02) (10.04)R 2=0.7831 R 2=0.7676 D 。
W 。
=1。
89 F=50。
53 RSS=0。
8232图1估计结果显示,其他收入而不是从事农业经营的收入的增长,对农户消费支出的增长更具有刺激作用.下面对该模型进行异方差性检验。
1.图示法。
首先做出Y与X1、X2的散点图,如下:图2X基本在其均值附近上下波动,而2X散点存在较为可见1明显的增大趋势.再做残差平方项2ˆi e与1ln X的散点图:ln X、2图3图4可见图1中离群点相对较少而图2呈现较为明显的单调递增的异方差性.故初步判断异方差性主要是2X引起的.2。



R案例分析_异方差异方差是指在统计分析中,随着自变量的不同取值,因变量的方差也随之发生变化的现象。
异方差问题在实际数据分析中经常遇到,其存在会对统计模型的准确性和效果产生重要影响。
本文将以一个实际案例为例,分析异方差问题及其解决办法。
假设我们是一家电商公司的数据分析师,负责分析产品销售情况。
在进行销售数据分析时,我们发现在不同的销售渠道下,产品的销售量存在差异。
为了更准确地分析销售情况,我们希望解决异方差问题。
首先,我们需要通过数据分析手段来确认异方差的存在。
我们可以绘制销售量和销售渠道的散点图,观察销售量在不同渠道下的分布情况。
如果不同渠道下的散点图呈现出不同的方差大小,则可以初步判断存在异方差问题。
确定存在异方差问题后,我们需要采取措施来解决。
以下是几种常见的异方差处理方法:1.数据变换:可以通过对因变量进行一些数学变换,如开方、取对数等。
这样可以将异方差问题转化为方差齐性问题,便于后续的数据分析。
但需要注意的是,变换后的数据在解释上可能会有所改变。
2. 加权最小二乘法(Weighted Least Squares, WLS):WLS是一种适用于异方差数据的回归分析方法。
其基本思想是根据异方差结构,对不同的观测值赋予不同的权重,从而修正回归模型的误差项。
3.方差分析(ANOVA):如果我们可以找到一些能够解释异方差的因素,可以通过方差分析来进行处理。
对于不同的因子水平,通过统计方法比较其差异性,进而确定是否存在异方差问题。
4. 偏最小二乘回归(Partial Least Squares Regression, PLS):PLS是一种非参数化的回归分析方法,可以在一定程度上克服异方差问题。
PLS通过找到主成分来降低变量间的相关性,从而改善模型的准确性。
在实际应用中,我们可以尝试使用上述方法中的一个或多个来解决异方差问题。
需要注意的是,不同的方法适用于不同的数据情况,选择合适的方法需要基于实际情况和数据分析的目的进行综合考虑。

异方差的例子异方差指的是在统计分析中,不同观测值的方差不相等。
这种情况下,使用传统的线性回归模型可能会导致结果的偏差和误差。
因此,为了得到更准确的结果,需要采取一些方法来处理异方差性。
下面将列举一些常见的异方差的例子,并介绍相应的处理方法。
1. 股票价格波动:股票价格的波动通常呈现出非常明显的异方差性。
在股票市场中,有些股票的价格非常波动,而有些股票的价格相对稳定。
这种情况下,可以使用加权最小二乘法来处理异方差。
2. 学生考试成绩:学生考试成绩的方差通常也会存在异方差性。
一些学生的考试成绩波动较大,而一些学生的考试成绩相对稳定。
在分析学生的考试成绩时,可以考虑使用方差齐性检验来确定是否存在异方差,并选择相应的处理方法。
3. 经济增长率:经济增长率在不同的时间段和地区通常也会呈现出异方差性。
一些地区的经济增长率波动较大,而一些地区的经济增长率相对稳定。
在分析经济增长率时,可以使用异方差稳健标准误来处理异方差。
4. 气温变化:气温在不同的季节和地区通常也会呈现出异方差性。
一些地区的气温波动较大,而一些地区的气温相对稳定。
在分析气温变化时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
5. 金融市场波动:金融市场的波动性也会导致异方差的问题。
一些金融资产的价格波动较大,而一些金融资产的价格相对稳定。
在分析金融市场波动时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
6. 人口增长率:人口增长率在不同的国家和地区也会呈现出异方差性。
一些国家的人口增长率波动较大,而一些国家的人口增长率相对稳定。
在分析人口增长率时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
7. 网络流量:网络流量在不同的时间段和地区也会呈现出异方差性。
一些地区的网络流量波动较大,而一些地区的网络流量相对稳定。
在分析网络流量时,可以使用加权最小二乘法或者异方差稳健标准误来处理异方差。
8. 土地价格:土地价格在不同的地区和时间段也会呈现出异方差性。

异方差实验报告异方差实验报告引言在统计学中,方差是一种衡量数据分布离散程度的重要指标。
然而,在实际应用中,我们常常会遇到方差不稳定的情况,即异方差。
异方差的存在会对统计分析结果产生显著影响,因此,我们需要探索异方差的原因和解决方法。
本实验旨在通过模拟数据和实际案例来探讨异方差的现象、原因和处理方法。
一、异方差现象的模拟实验为了更好地理解异方差的现象,我们首先进行了一系列的模拟实验。
我们生成了两组数据,一组是服从正态分布的数据,另一组是服从泊松分布的数据。
然后,我们分别对两组数据进行方差分析,并比较其结果。
实验结果显示,当数据服从正态分布时,方差分析的结果较为稳定,各组之间的方差差异不大。
然而,当数据服从泊松分布时,方差分析的结果却出现了明显的差异。
这说明泊松分布的数据具有异方差性质。
二、异方差的原因分析为了深入理解异方差的原因,我们进一步探究了几个可能导致异方差的因素。
1. 数据的变换我们对泊松分布的数据进行了对数变换,然后再进行方差分析。
实验结果显示,经过对数变换后,数据的异方差性质得到了明显改善。
这说明,数据的变换可以在一定程度上解决异方差问题。
2. 数据的离散程度我们生成了两组服从正态分布的数据,一组具有较小的离散程度,另一组具有较大的离散程度。
实验结果显示,离散程度较大的数据组具有更明显的异方差性质。
这表明,数据的离散程度与异方差之间存在一定的关联。
3. 样本容量我们通过不断调整样本容量,观察方差分析结果的变化。
实验结果显示,随着样本容量的增加,方差分析结果的稳定性得到了明显改善。
这说明,样本容量的大小对异方差的影响是显著的。
三、处理异方差的方法针对异方差问题,统计学家们提出了多种处理方法。
以下是一些常见的方法:1. 方差齐性检验在进行统计分析之前,我们可以先对数据进行方差齐性检验。
常用的方差齐性检验方法包括Levene检验和Bartlett检验。
如果检验结果表明数据存在异方差,我们可以采取相应的处理方法。

14异方差案例分析异方差(heteroscedasticity)是指随着自变量的变化,因变量的方差也发生变化的一种情况。
在统计分析中,当异方差存在时,会影响到参数估计的准确性和统计检验的可靠性,因此需要进行异方差的诊断和处理。
下面通过一个案例来分析异方差的问题。
假设有一家电子产品公司,想要研究其产品销售量与广告投入的关系。
公司从10个城市中随机选择了200家零售店作为样本,并分别统计了广告投入金额(自变量)和产品销售量(因变量)。
数据如下:店铺编号,广告投入金额(万元),产品销售量(千件)---------,-----------------,-----------------1,1.2,102,1.8,113,1.5,94,2.3,155,2.0,86,1.6,107,1.9,128,1.1,99,2.5,1610,2.2,14...,...,...200,3.4,18```pythonimport matplotlib.pyplot as pltadvertising = [1.2, 1.8, 1.5, 2.3, 2.0, 1.6, 1.9, 1.1, 2.5, 2.2, ...]sales = [10, 11, 9, 15, 8, 10, 12, 9, 16, 14, ...]plt.scatter(advertising, sales)plt.xlabel("Advertising Investment (million yuan)")plt.ylabel("Product Sales (thousand units)")plt.show```从散点图中我们可以看出,随着广告投入的增加,产品销售量并没有呈现出明显的线性增长趋势,同时也可以看到在销售量较低和高投入时,方差较大的情况。
为了进一步确定是否存在异方差的问题,我们可以进行异方差的诊断检验,最常用的方法是利用残差图。

stata沃尔德组间异方差检验下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!Stata沃尔德组间异方差检验简介Stata是一种统计分析软件,被广泛应用于各种研究领域。

第五章 案例分析一、问题的提出和模型设定根据本章引子提出的问题,为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
假定医疗机构数与人口数之间满足线性约束,则理论模型设定为i i i u X Y ++=21ββ (5.31)其中i Y 表示卫生医疗机构数,i X 表示人口数。
由2001年《四川统计年鉴》得到如下数据。
表5.1 四川省2000年各地区医疗机构数与人口数地区人口数(万人) X医疗机构数(个)Y地区人口数(万人) X医疗机构数(个)Y成都 1013.3 6304 眉山 339.9 827 自贡 315 911 宜宾 508.5 1530 攀枝花 103 934 广安 438.6 1589 泸州 463.7 1297 达州 620.1 2403 德阳 379.3 1085 雅安 149.8 866 绵阳 518.4 1616 巴中 346.7 1223 广元 302.6 1021 资阳 488.4 1361 遂宁 371 1375 阿坝 82.9 536 内江 419.9 1212 甘孜 88.9 594 乐山345.91132 凉山 402.41471 南充 709.24064二、参数估计进入EViews 软件包,确定时间范围;编辑输入数据;选择估计方程菜单,估计样本回归函数如下表5.2估计结果为56.69,2665.508..,7855.0)3403.8()9311.1(3735.50548.563ˆ2===-+-=F e s R X Y ii (5.32) 括号内为t 统计量值。
三、检验模型的异方差本例用的是四川省2000年各地市州的医疗机构数和人口数,由于地区之间存在的不同人口数,因此,对各种医疗机构的设置数量会存在不同的需求,这种差异使得模型很容易产生异方差,从而影响模型的估计和运用。
为此,必须对该模型是否存在异方差进行检验。

异方差性案例分析异方差性是统计学中一种常见的问题,指的是随机变量具有不同的方差或者方差不稳定的情况。
当异方差性存在时,会影响到统计模型的效果和结果的可信度。
本文将通过一个实际案例来分析异方差性的问题,并探讨如何解决这一问题。
假设我们进行了一项研究,调查了一批学生的学业成绩和上网时间的关系。
我们收集了60位学生的数据,其中包括学习时间(以小时为单位)和平均每周上网时间(以小时为单位)。
我们的研究目的是确定学生的学习时间与上网时间是否存在相关性,并且构建一个合适的回归模型来预测学生成绩。
首先,我们绘制了学习时间和上网时间的散点图,以探索两个变量之间的关系。
从散点图中,我们可以看到数据的分布情况和可能的相关性。
接下来,我们使用线性回归模型来分析学习时间和上网时间的关系。
我们假设学习时间是因变量,上网时间是自变量。
模型的形式为:学习时间=β0+β1*上网时间+ε其中,β0和β1是回归系数,ε是误差项。
我们利用最小二乘法估计出回归系数,进而得到回归模型。
然而,在进行异方差性检验时,我们发现了一个令人担忧的问题:残差的方差并不是恒定的。
简单说,残差并不是随机地围绕着回归线分布,而是变动的。
异方差性的存在会导致参数估计的不准确性,进而使统计结果产生偏差和误导性。
因此,解决异方差性问题是非常重要的。
为了解决这个问题,我们可以尝试使用加权最小二乘法,即引入一个权重系数来重新估计回归系数。
权重系数的选择与残差的方差相关,即越大的权重用于较小方差的观测值,越小的权重用于较大方差的观测值。
为了确定权重系数,我们可以进行一些统计方法的变换,例如对残差进行平方根、对数转换等。
我们还可以使用一些专门用于解决异方差性的模型,如加权最小二乘法(WLS)、广义最小二乘法(GLS)等。
在我们的案例中,我们尝试了通过对残差进行平方根转换来解决异方差性问题。
具体来说,我们计算了残差的平方根,并重新估计了回归系数。
经过尝试和比较,我们发现使用平方根转换的模型的残差方差相对于未加权的模型有了显著的改善。

第五章案例分析一、问题的提出和模型设定为了分析不同省份或城市的交通和通讯支出的规划提供依据,支配收入的关系,建立交通和通讯支出与可支配收入的回归模型。
支配收入满足线性约束,则理论模型设定为得到如下数据注:见数据文件 cumexp_income.csv利用最小二乘法估计模型(1 )的参数:mydata .lm <- lm(cumexp ~ in come) summary(mydata .Im) R 软件输出的结果为: Call:lm(formula = cumexp ~ in come) -97.465 -19.986 -5.111 15.532 184.115cum iin come i u i(1)其中cum i 表示交通和通讯支出,income i 表示可支配收入。
由1999年《中国统计年鉴》分析交通和通讯支出与可 假定交通和通讯支出与可f t . 可丸配收入 地 &t Ie宁n.尚議总江 内薫古 卅 中 北 南4009. 6] MSC 73 4112+ 41 4206. 61 421P. 42 4220.24 4240,13 4251. A2 4258. 50 4353.02 4&65+ 39 4617. 24 4770.47 4826, 36 ^852. 87159. 60137.11 231.51 172.65 bl 65 19】,76 197. 04 176.39 1S5. 7S 20«. 91 227. 2]201, &7237. lfi 2H. 37 265,朋册 河广t ;£云5000. 795084+ 64 5127,08 53S0. 085412. 24 5434.26 51G6. 57 6017, 85 6042. 78 £485.637110.54 7B36. 76 847 L 98 8773.10B839. 6Bcum212. 30270, Q9212,46 255.53 252.37255. 79 337. 83吳娠来画:中耳施计卑蓦,申M 皱计出蚤社卿参数估计Residuals:Min 1Q Median 3Q MaxI 单位=元}*4. I丈逋釦诞iff,支出incumJi &哥jt 配收人|交遇和道酬JI 出 ”- 一卜inCoefficie nts:Estimate Std. Error t value Pr(>|t|)(In tercept) -56.91798 36.20624 -1.5720.127in come 0.058080.006488.962 1.02e-09 ***Signif. codes: 0' *** ' 0.001' ** ' 0.01'* ' 1 0.05'. ' 0.1Residual sta ndard error: 50.48 on 28 degrees of freedom Multiple R-squared: 0.7415, Adjusted R-squared: 0.7323 F-statistic: 80.32 on 1 and 28 DF, p-value: 1.021e-09估计结果为:cuifl 56.92 0.06i ncome (36.21) (0.01)R 2 0.74 s.e. 5048 F 80.32括号内为标准差。
10.5 一个更完整的例子让我们来看一个更完整的基于横殿面的异方差的例子。
20世纪70年代中期,美国能源部门试图基于各地过去的汽油消耗量和人口变动情况以及其他一些因素给各地区、各州甚至各零售点直接分配汽油。
实现这种分配必须将大量因素作为各州(各地区)的燃油消耗量(应变量)的函数而建立模型。
而对于这样的横截面模型,即使是估计的模型,也很可能会具有异方差问题。
在模型中,应变量为各州的燃油消耗量,可能的解释变量包括:与各州规模大小相关的变量(例如公路里程数、注册的机动车数量和人口),以及与各州规模大小无关的变量(例如燃油税率和最高限速)。
因为在模型中反映各州规模大小的变量不应多于一个(如果包含过多变量容易导致多重共线性),因为有许多州的最高限速相同(但在时间序列模型中,它将是一个有用的变量)。
因此,一个合理的模型为:012(,)i i i i i PCON f REG TAX REG TAX εβββε+-=+=+++ (10-20)式中 i PCON ——第i 个州的燃油消耗量(百万BTU ), i REG ——第i 个州的注册机动车数量(千辆), i TAX ——第i 个州的燃油税率(美分/加仑), i ε——经典误差项。
我们可以认为一个州注册的汽车数量越多,该州所消耗的燃油也越多;而一个州的燃油税率越高则该州的燃油消耗量越小1。
我们搜集那一时期的数据(见表10-1)用于估计方程(10-20),得到:i i i TAX REG PCON 59.531861.07.551-+=∧(10-21)(0.0117) (16.86)15.88t = 3.18-20.861R =50N =表10-1 燃油消费例子中的数据PCON UHM TAX REG POP e state270 2.2 9 743 1136 62.335 Maine 122 2.4 14 774 948 176.52 New Hampshire58 0.7 11 351 520 30.481 Vermont 82120.69.937505750101.87Massachusetts1在方程中我们也可用*TAX REG 或者*TAX PO P (iPOP 代表第i 个州的人口)取代TAX 作为方程的解释变量。
固定效应模型异方差stata固定效应模型是一种常用的面板数据模型,它可以帮助研究人员解决面板数据中可能存在的异方差问题。
本文将介绍固定效应模型的基本原理和在STATA软件中的实现方法,并通过一个案例来说明如何应用固定效应模型来处理异方差问题。
1. 引言面板数据是指在时间上观察同一组个体的多次观测数据,它具有一定的时间维度和个体维度。
在面板数据中,个体间可能存在着不同的特征和差异,而时间序列之间也可能存在异方差问题。
异方差是指方差不恒定的现象,即在不同时间点,方差的大小存在差异。
在面板数据分析中,异方差的存在可能会影响模型的稳健性和效率性。
固定效应模型可以有效地解决异方差问题,因此在面板数据分析中得到了广泛应用。
2. 固定效应模型的基本原理固定效应模型通过引入个体固定效应来控制个体间的差异,从而消除由于异方差引起的估计偏误。
在固定效应模型中,个体固定效应被视为未被观测到的个体特征,与解释变量无关。
因此,个体固定效应可以被视为一个捕捉个体特征的虚拟变量,并通过引入虚拟变量进行估计。
3. STATA中固定效应模型的实现方法在STATA软件中,可以通过面板数据命令xtreg来实现固定效应模型的估计。
在估计固定效应模型之前,首先需要将面板数据进行排序和标识个体,然后将数据转化为面板数据形式。
接下来,利用xtreg命令进行模型的估计。
在xtreg命令中,可以通过选项fe来指定固定效应模型的估计,即引入个体固定效应。
4. 案例分析为了说明固定效应模型在处理异方差问题中的应用,假设有一个研究关于企业绩效的面板数据集。
数据集包括100家企业在10年内的绩效指标和影响绩效的解释变量。
首先,我们可以通过描述性统计分析来观察面板数据的特征和异方差现象。
然后,我们可以利用固定效应模型来研究解释变量对企业绩效的影响,同时控制个体固定效应。
最后,我们可以利用固定效应模型的估计结果来检验异方差是否还存在,并评估模型的拟合度和有效性。
目录案例引入 (2)数据分析 (4)建立多元线性模型及检验 (5)经济检验: (6)统计检验 (6)异方差检验 (7)异方差修正 (12)结果解释 (13)一、案例引入随着国内生产生产总值和城乡居民可支配收入的不断增长,使得人们的收入成倍增长,无论微观经济理论还是人们的感受,收入的增加能够满足人们的更多需求,从而是人们对生活状况的满意程度增加,即提升主观幸福感,增加生命质量得分。
同时,研究结果现实收入较低人群的生命质量得分均较低且与其他组间差异大。
随着收入的增加,生命质量有提升的趋势。
而在社会五大保险之中,只有医保与我们的生命息息相关,堪称社保之中的重中之重,医保的价值让我们的健康得到了保证。
数据(表1)为我们研究收入水平与医保对生命预期的影响提供了重要数据基础。
我们选择58国收入、医保、生命预期这3个变量的相关数据作为样本,进行研究。
观察值生命预期收入医保观察值生命预期收入医保1 71.8 2046 81 44 74.7 13410 1002 60.2 686 74 45 55.6 884 413 76.4 14862 100 46 77.4 14784 1004 75.9 11760 100 47 64.7 360 805 73.2 7944 100 48 45.0 150 306 49.8 296 18 49 46.8 230 497 51.6 3288 90 50 73.7 5842 1008 50.3 156 45 51 62.5 784 849 52.6 482 64 52 54.3 330 7310 64.5 1456 76 53 75.1 17714 10011 52.6 324 75 54 66.7 1322 10012 62.8 462 89 55 52.2 292 6113 50.3 292 56 56 49.5 306 4514 75.7 11924 100 57 77.7 14280 10015 48.0 294 28 58 49.3 360 5116 48.3 244 61 59 65.2 1124 6417 63.2 2560 90 60 47.5 472 4018 55.0 392 80 61 65.6 804 8019 66.8 1094 63 62 47.7 13730 10020 66.3 1038 89 63 46.7 186 1521 52.6 248 81 64 61.4 1056 3422 67.9 7794 100 65 51.5 270 2623 72.3 994 90 66 76.6 16192 10024 59.3 522 80 67 47.4 166 4925 53.6 384 61 68 70.4 2328 7226 70.7 4956 99 69 54.3 342 5527 74.6 13408 100 70 74.5 10490 10028 71.3 1974 100 71 76.8 19782 10029 62.1 3954 80 72 64.6 862 7030 45.5 420 30 73 65.1 1180 9131 44.0 252 43 74 60.9 604 7232 71.4 1472 97 75 70.1 396 9333 52.0 744 31 76 69.0 2736 9434 63.5 780 74 77 70.1 2142 10035 70.4 19182 90 78 74.4 1506 8036 74.7 11076 100 79 76.9 14472 10037 60.8 1078 75 80 72.9 15506 10038 52.2 980 81 81 68.0 1246 6039 74.1 16624 100 82 76.6 11060 10040 75.0 9898 100 83 46.5 160 2841 71.8 2036 82 84 61.0 862 5842 76.5 9532 100 85 50.1 638 4643 70.8 2366 100 ————数据来源:老师提供数据无需处理。
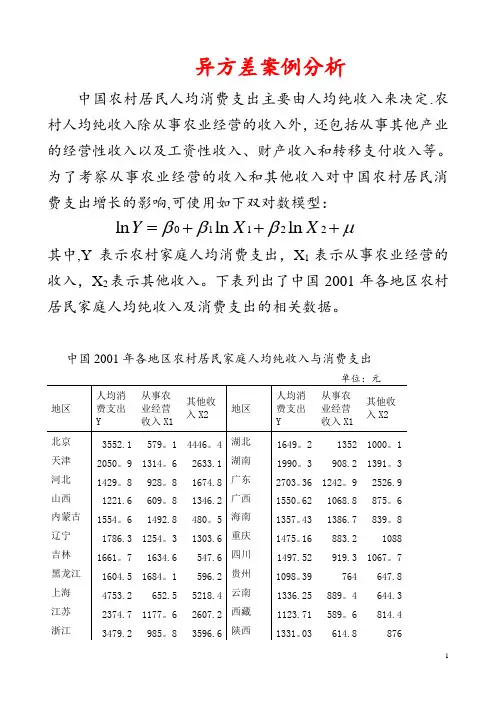
异方差案例分析
中国农村居民人均消费支出主要由人均纯收入来决定。
农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入等。
为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,可使用如下双对数模型:
1122ln ln ln Y X X βββμ0=+++
其中,Y 表示农村家庭人均消费支出,X 1表示从事农业经营的收入,X 2表示其他收入。
下表列出了中国2001年各地区农村居民家庭人均纯收入及消费支出的相关数据。
中国2001年各地区农村居民家庭人均纯收入与消费支出 单位:元
资料来源:《中国农村住户调查年鉴》(2002)、《中国统计年鉴》(2002)。
我们不妨假设该线性回归模型满足基本假定,采用OLS 估计法,估计结果如下:
12ˆln 1.6550.3166ln 0.5084ln Y
X X =++ (1.87) (3.02) (10.04)
R 2=0.7831 R 2=0.7676 D.W.=1.89 F=50.53 RSS=0.8232
图1
估计结果显示,其他收入而不是从事农业经营的收入的增长,对农户消费支出的增长更具有刺激作用。
下面对该模型进行异方差性检验。
1.图示法。
首先做出Y与X1、X2的散点图,如下:
图2
可见1X 基本在其均值附近上下波动,而2X 散点存在较为明显的增大趋势。
再做残差平方项2
ˆi e
与1ln X 、2ln X 的散点图:
图3
图4
可见图1中离群点相对较少而图2呈现较为明显的单调递增的
异方差性。
故初步判断异方差性主要是2X引起的。
2.G-Q检验
根据上述分析,首先将原始数据按X2升序排序,去掉中间7个数据,得到两个容量为12的子样本,记数据较小的样本为子样本1,数据较大的为子样本2。
对子样本1进行OLS回归,结果如下:
图5
得到子样本1的残差平方和RSS1=0.064806;
再对子样本2进行OLS回归,结果如下:
图6
得到子样本2的残差平方和RSS 2=0.279145。
计算F 统计量:
21RSS 0.279145F 4.3082
RSS 0.064806==≈
在5%的显著水平下,F 0.05(9,9)=3.18 < F,故应拒绝同方差假设,表明该总体随机干扰项存在单调递增的异方差。
3.white 检验
记原模型残差平方项为2ˆe
, 将其与X 1,X 2及其平方项与交叉项做辅助回归,结果如下:
图7
由各参数的t值可见各项都不是很显著,而且可决系数值也比较小,但white统计量nR2=31⨯0.464=14.38该值大于5%显著水平下自由度为5的2χ分布相应的临界值20.05
χ=11.07,因此应拒绝同方差假设。
去掉交叉项后的辅助回归结果如下:
图8
显然,X2和X2的平方项的参数的t检验是显著的,并且white 统计量nR2=31⨯0.437376=11.58656大于5%显著水平下自由度为5的2χ分布相应的临界值20.05
χ=11.07,因此应拒绝同方差假设。
4.异方差的修正——加权最小二乘法
我们以1/X2为权重进行异方差的修正。
加权后的估计结果如
下:
图9
可见修正后各解释变量的显著性总体相对提高。
其white检验结果如下:
精品
可编辑修改
图10
此时white 统计量nR 2=31⨯0.023325=0.723小于5%显著
水平下自由度为5的2
χ分布相应的临界值20.05χ=11.07,故此时满足同方差假设。
故修正后的估计结果为:
12
ˆln 2.3250.441ln 0.284ln Y X X =++。