16力矩分配法讲解

§8.1力矩分配法的基本概念力矩分配法是在位移法的基础上发展起来的一种渐近法，它主要应用于分析连续梁和无结点线位移的刚架。

杆端弯矩的正负号规定与位移法相同。

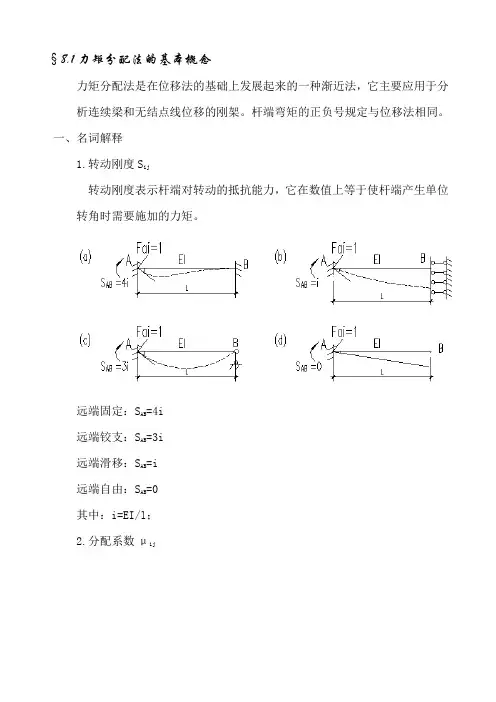
一、名词解释1.转动刚度S ij转动刚度表示杆端对转动的抵抗能力，它在数值上等于使杆端产生单位转角时需要施加的力矩。

远端固定：S AB=4i远端铰支：S AB=3i远端滑移：S AB=i远端自由：S AB=0其中：i=EI/l；2.分配系数μij由转动刚度的定义可知：M AB= S AB•θA=4i AB•θAM AC= S AC•θA=i AC•θAM AD= S AD•θA=3i AD•θA取结点A为隔离体，列ΣM=0，可得：M= S AB•θA+ S AC•θA+ S AD•θAM M∴θ= ──────── = ──S AB + S AC + S AD ΣSΣS表示各杆A端转动刚度之和，把θ反代入，可得：M AB=M• S AB/ΣS M AC=M• S AC/ΣS M AD=M• S AD/ΣS令μAj= S Aj/ΣS 则 M Aj=μAj•MμAj称为分配系数，等于某杆的转动刚度与交于结点的各杆的转动刚度之和的比值；同一结点各杆分配系数之间存在下列关系：ΣμAj=μAB +μAC +μAD = 13.传递系数C AjM AB =4i AB•θA，M BA =2i AB•θAM AC =i AC•θA， M CA = -i AC•θAM AD =3i AD•θA，M DA =0C AB= M BA / M AB =1/2∴远端固定：C=1/2远端滑动：C=-1远端铰支：C=0用下列公式表示传递系数的应用：M BA = C AB• M AB系数C AB称为由A端至B端的传递系数；二、力矩分配的基本概念如下图所示结构，用位移法计算时，此结构有一具未知量Z1，典型方程为：r11•Z1 + R1p = 0r11=3i12 + i13 + 4i14 = S12 + S13 + S14 =ΣSR1P =ΣM1j g =M12g +M13g =M1gR1P代表附加刚臂上反力矩，它等于汇交于结点1的各杆端的固端弯矩的代数和，用M1g表示。

结构力学——力矩分配法结构力学是研究物体在外力作用下的变形和破坏行为的学科。

其中，力矩分配法是一种求解结构梁的内力和变形的常用方法之一、本文将介绍力矩分配法的基本理论和应用。

首先，对于结构力学的研究，我们需要了解一些基本概念。

力矩是由力的作用点与旋转轴之间的距离和力的大小决定的。

在结构力学中，我们通常考虑作用在梁上的力和力矩。

梁是一种常见的结构元件，可以将其看作是在两个固定点之间作用的力的集合。

在力矩分配法中，我们将梁分割成若干个小段，然后逐段计算每个小段的内力和变形。

假设有一根长度为L，截面形状均匀的梁，并且在两个固定点之间施加了一系列分布力。

我们可以将梁分割成n个小段，每个小段的长度为Δx=L/n。

接下来，我们需要计算每个小段的内力和变形。

首先，我们可以根据材料力学的基本原理得出梁的拉伸、压缩和弯曲的力学方程。

然后，我们可以根据小段的切线方向和切线上的任意一点来推导出该小段的内力和弯曲方程。

最后，我们将内力分量在小段两端的力矩分配系数和位置矩分配系数进行合成，从而得出该小段的内力和弯曲方程。

在力矩分配法中，一个重要的概念是力矩分配系数。

力矩分配系数是一个无量纲的参数，用来表示力和力矩在小段两端分配的比例。

在计算力矩分配系数时，我们可以根据梁的几何形状和分布力的位置，利用力矩的基本原理进行推导。

力矩分配系数是力矩分配法的核心，它可以帮助我们计算出每个小段的内力和变形。

在实际应用中，力矩分配法通常用于求解多跨梁的内力和变形。

我们可以将多跨梁分割成若干个小段，并根据力矩分配法计算出每个小段的内力和变形。

然后，我们可以将各个小段的内力和变形进行叠加，得出整个多跨梁的内力和变形。

需要注意的是，力矩分配法具有一定的局限性。

首先，它只适用于存在弯曲变形的梁，对于其他类型的结构，如框架和板，需要采用其他的分析方法。

其次，力矩分配法仅适用于分布力作用在梁的直线部分上，对于弯曲部分或非均匀分布力的情况，需要采用其他的方法进行分析。

《建筑力学》15章丶16章_力矩分配法丶影响线第15章计算简支梁反力的力矩分配法力矩分配法是一种简化计算简支梁反力的方法，在工程实践中得到广泛应用。

该方法的基本原理是将荷载按照其作用位置分配给不同的支座，使得各支座所受的力矩之和等于梁所受外力的总力矩。

力矩分配法的步骤如下：1.绘制受荷简支梁的截面图，并标注各荷载作用的位置。

2.将受荷简支梁分割成若干个力矩区段。

3.分别计算各力矩区段的力矩，力矩的计算公式为：M=F*d，其中M 为力矩，F为作用力，d为力臂（即作用力到支座的距离）。

4.按照力矩区段所受作用力的大小，将外力分配给各支座，使得各支座所受的力矩之和等于梁所受外力的总力矩。

5.根据支座的几何条件，计算支座反力。

通过力矩分配法计算简支梁反力的优点是计算简单、便于手算，适用于一些简单的结构。

但是该方法的精度相对较低，对于要求较高精度的工程问题，不宜采用该方法。

第16章影响线及其应用影响线是指荷载施加在结构一些位置时，其引起的反力或变形与荷载在这个位置的拉力成正比的线。

影响线的性质及应用关系到结构分析和设计中的静力灵敏度、变形及挠度等问题。

影响线的构造方法包括弹性法和刚性法两种。

弹性法是基于杆件理论，假设结构杆件为弹性杆件，通过建立弹性杆件的力学方程组或位移表达式，推导出影响线方程。

刚性法是建立在结构平衡理论的基础上，结合位移条件，推导出刚度方程组，并解得影响线方程。

影响线的应用包括以下几个方面：1.静力灵敏度分析：通过计算不同位置上的影响线，可以分析和评估不同点荷载对结构响应的敏感程度。

2.变形和挠度计算：通过影响线法，可以很方便地计算结构在不同位置处的变形和挠度，并进一步进行结构设计和优化。

3.荷载位移计算：通过影响线，可以计算荷载移动导致的结构位移，有助于评估结构的安全性和稳定性。

总之，力矩分配法和影响线是建筑力学中重要的计算方法和分析工具，它们在结构分析和设计中具有广泛的应用价值。

对于工程师来说，掌握这些方法和工具，可以更好地分析和设计结构，提高工作效率和工作质量。