第16章 位移法及力矩分配法

第十八章力矩分配法力矩分配法理论基础：位移法；计算对象：杆端弯矩；适用范围：连续梁和无侧移刚架。

一、转动刚度转动刚度表示杆端对转动的抵抗能力。

它在数值上等于使杆端产生单位转角时需要施加的力矩，以SAB表示。

A是施力端（近端），B为远端。

1S AB=4i1S AB=3iS AB= i1S AB=0远端固定远端铰支远端滑动远端自由第一节力矩分配法的基本原理1S AB =4i1S AB =3iS AB = i 1S AB =0远端固定远端铰支远端滑动远端自由转动刚度远端固定，S =4i 远端简支，S =3i 远端定向，S =i 远端自由，S =0S AB 与杆的线刚度i 和远端支承情况有关。

i —杆件的线刚度，lEI i二、传递系数M AB = 4i AB ϕAM BA = 2i AB ϕA21==AB BA ABM M C M AB = 3i AB ϕA 0==ABBA ABM M C M AB = i AB ϕAM BA = -i AB ϕA1-==ABBA ABM M C ϕAlAB远端固定ABϕAϕAAB远端铰支远端滑动M BA = 0远端支承转动刚度传递系数固定S=4i C =1/2简支S=3i C =0定向S=i C = -1自由S=0三、力矩分配法的基本原理杆端弯距：取结点A 作隔离体，由∑M =0，得分配系数CA BDi ABi AC i ADAAB A AB AB S i M ϕϕ==4A AC A AC AC S i M ϕϕ==AAD A AD AD S i M ϕϕ==3}M M ABM ACM ADAAD AC AB S S S M ϕ)(++=∑=++=AAD AC AB A SMS S S M ϕMSSM AADAD ∑=M SS M A ABAB ∑=M S S M AACAC ∑=注：1）分配弯矩是杆端转动时产生的近端弯矩。

2）结点集中力偶顺时针为正。

∑=AAkAkSS μMM Ak Ak μ=分配弯矩A ϕM1321=++=∑A A A Ak μμμμ各杆的远端弯矩M kA 可以利用传递系数求出。

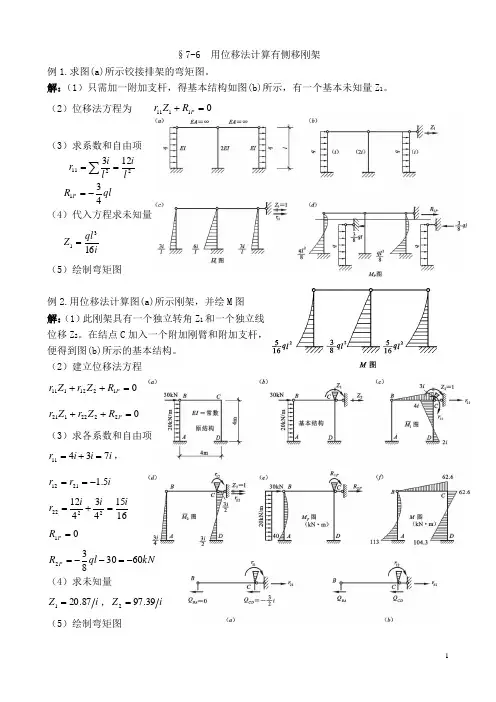
§7-6 用位移法计算有侧移刚架例1.求图(a)所示铰接排架的弯矩图。

解：（1）只需加一附加支杆，得基本结构如图(b)所示，有一个基本未知量Z 1。

（2）位移法方程为 01111=+P R Z r（3）求系数和自由项2211123l il i r ==∑ql R P 431-=（4）代入方程求未知量iql Z 1631=（5）绘制弯矩图例2.用位移法计算图(a)所示刚架，并绘M 图 解：（1）此刚架具有一个独立转角Z 1和一个独立线位移Z 2。

在结点C 加入一个附加刚臂和附加支杆，便得到图(b)所示的基本结构。

（2）建立位移法方程01212111=++P R Z r Z r 02222121=++P R Z r Z r （3）求各系数和自由项i i i r 73411=+=， i r r 5.12112-==1615434122222ii i r =+=01=P RkN ql RP 6030832-=--=（4）求未知量i Z 87.201=，i Z 39.972= （5）绘制弯矩图例3.用直接平衡法求刚架的弯矩图。

解：（1）图示刚架有刚结点C 的转角Z 1和结点C 、D 的水平线位移Z 2两个基本未知量。

设Z 1顺时针方向转动，Z 2向右移动。

（2）求各杆杆端弯矩的表达式3421+-=Z Z M CA 3221--=Z Z M AC 13Z M CD = 25.0Z M BD -= （3）建立位移法方程有侧移刚架的位移法方程，有下述两种：Ⅰ.与结点转角Z 1对应的基本方程为结点C 的力矩平衡方程。

∑=0CM ， 037021=+-⇒=+Z Z M M CD CAⅡ.与结点线位移Z 2对应的基本方程为横梁CD 的截面平衡方程。

∑=0xF， 0=+D C CA Q Q取立柱CA 为隔离体(图(d))，∑=0A M ， 331216262121-+-=---=Z Z ql Z Z Q CA 同样，取立柱DB 为隔离体（(e))，∑=0B M ， 2212165.0Z Z Q DB =--= 代入截面平衡方程得 03125012133121221=-+-⇒=+-+-Z Z Z Z Z（4）联立方程求未知量 Z 1=0.91 Z 2=9.37（5）求杆端弯矩绘制弯矩图将Z 1、Z 2的值回代杆端弯矩表达式求杆端弯矩作弯矩图。

1渐近法2用力法、位移法分析超静定结构，都需要求解多元联立方程组，求出基本未知量。

当未知量较多时，计算颇为繁重。

渐近法—采用逐步地逼近真实解的方法。

渐近法主要有：一、渐近法概述(1)力矩分配法：适于连续梁与无侧移刚架。

(2)无剪力分配法：适于规则的有侧移刚架。

(3)迭代法：适于梁的刚度大于柱刚度的各种刚架。

3力矩分配法理论基础：位移法；计算对象：杆端弯矩；计算方法：逐渐逼近的方法；适用范围：连续梁和无侧移刚架。

4只有结点角位移而无结点线位移的梁和刚架。

？力矩分配法的适用范围：力矩分配法的适用范围：5只有结点角位移而无结点线位移的梁和刚架。

√6力矩分配法以杆端弯矩为计算对象，采用：固定放松分配、传递逐次逼近杆端弯矩的精确解。

计算原理及符号规则均与位移法相同，只是计算过程不相同。

7计算过程：1.固定结点求出固定状态的杆端弯矩FijM 附加刚臂处的不平衡弯矩iM依次将结点上的不平衡弯矩反号分配于各杆近端，并传向远端。

2.逐次放松各结点8若干次循环计算= 也即逐次恢复转角的过程直接表达为各杆端弯矩逐次修正的过程放松结束，也即变形（转角）、内力趋于实际状态。

9——基本运算A BCM ABM BAM BC A BCM FAB M FBAM FBCM BM BM F BAM F BCM B =M F BA +M F BCABC－M BBAM ′BCM ′AB M ′0－M BBAM ′BCM ′)(B BA BAM M −⋅=′μ)(B BC BCM M −⋅=′μ+=最后杆端弯矩：M BA =M F BA +BAM ′M BC =M F BC +BCM ′M AB =M F AB +AB M ′然后各跨分别叠加简支梁的弯矩图，即得最后弯矩图。

固端弯矩带本身符号单结点的力矩分配分配系数分配弯矩10例1. 用力矩分配法作图示连续梁的弯矩图。

3m 3m 6m EI EI 200kN 20kN/m （1）固定B 结点A BC 200kN 20kN/m M F AB =M F BA =M F BC=mkN ⋅−=×−15086200m kN ⋅150m kN ⋅−=×−9086202M B =M F BA + M F BC =m kN ⋅60－150150－90（2）放松结点B，即加-60进行分配60A B C－60设i =EI/l 计算转动刚度：S BA =4iS BC =3i分配系数：571.0344=+=i i iBAμ429.073==iiBCμ0.5710.429分配力矩:3.34)60(571.0−=−×=′BAM 7.25)60(429.0−=−×=′BCM －34.3－25.7－17.2+(3) 最后结果。

力法位移法。

力矩分配法常见问题建筑力学常见问题解答6 超静定结构內力计算1．什么是超静定结构？它和静定结构有何区别？答：单靠静力平衡条件不能确定全部反力和內力的结构为超静定结构。

从几何组成的角度看，静定结构是没有多余约束的几何不变体系。

若去掉其中任何一个约束，静定结构即成为几何可变体系。

也就是说，静定结构的任何一个约束，对维持其几何不变性都是必要的，称为必要约束。

对于超静定结构，若去掉其中一个甚至多个约束后，结构仍可能是几何不变的。

2．什么是超静定结构的超静定次数？答：超静定结构多余约束的数目，或者多余约束力的数目，称为结构的超静定次数。

73．超静定结构的基本结构是否必须是静定结构？答：超静定结构的基本结构必须是静定结构。

4．如何确定超静定结构的超静定次数？答：确定结构超静定次数的方法是：去掉超静定结构的多余约束，使之变为静定结构，则去掉多余约束的个数，即为结构的超静定次数。

5．撤除多余约束的方法有哪几种？答：撤除多余约束常用方法如下：（1）去掉一根支座链杆或切断一根链杆，等于去掉一个约束。

（2）去掉一个固定铰支座或拆去一个单铰，等于去掉两个约束。

（3）去掉一个固定端支座或把刚性连接切开，等于去掉三个约束。

76．用力法计算超静定结构的基本思路是什么？答：用力法计算超静定结构的基本思路是：去掉超静定结构的多于约束，代之以多余未知力，形成静定的基本结构；取多余未知力作为基本未知量，通过基本结构的位移谐调条件建立力法方程，利用这一变形条件求解多余约束力；将已知外荷载和多余约束力所引起的基本结构的内力叠加，即为原超静定结构在荷载作用下产生的内力。

7．什么是力法的基本结构和基本未知量？答：力法的基本结构是：超静定结构去掉多余约束后得到的静定结构。

力法的基本未知量是对应于多余约束的约束反力。

8．简述n次超静定结构的力法方程，及求原结构的全部反力和內力的方法。

答：（1）n次超静定结构的力法方程对于n次超静定结构，撤去n个多余约束后77可得到静定的基本结构，在去掉的n 个多余约束处代以相应的多余未知力。

力法位移法力矩分配法《力法、位移法、力矩分配法：我的探索之旅》我呀，是一个对建筑结构特别感兴趣的小学生。

在我的小脑袋里呀，总是充满了各种各样关于房子、桥梁这些建筑怎么稳稳当当站立着的好奇想法。

今天呢，我就想和大家讲讲我正在学习的力法、位移法、力矩分配法，这就像是一场奇妙的冒险。

先说说力法吧。

我觉得力法就像是一个超级侦探在寻找真相。

你看，一座建筑受到各种各样的力，就像一群调皮的小怪兽在捣乱。

力法呢，就是要把这些力都搞清楚。

比如说，有一个大桥，上面有汽车在跑，风在吹，还有桥自身的重量。

这时候力法就登场了。

它会假设一些未知的力，就像在黑暗里猜宝藏在哪里一样。

然后呢，根据建筑的变形情况来找出这些真正的力。

这就好比我们玩猜谜语，根据谜面的一些提示，猜出正确的答案。

我记得有一次我和小伙伴们一起玩搭积木。

我们想搭一个超级高的大楼，可是搭到一半就倒了。

我当时就想啊，如果我会用力法就好了。

我就能算出每个小积木受到的力，知道怎么摆放它们才能稳稳当当的。

我就和小伙伴们说：“哎呀，咱们搭的这个就像一个没有规则受力的建筑，肯定会倒呀。

要是能像工程师叔叔阿姨那样会用力法，就不会这样啦。

”小伙伴们都似懂非懂地点点头。

再来说说位移法。

位移法在我眼里就像一个魔法。

想象一下，建筑就像一个有生命的巨人，当受到力的时候，它就会动一动，也就是产生位移。

位移法就是紧紧抓住这个位移的小尾巴，来弄清楚建筑内部的力是怎么分布的。

这就好比我们看一个会变形的机器人，它的每个关节动了多少，我们就能知道它内部的零件是怎么工作的。

我在书上看到一个例子，说有一个古老的钟楼，经过了很多年，有点倾斜了。

工程师们用位移法来研究这个钟楼，看看怎么去修复它。

我当时就想，哇，这也太神奇了吧。

我就跑去跟爷爷说：“爷爷，那个钟楼歪了，工程师叔叔用位移法就能知道怎么修呢。

”爷爷笑着说：“小家伙，你懂的还不少呢。

”我就特别得意，感觉自己像是掌握了一个大秘密。

最后就是力矩分配法啦。

第十六章
位移法和力矩分配法
思考题
1．什么是转动刚度？影响转动刚度确定的因素是什么？
2．分配系数与转动刚度有什么关系？为什么一刚结点处各杆端的分配系数之和等于1？
3．何为固端弯矩与不平衡力矩？如何计算不平衡力矩？为何将它反号才能进行分配？
4．当结构发生已知的支座移动时结点是有线位移的，可否用力矩分配法计算？
5．力矩分配法的计算过程为何是收敛的？
6．在力矩分配法的计算过程中，若仅是传递弯矩有误，杆端最后弯矩能否满足结点的力矩平衡条件？为什么？
习题
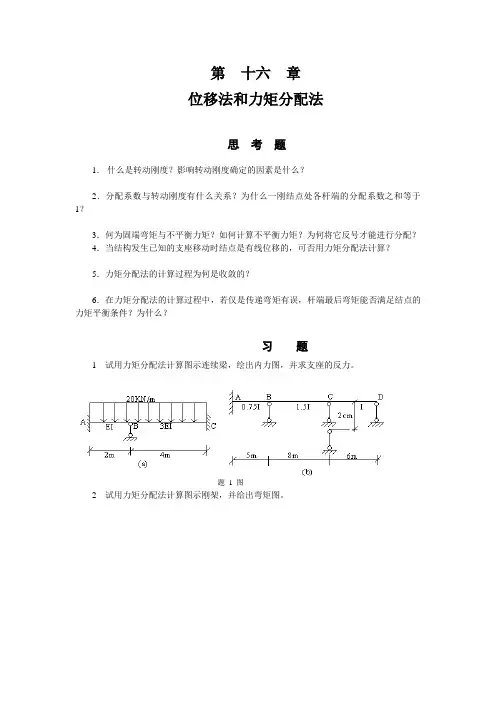
1 试用力矩分配法计算图示连续梁，绘出内力图，并求支座的反力。

题 1 图
2 试用力矩分配法计算图示刚架，并给出弯矩图。

题 2 图
3 试用无剪力分配法计算图示单跨对称刚架，作出弯矩图。

题3图
习题答案：
1. （a）M BC=-14.67 kN·m；F BY=48 kN（）
（b）M BC=-50 kN·m；M BA=-50 kN·m；F BY=27.5 kN（
2. M CD=-35 kN·m；M CA=5 kN·m
3. M BC=-150.35 kN·m；M BA=-136.28 kN·m。