弹性吊弦_计算资料
- 格式:ppt
- 大小:756.00 KB
- 文档页数:62

接触网常用计算公式接触网常用计算公式1. 平均温度t p 和链形悬挂无弛度温度t o 的计算① 2t t tp min max += ② 5-2t t t min max o +=弹 ③ 10-2t t t min max o +=简 式中 t p —平均温度℃(即吊弦、定位处于无偏移状态的温度);t o 弹、t o 简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃;t max —设计最高温度℃;t min —设计最低度℃;2. 当量跨距计算公式∑∑===n i In i I LLLD 113 式中L D —锚段当量跨距(m );).........(3323113n n i I L L L L+++=∑=—锚段中各跨距立方之和; ).........(211n n i I L L L L+++=∑=—锚段中各跨距之和;3. 定位肩架高度B 的计算公式2)101 +(hd h Ie H B ++≈ 式中 B —肩架高度(mm );H —定位点处接触线高度(mm );e —支持器有效高度(mm );I —定位器有效长度(包括绝缘子)(mm );d —定位点处轨距(mm );h —定位点外轨超高(mm );4. 接触线拉出值a 地的计算公式h dH a a -=地 式中 a 地—拉出值标准时,导线垂直投影与线路中心线的距离(mm )。
a 地为正时导线的垂直投影应在线路的超高侧,a 地为负时导线的垂直投影应在线路的低轨侧。
H —定位点接触线的高度(mm );a —导线设计拉出值(mm );h —外轨超高(mm );d —轨距(mm );5. 接触线定位拉出值变化量m ax a ∆的计算公式2max 2max E I I a z z --=∆式中 Δa max —定位点拉出值的最大变化量(mm );Z L —定位装置(受温度影响)偏转的有效长度(mm );max E —极限温度时定位器的最大偏移值(mm );由上式可知 E=0时 Δa=06. 定位器无偏移时拉出值a 15的确定:(取平均温度t p =15℃)max 2115a a a ∆±= 式中 a —导线设计拉出值(mm );Δa max —定位点拉出值的最大变化量(mm );15a —定位器无偏移时(即平均温度时)的拉出值(mm )。

吊弦安装计算一、执行接触网计算软件进入软件主菜单,选定“吊弦安装计算”栏,根据现场实际情况完成基本数据库、原始数据库数据输入。
二、字段说明1)悬挂类型——承导线型号2)导线高——导线高度3)悬挂单位自重——悬挂的每米质量(包括吊弦重、承力索和导线重)4)接触线单位自重——接触线的每米质量5)承力索额定张力——承力索设计的额定补偿张力6)接触线额定张力——接触线设计的额定补偿张力7)预留驰度率——接触线的预留驰度值8)吊弦线夹扣料值——承力索的顶面与导线的底面至吊弦环两端的长度之和9)跨距下限——吊弦布置数量相同的跨距范围的最小值(包括该值)10)跨距上限——吊弦布置数量相同的跨距范围的最大值(不包括该值)11)吊弦根数——分布在该跨距范围内吊弦的总数量12)未知间距数——该跨距范围内吊弦间距未确定的数量13)左1——该跨距内左支柱悬挂点至第一根吊弦的间距14)1-2——第一根吊弦至第二根吊弦的间距15)2-3——第二根吊弦至第三根吊弦的间距16)3-4、4-5、5-6、6-7、7-8、8-9、9-10——各间距类推17)10-右——第十根吊弦至右支柱悬挂点的间距18)跨距特征——该跨距内线路特征(集中负荷、曲线、竖曲线)19)承力索偏移值——承力索相对导线的偏移值20)曲线半径——该跨距所在范围内的线路曲线半径21)集中负荷——该跨距内集中负荷的重量22)竖曲线半径——该跨距内的竖曲线半径23)承力索高度——悬挂点处承力索相对于轨面中心的高度24)曲外超高——悬挂点处曲线的外轨超高25)集中负荷至左端距离——集中负荷中心至左悬挂点的距离26)吊弦1~10——吊弦从左到右的编号27)吊弦位置——吊弦至左侧支柱的距离28)吊弦长度——吊弦加吊弦线夹的长度和29)实际下料——吊弦实际有效长度,不含回头长度30)预留驰度——导线的设计预留驰度三、计算步骤:1)核对吊弦常用数据库、吊弦分布数据库是否正确。



附件一、接触网常用计算公式:1.平均温度t p和链形悬挂无弛度温度t o的计算t max+t min①t p=2t max+t min②t o弹= -52t max+t min③t o简= -102式中t p—平均温度℃(即吊弦、定位处于无偏移状态的温度);t o弹、t o简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃;t max—设计最高温度℃;t min—设计最低温度℃;2.当量跨距计算公式n∑L I3LD= i=1n∑L I√i=1式中L D—锚段当量跨距(m);n∑L I3=(L13+ L23+……+ L n3)—锚段中各跨距立方之和;i=1n∑L I=(L1+ L2+……+ L n)—锚段中各跨距之和;i=13.定位肩架高度B的计算公式B≈H+e+I(h/d+1/10)h/2式中B—肩架高度(mm);H—定位点处接触线高度(mm);e—支持器有效高度(mm);I—定位器有效长度(包括绝缘子)(mm);d—定位点处轨距(mm);h—定位点外轨超高(mm);4.接触线拉出值a地的计算公式Ha地=a-hd式中a地—拉出值标准时,导线垂直投影与线路中心线的距离(mm)。
a地为正时导线的垂直投影应在线路的超高侧,a地为负时导线的垂直投影应在线路的低轨侧。
H—定位点接触线的高度(mm);a—导线设计拉出值(mm);h—外轨超高(mm);d—轨距(mm);5.接触线定位拉出值变化量Δa max的计算公式Δa max=I z-√I2z-E2max式中Δa max—定位点拉出值的最大变化量(mm);I z—定位装置(受温度影响)偏转的有效长度(mm);E max—极限温度时定位器的最大偏移值(mm);由上式可知E=0时Δa=06.定位器无偏移时拉出值a15的确定:(取平均温度t p=15℃)a15=a±1/2Δa max式中a—导线设计拉出值(mm);Δa max—定位点拉出值的最大变化量(mm);a15—定位器无偏移时(即平均温度时)的拉出值(mm)。

整体吊弦长度计算整体吊弦长度计算是指在建筑结构中,将吊弦的长度计算为整体长度的方法。
吊弦通常用于吊挂悬挂系统,如天花板、吊顶、灯具等,该系统需要满足一定的静力学要求,如稳定性、可靠性和安全性。
因此,正确计算吊弦的长度对于设计和施工至关重要。
1.直线吊弦的计算直线吊弦是指吊弦的轮廓线是一条直线的情况。
在计算直线吊弦的长度时,可以使用三角形或平行四边形的几何性质来确定吊弦的长度。
具体计算步骤如下:1)确定吊弦的起始点和结束点。
2)根据起始点和结束点的位置关系,确定吊弦的直线方程。
3)计算吊弦的长度,可以使用勾股定理或坐标公式求解。
2.曲线吊弦的计算曲线吊弦是指吊弦的轮廓线不是直线,而是一条曲线。
计算曲线吊弦的长度需要考虑曲线的形状和曲线方程的表示方法。
常见的曲线吊弦有圆弧形吊弦和椭圆形吊弦。
具体计算步骤如下:1)确定吊弦的起始点和结束点。
2)根据吊弦的形状选择相应的曲线方程,如圆弧的方程或椭圆的方程。
3)计算曲线的弧长,可以通过积分或参数方程求解。
3.多段吊弦的计算多段吊弦是指吊弦由多个线段组成的情况。
在计算多段吊弦的长度时,需要将各个线段的长度相加,并考虑各个线段之间的转角。
1)确定吊弦的起始点和结束点。
2)选择适当的线段分段数目,将吊弦分割为若干个线段。
3)计算各个线段的长度,可以使用直线的长度计算方法。
4)考虑各个线段之间的转角,确定各个线段之间的连接方式,如直接相连或采用弯头连接。
总结起来,整体吊弦长度的计算方法根据吊弦的类型进行选择。
对于直线吊弦,可以使用几何方法进行计算;对于曲线吊弦,需要根据曲线的形状选择相应的曲线方程并计算弧长;对于多段吊弦,需要将各线段的长度相加,并考虑各个线段之间的转角。
无论吊弦的类型如何,正确进行吊弦长度的计算可以确保结构系统的稳定性和安全性。


新建铁路南京至杭州客运专线四电系统集成工程(电气化专业)吊弦及弹性吊索预配安装作业指导书编号:NH-DH-12编制:柴正均审核:罗林生批准:毛伟中铁建电气化局集团有限公司宁杭客专工程指挥部电气化项目部2023年 2月11日一、施工准备1、劳动组织2、工机具3、重要材料、设备二、工艺流程图1、施工准备承力索架设完毕,并倒鞍子,承力索中心锚结安装后,可进行弹性吊索安装。
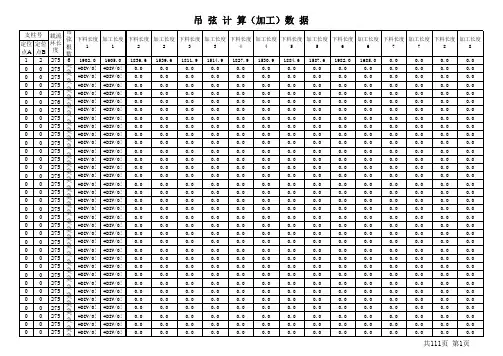
2、预制2.1、弹性吊索和吊弦计算结果相关说明宁杭客专的弹性吊索和吊弦计算结果包含图表1中的数据:图1 弹性吊索和吊弦计算结果2.1.1、图1中数据为弹性吊索和吊弦的分布情况,用来拟定吊弦之间间距,吊弦距离定位点的距离、弹性吊索长度及位置、复核吊弦长度等。
2.1.2、计算结果注解(1)、“左定位点”和“右定位点”下第一行数据代表“支柱号”如“4623”,第二行代表弹性吊索长度如“18.00”;(2)、“弹吊1”和“弹吊2”下面的第一行数据代表弹性吊弦心形环内侧到心形环内侧的距离如“1.155”,第二行数据代表弹性吊弦接触线中心至承力索中心的距离如“1.250”,第三行数据代表弹性吊弦下料长度如“1.452”,第四行数据代表弹性吊弦与相邻定位点或吊弦的间距如“7.07”,注意吊弦间距数据是一跨中从小里程的定位点往大里程定位点顺序排列的,如图1,“弹吊1”下面第四行数据是代表小里程定位点至“弹吊1”的距离,“弹吊2”下面第四行数据是代表小里程“吊4”至“弹吊2”的距离;(3)、“吊1”-“吊8”下面的第一行数据代表一般吊弦心形环内侧到心形环内侧的距离如“1.128”,第二行数据代表一般吊弦接触线中心至承力索中心的距离如“1.224”,第三行数据代表一般吊弦下料长度如“1.425”,第四行数据代表一般吊弦与相邻弹性吊弦或一般吊弦的间距如“7.07”;(4)、弹性吊索的长度应按照计算长度加200mm裁剪,因张力计紧弹性吊索张力时要安装紧线器。


接触悬挂吊弦计算方法研究郑积浩;翟铁久;李华伟;吴燕【摘要】对奥运工程京津城际专线的接触悬挂进行分析,计算整体吊弦的精确下料、长度和动力特性.接触网属于柔性悬挂结构,用传统的力矩计算方法要进行精确计算较为困难.有限元法是结构分析计算的有力工具,但在悬挂结构计算中应用较少.将接触网按照索结构原理建立计算模型,用非线形有限元方法建立方程,解决了吊弦长度的计算问题.算例表明,只要建立接触悬挂的刚度矩阵和荷载矩阵,就可以对接触网的吊弦长度进行准确的计算,这是传统的计算方法难以做到的.与传统的简化方法比较起来,用非线形有限元方法计算的结果更为精确,可大大提高施工下料的准确性,减少材料浪费,对我国电气化铁路的高速化有重要的意义.【期刊名称】《铁道建筑技术》【年(卷),期】2010(000)007【总页数】5页(P17-21)【关键词】悬索结构;接触网;有限元;非线形【作者】郑积浩;翟铁久;李华伟;吴燕【作者单位】北京交通大学电气工程学院,北京,100044;北京交通大学电气工程学院,北京,100044;北京交通大学电气工程学院,北京,100044;北京交通大学电气工程学院,北京,100044【正文语种】中文【中图分类】TM922.51 概述以一系列受拉索作为主要的受力构件,这些索按照一定规律组成各种不同形式的体系,并悬挂在相应的支撑结构上,一般称这样的结构体系为悬索结构。
悬索结构具有节省材料、施工快捷、适应多样化等特点,特别适用于各类大跨度建筑,在国外应用十分广泛。
以悬索系作为承重结构有着悠久的历史。
古代的帐篷式住屋就是悬挂屋盖的雏形。
我国人民早在 1 000多年以前已经用竹索或铁链建成跨越河谷的悬索桥,悬链线理论是在桥梁中发展起来的。
电力线路为连续跨理论提供了工程验证。
随着钢材的利用,现代化的大跨悬索桥开始出现,并且从本世纪初以来取得了可观的发展,促进了有限元的应用。
在房屋建筑方面,从 20世纪 50年代开始,悬索结构取得较大进展。