接触网常用计算公式

接触网常用计算公式接触网常用计算公式1. 平均温度t p 和链形悬挂无弛度温度t o 的计算① 2t t tp min max += ② 5-2t t t min max o +=弹 ③ 10-2t t t min max o +=简 式中 t p —平均温度℃（即吊弦、定位处于无偏移状态的温度）；t o 弹、t o 简—分别表示弹性链形悬挂和简单链形悬挂的无弛度温度℃；t max —设计最高温度℃；t min —设计最低度℃；2. 当量跨距计算公式∑∑===n i In i I LLLD 113 式中L D —锚段当量跨距（m ）；).........(3323113n n i I L L L L+++=∑=—锚段中各跨距立方之和； ).........(211n n i I L L L L+++=∑=—锚段中各跨距之和；3. 定位肩架高度B 的计算公式2)101 +(hd h Ie H B ++≈ 式中 B —肩架高度（mm ）；H —定位点处接触线高度（mm ）；e —支持器有效高度（mm ）；I —定位器有效长度（包括绝缘子）（mm ）；d —定位点处轨距（mm ）；h —定位点外轨超高（mm ）；4. 接触线拉出值a 地的计算公式h dH a a -=地 式中 a 地—拉出值标准时，导线垂直投影与线路中心线的距离（mm ）。

a 地为正时导线的垂直投影应在线路的超高侧，a 地为负时导线的垂直投影应在线路的低轨侧。

H —定位点接触线的高度（mm ）；a —导线设计拉出值（mm ）；h —外轨超高（mm ）；d —轨距（mm ）；5. 接触线定位拉出值变化量m ax a ∆的计算公式2max 2max E I I a z z --=∆式中 Δa max —定位点拉出值的最大变化量（mm ）；Z L —定位装置（受温度影响）偏转的有效长度（mm ）；max E —极限温度时定位器的最大偏移值（mm ）；由上式可知 E=0时 Δa=06. 定位器无偏移时拉出值a 15的确定：（取平均温度t p =15℃）max 2115a a a ∆±= 式中 a —导线设计拉出值（mm ）；Δa max —定位点拉出值的最大变化量（mm ）；15a —定位器无偏移时（即平均温度时）的拉出值（mm ）。

第四章 接触网设计计算原理4.1 接触网设计计算气象条件的确定接触网设计中所用到的气象资料包括；最高温度、最低温度、最大风速及其出现时的温度、线索覆冰厚度、覆冰时的风速及温度、雷电日(或小时)、接触线无弛度时的温度、吊弦及定位器处于正常位置时的温度、，此外还有线路横跨河滩及山谷时的最大风速等。

4.1.1气象条件的确定1、最大风速采用距地面10m 高处（基本风速高度），15年一遇的10分钟最大值。

其计算方法有：平均法、变通法和数理统计法，其中常用数理统计法。

（1）平均法平均法是将占有的年份气象资料分成若干组，然后求得各组最大风速值的平均值作为最大计算风速。

例如，没有M 年气象资料，按每5年为一组，可分为n /5组(取整数，如遇小数可四舍五入)，然后在M /5组资料中取每组中的最大值，再取最大值的平均值可得/5max1max /5n i i vv n ==∑ （4-1）式中max i v ——第i 组中最大风速值；n ——占有资料的年份数；/5n ——占有资料的组数。

（2）变通法变通法即是将求得的各组最大风速的平均值作为最大计算风速。

计算中只是所占有风速资料年份的分组方法与平均法不同。

即/5max1max 4n i i vv n ==-∑ （4-2）式中max i v ——第i 组中最大风速值；n ——占有资料的年份数； 4n -——划分的组数。

（3）数理统计法设计上要求一定概率下的最大风速，即一定重现期的年极大风速值。

在重现期内不出现这种极大风速的保证率是1/(1)p p -（4-3）而出现大于此值的极大风速的概率为1/1(1)p p -- （4-4）各种各样的统计方法归纳起来不外乎两个方面：一是从统计理论上确定年极大风速应该服从的概率线型，然后从实际资料决定其参数；二是从经验概率上确定年极大风速分布线型，然后从实际资料决定其参数。

其计算公式为1m p n =+ （4-5）式中P ——风速出现的频率； n ——占有资料的年份数；m ——将统计年份内出现的全部风速值由大到小按递减次序排列的序号数。

高速铁路有关术语
1、反射系数：接触网的振动波在非均质点被反射，如吊弦点、线夹处等。

反射系数用下式表示：
γ=√ρm.F m /（√ρc.F c + √ρm.F m ）
ρm.F m —分别代表承力索的线密度和承力索的张力；
ρc.F c ——分别代表接触线的线密度和接触线的张力。

2、多普勒因素：
α=（C – V）/（C + V）
V—行驶速度；
C—接触线波动传播速度，左右离线率和共振时的振幅。

3、增强因素：接触网的振动波在非均质处被反射，被反射回的波壁与该物体相向运动，并被继续向前运动的物体以输入能量的方式再次反射回去。

波的能量被增强，其增强系数用下式表示，为了使波能够衰减，必须满足γ<1的条件。

Φ = γ/α
γ—反射因素；
α—多普勒因素。

在上述三个动态标准中，最关键的动态标准为增强因素，应使增强因素尽可能的小。

因此，可通过减小反射系数，增大多普勒因素得以实现。

减少反射系数可以通过两个途径实现：减少承力索张力；增大接触线张力。

只有提高接触线的张力和波动传播速度才可能大幅度地减小增强因素，改善受流性能。

4、无量纲速度：β应小于0.7。

β= V/C。

接触网计算公式3 2接触网上部悬挂的载荷3 2 1负载分析接触网上部悬挂结构受到的主要外载荷包括：接触线和承力索在风作用下的风负载F风、以及接触线和承力索在覆冰作用下的冰负载Ft、接触线作用下的之字力P、地面对支柱的支持力F冰、受电弓作用下的抬升力N和其自身的重力Q。

由于接触网外部悬挂结构多种多样，但每一种结构的分析方法都大同小异。

本文选择一种典型的接触网上部悬挂结构作为研究对象，进行分析计算，即直线段中间支柱反定位悬挂形式。

其示意图如下其中F风=Pc+Pj，F冰.合成在Qo中以兰新线武威南至嘉峪关段直线段中间柱反安装为例，取侧面界限Cx=3.1m，安装角a=45°。

标准典型气象区选Ⅳ区，最大风度Vb=lOm/s，覆冰厚度b=5mm，吊弦单位长度自重取g。

=0.5×l03 KN/m，跨距取l =65m,拉出值a=200 mm。

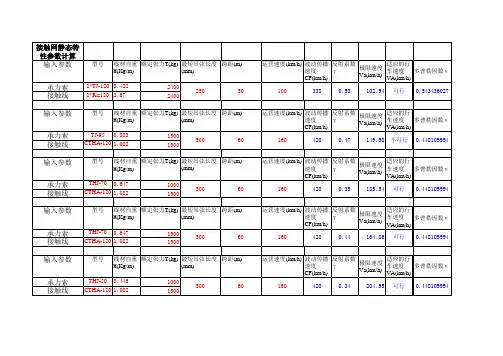
承力索和接舷线的相关参数如表3.1。

表3.1 承力索和接触线的参数接触线长度65m，考虑弛度的影响，承力索实际长度为L=l+8F/3l计算得到承力索实际长度l=65. 02m。

(1)单位长度风负载P =0.615akv2d×106（kN／m）式中p——绳索所受的实际风负载：a——风速不均匀系数；k——风负载体型系数；d——绳索的直径。

代入数据计算得到：单位长度承力索风负载：P cb=1.494×10-3(KN/m)单位长发接触线风负载：P jb=1.494×10-3 (KN/m)(2)单位长度冰负载g b=πr b b(b+ d)g H l0-9 (KN/m)式中g b——绳索的覆冰重力负载b——覆冰厚度；d——绳索直径；r b——覆冰密度：g H——重力加速度。

代入数据计算得到：承力索单位长度冰负载9hr =2. 003×l0-3 (KN/m) 接触线单位长度冰负载g。

=1. 082×10-3(KN/m)。