苏教版数学高一苏教版必修1学案对数函数的概念及基本性质

第二十教时教材：对数的基本概念目的：要求学生理解对数的概念，能够进行对数式与指数式的互化，并由此求一些特殊的对数式的值。

进程：一、引入：从指数导入，见P 80例题假设1995年我国的国民生产总值为 a 亿元，如每年平均增长8%，那么经过多少年国民生产总值是1995年的2倍？设：经过x 年国民生产总值是1995年的2倍则有 ()a a x 2%81=+ 208.1=x这是已知底数和幂的值，求指数的问题。

即指数式 N a b =中，已知a 和N 求b 的问题。

（这里 10≠>a a 且）二、课题：对数定义：一般地，如果 ()1,0≠>a a a 的b 次幂等于N , 就是 N a b=，那么数 b 叫做 a 为底 N 的对数，记作 b N a =log ，a 叫做对数的底数，N 叫做真数。

N a b =b N a =log1．在指数式中 N > 0 （负数与零没有对数） 2．Θ对任意 0>a 且 1≠a , 都有 10=a ∴01log =a同样易知： 1log =a a3．如果把 N a b = 中的 b 写成 N a log , 则有 N a Na=log（对数恒等式）三、对数式与指数式的互换，并由此求某些特殊的对数。

例如： 1642= 216log 4= 100102= 2100log 10=2421=212log 4= 01.0102=- 201.0log 10-=例一、P 81 例一、例二例二、1．计算： 27log 9，81log34，()()32log 32-+，625log435解：设 =x 27log 9 则 ,27=x a 3233=x , ∴23=x设 =x 81log34则8134=⎪⎭⎫ ⎝⎛x,4433=x,∴16=x令 =x ()()32log 32-+=()()13232log -+-, ∴()()13232-+=+x , ∴1-=x 令 =x 625log435, ∴625543=⎪⎪⎭⎫⎝⎛x , 43455=x , ∴5=x 2．求 x 的值：①43log 3-=x ②35log 2-=x③()()1123log 2122=-+-x x x ④()[]0log log log 432=x解：①2713443==-x②3212235==-x③2,00212123222-==⇒=+⇒-=-+x x x x x x x但必须：⎪⎪⎩⎪⎪⎨⎧>-+≠->-0123112012222x x x x ∴0=x 舍去 2-=x④()1log log 43=x , ∴3log 4=x , 6443==x3．求底数：533log -=x , 872log =x解：53355333---⎪⎪⎪⎭⎫ ⎝⎛==x, ∴353-=x87788722⎪⎪⎪⎭⎫ ⎝⎛==x , ∴2=x四、介绍两种特殊的对数：1．常用对数：以10作底 N 10log 写成 N lg 2．自然对数：以 e 作底 e 为无理数，e = 2.71828……N e log 写成 N ln五、小结：1°定义 2°互换 3°求值 六、作业：（练习） P 81 练习 P 84 习题2.7 1，2 《课课练》 P 79 课时练习 6—10。

对数的概念【教学目标】1.使学生理解对数的概念，能够进行对数式与指数式的互化。

2.培养学生应用数学的意识.【教学重点】对数的概念【教学难点】对数与指数的互化【教学过程】一.复习引入：某种放射性物质不断变化为其他物质,每经过一年,这种物质剩留的的质量是原来的84%,经过多少年这种物质的剩留量为原来的一半?二.新课讲解1. 定义：一般地，如果 ()1,0≠>a a a 的b 次幂等于N , 即 N a b =，那么数 b 叫做 a 为底 N 的对数，记作 b N a =log ，a 叫做对数的底数，N 叫做真数。

N a b = b N a =log【注】（1） 在指数式中 N > 0 （负数与零没有对数）；（2） 01log =a 1log =a a（3）对数恒等式： N a N a =log ；b a b a =log（4）常用对数：我们通常将以10为底的对数叫做常用对数。

为了简便,N 的常用对数log 10 N 简记作lg N例如：log 105简记作lg 5 log 103.5简记作lg3.5.（5）自然对数：在科学技术中常常使用以无理数e ＝2.71828……为底的对数，以e 为底的对数叫自然对数，为了简便，N 的自然对数log e N 简记作ln N 。

例如：log e 3简记作ln3 log e 10简记作ln102. 例题例1 将下列指数式改写成对数式：（1）54＝625 （2）2-6＝164 （3）3a ＝27 (4) （13 ）m ＝5.73 解：（1）log 5625＝4；（2）log 2 164 ＝－6；（3）log 327＝a ；（4）log 315.73＝m例2 将下列对数式写成指数式：（1）log 2116＝－4；（2）log 2128＝－7；（3）lg0.01＝－2；（4）ln10＝2.303解：（1）（12 ）－4＝16；（2）27＝128；（3）10－2＝0.01；（4）e 2.303＝10例3 求下列各式的值：（1） 64log 2 ；271log 3（2） 27log 9； 81log 34解：设 =x 27log 9 则 ,27=x a 3233=x , ∴23=x （3） ()[]81log log log 346（4） ()()32log 32-+（5） 5log 23log 14242-+-+例4 求 x 的值：（1） 43log 3-=x （2） ()()1123log 2122=-+-x x x （3） ()[]0log log log 432=x （4） 872log =x （5） 416log =x解：（1）2713443==-x （2）2,00212123222-==⇒=+⇒-=-+x x x x x x x但必须：⎪⎩⎪⎨⎧>-+≠->-0123112012222x x x x ∴0=x 舍去 2-=x（3） ()1log log 43=x , ∴3log 4=x , 6443==x（4） 787878878722)(2=∴==x x x （5） )(22164舍去或-=∴=x x【课堂小结】（1）定义 （2）互换 （3）求值大家要在理解对数概念的基础上，掌握对数式与指数式的互化，会计算一些特殊对数值。

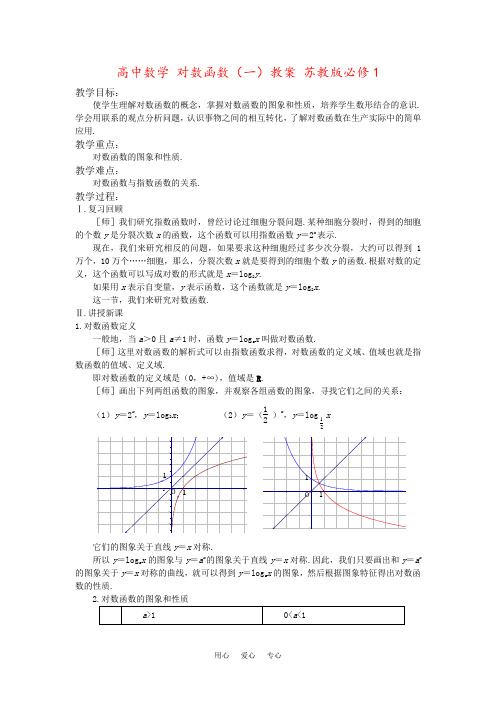
高中数学 对数函数（一）教案 苏教版必修1教学目标：使学生理解对数函数的概念，掌握对数函数的图象和性质，培养学生数形结合的意识.学会用联系的观点分析问题，认识事物之间的相互转化，了解对数函数在生产实际中的简单应用.教学重点：对数函数的图象和性质.教学难点：对数函数与指数函数的关系.教学过程：Ⅰ.复习回顾［师］我们研究指数函数时，曾经讨论过细胞分裂问题.某种细胞分裂时，得到的细胞的个数y 是分裂次数x 的函数，这个函数可以用指数函数y ＝2x表示.现在，我们来研究相反的问题，如果要求这种细胞经过多少次分裂，大约可以得到1万个，10万个……细胞，那么，分裂次数x 就是要得到的细胞个数y 的函数.根据对数的定义，这个函数可以写成对数的形式就是x ＝log 2y .如果用x 表示自变量，y 表示函数，这个函数就是y ＝log 2x . 这一节，我们来研究对数函数. Ⅱ.讲授新课 1.对数函数定义一般地，当a ＞0且a ≠1时，函数y ＝log a x 叫做对数函数.［师］这里对数函数的解析式可以由指数函数求得，对数函数的定义域、值域也就是指数函数的值域、定义域.即对数函数的定义域是（0，+∞)，值域是R .［师］画出下列两组函数的图象，并观察各组函数的图象，寻找它们之间的关系：（1）y ＝2x ，y ＝log 2x ； （2）y ＝（12）x，y ＝log 21x它们的图象关于直线y ＝x 对称.所以y ＝log a x 的图象与y ＝a x 的图象关于直线y ＝x 对称.因此，我们只要画出和y ＝a x的图象关于y ＝x 对称的曲线，就可以得到y ＝log a x 的图象，然后根据图象特征得出对数函数的性质.图 象32.521.510.5-0.5-1-1.5-2-2.5-11234567801132.521.510.5-0.5-1-1.5-2-2.5-11234567811性 质定义域：（0，+∞） 值域：R过点（1，0），即当x ＝1时，y ＝0 x ∈（0，1）时y ＜0 x ∈（1，＋∞）时y ＞0 x ∈（0，1）时y ＞0 x ∈（1，＋∞）时y ＜0在（0，+∞）上是增函数在（0，+∞）上是减函数［师］接下来，我们通过例题来看一下对数函数性质的简单应用.3.例题讲解［例1］求下列函数的定义域（1）y ＝log a x 2 (2)y ＝log a (4－x ) (3)y ＝log a (9－x 2) 分析：此题主要利用对数y ＝log a x 的定义域（0，+∞）求解解：（1）由x 2＞0，得x ≠0 所以函数y ＝log a x 2的定义域是{x |x ≠0} (2)由4－x ＞0，得x ＜4 所以函数y =log a (4－x )的定义域是{x |x ＜4}(3)由9－x 2＞0得－3＜x ＜3 所以函数y =log a (9－x 2)的定义域是{x |－3＜x ＜3} 评述：此题只是对数函数性质的简单应用，应强调学生注意书写格式. ［师］为使大家进一步熟悉对数函数的图象和性质，我们来做练习. Ⅲ.课堂练习 课本P 69练习1.画出函数y ＝log 3x 及y ＝x 31log 的图象，并且说明这两个函数的相同性质和不同性质.相同性质：两图象都位于y 轴右方，都经过点（1，0），这说明两函数的定义域都是（0，+∞），且当x ＝1，y ＝0.不同性质：y ＝log 3x 的图象是上升的曲线，y ＝x 31log 的图象是下降的曲线，这说明前者在（0，+∞）上是增函数，后者在（0，+∞）上是减函数.2.求下列函数的定义域：（1）y ＝log 5(1－x ) （2）y ＝1log 2x（3）y ＝log 711－3x（4）y ＝log 3x解：（1）由1－x ＞0得x ＜1 ∴所求函数定义域为{x |x ＜1}(2）由log 2x ≠0，得x ≠1，又x ＞0 ∴所求函数定义域为{x |x ＞0且x ≠1}(3)由⎩⎪⎨⎪⎧11－3x ＞01－3x ≠0 ，得x ＜13 ∴所求函数定义域为{x |x ＜13}(4)由⎩⎨⎧x ＞0log 3x ≥0 ，得⎩⎨⎧x ＞0x ≥1∴x ≥1∴所求函数定义域为{x |x ≥1} 要求：学生板演练习，老师讲评. Ⅳ.课时小结［师］通过本节学习，大家应逐步掌握对数函数的图象与性质，并能利用对数函数的性质解决一些简单问题，如求对数形式的复合函数的定义域问题. Ⅴ.课后作业（一）课本P 70习题1，2（二）1.预习内容：P 67例2、例3 2.预习提纲：（1）同底数的两对数如何比较大小？ （2）不同底数的两对数如何比较大小？对数函数（二）教学目标：使学生掌握对数函数的单调性，掌握比较同底与不同底对数大小的方法，培养学生数学应用意识；用联系的观点分析、解决问题，认识事物之间的相互转化.教学重点：利用对数函数单调性比较同底对数大小.教学难点：不同底数的对数比较大小.教学过程：Ⅰ.复习回顾［师］上一节，大家学习了对数函数的图象和性质，明确了对数函数的单调性，即： 当a ＞1时，y ＝log a x 在（0,+∞）上是增函数； 当0＜a ＜1时，y ＝log a x 在（0，+∞）上是减函数. 这一节，我们主要学习对数函数单调性的应用. Ⅱ.讲授新课［例1］比较下列各组数中两个值的大小：（1）log 23.4，log 28.5 (3)log 0.31.8，log 0.32.7 (3)log a 5.1，log a 5.9(a ＞0，a ≠1) 分析：此题主要利用对数函数的单调性比较两个同底数的对数值大小. 解：（1）考查对数函数y ＝log 2x ，因为它的底数2＞1，所以它在（0，+∞）上是增函数，于是log 23.4＜log 28.5(2)考查对数函数y ＝log 0.3x ，因为它的底数0＜0.3＜1，所以它在（0，+∞）上是减函数，于是log 0.31.8＞log 0.32.7［师］通过（1）、（2）的解答，大家可以试着总结两个同底数的对数比较大小的一般步骤：（1）确定所要考查的对数函数；（2）根据对数底数判断对数函数增减性；（3）比较真数大小，然后利用对数函数的增减性判断两对数值的大小.解：（3）当a ＞1时，y ＝log a x 在（0，+∞）上是增函数，于是log a 5.1＜log a 5.9当0＜a ＜1时，y ＝log a x 在（0，+∞）上是减函数，于是log a 5.1＞log a 5.9评述：对数函数的增减性决定于对数的底数是大于1还是小于1.而已知条件并未指明，因此需要对底数a 进行讨论，体现了分类讨论的思想，要求学生逐步掌握.［例2］比较下列各组中两个值的大小： （1）log 67，log 76 (2)log 3π，log 20.8分析：由于两个对数值不同底，故不能直接比较大小，可在两对数值中间插入一个已知数，间接比较两对数值的大小.解：（1）∵log 67＞log 66＝1，log 76＜log 77＝1，∴log 67＞log 76 （2）∵log 3π＞log 31＝0，log 20.8＜log 21＝0，∴log 3π＞log 20.8评述：例2仍是利用对数函数的增减性比较两个对数的大小，当不能直接比较时，经常在两个对数中间插入1或0等，间接比较两个对数的大小，例2（2）题也可与1比较. ［例3］求下列函数的定义域、值域：⑴ y ＝212--x －14⑵ y ＝log 2（x 2＋2x ＋5） ⑶ y ＝log 31（－x 2＋4x ＋5） ⑷ y ＝log a （－x 2－x ） （0＜a ＜1）解：⑴要使函数有意义，则须： 212--x －14≥0 即：－x 2－1≥－2 得－1≤x ≤1 ∵－1≤x ≤1 ∴－1≤－x 2≤0 从而 －2≤－x 2－1≤－1 ∴14 ≤212--x ≤12 ∴0≤212--x －14 ≤14 ∴0≤y ≤12∴定义域为[－1，1]，值域为[0，12]⑵∵x 2＋2x ＋5＝（x ＋1）2＋4≥4对一切实数都恒成立 ∴函数定义域为R从而log 2（x 2＋2x ＋5）≥log 24＝2 即函数值域为[2，＋∞）⑶要使函数有意义，则须： －x 2＋4x ＋5＞0得x 2－4x －5＜0解得－1＜x ＜5由－1＜x ＜5 ∴在此区间内 （－x 2＋4x ＋5）max ＝9∴ 0≤－x 2＋4x ＋5≤9从而 log 31（－x 2＋4x ＋5）≥log 319＝－2 即：值域为 y ≥－2∴定义域为[－1，5]，值域为[－2，＋∞）⑷要使函数有意义，则须：⎩⎨⎧≥-->--)2(0)(log )1(022x x x x a由①：－1＜x ＜0由②：∵0＜a ＜1时 则须 －x 2－x ≤1，x ∈R 综合①②得 －1＜x ＜0当－1＜x ＜0时 （－x 2－x ）max ＝14 ∴0＜－x 2－x ≤14∴log a （－x 2－x ）≥log a 14∴ y ≥log a 14∴定义域为(－1，0)，值域为[log a 14，＋∞）Ⅲ.课堂练习课本P 69练习3补充：比较下列各题中的两个值的大小（1）log 20.7，log 310.8 （2）log 0.30.7， log 0.40.3（3）log 3.40.7，log 0.60.8，（13）21- （4）log 0.30.1， log 0.20.1解：（1）考查函数y ＝log 2x∵2＞1， ∴函数y ＝log 2x 在（0，+∞）上是增函数 又0.7＜1， ∴log 20.7＜log 21＝0 再考查函数y ＝log 31x∵0＜13＜1 ∴函数y ＝log 31x 在（0，+∞）上是减函数又1＞0.8， ∴log 310.8＞log 311＝0∴log 20.7＜0＜log 310.8 ∴log 20.7＜log 310.8（2）log 0.30.7＜log 0.40.3（3）log 3.40.7＜log 0.60.8＜（13）21-（4）log 0.30.1＞log 0.20.1 要求：学生板演，老师讲评 Ⅳ.课时小结［师］通过本节学习，大家要掌握利用对数函数的增减性比较两对数大小的方法，并要能够逐步掌握分类讨论的思想方法. Ⅴ.课后作业课本P 70习题 3对数函数（三）教学目标：使学生掌握对数形式复合函数的单调性的判断及证明方法，掌握对数形式复合函数的奇偶性的判断及证明方法，培养学生的数学应用意识；认识事物之间的内在联系及相互转化，用联系的观点分析问题、解决问题.教学重点：函数单调性、奇偶性证明通法.教学难点：对数运算性质、对数函数性质的应用.教学过程：Ⅰ.复习回顾［师］上一节课后，我要求大家预习函数单调性，奇偶性的证明方法，现在，我们进行一下回顾.1.判断及证明函数单调性的基本步骤： 假设——作差——变形——判断说明：变形目的是为了易于判断；判断有两层含义：一是对差式正负的判断；二是对增减函数定义的判断.2.判断及证明函数奇偶性的基本步骤：①考查函数定义域是否关于原点对称；②比较f (－x )与f (x )或者－f (x )的关系；③根据函数奇偶性定义得出结论.说明：考查函数定义域容易被学生忽视，应强调学生注意. ［师］接下来，我们一起来看例题 Ⅱ.讲授新课［例1］判断下列函数的奇偶性：（1）f (x )＝lg 1－x 1＋x(2)f (x )＝ln(1+x 2－x )分析：首先要注意定义域的考查，然后严格按照奇偶性证明基本步骤进行. 解：（1）由1－x1＋x＞0可得－1＜x ＜1所以函数的定义域为：（－1，1）关于原点对称又f (－x )＝lg 1＋x 1－x ＝lg （1－x 1＋x ）－1＝－lg 1－x 1＋x ＝－f (x )即f (－x )＝－f (x )所以函数f (x )＝lg 1－x1＋x是奇函数评述：此题确定定义域即解简单分式不等式，函数解析式恒等变形需利用对数的运算性质，说明判断对数形式的复合函数的奇偶性，不能轻易直接下结论，而应注意对数式的恒等变形.解：（2）由1+x 2－x ＞0可得x ∈R 所以函数的定义域为R 关于原点对称又f (－x )＝ln(1+x 2＋x )＝ln (1+x 2+x ) (1+x 2－x )1+x 2－x＝ln11+x 2－x＝－ln(1+x 2－x )＝－f (x )即f (－x )＝－f (x )所以函数f (x )＝ln(1+x 2－x )是奇函数评述：此题定义域的确定可能稍有困难，可以讲解此点，而函数解析式的变形用到了分子有理化的技巧，应要求学生掌握.[例2]（1）证明函数f (x )＝log 2(x 2＋1)在（0，+∞）上是增函数（2）问：函数f (x )＝log 2(x 2＋1)在（－∞，0）上是减函数还是增函数？ 分析：此题目的在于让学生熟悉函数单调性证明通法，同时熟悉上一节利用对数函数单调性比较同底数对数大小的方法.（1）证明：设x 1,x 2∈(0,+∞)，且x 1＜x 2则f (x 1)－f (x 2)＝log 2(x 12+1)－log 2(x 22+1)∵0＜x 1＜x 2 ∴x 12+1＜x 22+1 又∵y ＝log 2x 在（0，+∞）上是增函数.∴log 2(x 12+1）＜log 2(x 22+1) 即f (x 1)＜f (x 2)∴函数f (x )＝log 2(x 2+1)在（0，+∞）上是增函数. （2）是减函数，证明可以仿照上述证明过程.评述：此题可引导学生总结函数f (x )＝log 2(x 2+1)的增减性与函数y ＝x 2+1的增减性的关系，并可在课堂练习之后得出一般性的结论.[例3]求函数y ＝log 21（x 2－2x －3）的单调区间.解：定义域x 2－2x －3＞0 解得x ＞3或x ＜－1 单调减区间是（3，＋∞）[例4] 已知y ＝log a (2－ax )在[0，1]上是x 的减函数，求a 的取值范围. 解：∵a ＞0且a ≠1 ∴函数t ＝2－ax 是减函数由y ＝log a (2－ax )在[0，1]上x 的减函数，知y ＝log a t 是增函数，∴a ＞1 由x ＝1时，2－ax ＝2－a ＞0，得a ＜2∴1＜a ＜2Ⅲ.课堂练习（1）证明函数y ＝log 21 (x 2+1)在（0，+∞）上是减函数；（2）判断函数y ＝log 21 (x 2+1)在（－∞,0）上的增减性.证明：（1）设0＜x 1＜x 2，则f (x 1)－f (x 2)＝log 21 (x 12+1)－log 21 (x 22+1)＝log 21x 12＋1x 22＋1∵0＜x 1＜x 2，∴0＜x 12＜x 22， ∴x 12＋1x 22＋1 ＜x 12＋1x 12＋1而log 21x 是减函数 ∴log 21x 12＋1x 22＋1 ＞log 21x 12＋1x 12＋1＝log 211＝0∴f (x 1)－f (x 2)＞0 即f (x 1)＞f (x 2) ∴函数y ＝ log 21 (x 2+1)在（0，+∞）上是减函数（2）设x 1＜x 2＜0，则f (x 1)－f (x 2)＝ log 21 (x 12+1)－log 21 (x 22+1)∵x 1＜x 2＜0，∴x 12＞x 22＞0而函数y ＝ log 21x 在（0，+∞）上是减函数.∴log 21 (x 12+1）＜log 21 (x 22+1) 即f (x 1)＜f (x 2)∴y ＝ log 21 (x 2+1)在（－∞，0）上是增函数.Ⅳ.课时小结［师］通过本节学习，大家能进一步熟悉对数函数的性质应用，并掌握证明函数单调性，奇偶性的通法，提高数学应用的能力. Ⅴ.课后作业（一）课本P 70 4，5，8 （二）补充1.求y ＝log 0.3(x 2－2x )的单调递减区间.解：先求定义域：由x 2－2x ＞0,得x (x －2)＞0∴x ＜0或x ＞2 ∵函数y ＝log 0.3t 是减函数故所求单调减区间即t ＝x 2－2x 在定义域内的增区间.又t ＝x 2－2x 的对称轴为x ＝1 ∴所求单调递减区间为（2，+∞）2.求函数y ＝log 2(x 2－4x )的单调递增区间解：先求定义域：由x 2－4x ＞0得x (x －4)＞0∴x ＜0或x ＞4 又函数y ＝log 2t 是增函数故所求单调递增区间为t ＝x 2－4x 在定义域内的单调递增区间.∵t ＝x 2－4x 的对称轴为x ＝2 ∴所求单调递增区间为：（4，+∞）3. 已知y ＝log a (2－a x)在［0，1］上是x 的减函数，求a 的取值范围.解：∵a＞0且a≠1 当a ＞1时，函数t ＝2－a x>0是减函数由y ＝log a (2－a x)在［0，1］上是x 的减函数，知y ＝log a t 是增函数，∴a＞1 由x ∈［0，1］时，2－a x≥2－a ＞0，得a ＜2, ∴1＜a ＜2当0<a <1时，函数t ＝2－a x>0是增函数由y ＝log a (2－a x)在［0，1］上x 的减函数，知y ＝log a t 是减函数，∴0<a<1 由x ∈［0，1］时，2－a x≥2－1＞0， ∴0<a<1 综上述，0<a<1或1＜a ＜2。

2012高一数学 对数函数（3）学案学习目标：1．进一步理解对数函数的性质，能运用对数函数的相关性质解决对数型函数的常见问题．2．培养学生数形结合的思想，以及分析推理的能力．课前预习：1．复习对数函数的性质．2．回答下列问题．（1）函数y ＝log 2x 的值域是 ；（2）函数y ＝log 2x (x ≥1)的值域是 ；（3）函数y ＝log 2x (0＜x ＜1)的值域是 ．问题解决：一、情境问题函数y ＝log 2(x 2＋2x ＋2)的定义域和值域分别如何求呢？二、学生活动探究完成情境问题．三、数学运用例1：求函数y ＝log 2(x 2＋2x ＋2)的定义域和值域例2：判断下列函数的奇偶性：（1）f (x )＝lgxx +-11 （2）f (x )＝ln(21x +－x )例3：已知log a 0.75＞1，试求实数a 取值范围．例4：已知函数y ＝log a (1－a x )(a ＞0，a ≠1)．（1）求函数的定义域与值域；（2）求函数的单调区间．练习反馈：（1）已知函数y ＝log 2x 的值域是[－2，3]，则x 的范围是________________．（2）函数12log y x =，x ∈(0，8]的值域是 ．（3）函数y ＝log 21(x 2－6x +17)的值域 ．（4）函数()212log 2y x=-的值域是_______________．课堂小结（1）借助于对数函数的性质研究对数型函数的定义域与值域；（2）换元法；（3）能画出较复杂函数的图象，根据图象研究函数的性质（数形结合）． 课后巩固：1．下列函数(1) y ＝x －1；(2) y ＝log 2(x －1)；(3) y (4)y ＝ln x ，其中值域为R 的有 (请写出所有正确结论的序号)．2．函数y ＝lg(x+12－1)的图象关于 对称． 3．已知函数1()log 1a mx f x x -=-(a ＞0，a ≠1)的图象关于原点对称，那么实数m ＝ ． 4．求函数)3(log )27(log 33x x y ⋅=，其中x ∈[127，9]的值域．变式：求函数的最值及取最值时x 的值.学习反思：。

2.3.2 对数函数（2）教学目标：1．掌握对数函数的性质，能初步运用性质解决问题．2．运用对数函数的图形和性质．3．培养学生数形结合的思想，以及分析推理的能力．教学重点：对数函数性质的应用．教学难点：对数函数图象的变换．教学过程：一、问题情境1．复习对数函数的定义及性质．2．问题：如何解决与对数函数的定义、图象和性质有关的问题？二、学生活动1．画出3log (2)y x =+、3log 2y x =+等函数的图象，并与对数函数3log y x =的图象进行对比，总结出图像变换的一般规律．2．探求函数图象对称变换的规律．三、建构数学1．函数log ()a y x b c =++（0,1a a >≠）的图象是由函数log a y x =的图象得到；2．函数|log |a y x =的图象与函数log a y x =的图象关系是 ；3．函数log ||a y x =的图象与函数log a y x =的图象关系是 ．四、数学运用例1 如图所示曲线是对数函数y ＝log a x 的图像，已知a 值取0.2，0.5，1.5，e ，则相应于C 1，C 2，C 3，C 4的a 的值依次为 ． 1C 2C 3C 4C 1 0 xy例2 分别作出下列函数的图象，并与函数y＝log3x的图像进行比较，找出它们之间的关系（1）y＝log3(x－2)；（2）y＝log3(x＋2)；（3）y＝log3x－2；（4）y＝log3x＋2．练习：1．将函数y＝log a x的图像沿x轴向右平移2个单位，再向下平移1个单位，所得到函数图像的解析式为．2．对任意的实数a(a＞0，a≠1)，函数y＝log a(x－1)＋2的图像所过的定点坐标为．3．由函数y＝log3(x＋2)，y ＝log3x的图象与直线y=－1，y＝1所围成的封闭图形的面积是．例3 分别作出下列函数的图象，并与函数y＝log2x的图像进行比较，找出它们之间的关系（1）y＝log2|x|；（2）y＝|log2x|；（3）y＝log2(－x)；（4）y＝－log2x．练习结合函数y＝log2|x|的图象，完成下列各题：（1）函数y＝log2|x|的奇偶性为；（2）函数y＝log2|x|的单调增区间为，减区间为．（3）函数y＝log2(x－2)2的单调增区间为，减区间为．（4）函数y＝|log2x－1|的单调增区间为，减区间为．五、要点归纳与方法小结（1）函数图象的变换（平移变换和对称变换）的规律；（2）能画出较复杂函数的图象，根据图象研究函数的性质(数形结合)．六、作业1．课本P70－6，8，9．2．课后探究：试说出函数y＝log212x的图象与函数y＝log2x图象的关系．。

高中数学6.3 对数函数教案教案名称：高中数学6.3 对数函数教学教案教学目标：1. 理解对数函数的定义和性质。

2. 掌握对数函数的图像、变化规律及其应用。

3. 能够应用所学知识解决相关问题。

教学重点：1. 对数函数的定义和性质。

2. 对数函数的图像和变化规律。

教学难点：1. 理解对数函数与指数函数之间的关系。

2. 掌握对数函数图像在平面直角坐标系中的绘制方法。

教学过程：Step 1：引入概念（10分钟）通过引导学生观察和思考，介绍什么是对数。

让学生了解对数是一个表示底数乘积的幂次方，强调在实际问题中，我们需要掌握对数运算和对数函数的基本概念，并通过实例演示，让学生理解并掌握如何求出零次方、一次方等特殊情况下的值。

Step 2：定义与性质（15分钟）介绍什么是对数函数及其基本性质。

讲解如何根据底数大小确定对数函数增减性及奇偶性，并通过具体例子演示，让学生掌握对数函数的定义和性质。

特别是要强调对数函数与指数函数之间的关系，引导学生理解它们之间的联系和区别。

Step 3：图像绘制（20分钟）详细讲解对数函数在平面直角坐标系中的图像及其变化规律。

通过演示和讲解，让学生深入理解对数函数的图像特点和变化趋势，并能够独立进行绘制。

同时，教师可以提供一些实例，让学生通过观察、分析和推理来确定图像的形状和位置。

Step 4：应用分析（20分钟）提供一些实际问题案例，让学生应用所学知识进行分析和解决。

例如，在一个 pH 值计算问题中求出氢离子浓度等参数。

教师可以给予指导和提示，引导学生利用所学知识进行推理和分析。

通过实例演示，让学生掌握如何运用所学知识解决实际问题，并能够独立应用于其他情境。

Step 5：练习与巩固（10分钟）提供一些涉及对数函数的练习题目，让学生独立或小组合作完成。

教师可以给予指导和反馈，帮助学生巩固所学知识。

鼓励学生自主思考，并培养他们灵活运用所学知识解决问题的能力。

Step 6：拓展与应用（10分钟）引导学生思考更复杂情境下的应用问题。

课堂导学三点剖析一、对数的定义【例1】 将下列指数式化成对数式，对数式化成指数式：(1)3x =271;(2)215=51;(3)x=log 2791. 答案：(1)log 3271=x;(2)log 551=-21;(3)27x = 91. 温馨提示(1)由对数定义，指数式a x =N 与log a N=x(a>0且a ≠1)可相互转化，因此本题容易完成转化.但是要注意两种表示形式中a 、x 、N 的相应位置.(2)x=log a N 实质上是N=a x 的另一种表示形式.二、对数概念的应用【例2】 求下列各式中的x 值： (1)x=161log 21; (2)21log x=-4;(3)log x 8=-3.解析：(1)把x=21log 161化成(21)x =161, 即(21)x =(21)4, ∴x=4. (2)把21log x=-4化为x=(21)-4=16. (3)把log x 8=-3化为x -3=8，即x=318 =21. 温馨提示对于对数和对数的底数与真数三者之间，已知其中两个就可利用对数式和指数式的互化求出另外一个.三、对数的实际应用【例3】 一种放射性元素，最初质量为500 g ，按每年10%衰减.（1）求t 年后，这种放射性元素质量s 的表达式；（2）根据求出的函数表达式，求这种放射性元素的半衰期.（精确到十分位）解析：（1）最初的质量为500 g.经过1年，s=500（1-10%）=500×0.9,经过2年，s=500×0.92,由此类推，t 年后，s=500×0.9t .(2)解方程：500×0.9t =250. 0.9t =0.5.lg0.9t =lg0.5,tlg0.9=lg0.5,t=9.0lg 5.0lg ≈6.6. 即这种放射性元素的半衰期为6.6年.温馨提示利用对数的定义解决有关的实际问题，有一定的能力要求，在解题过程中，要领会在什么时候取对数，怎样取对数，取了对数以后又怎样运算这些常见的问题.各个击破类题演练 1将下列指数形式化成对数形式：（1）54=625；（2）3-2=91.解析：（1）∵54=625，∴log 5625=4.(2)∵3-2=91,∴log 391=-2.变式提升 1将下列对数式化为指数式：（1）log 216=4；(2)log x 64=-6.答案：（1）24=16.（2）x -6=64.类题演练 2求下列各式中的x.（1）log 8x=-32;(2)log x 27=43.答案：（1）由log 8x=-32,得x=328-=323)2(-=2-2,即x=21.(2)由log x 27=43,得43x =27,即43x =33,故x=343)3(=34=81.变式提升 2(1)求log 84的值.（2）已知log a 2=m,log a 3=n,求a 2m +n 的值.解析：（1）设log 84=x,根据对数的定义有8x =4.即23x =22,∴x=32,即log 84=32.(2)∵log a 2=m,log a 3=n,∴a m =2,a n =3,则a 2m+n =(a m )2·a n =22×3=12.类题演练 3生物死亡后，体内的碳-14含量P 的衰变规律是P=5730)21(t .湖南长沙马王堆汉墓女尸出土时碳-14的残余量约占原始含量的76.7%，试推算马王堆汉墓的年代.解析：由对数与指数的关系，指数式P=5730)21(t 可写成对数式t=5 73021log P. 湖南长沙马王堆汉墓女尸中碳-14的残留量约占原始含量的76.7%，即P=0.767,那么t=5 73021log 0.767.由计算器可得t ≈2 193.所以，马王堆古墓约是2 100多年前的遗址.变式提升 3某城市现有人口总数为100万人，如果年自然增长率为1.2%，试解答下面的问题：（1）写出该城市人口总数y(万人)与年份x(年)的函数关系式；（2）计算10年以后该城市人口总数（精确到0.1万人）.解析：（1）x 年后该城市人口总数为y=100×(1+1.2%)x .(2)10年后人口数为100×(1+1.2%)10≈112.7(万).。

1§2.4 对数函数(1)教学任务：（1）通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；（2）能借助计算器或计算机画出具体对数函数的图象，探索并了解对数函数的单调性与特殊点；（3）通过比较、对照的方法，引导学生结合图象类比指数函数，探索研究对数函数的性质，培养学生数形结合的思想方法，学会研究函数性质的方法．教学重点：掌握对数函数的图象和性质．教学难点：对数函数的定义，对数函数的图象和性质及应用．教学过程： 一．问题情境 教材65P ：即细胞分裂次数x 是细胞个数y 的函数．由于我们习惯上是用x 表示自变量，用y 表示x 的函数，所以，在这个新的函数关系中，我们将x 、y 的身份交换一下，就得到：细胞分裂次数y 是细胞个数x 的函数：2log y x .2再看下面一个问题（教材52P 例４）：按照习惯，我们得到：经过的时间y （年）是物质剩留量x 的函数：0.84log y x =．二．对数函数的定义１．定义：函数log a y x =，（0,1a a >≠）叫做对数函数．注意：①对数函数的定义与指数函数类似，都是形式定义，注意辨别．如：x y 2log 2=，5log 5xy = 都不是对数函数，而只能称其为对数型函数．②对数函数对底数的限制：0(>a ，且)1≠a ．２．根据对数函数log a y x =（0,1a a >≠）的来历，我们把它叫做指数函数x ya =（0,1a a >≠）的反函数．（对反“字”的理解，只要从“对应法则”的关系上理解就可以了：确定对数函数的“对应法则”是确定指数函数的“对应法则”反过来的“对应法则”，故理所当然地应该称对数函数为指数函数的反函数．）（当然，我们也不难得出：指数函数x ya =，（0,1a a >≠）叫做对数函数log a y x =（0,1a a >≠）的反函数．）反函数的记号（教材67P ）：一般地，如果函数()y f x =存在反函数，那么它3的反函数记作1()yf x -=．思考（教材65P ）：指数函数xy a =，（0,1a a >≠）的值域是对数函数log a y x=（0,1aa >≠）的定义域；指数函数xy a =，（0,1a a >≠）定义域的是对数函数log a y x=（0,1a a >≠）的值域．上述结论反过来又可说成： 对数函数log a y x=，（0,1a a >≠）的值域是指数函数xy a =（0,1a a >≠）的定义域；对数函数log a y x=，（0,1a a >≠）定义域的是指数函数xy a =（0,1a a >≠）的值域．列成表即：综上，我们有：３．重要结论： 对数函数log a yx =，（0,1a a >≠）与指数函数xy a =（0,1a a >≠）的定义域与值域互换． 由此，立得：对数函数log a yx =，（0,1a a >≠）的定义域为(0,)+∞，4值域为(,)-∞+∞．（这是对数函数的性质之一！）根据这一性质，思考：例１（教材67P ）求下列函数的定义域： (1)0.2log (4)y x =-；(2)log a y= （0,1a a >≠）．分析：由对数函数的来历及得出来的性质知：零和负数没有对数．所以有： 由(1)得：40x ->时，即4x <时，0.2log (4)y x =-才有意义 ，所以函数0.2log (4)y x =- 的定义域是(,4)-∞；由(2)得：0>时，即1x >时log a y =才有意义，所以函数log a y =的定义域是(1,)+∞．说明：１．教材中说的“当4x ≥时，0.2log (4)y x =-没有意义” 、“当1x ≤时，log a y =没有意义”都是多余的说法，以后我们考虑问题是不要这样说．也就是说，当我们把“有意义”的情况都思考到了就行了，“没有意义”的可以省略不说．２．第(2)小题中，函数log a y=后面跟的（0,1a a >≠）是对函数解析式中的字母a 的限制条件，作为一个题目，给出的时候要考虑其严谨性，当然这个条件是不可缺少的．但是，在解题过程中，如果每写一个含字母a 的式子都把限制条件（0,1aa >≠）写一次，又会让人觉得多余，所以，在解题过程中通常就不再重复交代了．练习：（活页45P 第17课时:对数函数(1)例1）函数lg(1)y x =+的定义域为（ ）Ａ．(1,2)- Ｂ．(1,2]-5Ｃ．(1,0)(0,2]-U Ｄ．(1,0)(0,2)-U分析：当201011x x x -≥⎧⎪+>⎨⎪+≠⎩时，即：210x x x ≥⎧⎪>-⎨⎪≠⎩时，也就是x ∈(1,0)(0,2]-U时，函数lg(1)y x =+才有意义．所以，函数lg(1)y x =+的定义域为(1,0)(0,2]-U ．例２．（补充）求函数1()25xy =-的反函数．解：将函数1()25x y =-解析式变形为1()25xy =+，反解得15log (2)x y =+，将x 、y 互换得15log (2)y x =+；又由函数1()25xy =-得其值域为(2,)-+∞，所以，函数1()25xy =-的反函数为115()log (2)(2)f x x x -∴=+>-．三．对数函数的图像和性质问题1：你能类比前面讨论指数函数性质的思路，提出研究对数函数性质的内容和方法吗？研究方法：画出函数的图象，结合图象研究函数的性质．研究内容：定义域、值域、特殊点、单调性、最大（小）值、奇偶性．探索研究：○1 在同一坐标系中画出下列对数函数的图象；（可用描点法，也可借助科学计算器或计算机）6讲解：①：01在同一坐标系内作出2log yx =与2x y =的图像；（链接：D:\备课用包\2函数\附件\对数函数(1)课件.gsp ）02由函数2log y x =是函数2x y =的反函数，得知：若点Ｂ00(,)x y 在函数2log yx =的图像上，即有020log y x =，则有002y x =，所以，点Ａ00(,)y x 一定在2x y=的图像上；03观察得到：函数2log y x =的图像与函数2x y =的图像关于直线y x =对称．②：01在同一坐标系内作出12log y x =与1()2xy =的图像；（链接：D:\备课用包\2函数\附件\对数函数(1)课件.gsp ）2由函数12log y x =是函数1()2xy =的反函数，得知：若点Ｂ00(,)x y 在函数12log y x =的图像上，即有0102log y x =，则有001()2y x =，所以，点Ａ00(,)y x 一定在1()2xy =的图像上；3观察得到：函数12log y x =的图像与函数1()2xy =的图像也关于直线y x =对称．7由特殊到一般：（教材66P “思考”的答案：一般地，当0,1aa >≠时，函数x y a =与函数log a y x =的图像关于直线y x =对称．）③ 思考底数a 是如何影响函数x y a log =的．（学生独立思考，师生共同总结）规律：在第一象限内，逆时针方向，图象对应的对数函数的底数逐渐变小．在第一象限内，逆时针方向，图象对应的指数函数的底数逐渐变大．Ⅱ.性质D:\备课用包\2函数\附件\对数函数(1)课件.gsp例３．（教材67P 例２）比较下列各组数中两个值的大小：D:\备课用包\2函数\附件\对数函数(1)课件.gsp(1)log 3.4,log 3.822；(2)log 1.8,log 2.10.50.5；(3) log 5,log 776．练习: (课时训练P45例3)8利用对数函数的单调性,比较下列各组数的大小.(1) e π ;(2)132log 0.3,log 0.2 ;(3)34log 0.4,log 0.4 .(1)e π>(2) 找中间值 “1” (3) 先取倒数0.40.4log 3log 4>,再比较得34log 0.4log 0.4<(课时训练P45练习2) 若01a <<,则0.3133log ,log ,log a a a 的大小顺序是( )A.10.333log log log a a a >> B. 310.33log log log a a a >>C.0.3133log log log a a a >> D. 30.313log log log a a a >>解析: 先化同底111,,1log 0.3log 3log 3a a a∵1log 0.3log 0log 33a a a >>>9∴10.333log log 0log a a a >>> 应选A.四．【课堂小结】本节学习了如下内容：１．对数函数的概念；２．对数函数的性质． 五．〖课外作业〗 １．教材70P 习题2.3(2)第1、2、3题； ２．活页45P 第17课时：对数函数(1)．。