艾滋病疗法的评价及疗效预测模型
- 格式:doc
- 大小:1.02 MB
- 文档页数:32

艾滋病疗法的评价及疗效的预测摘要:艾滋病是当前人类社会最严重的瘟疫之一,从1981年发现以来的20多年间,它已经吞噬了近3000万人的生命。
所以对艾滋病相关用药的时间、疗法的选择、费用的考虑具有重要意义。
本文主要主要运用了层次分析法以及数据的差值和拟合来解决问题。
关键词:数据拟合;层次分析法;艾滋病疗法一、问题重述艾滋病是当前人类社会最严重的瘟疫之一,从1981年发现以来的20多年间,它已经吞噬了近3000万人的生命。
艾滋病的医学全名为“获得性免疫缺损综合症”,英文简称AIDS,它是由艾滋病毒(医学全名为“人体免疫缺损病毒”,英文简称HIV)引起的。
这种病毒破坏人的免疫系统,使人体丧失抵抗各种疾病的能力,从而严重危害人的生命。
人类免疫系统的CD4细胞在抵御HIV的入侵中起着重要作用,当CD4被HIV感染而裂解时,其数量会急剧减少,HIV将迅速增加,导致AIDS发作。
艾滋病治疗的目的,是尽量减少人体内HIV的数量,同时产生更多的CD4,至少要有效地降低CD4减少的速度,以提高人体免疫能力。
迄今为止人类还没有找到能根治AIDS的疗法,目前的一些AIDS疗法不仅对人体有副作用,而且成本也很高。
许多国家和医疗组织都在积极试验、寻找更好的AIDS疗法。
现在得到了美国艾滋病医疗试验机构ACTG公布的两组数据。
ACTG320(见附件1)是同时服用zidovudine(齐多夫定),lamivudine(拉美夫定)和indinavir(茚地那韦)3种药物的300多名病人每隔几周测试的CD4和HIV的浓度(每毫升血液里的数量)。
193A(见附件2)是将1300多名病人随机地分为4组,每组按下述4种疗法中的一种服药,大约每隔8周测试的CD4浓度(这组数据缺HIV浓度,它的测试成本很高)。
4种疗法的日用药分别为:600mg zidovudine或400mg didanosine(去羟基苷),这两种药按月轮换使用;600 mg zidovudine加2.25 mg zalcitabine(扎西他滨);600 mg zidovudine加400 mg didanosine;600 mg zidovudine加400 mg didanosine,再加400 mg nevirapine(奈韦拉平)。


艾滋病疗法的评价及疗效的预测帅治渝,梁文真,黄文婷指导教师 朱伟摘要:本文主要就艾滋病的疗法进行了评价,并针对所提供的数据分别利用一元多项式非线性回归模型和改进的平滑GM (1,1)模型-平滑灰度模型,对治疗方法的疗效进行了的预测,由此得出了不同方案下最佳停止治疗时间。
针对问题一,首先利用一元多项式非线性回归模型对问题进行分析,得出CD4和HIV 浓度的整体变化规律,然后利用平滑处理法,改变了灰色模型单调无限增加的特点,进而引入平滑灰度模型并对其求解,得出在各个病情阶段的最佳停止治疗时间。
针对问题二,根据如下疗法优劣评价准则:①服药过后CD4浓度维持“安全”水平的时间的长短。
②服药后,在相同时间内,CD4浓度含量变化速度的快慢,对疗法进行评价,判断得出疗法4的治疗效果是最好的。
最佳治疗时间为21周。
针对问题三,考虑到了经济因素,首先对四种疗法的费用进行了评价。
然后,结合各疗法的疗效,利用费用-效果比的方法对4种疗法进行评价。
得出疗法3的综合评价是最高的,进而利用一元多项式非线性回归求出采用疗法3时,最佳停止治疗时间为12周左右。
关键字:平滑GM(1,1)灰色模型;一元多项式非线性回归;期望;费用-效果比值1 问题假设1.假设两个相邻测试点之间每一个周的CD4浓度(HIV )变化率相等。
2.假设测试的病人在测试期间均未出现并发症,测量数据准确有说服力。
3.假设年龄对CD4浓度没有影响。
4.假设不考虑测试对象之间的个体差异。
5.假设不统计存在异常现象的个体数据。
6.假设病人每天都按时吃药。
7.假设每一个月有30天。
2 全局符号说明()y t :CD4浓度在t 时刻时0~t 的总和;α:平滑系数;t x :CD4在t 时刻进行测量时的浓度值;:第(1)i +个测试点与第i 个测试点之间CD4(HIV)的周均变化率;ˆt x:在t 时刻t x 的GM (1,1)的预测值;ˆt y :在t 时刻k y 的GM (1,1)的值;()i f t :第i 种疗法的费用函数;()i g t :第i 种疗法的疗效函数。

关于艾滋病疗法的评价及疗效预测的数学模型关于艾滋病疗法的评价及疗效预测的数学模型摘要艾滋病治疗的目的,是尽量减少人体内HIV的数量,同时产生更多的CD4,至少要有效地降低CD4减少的速度,以进步人体免疫才能。
艾滋病的实际治疗研究说明,CD4浓度增加,HIV浓度降低,艾滋病患者的病情会得到较好控制,但是,在治疗过程中发现,药物治疗的效果并非如我们想象的那样可以持久有效,即:在使用某1种药物治疗到达1定时间之后,无论是HIV还是CD4的含量都会出现反弹,而这个时间往往也因病人而异。
此外,在实际治疗时,不同的药物治疗的费用与治疗效果都不一样,在对病人进展治疗时常常会综合使用几种药物,如何恰当的混合使用药物来获得最好的治疗方案也是需要解决的1个问题。
针对这些问题,本文以美国艾滋病医疗试验机构ACTG(Aids Clincal Trials Group)公布的两组数据为根底,用数学建模的方法对药物最正确治疗终止时间预测及药物治疗方案评价问题进展了分析,并建立了相应的预测模型与评价模型。
结果说明,所构建的预测模型对大局部个体数据有较好的符合度,具有预测疗效、计算最正确治疗终止时间的作用;而所构建的评价模型能为艾滋病的实际治疗提供理论上的参考。
关键词: 治疗效果;最正确治疗时间;阻滞增长模型Mathematical Module For Appreciation Prediction of Efficiency on Medical Therapies Against AIDSAbstractPresently, AIDS(Acquired Immune Deficiency Syndromes) is one of the most serious epidemic in the world, which means ,since found in 1981,it has taken almost 30 million lives.The therapies aim at reducing the amount of HIV, and producing more CD4 as much as possible, at least slowing down the speed CD4 loses with, which will enhance humans immuning ability. The actual research on AIDS shows that with CD4 increases, HIV decreases, and the patient feelsbetter. .But, we also know that the efficiency cant last as long as we thought. Namely, after certain times, no matter HIV or CD4 may have a unpredictable phenomenon. And the standard for that differs. Also, in actual cruelty, different therapies have different fees and different efficiencies. So some kinds of medicine usually are used in certain approach. How to use them properly to obtain the best efficiency is our focus.Facing such problems, this article analyzes the prediction about best ending time and appreciation, building corresponding predicting-module and appreciating one.As result shows, predicting-module has a good coordination to major of data, and works well in predicting efficiency and puting the best ending time. Meanwhile, the appreciating one can be a theorical proof for AIDS actual operation.Keywords: Efficiency; Best Cure Time; Module of Preventing Increasement欢送访问。
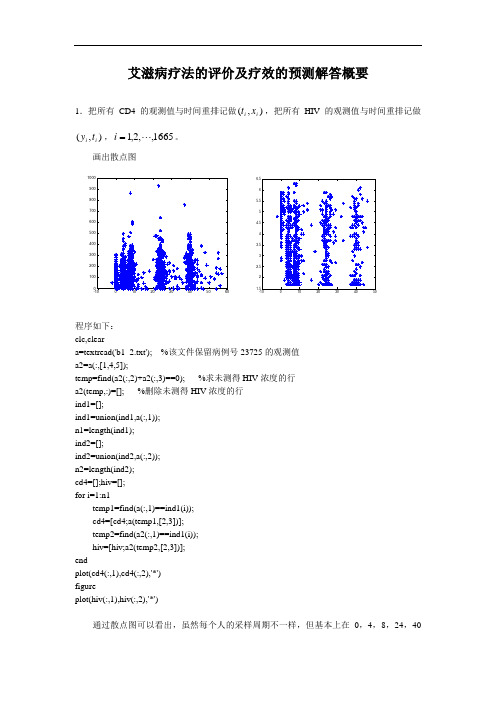
艾滋病疗法的评价及疗效的预测解答概要1.把所有CD4的观测值与时间重排记做),(i i x t ,把所有HIV 的观测值与时间重排记做),(i i t y ,1665,,2,1 i 。
画出散点图程序如下: clc,cleara=textread('b1_2.txt'); %该文件保留病例号23725的观测值 a2=a(:,[1,4,5]);temp=find(a2(:,2)+a2(:,3)==0); %求未测得HIV 浓度的行 a2(temp,:)=[]; %删除未测得HIV 浓度的行 ind1=[];ind1=union(ind1,a(:,1)); n1=length(ind1); ind2=[];ind2=union(ind2,a(:,2)); n2=length(ind2); cd4=[];hiv=[]; for i=1:n1temp1=find(a(:,1)==ind1(i)); cd4=[cd4;a(temp1,[2,3])]; temp2=find(a2(:,1)==ind1(i)); hiv=[hiv;a2(temp2,[2,3])]; endplot(cd4(:,1),cd4(:,2),'*') figureplot(hiv(:,1),hiv(:,2),'*') 通过散点图可以看出,虽然每个人的采样周期不一样,但基本上在0,4,8,24,40周左右进行采样。
我们可以不考虑具体的采样时间,只考虑5次采样,这5次采样时间都看作是在第0,4,8,24,40周进行。
我们建立logistic 模型,考虑到logistic 模型的增长曲线是单调的,不能在整个时间段上进行拟合,应当在每个单调区间上进行拟合。
我们利用前4次采样数据建立logistic 模型。
设)(t x 表示t 时刻CD4的浓度,对于logistic 连续模型,设微分方程为)1(bx ax dtdx-=,0)0(x x = (1)其中参数b a ,需要通过拟合得到。

艾滋病疗法的评价及疗效的预测摘要本题是一个根据ACTG所公布的数据对艾滋病的疗法进行评价,并对其疗效进行预测的问题。
在解决过程中,我们建立了四个数学模型,并给出了具体的数值结果。
针对问题一,我们建立了两个数学模型,从附件一中筛选了部分数据,从不同的角度解决了问题。
模型一运用了二元线性回归预测方法以最小二乘法为工具得到了二元经验线性回归方程及相应数值结果。
模型二为带有权重系数的Hammerstein模型,可视为模型一的推广。
在一般情况下,它是一个非线性的模型,因而我们用最速下降法给出了回归方程系数的数值解法。
问题二的解答利用了模型一、二中的相关结论,建立了一个多目标决策的数学模型。
该模型中,我们运用层次分析法得到了各评价因子的权重系数,并由此得出疗法的综合评价指数。
从附件二中筛选了部分数据,根据病情及年龄将其分为九类,对每一类患者选择了较优的疗法,并确定了最佳治疗终止时间。
在问题三的解决过程中,我们考虑了疗效和费用两因素,建立了模糊切比雪夫多目标决策模型,利用该模型我们得到了问题二的重新评价和预测结果。
问题一、二、三的具体数值结果如下:问题一:轻症患者最佳治疗终止时间为第76周,中症患者为第65周,重症患者为第54周。
问题二:对第1类病人第一种疗法的疗效较好,其最佳治疗终止时间为第78 周;对第3类病人第二种疗法较为有效,其最佳治疗终止时间为第20周;对第2类病人第三种疗法的治疗效果较好,其最佳治疗终止时间为第41周;对第48类病人第四种疗法较为有效,最佳治疗终止时间分别为第34,29,40,24,25周。
问题三:问题二中需要调整疗法的有:第3、第7、第8类病人,他们均可选用第三种疗法。
关键词:最小二乘法模糊切比雪夫多目标决策层次分析法一、问题的重述与分析1、问题的重述艾滋病是当前人类社会最严重的瘟疫之一,从1981年发现以来的20多年间,它已经吞噬了近3000万人的生命。
艾滋病的医学全名为“获得性免疫缺损综合症”,英文简称AIDS,它是由艾滋病毒(医学全名为“人体免疫缺损病毒”, 英文简称HIV)引起的。
艾滋病疗法的评价及疗效的预测摘要:艾滋病是当前人类社会最严重的瘟疫之一,近20多年来已吞噬了近3000万人的生命。
但人类迄今为止还没有找到能有效治疗艾滋病的疗法,为摆脱传统的高成本高副作用疗法,许多国家和医疗组织都在积极试验、寻找更好的疗法。
本文是研究艾滋病疗法的评价及疗效的预测的统计决策问题。
我们以美国艾滋病医疗试验机构ACTG 公布的两组数据ACTG320和193A 为资料,结合艾滋病治疗的现况,分别建立模型,分析求解。
针对问题一,我们根据实际情况——具体药物对不同程度患者疗效不同,先据此建立多元统计聚类分析模型(对患者进行患病轻重分类),通过提取出ACTG320中的各患者开始服药时(0周时)的CD4和HIV 的浓度值,运用SAS 进行聚类分析,将患者分为3类——重病、一般和轻度患者,具体每类见文中多元统计聚类分析模型结果;再建立多项式拟合模型Ⅰ,通过统计的CD4和HIV 的浓度值随时间周的变化关系,运用Matlab 提供的拟合函数polyfit 进行拟合,拟合曲线见图1~图3,并做出决策——重病、一般和轻度3类患者服用此药分别应该在开始服药后第34周、第18周和第29周停药。
针对问题二,我们先建立层次分析法模型,将不同年龄段作为准则层,4种疗法作为措施层,确定最优疗法作为目标层。
通过统计原数据,构造层次结构图的各层成对比较阵,运用Matlab 编程可判别第4种疗法最优;同样再建立多项式拟合模型Ⅱ,通过统计出的最优疗法中的3类病人对应的Log(CD4 count+1)值对时间周的变化关系,运用Matlab 提供的拟合函数polyfit 进行拟合,拟合曲线见图4~图6,并做出决策——青年、中年和老年3类患者服用此药分别应该在开始服药后第14周、第8周和第3周停药。
针对问题三,我们先建立模糊综合评判模型,以“平均疗效”和“平均价格的倒数”为因素集、以4种疗法为评判集,通过统计原数据,建立综合评判矩阵,根据人群的特性选择不同的权重,进行模糊综合评判,判别出对于一般人群和富有人群而言第四种疗法是最优,而对于贫困的人群而言选择第三种疗法则是最优;为了增强拟合效果,我们先对tit S L 建立差分模型;最后再建立多项式拟合模型Ⅲ,通过统计出的最优疗法中的3类病人对应的t y t ∆∆值对时间周的变化关系,运用Matlab 提供的拟合函数polyfit 进行拟合,拟合曲线见图7~图9,并做出决策——青年、中年和老年3类患者服用此药分别应该在开始服药后第20周、第8周和第10周停药。
承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):B甲1304所属学校(请填写完整的全名):山东理工大学参赛队员(打印并签名) :1.指导教师或指导教师组负责人(打印并签名):丁树江日期:2006 年 9月 18 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):艾滋病疗法的评价及疗效的预测摘要本文利用美国艾滋病医疗试验机构ACTG公布的ACTG320和193A数据,在合理的假设基础上,通过线性插值拟合均匀的模拟出每个被调查者每周身体中CD4细胞计数和HIV浓度,对所有的被调查者每周的CD4细胞计数和HIV浓度求平均值,这样可以得到一个关于该疗法的从时间序列角度来说较为完全的数据。
用SPSS模拟出最优曲线,得出该疗法对人体CD4细胞计数影响近似为三次曲线,而对人体HIV浓度的影响在四十周以前与四十周以后可以分别用S曲线和三次曲线较好的模拟,从而可以更好的预测未来疗效。
由于现行实验室艾滋病入选标准为CD4细胞计数,所以我们根据CD4细胞计数的拟合曲线,参考HIV 拟合曲线,得出应该在二十七周左右终止该疗法。
针对问题二中被随机分组的1300多名被调查者分别服用不同的药物组合的跟随检测数据,沿用问题一的数据处理方法,用均匀插值填充从第零周到最后一周的数据,得到四种疗法被调查者每周的CD4细胞计数时间序列数据,计算出使用各种疗法的所有被调查者在每个周次的CD4细胞计数的均值,合出较优的针对经过用SPSS多次模拟,拟每种疗法的模型,继而可用此模型分别预测每种疗法继续使用的疗效。
艾滋病疗法的评价及疗效预测模型摘要本文利用附件1和附件2中的测试数据,建立了基于差分方程的统计回归预测模型,对艾滋病患者的最佳治疗终止时间进行预测;并且对现有的4种艾滋病疗法建立评价预测模型。
统计预测模型的基本思想为:第一,筛选出附件1中的有效数据,采用插值的方法对数据进行补充;第二,利用模糊聚类分析法将被测试者分为三类,体内CD4和HIV含量均较高者为第一类,体内CD4和HIV含量均较低者为第二类,其他的为第三类;第三,将时间离散化,通过建立被测试者体内CD4浓度的差分方程,求解出被测试者服药治疗对体内CD4浓度的作用效果函数的差分方程。
同理求解出对HIV效果函数的差分方程。
第四,分别给出CD4和HIV效果函数的初值后,由差分方程迭代求得两组效果函数值;第五,使用回归分析的方法求出效果函数的表达式,求其加权和即得综合疗效。
综合疗效达到最大的时刻即为最佳治疗终止时间。
对于问题一,通过统计预测模型,对附件1中的数据求解,其结果如下:评价预测模型的基本思想为:首先,筛选出附件2中的有效数据后进行插值;其次,按年龄将被测试者分为青年组和中年组;再次,确定评价目标为:CD4浓度增长的效果、有效治疗时间和疗法的费用,并对其作无量纲化处理,统一评价标准;最后,以测试时间为约束建立多目标规划模型,对4种疗法进行评价。
对于问题二,仅以CD4为标准,取治疗费用的偏好系数为零,利用评价预测模型对对于问题三,评价时需要考虑4种疗法的费用。
在评价预测模型中固定有效治疗时间的偏好系数,当费用偏好系数变化时,利用模拟的方法评价出最优疗法,并求其最佳终止治疗时间。
通过此法对附件2求解,得:每一个费用偏好系数P3的变动区间,均有对应的最佳终止治疗的估计区间。
关键词:偏好系数聚类分析回归分析多目标规划1.背景及问题提出艾滋病是当前人类社会最严重的瘟疫之一,从1981年发现以来的20多年间,已吞噬了近3000万人的生命。
艾滋病的医学全名为“获得性免疫缺损综合症”,英文简称AIDS,它是由艾滋病毒(医学全名为“人体免疫缺损病毒”, 英文简称HIV)引起的。
这种病毒破坏人的免疫系统,使人体丧失抵抗各种疾病的能力,从而严重危害人的生命。
人类免疫系统的CD4细胞在抵御HIV的入侵中起着重要作用,当CD4被HIV感染而裂解时,其数量会急剧减少,HIV将迅速增加,导致AIDS发作。
艾滋病治疗的目的是尽量减少人体内HIV的数量,同时产生更多的CD4细胞,至少要有效地降低CD4减少的速度,以提高人体免疫能力。
现有美国艾滋病医疗试验机构ACTG公布的两组数据。
ACTG320(见附件1)是同时服用zidovudine(齐多夫定),lamivudine(拉美夫定)和indinavir(茚地那韦)3种药物的300多名病人每隔几周测试的CD4和HIV的浓度(每毫升血液里的数量)。
193A (见附件2)是将1300多名病人随机地分为4组,每组按下述4种疗法中的一种服药,大约每隔8周测试的CD4浓度(这组数据缺HIV浓度,它的测试成本很高)。
4种疗法的日用药分别为:600mg zidovudine或400mg didanosine(去羟基苷),这两种药按月轮换使用;600 mg zidovudine加2.25 mg zalcitabine(扎西他滨);600 mg zidovudine 加400 mg didanosine;600 mg zidovudine加400 mg didanosine,再加400 mg nevirapine (奈韦拉平)。
基于上述条件完成以下问题:(1)利用附件1的数据,预测继续治疗的效果,或者确定最佳治疗终止时间。
(2)利用附件2的数据,评价4种疗法的优劣(仅以CD4为标准),并对较优的疗法预测继续治疗的效果,或者确定最佳治疗终止时间。
(3) 艾滋病药品的主要供给商对不发达国家提供的药品价格如下:600mg zidovudine 1.60美元,400mg didanosine 0.85美元,2.25 mg zalcitabine 1.85美元,400 mg nevirapine 1.20美元。
如果病人需要考虑4种疗法的费用,对(2)中的评价和预测(或者提前终止)有什么改变。
2.问题分析本题针对艾滋病治疗情况,提供被测试者的治疗数据,要求建立模型预测治疗效果(或确定最佳治疗终止时间),并且评价4种治疗方案。
2.1.CD4和HIV的关系医学研究表明:在T淋巴细胞分类中,CD4代表T辅助细胞。
CD4细胞是HIV感染的主要靶细胞,而其本身又是免疫反应的中心细胞。
人体感染了HIV后,主要表现为:CD4细胞的丢失,绝对数量的减少。
而HIV病毒和CD4细胞自身都有增长的能力,因此可以认为二者是相互竞争对抗的,又是相互影响的。
2.2.“预测继续治疗效果和最佳治疗终止时间”的理解2.2.1.治疗效果是指疗法对测试者体内的CD4以及HIV数量变化的影响。
因此为了得到精确的预测结果,需要充分考虑被测试者的身体状况及其病情严重程度等因素。
故可将被测试者进行分类,按类别预测继续治疗的效果。
2.2.2.继续治疗指在测试终止后继续服药。
最佳治疗终止时间,指由于继续服药效果下降而停止治疗的时间。
预测继续治疗效果的依据是效果函数的变化趋势,而最佳治疗终止时间也体现了治疗效果的变化趋势,两者可以看作同一个问题。
由此本文针对不同类别被测试者分别计算其最佳治疗终止时间。
2.3.预测方法步骤利用附件中提供的测试数据进行统计预测。
根据预测的连贯原则(预测对象的发展始终都按一定的规律进行的原则)和类推原则(预测对象必须有某种结构,其升降起伏变动是有章可循的原则),利用数学方法模拟治疗效果的内部结构,进而建立适当的预测模型,对治疗效果进行近期预测。
统计预测的具体过程如下图:图1统计预测过程流程图2.4.疗法优劣的评价标准迄今为止人类还没有找到根治AIDS的疗法。
因此要对第二问中给出的4种疗法进行评价,就不能以疗法是否可以治愈艾滋病为标准。
本文从治疗效果、治疗周期、治疗费用等多方面考虑,对四种疗法进行综合评价及预测。
目前的一些AIDS疗法不仅对人体有副作用,而且成本也很高。
第三问中需要考虑疗法的费用问题,因此第三问的求解是在第二问的基础上,将治疗费用添加到评价因素中,重新对四种疗法进行的评价及预测。
3.基本假设(1)忽略测试数据中的误差。
(2)HIV的增加速率、CD4的减少速率是随时间变化的连续函数。
(3)由于HIV病毒自身的繁殖能力很强,从而可以忽略HIV阻碍自身增长的作用。
4.符号说明5. 关于问题一的预测模型5.1.问题准备5.1.1 数据处理插值——附件1是被测试者每隔几周的测试数据,然而要预测被测试者继续治疗的效果,需要得到反映被测试者每周身体状况的数据。
我们采用样条插值的方法得到所需数据,具体步骤如下:Step1:从附件1中读取原始数据。
Step2:对于有CD4(t)和HIV 的测试值为空值的数据,将其删除。
Step3:剔除无效数据后对相关节点进行三次样条插值。
筛选有效数据——被测试者接受测试的时间长短是不同的,因此插值时不能保证结果都是经内插得到的结果。
当结点不在所选插值区间时,不能保证插值得到的结果是正值,为保证求解的精确性将这些数据去除。
经统计,绝大多数被测试者接受测试的时间在40周以内,所以选取0-40周为插值区间,舍弃其它的数据。
注*插值程序见附录一程序1-1,结果存储在‘data.mat ’源文件中。
5.1.2 Fuzzy 聚类第一问要预测治疗效果,相同的治疗效果在不同被测试者身上的体现是不同的,被测试者的测试效果会产生差别。
如果直接将所有被测试者视为一类人来预测,由于初始的身体状况对治疗效果的影响,预测结果的误差会较大。
所以要根据第一步处理过的数据,将被测试者分类。
被测试者得身体状况不能明确的量化表示,属于模糊概念,并且不同被测试者的身体状况也不容易比较,因此选用模糊聚类分析的方法对被测试者进行分类。
聚类分析的基本思想是用相似性尺度来衡量事物之间的亲属程度,并以此来实现分类,Fuzzy 聚类分析中的衡量尺度不是明确的,而是根据研究对象本身的属性来构造Fuzzy 矩阵,在此基础上根据一定的隶属度来确定其分类关系。
(注*相关概念见附录二。
)模糊聚类分析步骤如下:第一,建立Fuzzy 相似矩阵。
在实际中有很多建立相似矩阵的方法,经常使用的方法是“最大最小法”: n j i x xx xr m k jk ikm k jk ik ij ,,2,1,)()(11 =∨∧=∑∑== (5.1) 第二,改造Fuzzy 相似矩阵为Fuzzy 等价矩阵。
用上述方法建立相似矩阵R 后要将R 改造成Fuzzy 等价矩阵,从而得到聚类图,在适当的阈值上进行截取,便可得到所需要的分类。
由附录二中的定理可知:将Fuzzy 相似矩阵改造成Fuzzy 等价矩阵的可行性。
事实上,用求传递闭包的方法可将R 改造成)(R t ,具体方法如下:依次计算2422l t tR R RR R R R R R ===当第一次出现k k k R R R =时,必有k R R t =)(,因此k R 就是由n n ij r R ⨯=)(改造的模糊等价矩阵。
第三,进行Fuzzy 聚类。
对Fuzzy 等价矩阵)(R t 进行聚类处理,给定的分类置信水平的α,令1,0,ij ij ij r r r ααα>⎧⎪=⎨≤⎪⎩ (5.2) 得到矩阵α)(R t 。
如果ααik ij r r =则说明第j 个元素和第k 个元素是同一类的。
5.2.模型建立要对继续治疗的效果进行预测,应明确预测目标是治疗的效果。
为此,确定治疗效果函数是建立预测模型的基础。
5.2.1.确定治疗效果函数由题目可知:艾滋病治疗的目的是尽量减少人体内HIV 的数量,同时产生更多的CD4,至少要有效地降低CD4减少的速度。
因此我们认为,CD4细胞和HIV 在人体内是相互竞争的关系。
艾滋病治疗对人体内CD4细胞数量的增长起到正面效果,对HIV 数量的增长起到负面的效果。
据此确定被测试者服药治疗后体内CD4细胞和HIV 数量的变化规律。
附件1中给出的数据是300多名病人每隔几周测试的CD4和HIV 的浓度,时间是离散化的,因此建立差分方程,描述CD4和HIV 的浓度的变化规律。
5.2.1.1建立差分方程,确定药物对CD4数量的效果函数通常情况下人体内的CD4数量在800—1200个,最低不少于400个,由此假设CD4的最大含量4CD N 为1200个。
人体内CD4数量的变化量,由以下三部分构成:(1)CD4细胞的自然增长作用,增加的CD4细胞数量;(2)HIV 的入侵对CD4细胞的裂解作用,减少的CD4细胞数量;(3)药物治疗作用,增加的CD4细胞数量。