北京四中数学必修五练习第三章 不等式综合之提高篇

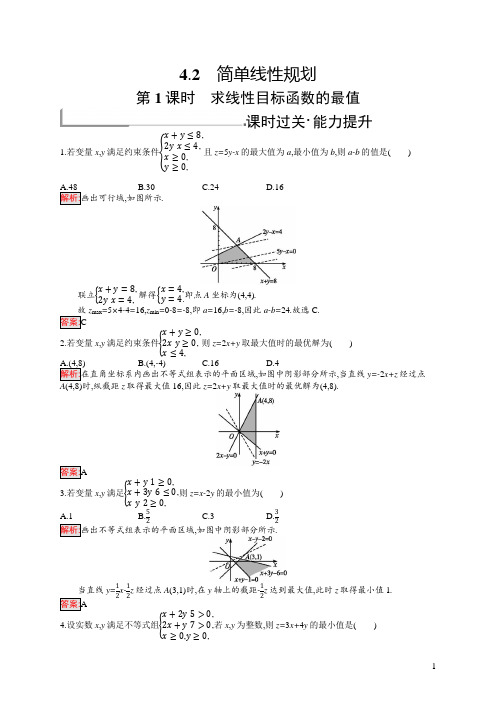
4.2 简单线性规划第1课时 求线性目标函数的最值课时过关·能力提升1.若变量x ,y 满足约束条件{x +y ≤8,2y -x ≤4,x ≥0,y ≥0,且z=5y-x 的最大值为a ,最小值为b ,则a-b 的值是( )B.30C.24D.16 ,如图所示.联立{x +y =8,2y -x =4,解得{x =4,y =4.即点A 坐标为(4,4).z max =5×4-4=16,z min =0-8=-8,即a=16,b=-8,因此a-b=24.故选C . 2.若变量x ,y 满足约束条件{x +y ≥0,2x -y ≥0,x ≤4,则z=2x+y 取最大值时的最优解为( )B.(4,-4)C.16D.4,如图中阴影部分所示,当直线y=-2x+z 经过点,纵截距z 取得最大值16,因此z=2x+y 取最大值时的最优解为(4,8).3.若变量x ,y 满足{x +y -1≥0,x +3y -6≤0,x -y -2≥0,则z=x-2y 的最小值为( )A.1B.52C.3D.32解析:画出不等式组表示的平面区域,如图中阴影部分所示.当直线y=12x-12z 经过点A (3,1)时,在y 轴上的截距-12z 达到最大值,此时z 取得最小值1.4.设实数x ,y 满足不等式组{x +2y -5>0,2x +y -7>0,x ≥0,y ≥0,若x ,y 为整数,则z=3x+4y 的最小值是( )A.14B.16 D.19{x +2y -5>02x +y -7>0x ≥0,y ≥0表示的平面区域,如图中阴影部分所示.x ,y 为整数,所以z=3x+4y 在点A (4,1)处取到最小值16.x ,y 满足|x|+|y|≤1,z=2x+y ,则z 的最大值和最小值分别为( ) B.2,-2 C.1,-2 D.2,-1≤1表示的平面区域如图阴影部分所示.y=-2x+z 过点(1,0)时,z 最大;当直线y=-2x+z 过点(-1,0)时,z 最小,则z 的最大值为2,最小值为-2.6.设变量x ,y 满足约束条件{x -2≤0,x -2y ≤0,x +2y -8≤0,则目标函数z=3x+y 的最大值为( )B .8C .9D .14 解析:画出题中约束条件满足的可行域,如图中阴影所示.目标函数z=3x+y 可化为y=-3x+z ,平移目标函数线当其过点A 时,z 取最大值.由{x =2,x +2y -8=0得{x =2,y =3.A 的坐标为(2,3),z max =3×2+3=9.7.若实数x ,y 满足不等式组{x +y ≥2,2x -y ≤4,x -y ≥0,则z=2x+3y 的最小值是 ..当直线y=-23x+z 过点A (2,0)时,z=2x+3y 有最小值4.8.若实数x ,y 满足{y ≤2x ,y ≥-2x ,x ≤3,则目标函数z=x-2y 的最小值是 .画出满足不等式组的可行域如图阴影部分所示,目标函数化为y=12x-z ,当直线经过点A 时,-z 的值最,点A 坐标为(3,6),所以z 的最小值为3-2×6=-9. 99.若x ,y 满足不等式组{x -y +1≥0,x +y +1≥0,x +2y -2≤0,x -2y -2≤0,则z=3x+y-7的最大值为 .解析:画出可行域如图阴影部分所示.当直线y=-3x+z 0经过点A (2,0)时,直线在y 轴上的截距z 0最大,所以z 0=3x+y 有最大值6,故7有最大值-1. 110.设z=2y-2x+4,式中x ,y 满足{0≤x ≤1,0≤y ≤2,2y -x ≥1,求z 的最大值和最小值.{0≤x ≤1,0≤y ≤2,2y -x ≥1的可行域,如图阴影部分所示,作直线l :2y-2x=z-4,当直线l 经过点时,z max =2×2-2×0+4=8;当直线l 经过点B (1,1)时,z min =2×1-2×1+4=4.★11.求z=5x-8y 的最大值,式中的x ,y 满足约束条件{x +y ≤6,5x +9y ≤45,x ≥0,y ≥0.{x +y ≤6,5x +9y ≤45,x ≥0,y ≥0的可行域,如图阴影部分所示.作直线l 0:5x-8y=0,平移直线l 0,由图可知,当直线平移到经过点A 时,z 取最大值.解方程组{x +y =6,y =0,得A (6,0),所以z max =5×6-8×0=30. ★12.若实数x ,y 满足不等式组{2≤2x -y ≤4,x ≤3,y ≥-3,求下列目标函数的最大值,以及此时x ,y 的值.(1)z=x-y ; 3y+1.解:在平面直角坐标系中画出可行域,如图阴影部分所示.(1)当直线y=x-z 移动到经过点A (12,-3)时,直线在y 轴上的截距-z 最小,为-72,所以当x=12,y=-3时,z取得最大值72.(2)当直线y=-13x+z -13移动到经过点B (3,4)时,直线在y 轴上的截距z -13最大,为5,所以当x=3,y=4时,z 取得最大值16.。

3.2 基本不等式与最大(小)值第1课时 利用基本不等式求最值课时过关·能力提升1.设a>0,b>0,若√3是3a 与3b 的等比中项,则1a +1b 的最小值为( ) A.8B.4C.1D.143a ·3b =3,所以a+b=1,所以1a +1b =(a+b )(1a +1b )=2+ba +ab ≥2+2√b a ·ab =4,当且仅当ba =ab ,即a=b=2时,等号成立. 2.若x>0,则y=33x 1x的最大值是( ) B.33√2C.32√3D.133x 1x =3(3x +1x )≤32√3x ·1x =32√3,当且仅当3x=1x ,即x=√33时,等号成立. 3.已知a>0,b>0,则1a +1b +2√ab 的最小值是( ) B.2√2C.4D.51b +2√ab ≥2√1ab +2√ab ≥2√2√1ab ·2√ab =4.当且仅当{1a =1b ,√1ab=√ab ,即a=b=1时,等号成立,故1a +1b +2√ab 的最小值为4.4.若x>1,则函数y=x 2+11-x2的最大值为( )B.0C.1D.2x>1时,x 2+1x 2-1=x 21+1x 2-1+1≥2√(x 2-1)·1x 2-1+1=3,当且仅当x=√2时,等号成立,所以x 2+1-x 2≤3. 5.若a>0,b>0,a+b=2,则y=1a+4b的最小值是( ) A.72B.4C.92D.5a+b=2,∴1=a+b2,4=2(a+b ).∴y=1a +4b =a+b 2a +2(a+b )b=12+b 2a +2a b +2=52+(b 2a +2a b)≥52+2√b 2a ·2a b=92,当且仅当a=13,b=23时,.6.若p>0,q>0,p ,q 的等差中项是12,x=p+1p ,y=q+1q ,则x+y 的最小值为( ) B.5C.4D.3p+q=1,p>0,q>0,∴x+y=p+q+1p +1q =1+1pq ≥1+1(p+q 2)2=5.当且仅当p=q=12时,等号成立.7.若2x +2y =1,则x+y 的取值范围是( ) A.[0,2] B.[2,0] ∞) D.(∞,2]2x +2y ≥2√2x ·2y =2√2x+y ,∴√2x+y ≤12,2x+y ≤14. ∴x+y ≤2.D .8.已知函数f (x )=4x+ax(x>0,a>0)在x=3时取得最小值,则a= .4x+a x ≥2√4a ,当且仅当4x=ax 时,等号成立,∴4x 2=a ,∴a=4×32=36.9.若a+b=2,b>0,则12|a |+|a |b 的最小值为 .|a |b=a+b 4|a |+|a |b=a 4|a |+b 4|a |+|a |b≥a 4|a |+1≥14+1=34,当且仅当b4|a |=|a |b,a<0,即a=2,b=4时,等号故12|a |+|a |b 的最小值是34.x ,y 满足x 2+y 2+xy=1,则x+y 的最大值是 .x 2+y 2+xy=1,(x+y )2=xy+1.又xy ≤(x+y 2)2,∴(x+y )2≤(x+y 2)2+1,即34(x+y )2≤1. ∴(x+y )2≤43,当且仅当|x|=|y|=√33时,等号成立. ∴2√33≤x+y ≤2√33,∴x+y 的最大值为2√33.★11.求下列函数的最值. (1)y=x (25x ),x ∈(0,25); ·√3-x 2,x ∈(0,√3).∵x ∈(0,25),∴x>0,25x>0,y=x (25x )=15·5x (25x )≤15·(5x+2-5x 2)2=15.当且仅当5x=25x ,即x=15时,等号成立. ∴y=x (25x )的最大值为15.(2)∵x ∈(0,√3), ∴x>0,3x 2>0.∴y=x ·√3-x 2≤x 2+3-x 22=32.当且仅当x=√3-x 2,即x=√62时,等号成立.∴y=x ·√3-x 2的最大值为32.★12.当x>12时,求函数y=x+82x -1的最小值,并求出当函数取得最小值时x 的值.y=x+82x -1=x+4x -12=x 12+4x -12+12.因为x>12,所以x 12>0.所以y ≥2√4+12=92.当且仅当x 12=4x -12,即x=52时,等号成立.所以函数的最小值为92,且函数取最小值时x=52.。

高中数学学习材料唐玲出品第三章不等式（数学北京师大版必修5）8.已知不等式（x+y ）(1ax y+)≥9对任意正实数x ，y 恒成立，则正实数a 的最小值为（ ） A.2 B.4 C.6 D.89.满足不等式y 2-x 2≥0的点（x ，y ）的集合（用阴影表示）是（ ）10.如果正数a ，b ，c ，d 满足a+b =cd =4，那么（ ） A .ab ≤c+d ，且等号成立时a ，b ，c ，d 的取值唯一 B .ab ≥c+d ，且等号成立时a ，b ，c ，d 的取值唯一 C .ab ≤c+d ，且等号成立时a ，b ，c ，d 的取值不唯一D .ab ≥c+d ，且等号成立时a ，b ，c ，d 的取值不唯一11.设，且a b （a 、b 、 ），则M 的取值范围是（ ） A . ，18B . ［，1）C .［ ， ）D .［8，+∞）12.对于满足等式x 2+（y-1）2=1的一切实数x 、y ，不等式x+y+c ≥0恒成立，则实数c 的取值范围 是（ ）A .（-∞，0］B .，+∞） C .-1，+∞） D .［1，+∞）13.不等式2242x x +-≤12的解集为 . 14.若不等式x 22a xa ＞0对x恒成立，则关于t 的不等式a 2t 1＜at22t 3的解集为 .15.设x ，y ，z ，则x 2y z的最大值是 .16.函数y =1x a -（a ＞0，a ≠1）的图像恒过定点A ，若点A 在直线mx+ny-1=0（mn ＞0）上，则1m +1n的最小值为 .三、解答题（共74分）17.（12分）如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏目的面积之和为18 000 cm 2，四周空白的宽度为10 cm ，两栏之间的中缝空白的宽度为 5 cm.怎样确定广告的高与宽的尺寸（单位： ）能使矩形广告的面积最小？第17题图18.（12分）不等式（m 2-2m-3）x 2-（m-3）x-1<0对一切x ∈R 恒成立，求实数m 的取值范围.19.（12分）制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目，根据预测，甲、乙两个项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，则投资人对甲、乙两个项目各投资多少万元才能使可能的盈利最大？20.（12分）已知二次函数f（x）满足f（-2）=0，且2x≤f（x）≤242x+对一切实数x都成立.（1）求f（2）的值；（2）求f（x）的解析式；（3）设b n=1()f n，数列{b n}的前n项和为S n，求证：S n＞43(3)nn+.21.（12分）已知a，b，c是不全相等的正数，求证：a b22b2a2a2b2＞6a b 22.（14分）某村计划建造一个室内面积为72 m2的矩形蔬菜温室.在温室内，沿左、右两侧与后侧内墙各保留1 m宽的通道，沿前侧内墙保留3 m宽的空地.当矩形温室的边长各为多少时蔬菜的种植面积最大？最大种植面积是多少？第三章不等式（数学北京师大版必修5）答题纸得分：一、选择题二、填空题13． 14． 15． 16．三、计算题17．18.19.20.21.22.第三章 不等式（数学北京师大版必修5）参考答案一、选择题1.D 解析： y2x是增函数，而0＜b ＜a ＜1，1＜2b ＜2a＜2 .2.D 解析：∵ t a b a b b ，∴ t ≤s .3.C 解析：依题意得x ， x x x 或 x ， x x x ，所以 x ，x 或 或-1≤x -1x -1，故选C.4.A 解析：不等式组可化为x y ＞0，xy ＞0，0 x 2，或 xy ＜0，xy ＜0，0 x 2，在平面直角坐标系中作出符合上面两个不等式组的平面区域，如图中的阴影部分所示， ∴ 不等式组x y xy ＞0，0 x 2表示的平面区域为三角形.5.D 解析：∵ x ＞2，∴ f （x ）=x + 1x 2=x -2+1x 2+2≥2 x21x 2+2=4，当且仅当 x 21x 2，即x3时等号成立.故选D.6.C 解析：不等式组表示的平面区域如图中阴影部分所示，由34,34x y x y +=⎧⎨+=⎩得交点A 的坐标为（1，1），又B ，C 两点的坐标分别为（0，4）， ，43， 故S △ABC12 43×1 43. 7.B 解析：特殊值法.令a =7，b =3，c =1，满足a ＞b ＞c ＞0， ∴2log (11)1+＞2log (31)3+＞2log (71)7+.8.B 解析：不等式 x y1a x y + ≥9对任意正实数x ，y 恒成立，则1+a+y axx y+≥a+1≥9，∴2-4（舍去），∴ 正实数a 的最小值为4.9.B 解析：取测试点（0，1）可知C ，D 错；再取测试点（0，-1）可知A 错，故选B .又cd ≤2()4c d +，故 ≥4，所以ab ≤c+d ，当且仅当a =b =c =d =2时，等号成立.故应选A .11.D 解析：M≥12.C 解析：令x θ，y θ，则 x y θ θ θπ4∴ x y max -1.∵ x y 恒成立，故c ≥ x y max -1，故选C.13. x x 解析：依题意得x x ≤-1 x x ≤0 x ∈［-3，1］.14.（-2，2）解析：由x 22a x a ＞0对x 恒成立得Δ 4a24a ＜0，即0＜a ＜1， 函数yax是 上的减函数，∴ 2t 1＞t22t 3，解得-2＜t ＜2.15.222解析： x22y 2z2222 21 22xy z 2x 22y 2z 21122xy z 2.16.4 解析：由题意知 （ ， ），∴ n ，∴ n ， ∴n17.解：设矩形栏目的高为a cm ，宽为b cm ，则ab =9 000.① 广告的高为a+20，宽为2b+25，其中a ＞0，b ＞0.广告的面积 a b ab b a a b ≥ a b 18 500+2 ab 24 500.当且仅当25a =40b 时等号成立，此时b =58a ，代入①式得a =120，从而b =75，即当a =120，b =75时，S 取得最小值24 500.故广告的高为140 cm ，宽为175 cm 时，可使矩形广告的面积最小. 18.解：若m 2-2m-3 0，则m -1或m 3.当m -1时，不合题意；当m 3时，符合题意.若m 2-2m-3≠0，设f （x ）=（m 2-2m-3）x 2-（m-3）x-1，则由题意得，22230,230,m m m m m ∆2⎧--<⎨=[-(-3)]+4(--)<⎩解得-15<m<3.综上可得，-15<m≤3.19.解：设投资人分别用x，y万元投资甲，乙两个项目，由题意得，10,0.30.1 1.8,0,0,x yx yxy+≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩目标函数为z x y第19题答图上述不等式组表示的平面区域如图阴影部分所示，作直线x y，并作平行于直线l0的一组直线x y z，z∈R，与可行域相交，其中有一条直线经过可行域上的点M，此时z最大，这里点M是直线x与直线 x y的交点.解方程组10,0.30.1 1.8,x yx y+=⎧⎨+=⎩得4,6,xy=⎧⎨=⎩此时，z=4+0.5×6=7（万元）.∴当x，y时，z取得最大值.答：投资人用4万元投资甲项目，6万元投资乙项目，才能使可能的盈利最大.20.（1）解：∵2x≤f（x）≤242x+对一切实数x都成立，∴4≤f（2）≤4，∴f（2）=4.（2）解：设f（x）=ax2+bx+c（a≠0），∵f（-2）=0，f（2）4，∴424,1, 42024.a b c ba b c c a++==⎧⎧⇒⎨⎨-+==-⎩⎩∵ax2+bx+c≥2x，即ax2-x+2-4a≥0，∴ a a a，∴a 14，c2-4a1，故f（x）=24x+x+1.（3）证明：∵b n1()f n24(2)n+＞4(2)(3)n n++412n+13n+，∴S n b1+b2+…+b n＞41314141512n+13n+=4× nn21.证明：∵ b222b， a b222a b①同理b2a22a b，②a2b22a b. ③∵a，b，c是不全相等的正数，∴b222b，2a22a，a2b22a b三式中不能全取“＝”，∴①②③三式相加，得a b22b2a2 a2b2＞6a b.22.解：设矩形温室的左侧边长为a m，后侧边长为b m，则ab=72，蔬菜的种植面积S=（a-4）（b-2）=ab-4b-2a+8=80-2(a+2b)≤80-.当且仅当a=2b，即a，b=6时，S max=32.答：矩形温室的边长分别为6 m，12 m时，蔬菜的种植面积最大，最大种植面积是32 m2.。

北师大版必修5编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016-2017学年高中数学第三章不等式3.4.2 简单线性规划课后演练提升北师大版必修5）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016-2017学年高中数学第三章不等式3.4.2 简单线性规划课后演练提升北师大版必修5的全部内容。

练提升北师大版必修5一、选择题(每小题5分，共20分)1．若x，y∈R，且错误!则z＝x＋2y的最小值等于( )A．2 B．3C．5 D．9解析：作出可行域如图所示，目标函数y＝－错误!x＋错误!z，则过B(1,1）时z取最小值z min＝3。

答案：B2．若实数x，y满足不等式组错误!则x＋y的最大值为( ）A．9 B.错误!C．1 D.错误!解析：作出可行域如图所示令z＝x＋y，则y＝－x＋z，∴y＝－x＋z过A(4，5）时，z取最大值z＝9。

max答案：A3．若实数x，y满足错误!则错误!的取值范围是( )A．(－1，1) B．(－∞，－1)∪(1，＋∞）C．(－∞,－1) D．[1，＋∞）解析：可行域如图阴影，错误!的几何意义是区域内点与（1，0)连线的斜率，易求得错误!＞1或错误!＜－1。

答案:B4．若实数x,y满足不等式组错误!且x＋y的最大值为9,则实数m＝( ）A．－2 B．－1C．1 D．2解析：令z＝x＋y，则y＝－x＋z，斜率为－1的直线向上平移时z逐渐增大，则过直线2x－y－3＝0与x－my＋1＝0的交点时z取到最大值联立错误!，可得y＝错误!,x＝错误!，x＋y＝3m＋62m－1＝9，解得m＝1。

答案：C二、填空题（每小题5分，共10分)5．已知错误!则x2＋y2的最小值是________．解析：画出错误!所表示的平面区域如图所示：由错误!解得A(1，2）．而x2＋y2表示阴影部分的点到原点的距离的平方,由图可知A点到原点的距离为错误!,∴x2＋y2的最小值为5.答案：56．线性目标函数z＝3x＋2y,在线性约束条件错误!下取得最大值时的最优解只有一个,则实数a的取值范围是________．解析：作出线性约束条件错误!表示的平面区域，如图中阴影部分所示．因为取得最大值时的最优解只有一个，所以目标函数对应的直线与平面区域的边界线不平行，根据图形及直线的斜率，可得实数a的取值范围是[2,＋∞)．答案：［2，＋∞）三、解答题(每小题10分,共20分)7．设z＝2x＋y,此函数解析式中变量x、y满足下列条件：错误!求z的最大值和最小值．针对上述问题，请指出该问题中的目标函数、可行解、可行域以及最优解．解析：作出二元一次不等式组错误!所表示的平面区域（如图所示），即为可行域；z＝2x ＋y即为目标函数；阴影部分内的每一组（x，y）均为可行解．考虑z＝2x＋y，将它变形为y＝－2x＋z，这是斜率为－2,随z变化的一族平行直线，z 是直线在y轴上的截距，当直线截距最大时，z的值最大．在直线与平行域相交的条件下,即在满足约束条件时目标函数z＝2x＋y取得最大值；当直线截距最小时，z的值最小，即在满足约束条件时目标函数z＝2x＋y取得最小值．由图可见，当直线z＝2x＋y经过可行域上的A点时，截距最大,即z最大．解方程组错误!得A的坐标为(5，2)．所以z max＝2×5＋2＝12.当直线z＝2x＋y经过可行域上的点B时,截距最小，即z最小．解方程组{x－4y＋3＝0，，x＝1.得B的坐标为（1，1)．所以z min＝2x＋y＝2×1＋1＝3.故使z＝2x＋y取得最大值的最优解为（5，2)，取得最小值的最优解为（1，1）．8．已知x、y满足错误!。

第2课时 一元二次不等式根的分布及实际应用问题课时过关·能力提升1.不等式4x -2≤x-2的解集是( ) A.(-∞,0]∪(2,4]B.[0,2)∪[4,+∞)C.[2,4)∪(4,+∞) 原不等式等价于4x -2-(x-2)≤0, 即x 2-4x x -2≥0,即{x (x -4)(x -2)≥0,x -2≠0,0≤x<2或x ≥4,故选B .x 的方程x 2+(a 2-1)x+a-2=0的一个根比1大且另一个根比1小,则a 的取值范围是( )A.-1<a<1B.a<-1或a>1 1 D.a<-2或a>1f (x )=x 2+(a 2-1)x+a-2.由题意知,f (1)=1+a 2-1+a-2=a 2+a-2=(a-1)(a+2)<0,则-2<a<1. x 的方程9x +(4+a )3x +4=0有解,则实数a 的取值范围为( )A.(-∞,-8]B.(-∞,-8]∪[0,+∞)C.(-∞,-4)3x =t ,t ∈(0,+∞),则t 2+(4+a )t+4=0有正数解,所以{Δ=(4+a )2-16≥0,-(4+a )>0,解得a ≤-8. x 的方程x 2-(m+3)x+m 2=0有两个不相等的正根,则m 的取值范围是 .x 1,x 2是方程的两根,则由题意知x 1≠x 2,且x 1>0,x 2>0, 所以{Δ>0,x 1+x 2>0,x 1x 2>0,即{(m +3)2-4m 2>0,m +3>0,m 2>0,-1<m<0或0<m<3.-1,0)∪(0,3)98万元购买一艘捕鱼船,第一年花费各种费用12万元,以后每年都增加4万元,50万元,则第 年开始获利.n 年开始获利,则98+12n+4+8+…+(n-1)·4-50n>0,即n 2-20n+49>0,解得10-10+√51.因为n ∈N +,所以3≤n ≤17.3年开始获利.A={x|x 2+3x-18>0},B={x|(x-k )·(x-k-1)≤0},若A ∩B ≠⌀,求k 的取值范围.A ,B ,即解出一元二次不等式后,根据A ∩B ≠⌀来研究集合端点值的关系,列不等式组求得k .x 2+3x-18>0,得x>3或x<-6,{x|x>3或x<-6}.由(x-k )(x-k-1)≤0,得k ≤x ≤k+1,故B={x|k ≤x ≤k+1}.∵A ∩B ≠⌀,作出图形,如图所示,∴k+1>3或k<-6, 的取值范围是{k|k<-6或k>2}.A ∩B=⌀时k 的取值范围.,得A={x|x<-6或x>3},B={x|k ≤x ≤k+1}.∵A ∩B=⌀,则{k +1≤3,k ≥-6,即-6≤k ≤2, ∴A ∩B ≠⌀的k 的取值范围是{k|k<-6或k>2}.★7.如图所示,将一个矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求点B 在AM 上,点D 在AN 上,且对角线MN 过点C ,已知AB=3,AD=2,要使矩形AMPN 的面积大于32,则DN 的长度应在什么范围内?DN=x (x>0),则AN=x+2,由DN AN =DC AM ,得AM=3(x+2)x,故S 矩形AMPN =AN ·AM=3(x+2)2x (x>0), 由S 矩形AMPN >32,得3(x+2)2x >32(x>0),即3x 2-20x+12>0(x>0),解得0<x<23或x>6, 即DN 长度的取值范围是(0,23)∪(6,+∞). ★8.两位同学合作学习,对问题“已知由不等式xy ≤ax 2+2y 2中的数对(x ,y )组成的点在区域Ω={(x ,y )|1≤x ≤2,2≤y ≤3}中,求a 的取值范围”提出了各自的解题思路.甲说:“寻找x 与y 的关系,再作分析.”乙说:“把字母a 单独放在一边,再作分析.”参考上述思路,或用自己的其他解法,求出实数a 的.,原不等式可变形为y x ≤a+2(y x )2,记t=y x ,得2t 2-t+a ≥0, ={(x ,y )|1≤x ≤2,2≤y ≤3}时,1≤t ≤3.令f (t )=2t 2-t+a ,其对称轴为直线t=14,故由{f (1)=2-1+a ≥0,f (3)=18-3+a ≥0,得a ∈[-1,+∞).,原不等式可变形为a ≥xy -2y 2x 2=-2(y x )2+y x =-2(y x -14)2+18, 当Ω={(x ,y )|1≤x ≤2,2≤y ≤3}时,1≤y x ≤3,当y x =1时,(xy -2y 2x 2)max =-1,所以a ∈[-1,+∞).★9.某蛋糕厂生产某种蛋糕的成本为40元/个,出厂价为60元/个,日销售量为1 000个,为适应市场需求,计划提高蛋糕档次,适度增加成本.若每个蛋糕成本增加的百分率为x (0<x<1),则每个蛋糕的出厂价相应提高的百分率为0.5x ,同时预计日销售量增加的百分率为0.8x ,已知日利润=(出厂价-成本)×日销售量,且设增加成本后的日利润为y.(1)写出y 与x 的关系式;,求x 的取值范围.根据日利润=(出厂价-成本)×日销售量列出y 与x 的关系式;(2)日利润有所增加的含义是增,转化为解一元二次不等式.由题意,得y=[60×(1+0.5x )-40×(1+x )]×1 000×(1+0.8x )=2 000(-4x 2+3x+10)(0<x<1).(2)要保证日利润有所增加,则{y >(60-40)×1 000,0<x <1,即{-4x 2+3x >0,0<x <1,解得0<x<34. 所以为保证日利润有所增加,x 的取值范围是(0,34).。

2016-2017学年高中数学第三章不等式本章高效整合北师大版必修5 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016-2017学年高中数学第三章不等式本章高效整合北师大版必修5）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016-2017学年高中数学第三章不等式本章高效整合北师大版必修5的全部内容。

2016—2017学年高中数学第三章不等式本章高效整合北师大版必修5一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中,只有一项是符合题目要求的)1．设集合A＝{x|x2－1＞0｝，B＝{x|log2x＞0｝，则A∩B等于（）A．{x｜x＞1} B．{x｜x＞0}C．｛x|x＜－1｝D．{x|x＜－1,或x＞1}解析: ∵x2－1＞0，x2＞1，∴x＞1或x＜－1，∴A＝｛x|x＞1，或x＜－1｝,又log2x＞0，即log2x＞log21。

∴x＞1，∴B＝｛x|x＞1}，∴A∩B＝{x|x＞1}．答案：A2．已知t＝a＋2b，s＝a＋b2＋1，则t和s的大小关系正确的是( )A．t＞s B．t≥sC．t＜s D．t≤s解析: ∵t－s＝a＋2b－a－b2－1＝－(b－1）2≤0，∴t≤s。

答案：D3．当x∈R时，不等式kx2－kx＋1＞0恒成立，则k的取值范围是( ）A．(0，＋∞）B．［0，＋∞)C．［0,4) D．(0,4）解析: （1)当k＝0时，不等式变为1＞0成立；（2）当k≠0时，不等式kx2－kx＋1＞0恒成立，则错误!即0＜k＜4，所以0≤k＜4.答案:C4．不等式x2－ax－12a2＜0(其中a＜0)的解集为( ）A．(－3a,4a) B．（4a,－3a)C．(－3,4）D．（2a,6a）解析: 方程x2－ax－12a2＝0的两根为4a，－3a，且4a＜－3a，∴4a＜x＜－3a.答案：B5．已知不等式x2－2x－3<0的解集为A，不等式x2＋x－6〈0的解集为B,不等式x2＋ax＋b<0的解集是A∩B,那么a＋b等于（）A．－3 B．1C．－1 D．3解析：由题意：A＝{x|－1<x<3}，B＝｛x｜－3〈x〈2}．A∩B＝{x|－1〈x〈2｝，由根与系数的关系可知:a＝－1，b＝－2，∴a＋b＝－3，故选A.答案：A6．已知正实数a，b满足4a＋b＝30，当错误!＋错误!取最小值时，实数对（a，b)是( ) A．（5,10) B．（6，6)C．(10,5）D．(7，2）解析: 错误!＋错误!＝错误!·错误!·30＝错误!错误!(4a＋b）＝错误!错误!≥错误!错误!＝3.10当且仅当错误!，即错误!时取等号．故选A。

北师大版必修5编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2016-2017学年高中数学第三章不等式3.3.1 基本不等式课后演练提升北师大版必修5）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2016-2017学年高中数学第三章不等式3.3.1 基本不等式课后演练提升北师大版必修5的全部内容。

升北师大版必修5一、选择题（每小题5分，共20分）1．若0＜a＜1，0＜b＜1，且a≠b，则a＋b,2错误!，a2＋b2,2ab中最小的一个是（）A．a2＋b2B．2abC．2ab D．a＋b解析：由基本不等式得错误!＞错误!，∴a＋b＞2错误!.又∵0＜a＜1,0＜b＜1，∴ab＜1，∴ab＜1，∴2错误!·错误!＜2错误!，即2ab＜2错误!.又2ab＜a2＋b2，∴2ab最小．答案：C2．设M＝错误!,N＝（错误!)x＋y,P＝3错误!(其中0＜x＜y），则M、N、P的大小顺序是（）A．P＜N＜M B．N＜P＜MC．P＜M＜N D．M＜N＜P解析: 由基本不等式知错误!＞错误!＝错误!＝（错误!)x＋y，即M＞N.又∵错误!＞错误!，而（3)x＋y＝3错误!＞3错误!，即N＞P，∴M＞N＞P.答案：A3．已知a≥0，b≥0，且a＋b＝2，则( )A．ab≤错误!B．ab≥错误!C．a2＋b2≥2 D．a2＋b2≤3解析：∵a＋b＝2,∴（a＋b）2＝4，即a2＋b2＋2ab＝4，又∵a2＋b2≥2ab，∴2（a2＋b2）≥4，∴a2＋b2≥2.答案:C4．已知a、b∈（0，＋∞)且a＋b＝1,则下列各式恒成立的是( ）A。

【巩固练习】 一、选择题1．不等式ax 2+5x+c ＞0的解集为11{|}32x x <<，则a ，c 的值为（ ） A ．a=6，c=1 B ．a=－6，c=－1 C ．a=1，c=1 D ．a=－1，c=－6 2．若0＜t ＜1，则不等式1()()0x t x t--<的解集为( ) A.1|x x t t⎧⎫<<⎨⎬⎩⎭B.1|x x x t t⎧⎫><⎨⎬⎩⎭或 C.1|x x x t t⎧⎫<>⎨⎬⎩⎭或D.1|x t x t ⎧⎫<<⎨⎬⎩⎭3．已知不等式ax 2－bx －1≥0的解集是11,23⎡⎤--⎢⎥⎣⎦，则不等式x 2－bx －a ＜0的解集是( )A ．(2,3)B ．(－∞，2)∪(3，＋∞) C.11,32⎛⎫⎪⎝⎭ D.11,,32⎛⎫⎛⎫-∞+∞ ⎪⎪⎝⎭⎝⎭4．在R 上定义运算⊗：x ⊗y ＝x (1－y )．若不等式(x －a )⊗(x ＋a )＜1对任意实数x 恒成立，则( )A ．－1＜a ＜1B ．0＜a ＜2C ．1322a -<< D ．3122a -<< 5．不等式x 2－ax －b ＜0的解集是{x|2＜x ＜3}，则bx 2－ax －1＞0的解集是（ ） A ．{|23}x x << B ．11{|}32x x << C ．11{|}23x x -<<- D ．{|32}x x -<<-6. 关于x 的不等式(1＋m )x 2＋mx ＋m ＜x 2＋1对x ∈R 恒成立，则实数m 的取值范围是( )A ．(－∞，0)B ．4(,0),3⎛⎫-∞+∞ ⎪⎝⎭ C ．(－∞，0] D ．4(,0],3⎛⎫-∞-+∞ ⎪⎝⎭二、填空题7．若函数是定义在(0，＋∞)上的增函数，且对一切x ＞0，y ＞0都有f (xy )＝f (x )＋f (y )，则不等式f (x ＋6)＋f (x )＜2f (4)的解集为________．8．如果关于x 的方程x 2－(m －1)x+2－m=0的两根为正实数，则m 的取值范围是________.9. 函数()f x =的定义域是R ，则实数a 的取值范围为________．10. 已知函数21, 0()1, 0x x f x x ⎧+≥=⎨<⎩，则满足不等式f (1－x 2)＞f (2x )的x 的范围是________．三、解答题 11.解下列不等式(1)2x 2＋7x ＋3＞0； (2)－x 2＋8x －3＞0；12. 不等式mx 2+1＞mx 的解集为实数集R ，求实数m 的取值范围． 13. 解关于x 的不等式m 2x 2＋2mx －3＜0(其中m ∈R )． 14．已知2()2(2)4f x x a x =+-+，(1)如果对一切x ∈R ，f(x)>0恒成立，求实数a 的取值范围； (2)如果对x ∈[-3，1]，f(x)>0恒成立，求实数a 的取值范围.15. 已知a 为实数，A 为不等式x 2－(2a ＋1)x ＋(a ＋2)(a －1)≥0的解集，B 为不等式x 2－a (a ＋1)x ＋a 3＜0的解集．(1)用区间表示A 和B ；(2)是否存在实数a ，使A ∪B ＝R ？并证明你的结论．【答案与解析】1.【答案】B【解析】由题意可知方程250ax x c ++>的两根为12x =和13x =，由韦达定理得：11115,2323c a a ⨯=+=-，求得a=－6，c=－12．【答案】 D【解析】 ∵0＜t ＜1，∴11t >，∴1t t< ∴11()()0x t x t x t t--<⇔<<.3. 【答案】 A 【解析】 由题意知12-，13-是ax 2－bx －1＝0的两实根， ∴112311123baa ⎧⎛⎫-+-= ⎪⎪⎪⎝⎭⎨⎛⎫⎪-⨯-=-⎪⎪⎝⎭⎩.解得65a b =-⎧⎨=⎩.∴x 2－bx －a ＜0⇔x 2－5x ＋6＜0⇔2＜x ＜3.4. 【答案】 C【解析】 因为(x －a )⊗(x ＋a )＝(x －a )(1－x －a )，又不等式(x －a )⊗(x ＋a )＜1对任意实数x 恒成立，所以(x －a )(1－x －a )＜1对任意实数x 恒成立，即x 2－x －a 2＋a ＋1＞0对任意实数x 恒成立，所以Δ＝(－1)2－4(－a 2＋a ＋1)＜0，解得1322a -<<，故选C.5.【答案】C【解析】由题意得，方程x 2－ax －b=0的两根为x=2,x=3,由韦达定理得23a +=，23b ⨯=-，求得5 a =，b=-6，从而解得bx 2－ax －1＞0的解集为11{|}23x x -<<-6. 【答案】 C【解析】 原不等式等价于mx 2＋mx ＋m －1＜0对x ∈R 恒成立， 当m ＝0时，0·x 2＋0·x －1＜0对x ∈R 恒成立． 当m ≠0时，由题意，得22000404103403m m m m m m m mm m m <⎧<<⎧⎧⎪⇔⇔⇔<⎨⎨⎨<>∆=--<->⎩⎩⎪⎩或. 综上，m 的取值范围为(－∞，0]．7．【答案】 {x |0＜x ＜2}【解析】 由已知得f (x ＋6)＋f (x )＝f [x (x ＋6)]， 2f (4)＝f (4)＋f (4)＝f (4×4)＝f (16)，∴原不等式等价于6000002(6)1682[(6)]16x x x x x x x x f x x f +>⎧>>⎧⎧⎪>⇔⇔⇔<<⎨⎨⎨+<-<<⎩⎩⎪+<⎩.8．【答案】{|12}m m -+<< 【解析】由题意得：1212000x x x x ∆>⎧⎪+>⎨⎪>⎩，解得12m -+<<9. 【答案】 40,9⎡⎫⎪⎢⎣⎭【解析】 由已知f (x )的定义域是R . 所以不等式ax 2＋3ax ＋1＞0恒成立．(1)当a ＝0时，不等式等价于1＞0，显然恒成立； (2)当a ≠0时，则有2000400(94)09(3)40a a a a a a a a >>>⎧⎧⎧⇔⇔⇔<<⎨⎨⎨∆<-<-<⎩⎩⎩. 由(1)(2)知，409a ≤<. 即所求a 的取值范围是40,9⎡⎫⎪⎢⎣⎭.10. 【答案】 (－1，2－1) 【解析】若x ≥0，则2211101112x x x x x -<<⎧⎧->⎪⎪⇒⎨⎨<<->⎪⎪⎩⎩1101x x ⇒-<<⇒≤< 若x ＜0，则1－x 2＞0 ∴－1＜x ＜0综上11x -<<11．【解析】(1)因为Δ＝72－4×2×3＝25＞0，所以方程2x 2＋7x ＋3＝0有两个不等实根x 1＝－3，212x =-. 又二次函数y ＝2x 2＋7x ＋3的图象开口向上， 所以原不等式的解集为1|32x x x ⎧⎫>-<-⎨⎬⎩⎭或. (2)因为Δ＝82－4×(－1)×(－3)＝52＞0， 所以方程－x 2＋8x －3＝0有两个不等实根14x =24x =又二次函数y ＝－x 2＋8x －3的图象开口向下，所以原不等式的解集为{|44x x <<．12.【答案】{m|0≤m<4} 【解析】当m ＝0时，不等式即为1＞0，满足条件．当m≠0时，若不等式的解集为R ，则应有⎪⎩⎪⎨⎧<--=∆>0m 4)m (0m 2， 解得0＜m ＜4．综上，m 的取值范围是{m|0≤m<4}.13.【解析】 当m ＝0时，原不等式可化为－3＜0，其对一切x ∈R 都成立， 所以原不等式的解集为R . 当m ≠0时，m 2＞0，由m 2x 2＋2mx －3＜0，得(mx －1)(mx ＋3)＜0， 即130x x m m ⎛⎫⎛⎫-+< ⎪⎪⎝⎭⎝⎭， 若m ＞0，则13m m>-， 所以原不等式的解集为31,m m ⎛⎫- ⎪⎝⎭； 若m ＜0，则13m m<-， 所以原不等式的解集为13,m m ⎛⎫-⎪⎝⎭.综上所述，当m ＝0时，原不等式的解集为R ； 当m ＞0时，原不等式的解集为31,m m ⎛⎫- ⎪⎝⎭； 当m ＜0时，原不等式的解集为13,m m ⎛⎫- ⎪⎝⎭.14．【解析】(1)由题意得：△=2[2(2)]160a --<，即0<a<4； (2)由x ∈[-3，1]，f(x)>0得，有如下两种情况：2[3,1](3)0(1)0a f f -∉-⎧⎪->⎨⎪>⎩或2[3,1](2)0a f a -∈-⎧⎨->⎩ 综上所述：1,42a ⎛⎫∈- ⎪⎝⎭.15. 【解析】 不等式x 2－(2a ＋1)x ＋(a ＋2)(a －1)≥0可以转化为[x －(a ＋2)][x －(a －1)]≥0，不等式x 2－a (a ＋1)x ＋a 3＜0可以转化为(x －a )(x －a 2)＜0.(1)因为对任意实数a 都有a －1＜a ＋2， 所以A ＝(－∞，a －1]∪[a ＋2，＋∞)． 当a 2≥a ，即a ≥1或a ≤0时，B ＝(a ，a 2)； 当a 2＜a ，即0＜a ＜1时，B ＝(a 2，a )． (2)要使A ∪B ＝R ，则 当a ≥1或a ≤0时，需212a a a a ≤-⎧⎨≥+⎩，该不等式组无解；当0＜a ＜1时，需212a a a a ⎧≤-⎨≥+⎩，该不等式组无解．所以不存在实数a ，使得A ∪B ＝R .。

【巩固练习】1．首项为-24的等差数列,从第10项起开始为正数,则公差d 的取值范围是 ( ) (A)83d >(B)3d < (C)833d ≤< (D)833d <≤ 2．在ABC ∆中,若0AB BC ⋅>,则ABC ∆的形状是（ ）(A)锐角三角形 (B)钝角三角形 (C) 直角三角形 (D)正三角形 3.“22<-<b a 且”是“函数[)+∞-∈-+=,1,)(x ax bx x f 是增函数”的 （ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件4.在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立,则 （ ）（A ）11<<-a（B ）20<<a（C ）2321<<-a （D ）2123<<-a 5.已知奇函数)(,)(2121x x x x x f ≠对任意的正实数恒有0))()()((2121>--x f x f x x ,则一定正确的是（ ）A ．)6()4(->f fB ．)6()4(-<-f fC ．)6()4(->-f fD ．)6()4(-<f f6.设a 、b 、c 是互不相等的正数,则下列等式中不恒成立．．．．的是（ ） A.||||||c b c a b a -+-≤- B.aa a a 1122+≥+ C.21||≥-+-ba b a D.a a a a -+≤+-+213 7．函数1|cos |2-=x y 的定义域为8．如果函数213log (23)y x x =--的单调递增区间是(-∞,a ],那么实数a 的取值范围是9. 若对]1,(--∞∈x 时,不等式1)21(2)(2<--xx m m 恒成立,则实数m 的取值范围是10. 已知直线:2l y ax =+和A （1,4）,B （3,1）,若直线l 和线段AB 相交,则a 的取值范围是11.已知f(x)是定义在[-1,1]上的奇函数,f(1)＝1,且当a,b ∈[-1,1],a+b ≠0时,有()()0f a f b a b+>+(1)若f(x)≤m 2-2m +1,对所有x ∈[-1,1],恒成立,求实数m 的取值范围; (2)解不等式11()()21f x f x +<-。