叠加弯矩图最简单原理
- 格式:ppt
- 大小:362.00 KB
- 文档页数:9




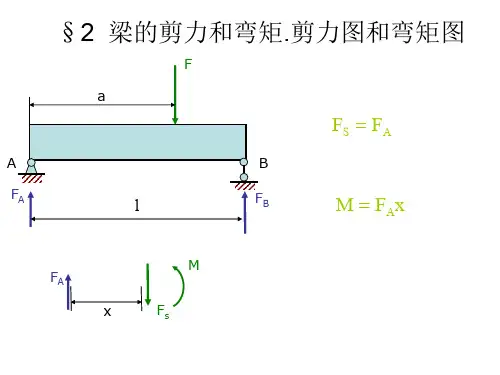
2.6叠加法作弯矩图当梁在荷载作用下变形微小,因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算,且所得结果与梁上荷载成正比。
在这种情况下,当梁上有几项荷载作用时,由每一项荷载所引起的梁的支反力或内力,将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时,只需先分别算出各项荷载单独作用时在该截面上引起的弯矩,然后求它们的代数和即得到该截面上的总弯矩。
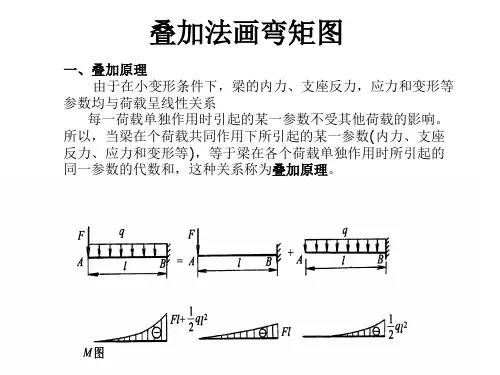
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法,称为叠加法。
叠加法的应用很广,它的应用条件是:需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说,该物理量的荷载表达式中既不包含荷载的一次方以上的项,也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解:先将梁上每一项荷载分开(见图(b)、图(c)),分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号,在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分,其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图,即得通常形式的弯矩图(见图(曲)。
求极值弯矩时,先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图(g)可见,全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时,也可将梁按荷载情况分段,求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力,不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩,故在作弯矩图时可将它略去,剩下的梁端剪力1Q,2Q和梁端弯矩1M、2M,及荷载对梁段的作用,可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供,故图中未画出)。



叠加法在绘制弯矩图中的应用作者:詹景元石煜威朱芳振来源:《建材发展导向》2015年第03期摘要:弯矩图是结构力学最为重要和基础的知识点,是后续变形和位移计算的关键内容。
但是现在的大部分教材对于弯矩图的绘制技巧和一些特殊情况的处理方法的介绍并不是很多,只是通过几道例题去将弯矩图的画法展现出来,让学生自己去理解,这便使得不少学生对于弯矩图的绘制感到无从下手。
文章通过对书本上例题的理解分析,总结出叠加法运用在绘制弯矩图中的一些简单的基本理念和分析方法。
关键词:弯矩图;叠加法;静定结构1 叠加法的介绍1.1 叠加法的前提条件材料力学讨论的杆件均满足几个基本假设,其中,小变形假设是指构件在承受荷载作用时,所产生的变形和构件的原始尺寸相比非常微小。
由于变形量微小,我们在研究杆件的支反力、内力、应力、变形等问题时都可以用构件的原始尺寸和形状进行计算,不必考虑构件受荷变形后尺寸变化给计算带来的影响。
同时,采用构件的原始尺寸进行计算所得的支反力、内力、应力、变形均与梁上的荷载保持线性关系。
1.2 叠加法的使用条件叠加法的理论依据就是叠加原理,它不仅可以用来梁的位移,也可用来计算梁的支反力、内力和应力;它不仅可用于梁,也可用于拉(压)杆和其他结构。
一般来说,当构件或结构上同时作用几个荷载时,如果各荷载产生的效果(应力、反力、内力和位移等)互不影响(或影响甚小可忽略不计),则它们所产生的总效果即等于各荷载单独作用时所产生的效果总和(或为代数和,或为矢量和,由所求的物理量的性质而定)。
在土木工程实践中,一般的梁工作时变形很小,由梁上荷载产生的剪力和弯矩与荷载呈线性关系,并且其跨长的改变可以略去不计。
因此当梁上同时受到几个载荷作用时,由每一个载荷所引起的梁的内力将不受其他载荷的影响,满足叠加原理的条件,即可用叠加法来计算梁的内力(包括剪力、弯矩等)。
1.3 叠加法的使用准备梁的内力采用叠加法来求解时,必须要对简单梁承受单个基本荷载时的内力分布比较熟悉,这样叠加计算才会比较简单便捷。

2.6叠加法作弯矩图当梁在荷载作用下变形微小,因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算,且所得结果与梁上荷载成正比。
在这种情况下,当梁上有几项荷载作用时,由每一项荷载所引起的梁的支反力或内力,将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时,只需先分别算出各项荷载单独作用时在该截面上引起的弯矩,然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法,称为叠加法。
叠加法的应用很广,它的应用条件是:需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说,该物理量的荷载表达式中既不包含荷载的一次方以上的项,也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解:先将梁上每一项荷载分开(见图(b)、图(c)),分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号,在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分,其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图,即得通常形式的弯矩图(见图(曲)。
求极值弯矩时,先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图(g)可见,全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
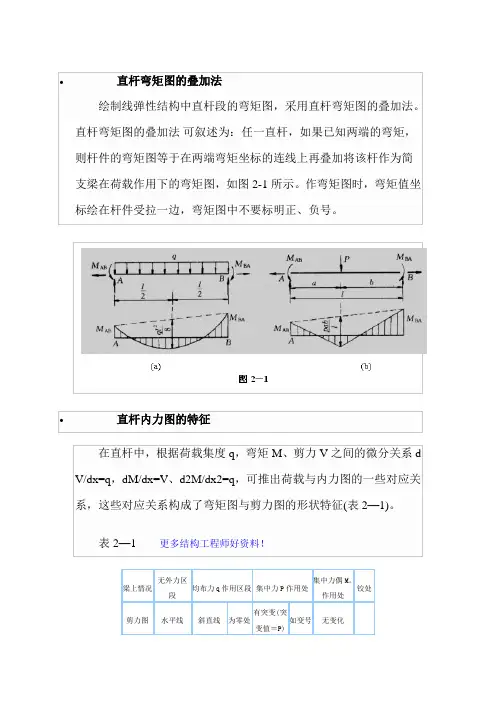
当梁上的荷载较复杂时,也可将梁按荷载情况分段,求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力,不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩,故在作弯矩图时可将它略去,剩下的梁端剪力1Q,2Q和梁端弯矩1M、2M,及荷载对梁段的作用,可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供,故图中未画出)。
转贴
[解] 此组合结构中,除AC、BC杆为受弯杆件外,其余均为轴力杆。
(1)求支座反力
由整体平衡条件,得VA=VB=75kN,HA=0.
(2)通过铰C作I—I截面,由该截面左边隔离体的平衡条件ΣMc=0,得NDE=135kN(拉力);由ΣY=0,Qc=—15kN;由ΣX=0,得NC =—135kN(压力)。
(3)分别由结点D、E的平衡条件,得NDA=NEB=151kN(拉力),NDF=NEG=67.5kN(压力)。
更多结构工程师好资料!(4)根据铰C处的剪力Qc及轴力Nc,并按直杆弯矩图的叠加法就可绘出受弯杆AFC、BGC的弯矩图。
(5)M、Q、N图分别如图2—17b、c、d所示。
广义力和广义位移
以各种不同方式作用在结构上的力,如集中力、集中力偶、分布力、分布力偶等都称为广义力,它可以是外力,也可以是内力。
与广义力对应的位移称为广义位移。
或能唯一地决定结构几何位置改变的彼此独立的量称为广义位移,如线位移、角位移、相对线位移、相对角位移等。
更多结构工程师好资料!
本节主要介绍静定结构在广义力、温度变化、支座位移等因素作用下的广义位移计算。
转贴
[解] 此组合结构中,除AC、BC杆为受弯杆件外,其余均为轴力杆。
(1)求支座反力
由整体平衡条件,得VA=VB=75kN,HA=0.
(2)通过铰C作I—I截面,由该截面左边隔离体的平衡条件ΣMc=0,得NDE=135kN(拉力);由ΣY=0,Qc=—15kN;由ΣX=0,得NC =—135kN(压力)。
(3)分别由结点D、E的平衡条件,得NDA=NEB=151kN(拉力),NDF=NEG=67.5kN(压力)。
更多结构工程师好资料!(4)根据铰C处的剪力Qc及轴力Nc,并按直杆弯矩图的叠加法就可绘出受弯杆AFC、BGC的弯矩图。
(5)M、Q、N图分别如图2—17b、c、d所示。
广义力和广义位移
以各种不同方式作用在结构上的力,如集中力、集中力偶、分布力、分布力偶等都称为广义力,它可以是外力,也可以是内力。
与广义力对应的位移称为广义位移。
或能唯一地决定结构几何位置改变的彼此独立的量称为广义位移,如线位移、角位移、相对线位移、相对角位移等。
更多结构工程师好资料!
本节主要介绍静定结构在广义力、温度变化、支座位移等因素作用下的广义位移计算。
1.1.3区段叠加法作直梁弯矩图
在小变形情况下,依据力的独立性原理,复杂荷载引起的弯矩图,可分区段用单一荷载引起的弯矩图叠加的方法,即区段叠加法进行
绘制。
可按以下三个步骤进行:
●一求控制弯矩:首先,求两杆端的弯矩,常可直接判断(对于简支梁两端铰支处、悬臂梁的悬臂端,若无集中力偶作用,其弯
矩均为零;若有集中力偶作用,其弯矩即等于该集中力偶);其次,求外力不连续点处的弯矩(如集中力作用点、均布荷载的起点和终点、集中力偶作用点两侧的弯矩),用载面法即可方便求得。
●二引直线相连:将相邻二控制弯矩用直线相连(当二控制截面间无横向荷载作用时,用实线连接,即为该区段弯矩图形;当二
控制截面间尚有横向荷载作用时,则用虚线连接,作为新的“基线”,然后再按下面的第“三”步叠加)。
●三叠简支弯矩:在新的“基线”上,叠加该区段按简支梁求得的弯矩图(注意:所叠加的二竖标均应垂直于原杆轴)。
现以图1-3所示简支伸臂梁为例,用区段叠加法绘制其弯矩图。
其计算步骤示于图1-3b-d中(具体计算过程从略)。
图1-3“区段叠加法”分步示意图
(二)对于曲线弯矩图叠加曲线弯矩图的情况
找出一些控制弯矩值(至少三点),中间连以适当曲线,主要是定好弯曲方向,一般为连续光滑曲线。