叠加法作弯矩图
- 格式：ppt
- 大小：776.50 KB
- 文档页数：14
下载文档原格式
合集下载
叠加法作弯矩图
1/2qL2
FL
F A
m 1 Fl
4A
F
C
B
B
l2 l2
1 Fl 4
-
+ 1 Fl 8
l2 l2
+
1 Fl 4
A C
m 1 Fl 4 C
l
1 Fl
-4
6kN
6kN 2kN m
AC
B
D
2m 2m 2m
4
+
-
6
+
4
2kN m
2m 2m 2m
4
-
MA
q
A
l
MB BA
+ MB
A
1/8qL2
q
l
+
1/8qL2
6kN 2kN m
AC
B
D
2m 2m 2m
4
B
2
A1DFra bibliotek4支座反力 RA=15KN
6KN q=2KN/m
8KN q=2KN/m
RB=11KN
C 2m
梁分CA、AD、DB、BF段。
各控制面弯矩分别为：
A 4m
RA
D
E
2m 2m
BF 2m
RB
MA=-12KN MD=8KN MB=-4KN
12 4
8
10
MA B
A
MB B
l
+ MB MA
能用叠加法画下图所示梁的弯矩图吗？
q
P
A
B
方法四
区段叠加法——用叠加法 作某一段梁弯矩图的方法
原理
q
A MA
A VA MA
区段叠加法作弯矩图
叠加法作弯矩图 教学目的：
1、掌握叠加原理； 2、会用叠加法作弯矩图； 3、会用区段叠加法作弯矩图
重 点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难 点
区段叠加法绘制弯矩图
叠加原理： 几个载荷共同作用的效果，等于各个载荷单独作用效果之和 “效果”——指载荷引起的反力、内力、应力或变形 “之和”——代数和 叠加原理成立的前提条件：小变形条件
+
1 Fl 8
+
1 Fl 4
6kN 6kN
A
2kN m
B
2kN m
D
C
2m
2m
4
2m
2m
2m
2m
+
+
4
6
4
-
MA A
q
MB B
l A
q
B A
MA
MB B
l
l
+
MA 1/8qL2
+
MB 1/8qL2 MA
+
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
M x M1 x M 2 x
qx2 M x Fx 2
q
B
A F
X
l
叠加法——用叠加原理绘制弯矩图的方法
叠加时，易先画直线形的弯矩图，再叠加曲线形或折线形 的弯矩图 由于剪力图比较好画，重点介绍用叠加法画弯矩图
步骤：
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
注意：
弯矩图的叠加， 不是两个图形的简单叠加， 而是对应点处纵坐标的相加。
1、掌握叠加原理； 2、会用叠加法作弯矩图； 3、会用区段叠加法作弯矩图
重 点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难 点
区段叠加法绘制弯矩图
叠加原理： 几个载荷共同作用的效果，等于各个载荷单独作用效果之和 “效果”——指载荷引起的反力、内力、应力或变形 “之和”——代数和 叠加原理成立的前提条件：小变形条件
+
1 Fl 8
+
1 Fl 4
6kN 6kN
A
2kN m
B
2kN m
D
C
2m
2m
4
2m
2m
2m
2m
+
+
4
6
4
-
MA A
q
MB B
l A
q
B A
MA
MB B
l
l
+
MA 1/8qL2
+
MB 1/8qL2 MA
+
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
M x M1 x M 2 x
qx2 M x Fx 2
q
B
A F
X
l
叠加法——用叠加原理绘制弯矩图的方法
叠加时，易先画直线形的弯矩图，再叠加曲线形或折线形 的弯矩图 由于剪力图比较好画，重点介绍用叠加法画弯矩图
步骤：
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
注意：
弯矩图的叠加， 不是两个图形的简单叠加， 而是对应点处纵坐标的相加。
结构力学 叠加法
2．6叠加法作弯矩图当梁在荷载作用下变形微小，因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算，且所得结果与梁上荷载成正比。
在这种情况下，当梁上有几项荷载作用时，由每一项荷载所引起的梁的支反力或内力，将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时，只需先分别算出各项荷载单独作用时在该截面上引起的弯矩，然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法，称为叠加法。
叠加法的应用很广，它的应用条件是：需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说，该物理量的荷载表达式中既不包含荷载的一次方以上的项，也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
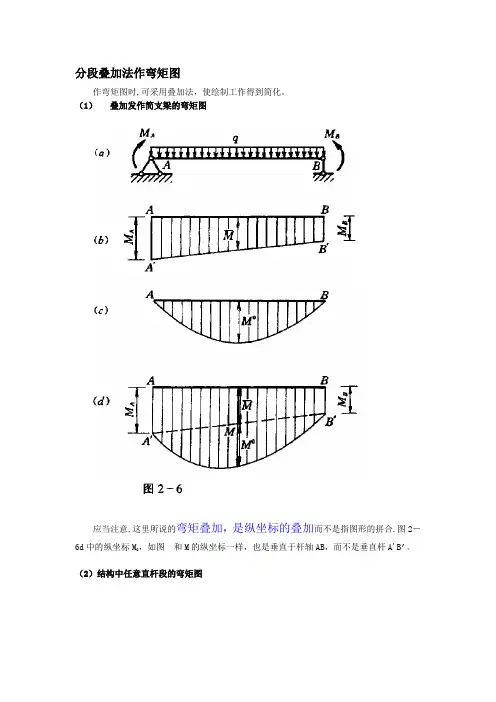
解：先将梁上每一项荷载分开(见图(b)、图(c))，分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号，在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分，其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图，即得通常形式的弯矩图(见图(曲)。
求极值弯矩时，先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图（g)可见，全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时，也可将梁按荷载情况分段，求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力，不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩，故在作弯矩图时可将它略去，剩下的梁端剪力1Q，2Q和梁端弯矩1M、2M，及荷载对梁段的作用，可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供，故图中未画出)。
叠加法作弯矩图32
D
4
支座反力 RA=15KN
6KN q=2KN/m
8KN q=2KN/m
RB=11KN
C 2m
梁分CA、AD、DB、BF段。
各控制面弯矩分别为：
A 4m
RA
D
E
2m 2m
BF 2m
RB
MA=-12KN MD=8KN MB=-4KN
12 4
8
10
的拼凑。
ql2/8
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁
的弯矩图。
支座反力（可不求） 梁分两段：AB段和BD段。
AB段： A端弯矩MAB=0， B端弯矩MBA=-4KN•m BD段： B端弯矩MBD=-4KN•m D端弯矩MDB=0
6kN 2kN m
AC
B
D
2m 2m 2m
4
B
2
A
1
步骤：1. 荷载分解(分解）
2. 作分解荷载的弯矩图（查表9-1）
3. 作荷载共同作用下的弯矩图（叠加）
注意：
弯矩图的叠加，不是两个图形的简单叠加，而是对应点处 纵坐标的相加。
叠加法作弯矩图举例
F
q
F
q
=
+
A
BA l
B l
A
B
l
1/2qL2+FL
1/2qL2
FL
F A
m 1 Fl
4A
F
C
B
B
l2 l2
1 Fl 4
-
+ 1 Fl 8
l2 l2
+
1 Fl 4
A C
m 1 Fl 4 C
l
1 Fl
直杆弯矩图的叠加法
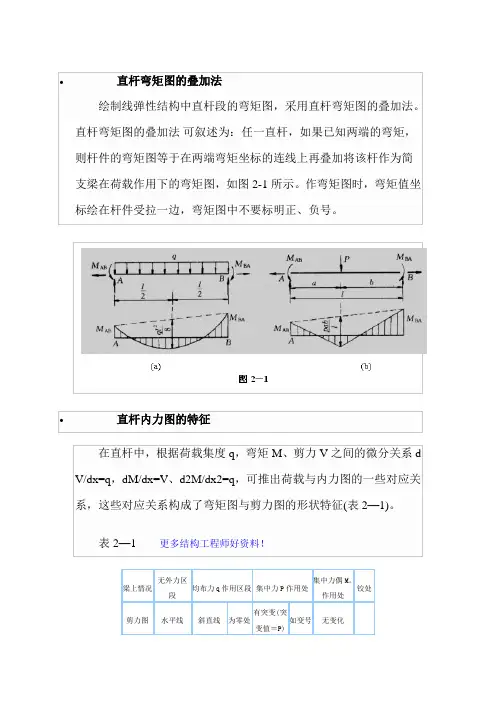
直杆弯矩图的叠加法直杆弯矩图的叠加法 ,绘制线弹性结构中直杆段的弯矩图，采用直杆弯矩图的叠加法。
直杆弯矩图的叠加法可叙述为:任一直杆，如果已知两端的弯矩，则杆件的弯矩图等于在两端弯矩坐标的连线上再叠加将该杆作为简支梁在荷载作用下的弯矩图，如图2-1所示。
作弯矩图时，弯矩值坐标绘在杆件受拉一边，弯矩图中不要标明正、负号。
直杆内力图的特征 ,在直杆中，根据荷载集度q，弯矩M、剪力V之间的微分关系dV/dx=q，dM/dx=V、d2M/dx2=q，可推出荷载与内力图的一些对应关系，这些对应关系构成了弯矩图与剪力图的形状特征(表2—1)。
表2—1 更多结构工程师好资料～无外力区集中力偶M。
梁上情况均布力q作用区段集中力P作用处铰处段作用处有突变(突剪力图水平线斜直线为零处如变号无变化变值,P)抛物线(凸有尖角(尖一般为斜有突变(突弯矩图出方向同有极值角指向同P有极值为零直线变值—M。
) q指向) 指向)注意到截面上轴力与剪力是互相垂直的，只要根据剪力图的特征，并结合杆件上的荷载情况，就可得到轴力图的特征。
熟悉掌握内力图的特征，便于绘制和校核内力图。
(二)三铰拱的合理拱轴 ,在某种固定荷载作用下，拱的所有截面的弯矩均为零的轴线称为合理拱轴。
三铰拱在竖向荷载作用下合理拱轴的一般表达式，可根据合理拱轴的定义，令式 (2—4)等于零，得合理拱轴方程为更多结构工程师好资料～y,M0,H (2—7)图2—8a所示三铰拱承受满跨均布荷载q作用，其具体的合理拱轴方程可按式(2,7)推导如下:按图2—8a所示坐标系，将代梁(图2—8b)的弯矩方程M0,qx(l,x),2及拱的水平推力H,MC0,f,ql2,8f代人式(2—7)得拱的合理拱轴方程为y,4fx(l,x),l2 (2—8)顺便指出，三铰拱在满跨填料重量作用下的合理拱轴为悬链曲线;在径向均布荷载作用下的合理拱轴为圆弧线。
(三)三铰刚架的内力计算分析图2—9a所示的三铰刚架，绘制其弯矩、剪力、轴力图。
按叠加原理作弯矩图
F
x
F, q 作用该截面上的弯矩等于F, q 单独作 用该截面上的弯矩的代数和
q
qx M ( x ) Fx 2
2
x
3
(Internal forces in beams)
F
q
2 ql 6
+
2l/3
2 ql 81
M F ( x ) Fx
+
x l
Fl
F
2
ห้องสมุดไป่ตู้
qx M q ( x) 2
2 ql 6
1
(Internal forces in beams)
三、步骤 (Procedure)
（1）分别作出各项荷载单独作用下梁的弯矩图;
（2）将其相应的纵坐标叠加即可（注意：不是图形的简单拼凑） 例16 悬臂梁受集中荷载 F 和均布荷载 q 共同作用, 试按叠加 原理作此梁的弯矩图. F=ql/3 q
x
F2 F1 F3
a
122
a
a
a
d
a
+
c
d
a
c
b
e
d
a
c
b
5 215
e
b
e 291
(Internal forces in beams)
F1
D a A
F2
C B
F3
E
d
a
c
b
e
291 a a c 131 215 291 a a
122
d
a
d
a
1 1 M C ( 291 ) 122 ( 215 ) 131kN m 2 2
FS (F1 ,F2 , ,Fn ) = FS (F1 ) + FS ( (F2 ) + + FS (Fn )
结构力学 叠加法
2．6叠加法作弯矩图当梁在荷载作用下变形微小，因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算，且所得结果与梁上荷载成正比。
在这种情况下，当梁上有几项荷载作用时，由每一项荷载所引起的梁的支反力或内力，将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时，只需先分别算出各项荷载单独作用时在该截面上引起的弯矩，然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法，称为叠加法。
叠加法的应用很广，它的应用条件是：需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说，该物理量的荷载表达式中既不包含荷载的一次方以上的项，也不包含荷载的零次项。
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解：先将梁上每一项荷载分开(见图(b)、图(c))，分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号，在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分，其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图，即得通常形式的弯矩图(见图(曲)。
求极值弯矩时，先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图（g)可见，全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时，也可将梁按荷载情况分段，求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力，不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩，故在作弯矩图时可将它略去，剩下的梁端剪力1Q，2Q和梁端弯矩1M、2M，及荷载对梁段的作用，可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供，故图中未画出)。
直杆弯矩图的叠加法
转贴
[解] 此组合结构中，除AC、BC杆为受弯杆件外，其余均为轴力杆。
（1）求支座反力
由整体平衡条件，得VA＝VB＝75kN，HA＝0.
（2）通过铰C作I—I截面，由该截面左边隔离体的平衡条件ΣMc=0，得NDE＝135kN（拉力）；由ΣY=0，Qc＝—15kN；由ΣX=0，得NC ＝—135kN（压力）。
（3）分别由结点D、E的平衡条件，得NDA＝NEB＝151kN（拉力），NDF＝NEG＝67.5kN（压力）。
更多结构工程师好资料！（4）根据铰C处的剪力Qc及轴力Nc，并按直杆弯矩图的叠加法就可绘出受弯杆AFC、BGC的弯矩图。
（5）M、Q、N图分别如图2—17b、c、d所示。
广义力和广义位移
以各种不同方式作用在结构上的力，如集中力、集中力偶、分布力、分布力偶等都称为广义力，它可以是外力，也可以是内力。
与广义力对应的位移称为广义位移。
或能唯一地决定结构几何位置改变的彼此独立的量称为广义位移，如线位移、角位移、相对线位移、相对角位移等。
更多结构工程师好资料！
本节主要介绍静定结构在广义力、温度变化、支座位移等因素作用下的广义位移计算。
分段叠加法作弯矩图
分段叠加法作弯矩图
作弯矩图时,可采用叠加法，使绘制工作得到简化。
（1）叠加发作简支梁的弯矩图
应当注意,这里所说的弯矩叠加，是纵坐标的叠加而不是指图形的拼合.图2－6d中的纵坐标M0，如图 和M的纵坐标一样，也是垂直于杆轴AB，而不是垂直杆A'段的弯矩图的特性和与其相应的（长度、承受荷载q和两端弯矩MA、MB均相同）简支梁的竖向力YA、YB(Y0A、Y0B）和弯矩图完全相同，因此,我们可以用前面所属的叠加法来绘制任意直杆段的弯矩图。
（2）分段画弯矩图。当控制截面之间无荷载时，该段弯矩图是直线图形。当控制截面之间有荷载时，用叠加法作该段的弯矩图。
具体作法如下：先求出杆段两端截面的弯矩图MA、MB。作直线的 图, 然后依此直线为基线，叠加相应简支梁在跨间荷载作用下的M0图（如d所示）
小结：梁弯矩图的一般作法
利用内力图的特性和弯矩图叠加法，将梁弯矩图的一般作法归纳如下：
（1）选定外力的不连续点（如集中力、集中力偶的作用点,分布力的起点和终点等)为控制截面,求出任制裁面的弯矩值。
作弯矩图时,可采用叠加法，使绘制工作得到简化。
（1）叠加发作简支梁的弯矩图
应当注意,这里所说的弯矩叠加，是纵坐标的叠加而不是指图形的拼合.图2－6d中的纵坐标M0，如图 和M的纵坐标一样，也是垂直于杆轴AB，而不是垂直杆A'段的弯矩图的特性和与其相应的（长度、承受荷载q和两端弯矩MA、MB均相同）简支梁的竖向力YA、YB(Y0A、Y0B）和弯矩图完全相同，因此,我们可以用前面所属的叠加法来绘制任意直杆段的弯矩图。
（2）分段画弯矩图。当控制截面之间无荷载时，该段弯矩图是直线图形。当控制截面之间有荷载时，用叠加法作该段的弯矩图。
具体作法如下：先求出杆段两端截面的弯矩图MA、MB。作直线的 图, 然后依此直线为基线，叠加相应简支梁在跨间荷载作用下的M0图（如d所示）
小结：梁弯矩图的一般作法
利用内力图的特性和弯矩图叠加法，将梁弯矩图的一般作法归纳如下：
（1）选定外力的不连续点（如集中力、集中力偶的作用点,分布力的起点和终点等)为控制截面,求出任制裁面的弯矩值。
建筑力学中应用叠加法绘制弯矩图的新探讨
建筑力学中应用叠加法绘制弯矩图的新探讨程晶晶(兰州现代职业学院城市建设学院 甘肃兰州 730030)摘要：建筑设计流体力学是指人们通过对自然界现象的观察，以及在劳动中的经验总结。
建筑设计流体力学在由建筑物结构所形成的客观世界中，起到了最基本的认识功能。
在工程流体力学中，利用叠加法在绘制最大弯矩图中具有很大的意义。
通常的绘制最大弯矩图的办法主要有方程法、规则法和叠加法，其中利用叠加法是一个比较实用、便捷的办法，在工程流体力学计算中也被普遍应用。
该文重点探讨了运用叠加法怎样描绘杆系构件的最大弯矩图形，为建筑力学实验教学中提出了有益的借鉴。
关键词：建筑力学 叠加法 矩图 探讨中图分类号：G64文献标识码：A 文章编号：1672-3791(2023)16-0150-04 New Discussion of Using the Superposition Method to Draw Bending Moment Diagrams in Architectural MechanicsCHENG Jingjing(School of Urban Construction, Lanzhou Modern Vocational College, Lanzhou, Gansu Province, 730030 China) Abstract:Architectural design fluid mechanics refers to the summary of people's experience in labor through the observation of natural phenomena. Architectural design fluid mechanics plays the most basic cognitive function in the objective world formed by the structure of buildings. In engineering fluid mechanics, the use of the superposi‐tion method is of great significance in drawing the maximum bending moment diagram. The common methods for drawing the maximum bending moment diagram mainly include the equation method, rule method and superposi‐tion method, among which the superposition method is a more practical and convenient method, and it is also widely used in the calculation of engineering fluid mechanics. This paper mainly discusses how to use the superpo‐sition method to describe the maximum bending moment figure of the member system, which provides a useful reference for the experimental teaching of engineering mechanics.Key Words: Architectural mechanics; Superposition method; Bending moment diagram; Discussion力学的概念起源于古人对自然现象的观察、在自然界生产活动过程中总结的经验。
区段叠加法
1.1.3区段叠加法作直梁弯矩图
在小变形情况下，依据力的独立性原理，复杂荷载引起的弯矩图，可分区段用单一荷载引起的弯矩图叠加的方法，即区段叠加法进行
绘制。
可按以下三个步骤进行：
●一求控制弯矩：首先，求两杆端的弯矩，常可直接判断（对于简支梁两端铰支处、悬臂梁的悬臂端，若无集中力偶作用，其弯
矩均为零；若有集中力偶作用，其弯矩即等于该集中力偶）；其次，求外力不连续点处的弯矩（如集中力作用点、均布荷载的起点和终点、集中力偶作用点两侧的弯矩），用载面法即可方便求得。
●二引直线相连：将相邻二控制弯矩用直线相连（当二控制截面间无横向荷载作用时，用实线连接，即为该区段弯矩图形；当二
控制截面间尚有横向荷载作用时，则用虚线连接，作为新的“基线”，然后再按下面的第“三”步叠加）。
●三叠简支弯矩：在新的“基线”上，叠加该区段按简支梁求得的弯矩图（注意：所叠加的二竖标均应垂直于原杆轴）。
现以图1-3所示简支伸臂梁为例，用区段叠加法绘制其弯矩图。
其计算步骤示于图1-3b-d中（具体计算过程从略）。
图1-3“区段叠加法”分步示意图
（二）对于曲线弯矩图叠加曲线弯矩图的情况
找出一些控制弯矩值（至少三点），中间连以适当曲线，主要是定好弯曲方向，一般为连续光滑曲线。
理论力学-叠加法
2a
(h)
a
1 1 M C ( 291 ) 122 ( 215 ) 131KN m 2 2
绘出叠加后的弯矩图如图 e 所示。
P1
D
P2
A C B
P3
E D
P1
A B
E
a
a
a
a
(f)
a
2a
(e)
E3 P D A B D
P2
A C B E
a
(h)
a
(g)
2a
a
+
P
x q
(c)
x
叠加原理：由几个外力共同作用时所引起的某一参数 （内力，应力，位移），就等于每个外力单独作用时所 引起的该参数值的代数和。 例题4-17 试按叠加原理作图 a 所示简支梁的弯矩图， 设 m
ql ，求梁的极值弯矩和最大弯矩。 8
m q
A
2
x
l
m
m
q
A
q
B
A B A B
x
l
l
l
+
+
D
a
a
(a)
a
a
a
2a
(b)
P2
A C B
E D
P3
A B E
a
(C)
a 例题4-18图
2a
(d)
a
P1
D
A B
P2
E D
A C B
E
a
2a
(g)
a
a
(f)
+
P3
D A B E
M A 291 0 0 291KN m M B 0 0 215 215KN m
结构力学第三章叠加法作弯矩图
2kN· m
（3）叠加得弯矩图
4kN· m
4kN· m
MA A
MB
B
l
MB
MA
MA A
q B
MB
l
MA
ql 8
2
MB
8kN· m
2kN/m
3m
3m
2m
（1）悬臂段分布荷载作用下
4kN· m
2kN· m
（2）跨中集中力偶作用下
4kN· m
4kN· m
（3）叠加得弯矩图
6kN· m
4kN· m
2kN· m
+
所以：M2＝375kN.m （左拉） FN1=141×0.707=100kN
FQ1= 50 +5×5 －141×0.707 =－25kN
(取外力矩逆时针转向为正方向) (下拉）
M1=125 +141×0.707×10－50×5－5/2×5²=812.5kNm
注意：外力矩的正负是为了区分它的两种不同的转向。
qba30因此上图梁中ab段的弯矩图可以用与简支梁相同的方法绘制即把m以直线然后在此直线上叠加上节间荷载单独作用在简支梁上时的弯矩图为此必须先求出mql区段弯矩图叠加法32qlqlqlqlqlqlql区段弯矩图叠加法3310knm15kn60knm2m2m2m2m20knm3055303030303030303030303030348kn4knm16knm1m2m2m1m1730237kn1m1m35利用上述关于内力图的特性和弯矩图的分段叠加法可将梁的弯矩图的一般作法归纳如1选定外力的不连续点如集中力作用点集中力偶作用点分布荷载的起点和终点等为控制截面求出控制截面的弯矩值连一虚线然后以该虚线为基线叠加上简支梁在跨间荷载作用下的弯矩图
（3）叠加得弯矩图
4kN· m
4kN· m
MA A
MB
B
l
MB
MA
MA A
q B
MB
l
MA
ql 8
2
MB
8kN· m
2kN/m
3m
3m
2m
（1）悬臂段分布荷载作用下
4kN· m
2kN· m
（2）跨中集中力偶作用下
4kN· m
4kN· m
（3）叠加得弯矩图
6kN· m
4kN· m
2kN· m
+
所以：M2＝375kN.m （左拉） FN1=141×0.707=100kN
FQ1= 50 +5×5 －141×0.707 =－25kN
(取外力矩逆时针转向为正方向) (下拉）
M1=125 +141×0.707×10－50×5－5/2×5²=812.5kNm
注意：外力矩的正负是为了区分它的两种不同的转向。
qba30因此上图梁中ab段的弯矩图可以用与简支梁相同的方法绘制即把m以直线然后在此直线上叠加上节间荷载单独作用在简支梁上时的弯矩图为此必须先求出mql区段弯矩图叠加法32qlqlqlqlqlqlql区段弯矩图叠加法3310knm15kn60knm2m2m2m2m20knm3055303030303030303030303030348kn4knm16knm1m2m2m1m1730237kn1m1m35利用上述关于内力图的特性和弯矩图的分段叠加法可将梁的弯矩图的一般作法归纳如1选定外力的不连续点如集中力作用点集中力偶作用点分布荷载的起点和终点等为控制截面求出控制截面的弯矩值连一虚线然后以该虚线为基线叠加上简支梁在跨间荷载作用下的弯矩图
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
叠加原理成立的前提条件：小变形条件
q
M x Fx qx2
2
Mx M1x M2x
AX l
B
F
叠加法——用叠加原理绘制弯矩图的方法
叠加时，易先画直线形的弯矩图，再叠加曲线形或折线形 的弯矩图
由于剪力图比较好画，重点介绍用叠加法画弯矩图
步骤： 注意：
1. 荷载分解 2. 作分解荷载的弯矩图
l
1 Fl
-4
6kN
6kN 2kN m
AC
B
D
2m 2m 2m
4
+
-
6+ຫໍສະໝຸດ 42kN m2m 2m 2m
4
-
MA A
MA
q
MB
B
l
q
A
l
+
+
MB
1/8qL2
1/8qL2
MA BA
l
+
MA
MB B
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
130
Fab 1601 2 107
L
3
30
ql2 40 16 80 KN m
8
8
130
40kN m
40kN
BF
310kN
4m
2m
120
40
kN
190 160
kNm
210 280
340
3. 叠加作荷载共同作用下 的弯矩图
弯矩图的叠加， 不是两个图形的简单叠加， 而是对应点处纵坐标的相加。
叠加法作弯矩图
F
q
F
q
A
BA
＋
B
A
B
l
l
l
1/2qL2+FL
1/2qL2
FL
F A
m 1 Fl
4A
F
C
B
B
l2 l2
1 Fl 4
-
+ 1 Fl 8
l2 l2
+
1 Fl 4
A C
m 1 Fl 4 C
梁分一段： A端截面弯矩：M=MA B端截面弯矩：M=MB
MA A
A
MA
q
MB
B
l
B
MB
1/8qL2
梁分两段：AB段和BD段。 AB段A端弯矩MAB=0， B端弯矩MBA=-4KN•m BD段B端弯矩MBD=-4KN•m D端弯矩MDB=0
6kN 2kN m
AC
B
D
2m 2m 2m
4 B 2
A
D
叠加法作弯矩图
教学目的：
1、掌握叠加原理； 2、会用叠加法作弯矩图； 3、会用区段叠加法作弯矩图
重点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难点
区段叠加法绘制弯矩图
叠加原理：
几个载荷共同作用的效果，等于各个载荷单独作用效果之和
“效果”——指载荷引起的反力、内力、应力或变形
“之和”——代数和
1
4
支座反力RA=15KN RB=11KN
梁分CA、AD、DB BF段。
各控制面弯矩分别为：
MA=-12KN MD=8KN MB=-4KN
6KN q=2KN/m
C 2m
A 4m
RA
12
8KN q=2KN/m
D
E
2m 2m
BF 2m
RB
4
8
10
80kN m 160kN
C A
DE 130kN
1m 1m 2m