事件的运算与关系解读
- 格式:ppt
- 大小:892.00 KB
- 文档页数:22




事件的关系和运算事件的关系常用的有包含关系、互斥关系和独立关系。
事件的运算常用的有并运算、交运算、差运算和补运算。
1. 包含关系:如果事件A发生必然导致事件B发生,则称事件B包含事件A,记作A⊆B。
例如,事件A为"今天下雨",事件B为"今天有降水",则A⊆B,因为当今天下雨时,当然也说明今天有降水。
2. 互斥关系:如果事件A和事件B不能同时发生,则称事件A和事件B互斥,记作A∩B=Ø。
例如,事件A为"掷一次骰子,结果为奇数",事件B为"掷一次骰子,结果为偶数",则A∩B=Ø,因为掷一次骰子的结果不可能既是奇数又是偶数。
3. 独立关系:如果事件A的发生与发生或不发生事件B无关,则称事件A和事件B独立,记作P(A|B) = P(A),其中P(A|B)表示在事件B发生的条件下事件A发生的概率。
例如,事件A为"掷一次骰子,结果为1",事件B为"抽一张牌,结果为红心",则A和B是独立事件,因为掷骰子的结果不会受到抽牌的影响。
事件的运算包括:1. 并运算:事件A∪B表示事件A和事件B中至少一个事件发生的情况。
例如,事件A为"今天下雨",事件B为"今天有降雨",则A∪B表示今天下雨或者今天有降雨。
2. 交运算:事件A∩B表示事件A和事件B同时发生的情况。
例如,事件A为"掷一次骰子,结果为奇数",事件B为"掷一次骰子,结果为3",则A∩B表示掷一次骰子的结果既是奇数又是3。
3. 差运算:事件A-B表示事件A发生但事件B不发生的情况。
例如,事件A为"今天下雨",事件B为"今天有降雨",则A-B表示今天下雨但今天没有降雨。
4. 补运算:事件A的补事件表示事件A不发生的情况,记作A'或Ac。

概率事件的关系与运算知识点总结一、事件的关系。
1. 包含关系。
- 定义:如果事件A发生必然导致事件B发生,那么称事件B包含事件A,记作A⊆ B。
例如,在掷骰子试验中,设事件A=“掷出的点数为1”,事件B=“掷出的点数为奇数”,那么A发生时B一定发生,所以A⊆ B。
- 特殊情况:如果A⊆ B且B⊆ A,那么A = B,即这两个事件是同一个事件。
2. 互斥关系(互不相容关系)- 定义:如果事件A与事件B不能同时发生,即A∩ B=varnothing (varnothing为空集),那么称A与B是互斥事件。
例如,掷一枚硬币,事件A=“正面朝上”,事件B=“反面朝上”,A和B不可能同时发生,所以A与B互斥。
3. 对立关系。
- 定义:如果A∩ B=varnothing且A∪ B=varOmega(varOmega为样本空间),那么称A与B是对立事件,B叫做A的对立事件,记作B=¯A。
例如,在掷骰子试验中,设事件A=“掷出的点数为偶数”,事件B=“掷出的点数为奇数”,A∩ B=varnothing且A∪ B={1,2,3,4,5,6}(整个样本空间),所以A与B是对立事件。
- 关系:对立事件一定是互斥事件,但互斥事件不一定是对立事件。
4. 独立关系(如果涉及到选修内容)- 定义:设A,B是两个事件,如果P(AB)=P(A)P(B),则称事件A与事件B相互独立。
例如,连续掷两次硬币,事件A=“第一次正面朝上”,事件B=“第二次正面朝上”,P(A)=(1)/(2),P(B)=(1)/(2),P(AB)=(1)/(4),满足P(AB) = P(A)P(B),所以A与B相互独立。
二、事件的运算。
1. 事件的并(和)运算。
- 定义:事件A与事件B的并(和)事件A∪ B是由所有A发生或B发生的基本事件组成的集合。
例如,掷骰子试验中,设事件A=“掷出的点数为1或2”,事件B=“掷出的点数为3或4”,那么A∪ B=“掷出的点数为1、2、3或4”。

事件间的关系及运算事件间的关系可以通过运算来描述和计算。
常见的事件运算包括并、交、差和补等。
1. 并运算(Union):表示将两个或多个事件合并在一起。
记作A∪B,表示事件A和事件B至少发生一个。
并运算的计算规则如下:- 若A和B是两个不相交的事件(即A∩B=∅),则A∪B 的概率等于A和B的概率之和:P(A∪B) = P(A) + P(B)。
- 若A和B是两个有交集的事件(即A∩B≠∅),则A∪B 的概率等于A和B的概率之和减去A和B的交集的概率:P(A∪B) = P(A) + P(B) - P(A∩B)。
2. 交运算(Intersection):表示两个事件同时发生的情况。
记作A∩B,表示事件A和事件B同时发生。
交运算的计算规则如下:- 若A和B是两个不相交的事件(即A∩B=∅),则A∩B的概率为0:P(A∩B) = 0。
- 若A和B是两个有交集的事件(即A∩B≠∅),则A∩B的概率等于A和B的概率之和减去A和B的并集的概率:P(A∩B) = P(A) + P(B) - P(A∪B)。
3. 差运算(Difference):表示事件A发生而事件B不发生的情况。
记作A-B,表示事件A发生而事件B不发生。
差运算的计算规则如下:- A-B等于事件A和事件B的交集的补集:A-B = A∩B'。
- 若A和B是两个不相交的事件(即A∩B=∅),则A-B的概率等于A的概率减去B的概率:P(A-B) = P(A) - P(B)。
4. 补运算(Complement):表示事件A不发生的情况。
记作A'或A^C,表示事件A不发生。
补运算的计算规则如下:- 若样本空间为S,则事件A的补集为S-A,即事件A不发生的情况。
- 若事件A是必然发生的事件(即A=S),则A的补集为空集:A' = ∅。
- 若事件A是不可能发生的事件(即A=∅),则A的补集为整个样本空间:A' = S。

事件的关系和运算一、引言在我们的日常生活中,我们经常遇到一些事件,这些事件之间存在着各种关系。
通过对这些关系的运算和分析,我们可以更好地理解事件之间的联系,并从中获得更多的信息和启示。
本文将探讨事件的关系和运算,希望能够给读者带来一些思考和启发。
二、事件的关系事件的关系是指事件之间的相互联系和相互作用。
在我们生活中,事件之间的关系可以是因果关系、逻辑关系、时间关系等。
下面我们将分别介绍这些关系。
1. 因果关系因果关系是指一个事件的发生导致另一个事件的发生。
例如,下雨导致地面湿滑,人们走路容易摔倒;吃太多甜食导致牙齿蛀坏。
因果关系是我们日常生活中最常见的一种关系,我们需要通过观察和分析来确定事件之间的因果关系。
2. 逻辑关系逻辑关系是指事件之间的合理性和推理性联系。
逻辑关系可以有推理关系、蕴含关系、对立关系等。
例如,如果A是B的子集,那么B一定是A的超集;如果一个命题是真的,那么它的否定命题一定是假的。
逻辑关系是我们进行思考和推理的基础,通过分析逻辑关系,我们可以得出正确的结论。
3. 时间关系时间关系是指事件之间的先后顺序和时间间隔。
事件之间的时间关系可以是同时发生、先后发生、持续发生等。
例如,早上起床后刷牙洗脸是先后发生的事件;午饭和晚饭是同时发生的事件。
时间关系帮助我们理清事件之间的顺序和关联,从而更好地安排和管理时间。
三、事件的运算事件的运算是指对事件进行组合、分解和变换的操作。
通过事件的运算,我们可以得到新的事件,并从中获得更多的信息和启示。
下面我们将介绍一些常见的事件运算。
1. 事件的组合事件的组合是指将多个事件合并成一个事件。
事件的组合可以有并集、交集、差集等。
例如,假设事件A表示今天下雨,事件B表示今天有雾,那么事件A和事件B的并集表示今天下雨或有雾;事件A和事件B的交集表示今天既下雨又有雾。
事件的组合帮助我们分析多个事件之间的关系和影响。
2. 事件的分解事件的分解是指将一个事件拆分成多个事件。

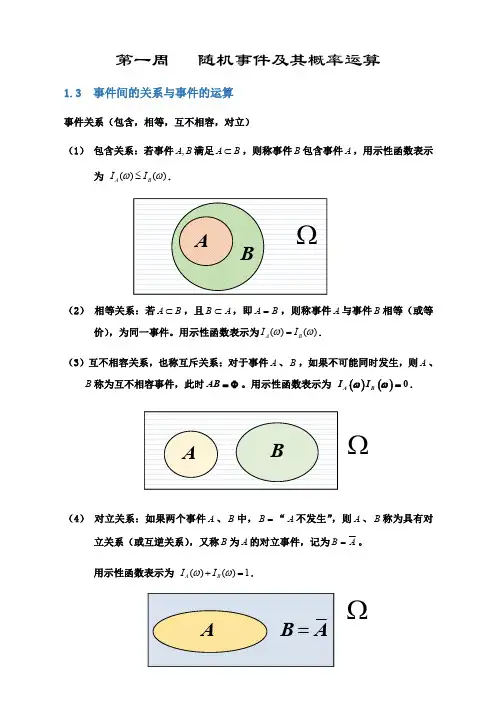
第一周随机事件及其概率运算1.3事件间的关系与事件的运算事件关系(包含,相等,互不相容,对立)(1)包含关系:若事件,A B 满足A B⊂,则称事件B 包含事件A ,用示性函数表示为()()ωω≤A B I I .(2)相等关系:若A B ⊂,且A B ⊂,即B A =,则称事件A 与事件B 相等(或等价),为同一事件。
用示性函数表示为()()A B I I ωω=.(3)互不相容关系,也称互斥关系:对于事件A 、B ,如果不可能同时发生,则A 、B 称为互不相容事件,此时AB =Φ。
用示性函数表示为()()0A B I I ωω=.(4)对立关系:如果两个事件A 、B 中,=B “A 不发生”,则A 、B 称为具有对立关系(或互逆关系),又称B 为A 的对立事件,记为A B =。
用示性函数表示为()()1ωω+=A B I I .ΩΩ*********************************************************事件运算(和,积,差,交换律,结合律,分配律,结合律,对偶律)(1)事件的和:事件A 与事件B 的并集构成的事件称为事件A 与事件B 的和事件,记为A B 或A B +,即{}|A B x x A x B =∈∈ 或,如图所示的阴影部分.显然,当且仅当事件A 与事件B 至少有一个发生时,事件A B 才发生。
n 个事件n A A A ,,,21 的和事件,即为n 个集合的并集 n k k A 1=。
(2)事件的积(或交):事件A 与事件B 的交集构成的事件称为事件A 与事件B 的积(或交)事件,事件A 与事件B 同时发生。
记为A B 或AB 。
n 个事件n A A A ,,,21 的积事件,即为n 个集合的交集 nk k A 1=。
(3)事件的差:事件A 与事件B 的差集所构成的事件称为事件A 与事件B 的差事件,记为B A -。
{}|A B x x A x B AB -=∈∉=且。

