相贯线展开图坐标
- 格式:xls
- 大小:24.50 KB
- 文档页数:1
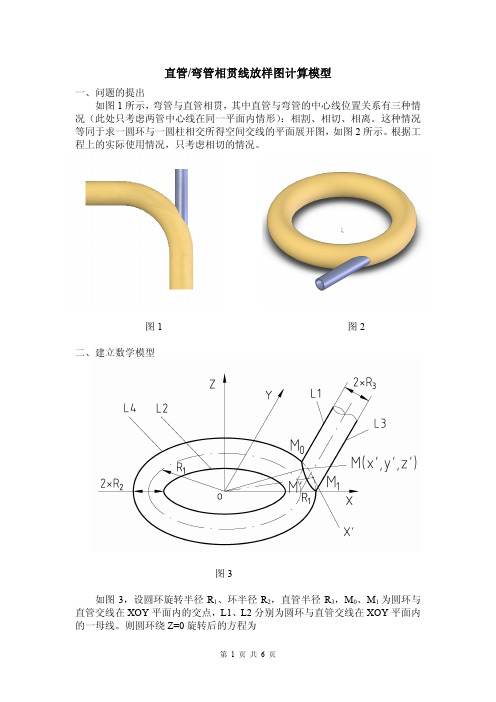
直管/弯管相贯线放样图计算模型一、问题的提出如图1所示,弯管与直管相贯,其中直管与弯管的中心线位置关系有三种情况(此处只考虑两管中心线在同一平面内情形):相割、相切、相离。
这种情况等同于求一圆环与一圆柱相交所得空间交线的平面展开图,如图2所示。
根据工程上的实际使用情况,只考虑相切的情况。
图1 图2二、建立数学模型图3如图3,设圆环旋转半径R1、环半径R2,直管半径R3,M0、M1为圆环与直管交线在XOY平面内的交点,L1、L2分别为圆环与直管交线在XOY平面内的一母线。
则圆环绕Z=0旋转后的方程为()22212R zR −+=……………………… ①或2222212x y R z R R +++−=± (注:圆环关于XOY 平面对称) 直管圆柱面方程为()22213x R z R −+=……………………… ②联立①②,则得圆环与直管的交线(即相贯线)方程()()2221222213R z R x R z R ⎧+=⎪⎨⎪−+=⎩……………………… ③ 为便于求解,只求第一象限的交线,则定义域为1313122300{,}R R x R R y R R z MAX R R −≤≤+⎧⎪≤≤+⎨⎪≤≤⎩三、求解直管沿母线L1剪切展开后的图形大致类似于图4,圆环沿母线L2剪切展开后的图形大致类似于图5。
图4 图5在图3任取一动点M(x’,y’,z’),当点 M(x’,y’,z’)沿方程③运动时,对应于图4、图5中点M(x,y)的运动轨迹即为所求。
从图3和方程组③中可以得知,图4、图5的曲线是关于y 轴对称的,所以只需研究图3第一象限上半部分的曲线展开方程,即图4、图5中的第二象限部分曲线方程。
1、直管相贯线展开方程X =-(图3中直管上的截面圆上点M 到M 1所在母线L3的一段弧长) Y =图3中M 的Y 坐标值-图3中M 1的Y坐标值第 3 页 共 6 页X 的具体求解方法为:将直管投影在XOZ 平面上(见图6)。




第二节相贯线的作图求解一、轴线互相垂直的两圆柱的相贯线当圆柱体轴线垂直于投影面时,其圆柱表面在该投影面上的投影有积聚性,所以两圆柱轴线互相垂直的相贯线可利用积聚性投影取点作图法求解。
1、轴线正交两圆柱的相贯线图10-2如图10-2所示两圆柱轴线垂直相交,且分别垂直于H面和W面,因此俯视图中相贯线的投影积聚在小圆柱的投影(圆)上;左视图中相贯线的投影积聚在小圆柱两条转向轮廓线之间的大圆柱面投影(圆)上。
这样由相贯线的两个已知投影,可作出它的V面投影。
利用积聚性投影取点作图求相贯线的作图步骤如图10-3所示:图10-3 柱-柱相交相贯线作图步骤(1)求特殊点图10-3.b所示相贯线上I、V两点分别位于两圆柱对V面的转向线上,是相贯线上的最高点,也分别是相贯线上的最左点和最右点。
Ⅲ、Ⅶ两点分别位于小圆柱对W面的转向线上,它们是相贯线上的最低点,也分别是相贯线上的最前点和最后点。
在投影图上可直接作投影连线求得1’、3’、5’、7’。
(2)求一般点先在俯视图中的小圆柱投影圆上,适当地确定出若干个一般点的投影,如图10-3.c所示中的2、4、6、8等点,再按点的三面投影规律,作出W面投影2"(4")、8" (6")和V面投影2’(8’)4’(6’)点。
(3)判断可见性及圆滑连接由于该相贯线前后前部分对称,且形状相同,所以在V面投影中可见与不可见部分重合,按1’-2’-3’-4’-5’顺序用粗实线圆滑地连接起来。
(4)按图线要求描深各图线,完成两圆柱正交立体的三视图(图10-3.d)。
2、轴线正交内、外圆柱面的相贯线由于圆柱有实体圆柱和空心圆柱之分,因此圆柱面又有外圆柱面和内圆柱面之别。
故两圆柱面相交会产生三种情况:(1)两外圆柱面相交,如图10-4.a所示;(2)外圆柱面与内圆柱面相交,即圆柱与圆孔相交,如图10-4.b所示;(3)两内圆柱面相交,即圆孔与圆孔相交,如图10-4.c所示。
