管子相贯线展开的方程式
- 格式:xls
- 大小:316.50 KB
- 文档页数:4
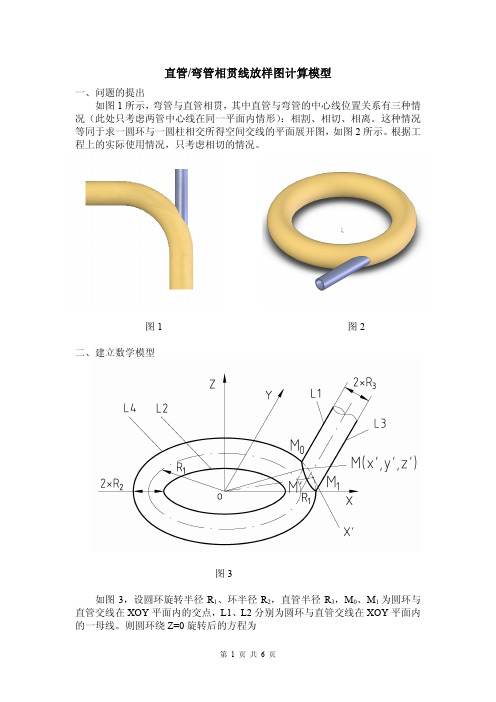
直管/弯管相贯线放样图计算模型一、问题的提出如图1所示,弯管与直管相贯,其中直管与弯管的中心线位置关系有三种情况(此处只考虑两管中心线在同一平面内情形):相割、相切、相离。
这种情况等同于求一圆环与一圆柱相交所得空间交线的平面展开图,如图2所示。
根据工程上的实际使用情况,只考虑相切的情况。
图1 图2二、建立数学模型图3如图3,设圆环旋转半径R1、环半径R2,直管半径R3,M0、M1为圆环与直管交线在XOY平面内的交点,L1、L2分别为圆环与直管交线在XOY平面内的一母线。
则圆环绕Z=0旋转后的方程为()22212R zR −+=……………………… ①或2222212x y R z R R +++−=± (注:圆环关于XOY 平面对称) 直管圆柱面方程为()22213x R z R −+=……………………… ②联立①②,则得圆环与直管的交线(即相贯线)方程()()2221222213R z R x R z R ⎧+=⎪⎨⎪−+=⎩……………………… ③ 为便于求解,只求第一象限的交线,则定义域为1313122300{,}R R x R R y R R z MAX R R −≤≤+⎧⎪≤≤+⎨⎪≤≤⎩三、求解直管沿母线L1剪切展开后的图形大致类似于图4,圆环沿母线L2剪切展开后的图形大致类似于图5。
图4 图5在图3任取一动点M(x’,y’,z’),当点 M(x’,y’,z’)沿方程③运动时,对应于图4、图5中点M(x,y)的运动轨迹即为所求。
从图3和方程组③中可以得知,图4、图5的曲线是关于y 轴对称的,所以只需研究图3第一象限上半部分的曲线展开方程,即图4、图5中的第二象限部分曲线方程。
1、直管相贯线展开方程X =-(图3中直管上的截面圆上点M 到M 1所在母线L3的一段弧长) Y =图3中M 的Y 坐标值-图3中M 1的Y坐标值第 3 页 共 6 页X 的具体求解方法为:将直管投影在XOZ 平面上(见图6)。



(princ "直圆管展开图(来自化缘敲鱼) 命令:zkx") (defun c:zkx (/ l0 lsslss_mptss df_dx0 n ptptstpten) (setvar "cmdecho" 0)(command "undo" "be")(command "ucs" "w")(princ "\n请选择轴线:")(setq l0 (car (entsel)))(princ "\n半径:")(princ r)(princ "\n请选择切割线:")(setqlss (ssget))(command "ucs" "ob" l0)(setq m 0)(while (< m (sslengthlss))(setqlss_m (ssnamelss m))(setqptss (list))(setq df_dx0 (entlast))(command "divide" lss_m 200) ;100等分对象(setq n 0)(while (= n 0)(if (equal df_dx0 (entlast))(setq n 1)(progn(if (eq (cdr (assoc '0 (entget (entlast)))) "POINT")(progn(setqpt (cdr (assoc '10 (entget (entlast)))))(setqpt (trans pt 0 1))(setqptss (cons ptptss))))(command "ERASE" "l" ""))))(setqptst (vlax-curve-getstartPointlss_m))(setqpten (vlax-curve-getEndPointlss_m))(setqptst (trans ptst 0 1))(setqpten (trans pten 0 1))(if (> (distance ptst (nth 0 ptss)) 0.01)(setqptss (cons ptstptss)))(if (> (distance pten (nth 0 (reverse ptss))) 0.01)(setqptss (reverse (cons pten (reverse ptss)))))(command "pline")(setq n 0)(while (< n (length ptss))(setqpt (nth n ptss))(setq x (nth 0 pt))(setq y (nth 1 pt))(setq z (nth 2 pt))(setqang (* -1 (- (angle (list 0 0 0) (list z y 0)) pi)))(setq r (distance (list 0 0 0) (list 0 y z)))(setqpt (list x (* ang r)))(commandpt)(setq n (1+ n)))(command "")(setq m (1+ m)))(command "ucs" "p")(command "undo" "e")(princ))。

计算机辅助绘制圆管相贯线展开图的方法与技巧殷刚沈阳远大企业集团研究所计算机应用室沈阳110161【摘要】本文介绍了沈阳远大企业集团研究所计算机应用室自主开发的“远大空间管桁结构相贯节点放样工具软件”的使用方法和圆管相贯构件展开放样的基本原理,阐述了用计算机实现辅助绘制圆管相贯线展开图的方法,通过典型实例分析了绘制多个圆管相贯线展开图的技巧。
【关键词】计算机辅助设计钣金展开放样1 概述在工程的生产加工过程中,我们会经常遇到两个(或几个)圆管相贯的情况。
在正式加工前,须作出这些相贯线的全部或部分展开图样线,然后才能裁剪制成。
这些相贯线的展开图样线是否正确以及精度如何,将直接影响到产品的质量。
本文介绍的就是利用计算机来实现辅助绘制相贯线的展开图样线的基本方法和一些技巧。
熟练地掌握这些方法和技巧,既可以帮助设计人员和工艺人员进行现场的展开放样,提高工作效率和产品质量,又可以为公司节省工料,降低成本。
2 钣金展开放样的基本方法绘制相贯线的展开图样线的基本方法大体有两种。
第一种是图解法,它运用投影原理作图,进行展开放样。
首先按投影原理绘制出构件的有关视图,并画出辅助线,求出实长、实形等,然后再作出相贯线的展开图样线。
图解法作图繁琐,手工作图误差较大,影响加工质量。
计算机辅助绘图虽可提高精度,但是模块化程度不高,不易于程序设计。
第二种是计算法,它通过理论计算,进行展开放样。
首先示意性的画出必要的视图,然后将圆管断面等分,将圆周上等分点折算成角度依次计算,再根据计算结果描点进行放样,作出相贯线的展开图样线。
计算法作图迅速,虽然是近似计算,但等分点愈多展开图愈准确,足以满足工程需要。
计算法繁琐的计算过程因其模块化程度高,可以通过程序设计来实现,精确的描点绘图也可由计算机来完成,可以确保产品质量,提高工作效率。
本文讨论的就是如何通过计算法进行展开放样。
3 典型圆管构件的放样计算原理圆管构件在钣金结构中较为普遍,而且类型较多,不能一一例举。
一、Y形管展开计算
图1-19所示为等径Y形管,已知尺寸为d、l、h、t、β,放样计算式:
式中 y n——展开图圆周长度等分点至曲线坐标值; d——圆管外径;
αn——辅助圆等分角度。
图1-19
下面推导当β=60°时各等分数的计算式。
当n=12时
计算式:
用同样方法可推导出支管轴线交角β=90°Y形管展开曲线坐标值。
为便于使用,将β=60°、β=90°不同等分数的Y形管展开曲线坐标值,列于表1-18、表1-19中。
表1-18 β=60°Y形管展开图曲线坐标值
注:y—圆管展开周长等分点至曲线距离;d—圆管外径;n—圆周长度等分数。
表1-19 β=90°Y形管展开图曲线坐标值
注:y—圆管展开周长等分点至曲线距离;d—圆管外径;n—圆周长度等分数。
例题计算
已知等径Y形管支管轴线交角β=60°,圆管外径d=240,板厚t=4,主管高h=280,支管长l=350,试用计算放样。
解:设圆周长度等分数n=12,查表1-18得:
y0=0.134×240=32
y1=0.116×240=27.8
y2=0.067×240=16
y3=0
y4=0.433×240=104
y=0.75×240=180
y6=0.866×240=207.8
圆周长 S=π(d-t)=3.1416×(240-4)=741.4
根据以上各计算值即可画出展开图,如图1-18所示,说明省略。
图1-18。
圆管相贯线三维坐标方程的推导在采用数控机床加工零件时,往往会遇到零件形状是由复杂的空间曲线构成。
已知条件是曲线的方程,这些方程可能是直接得到的,或者是通过轮廓形状上的一些关键点,通过拟合的方法得到近似的曲线方程。
特别在起重机、锅炉制造等行业经常有不同管径的圆管交叉连接。
其中两管相贯线的确定和精确切割加工是一个难点。
常用的方法是在知道管的相对位置等条件下,经过计算手工制出模板,用模板画线,手工切割。
其过程十分烦琐,且切割精度也无法保证。
数控加工的目的在于按照已知的曲线方程加工零件,因此将曲线转换为数控加工需要的数控代码是很重要的一个环节。
如果用手工编程,则效率低、可靠性差,不能充分发挥机床的功能和性能。
随着CAD/CAM技术的发展,国外许多高档的CAD软件都具有相应的CAM模块。
例如美国SRDC公司的I_DEAS、PTC公司的Pro/E、UG、SolidWork等性能良好的CAM模块。
利用其三维实体数据生成数控加工代码,通过通讯接口传输到数控机床的数控系统。
也有一些第三方开发的CAM模块,可与CAD软件无缝集成,完成数控代码的生成。
然而,这些软件相对来说要求高,价格昂贵。
且没有配置专用的后置处理器,或者只配置了通用的后置处理器而没有根据数控机床的特点进行二次开发,由此产生的代码还需要做大量的手工修改。
本文以Autodesk公司的AutoCAD2000为平台,利用其内嵌的ARX编程工具,针对生产现场的数控切割机床加工两管的相贯线,开发了一套能够计算并自动获得相贯线数控加工代码的系统。
通过设置刀具路径等工艺参数和后置处理,最后生成NC代码,供数控机床加工零件。
此过程可以节省大量的人力和时间。
并且最大限度的减少人为和系统因素的影响,使管缝切割精度高,保证焊接质量更加稳定可靠。
在一定程度上弥补了零件制造从设计到成型的薄弱环节。
1.数学模型的建立两个圆管的相交形式多样。
但都是两个相同或者不同直径的圆柱面以一定的角度相交形成的空间曲线。