厂商理论概述
- 格式:doc
- 大小:643.50 KB
- 文档页数:15





微观经济学–厂商理论1. 引言微观经济学是研究个体经济行为和市场机制的经济学分支。
在微观经济学中,厂商理论是一个重要的研究领域,主要关注厂商的行为和决策,探讨企业如何在市场环境下最大化利润。
在本文中,我们将介绍厂商理论的基本概念、分析框架和重要结论。
首先,我们将讨论企业的目标与约束条件。
然后,我们将介绍生产函数和成本函数的概念,并解释厂商的生产决策。
接下来,我们将讨论厂商的市场行为,包括定价策略和市场份额的决策。
最后,我们将讨论厂商的市场结构和行业竞争对厂商行为的影响。
2. 企业的目标与约束条件在厂商理论中,企业的目标通常是利润最大化。
利润最大化是指企业通过在给定的市场环境下做出最佳决策,使其总收入减去总成本最大化。
企业的利润可以分为两部分:显性利润和隐性利润。
显性利润是指企业从市场销售商品或服务所获得的收入超过其成本的部分。
隐性利润是指企业在做出决策时所获得的非货币性收益,如知名度、品牌价值等。
此外,企业在决策过程中还有一些约束条件。
其中,技术约束是指企业所使用的技术和生产方法对企业决策的影响。
市场约束是指企业在市场竞争中所面临的约束,如市场供求关系、价格竞争等。
3. 生产函数和成本函数在厂商理论中,生产函数和成本函数是分析企业生产决策的重要工具。
生产函数描述了输入要素和产出之间的关系。
一般来说,生产函数可以表示为Y = f(X1, X2, …, Xn),其中 Y 表示产出,X1, X2, …, Xn 表示输入要素,如劳动力、资本等。
生产函数的形式和参数决定了企业的生产能力和生产效率。
成本函数描述了企业的成本与产出之间的关系。
一般来说,成本可以分为两部分:固定成本和可变成本。
固定成本是企业不随产量变化的成本,如租金、管理费用等。
可变成本是随着产量变化的成本,如原材料、劳动力成本等。
成本函数可以表示为 C = C(Q),其中 C 表示总成本,Q 表示产量。
4. 厂商的生产决策在厂商理论中,生产决策是指企业如何在给定的技术和成本条件下选择产量水平和输入要素的组合。
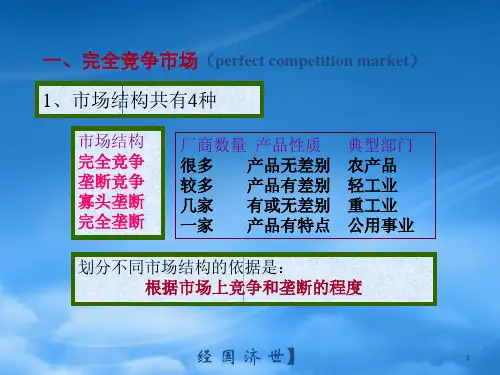





《西方经济学》第五章厂商理论教学目标及基本要求:通过本章教学,掌握短期和长期成本函数的分类与相互关系,掌握利润最大化原则,能运用有关成本理论进行成本决策。
了解厂商在不同市场上的行为即在不同的市场上厂商如何通过价格与产量的决定来实现利润最大化.教学重点:成本与收益;各种市场结构下的短期均衡与长期均衡;教学难点:各种市场结构下的短期均衡与长期均衡的条件;第一节成本与收益本节讨论厂商的生产成本和产量之间的关系。
企业要决定最佳的产量,必须经过充分的成本分析。
本节假定厂商只能被动地接受生产要素的市场价格,即假定生产要素市场是完全竞争的.一、短期成本短期成本:是指厂商只调整某些生产要素时所发生的成本.长期成本:是指厂商调整全部生产要素发生的成本。
1、短期成本的分类已知短期生产函数为:Q = f ( L , K)其中 K 为常数,则厂商在每一个产量水平上所对应的短期总成本为: STC = w· L(Q) + r · K短期成本的分类总固定成本 TFC = r K总可变成本 TVC = w L(Q) = TVC(Q)总成本 TC = TFC + TVC平均固定成本 AFC = TFC / Q平均可变成本 AVC = TVC / Q平均成本 AC = TC / Q=AFC+AVC边际成本 MC = dTC / dQ2、短期成本的变动规律及其关系(1)短期总成本(shortrun total cost)STC短期成本分为:固定成本FC和可变成本VC。
STC = FC + VC固定成本FC:固定不变,不随产量变动而变动,厂商在短期内必须支付的不能调整的生产要素的费用。
包括:厂房和设备的折旧,以及管理人员的工资.可变成本VC:随产量变动而变动。
短期内可以调整。
包括:原材料、燃料支出和生产工人的工资.短期总成本曲线STC = FC + VC它不从原点出发,而从固定成本FC出发;没有产量,短期总成本最小也等于固定成本.陡--平——陡(2)短期平均成本SAC短期平均成本:生产每一单位产品平均所需要的成本.SAC =平均固定成本 +平均可变成本= AFC+ AVC平均固定成本AFC随产量Q的增加而递减——一直趋于减少。
厂商理论在这一章里我们研究经济的供给边,研究商品和服务是任何生产出来的,生产商品和服务的基本单位我们称之为厂商。
这里研究的厂商是完全竞争的厂商,它们的市场力很小,不能影响商品和服务的价格,每一个厂商是无数多个厂商中的一个。
4.1 生产集和以前一样,我们假设商品的个数为n 。
一个生产向量(投入-产出向量或生产计划)是一个向量n n R y y y ∈=),(1 ,其中正数表示产出,负数表示投入,并且生产向量的元素可以等于0,这意味着这个商品既没有被生产也没有用来作为投入。
例如如果)0,3,6,2,5(,5--==y n 意味着利用5个单位的商品1和6个单位的商品3生产出2个单位的商品2和3个单位的商品4,商品5既没有被生产也没有用来作为投入。
并不是每一个生产向量都是技术上可行的,所有的技术上可行的生产向量构成的集合称为生产集,记为Y 。
Y 就代表了厂商的技术水平。
从短期看,有些投入是固定的,集合}:{)(i z y Y y z Y i 对某个=∈=称为短期或约束生产集。
有时我们也用一个函数)(⋅F 来描述生产集,这个函数称为变换函数,它满足如下性质:}0)(:{≤∈=y F Y y Y 并且0)(=y F 当且仅当y 是Y 的边界元。
集合{}0)(:=∈y F R y n称为变换边界。
如果)(⋅F 是可微的,生产向量y 满足0)(=y F ,那么对于任意的商品k l 和,比率 k llk y y F y y F y MRT ∂∂∂∂=)()()(被称为商品l 对于商品k 在y 处的边际变换率,它测度的是如果减少一个单位的商品l 应该增加多少单位的商品k 。
因为,由0)(=y F ,我们有0)()(=∂∂+∂∂l lk k dy y y F dy y y F故有 k l l k y y F y y F dy dy ∂∂∂∂-=)()( 生产向量Y y ∈称为有效的,如果不存在y y Y y >'∈',。
如果厂商只生产一种商品,不妨设为第n 种商品,那么生产集中的元素可写为),(y x -,其中+-+∈∈R y R x n ,1。
集合}),(:{)(1Y y x R x y V n ∈-∈=-+称为投入要求集。
)(y V 表示的是所有能生产出y 单位产出的投入组合集。
集合})()(:{)(1y y y V x y V x R x y Q n >''∉∈∈=-+对所有但称为等产量集,它表示恰好能生产y 单位产出的投入组合集。
}),(:max{)(Y y x y x f ∈-=称为生产函数。
固定产出水平为y 且y x f =)(,我们能定义投入l 关于投入k 在x 处的边际技术替代率为 k llk x x f x x f x MRTS ∂∂∂∂=)()()(,它测度的是为保持产出水平不变减少一个单位的投入l 需增加多少单位的投入k 。
事实上,由y x f =)(,我们有 0)()(=∂∂+∂∂k kl l dx x x f dx x x f ,故有 k l l k x x f x x f dx dx ∂∂∂∂-=)()(。
例子4.1.1:柯比-道格拉斯技术假设a 是一个参数,且10<<a ,柯比-道格拉斯技术能用下列生产集表示}:),,{(121321a a x x y R y x x Y -≤∈--=相应地有}:),{()(121221a a x x y R x x y V -+≤∈=}:),{()(121221a a x x y R x x y Q -+=∈=},:),,{()(2121321z x x x y R y x x z Y a a =≤∈--=-aa x x y y x x F --=--12121),,(a a x x x x f -=12121),(例子4.1.2:里昂惕夫技术假设b a ,是参数,且0,0>>b a 。
里昂惕夫技术由下述生产集表示 )},m in(:),,{(21321bx ax y R y x x Y ≤∈--=相应地有)},m in(:),{()(21221bx ax y R x x y V ≤∈=+)},m in(:),{()(21221bx ax y R x x y Q =∈=+ ),mi n (),,(2121bx axy y x x F -=-- ),mi n (),(2121bx axx x f =4.2 生产集的性质在这一节里我们给出生产集的性质,这些性质通常被假设生产集具有。
它们中的每一个都是在特定的环境下成立,甚至下列性质有些是相互排斥的。
(1)Y 是非空的。
这个假设是说厂商一定有事情可干,否则我们没有必要研究它的行为。
(2)Y 是闭集。
也即如果,,y y Y y n n →∈那么Y y ∈。
这个假设纯粹是技术上的考虑。
(3)没有免费的午餐。
如果Y y ∈,0≥y ,那么一定有0=y 。
这也即是说没有任何投入是不可能生产出产出的。
(4)不生产是可能的。
这也即是说Y ∈0。
(5)自由处置。
它的意思是如果y y Y y ≤'∈,,那么一定有Y y ∈'。
或Y R Y n ⊂-+。
经济解释为额外数量的投入能够自由处置。
(6)不可逆性。
假设0,≠∈y Y y 。
不可逆性是说Y y ∈-。
换句话说,一旦一定量的投入组合产生了一定量的产出,要想使同样的产出转换成同样的投入是不可能的。
(7)非递增的规模报酬。
如果对于任意的,Y y ∈]1,0[∈α,有α,Y y ∈那么生产技术Y 具有非递增的规模报酬。
换句话说,任意可行的投入-产出向量的规模能够被成比例地减少。
注意到,非递增的规模报酬蕴涵不生产是可能的。
(8)非递减的规模报酬。
如果对于任意的,Y y ∈1≥α,有α,Y y ∈那么生产技术Y 具有非递减的规模报酬。
换句话说,任意可行的投入-产出向量的规模能够被成比例地增加。
(9)常数规模报酬。
如果对于任意的,Y y ∈0≥α,有α,Y y ∈那么生产技术Y 具有常数规模报酬。
(10)可加性。
假设,Y y ∈,Y y ∈'可加性要求Y y y ∈'+。
或简单地,Y Y Y ⊂+。
这蕴涵着对于任意的正整数k ,有Y ky ∈。
(11)凸性。
假设生产集Y 是凸的,也即如果,Y y ∈,Y y ∈']1,0[∈α,那么Y y y ∈'-+)1(αα。
这是微观经济学中的基本假设之一。
如果不生产是可能的,也即Y ∈0,那么凸性蕴涵Y 具有非递增的规模报酬。
(12)Y 是一个凸锥。
如果,Y y ∈,Y y ∈'常数0,0≥≥βα,有Y y y ∈'+βα,那么Y 是一个凸锥。
命题4.2.1 :生产集Y 是可加的并且满足非递增报酬条件当且仅当它是一个凸锥。
证明:凸锥的定义直接蕴涵可加性和非递增报酬。
反过来,如果可加性和非递增报酬成立,我们想要证明对于任意,Y y ∈,Y y ∈'常数0,0≥≥βα,有Y y y ∈'+βα。
为此,设k 是满足},max{βα>k 的整数,由可加性,Y ky ∈,Y y k ∈'。
由于ky k y )/(αα=,非递增报酬条件蕴涵Y y ∈α。
相似地,Y y ∈'β。
又由可加性,Y y y ∈'+βα。
4.3 利润最大化和成本最小化在这一节里,我们开始研究厂商的市场行为。
和研究消费需求一样,我们假设n 种商品的价格为,0),,(1>>=n p p p 并且它是独立于厂商的生产计划的。
我们假设厂商的目标是最大化它的利润。
并且,我们一直假设厂商的生产集Y 满足非空性,闭性和自由处置。
4.3.1 利润最大化问题给定一个价格向量0),,(1>>=n p p p 和一个生产计划n R y ∈,厂商选择生产计划n R y ∈所产生的利润为l nl l y p py ∑==1。
由于在一个生产计划中,投入被记为负数,产出被记为正数,从而l nl l y p py ∑==1刚好是总收益减去总的成本,也即利润。
给定厂商的技术约束,它由生产集Y 表示,厂商的利润最大化问题为:Yy t s y p Max y∈⋅.. 如果使用表示生产集Y 的变换函数)(⋅F ,那么厂商的利润最大化问题可以等价地写为: 0)(..≤⋅y F t s yp Max y给定生产集Y ,对应每一个价格向量0),,(1>>=n p p p ,厂商的利润函数}:{)(Y y y p Max p ∈⋅=π,也即是利润最大化问题的解的值。
厂商的供给对应)}(:{)(p y p Y y p y π=⋅∈=,也即是使得利润达到最大的生产计划的集合。
一般地,)(p y 是一个集合,而不是一个单个的向量。
也有可能不存在使得利润达到最大的生产计划。
例如,假设2=n ,厂商使用一个单位的物品1生产出一个单位的物品2,也即是它的生产技术是常数规模报酬的,如果12p p ≤,那么0)(=p π。
如果12p p >,那么厂商的利润为212)(y p p -,这里2y 是物品2 的产出水平,显然,选择适当的2y ,可以使得利润任意大。
因此,如果12p p >,+∞=)(p π。
如果变换函数)(⋅F 是可微的,那么利润最大化问题的解可以用一阶条件来刻划。
如果)(*p y y ∈,那么,对于某个0≥λ,*y 必须满足如下的一阶条件:n l y y F p ll ,,1,)(* =∂∂=λ 或,用矩阵记号,上面的一阶条件可表示为:)(*y F p ∇=λ (4.3.1) 由此一阶条件可得到下列等式: ),(/*y MRT p p lk k l =对于所有的k l ,如果不是这样,厂商的生产计划的一个微小的改变能够增加它的利润。
当生产集Y 对应的是具有可微生产函数)(z f 的单产出的技术时,我们能够把厂商的决策问题归结为对投入水平z 的选择。
在这种特殊的情形下,我们用标量0>p 记为厂商的产品的价格,向量0>>w 记为厂商的投入的价格。
此时厂商的利润最大化问题可表示为:z w z pf Max z ⋅-≥)(0如果*z 是最优的,那么它必须满足如下的一阶条件: l lw z z f p ≤∂∂)(*,如果0*>l z 取等号,1.,1-=n l 。
或,用矩阵记号,上面的一阶条件可表示为:0])([,)(***=⋅-∇≤∇z w z f p w z f p (4.3.2)因此,每一个被使用的投入品l (也即0*>l z )的边际产品等于它的相对于产品的价格,p w l /。
对于任意两种投入品l 和k ,只要0),(**>>k l z z ,上面的条件蕴涵着k l lk w w MRTS /=。