递归求解m个白球和n个黑球
- 格式:doc
- 大小:23.50 KB
- 文档页数:2
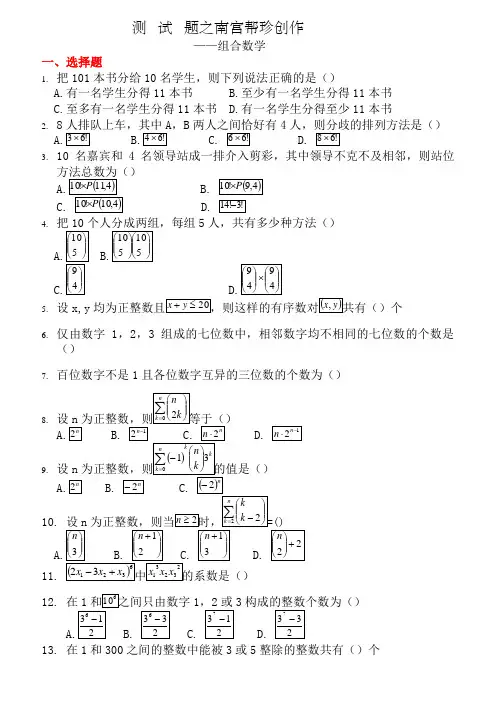
测试题之南宫帮珍创作——组合数学一、选择题1.把101本书分给10名学生,则下列说法正确的是()A.有一名学生分得11本书B.至少有一名学生分得11本书C.至多有一名学生分得11本书D.有一名学生分得至少11本书2.8,B43.10名嘉宾和4名领导站成一排介入剪彩,其中领导不克不及相邻,则站位4.5人,共有多少种方法()5.设x,y6.仅由数字1,2,3组成的七位数中,相邻数字均不相同的七位数的个数是()7.百位数字不是1且各位数字互异的三位数的个数为()8.9.设n12. 1313. 在1和300之间的整数中能被3或5整除的整数共有()个14.Fibonacci18.19.把15个相同的足球分给4个人,使得每人至少分得3个足球,分歧的分法共有()种20. 5-排列数为()21. 部分数为3且没有等于1的部分的15-分拆的个数为()22. 设n,kk 的n-值是()23. 设A ,B ,C 是实数且对任意正整数nB的值是()24.25.二、填空题1. 在1和2000之间能被6整除但不克不及被15整除的正整数共有_________个2. 用红、黄、蓝、黑4_______种3.2,则其通解为4.3个分歧的房间,每个房间至少1人的分法数为5.___________ 6. 由5个字母a,b,c,d,e 作成的6次齐次式最多可以有_________个分歧类8. 求由2个0,3个1和3个2作成的八位数的个数______________9.含3个变元x, y, z 的一个对称多项式包含9个项,其中4项包含x,2项n的3次多项式则11. n 元集划分成k 个元素个数均不小于2的子集的分歧方法12.部分数为3且没有等于k 的部分的n-分拆数________________13. 把24颗糖分成5堆,每堆至少有3颗糖,则有___________种分法三、计算题1.在1000至9999之间有多少个数字分歧的奇数?2、以3种分歧的长度,8种分歧的颜色和4种分歧的直径生产粉笔,试问总共有多少种分歧种类的粉笔?3、至多使用4位数字可以写成多少个2进制数!(2进制数只能用符号0或1)4、由字母表L={a,b,c,d,e}中字母组成的分歧字母且长度为4的字符串有多少个?如果允许字母重复出现,则由L 中字母组成的长度为3的字符串有多少个?5、从{1,2,3……9}中选取分歧的数字且使5和6不相邻的7位数有多少?6、已知平面上任3点不共线的25个点,它们能确定多少条直线?能确定多少个三角形?7、计算数字为1,2,3,4,5且满足以下两个性质的4位数的个数: (a)数字全不相同; (b)数为偶数8、正整数7715785有多少个分歧的正因子(1除外)?9、50!中有多少个0在结尾处?10、比5400大而且只有下列性质的数有多少? (a)数字全不相同; (b)不出现数字2和711. 将m=3761写成阶乘和的形式。

VB排列递归算法是一种用于处理组合问题的经典算法。
它可以帮助我们在给定一组数的情况下,找出其中任意个数的排列组合。
在使用中,我们可以输入随机n个数,然后利用VB排列递归算法输出m个数的组合。
今天,我们就来详细介绍一下VB排列递归算法的原理和操作步骤。
一、VB排列递归算法的原理1.1 递归算法递归算法是一种常见的解决问题的方法,它是指在函数的定义中使用函数本身的方法。
在VB排列递归算法中,递归的核心思想是将大问题分解为小问题,然后通过递归调用来解决小问题。
1.2 排列组合在数学中,排列和组合是常见的概念。
排列是指从给定的元素中按照一定顺序选取一定数量的元素,而组合是指从给定的元素中选取一定数量的元素,顺序无关紧要。
VB排列递归算法可以帮助我们高效地求解排列和组合的问题。
二、VB排列递归算法的操作步骤现在,我们来介绍一下使用VB排列递归算法求解组合问题的具体操作步骤。
2.1 输入随机n个数我们需要输入一组随机的n个数,这些数可以是整数、小数或者是字符串,根据实际需求而定。
2.2 设置输出m个数的组合接下来,我们需要设置输出m个数的组合,即从输入的n个数中选取m个数进行组合。
2.3 编写VB排列递归算法在VB编程环境中,我们需要编写排列递归算法的具体代码。
这部分代码主要涉及递归函数的定义和递归调用的实现,通过递归的方式来实现排列组合的求解。
2.4 执行VB排列递归算法一切准备就绪后,我们可以执行VB排列递归算法,得到输出m 个数的组合结果。
这些组合结果可以是打印输出、保存到文件或者在界面中展示,根据实际需求进行选择。
三、VB排列递归算法的应用实例现在,我们通过一个具体的示例来演示VB排列递归算法的应用过程。
3.1 示例说明假设我们有一组数字{1, 2, 3, 4, 5},我们需要从中选取3个数字进行组合,那么该怎么做呢?接下来,我们就通过VB排列递归算法来解决这个问题。
3.2 操作步骤我们需要输入数字{1, 2, 3, 4, 5},然后设置输出3个数字的组合。


1. 第二章2. 设随机变量X 的分布律为:2(), 1,2,33xP X x c x ⎛⎫=== ⎪⎝⎭求c 的值。
解:由分布律的性质:31()1x P X x ===∑,得312381327xx c c =⎛⎫== ⎪⎝⎭∑ 所以有 2738c =3. 一口袋中装有m 个白球,n − m 个黑球,连续无放回地从袋中取球,直到取出黑球为止,此时取出了X 个白球,求X 的分布律。
解:由题设知,随机变量X 的可能取值为:0,1,2,,m ,且事件()(0,1,2,,)X k k m ==表示一共取了k +1次球,前k 次取到的都是白球,第k +1次取到的是黑球。
所以有11(), 0,1,2,,.k m n mk nC C P X k k m C -+===4. 设一个试验只有两个结果:成功或失败,且每次试验成功的概率为 (01)p p <<,现进行重复试验,求下列X 的分布律。
(1) 将试验进行到出现一次成功为止,以X 表示所需的试验次数(几何分布)(2) 将试验进行到出现k 次成功为止,以X 表示获得k 次成功时的试验次数(巴斯卡分布) 解:(1)由题设知,随机变量X 的可能取值为:1,2,,且事件()(1,2,)X n n ==表示一共进行了n 次试验,且前n − 1次均是失败,而第n 次成功。
所以有1()(1), 1,2,.n P X n p p n -==-=(2) 由题设知,随机变量X 的可能取值为:,1,2,k k k ++,且事件()(,1,2,)X n n k k k ==++表示一共进行了n 次试验,且前n − 1次中成功了k − 1次,而第n 次也成功。
所以有11()(1), ,1,2,.k n kk n P X n C p p n k k k ---==-=++5. 求k 使得二项分布(;,)b k n p 达到最大值。
解:假设有0()max ()l nP X k P X l ≤≤===则有:()(1)()(1)P X k P X k P X k P X k =≥=-⎧⎨=≥=+⎩ 11(1)11(1)(1)(1)(1)(1)k k n k k k n k n n k kn k k k n k n n C p p C p p C p p C p p ------++-+⎧-≥-⇒⎨-≥-⎩ (1)(1)(1)(1)()n k p k p k p n k p-+≥-⎧⇒⎨+-≥-⎩ (1)(1)1k n pk n p ≤+⎧⇒⎨≥+-⎩ 所以当(1)n p +为整数时,(1)1k n p =+-或(1)k n p =+时,()P X k =的值最大; 当(1)n p +不是整数时,[(1)]k n p =+([]x 表示不超过x 的最大整数)时,()P X k =的值最大。

dic递归基础练习题:1.求1+2+3+……+n的值int sum(int a,int b){if(b==a) return a;return a+sum(a+1,b);}2. 求1*2*3*……*n的值cheng(int begin,int end){if(begin==end) return begin;return begin * cheng(begin+1,end);}3. 数的全排列问题。
将n个数字1,2,…n的所有排列按字典顺序枚举出猴2 3 12 1 33 1 23 2 14. 数的组合问题。
从1,2,…,n中取出m个数,将所有组合按照字典顺序列出。
如n=3,m=2时,输出:1 21 32 35. 小猴子第一天摘下若干桃子,当即吃掉一半,又多吃一个.第二天早上又将剩下的桃子吃一半,又多吃一个.以后每天早上吃前一天剩下的一半另一个.到第10天早上猴子想再吃时发现,只剩下一个桃子了.问第一天猴子共摘多少个桃子?fruit(int begin,int times){if(times==10) return begin;return fruit((begin+1)*2,times+1);}6. 有雌雄一对兔子,假定过两个月便可繁殖雌雄各一的一对小兔子。
问过n个月后共有多少对兔子?7. 一个人赶着鸭子去每个村庄卖,每经过一个村子卖去所赶鸭子的一半又一只。
这样他经过了七个村子后还剩两只鸭子,问他出发时共赶多少只鸭子?经过每个村子卖出多少只鸭子?duck(int begin,int times){if(times==7) return begin;return duck((begin+1)*2,times+1);}8.著名的菲波拉契(Fibonacci)数列,其第一项为0,第二项为1,从第三项开始,其每一项都是前两项的和。
编程求出该数列前N项数据。
int fbi(int i){if(i<2){if(i == 0) return 0;else return 1;}return fbi(i-1) +fbi(i-2);}9. 求两个数的最大公约数。

c语言黑白球算法题
黑白球算法题是一个经典的C语言编程问题,通常涉及使用条件语句和循环来解决。
这个问题的典型描述是,有一个盒子里面有n个黑球和m个白球,现在要将这些球依次拿出并排成一排,要求相邻的球不能颜色相同,问有多少种排列方法?
首先,我们可以使用递归的方法来解决这个问题。
我们可以定义一个递归函数,该函数的参数包括剩余的黑球数、白球数以及上一个放置的球的颜色。
在递归函数中,我们可以不断尝试放置黑球或白球,并在放置后调用递归函数来处理剩余的球。
通过不断尝试不同的放置方式,我们可以统计出所有满足条件的排列方式。
另外,我们也可以使用动态规划来解决这个问题。
我们可以定义一个二维数组dp,其中dp[i][0]表示放置了i个球且最后一个球是黑色的方案数,dp[i][1]表示放置了i个球且最后一个球是白色的方案数。
然后我们可以通过状态转移方程来更新dp数组,最终得到放置所有球且满足条件的排列方式数目。
除了递归和动态规划,我们还可以尝试使用数学方法来解决这个问题。
我们可以考虑排列组合的方法,通过计算不同颜色的球的
排列方式数目来得到最终的结果。
总之,黑白球算法题是一个涉及排列组合和条件限制的经典编
程问题,可以通过递归、动态规划或数学方法来解决。
在C语言中,我们可以利用条件语句和循环来实现相应的算法。
希望这个回答能
够帮助你更好地理解和解决这个问题。

多米诺骨牌上的数学——数学归纳法五十多年前,清华大学数学系赵访熊教授在给大学一年级学生讲高等数学课,总要先讲讲数学的基本概念和方法,他在讲解数学归纳法的时候,先讲了这样一个故事:某主妇养小鸡十只,公母各半。
她预备将母鸡养大留着生蛋,公鸡则养到一百天就陆续杀以佐餐。
天天早晨她拿米喂鸡。
到第一百天的早晨,其中的一只公鸡正在想:“第一天早晨有米吃,第二天早晨有米吃,……第九十九天早晨有米吃,所以今天,第一百天的早晨,一定有米吃。
”这时,该主妇来了,正好把这只公鸡抓去杀了。
这只公鸡在第一百天的早晨不但没有吃着米,反而被杀了,虽然它已有九十九天吃米的经验,但不能证明第一百天一定有米吃。
(赵访熊,1908年——1996年,我国最早提倡和从事应用数学与计算数学的教学与研究的学者之一。
)赵先生把这只公鸡的推理戏称为“公鸡归纳法”。
显然这是一种错误的不完全归纳法。
我们经常会遇到涉及全体自然数的命题,对待这种问题,如果要否定它,你只要能举出一个反例即可。
如果要证明它,由于自然数有无限多个,若是一个接一个地验证下去,那永远也做不完。
怎么办?数学家想出了一种非常重要的数学方法来解决这类问题,那就是数学归纳法。
【数学史话】欧几里得的开端实际上,人们很早就遇到了无限集合的问题,而当时具体的推导或计算都只是针对有限对象,实施有限次论证。
怎样在具体的推导或计算中把握无限的难题,很早就摆在数学家面前了。
(欧几里得,公元前330年—公元前275年,古希腊伟大的数学家,被称为数学之父)最先是古希腊数学家欧几里得在他的《几何原本》中采用了近似于数学归纳法的思想。
该书第九卷第20命题是:“素数比任何给定的一批素数都多。
”欧几里得在证明这一命题时采用了独特的“几何”方式,他把数视为线段:设有素数a、b、c,另设d=a·b·c+1,则d或是素数或不是素数。
如果d是素数,则d是与a、b、c三者都不同的素数。
如d不是素数,则它必有素因数e,并且e与a、b、c都不同,所以一定有比给定的素数更多的素数。

c语言,使用递归方法,求n的累加1.引言1.1 概述概述部分的内容可以描述本文的主要内容和目标。
可以按照以下方式编写:概述在计算机科学中,递归是一种常用的问题解决方法。
它通过将一个问题分解为一个或多个相同类型的子问题,并通过解决这些子问题来解决原始问题。
在本文中,我们将探讨如何使用递归方法求解一个常见的问题:求n的累加。
本文主要介绍了递归方法以及如何在C语言中使用递归方法来进行求解。
递归方法的核心思想是将一个大问题分解为更小的子问题,并且每一个子问题都可以通过调用相同的函数来解决。
在C语言中,递归方法可以通过函数的自我调用来实现。
通过本文的学习,读者将了解到递归方法的基本原理和应用场景。
此外,我们将详细介绍如何在C语言中编写递归函数求解n的累加问题,并通过具体的示例代码来演示其实现过程。
最后,本文将对递归方法的优缺点进行总结,并对求解n的累加问题的结果进行分析。
通过本文的学习,读者将能够更好地理解递归方法的思想,并能够灵活运用该方法解决实际问题。
接下来,我们将首先介绍递归方法的基本概念和原理,然后详细讨论如何在C语言中使用递归方法求解n的累加问题。
让我们开始吧!1.2 文章结构2. 正文2.1 递归方法的介绍2.2 C语言中的递归方法2.1 递归方法的介绍递归是一种算法或函数调用自身的方式。
它在解决问题时,将问题分解为相同类型的子问题,并通过不断调用自身来解决这些子问题,最终得到原始问题的解答。
递归方法一般包括两个要素:基本条件和递归条件。
基本条件是指递归结束的条件,当满足这个条件时,递归将停止。
递归条件则是指问题分解的规则或方式。
递归方法常应用于数学、计算机科学和编程等领域。
它能够有效地解决一些具有重复性质的问题,使问题的解决过程更加简洁和优雅。
2.2 C语言中的递归方法在C语言中,递归方法的使用需要遵循一定的规则。
首先,递归方法必须具备基本条件,否则将导致无限递归,最终导致栈溢出。
其次,在递归方法中,需要将原始问题通过子问题的方式进行分解,直到满足基本条件。

c语言递归算法经典实例递归算法是计算机科学中的重要概念,也是C语言编程中常用的技术手段之一。
它可以用于解决各种问题,包括数学、图形、排序、搜索等领域。
在本文中,我们将以中括号内的内容为主题,详细介绍C语言递归算法的经典实例,并逐步回答一些相关问题。
首先,让我们从递归算法的定义开始。
递归算法是一种通过将问题分解为更小的子问题来解决问题的方法。
在使用递归算法时,我们首先解决最小的问题,然后逐步解决更大的问题,直到最终解决整个问题。
这种分而治之的思想是递归算法的核心。
接下来,让我们以斐波那契数列为例,详细介绍递归算法的应用。
斐波那契数列是一个经典的数学问题,其中每个数字都是前两个数字之和。
例如,序列的前几个数是1、1、2、3、5、8、...。
我们可以使用递归算法来计算斐波那契数列中的任意项。
首先,我们定义一个函数fibonacci,用来计算斐波那契数列中的第n项。
函数的定义如下:cint fibonacci(int n) {if (n <= 1) {return n;} else {return fibonacci(n-1) + fibonacci(n-2);}}在这个函数中,我们首先检查n是否小于或等于1。
如果小于或等于1,则直接返回n作为结果。
否则,我们通过递归调用fibonacci函数来计算n-1和n-2两个子问题的解,然后将它们相加。
接下来,让我们回答第一个问题:如何使用递归算法计算斐波那契数列的第n项?我们可以通过调用fibonacci函数来计算斐波那契数列中的第n项。
例如,要计算第10项的值,我们可以使用以下代码:cint result = fibonacci(10);printf("第10项的值是:d\n", result);这将打印出“第10项的值是:55”,因为斐波那契数列的第10项是55。
接下来,让我们回答第二个问题:递归算法如何工作?当我们调用fibonacci函数时,它会检查传递给它的参数n的值。

一.问答题(共4题,每题5分,共计20分)1.什么叫随机试验?什么叫基本事件?什么叫样本空间?什么叫事件?2.试写出随机变量X的定义.3.试写出贝叶斯公式.4.试写出连续型随机变量的数学期望和方差的定义.二.填空题(共6题,每题5分,共计30分)1.设有N件产品,其中有M件次品,若从N件产品中任意抽取n件,则抽到的n件中检有m(m≤M)件次品的概率为2.设P(B)=0.8,P(A|B)=0.75,则由概率的乘法公式知,P(AB)= 0.6.3.(泊松分布定义)若随变量X的分布列为,k=0,1,2…,其中λ为正常数,则称X服从参数为λ的泊松分布,记作X~P( λ )。
4.(正态分布定义)若连续型随机变量X的密度函数为,(-∞<x<+∞),其中μ,σ为常数,且σ>0,则称X服从参数为μ,σ的正态分布(或高斯分布),记作。
5.设(X1,X2,…X n)为总体X的一个容量为n的样本,则称统计量(1)为样本均值;(2)为样本方差;(3)为修正样本方差.6.设P(B)=0.8,P(AB)=0.6,则由条件概率知,P(A|B)=().三.计算题(共6题,每题6分,共计36分)1.一批产品有10件,其中4件为次品,现从中任取3件,求取出的3件产品中有次品的概率。
解:样本点总数. 设A={取出的3件产品中有次品}..2、设A,B为随机事件,P(A)=0.2,P(B)=0.45,P(AB)=0.15,求:P(A|B);P(B|A);。
解:3、一袋中有m个白球,n个黑球,无放回地抽取两次,每次取一球,求:(1)在第一次取到白球的条件下,第二次取到白球的条件概率;(2)在第一次取到黑球的条件下,第二次取到白球的条件概率。
解:用A表示“第一次取到白球”,B表示“第二次取到白球”。
(1)袋中原有m+n个球,其中m个白球。
第一次取到白球后,袋中还有m+n-1球,其中m-1个为白球。
故;(2)袋中原有m+n个球,其中m个白球,第一次取到黑球后,袋中还有m+n-1个球,其中m个为白球。

m选n组合算法M选N组合算法是一种常用的数学算法,用于从给定的M个元素中选取N个元素的所有可能组合。
本文将介绍M选N组合算法的原理和实现,并通过示例进行说明。
一、算法原理M选N组合算法的原理是通过递归实现,具体步骤如下:1. 初始化一个空数组result,用于存储所有的组合结果;2. 从M个元素中选择一个元素,将其添加到组合中,并将N减1;3. 如果N为0,表示已经选取了N个元素,将组合添加到result 数组中;4. 否则,从选择的元素的下一个元素开始,递归调用M选N组合算法,将结果添加到result数组中;5. 返回result数组,即为所有的组合结果。
二、算法实现下面以Python语言为例,给出M选N组合算法的实现代码:```def combine(m, n):result = []combineHelper(m, n, 1, [], result)return resultdef combineHelper(m, n, start, temp, result):if n == 0:result.append(temp[:])returnfor i in range(start, m + 1):temp.append(i)combineHelper(m, n - 1, i + 1, temp, result)temp.pop()# 示例result = combine(5, 3)print(result)```三、示例说明假设有5个元素[1, 2, 3, 4, 5],需要从中选取3个元素的组合。
根据M选N组合算法,可以得到以下所有的组合结果:```[[1, 2, 3],[1, 2, 4],[1, 2, 5],[1, 3, 4],[1, 3, 5],[1, 4, 5],[2, 3, 4],[2, 3, 5],[2, 4, 5],[3, 4, 5]]```四、总结M选N组合算法是一种常用的数学算法,通过递归实现从给定的M 个元素中选取N个元素的所有可能组合。
N个不同球取出M个的组合个数求解Technorati 标签: 组合,概率从N个不同的球中取出M个,一共有多少种取法?这个问题是组合数据的基本问题,考虑拿出球是否放回,拿出去的球是否有序,它有4种变体:1.不放回,有序;2.不放回,无序;3.放回,无序;4.放回,有序;对于第一种,取出M个球,第一个有N种可能,第二个N-1种可能,依次类推,M个球共有:N*(N-1)*(N-2)*..*(N-M+1),举个例子:3个同学(A,B,C),从中取出2位同学,那么可能的组合是:共计6种,刚好是3*(3-2+1)=6种。
--------------接着看第二种,不放回,无序。
由于是无序的,那么上面(无放回有序)的排列显然存在重复,重复的次数正好等于M的全排列。
因此它的组合数等于:N*...*(N-M+1) / (M*(M-1)* (1)如果用推理计算的方式,我们可以得到一个递归式子:f(n,m)= f(n-1,m)+f(n-1,m-1),表示如果包含头元素f(n-1,m-1)种,不包含则为f(n-1,m)种。
--------------第三种,有放回,有序。
由于是有序的,M个球,第一个有N种可能,第二个球也有N种可能,。
依次类推,因此共有N*N*。
*N,共M个N相乘。
举个例子,3个球A,B,C,取出2个,那么可能的组合是:--------------第四种,有放回,无序,是这里面最麻烦的一种。
最直观的做法,是和“无放回”的对应的,类比它们的做法,在结果(3)上除以一个因子:M的全排列。
但是这里略有区别,因为在“无放回”的例子中,取出的球是不同的,因此不同的排列是M的阶乘;但是在本case中,取出的球是有重复的,再除以M!就不对了。
举个例子,3个球取2个,有放回,无序:显然是6种,并不是3*3/2种,后者竟然不是个整数。
那么正确的建模方式是什么呢?首先:把M次取出球当成是M个标签(相同的标签,因为是无序的),把这些标签贴到任意的球上,都贴在一个球上也没有关系。
高考数学中的置换组合问题解决方法高考数学中,置换组合问题是一个经典的题型。
这类题目考察的是置换和组合数学的相关概念与运算,需要学生理解和掌握置换群的概念、行列式的运算等高阶数学知识。
本文将分析一些典型的置换组合问题,并给出解决方法。
一、置换群的基本概念置换群是指同一个元素集合上的一些可能存在的变换所形成的群。
其中,每个变换都称为一个置换,所有置换构成的集合称为置换群,通常用S_n表示,其中n为元素集合的元素数量。
例如,如果元素集合为{1,2,3},那么S_3就是由这三个元素的所有置换所构成的群。
置换群的基本性质是它是封闭的、可逆的和结合的。
封闭性指的是对于S_n中的任意两个置换,它们的复合操作仍然属于S_n 中;可逆性指的是对于S_n中的任意置换,它都有一个逆置换存在,使得它们的复合操作等于单位置换;结合性指的是对于S_n中的任意三个置换,在任意复合顺序下它们的结果都是相同的。
二、置换组合问题的解决方法在高考数学中,置换组合问题一般形式为:有n个不同的数,对它们进行若干次置换后,求出有多少个置换不改变这n个数的相对位置。
下面以一个典型的置换组合问题为例进行说明。
例1:有6个独立的物体放在数据线上,现要对它们进行随机的交换和移动操作,问有多少种操作方式,才能把数据线变为原始状态?解:首先,我们需要求解6个元素的置换群S_6中,有多少个置换能够将6个物体变回原始状态。
设A为将6个物体变回原始状态的置换集合,那么|A|表示置换集合A中元素的数量。
由于A中的每一个置换操作都是可逆的,只需要找到其中一个操作,后面的操作就可以根据该操作的逆置换进行计算。
换句话说,假设存在一个合法操作将这6个物体变为原始状态,那么我们可以考虑该操作能够带来些什么变化,进而推导出其他合法操作的数量。
对于该操作,我们假设其将第1个物体移动到了第k个位置,然后根据k和其他物体的位置确定该置换。
不难发现,由于6个物体原来的位置已经确定,第1个物体此时只能被移到5个特定的位置上,也就是第2个物体到第6个物体所在的位置。
多米诺骨牌上的数学——数学归纳法五十多年前,清华大学数学系赵访熊教授在给大学一年级学生讲高等数学课,总要先讲讲数学的基本概念和方法,他在讲解数学归纳法的时候,先讲了这样一个故事:某主妇养小鸡十只,公母各半。
她预备将母鸡养大留着生蛋,公鸡则养到一百天就陆续杀以佐餐。
天天早晨她拿米喂鸡。
到第一百天的早晨,其中的一只公鸡正在想:“第一天早晨有米吃,第二天早晨有米吃,……第九十九天早晨有米吃,所以今天,第一百天的早晨,一定有米吃。
”这时,该主妇来了,正好把这只公鸡抓去杀了。
这只公鸡在第一百天的早晨不但没有吃着米,反而被杀了,虽然它已有九十九天吃米的经验,但不能证明第一百天一定有米吃。
(赵访熊,1908年——1996年,我国最早提倡和从事应用数学与计算数学的教学与研究的学者之一。
)赵先生把这只公鸡的推理戏称为“公鸡归纳法”。
显然这是一种错误的不完全归纳法。
我们经常会遇到涉及全体自然数的命题,对待这种问题,如果要否定它,你只要能举出一个反例即可。
如果要证明它,由于自然数有无限多个,若是一个接一个地验证下去,那永远也做不完。
怎么办?数学家想出了一种非常重要的数学方法来解决这类问题,那就是数学归纳法。
【数学史话】欧几里得的开端实际上,人们很早就遇到了无限集合的问题,而当时具体的推导或计算都只是针对有限对象,实施有限次论证。
怎样在具体的推导或计算中把握无限的难题,很早就摆在数学家面前了。
(欧几里得,公元前330年—公元前275年,古希腊伟大的数学家,被称为数学之父)最先是古希腊数学家欧几里得在他的《几何原本》中采用了近似于数学归纳法的思想。
该书第九卷第20命题是:“素数比任何给定的一批素数都多。
”欧几里得在证明这一命题时采用了独特的“几何”方式,他把数视为线段:设有素数a、b、c,另设d=a·b·c+1,则d或是素数或不是素数。
如果d是素数,则d是与a、b、c三者都不同的素数。
如d不是素数,则它必有素因数e,并且e与a、b、c都不同,所以一定有比给定的素数更多的素数。
用递归方法求n阶勒让德多项式的值什么是勒让德多项式?勒让德多项式(Legendre Polynomials)是数学中的一类多项式,由法国数学家阿道夫·勒让德(Adrien-Marie Legendre)在18世纪提出。
它在物理学、工程学和数学分析中有广泛的应用。
n阶勒让德多项式记作Pn(x),其中n为多项式的阶数。
数学定义中,勒让德多项式可以通过Rodrigues公式或正交性条件来定义。
在这篇文章中,我们将使用递归方法来计算n阶勒让德多项式的值。
递归方法求解勒让德多项式为了计算n阶勒让德多项式的值,我们可以利用其递推关系式。
首先,我们需要知道勒让德多项式的前两项P0(x)和P1(x),然后可以利用递推公式计算后续项。
在计算Pn(x)时,我们可以利用以下递推公式:Pn(x) = ((2n-1) * x * Pn-1(x) - (n-1) * Pn-2(x)) / n这个递推公式描述了n阶勒让德多项式与低阶多项式的关系。
通过使用递推公式,我们可以从低阶多项式逐步计算出高阶多项式的值。
代码实现下面是用C语言编写的递归方法求解n阶勒让德多项式的代码:#include <stdio.h>double legendre(int n, double x) {if (n == 0) {return 1.0;} else if (n == 1) {return x;} else {return ((2 * n - 1) * x * legendre(n - 1, x) - (n - 1) * legendre(n - 2, x)) / n;}}int main() {int n;double x;printf("Enter the order of Legendre polynomial (n): ");scanf("%d", &n);printf("Enter the value of x: ");scanf("%lf", &x);double result = legendre(n, x);printf("The value of P%d(%.2f) is %.6f\n", n, x, result);return 0;}在上面的代码中,我们首先定义了一个函数legendre来计算n阶勒让德多项式的值。