课时集训七年级数学上册 6.9 直线的相交试题1 (新版)浙教版

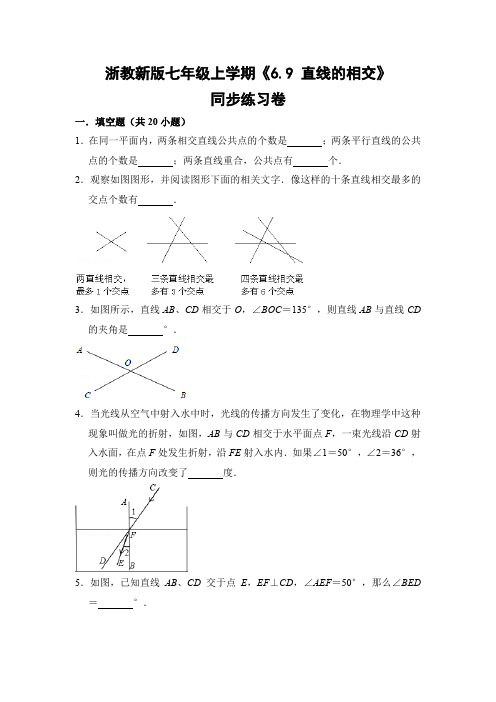
浙教新版七年级上学期《6.9 直线的相交》同步练习卷一．填空题（共20小题）1．在同一平面内，两条相交直线公共点的个数是；两条平行直线的公共点的个数是；两条直线重合，公共点有个．2．观察如图图形，并阅读图形下面的相关文字．像这样的十条直线相交最多的交点个数有．3．如图所示，直线AB、CD相交于O，∠BOC＝135°，则直线AB与直线CD 的夹角是°．4．当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，如图，AB与CD相交于水平面点F，一束光线沿CD射入水面，在点F处发生折射，沿FE射入水内．如果∠1＝50°，∠2＝36°，则光的传播方向改变了度．5．如图，已知直线AB、CD交于点E，EF⊥CD，∠AEF＝50°，那么∠BED＝°．6．如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1＝30°，则∠2＝．7．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是．8．如图，点P在直线l外，PB⊥l于B，A为l上任意一点，则P A与PB的大小关系是P A PB．9．在△ABC中∠B＝90°，BC＝5，AB＝12，AC＝13，则点B到斜边AC的距离是．10．如图，BC⊥AC，BC＝8，AC＝6，AB＝10，则点C到线段AB的距离是．11．平面内有10条直线两两相交，交点个数最多有m个，最少有n个，则m+n 的值为．12．平面内有n条直线，任意两条直线都相交，则最多有个交点．13．已知，直线AB和直线CD交于点O，∠BOD是它的邻补角的3倍，则直线AB与直线CD的夹角是度．14．如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE 表示正东方向，已知射线OB的方向是南偏东60°，射线OC在∠NOE内，且∠NOC与∠BOS互余，射线OA平分∠BON，图中与∠COA互余的角是．15．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON＝2∠COM，则∠BOD的度数为．16．如图，已知AO⊥BC于O，∠AOD＝30°，那么∠DOC＝°．17．如图，体育课上老师测量跳远成绩是这样操作的：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是．18．如图，点A，B，C，D，E在直线l上，点P在直线l外，PC⊥l于点C，在线段P A，PB，PC，PD，PE中，最短的一条线段是，理由是19．如图，CD⊥AB，点E、F在AB上，且CE＝10cm，CD＝8cm，CF＝12cm，则点C到AB的距离是．20．如图，点B到直线DC的距离是指线段的长度．二．解答题（共15小题）21．在同一平面内有四条直线（1）这四条直线的交点个数可能有哪些？（2）请你画出两种交点个数是4的图形．22．如图，直线AB，CD相交于点O，OF平分∠AOC，∠COE＝90°，∠DOF ＝160°．（1）求∠COF的度数；（2）求∠BOE的度数．23．如图，直线AB，CD相交于点O，OE⊥CD于点0，OD平分∠BOF，∠BOE ＝50°，求∠AOC，∠AOF，∠EOF的度数．24．如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．（1）在直线MN上取一点C，使线段AC最短．依据是．（2）在直线MN上取一点D，使线段AD+BD最短．依据是．25．如图，点A表示小雨家，点B表示小樱家，点C表示小丽家，她们三家恰好组成一个直角三角形，其中AC⊥BC，AC＝900米，BC＝1200米，AB＝1500米．（1）试说出小雨家到街道BC的距离以及小樱家到街道AC的距离．（2）画出表示小丽家到街道AB距离的线段．26．观察下列图形，阅读下面的相关文字并回答以下问题：两条直线相交三条直线相交四条直线相交只有一个交点最多的3个交点最多有6个交；猜想：①5条直线相交最多有几个交点？②6条直线相交最多有几个交点？③n条直线相交最多有n个交点？27．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？28．如图，直线AB，CD相交于点O，OA平分∠EOC．若∠EOC＝68°，求∠BOD的度数．29．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝80°，求∠BOD的度数；（2）若∠EOC＝∠EOD，求∠BOD的度数．30．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD＝38°，求∠AOC和∠COB的大小．31．如图，AOB为一直线，∠AOD：∠DOB＝3：1，OD平分∠COB．请判断AB与OC的位置关系．32．已知：点P是直线MN外一点，点A、B、C是直线MN上三点，分别连接P A、PB、PC．（1）通过测量的方法，比较P A、PB、PC的大小，直接用“＞”连接；（2）在直线MN上能否找到一点D，使PD的长度最短？如果有，请在图中作出线段PD，并说明它的理论依据；如果没有，请说明理由．33．如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．（1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是；（2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是．34．如图，点M，N分别在直线AB，CD上．（1）请在图中作出表示M，N两点间的距离的线段a，和表示点N到直线AB的距离的线段b；（2）请比较（1）中线段a，b的大小，并说明理由．35．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；（1）过点P画OA的垂线，垂足为H；（2）线段PH的长度是点P到的距离，是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是（用“＜”号连接）浙教新版七年级上学期《6.9 直线的相交》同步练习卷参考答案与试题解析一．填空题（共20小题）1．在同一平面内，两条相交直线公共点的个数是1个；两条平行直线的公共点的个数是0个；两条直线重合，公共点有无数个．【分析】先画出两条直线平行、相交及重合的图示，再由其交点情况进行解答．【解答】解：如图所示：由（1）可知同一平面内，两条相交直线公共点的个数是1个；由（2）可知两条平行直线的公共点的个数是0个；由（3）可知两条直线重合，公共点有无数个．故答案为：一个、0个、无数．【点评】本题考查的是两条直线的位置关系，即相交、平行、重合．2．观察如图图形，并阅读图形下面的相关文字．像这样的十条直线相交最多的交点个数有45．【分析】根据直线两两相交且不交于同一点，可得答案．【解答】解：十条直线相交最多的交点个数有＝45，故答案为：45．【点评】本题考查了相交线，n每条直线都与其它直线有一个交点，可有（n﹣1）个交点，n条直线用n（n﹣1）个交点，每个交点都重复了一次，n条直线最多有个交点．3．如图所示，直线AB、CD相交于O，∠BOC＝135°，则直线AB与直线CD 的夹角是45°．【分析】先根据邻补角的定义求出∠AOC，再根据直线的夹角为锐角解答．【解答】解：∵∠BOC＝135°，∴∠AOC＝180°﹣∠BOC＝180°﹣135°＝45°，∴直线AB与直线CD的夹角是45°．故答案为：45．【点评】本题考查了邻补角的定义，要注意直线的夹角是锐角．4．当光线从空气中射入水中时，光线的传播方向发生了变化，在物理学中这种现象叫做光的折射，如图，AB与CD相交于水平面点F，一束光线沿CD射入水面，在点F处发生折射，沿FE射入水内．如果∠1＝50°，∠2＝36°，则光的传播方向改变了14度．【分析】根据对顶角相等得出∠DFB＝∠1，进而解答即可．【解答】解：∵∠1＝50°，∴∠DFB＝∠1＝50°，∵∠2＝36°，∴∠DFE＝50°﹣36°＝14°，故答案为：14【点评】此题考查对顶角问题，关键是根据对顶角相等得出∠DFB＝∠1．5．如图，已知直线AB、CD交于点E，EF⊥CD，∠AEF＝50°，那么∠BED＝40°．【分析】根据垂直的定义可得∠CEF＝90°，然后求出∠AEC，再根据对顶角相等解答．【解答】解：∵EF⊥CD，∴∠CEF＝90°，∴∠AEC＝∠CEF﹣∠AEF＝90°﹣50°＝40°，∴∠BED＝∠AEC＝40°．故答案为：40．【点评】本题考查了垂线的定义，对顶角相等的性质，是基础题，准确识图是解题的关键．6．如图，直线AB，CD，EF相交于点O，且AB⊥CD，∠1＝30°，则∠2＝60°．【分析】根据对顶角相等求出∠EOD，继而得出∠2．【解答】解：∵∠EOD与∠1互为对顶角，∴∠EOD＝∠1＝30°，又∵AB⊥CD，∴∠AOD＝∠BOD＝90°，∴∠2＝90°﹣∠EOD＝60°．故答案为：60°．【点评】本题考查了垂线的定义，用到的知识点为：对顶角相等，垂线产生直角．7．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是垂线段最短．【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短．据此作答．【解答】解：其依据是：连接直线外一点与直线上各点的所有线段中，垂线段最短．故答案为：垂线段最短．【点评】本题考查了垂线的性质在实际生活中的运用，关键是掌握垂线段的性质：垂线段最短．8．如图，点P在直线l外，PB⊥l于B，A为l上任意一点，则P A与PB的大小关系是P A≥PB．【分析】由垂线段的定义可知，线段PB为垂线段，再根据垂线段的性质判断．【解答】解：∵PB⊥l于B，∴线段PB为点P到直线l的垂线段．根据从直线外一点到这条直线上各点所连的线段中，垂线段最短．可知P A≥PB．故答案为：≥．【点评】此题主要考查了从直线外一点到这条直线上各点所连的线段中，垂线段最短的性质．9．在△ABC中∠B＝90°，BC＝5，AB＝12，AC＝13，则点B到斜边AC的距离是．【分析】设AC边上的高为h，再根据三角形的面积公式即可得出结论．【解答】解：设AC边上的高为h，∵在Rt△ABC中，∠B＝90°，AB＝5，BC＝12，AC＝13，∴AB•BC＝AC•h，∴h＝＝＝．故答案为：．【点评】本题考查的是三角形的面积，熟知三角形的面积公式是解答此题的关键．10．如图，BC⊥AC，BC＝8，AC＝6，AB＝10，则点C到线段AB的距离是 4.8．【分析】设点C到线段AB的距离是x，然后根据△ABC的面积列方程求解即可．【解答】解：设点C到线段AB的距离是x，∵BC⊥AC，＝AB•x＝AC•BC，∴S△ABC即×10•x＝×6×8，解得x＝4.8，即点C到线段AB的距离是4.8．故答案为：4.8．【点评】本题考查了点到直线的距离，解题的关键在于利用三角形的面积列出方程．11．平面内有10条直线两两相交，交点个数最多有m个，最少有n个，则m+n 的值为46．【分析】由题意可得10条直线相交于一点时交点最少，任意两直线相交都产生一个交点时交点最多，由此可得出m，n的值，从而得出答案．【解答】解：根据题意可得：10条直线相交于一点时交点最少，此时交点为1个，即n＝1；任意两直线相交都产生一个交点时，交点最多，∴此时交点为：10×（10﹣1）÷2＝45，即m＝45；则m+n＝45+1＝46．故答案为：46．【点评】本题考查直线的交点问题，注意掌握直线相交于一点时交点最少，任意n条直线两两相交时交点最多为n（n﹣1）个．12．平面内有n条直线，任意两条直线都相交，则最多有个交点．【分析】分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数，找出规律即可解答．【解答】解：2条直线相交最多有1个交点；3条直线相交最多有1+2个交点；4条直线相交最多有1+2+3个交点；5条直线相交最多有1+2+3+4个交点；6条直线相交最多有1+2+3+4+5个交点；…n条直线相交最多有1+2+3+4+5+…+（n﹣1）＝个交点．故答案为：．【点评】本题考查的是多条直线相交的交点问题，解答此题的关键是根据2条、3条、4条、5条、6条直线相交时最多的交点个数发现规律．13．已知，直线AB和直线CD交于点O，∠BOD是它的邻补角的3倍，则直线AB与直线CD的夹角是45度．【分析】设∠BOD＝x°，则它的补角为3x°，根据邻补角互补可得x+3x＝180，再解方程即可．【解答】解：设∠BOD＝x°，则它的补角为3x°，x+3x＝180，x＝45，故答案为：45°．【点评】此题主要考查了邻补角，关键是掌握邻补角互补．14．如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向，已知射线OB的方向是南偏东60°，射线OC在∠NOE内，且∠NOC与∠BOS互余，射线OA平分∠BON，图中与∠COA互余的角是∠BOC、∠NOA、∠AOB、∠COE．【分析】根据方位角的定义及角平分线的定义、余角的概念分别求出∠BOS、∠NOC、∠NOA、∠AOB的度数可得答案．【解答】解：∵∠BOS＝60°、∠NOC与∠BOS互余，∴∠NOC＝30°，∠BON＝120°，又∵OA平分∠BON，∴∠NOA＝∠AOB＝60°，则∠AOC＝∠NOA﹣∠NOC＝30°，∵∠NOE＝90°、∠NOC＝30°，∴∠COE＝60°，综上，∠COA互余的角有∠BOS、∠NOA、∠AOB、∠COE，故答案为：∠BOS、∠NOA、∠AOB、∠COE．【点评】本题主要考查方位角、余角和补角，解题的关键是掌握方位角的定义及角平分线的定义、余角的概念．15．如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON＝2∠COM，则∠BOD的度数为60°．【分析】根据垂直得出∠NOM＝90°，根据角平分线定义得出∠AOM＝∠COM，再利用∠CON＝2∠COM，即可得出答案．【解答】解：∵ON⊥OM，∴∠NOM＝90°，∵∠CON＝2∠COM，∴设∠COM＝x，则∠CON＝2x，故x+2x＝90°，解得：x＝30°，∵射线OM平分∠AOC，∴∠AOM＝∠COM＝30°，∴∠AOC＝∠BOD＝2∠COM＝60°，故答案为：60°．【点评】本题考查了垂直定义，角平分线定义等知识点，能求出∠COM的度数是解此题的关键．16．如图，已知AO⊥BC于O，∠AOD＝30°，那么∠DOC＝60°．【分析】根据垂直的定义得到∠AOC＝90°，结合图形找到相关角间的和差关系进行解答即可．【解答】解：如图，∵AO⊥BC，∴∠AOC＝90°，又∠AOD＝30°，∴∠DOC＝90°﹣∠AOD＝60°．故答案是：60．【点评】本题考查了垂直的定义，如果两个角的和等于90°，两个角互为余角．17．如图，体育课上老师测量跳远成绩是这样操作的：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是垂线段最短．【分析】根据垂线段的性质，可得答案．【解答】解：用一块直角三角板的一边附在踏跳板上，另一边与拉直的皮尺重合，并且使皮尺经过被测试同学的落点，这样做的理由是垂线段最短，故答案为：垂线段最短．【点评】本题考查了垂线段，利用垂线段的性质是解题关键．18．如图，点A，B，C，D，E在直线l上，点P在直线l外，PC⊥l于点C，在线段P A，PB，PC，PD，PE中，最短的一条线段是PC，理由是垂线段最短【分析】点到直线的距离是指该点到直线的垂线段的长，根据定义即可选出答案．【解答】解：根据点到直线的距离的定义得出线段PC的长是点P到直线l的距离，从直线外一点到这条直线所作的垂线段最短．故答案是：PC；垂线段最短．【点评】本题考查了对点到直线的距离的应用，注意：点到直线的距离是指该点到直线的垂线段的长．19．如图，CD⊥AB，点E、F在AB上，且CE＝10cm，CD＝8cm，CF＝12cm，则点C到AB的距离是8cm．【分析】根据点到直线的距离是垂线段的长度，可得答案．【解答】解：∵CD⊥AB，点E、F在AB上，CD＝8cm，∴点C到AB的距离是CD＝8cm，故答案为：8cm．【点评】本题考查了点到直线的距离，利用点到直线的距离是垂线段的长度是解题关键．20．如图，点B到直线DC的距离是指线段BC的长度．【分析】直接利用直线外一点到直线的垂线段的长度，叫做点到直线的距离，进而得出答案．【解答】解：点B到直线DC的距离是指线段BC的长度．故答案为：BC．【点评】此题主要考查了点到直线的距离，正确把握相关定义是解题关键．二．解答题（共15小题）21．在同一平面内有四条直线（1）这四条直线的交点个数可能有哪些？（2）请你画出两种交点个数是4的图形．【分析】（1）根据两直线的位置即确定；（2）四条直线两两相交有6个交点，交点的个数是4，即6个中的三个重合．【解答】解：（1）这四条直线的交点个数可能是：0，1，4，5，6；（2）作图如下：【点评】本题考查了相交线的应用，主要考查学生的画图能力和理解能力．22．如图，直线AB，CD相交于点O，OF平分∠AOC，∠COE＝90°，∠DOF ＝160°．（1）求∠COF的度数；（2）求∠BOE的度数．【分析】（1）根据∠COF＝∠DOC﹣∠DOF求出即可；（2）先根据角平分线定义求出∠AOC，根据对顶角求出∠BOD，求出∠DOE，即可求出答案．【解答】解：（1）∵∠DOC＝180°，∠DOF＝160°，∴∠COF＝∠DOC﹣∠DOF＝20°；（2）∵∠COF＝20°，OF平分∠AOC，∴∠AOC＝2∠COF＝40°，∴∠DOB＝∠AOC＝40°，∵∠COE＝90°，∴∠DOE＝180°﹣90°＝90°，∴∠BOE＝∠BOD+∠DOE＝40°+90°＝130°．【点评】本题考查了对顶角、邻补角、角平分线定义等知识点，能求出各个角的度数是解此题的关键．23．如图，直线AB，CD相交于点O，OE⊥CD于点0，OD平分∠BOF，∠BOE ＝50°，求∠AOC，∠AOF，∠EOF的度数．【分析】根据题意即可推出∠EOD＝90°，∠BOD＝40°，既而得，∠AOC＝40°，∠BOF＝80°，得：∠EOF＝130°，∠AOF＝100°．【解答】解：∵OE⊥CD于点O，∴∠EOD＝90°（垂直的定义）∵∠BOE＝50°，∴∠BOD＝90°﹣50°＝40°，∴∠AOC＝∠BOD＝40°（对顶角相等）．∵OD平分∠BOF，∴∠BOF＝2∠BOD＝80°（角平分线的定义），∴∠AOF＝180°﹣80°＝100°，（平角的定义）∴∠EOF＝∠EOB+∠BOF＝130°．答：∠AOC＝40°，∠AOF＝100°，∠EOF＝130°．【点评】本题主要考查垂线的定义、角平分线的定义、对顶角的性质、邻补角的性质，关键在于熟练运用各性质定理，推出相关角的度数．24．如图，在直线MN的异侧有A、B两点，按要求画图取点，并注明画图取点的依据．（1）在直线MN上取一点C，使线段AC最短．依据是垂线段最短．（2）在直线MN上取一点D，使线段AD+BD最短．依据是两点之间线段最短．【分析】（1）过A作AC⊥MN，AC最短；（2）连接AB交MN于D，这时线段AD+BD最短．【解答】解：（1）过A作AC⊥MN，根据：垂线段最短．（2）连接AB交MN于D，根据是：两点之间线段最短．【点评】此题主要考查了垂线段的性质和线段的性质，关键是掌握垂线段最短；两点之间线段最短．25．如图，点A表示小雨家，点B表示小樱家，点C表示小丽家，她们三家恰好组成一个直角三角形，其中AC⊥BC，AC＝900米，BC＝1200米，AB＝1500米．（1）试说出小雨家到街道BC的距离以及小樱家到街道AC的距离．（2）画出表示小丽家到街道AB距离的线段．【分析】（1）利用点到直线的距离定义分别得出答案；（2）过点C作CD⊥AB进而得出答案．【解答】解：（1）∵AC＝900米，BC＝1200米，AB＝1500米，∴AC⊥BC，∴小雨家到街道BC的距离为：900m，小樱家到街道AC的距离为：1200m；（2）如图所示：CD即为小丽家到街道AB距离．【点评】此题主要考查了点到直线的距离定义，正确把握定义是解题关键．26．观察下列图形，阅读下面的相关文字并回答以下问题：两条直线相交三条直线相交四条直线相交只有一个交点最多的3个交点最多有6个交；猜想：①5条直线相交最多有几个交点？②6条直线相交最多有几个交点？③n条直线相交最多有n个交点？【分析】先观察图形，找出交点的个数与直线的条数之间的关系，然后进行计算即可．【解答】解：①5条直线相交最多有＝10个交点；②6条直线相交最多有＝15个交点；③n条直线相交最多有个交点．【点评】此题考查了相交线，关键是观察图形，找出规律，用到的知识点是同一平面内内n条直线相交最多有个交点．27．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量？【分析】延长∠AOB的一边，然后根据邻补角的和等于180°即可求解．【解答】解：如图，延长AO，先测量出∠BOC的度数，然后根据∠AOB与∠BOC是邻补角即可求解，∠AOB＝180°﹣∠BOC．【点评】本题考查了相交线的性质，主要利用了邻补角的和等于180°的性质．28．如图，直线AB，CD相交于点O，OA平分∠EOC．若∠EOC＝68°，求∠BOD的度数．【分析】根据角平分线定义得到∠AOC＝∠EOC＝×68°＝34°，然后根据对顶角相等得到∠BOD＝∠AOC＝34°．【解答】解：∵OA平分∠EOC，∴∠AOC＝∠EOC＝×68°＝34°，∴∠BOD＝∠AOC＝34°．【点评】本题考查了角的计算：1直角＝90°；1平角＝180°．也考查了角平分线的定义和对顶角的性质．解决本题的关键是熟记对顶角相等．29．如图，直线AB，CD相交于点O，OA平分∠EOC．（1）若∠EOC＝80°，求∠BOD的度数；（2）若∠EOC＝∠EOD，求∠BOD的度数．【分析】（1）根据角平分线定义得到∠AOC＝∠EOC＝×80°＝40°，然后根据对顶角相等得到∠BOD＝∠AOC＝40°；（2）先设∠EOC＝x，∠EOD＝x，根据平角的定义得x+x＝180°，解得x＝90°，则∠EOC＝x＝90°，然后与（1）的计算方法一样．【解答】解：（1）∵OA平分∠EOC，∴∠AOC＝∠EOC＝×80°＝40°，∴∠BOD＝∠AOC＝40°；（2）设∠EOC＝x，∠EOD＝x，根据题意得x+x＝180°，解得x＝90°，∴∠EOC＝x＝90°，∴∠AOC＝∠EOC＝×90°＝45°，∴∠BOD＝∠AOC＝45°．【点评】考查了角的计算：1直角＝90°；1平角＝180°．也考查了角平分线的定义和对顶角的性质．30．如图，直线AB、CD相交于点O，OE⊥AB，O为垂足，如果∠EOD＝38°，求∠AOC和∠COB的大小．【分析】由OE⊥AB，可得出∠EOB＝90°，结合∠EOD＝38°可求出∠DOB 的度数，根据对顶角相等即可求出∠AOC的度数，再由∠COB与∠AOC互补可求出∠COB的大小．【解答】解：∵OE⊥AB，∴∠EOB＝90°，又∠EOD＝38°，∴∠DOB＝90°﹣38°＝52°，∵∠AOC＝∠DOB，∴∠AOC＝52°．∵∠COB与∠AOC互补，∴∠COB＝180°﹣52°＝128°．【点评】本题考查了垂线、对顶角以及邻补角，牢记“对顶角相等、邻补角互补”是解题的关键．31．如图，AOB为一直线，∠AOD：∠DOB＝3：1，OD平分∠COB．请判断AB与OC的位置关系．【分析】由已知条件和观察图形可知∠AOD与∠DOB互补，利用∠AOD：∠DOB ＝3：1及角平分线的定义这些关系，得出∠AOC＝90°，可证垂直．【解答】解：AB⊥OC．∵∠AOD：∠DOB＝3：1∴∠AOD＝3∠DOB∵∠AOB＝180°∴∠AOD+∠DOB＝180°即3∠DOB+∠DOB＝180°∴∠DOB＝45°又∵OD平分∠COB，有∠COD＝∠DOB＝45°，∴∠BOC＝∠DOB+∠COD＝45°+45°＝90°．由∠BOC＝90°，可知AB⊥OC．【点评】利用垂直的定义除了由垂直得直角外，还能由直角判定垂直，判断两直线的夹角是否为90°是判断两直线是否垂直的基本方法．32．已知：点P是直线MN外一点，点A、B、C是直线MN上三点，分别连接P A、PB、PC．（1）通过测量的方法，比较P A、PB、PC的大小，直接用“＞”连接；（2）在直线MN上能否找到一点D，使PD的长度最短？如果有，请在图中作出线段PD，并说明它的理论依据；如果没有，请说明理由．【分析】（1）根据测量可直接得出结论；（2）过点P作PD⊥MN，根据点到直线距离的定义可得出结论．【解答】解：（1）通过测量可知，P A＞PB＞PC；（2）过点P作PD⊥MN，则PD最短（垂线段最短）．【点评】本题考查的是垂线段最短，熟知从直线外一点到这条直线所作的垂线段最短是解答此题的关键．33．如图，点P，点Q分别代表两个村庄，直线l代表两个村庄中间的一条公路．根据居民出行的需要，计划在公路l上的某处设置一个公交站．（1）若考虑到村庄P居住的老年人较多，计划建一个离村庄P最近的车站，请在公路l上画出车站的位置（用点M表示），依据是直线外一点与直线上各点连接的所有线段中垂线段最短；（2）若考虑到修路的费用问题，希望车站的位置到村庄P和村庄Q的距离之和最小，请在公路l上画出车站的位置（用点N表示），依据是两点之间线段最短．【分析】（1）直接利用点到直线的距离的定义得出答案；（2）利用线段的性质得出答案．【解答】解：（1）如图，点M即为所示．依据是直线外一点与直线上各点连接的所有线段中垂线段最短（2）如图，点N即为所示．依据是两点之间线段最短；故答案为：直线外一点与直线上各点连接的所有线段中垂线段最短；两点之间线段最短．【点评】此题主要考查了应用设计与作图，正确理解线段的性质是解题关键．34．如图，点M，N分别在直线AB，CD上．（1）请在图中作出表示M，N两点间的距离的线段a，和表示点N到直线AB 的距离的线段b；（2）请比较（1）中线段a，b的大小，并说明理由．【分析】（1）根据线段的意义，点到直线的距离，可得答案；（2）根据垂线段的性质，可得答案．【解答】解：（1）连接MN，过N作NE⊥AB，如图，（2）由垂线段最短，得MN＞NE，即a＞b，理由是垂线段最短．【点评】本题考查了点到直线的距离，利用垂线段的性质是解题关键35．如图，点P是∠AOB的边OB上的一点，过点P画OB的垂线，交OA于点C；（1）过点P画OA的垂线，垂足为H；（2）线段PH的长度是点P到OA的距离，线段CP的长度是点C到直线OB的距离．线段PC、PH、OC这三条线段大小关系是PH＜PC＜OC（用“＜”号连接）【分析】（1）过点P画OA的垂线，即过点P画∠PHO＝90°即可，（2）利用点到直线的距离可以判断线段PH的长度是点P到OA的距离，PC是点C到直线OB的距离，线段PC、PH、OC这三条线段大小关系是PH＜PC ＜OC．【解答】解：（1）如图：（2）线段PH的长度是点P到直线OA的距离，线段CP的长度是点C到直线OB的距离，根据垂线段最短可得：PH＜PC＜OC，故答案为：OA，线段CP，PH＜PC＜OC．【点评】本题主要考查了基本作图﹣﹣﹣﹣作已知直线的垂线，另外还需利用点到直线的距离才可解决问题．。

《直线的相交一》习题一、选择题1.下列语句中，是对顶角的语句为( )A .两条直线相交所成的角B .有公共顶点且方向 相反的两个角C .两条直线相交所成的角，且有一个公共顶点，而没有公共边D .有公共顶点并且相等的两个角2.图中，∠∠12、是对顶角的为( )1 2A B C D121122 3.三条直线相交于一点，所成的对顶角的对数是( )A .3B .4C .5D .64.点到直线的距离是指这点到这条直线的( )A .垂线段B .垂线的长C .长度D .垂线段的长度5.如图，三条直线l l l 123，，相交于点O ，则∠+∠+∠=123( )A .90︒B .120︒C .180︒D .360︒1 O 32 l 1l 2l 3二、填空题6.两个互为邻补角的角平分线___________；两个对顶角的角平分线形成___________.7.直线AB 与CD 互相垂直，垂足为O ，P 是直线CD 上一点，则P 到AB 的距离是__________.8.如图1，直线AB 、CD 、EF 都经过O 点，并且已知∠=︒∠=︒AOC COE 3546，，则∠=EOB __________，∠=BOC _________，∠=DOF ________，∠=FOA ______.A FC O DE B图19.如图，直线AB 、CD 、EF 相交于O ，且AB CD ⊥，∠=︒127，则∠=2_______，∠=FOB __________.CEA 2 OB 1FD10.已知：如图，AO BO ⊥∠=∠，12.求证：CO DO ⊥.BCD2 31O A。

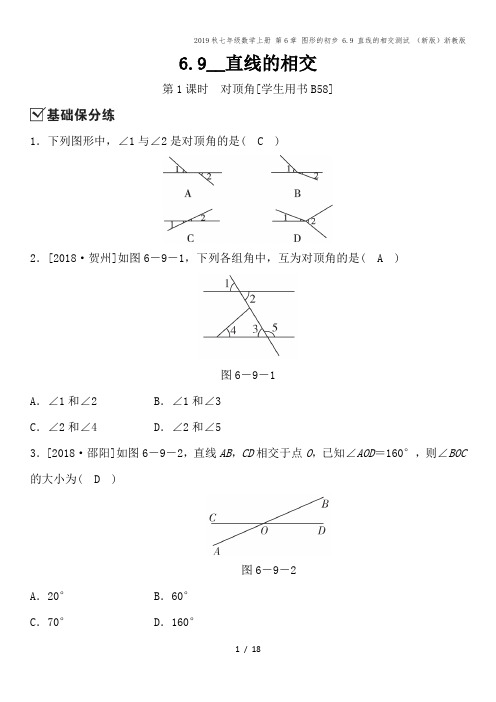
6.9__直线的相交第1课时对顶角[学生用书B58]1．下列图形中，∠1与∠2是对顶角的是( C )2．[2018·贺州]如图6－9－1，下列各组角中，互为对顶角的是( A )图6－9－1A．∠1和∠2 B．∠1和∠3C．∠2和∠4 D．∠2和∠53．[2018·邵阳]如图6－9－2，直线AB，CD相交于点O，已知∠AOD＝160°，则∠BOC 的大小为( D )图6－9－2A．20° B．60°C．70° D．160°【解析】∵∠AOD＝160°，∴∠BOC＝∠AOD＝160°.4．如图6－9－3，直线AB，CD相交于点O，OE，OF是过点O的两条射线，其中构成对顶角的是( C )图6－9－3A．∠AOF与∠DOEB．∠EOF与∠BOEC．∠BOC与∠AODD．∠COF与∠BOD5．如图6－9－4，直线AB，CD，EF相交于O，则∠1＋∠2＋∠3的度数等于( C )图6－9－4A．90° B．150°C．180° D．210°6．如图6－9－5所示，直线AB，CD，EF，MN，GH相交于点O，则图中对顶角共有( D )图6－9－5A．3对B．6对C．12对D．20对【解析】 2条直线交于一点，对顶角有2对，2＝2×1；3条直线交于一点，对顶角有6对，6＝3×2；4条直线交于一点，对顶角有12对，12＝4×3；由规律可得，n条不同的直线相交于一点，可以得到n(n－1)对对顶角，∴直线AB，CD，EF，MN，GH相交于点O，对顶角共有5×4＝20对，故选D.7．图6－9－6中是对顶角量角器，用它测量角的原理是__对顶角相等__．图6－9－68．如图6－9－7，直线AB，CD相交于点O，若∠AOD＝28°，则∠BOC＝__28°__，∠AOC ＝__152°__.图6－9－79．如图6－9－8，直线AB，CD相交于点O，则：图6－9－8(1)若∠1＋∠3＝68°，则∠1＝__34°__；(2)若∠2∶∠3＝4∶1，则∠2＝__144°__；(3)若∠2－∠1＝100°，则∠3＝__40°__．【解析】(1)∵∠1＝∠3，∠1＋∠3＝68°，∴2∠1＝68°，∴∠1＝34°；(2)设∠3＝x，则∠2＝4x，于是x＋4x＝180°，则x＝36°，∴∠2＝4×36°＝144°；(3)设∠1＝x，则∠2＝100°＋x.∵∠1＋∠2＝180°，∴x＋100°＋x＝180°，∴x＝40°，∴∠3＝∠1＝x＝40°.10．如图6－9－9，已知直线AB，CD，MN相交于点O，若∠1＝22°，∠2＝46°，则∠3＝__112°__．图6－9－9【解析】∵∠AOM＝∠1＝22°，∴∠3＝180°－∠AOM－∠2＝180°－22°－46°＝112°.11．[2018春·娄星区期末]如图6－9－10，直线AB，CD相交于点O，OA平分∠EOC.图6－9－10(1)若∠EOC＝80°，求∠BOD的度数；(2)若∠EOC＝∠EOD，求∠BOD的度数．解：(1)∵OA平分∠EOC，∴∠AOC＝12∠EOC＝12×80°＝40°，∴∠BOD＝∠AOC＝40°；(2)设∠EOC＝x，∠EOD＝x，根据题意，得x＋x＝180°，解得x＝90°，∴∠EOC＝x＝90°，∴∠AOC＝12∠EOC＝12×90°＝45°，∴∠BOD＝∠AOC＝45°.12．如图6－9－11，直线a，b，c相交于点O，若∠1＝2∠2，∠3－∠1＝30°，则∠4等于( A )图6－9－11A．30° B．60°C．20° D．15°【解析】∵∠1＋∠2＋∠3＝180°，又∠1＝2∠2，∠3－∠1＝30°，∴∠3＝30°＋∠1＝30°＋2∠2，∴2∠2＋∠2＋30°＋2∠2＝180°，即5∠2＝150°，∴∠2＝30°，∴∠4＝∠2＝30°.故选A.13．如图6－9－12，直线EF分别交∠AOB的两边于C，D两点，图中有哪几对对顶角？图6－9－12解：图中的对顶角有∠OCE与∠ACD，∠ACE与∠OCD，∠CDO与∠BDF，∠CDB与∠ODF，共4对对顶角．14．[2017秋·越城区期末]如图6－9－13，直线AB，CD相交于点O，∠BOM＝90°，∠DON＝90°.(1)若∠COM＝∠AOC，求∠AOD的度数；(2)若∠COM＝14∠BOC，求∠AOC和∠MOD.图6－9－13解：(1)∵∠COM＝∠AOC，∴∠COM＝12∠AOM，∵∠BOM＝90°，∴∠AOM＝90°，∴∠AOC＝45°，∴∠BOD＝45°，∴∠AOD＝180°－∠BOD＝135°；(2)设∠COM＝x，则∠BOC＝4x，∴∠BOM＝3x，∵∠BOM＝90°，∴3x＝90°，即x＝30°，∴∠AOC ＝60°，∠MOD ＝90°＋∠BOD ＝90°＋∠AOC ＝150°.15．[2017秋·拱墅区期末]如图6－9－14，直线AE 与CD 相交于点B ，射线BF 平分∠ABC ，射线BG 在∠ABD 内，图6－9－14(1)若∠DBE 的补角是它的余角的3倍，求∠FBC 的度数； (2)在(1)的件下，若∠DBG ＝∠ABG －33°，求∠ABG 的度数； (3)若∠FBG ＝100°，求∠ABG 和∠DBG 的度数的差．解：(1)设∠DBE ＝α，则∠DBE 的补角是180°－α，它的余角是90°－α，依题意，得180°－α＝3(90°－α)，解得α＝45°， ∴∠ABC ＝45°，∴∠FBC ＝12∠ABC ＝22.5°；(2)设∠ABG ＝x ，∠DBG ＝x －33°，依题意得x ＋x －33°＝135°， 解得x ＝84°，∠DBG ＝x －33°＝51°， ∴∠ABG ＝∠ABD －∠DBG ＝84°； (3)∵射线BF 平分∠ABC ，∴可设∠ABF ＝∠CBF ＝β，又∵∠FBG ＝100°，∴∠ABG ＝100°－β，∠DBG ＝180°－100°－β＝80°－β， ∴∠ABG －∠DBG ＝(100°－β)－(80°－β)＝20°，即∠ABG和∠DBG的度数的差为20°.16．[2017秋·松滋期末]如图6－9－15，已知直线AB与直线CD相交于点O，∠BOE ＝90°，OF平分∠BOD，∠BOC∶∠AOC＝1∶3.(1)求∠DOE，∠COF的度数；(2)若射线OF，OE同时绕O点分别以2°/s，4°/s的速度，顺时针匀速旋转，当射线OE，OF的夹角为90°时，两射线同时停止旋转．设旋转时间为t，试求t的值．图6－9－15解：(1)∵∠BOC∶∠AOC＝1∶3，∴∠BOC＝180°×11＋3＝45°，∴∠AOD＝45°，∵∠BOE＝90°，∴∠AOE＝90°，∴∠DOE＝45°＋90°＝135°，∠BOD＝180°－45°＝135°，∵OF平分∠BOD，∴∠DOF＝∠BOF＝67.5°，∴∠COF＝180°－67.5°＝112.5°；(2)∠EOF＝90°＋67.5°＝157.5°，依题意有4t－2t＝157.5－90，解得t＝33.75.第2课时垂线[学生用书A60]1．两条直线相交所成的四个角中，下列说法正确的是( D )A．一定有一个锐角B．一定有一个钝角C．一定有一个直角D．一定有一个不是钝角【解析】因为两条直线相交，分为垂直相交和斜交，故分两种情况讨论：①当两直线垂直相交时，四个角都是直角，故A，B错误；②当两直线斜交时，有两个角是锐角，两个角是钝角，故C错误．综上所述，D正确．故选D.2．在数学课上，同学们在练习过点B作线段AC所在直线的垂线段时，有一部分同学画出了如图6－9－16 所示的四种图形，请你数一数，错误的个数为( C )图6－9－16A．1 B．2 C．3 D．43．[2018春·安国期末]如图6－9－17，因为直线AB⊥l于点B，BC⊥l于点B，所以直线AB和BC重合，则其中蕴含的数学原理是( A )图6－9－17A．平面内，过一点有且只有一条直线与已知直线垂直B．垂线段最短C．过一点只能作一条直线D．两点确定一条直线4．[2017·北京]如图6－9－18所示，点P到直线l的距离是( B )图6－9－18A．线段PA的长度B．线段PB的长度C．线段PC的长度D．线段PD的长度5．若A，B，C是直线l上的三点，P是直线l外一点，且PA＝6 cm，PB＝5 cm，PC ＝4 cm，则点P到直线l的距离( C )A．等于4 cmB．大于4 cm而小于5 cmC．不大于4 cmD．小于4 cm6．如图6－9－19，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有( D )图6－9－19A．2条B．3条C．4条D．5条【解析】如图所示：线段AB是点B到AC的距离，线段CA是点C到AB的距离，线段AD是点A到BC的距离，线段BD是点B到AD的距离，线段CD是点C到AD的距离，故图中能表示点到直线距离的线段共有5条．7．[2017春·桂林期末]如图6－9－20，在立定跳远中，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在起跳线上，另一边与拉直的皮尺重合，这样做的理由是( C )图6－9－20A．两点之间线段最短B．过两点有且只有一条直线C．垂线段最短D．过一点可以作无数条直线8．[2018·益阳]如图6－9－21，直线AB，CD相交于点O，EO⊥CD.下列说法错误的是( C )图6－9－21A．∠AOD＝∠BOCB．∠AOE＋∠BOD＝90°C．∠AOC＝∠AOED．∠AOD＋∠BOD＝180°【解析】 A．∠AOD与∠BOC是对顶角，所以∠AOD＝∠BOC，此选项正确；B．由EO⊥CD知∠DOE＝90°，所以∠AOE＋∠BOD＝90°，此选项正确；C．∠AOC与∠BOD是对顶角，所以∠AOC＝∠BOD，此选项错误；D．∠AOD与∠BOD是邻补角，所以∠AOD＋∠BOD＝180°，此选项正确．9．如图6－9－22，已知直线AB，CD都过点O，OE是射线，若∠1＝30°，∠2＝60°，则OE与AB的位置关系是__垂直__．图6－9－22【解析】∵∠1＋∠2＝30°＋60°＝90°，∴∠AOE＝180°－(∠1＋∠2)＝180°－90°＝90°，∴OE⊥AB.10．如图6－9－23，过△ABC的三个顶点A，B，C分别作BC，AC，AB的垂线，并用垂直符号表示出来．图6－9－23解：略．11．在直线AB上任取一点O，过点O作射线OC，OD，使OC⊥OD，当∠AOC＝30°时，则∠BOD的度数是( D )A．60° B．120°C．60°或90° D．60°或120°【解析】此题可分两种情况，即OC，OD在直线AB的一边时和在直线AB的两边时，分别求解即可．第11题答图①当OC，OD在AB的一边时，如答图①.∵OC⊥OD，∴∠COD＝90°.又∵∠AOC＝30°，∴∠BOD＝180°－∠COD－∠AOC＝60°；②当OC，OD在直线AB的两边时，如答图②.∵OC⊥OD，∠AOC＝30°，∴∠AOD＝60°，∴∠BOD＝180°－∠AOD＝120°.综上所述，∠BOD为60°或120°.故选D.12．如图6－9－24，直线AB与CD相交于点O，OE⊥AB，OF⊥CD.图6－9－24(1)图中∠AOF的余角是__∠EOF，∠DOB，∠AOC__(把符合条件的角都填写出来)；(2)图中除直角相等外，还有相等的角，请写出两对：①__∠AOC＝∠DOB＝∠EOF__，②__∠AOF＝∠EOD或∠AOD＝∠BOC(写出两对即可)__；(3)如果∠AOD＝140°，那么根据__对顶角相等__，可得∠BOC＝__140°__，如果∠AOF ＝70°，可得∠DOB＝__20°__．13．[2018春·香坊区期末]如图6－9－25，AB，CD交于点O，OE⊥AB，且OC平分∠AOE.(1)如图①，求∠BOD的度数；(2)如图②，过O点作射线OF，且∠DOF＝4∠AOF，求∠FOC的度数．图6－9－25解：(1)∵OE⊥AB，∴∠AOE＝90°，又∵OC平分∠AOE，∴∠AOC＝12∠AOE＝12×90°＝45°，∴∠BOD＝∠AOC＝45°；(2)∵∠COD＝180°，∴∠AOD＝∠COD－∠AOC＝180°－45°＝135°，∵∠DOF＝4∠AOF，∴∠AOD＝∠DOF＋∠AOF＝4∠AOF＋∠AOF＝5∠AOF＝135°，∴∠AOF＝27°，∴∠FOC＝∠AOF＋∠AOC＝72°.14．如图6－9－26，平原上有A，B，C，D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池．(1)不考虑其他因素，请你画图确定蓄水池H点的位置，使它到四个村庄距离之和最小；(2)计划把河水引入蓄水池H中，怎样开渠最短？请说明根据．图6－9－26第14题答图解：(1)如答图，∵两点之间线段最短，∴连结AD，BC交于H，则H为蓄水池位置，它到四个村庄距离之和最小；(2)如答图，过H作HG⊥EF，垂足为G.“过直线外一点与直线上各点的连线中，垂线段最短”是把河水引入蓄水池H中开渠最短的根据．15．[2017秋·渝中区校级期末]如图6－9－27①，已知A ，O ，B 三点在同一直线上，射线OD ，OE 分别平分∠AOC ，∠BOC . (1)求∠DOE 的度数；(2)如图②，在∠AOD 内引一条射线OF ⊥OC ，其他不变，设∠DOF ＝α(0°＜α＜90°)． ①求∠AOF 的度数(用含α的代数式表示)； ②若∠BOD 是∠AOF 的2倍，求∠DOF 的度数．图6－9－27解：(1)∵点A ，O ，B 在同一条直线上， ∴∠AOC ＋∠BOC ＝180°，∵射线OD 和射线OE 分别平分∠AOC 和∠BOC ， ∴∠COD ＝12∠AOC ，∠COE ＝12∠BOC ，∴∠COD ＋∠COE ＝12(∠AOC ＋∠BOC )＝90°，∴∠DOE ＝90°；(2)①∵OC ⊥OF ，∴∠COF ＝90°， ∵∠DOF ＝α，∴∠COD ＝90°－α， ∵∠AOD ＝∠COD ，∴∠AOF ＝∠AOD －∠DOF ＝90°－α－α＝90°－2α； ②∵∠BOD 是∠AOF 的2倍，∴180°－(90°－α)＝2(90°－2α)，解得α＝18°，即∠DOF ＝18°.16．[2017春·港南区期末]如图6－9－28，直线EF ，CD 相交于点O ，OA ⊥OB ，且OC 平分∠AOF ，(1)若∠AOE ＝40°，求∠BOD 的度数；(2)若∠AOE ＝α，求∠BOD 的度数；(用含α的代数式表示) (3)从(1)(2)的结果中能看出∠AOE 和∠BOD 有何关系？图6－9－28解：(1)∵∠AOE ＋∠AOF ＝180°(互为补角)，∠AOE ＝40°， ∴∠AOF ＝140°，又∵OC 平分∠AOF ， ∴∠AOC ＝12∠AOF ＝70°，∴∠BOD ＝180°－∠BOA －∠AOC ＝180°－90°－70°＝20°； (2)∵∠AOE ＋∠AOF ＝180°(互为补角)，∠AOE ＝α， ∴∠AOF ＝180°－α，又∵OC 平分∠AOF ， ∴∠AOC ＝12∠AOF ＝90°－12α，∴∠BOD ＝180°－∠AOC －∠AOB ＝180°－⎝⎛⎭⎪⎫90°－12α－90°＝12α；(3)从(1)(2)的结果中能看出∠AOE ＝2∠BOD .。

6.9直线的相交同步测试【浙教版】参考答案与试题解析一．选择题1．（2020秋•香坊区校级期中）在下列图中，∠1与∠2属于对顶角的是（）A．B．C．D．【思路点拨】根据对顶角的定义：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角，可得结论．【答案】解：在选项A、C、D中，∠1与∠2的两边都不互为反向延长线，所以不是对顶角，是对顶角的只有选项B．故选：B．【点睛】本题主要考查了对顶角的定义，熟记有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角是解答此题的关键．2．（2020春•老城区校级月考）如图，AC⊥BC，CD⊥AB，下列结论中，正确的结论有（）①线段CD的长度是C点到AB的距离；②线段AC是A点到BC的距离；③AB＞AC＞CD．A．0个B．1个C．2个D．3个【思路点拨】根据垂直的定义，点到直线距离的定义对各选项进行逐一分析即可．【答案】解：①线段CD的长度是C点到AB的距离，故结论正确；②应该是线段AC的长度是A点到BC的距离，结论错误，；③在同一直角三角形中，斜边大于直角边，所以AB＞AC＞CD，故结论正确；故选：C．【点睛】本题考查的是点到直线的距离、垂直的定义，熟记定义并准确识图是解题的关键．特别注意点到直线的距离指的是点到直线的垂线段的长度，互相垂直指夹角为90°．3．（2020春•荥阳市期中）如图，下列工具的图片中，有对顶角的是（）A．B．C．D．【思路点拨】利用对顶角的定义解答即可．【答案】解：根据对顶角的定义可知，选项B是对顶角，其它都不是，故选：B．【点睛】本题主要考查了对顶角的定义，熟练掌握定义是解答此题的关键．4．（2020春•长安区校级月考）下列说法：①两点之间的所有连线中，线段最短；②在同一平面内，过一点有且只有一条直线与已知直线垂直；③连接直线外一点与直线上各点的所有线段中，垂线段最短；④直线外一点到这条直线的垂线段叫做点到直线的距离，其中正确的个数有（）A．4个B．3个C．2个D．1个【思路点拨】根据线段、点到直线的距离，垂线的概念或性质逐项分析即可．【答案】解：①两点之间的所有连线中，线段最短，说法正确；②在同一平面内，过一点有且只有一条直线与已知直线垂直，说法正确；③连接直线外一点与直线上各点的所有线段中，垂线段最短，说法正确；④直线外一点到这条直线的垂线段的长度叫做点到直线的距离，说法错误．故选：B．【点睛】本题主要考查了线段、点到直线的距离，垂线的概念及性质，理解概念是解答此题的关键．5．（2020春•新乡期末）如图，田地A的旁边有一条小河l，要想把小河里的水引到田地A处，为了省时省力需要作AB⊥l，垂足为B，沿AB挖水沟，则水沟最短，理由是（）A．点到直线的距离B．两点确定一条直线C．垂线段最短D．两点之间，线段最短【思路点拨】根据垂线段的性质：垂线段最短，可得答案．【答案】解：把小河里的水引到田地A处，则作AB⊥l，垂足为点B，沿AB挖水沟，依据为：垂线段最短．故选：C．【点睛】此题主要考查了垂线段的性质，关键是熟练掌握从直线外一点到这条直线所作的垂线段最短．6．（2020春•夏邑县期末）如图所示，已知AB和CD相交于点O，OE⊥AB于点O，如果∠COE＝70°，则∠AOD＝（）A．30°B．20°C．25°D．15°【思路点拨】由垂直的性质可得∠BOE＝90°，易得∠BOC＝20°，利用对顶角的定义可得结果．【答案】解：∵OE⊥AB，∴∠BOE＝90°，∵∠COE＝70°，∴∠BOC＝∠BOE﹣∠COE＝90°﹣70°＝20°，∴∠AOD＝∠BOC＝20°，故选：B．【点睛】本题主要考查了垂直的性质，对顶角的性质，熟练掌握性质定理是解答此题的关键．7．（2020春•禅城区期末）平面上4条不重合的直线两两相交，交点最多的个数是（）A．4个B．3个C．6个D．5个【思路点拨】4条直线相交，有3种位置关系，画出图形，进行解答．【答案】解：若4条直线相交，其位置关系有3种，如图所示：则交点的个数有1个或4个或6个．所以最多有6个交点．故选：C．【点睛】本题主要考查了直线相交时交点的情况，关键是画出图形．8．（2019秋•海口期末）如图，AO⊥BO于点O，CO⊥DO，若∠AOD＝152°40'，则∠BOC等于（）A．62°40'B．31°20'C．28°20'D．27°20'【思路点拨】根据垂直的定义，得∠AOB＝∠COD＝90°，再结合图形的重叠特点求∠BOC的度数．【答案】解：∵AO⊥BO，CO⊥DO，∴∠AOB＝∠COD＝90°，∴∠BOC＝∠AOB+∠COD﹣∠AOD＝180°﹣152°40'＝27°20'．故选：D．【点睛】本题考查了垂直的定义以及角的计算，要注意领会由垂直得直角这一要点．9．（2019秋•嘉兴期末）如图，直线AB与直线CD相交于点O，∠BOD＝40°，若过点O作OE⊥AB，则∠COE的度数为（）A．50°B．130°C．50°或90°D．50°或130°【思路点拨】根据题意画出图形，根据垂直定义可得∠AOE＝90°，根据对顶角相等可得∠AOC＝40°，然后可得答案．【答案】解：如图1，∵OE⊥AB，∴∠AOE＝90°，∵∠BOD＝40°，∴∠AOC＝40°，∴∠EOC＝130°；如图2，∵OE⊥AB，∴∠AOE＝90°，∵∠BOD＝40°，∴∠AOC＝40°，∴∠EOC＝50°，综上所述：∠COE的度数为50°或130°．故选：D．【点睛】此题主要考查了垂线，关键是正确画出图形，分情况讨论，不要漏解．10．（2019秋•克东县期末）下列结论：①平面内3条直线两两相交，共有3个交点；②在平面内，若∠AOB ＝40°，∠AOC＝∠BOC，则∠AOC的度数为20°；③若线段AB＝3，BC＝2，则线段AC的长为1或5；④若∠α+∠β＝180°，且∠α＜∠β，则∠α的余角为（∠β﹣∠α）．其中正确结论的个数有（）A．1个B．2个C．3个D．4个【思路点拨】根据线段的和差，相交线的定义，角平分线的定义，余角和补角的定义进行判断找到正确的答案即可．【答案】解：①平面内3条直线两两相交，有1个或3个交点；故错误；②在平面内，若∠AOB＝40°，∠AOC＝∠BOC，则∠AOC的度数为20°或160°；故错误；③若线段AB＝3，BC＝2，则线段AC的长为1或5；点C不一定在直线AB上，故错误；④若∠α+∠β＝180°，且∠α＜∠β，则∠α的余角为（∠β﹣∠α），故正确．故选：A．【点睛】本题考查了基本的几何定义，比较简单，属于基础题．二．填空题11．（2020秋•香坊区校级期中）如图，直线a、b相交，∠1＝36°，则∠2﹣∠3＝108°．【思路点拨】根据对顶角、邻补角的性质及∠1＝36°可求出∠2和∠3的度数，进而能得出∠2﹣∠3的值．【答案】解：∵直线a、b相交，∠1＝36°，∴∠3＝∠1＝36°，∠2＝180°﹣∠1＝144°，∴∠2﹣∠3＝144°﹣36°＝108°．故答案为：108°．【点睛】本题考查了对顶角、邻补角．解题的关键是掌握对顶角、邻补角的性质．对顶角的性质：对顶角相等．邻补角的性质：邻补角互补，即和为180°．12．（2020春•沙河口区期末）如图，在灌溉时，要把河中的水引到农田P处，并要求所挖的渠道最短．小明画线段PM，他的根据是垂线段最短．【思路点拨】根据垂线段的性质，可得答案．【答案】解：要把河中的水引到水池P处，小明画线段PM垂直河岸，使挖的水渠的长度最短，这样做依据的几何学原理是垂线段最短，故答案为：垂线段最短．【点睛】本题考查了垂线段最短，利用了垂线段的性质：直线外的点与直线上所有点的连线：垂线段最短．13．（2019春•和平区期中）如图，在线段AB，AD，AE，AF，AC中，AE最短．张明同学说：“垂线段最短，因此线段AE的长是点A到线段BC的距离．”对张明同学说法，你认为不对．（选填“对”或“不对”）．【思路点拨】点到直线的距离是指垂线段的长度．【答案】解：虽然在线段AB，AD，AE，AF，AC中，AE最短，但AE不是垂线段，故张明的说法不对．故答案为：不对．【点睛】本题考查了点到直线的距离的定义，注意是垂线段最短，但在已知的一些线段中，最短的线段不一定是垂线段．14．（2019秋•建湖县期末）如图，直线AB和直线CD相交于点O，∠BOE＝90°，有下列结论：①∠AOC 与∠COE互为余角；②∠AOC＝∠BOD；③∠AOC＝∠COE；④∠COE与∠DOE互为补角；⑤∠AOC 与∠DOE互为补角；⑥∠BOD与∠COE互为余角．其中错误的有③⑤．（填序号）【思路点拨】根据对顶角相等、邻补角、垂直的意义、等量代换等知识，逐个进行判断即可．【答案】解：∵∠BOE＝90°，∴∠AOE＝180°﹣∠BOE＝180°﹣90°＝90°＝∠AOC+∠COE，因此①不符合题意；由对顶角相等可得②不符合题意；∵∠AOE＝90°＝∠AOC+∠COE，但∠AOC与∠COE不一定相等，因此③符合题意；∠COE+∠DOE＝180°，因此④不符合题意；∠EOC+∠DOE＝180°，但∠AOC与∠COE不一定相等，因此⑤符合题意；∠BOD＝∠AOC，且∠COE+∠AOC＝90°，因此⑥不符合题意；故答案为：③⑤【点睛】考查对顶角、邻补角、垂直的意义等知识，等量代换在寻找各个角之间关系时起到十分重要的重要．15．（2019春•诸城市期中）已知∠α与∠1是对顶角，∠1的余角是55°18′36″，则∠α＝34°41′24″．【思路点拨】直接利用对顶角的性质结合度分秒的换算法则计算得出答案．【答案】解：∵∠α与∠1是对顶角，∴∠α＝∠1，∵∠1的余角是55°18′36″，∴∠α＝90°﹣55°18′36″＝34°41′24″，故答案为：34°41′24″．【点睛】此题主要考查了对顶角和度分秒换算，正确掌握相关运算法则是解题关键．16．（2019春•望花区校级月考）点O在直线AB上，射线OC⊥射线OD，若∠AOC＝35°，则∠BOD的度数是55°或125°．【思路点拨】此题可分两种情况，即OC，OD在AB的一边时和在AB的两边，分别求解．【答案】解：①当OC、OD在AB的一旁时，如图1，∵OC⊥OD，∴∠COD＝90°，∵∠AOC＝35°，∴∠BOD＝180°﹣∠COD﹣∠AOC＝55°；②当OC、OD在AB的两旁时，如图2，∵OC⊥OD，∠AOC＝35°，∴∠AOD＝55°，∴∠BOD＝180°﹣∠AOD＝125°．故答案为：55°或125°【点睛】此题主要考查了垂线的定义，利用数形结合分析是解题关键．同时，值得注意的是，要记得分类讨论，不要漏掉其中一种情况．三．解答题17．各图中，用三角板分别过点C画线段AB的垂线．【思路点拨】根据垂直的定义，借助三角板的直角可画出垂线段．【答案】解：【点睛】本题主要考查了垂线段的画法．18．（2019秋•姜堰区期末）如图，直线AB、CD相交于点O，OM⊥AB．（1）若∠1＝∠2，求∠NOD的度数；（2）若∠AOD＝3∠1，求∠AOC和∠MOD的度数．【思路点拨】（1）利用垂直的定义得出∠2+∠AOC＝90°，进而得出答案；（2）根据题意得出∠1的度数，即可得出AOC和∠MOD的度数．【答案】证明：（1）∵OM⊥AB，∴∠AOM＝∠BOM＝90°，∴∠1+∠AOC＝90°，∵∠1＝∠2，∴∠2+∠AOC＝90°，即∠CON＝90°，∴∠NOD＝180°﹣∠CON＝180°﹣90°＝90°；（2）∵∠AOD＝3∠1，∴∠NOD＝2∠1＝90°，解得：∠1＝45°，∴∠AOC＝∠AOM﹣∠1＝90°﹣45°＝45°；∴∠BOD＝90°﹣45°＝45°，∴∠MOD＝∠BOD+∠BOM＝45°+90°＝135°．故答案为：（1）90°；（2）45°，135°．【点睛】此题主要考查了垂直的定义以及邻补角、对顶角等知识，正确把握垂直的定义是解题关键．19．如图，直线AB，CD，EF相交于点O，∠AOE：∠AOD＝1：3，∠COB：∠DOF＝3：4，求证，CD⊥EF．【思路点拨】设∠AOE＝x，则∠AOD＝3x，得出∠COE＝DOF＝4x，列出方程4x+x+3x＝180°，解方程即可得出结论．【答案】证明：设∠AOE＝x，则∠AOD＝3x，∴∠COB＝∠AOD＝3x，∴∠DOF＝4x，∵∠COE＝DOF＝4x，∠COE+∠AOE+∠AOD＝180°，∴4x+x+3x＝180°，∴x＝22.5°，∴∠COE＝4×22.5°＝90°，∴CD⊥EF．【点睛】本题考查了垂线．对顶角、邻补角的定义；弄清各个角之间的数量关系是解决问题的关键．20．（2019秋•句容市期末）已知如图，直线AB、CD相交于点O，∠COE＝90°．（1）若∠AOC＝36°，求∠BOE的度数；（2）若∠BOD：∠BOC＝1：5，求∠AOE的度数；（3）在（2）的条件下，过点O作OF⊥AB，请直接写出∠EOF的度数．【思路点拨】（1）根据平角的定义求解即可；（2）根据平角的定义可求∠BOD，根据对顶角的定义可求∠AOC，根据角的和差关系可求∠AOE的度数；（3）先过点O作OF⊥AB，再分两种情况根据角的和差关系可求∠EOF的度数．【答案】解：（1）∵∠AOC＝36°，∠COE＝90°，∴∠BOE＝180°﹣∠AOC﹣∠COE＝54°；（2）∵∠BOD：∠BOC＝1：5，∴∠BOD＝180°×＝30°，∴∠AOC＝30°，∴∠AOE＝30°+90°＝120°；（3）如图1，∠EOF＝120°﹣90°＝30°，或如图2，∠EOF＝360°﹣120°﹣90°＝150°．故∠EOF的度数是30°或150°．【点睛】本题主要考查了角的计算，涉及到的角有平角、直角；熟练掌握平角等于180度，直角等于90度，是解答本题的关键．21．探究型问题如图所示，在同一平面内，两条直线相交时最多有1个交点，三条直线相交时最多有3个交点，四条直线相交时最多有6个交点．（1）当五条直线相交时交点最多会有多少个？（2）猜想n条直线相交时最多有几个交点？（用含n的代数式表示）（3）算一算，同一平面内10条直线最多有多少个？（4）平面上有10条直线，无任何3条交于一点（3条以上交于一点也无），也无重合，它们会出现31个交点吗？如果能给出一个画法；如果不能请说明理由．【思路点拨】（1）要探求相交直线的交点的最多个数，则应尽量让每两条直线产生不同的交点．根据两条直线相交有一个交点，画第五条直线时，应尽量和前面四条直线都产生交点，即增加4个交点，则有6+4＝10个交点；（2）根据已知条件，求得n条直线相交，最多有1+2+3+…+（n﹣1）＝个交点；（3）将n＝10代入上式即可求解；（4）可使5条直线平行，另3条直线平行且都与这5条相交，再有2条直线平行且都与这5条直线相交，且3条和2条也有相交．【答案】解：（1）如图，∵两条直线相交，最多有1个交点，三条直线相交，最多有1+2＝3个交点，四条直线相交，最多有1+2+3＝6个交点．∴五条直线相交，最多有1+2+3+4＝10个交点；（2）n条直线相交，最多有1+2+3+…+（n﹣1）＝个交点；（3）10条直线相交，最多有＝45个交点；（4）会出现31个交点，如下图所示：【点睛】此题考查平面内不重合直线的位置关系，是寻找规律的题型，找到n条直线相交，最多有个交点是解题的关键．22．（2019秋•市中区期末）将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起．（1）如图（1），若∠BOD＝35°，则∠AOC＝145°；若∠AOC＝135°，则∠BOD＝45°；（直接写出结论即可）（2）如图（2），若∠AOC＝140°，则∠BOD＝40°；（直接写出结论即可）（3）猜想∠AOC与∠BOD的大小关系，并结合图（1）说明理由；（4）三角尺AOB不动，将三角尺COD的OD边与OA边重合，然后绕点O按顺时针或逆时针方向任意转动一个角度，当锐角∠AOD等于多少度时，这两块三角尺各有一条边互相垂直，直接写出∠AOD角度所有可能的值，不用说明理由．【思路点拨】（1）由于是两直角三角形板重叠，根据∠AOC＝∠AOB+∠COD﹣∠BOD可分别计算出∠AOC、∠BOD的度数；（2）根据∠BOD＝360°﹣∠AOC﹣∠AOB﹣∠COD计算可得；（3）由∠AOD+∠BOD+∠BOD+∠BOC＝180°且∠AOD+∠BOD+∠BOC＝∠AOC可知两角互补；（4）分别利用OD⊥AB、CD⊥OB、CD⊥AB、OC⊥AB分别求出即可．【答案】解：（1）若∠BOD＝35°，∵∠AOB＝∠COD＝90°，∴∠AOC＝∠AOB+∠COD﹣∠BOD＝90°+90°﹣35°＝145°，若∠AOC＝135°，则∠BOD＝∠AOB+∠COD﹣∠AOC＝90°+90°﹣135°＝45°；故答案为：145°；45°；（2）如图2，若∠AOC＝140°，则∠BOD＝360°﹣∠AOC﹣∠AOB﹣∠COD＝360°﹣140°﹣90°﹣90°＝40°；故答案为：40°；（3）∠AOC与∠BOD互补．∵∠AOB＝∠COD＝90°，∴∠AOD+∠BOD+∠BOD+∠BOC＝180°．∵∠AOD+∠BOD+∠BOC＝∠AOC，∴∠AOC+∠BOD＝180°，即∠AOC与∠BOD互补．（4）OD⊥AB时，∠AOD＝30°，CD⊥OB时，∠AOD＝45°，CD⊥AB时，∠AOD＝75°，OC⊥AB时，∠AOD＝60°，即∠AOD角度所有可能的值为：30°、45°、60°、75°．【点睛】本题主要考查了互补、互余的定义，垂直的定义以及三角形内角和定理等知识的综合运用，解决本题的关键是掌握：如果两个角的和等于180°（平角），就说这两个角互为补角，其中一个角是另一个角的补角．。

6.9直线的相交一．选择题（共8小题）1．同一平面内，三条不同直线的交点个数可能是（）个．A．1或3 B．0、1或3 C．0、1或2 D．0、1、2或32．下列各组角中，∠1与∠2是对顶角的为（）A． B．C． D．3．如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O，已知∠AOD=136°，则∠COM的度数为（）A．36° B．44° C．46° D．54°4．如图，把水渠中的水引到水池C，先过C点向渠岸AB画垂线，垂足为D，再沿垂线CD开沟才能使沟最短，其依据是（）A．垂线最短B．过一点确定一条直线与已知直线垂直C．垂线段最短D．以上说法都不对5．已知△ABC中，BC=6，AC=3，CP⊥AB，垂足为P，则CP的长可能是（）A．2 B．4 C．5 D．76．如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有（）A．2条B．3条C．4条D．5条7．已知∠α的两边分别与∠β的两边垂直，且∠α=20°，则∠β的度数为（）A．20° B．160°C．20°或160°D．70°8．如图，点A在直线l1上，点B，C分别在直线l2上，AB⊥l2，AC⊥l1，AB=4，BC=3，则下列说法正确的是（）A．点B到直线 l1的距离等于4 B．点C到直线l1的距离等于5C．直线l1，l2的距离等于4 D．点B到直线AC的距离等于3二．填空题（共4小题）9．如图，直线AB、CD相交于点O，∠1=50°，则∠2= 度．10．已知，如图，直线AB与CD相交于点O，OE平分∠AOC，若∠EOC=25°，则∠BOD的度数为．11．如图，直线AB与CD相交于E点，EF⊥AB，垂足为E，∠1=130°，则∠2= 度．12．如图，直线a，b相交，∠2=3∠1，则∠3= °．三．解答题（共3小题）13．如图，直线AB，CD相交于O，射线OM平分∠AOC，若∠BOD=80°，求∠BOM的度数．14．如图，直线AB与CD相交于点O，OD恰为∠BOE的角平分线．（1）请直接写出和∠AOD能成为互为补角的角；（把符合条件的角都填出来）（2）若∠AOD=142°，求∠AOE的度数．15．如图，直线AB与CD相交于点O，∠AOM=90°．（1）如图1，若OC平分∠AOM，求∠AOD的度数；（2）如图2，若∠BOC=4∠NOB，且OM平分∠NOC，求∠MON的度数．\初中数学试卷。

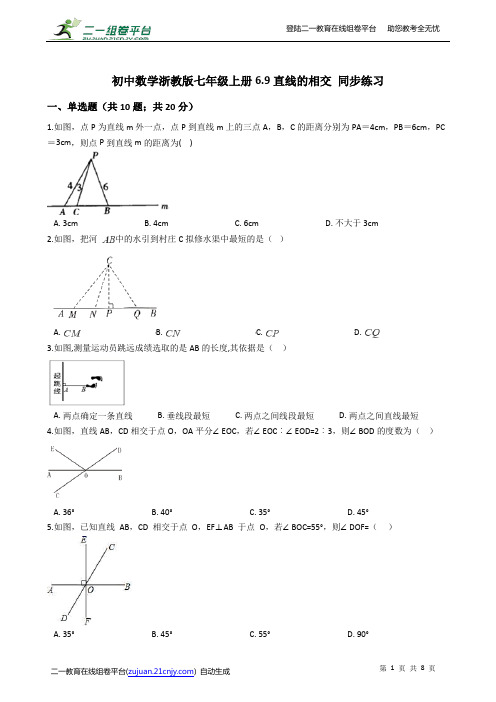
初中数学浙教版七年级上册6.9直线的相交同步练习一、单选题（共10题；共20分）1.如图，点P为直线m外一点，点P到直线m上的三点A，B，C的距离分别为PA＝4cm，PB＝6cm，PC ＝3cm，则点P到直线m的距离为( )A. 3cmB. 4cmC. 6cmD. 不大于3cm2.如图，把河中的水引到村庄C拟修水渠中最短的是（）A. B. C. D.3.如图,测量运动员跳远成绩选取的是AB的长度,其依据是（）A. 两点确定一条直线B. 垂线段最短C. 两点之间线段最短D. 两点之间直线最短4.如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC︰∠EOD=2︰3，则∠BOD的度数为（）A. 36°B. 40°C. 35°D. 45°5.如图，已知直线AB，CD 相交于点O，EF⊥AB 于点O，若∠BOC=55°，则∠DOF=（）A. 35°B. 45°C. 55°D. 90°6.如图，在平面内作已知直线m的垂线，可作垂线的条数有（）A. 0条B. 1条C. 2条D. 无数条7.下列各图中，过直线外的点画直线的垂线，三角尺操作正确的是（）A. B.C. D.8.下列说法中不正确的是( )A. 在同一平面内，经过一点能画一条且只能画一条直线与已知直线垂直B. 从直线外一点到这条直线的垂线段叫做点到直线的距离C. 一条直线的垂线可以画无数条D. 连接直线外一点与直线上各点的所有线段中，垂线段最短9.三条共点直线都与第四条直线相交，一共有（）对对顶角.A. 12B. 24C. 7D. 1110.下列语句中，正确的是（）A. 相等的角一定是对顶角B. 互为补角的两个角不相等C. 有一个公共顶点，两边互为反向延长线的两个角是对顶角D. 交于一点的三条直线形成3对对顶角二、填空题（共5题；共6分）11.经过一点________一条直线垂直于已知直线．12.如图，AC⊥BC, 且BC=6，AC=8，AB=10，则点A到BC的距离是________点B到点A的距离是________．13.如图所示，其中共有________对对顶角．14.如图，CD⊥AB，垂足是点D，AC＝7，BC＝5，CD＝4，点E是线段AB上的一个动点（包括端点），连接CE，那么CE长的范围是________．15.如图，直线AB，CD相交于点O，若∠AOC=20°，则∠BOD的大小为________（度）．三、解答题（共3题；共20分）16.画一条线段的垂线，就是画它所在直线的垂线．如图，请你过点P画出线段的垂线，垂足分别为点．17.如图，∠1=28°，AB⊥CD，垂足为O，EF经过点O.求∠2、∠3的度数.18.如图，直线与相交于点O，平分，．（1）若，求的度数；（2）在的内部作射线，探究与之间有怎样的关系？并说明理由．答案解析部分一、单选题1.【答案】D【解析】【解答】解：∵点P到直线m上的三点A，B，C的距离分别为PA＝4cm，PB＝6cm，PC＝3cm，∴点P到直线m的距离为不大于3cm.故答案为：D.【分析】根据垂线段最短，可得点P到直线m的距离的取值范围。

《6.9 直线的相交》课时同步练习2020-2021年数学浙教新版七（上）一．选择题（共8小题）1．在同一平面内，不重合的三条直线的交点有（）个．A．1或2B．2或3C．1或3D．0或1或2或3 2．如图，沿笔直小路DE的一侧栽植两棵小树B，C，小明在A处测得AB＝5米，AC＝7米，则点A到DE的距离可能为（）A．4米B．5米C．6米D．7米3．下列图形中，线段PQ的长表示点P到直线MN的距离是（）A．B．C．D．4．下列四个图形中，∠1与∠2是对顶角的是（）A．B．C．D．5．如图，CD⊥AB于D．且BC＝4，AC＝3，CD＝2.4．则点C到直线AB的距离等于（）A．4B．3C．2.4D．26．如图，直线AB，CD相交于点O，EO⊥AB，垂足为O，∠EOC＝40°，求∠AOD的度数（）A．110°B．120°C．130°D．140°7．如图，直线AB，CD相交于点O，已知∠AOC＝80°，∠BOE：∠EOD＝3：2，则∠AOE 的度数是（）A．100°B．116°C．120°D．132°8．如图，直线AB和CD相交于点O，OE⊥AB于点O，∠COE＝55°，则∠AOD的度数为（）A．145°B．135°C．125°D．155°二．填空题（共8小题）9．如图，直线AC和直线BD相交于点O，OE平分∠BOC，若∠1+∠2＝80°，则∠3的度数为°．10．如图，点O在直线AB上，OD⊥OE，垂足为O，OC是∠DOB的平分线，若∠AOD＝70°，则∠BOE＝度，∠COE＝度．11．如图，∠C＝90°，线段AB＝15cm，线段AD＝12cm，线段AC＝9cm，则点A到BC 的距离为cm．12．如图，想过点A建一座桥，搭建方式最短的是垂直于河两岸的AO，理由是．13．如图，已知BO⊥AD于点O，∠COE＝90°，且∠BOC＝4∠AOC，则∠BOE的度数为度．14．已知：如图，直线AB、CD相交于点O，∠COE＝90°，∠BOD：∠BOC＝1：5，过点O作OF⊥AB，则∠EOF的度数为．15．如图，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM＝d．我们把圆上到直线l的距离等于1的点的个数记为m．如d＝0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m＝4，由此可知：当m＝2时，d 的取值范围是．16．平面内有n条直线（n≥2），这n条直线两两相交，最多可以得到a个交点，最少可以得到b个交点，则a+b＝．三．解答题（共4小题）17．如图，已知直线AB，CD相交于点O，射线OE把∠AOC分成两部分．（1）写出图中∠AOC的对顶角，∠COE的补角是；（2）已知∠AOC＝60°，且∠COE：∠AOE＝1：2，求∠DOE的度数．18．如图，直线AB、CD相交于点O，∠AOC＝58°，∠1＝20°．（1）求∠2的度数；（2）若OF⊥OE，求∠DOF的度数．19．已知一个角的两边与另一个角的两边分别垂直，如图所示，解答下列问题：（1）如图1，AB⊥DE，BC⊥EF，∠1与∠2的数量关系是；（2）如图2，AB⊥DE，BC⊥EF，∠1与∠2的数量关系是；（3）由（1）（2）得出的结论是；（4）若两个角的两边互相垂直，且一个角比另一个角的2倍少30°，则这两个角的度数分别是多少？20．如图1，点A，O，B依次在直线MN上，现将射线OA绕点O沿顺时针方向以每秒4°的速度转动，同时射线OB绕点O沿逆时针方向以每秒6°的速度转动，直线MN保持不动，如图2，设转动时间为t（0≤t≤60，单位：秒）（1）当t＝3时，求∠AOB的度数；（2）在转动过程中，当∠AOB第二次达到80°时，求t的值；（3）在转动过程中是否存在这样的t，使得射线OB与射线OA垂直？如果存在，请求出t的值：如果不存在，请说明理由．参考答案一．选择题（共8小题）1．解：因为三条直线位置不明确，所以分情况讨论：①三条直线互相平行，有0个交点；②一条直线与两平行线相交，有2个交点；③三条直线都不平行，有1个或3个交点；所以交点的个数可能为0个或1个或2个或3个．故选：D．2．解：根据垂线段最短得，点A到DE的距离＜AB，故选：A．3．解：由题意得PQ⊥MN，P到MN的距离是PQ垂线段的长度，故选：A．4．解：A、∠1的两边不是∠2的两边的反向延长线，不是对顶角，不合题意；B、∠1的两边不是∠2的两边的反向延长线，不是对顶角，不合题意；C、∠1的两边是∠2的两边的反向延长线，是对顶角，符合题意；D、∠1的两边与∠2没有公共顶点，不是对顶角，不合题意；故选：C．5．解：由题意得点C到直线AB的距离等于CD的长，故选：C．6．解：∵EO⊥AB，∴∠EOB＝90°，又∵∠EOC＝40°，∴∠AOD＝∠BOC＝∠EOB+∠EOC＝90°+40°＝130°，故选：C．7．解：∵∠AOC＝80°，∴∠DOB＝80°，∠AOD＝100°，∵∠BOE：∠EOD＝3：2，∴∠DOE＝80°×＝32°，∴∠AOE＝100°+32°＝132°，故选：D．8．解：∵OE⊥AB于O，∴∠BOE＝90°，∵∠COE＝55°，∴∠BOC＝∠BOE+∠COE＝90°+55°＝145°，∴∠AOD＝∠BOC＝145°（对顶角相等）．故选：A．二．填空题（共8小题）9．解：∵∠1＝∠2，∠1+∠2＝80°，∴∠1＝∠2＝40°，∴∠BOC＝180°﹣∠1＝140°，又∵OE平分∠BOC，∴∠3＝×140°＝70°．故答案为：70．10．解：∵∠BOD＝180°﹣∠AOD＝110°，又∵OC是∠DOB的平分线．∴∠DOC＝∠COB＝∠BOD＝55°，∵OD⊥OE，垂足为O．∴∠COE＝90°﹣∠DOC＝90°﹣55°＝35°，∠BOE＝∠COB﹣∠COE＝55°﹣35°＝20°．故答案是：20和35．11．解：因为∠C＝90°，所以AC⊥BC，所以A到BC的距离是AC，因为线段AC＝9cm，所以点A到BC的距离为9cm．故答案为：9．12．解：∵AO⊥BD，∴由垂线段最短可知AO是最短的，故答案为：垂线段最短．13．解：∵BO⊥AD，∴∠AOB＝90°，即∠AOC+∠BOC＝90°，∵∠BOC＝4∠AOC，∴∠AOC+4∠AOC＝90°，∵∠AOC＝18°，∴∠BOC＝72°，∵∠COE＝90°，∴∠BOE＝90°﹣∠BOC＝90°﹣72°＝18°．故答案为：18．14．解：∵∠BOD：∠BOC＝1：5，∠BOD+∠BOC＝180°，∴∠BOD＝×180°＝30°，∵∠COE＝90°，∴∠EOD＝180°﹣∠COE＝90°，∵OF⊥AB，∴∠BOF＝90°，∴∠DOF＝∠BOF﹣∠BOD＝90°﹣30°＝60°，∴∠EOF＝∠EOD+∠DOF＝90°+60°＝150°．故答案为：150°．15．解：当d＝3时，m＝1；当d＝1时，m＝3；∴当1＜d＜3时，m＝2，故答案为：1＜d＜3．16．解：如图：2条直线相交有1个交点，3条直线相交有1+2个交点，4条直线相交有1+2+3个交点，5条直线相交有1+2+3+4个交点，6条直线相交有1+2+3+4+5个交点，…n直线相交有个交点．∴，而b＝1，∴故答案为：．三．解答题（共4小题）17．解：（1）由图形可知，∠AOC的对顶角是∠BOD，∠COE的邻角是∠DOE；（2）设∠COE＝x，则∠AOE＝2x，∵∠AOC＝60°，∴x+2x＝60，解得x＝20，即∠COE＝20°，∠AOE＝40°，∵∠AOC+∠AOD＝180°，∴∠AOD＝120°，∴∠DOE＝∠AOE+∠AOD＝40°+120°＝160°．18．解：（1）∵∠AOC＝∠BOD，∠AOC＝58°．∴∠BOD＝58°．∵∠1＝20°．∴∠2＝∠BOD﹣∠1＝38°．（2）∵OF⊥OE．∴∠EOF＝90°．∴∠DOF＝90°﹣∠2＝52°．19．解：（1）如图1，∵AB⊥DE，BC⊥EF，∴∠EGB＝90°，∠EHB＝90°，∴∠2+∠4＝90°，∠1+∠3＝90°，∵∠3＝∠4，∴∠1＝∠2．故答案为：相等．（2）如图2，∵AB⊥DE，BC⊥EF，∴∠EGB＝90°，∠EHB＝90°，∴∠1+∠2+∠EGB+∠EHB＝360°，∴∠1+∠2＝180°．故答案为：互补．（3）由（1）（2）的分析可得结论：如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等或互补；故答案为：如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等或互补；（4）设另一个角的度数为α，则一个角的度数为2α﹣30°，根据题意可得，α＝2α﹣30°或α+2α﹣30°＝180°，解得α＝30°，或α＝70°，当α＝30°时，2α﹣30°＝30°，当α＝70°时，2α﹣30°＝110°，∴这两个角的度数为30°，30°或110°，70°．20．解：（1）当t＝3时，∠AOB＝180°﹣4°×3﹣6°×3＝150°．（2）依题意，得：4t+6t＝180+80，解得t＝26，答：当∠AOB第二次达到80°时，t的值为26秒．（3）当0≤t≤18时，180﹣4t﹣6t＝90，解得t＝9，当18≤t≤60时，4t+6t＝180+90或4t+6t＝180+270，解得t＝27或t＝45．答：在旋转过程中存在这样的t，使得射线OB与射线OA垂直，t的值为9秒、27秒或45秒。

章节测试题1.【答题】如图，在所标识的角中，互为对顶角的两个角是（）A.∠2和∠3B.∠1和∠3C.∠1和∠4D.∠1和∠2【答案】A【分析】两条直线相交后，所得的只有一个公共顶点，且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角．【解答】解：根据同位角、同旁内角、邻补角、对顶角的定义进行判断，A、∠2和∠3是对顶角，正确；B、∠1和∠3是同旁内角，错误；C、∠1和∠4是同位角，错误；D、∠1和∠2的邻补角是内错角，错误．选A.2.【答题】如图，直线a、b相交于点O，若∠1等于40°，则∠2等于（）A.50°B.60°C.140°D.160°【答案】C【分析】因∠1和∠2是邻补角，且∠1=40°，由邻补角的定义可得∠2=180°﹣∠1=180°﹣40°=140°．【解答】解：∵∠1+∠2=180°又∠1=40°∴∠2=140°．选C.3.【答题】如图，某同学在课桌上随意将一块三角板的直角叠放在直尺上，则∠1+∠2的度数是（）A.45°B.60°C.90°D.180°【答案】C【分析】由图可知，直角三角形的两个锐角正好是∠1和∠2的对顶角，而直角三角形的两个锐角之和是90°，那么就可得知∠1+∠2的度数．【解答】解：由图可知，∠1和∠2的对顶角互余，所以∠1+∠2=90°．选C.4.【答题】如图，已知直线AB、CD相交于点O，OA平分∠EOC，∠EOC=110°，则∠BOD的度数是（）A.25°B.35°C.45°D.55°【答案】D【分析】根据角平分线的定义求出∠AOC的度数，再根据对顶角相等即可求解．【解答】解：∵OA平分∠EOC，∠EOC=110°，∴∠AOC=∠COE=55°，∴∠BOD=∠AOC=55°．选D.5.【答题】如图，已知直线AB，CD相交于点O，OA平分∠EOC，∠EOC=100°，则∠BOD的度数是（）A.20°B.40°C.50°D.80°【答案】C【分析】利用角平分线的性质和对顶角相等即可求得．【解答】解：∵∠EOC=100°且OA平分∠EOC，∴∠BOD=∠AOC=×100°=50°．选C.6.【答题】如图，直线AB，CD相交于O点，若∠1=30°，则∠2，∠3的度数分别为（）A.120°，60°B.130°，50°C.140°，40°D.150°，30°【答案】D【分析】首先判断所求角与∠1的关系，然后利用对顶角、邻补角的性质求解．【解答】解：∵∠1与∠3是对顶角，∴∠3=∠1=30°，∵∠1与∠2是邻补角，即∠1+∠2=180°，∴∠2=180°﹣30°=150°．选D.7.【答题】如图，已知直线AB、CD相交于点O，OE平分∠COB，若∠BOD=70°，则∠COE的度数是（）A.45°B.70°C.55°D.110°【答案】C【分析】根据邻补角的性质可得∠COB=110°，再根据角平分线的性质课可得∠COE=∠COB，进而得到答案．【解答】解：∵∠BOD=70°，∴∠COB=110°，∵OE平分∠COB，∴∠COE=∠COB=55°，选：C.8.【答题】如图，直线AB和CD相交于点O，若∠AOD=55°，则∠AOC=（）A.115°B.120°C.125°D.130°【答案】C【分析】根据互为邻补角的两个角的和等于180°列式计算即可得解．【解答】解：∵∠AOD=55°，∴∠AOC=180°﹣55°=125°．选C.9.【答题】如图，直线AB、CD相交于点O，OE平分∠BOD，若∠COE=160°，则∠AOC等于（）A.20°C.60°D.80°【答案】B【分析】根据邻补角的定义求出∠DOE，再根据角平分线的定义求出∠BOD，然后根据对顶角相等求解即可．【解答】解：∵∠COE=160°，∴∠DOE=180°﹣∠COE=180°﹣160°=20°，∵OE平分∠BOD，∴∠BOD=2∠DOE=2×20°=40°，∴∠AOC=∠BOD=40°．选B.10.【答题】如图，直线AB与直线CD相交于点O，OE平分∠AOD，已知∠BOD=30°，则∠AOE的度数是（）A.75°C.120°D.150°【答案】A【分析】先求得∠AOD的度数，再根据角平分线的性质，求出∠AOE的度数．【解答】解：∵∠BOD=30°，∴∠AOE=150°，∵OE平分∠AOD，∴∠AOE=∠AOD=×150°=75°，选A.11.【答题】如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（）A.36°B.72°C.108°D.120°【答案】B【分析】设∠DOE=x，根据题意得到∠BOE=2x，∠AOC=∠COD=72°﹣x，再根据平角为180度，得到2×（72°﹣x）+3x=180°，解得x=36°，即可得到∠BOE的度数．【解答】解：如图，设∠DOE=x，∵∠DOE=∠BOD，∴∠BOE=2x，又∵OC是∠AOD的平分线，∠COE=72°，∴∠AOC=∠COD=72°﹣x；∴2×（72°﹣x）+3x=180°，解得x=36°，∴∠BOE=2x=2×36°=72°．选B.12.【答题】下列说法正确的是（）A.相等的两个角是对顶角B.和等于90°的两个锐角互为余角C.如果∠1+∠2+∠3=180°，那么∠1、/2、∠3互为补角D.一个角的补角一定大于这个角【答案】B【分析】根据余角、补角、对顶角的定义进行判断即可．【解答】解：A、两个对顶角相等，但相等的两个角不一定是对顶角；故A错误；B、如果两个角的和是一个直角，那么这两个角互为余角；故B正确；C、余、补角是两个角的关系，故C错误；D、锐角的补角都大于这个角，而直角和钝角不符合这样的条件，故D错误．选B.13.【答题】下列说法错误的是（）A.53°38′角与36°22′角互为余角B.如果∠1+∠2=180°，那么∠1与∠2是邻补角C.两个角互补，如果其中一个是锐角，那么另一个一定是钝角D.一个角的补角比这个角的余角大90°【答案】B【分析】根据（1）余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．（2）补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．（3）邻补角：只有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．由此即可作出判断．【解答】解：A、53°38′+36°22′=90°，故53°38′角与36°22′角互为余角是正确的，不符合题意；B、如果∠1+∠2=180°，那么∠1与∠2互为补角，故如果∠1+∠2=180°，那么∠1与∠2是邻补角是错误的，符合题意；C、两个角互补，如果其中一个是锐角，那么另一个一定是钝角是正确的，不符合题意；D、由于180°﹣90°=90°，故一个角的补角比这个角的余角大90°是正确的，不符合题意．选B.14.【答题】如图，直线AB、CD、EF相交于O，图中对顶角共有（）A.3对B.4对C.5对D.6对【答案】D【分析】根据对顶角的定义，对顶角的两边互为反向延长线，可以判断．【解答】解：图中对顶角有：∠AOF与∠BOE、∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF，共6对．选D.15.【答题】如图，直线AB、CD相交于O点，∠AOD+∠BOC=236°，则∠AOC=（）A.72°B.62°C.124°D.144°【答案】B【分析】由两直线相交，对顶角相等，可得∠AOD=∠BOC，已知∠AOD+∠BOC=236°，可求∠AOD；又∠AOC与∠AOD互为邻补角，即∠AOC+∠AOD=180°，将∠AOD的度数代入，可求∠AOC.【解答】解：∵∠AOD与∠BOC是对顶角，∴∠AOD=∠BOC，又已知∠AOD+∠BOC=236°，∴∠AOD=118°．∵∠AOC与∠AOD互为邻补角，∴∠AOC=180°﹣∠AOD=180°﹣118°=62°．选B.16.【答题】两条直线相交，有______对对顶角，三条直线两两相交，有______对对顶角.【答案】两六【分析】根据对顶角的定义解答即可。

6．9 直线的相交(1)1．下列选项中，∠1与∠2是对顶角的是(C)2．如图，三条直线AB，CD，EF交于点O，则∠AOE＋∠DOB＋∠COF等于(B)A．150° B．180° C．210° D．120°,(第2题)) ,(第3题))3．如图，直线AB，CD交于点O，则图中共有对顶角(B)A．1对 B．2对 C．3对 D．4对4．下列说法中正确的是(A)A．若两个角是对顶角，则这两个角相等B．若两个角相等，则这两个角是对顶角C．若两个角不是对顶角，则这两个角不相等D．以上说法都不正确5．如图，直线AB，CD交于点O，射线OM平分∠AOC.若∠BOD＝76°，则∠BOM等于(C) A．38° B．104° C．142° D．144°,(第5题)) ,(第6题))6．如图，当剪刀口∠AOB增大15°时，∠COD增大__15°__．7．若∠1的对顶角是∠2，∠2的补角是∠3，且∠3＝54°，则∠1＝__126°__．8．如图，两直线AB ，CD 交于点O ，∠EOD ＝90°，且∠BOE ＝13∠BOC ，则∠AOC 的度数为__45°__．,(第8题)) ,(第9题))9．如图，直线AB ，CD ，EF 交于点O ，且∠EOD ＝90°.若∠COA ＝28°，则∠AOF ，∠BOC 和∠EOA 的度数分别是62°，152°，118°．10．如图，直线AB ，CD 交于点O ，OE 平分∠COD ，∠BOE ＝68°，则∠AOC ＝22°．,(第10题)) ,(第11题))11．如图，直线AB ，CD 交于点O ，OE 平分∠AOD ，OF 平分∠BOD .已知∠AOF ＝160°，那么∠COE ＝__110°__．12．如图，直线AB ，CD 交于点O ，OE 平分∠BOD ，且∠AOC ＝∠AOD －80°，求∠AOE 的度数．(第12题)【解】 ∵∠AOD ＝180°－∠AOC (平角的定义)， ∠AOC ＝∠AOD －80°(已知)， ∴∠AOC ＝180°－∠AOC －80°. ∴∠AOC ＝50°，∠AOD ＝130°. ∴∠BOD ＝∠AOC ＝50°(对顶角相等)． ∵OE 平分∠BOD (已知)，∴∠DOE ＝12∠BOD ＝25°(角平分线的意义)．∴∠AOE ＝∠AOD ＋∠DOE ＝130°＋25°＝155°.(第13题)13．如图，直线AB ，CD 交于点O ，OE 平分∠BOD . (1)若∠AOC ＝70°，∠DOF ＝90°，求∠EOF 的度数； (2)若OF 平分∠COE ，∠BOF ＝15°，求∠AOC 的度数． 【解】 (1)∵OE 平分∠BOD ，∠BOD ＝∠AOC ＝70°， ∴∠DOE ＝12∠BOD ＝35°.∴∠EOF ＝∠DOF －∠DOE ＝90°－35°＝55°. (2)设∠AOC ＝x ，则∠BOD ＝x . ∵OE 平分∠BOD ，∴∠DOE ＝∠EOB ＝12∠BOD ＝x2.∴∠COE ＝180°－∠DOE ＝180°－x2.∵∠EOF ＝∠EOB ＋∠BOF ， ∴∠EOF ＝x2＋15°.∵OF 平分∠COE ， ∴∠COE ＝2∠EOF .∴180°－x 2＝2⎝ ⎛⎭⎪⎫x2＋15°， 解得x ＝100°，即∠AOC ＝100°.14．如图，直线AB ，CD 交于点M ，MN 是∠BMC 的平分线，∠AMN ＝136°，求∠AMD 的度数．(第14题)【解】 ∵∠AMN＝136°， ∴∠BMN ＝44°.又∵MN 是∠BMC 的平分线， ∴∠AMD ＝∠BMC ＝2∠BMN ＝88°.15．如图，已知直线AB 与CD 交于点O ，OE 平分∠BOD ，OF 平分∠AOB . (1)若∠BOE ＝40°，求∠AOF 与∠COF 的度数；(2)若∠BOE ＝x (x ＜45°)，请用含x 的代数式表示∠COF 的度数．(第15题)【解】(1)∵OE 平分∠BOD ， ∴∠BOE ＝12∠BOD .∵∠BOE ＝40°， ∴∠BOD ＝80°， ∴∠BOC ＝100°. ∵OF 平分∠AOB ， ∴∠AOF ＝∠BOF ＝90°， ∴∠COF ＝100°－90°＝10°.(2)∠COF ＝180°－2x －90°＝90°－2x .。

6.9 直线的相交第1课时对顶角知识点1 对顶角的意义1．下列图形中，∠1与∠2是对顶角的是( )图6－9－12．如图6－9－2所示，BE，CF相交于点O，OA，OD是射线，其中构成对顶角的角是____________．图6－9－2知识点2 对顶角的性质3．如图6－9－3，直线a，b相交于点O，∠1＋∠3＝________，∠2＋∠3＝________(邻补角的定义)，所以∠1________∠2(同角的补角相等)．由此可知对顶角________．图6－9－34．已知∠α和∠β是对顶角，∠α＝30°，则∠β的度数为( )A．30° B．60° C．70° D．150°5．如图6－9－4，图中是对顶角量角器，用它测量角的原理是______________.图6－9－46．如图6－9－5，直线AB，CD，EF交于一点O.图6－9－5(1)∠EOB的对顶角是________；(2)________是∠AOE的对顶角；(3)若∠AOC＝76°，则∠BOD的度数为________．7．如图6－9－6所示，直线AB与CD相交于点O，若∠AOC＋∠BOD＝90°，则∠BOC＝________°.图6－9－68．如图6－9－7所示，∠1＝120°，∠2＋∠3＝180°，则∠4＝________°.图6－9－79. 如图6－9－8，直线AB，CD相交于点O，∠1＝40°，求∠2，∠3，∠4的度数．图6－9－810．如图6－9－9所示，直线AB，CD相交于点O，OE平分∠AOC，∠EOC＝35°，求∠BOD 的度数．图6－9－911．如图6－9－10，直线AB，CD，EF相交于点O，∠AOD＝150°，∠EOD＝80°，求∠AOF 的度数．图6－9－1012．如图6－9－11，直线AB，CD相交于点O，OE平分∠AOC，OF平分∠DOB，则点E，O，F在同一直线上，请说明理由．(补全解答过程)图6－9－11解：∵直线AB，CD相交于点O，∴∠AOC＝________(对顶角相等)．∵OE平分∠AOC，OF平分∠DOB，∴∠AOE＝______∠AOC，∠BOF＝______∠DOB，∴∠AOE＝________．∵∠AOF＋∠BOF＝∠AOB＝180°，∴∠AOF＋∠AOE＝∠EOF＝180°，∴点E，O，F在同一直线上．13．如图6－9－12，直线AB与CD相交于点O，∠BOE＝∠COF＝90°，且∠BOF＝32°，求∠AOC与∠EOD的度数．图6－9－1214．已知：如图6－9－13所示，直线AB，CD，EF相交于点O，∠1∶∠3＝3∶1，∠2＝30°，求∠BOE的度数．图6－9－1315．观察图6－9－14，回答下列各题．(1)图①中，共有________对对顶角，可以看作________＝________×________；(2)图②中，共有________对对顶角，可以看作________＝________×________；(3)图③中，共有________对对顶角，可以看作________＝________×________；(4)通过(1)～(3)各题中直线条数与对顶角对数之间的关系，若有n(n≥2)条直线相交于一点，则可形成几对对顶角？图6－9－141．C 2.∠EOF和∠BOC，∠COE和∠BOF3．180°180°＝相等4．A 5.对顶角相等6．(1)∠AOF(2)∠BOF(3)76°7．135 8.609．解：∵∠1＝40°，∠1＝∠2，∴∠2＝40°. ∵∠1＝40°，∠1＋∠3＝180°，∴∠3＝140°. 又∵∠3＝∠4，∴∠4＝140°.10. 解：∵OE平分∠AOC，∠EOC＝35°，∴∠AOC＝2∠EOC＝35°×2＝70°.由对顶角相等可知：∠BOD＝∠AOC＝70°. 11．解：∵∠AOD＝150°，∠AOD＋∠BOD＝180°，∴∠BOD＝30°.又∵∠EOD＝80°，∴∠EOB＝80°－30°＝50°，∴∠AOF＝∠EOB＝50°.12．∠DOB 1212∠BOF13．解：∵∠COF＝90°，∠BOF＝32°，∴∠COB＝90°－32°＝58°＝∠AOD.∵∠BOE＝90°，∴∠EOA＝180°－90°＝90°，∠EOC＝90°－∠COB＝32°，∴∠AOC＝∠EOA＋∠EOC＝122°，∠EOD＝∠EOA＋∠AOD＝148°.14．解：∵∠1＋∠2＋∠3＝180°，且∠1∶∠3＝3∶1，∠2＝30°，∴∠1＝112.5°，∠3＝37.5°，∴∠BOE＝∠1＝112.5°.15．解：(1)共有2对对顶角，可以看作2＝2×1.(2)单个角是对顶角的有3对，两个角组成复合角的对顶角有3对，共有6对，可以看作6＝3×2.(3)单个角是对顶角的有4对，两个角组成复合角的对顶角有4对，三个角组成复合角的对顶角有4对，共有12对，可以看作12＝4×3.(4)n(n≥2)条直线相交于一点，可形成n(n－1)对对顶角．。