离散系统1解析

自动控制原理离散系统知识点总结自动控制原理中的离散系统是指在时间域和数值范围上都是离散的系统。

在离散系统中，信号是以离散时间点的形式传递和处理的。

本文将对自动控制原理离散系统的知识点进行总结，包括离散系统的概念、离散信号与离散系统的数学表示、离散系统的稳定性分析与设计等。

一、离散系统的概念与特点离散系统是指系统输入、输出和状态在时间上都是以离散的方式存在的系统。

与连续系统相比，离散系统具有以下特点：1. 离散时间：离散系统的输入、输出和状态是在离散时间点上采样得到的，而不是连续的时间信号。

2. 离散数值：离散系统的输入、输出和状态都是以离散数值的形式存在的，而不是连续的模拟数值。

二、离散信号与离散系统的数学表示离散信号是指在离散时间点上采样得到的信号。

离散系统可以通过离散信号的输入与输出之间的关系进行描述。

常见的离散系统数学表示方法有差分方程和离散时间传递函数。

1. 差分方程表示：差分方程是通过离散时间点上的输入信号和输出信号之间的关系来描述离散系统的。

差分方程可以是线性的或非线性的，可以是时不变的或时变的。

2. 离散时间传递函数表示：离散时间传递函数描述了离散系统输入与输出之间的关系，类似于连续时间传递函数。

离散时间传递函数可以通过Z变换得到。

三、离散系统的稳定性分析与设计离散系统的稳定性是指系统的输出在有限时间内收敛到有限范围内，而不是无限增长或震荡。

离散系统的稳定性分析与设计是自动控制原理中的重要内容。

1. 稳定性分析：离散系统的稳定性可以通过判断系统的极点位置来进行分析。

若系统的所有极点都位于单位圆内，则系统是稳定的；若存在至少一个极点位于单位圆外，则系统是不稳定的。

2. 稳定性设计：若离散系统不稳定，可以通过调整系统的参数或设计控制器来实现稳定性。

常见的稳定性设计方法包括PID控制器调整、根轨迹设计等。

四、离散系统的性能指标与优化离散系统的性能指标与优化是指通过调整控制器参数或控制策略，使离散系统的性能得到优化。

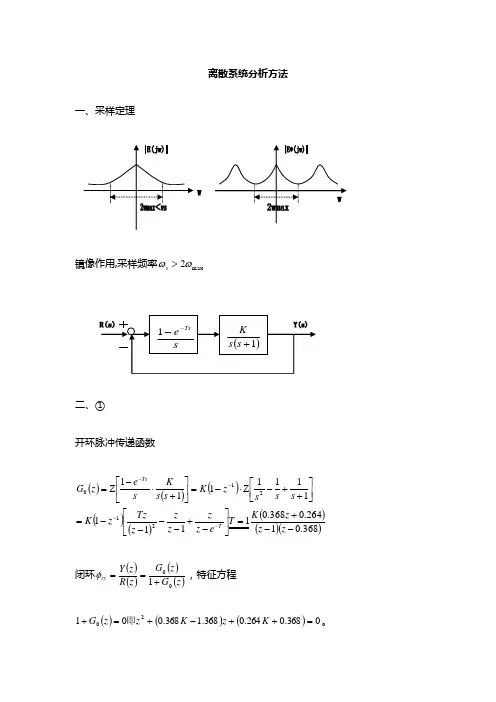
离散系统分析方法一、采样定理镜像作用,采样频率max 2ωω>s 二、①开环脉冲传递函数()()()()()()()()368.01264.0368.01111111111121210--+=⎥⎦⎤⎢⎣⎡-+----=⎥⎦⎤⎢⎣⎡++-Z ⋅-=⎥⎦⎤⎢⎣⎡+⋅-Z =----z z z K T e z z z z z Tz z K s s s z K s s K se z G T Ts闭环()()()()z G z G z R z Y ry 001+==φ，特征方程 ()()()0368.0264.0368.1368.00120=++-+=+K z K z z G 即。

②判断稳定性：用双线性变换11-+=ωωz ，将其代入特征方程中，再用劳斯判据。

如果K 给定，则直接解特征方程，若|z|<1则稳定，若|z|>1则不稳定。

③()()[]s G z G Z =0，对参考输入有：()()()()()()()()()()()()()()><-=Φ=⋅==-=⋅=⋅=-=+=⋅==→-→-→→定理此时必须且唯有用终值有干扰时，时，当时，当时，当z E z e z z N z E K T c e ct t r z G zK K T b e t b t r z G z K K a e t a t r z G K z ssn en ass z a vss z v pss z p 1lim ,21,1lim ,1lim 11,lim 122021101101④求()()()()()[]()()[]z R z z Y t y z R z z Y ry ry φφ11*,--Z =Z =⋅=时，可以用两种方法： a ）部分分式法；b ）长除方法⑤z 变换公式：()()()()()()()()()()()()()()()()323222111211111111-+===-===-=+==-===--z z z z T z X ss X t t x z Tzz X s s X t t x e z zz X a s s X e t x z z X ss X t t x atat 如：()()()⎥⎦⎤⎢⎣⎡++⋅-Z =-3210s s Ks e s G Ts()()......133********⋅-=⎥⎦⎤⎢⎣⎡+++-+Z ⋅-=--K z s s sK z σ 非线性系统分析方法注：1为sinwt ；2为基波和高次谐波经过G （s ）后剩下的基波。

实验二离散控制系统的性能分析（时域/频域）一、实验目的1．掌握离散闭环系统的动态性能时域参数的分析与计算方法；2．掌握离散系统稳定性的频域典型参数分析与计算方法。

二、实验工具1．MATLAB 软件（6.5 以上版本）；2．每人计算机一台。

三、实验内容1．在 Matlab 语言平台上，通过给定的闭环离散系统，深刻理解时域参数的物理意义与计算方法，内容包括如下：●阻尼比参数分析：Z 平面与 S 平面的极点相互转换编程实现；分析 S/Z 两个平面域特殊特性（水平线、垂直线、斜线、圆周等）的极点轨迹相互映射方法；系统阶跃响应参数：上升时间和超调量等。

2．采用频域分析方法，通过编程计算，进一步理解离散系统的稳定性参数，包括如下：●通过幅频图，进行增益裕度分析；●通过相频图，进行相位裕度分析。

四、实验步骤1.阻尼比计算注释：Example 1 Damping ratio computationts=0.1;gp=tf(1,[1 1 0])gz=c2d(gp,ts,'zoh')kz=tf(5*[1,-0.9],[1 -0.7],ts);sys_ta=feedback(gz*kz,1,-1)p=pole(sys_ta)- 2 -radii=abs(p);angl=angle(p)damp(sys_ta)real_s=log(radii)/tsimg_s=angl/tszeta=cos(atan(-img_s./real_s))wn=sqrt(real_s.^2+img_s.^2)运行结果：2.水平 S 平面线到 z 平面的映射注释：Example 2 Mapping of horizontal s-plane line to z-planexx=[0:0.05:1]'N=length(xx)s0=-xx*35;s=s0*[1 1 1 1 1]+j*ones(N,1)*[0,0.25,0.5,0.75,1]*pi/tsplot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',... real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',... real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid3.垂直 S 平面线到 z 平面的映射注释：Example 3 Mapping of vertical s-plane line to z-planes0=j*xx*pi/ts;s=ones(N,1)*[0,-5,-10,-20,-30]+s0*[1 1 1 1 1]plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid4.恒定阻尼比 S 平面线映射到 z 平面注释：Example 4 Mapping of constant damping ratio s-plane lines into z-plane s=s0*[1 1 1 1]-imag(s0)*[0,1/tan(67.5*pi/180),...1/tan(45*pi/180),1/tan(22.5*pi/180)]s=[s,real(s(:,4))];plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid5.将圆 s 平面线映射到 z 平面注释：Example 5 Mapping of circle s-plane line to z-planephi=xx*pi/2s0=(pi/ts)*(-cos(phi)+j*sin(phi))s=s0*[1,0.75,0.5,0.25,0]plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',... real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...real(s(:,5)),imag(s(:,5)),'-v'),sgridz=exp(s*ts)plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',... real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...real(z(:,5)),imag(z(:,5)),'-v'),zgrid6.阶跃响应注释：Example 6 Step response measurek=[0:1:60];step(sys_ta,k*ts);7.根轨迹注释：Example 7 Root-locus analysisrlocus(gz*kz)Amplitude；注释：Example 8 Root-locus analysis in page 56 numg=[1 0.5];deng=conv([1 -0.5 0],[1 -1 0.5]);sys_z=tf(numg,deng,-1)rlocus(sys_z)注释：Example 9 Root-locus analysis in page 57numg=[1];deng=[1 4 0];ts=0.25sys_s2=tf(numg,deng)sys_z2=c2d(sys_s2,ts,'imp')rlocus(sys_z2)8.频率响应注释：Example 10 Analysis of frequency response and roots locus in page 59 a=1.583e-7;k=[1e7,6.32e6,1.65e6];w1=-1;w2=1;ts=0.1;v=logspace(w1,w2,100);deng=[1.638 1 0];numg1=k(1,1)*a*[-1 1]numg2=k(1,2)*a*[-1 1]numg3=k(1,3)*a*[-1 1]sys_s1=tf(numg1,deng)sys_s2=tf(numg2,deng)sys_s3=tf(numg3,deng)bode(sys_s1,sys_s2,sys_s3,v),grid onnumg=1.2e-7*[1 1]deng=conv([1 -1],[1 -0.242]);sys_z2=tf(numg,deng,ts)rlocus(sys_z2),grid on五、实验思考1. S 平面与 Z 平面不同位置的映射关系分析s平面虚轴的映射s平面整个虚轴映射为z平面单位圆，左半平面任一点映射在z平面单位圆内，右半平面任一点映射在单位圆外。

离散控制系统离散系统导入与概念（压缩控制过程，提高效率）前面几章我们学习的都是连续控制系统，连续系统的特点是系统中各元件的输入与输出信号都是时间的连续函数。

（但是我们现在所接触到的很多都是离散的信号，比如说计算机信息处理（举例，图片）。

）但是近些年来，随着计算机以及数字式通信电路的大量使用，很多情况下信号不是连续的，而是离散的数字信号，很多过程用模拟控制器无法实现，我们只能借助于软件编程的方式。

同时数字控制有很好的通用性可以很方便的改变控制规律。

而且数字设备所能达到的精度和性能远远高于连续模拟设备，使得绝大多数的精密控制系统和复杂的过程走向数字化。

因此，离散控制系统也显得越来越重要。

那为什么我们在前面花了绝大多数时间学习的都是连续系统，而只花三次课的时间去学习离散系统呢？这就是因为离散系统的研究与分析方法在很大程度上与连续系统是相似的。

我们在实验或者研究过程中使用实际的连续模拟系统，等我们把连续系统研究的比较成熟了，再借助这个平台，利用他们的相似性，把连续系统的控制理论和方法推广到离散系统，这样就极大地简化了研究或者设计的过程。

需要说明的是，离散系统与连续系统在本质上是不同的，但是对于某些系统，比如说线性系统，离散线性系统和连续线性系统性质上有很大的相似性，我们就可以借助已经学习的连续线性系统的分析研究方法去研究分析离散线性系统，从而满足我们的需要。

这一点我们在其他课程比如说数字信号处理中也接触过。

离散系统概念以及常用术语离散系统：当系统中只要有一处的信号是脉冲信号或者数码的，就是离散系统。

也就是说这些信号是定义在离散时间上的，在间隔上没有定义。

脉冲控制系统：系统中的离散信号是脉冲序列即为脉冲控制系统。

时间上离散分布，幅值上任意可取的，幅值代表脉冲强度，也叫采样控制系统。

数码控制系统：系统中的离散信号是数码的极为数码控制系统。

时间上离散对应，幅值上整量化。

也就是一个基数的整数倍。

一般情况下，这个基数可以取得很小，也就实现了数码信号的连续性，也可以看成是脉冲信号，所以区别这两个意义不是很大，在理想采样与忽略误差情况下，数码控制系统近似于脉冲控制系统，他们统称为离散系统，分析和设计的理论方法都是一致的。

离散系统的分析1、连续系统的离散化功能：在离散控制系统中，会涉及到对模拟控制器的离散化，也会涉及到对系统的不可变部分的离散化问题，MATLAB对于离散化转换可采用相应的函数进行。

格式：[Ad,Bd]=c2d(A,B,ts)[Ad,Bd,Cd,Dd]=c2dm(A,B,ts,’method’)，[numz,denz]=c2dm(num,den,ts,’method’)说明：1) c2d命令使用离散化的零阶保持器方法，它只有状态空间形式；2) c2dm既有状态空间形式，又有传递函数形式；3) 参数ts是采样周期T；4) method指定转换方式，其中“zoh”表示采用零阶保持器；“foh”表示采用三角形近似；“tustin”表示采用双线性变换；“prewarp”表示采用指定转折频率的双线性变换，其转折频率Wc 由c2d （sysc ，T ，‘prewarp ’，Wc ）确定，系统默认为零阶保持器法。

5) A 、B 、num 、den 为连续域的数学模型，返回的是离散化以后的数学模型。

例已知系统的被控对象传递函数为：)5)(2(10)(++=s s s G采样周期T ＝0.1秒,试将其进行离散化处理。

解：将连续系统的传递函数G （s ）用零阶保持器法转换成离散系统的脉冲传递函数G(z)，并运行下面的程序。

num=10; den=[1,7,10]; ts=0.1; [n_zoh,d_zoh]=c2dm(num,den,ts) ; tf(n_zoh,d_zoh,ts)运行结果：Transfer function:0.0398 z + 0.03152 -------------------------- z^2 - 1.425 z + 0.49662、离散系统单位阶跃响应功能：对离散系统进行阶单位跃响应分析，给出一组阶跃响应的数据，并绘制其响应曲线。

格式： [y,x]=dstep(A,B,C,D,ui,n)[y,x]=dstep(num,den,n)说明：1) 若无左边的输出参数，则自动地绘制出响应曲线； 2) 参数ui 和n 为可选项，对于多输入系统是用于指定哪个输入通道，n 是指采样数； 3) 和连续系统中step 命令有关的所有命令都可以在离散系统中应用； 4) 其它时间响应命令是dimpulse 、dinitial 、dlsim 。